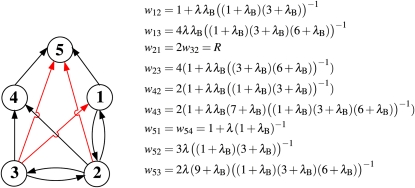Linkage Disequilibrium Under Recurrent Bottlenecks

Abstract

To model deviations from selectively neutral genetic variation caused by different forms of selection, it is necessary to first understand patterns of neutral variation. Best understood is neutral genetic variation at a single locus. But, as is well known, additional insights can be gained by investigating multiple loci. The resulting patterns reflect the degree of association (linkage) between loci and provide information about the underlying multilocus gene genealogies. The statistical properties of two-locus gene genealogies have been intensively studied for populations of constant size, as well as for simple demographic histories such as exponential population growth and single bottlenecks. By contrast, the combined effect of recombination and sustained demographic fluctuations is poorly understood. Addressing this issue, we study a two-locus Wright–Fisher model of a population subject to recurrent bottlenecks. We derive coalescent approximations for the covariance of the times to the most recent common ancestor at two loci in samples of two chromosomes. This covariance reflects the degree of association and thus linkage disequilibrium between these loci. We find, first, that an effective population-size approximation describes the numerically observed association between two loci provided that recombination occurs either much faster or much more slowly than the population-size fluctuations. Second, when recombination occurs frequently between but rarely within bottlenecks, we observe that the association of gene histories becomes independent of physical distance over a certain range of distances. Third, we show that in this case, a commonly used measure of linkage disequilibrium, ${\sigma }_{\text{d}}^2$ (closely related to ${\widehat{r}}^2$), fails to capture the long-range association between two loci. The reason is that constituent terms, each reflecting the long-range association, cancel. Fourth, we analyze a limiting case in which the long-range association can be described in terms of a Xi coalescent allowing for simultaneous multiple mergers of ancestral lines.

GENETIC variation at a single neutral locus has been investigated in great detail for population models under different demographic processes, such as population expansions, single bottlenecks, or genetic hitchhiking caused by nearby selective sweeps (see, for example, Eriksson et al. 2008 for a review of such models). Biological populations exhibit abundance fluctuations on both short and long timescales, caused by, e.g., environmental and ecological changes. Such size fluctuations in the form of repeated bottlenecks are characteristic of populations expanding into new territories. Examples include the human out-of-Africa scenario (Ramachandran et al. 2005; Liu et al. 2006), the accompanying expansion of the parasite Plasmodicum falciparum causing severe malaria (Tanabe et al. 2010), and the recolonization by the marine snail Littorina saxatilis of Sweden’s west coast archipelago (Johannesson 2003). Genetic variation in populations subject to bottlenecks is now routinely investigated in the laboratory. England et al. (2003), for example, have studied genetic variation in Drosophila melanogaster populations subjected to bottlenecks of different durations and strengths. Last but not least, bottlenecks can also be due to environmental fluctuations. Pujolar et al. (2011), for example, have investigated populations of Salmo marmoratus subject to weather-induced recurrent bottlenecks.

It is common practice to accommodate such fluctuations in the theory by using an effective population size instead of the census population size. See Ewens (1982) for a review of different measures of the effective population size.

Recent research has highlighted the importance of two competing timescales in the context of such effective population-size approximations: the timescale of the population-size fluctuations and the coalescent timescale (which reflects the time to the most recent common ancestor, MRCA). When demographic fluctuations are much slower than the coalescent timescale, they can be ignored and the effective population size can be approximated by the initial population size (Sjödin et al. 2005). In the opposite case of rapid demographic fluctuations, it has been argued (Wright 1938; Crow and Kimura 1970) that genetic variation is well described in terms of a population with effective population size N_eff, given by the harmonic average of the population size:

$$N_{\text{eff}}=\underset{T\to \mathrm{\infty }}{\lim }{\left(\frac{1}{T}{\displaystyle \sum _{\tau =0}^T\frac{1}{N_{\tau }}}\right)}^{-1}.$$ (1)

Here N_τ is the population size in generation τ. See Jagers and Sagitov (2004), Sjödin et al. (2005), and Wakeley and Sargsyan (2009) for recent developments of the concept of an effective population size. In conclusion, for both fast and slow demographic fluctuations, the statistical properties of single-locus gene genealogies agree with those of the constant population-size model. By contrast, when both timescales are of the same order, it has been shown (Kaj and Krone 2003; Nordborg and Krone 2002; Sjödin et al. 2005; Eriksson et al. 2010) that the distribution of total branch lengths in samples of single-locus gene genealogies does not in general agree with that predicted by the standard coalescent approximation. But Eriksson et al. (2010) have shown how to compute moments of the distribution of the total branch lengths of gene genealogies at a single locus, conditional on a given demographic history (see also Zivkovic and Wiehe 2008). In summary, the effect of population-size fluctuations upon genetic variation at a single locus is well understood.

But how do population-size fluctuations affect multilocus patterns of genetic variation on the same chromosome? Such patterns are influenced by recombination. Genetic recombination introduces a new timescale that is inversely proportional to r, the probability of recombination between a pair of loci per generation. As is well known, genetic recombination plays an important role in shaping empirically observed multilocus patterns of genetic variation in biological populations. Measures of linkage disequilibrium quantify the degree of association of genetic variation at pairs of loci on the same chromosome. Common measures of linkage disequilibrium, such as ${\widehat{r}}^2$ (Hill and Robertson 1968), and its approximation ${\sigma }_{\text{d}}^2$ (Ohta and Kimura 1971; McVean 2002), depend upon the allelic frequencies at two loci. These measures are thus closely related to the covariance of the times (i.e., the number of generations) to the MRCA of the underlying gene genealogies (McVean 2002).

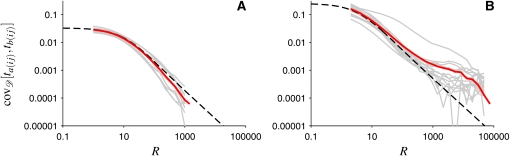
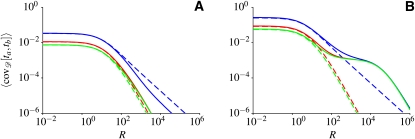
Figure 1 shows this covariance as a function of genetic distance between the two loci. The results shown were obtained by computer simulations of the Wright–Fisher dynamics (Fisher 1930, 1999; Wright 1931) of a population experiencing recurrent bottlenecks, with random durations of and random separations between bottlenecks. Details of the model are given in the Model section. In Figure 1, gray lines show how the covariance of the times to the MRCA for two chromosomes at two loci (averaged over all pairs of loci the same distance apart) depends on genetic distance. Each gray line corresponds to a single realization of the sequence of bottlenecks. The red lines in Figure 1 are the averages of the covariances within each panel. Figure 1, A and B, shows results for two different sets of parameters of the model. In Figure 1A, the bottlenecks happen frequently and have short durations. In this case, the single-locus properties are expected to be in good agreement with those of a population with effective population size given by Equation 1. For such populations, the coalescent approximation predicts

$$\text{cov}\left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]=x_{\text{eff}}^2\frac{R{x}_{\text{eff}}+18}{{\left(R{x}_{\text{eff}}\right)}^2+13R{x}_{\text{eff}}+18}.$$ (2)

(Griffiths 1981; Hudson 1983, 1990). Here t_a(ij) and t_b(ij) denote the times to the MRCA of two loci (called a and b) in a sample of two chromosomes (denoted by i and j). In Equation 2, R = 2N₀r is a scaled recombination rate, and x_eff = N_eff/N₀ is the effective population size relative to the population size at the present time, denoted by N₀. Units of time are chosen so that τ = ⌊tN₀⌋, and ⌊tN₀⌋ is the largest integer not larger than tN₀. In Figure 1 effective population-size approximations, according to Equation 2, are shown as dashed lines. In Figure 1A we observe good agreement between Equation 2 and the average covariance of the times to the MRCA obtained from computer simulations of the model. However, in Figure 1B, Equation 2 agrees with the simulated covariance only for short genetic distances. For large genetic distances, by contrast, Figure 1B shows that the covariance decreases much more slowly than expected according to Equation 2. Thus, the results shown in Figure 1B imply long-range association between two loci.

Figure 1.

Covariance of the times to the MRCA at two loci, in a sample of two chromosomes in a population subject to repeated bottlenecks (details in Model section). (A) Rapid population-size fluctuations. Wright–Fisher simulations are shown for 10 random sequences of bottlenecks with p = 10⁻³, q = 10⁻³, N₀ = 10⁵, and N_B = 10⁴ (gray lines). Each gray line is obtained by first generating a random sequence of bottlenecks and then averaging over an ensemble of 1000 gene genealogies. The red line shows the covariance averaged over demographic histories. The dashed line shows the result of the effective population-size approximation (Equation 2). (B) Same as in A, but for the case of severe reductions of population size during bottlenecks. Wright–Fisher simulations are shown for 15 randomly generated sequences of bottlenecks, with parameters p = 10⁻⁵, q = 2 × 10⁻², N₀ = 10⁶, and N_B = 5 × 10². Averages are over 100 gene genealogies for each demographic history.

The examples shown in Figure 1 raise many questions. What are the conditions for the effective population-size approximation to be valid in the multilocus case? Why does it fail when these conditions are not met? How significant are deviations of the exact result from the effective population-size approximation? Why does long-range association between two loci appear in some cases? How large are fluctuations around the covariance of the coalescent times, averaged over an ensemble of gene genealogies and over different demographic histories? What is the significance of the fluctuations around such averages for data analysis?

The aim of this article is to provide answers to the above questions by computing the covariance of the times to the MRCA for a pair of chromosomes under a model of recurrent bottlenecks introduced below in the Model section. Our analysis enables us to qualitatively and quantitatively determine the effects of fluctuating population size on the two-locus statistics in terms of the timescales of population-size fluctuations, of coalescence, and of recombination. Using both analytical (Covariance of the Times to the MRCA) and numerical approaches (Comparison of the Coalescent Calculations to the Wright–Fisher Simulations), we estimate the range of validity of the effective population-size approximation for the two-locus case. We find that the effective population-size approximation inevitably fails for large recombination rates: the failure is sometimes minor (as in the case shown in Figure 1A) and sometimes significant (as in the case shown in Figure 1B). By taking different limits of the parameters of the model, we provide both a qualitative and a quantitative understanding of how the effective population-size approximation may fail in predicting the long-range association between two loci. We demonstrate in The Effect of Recurrent Bottlenecks upon ${\sigma }_d^2$ that the long-range association has a surprisingly small effect upon ${\sigma }_{\text{d}}^2$. In the Discussion we review our results. In particular, in the limit where bottlenecks correspond to severe reductions of population size during bottlenecks, we show that gene genealogies in our model can be described in terms of the so-called Xi coalescent (Schweinsberg 2000; Möhle and Sagitov 2001; Sagitov 2003), which allows for simultaneous multiple coalescent events (called multiple mergers below).

In summary we describe in this article how sustained population-size variations in the form of sequences of bottlenecks influence two-locus patterns of genetic variation. We conclude this Introduction by briefly commenting on related models. The effect of recurrent bottlenecks on single-locus statistics was investigated by Sjödin et al. (2005) and also by Eriksson et al. (2010). The model introduced by Sargsyan and Wakeley (2008) contains a recurrent bottleneck model for a single locus as a special case. Sargsyan and Wakeley (2008) show under which conditions single-locus gene genealogies in their model can be approximated by either Kingman's coalescent or the Xi coalescent. Eldon and Wakeley (2008), finally, have analyzed two-locus gene genealogies under a population model allowing for skewed reproduction. We discuss the connection between the results of Eldon and Wakeley (2008) and our results in the Discussion (see Equation 14).

Model

Using a Wright–Fisher model of a population of gametes, we trace the ancestry of two loci on a pair of gametes backward in time, until the MRCA of both loci is found. In each generation τ we perform two steps. In the first step, each gamete is independently subjected to recombination such that, with probability r, the two loci segregate onto two different gametes (corresponding to different parents). We assume that r is approximately proportional to the physical distance between the given loci (see McPeek and Speed 1995 for a review of the general relation between recombination rate and physical distance). Because of this step, the ancestors of the original loci may be spread over up to four different gametes in any given generation in the past (if recombination leads to a gamete where neither locus is ancestral to the original sample, that gamete is dropped from further consideration). In the second step, the parent of each gamete is chosen randomly from the gametes in the parental generation. Whenever a pair of gametes have the same parent, the ancestries of these gametes are the same, and the number of gametes to be traced is reduced.

To investigate the effect of population-size fluctuations on genetic variation, we consider a model of recurrent bottlenecks in which the population size can take one of two values, N₀ or N_B. Here N_B denotes the population size in the bottlenecks, and N₀ stands for the population size between bottlenecks. We write N_B = xN₀, with 0 < x < 1. The probability of changing the population size, going one generation back in time, depends on the population size at the current time. The switching probabilities are denoted by p and q when the current population sizes are N₀ and N_B, respectively. Hence, the expected durations of the high and the low population-size phases are 1/p and 1/q generations, respectively. The population size in the first generation is taken to be N₀. For a single locus, as mentioned above, such a model has been investigated by Sjödin et al. (2005) and Eriksson et al. (2010); see also Sargsyan and Wakeley (2008).

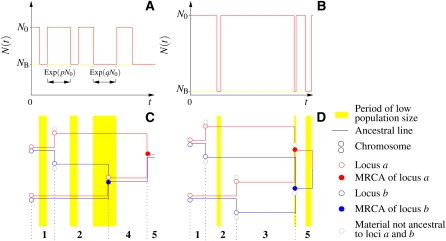
Figure 2, A and B, illustrates population-size fluctuations in this recurrent bottleneck model. In Figure 2, C and D, examples of gene genealogies of two loci (called a and b) in a sample of two chromosomes are shown. In Figure 2, C and D, generations with low population size (N_B) are marked yellow, and otherwise the population size is N₀. Each chromosome is represented by a pair of lines (red and blue lines correspond to loci a and b, respectively). In generations where a common ancestor is found for a pair of ancestral lines or recombination between two loci occurs, the chromosomes are represented by circles instead of lines. MRCAs are shown as solid circles. In some cases recombination causes the ancestry of one locus to become associated with a chromosome that lacks direct descendants in the sample (open gray circles). The ancestries of such segments of DNA are irrelevant to the gene genealogy of the sample, and these ancestral lines are not traced further.

Figure 2.

(A and B) Two realizations of the population-size curve, N(t), backward in time (t = 0 denotes the present time). Initially, the population size is N₀. Going backward in time, the population size randomly jumps between two values, N₀ and N_B, with transition rates pN₀ (from N₀ to N_B) and qN₀ (from N_B to N₀). (C and D) Examples of ancestral histories of two loci (blue and red open circles correspond to two loci, called a and b) subject to genetic recombination in a sample of two chromosomes. Times at which the population was subject to a bottleneck are shaded yellow. Two joint circles depict two loci in the same chromosome. The numbers 1, … , 5 denote the possible states of the system (they are explained in detail in Figure 3). Gray circles denote genetic material not ancestral to the sampled loci. Blue and red solid circles indicate that the corresponding loci have found their most recent common ancestor. Note that bottlenecks can host more than one coalescent event. In the case of severe reductions of population size during bottlenecks, such multiple coalescences appear as simultaneous multiple mergers on the timescale of the gene genealogy. An example is shown in D: an almost instantaneous transition from state 3 to state 5.

Covariance of the Times to the MRCA

Consider a sample of two chromosomes (denoted by i and j) and two loci (called a and b). As in the Introduction, the time to the MRCA at locus a is denoted by t_a(ij) [and t_b(ij) at locus b]. Consider ${\text{cov}}_{\mathcal{D}}$ [t_a(ij), t_b(ij)], the covariance conditional on a particular demographic history $\mathcal{D}$. Taking the average of the conditional covariance over random demographic histories, we have

$$\begin{array}{l}\langle {\text{cov}}_{\mathcal{D}} \left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]\rangle \\ \hspace{1em}=\langle \langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}|\mathcal{D}\rangle -\langle t_{a\left(ij\right)}|\mathcal{D}\rangle \langle t_{b\left(ij\right)}|\mathcal{D}\rangle \rangle \\ \hspace{1em}=\langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}\rangle -\langle {\langle t_{a\left(ij\right)}|\mathcal{D}\rangle }^2\rangle .\end{array}$$ (3)

Here 〈… |$\mathcal{D}$〉 denotes the expectation conditional on a particular demographic history $\mathcal{D}$. In the second equality we have used that the expected times to the MRCA are the same for both loci. Note that the averaged conditional covariance is not the same as the unconditional covariance of the times to the MRCA for the full process. The latter is given by

$$\langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}\rangle -{\langle t_{a\left(ij\right)}\rangle }^2\equiv \langle {\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]\rangle +\text{var}\left[\langle t_{a\left(ij\right)}|\mathcal{D}\rangle \right].$$ (4)

We remark that biological data correspond to a particular individual realization $\mathcal{D}$. The additional term in Equation 4 reflects the variance over different demographic histories of the average time to the MRCA at a single locus and is thus irrelevant to analyzing the covariance of the times to the MRCA in a particular empirical data set.

We now derive an approximate expression for 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉, Equation 3. The method we employ requires the typical timescales of coalescence, of population-size fluctuations, and of recombination to be large. We require that

$$N_0\gg 1,\hspace{0.5em}{N}_{\text{B}}\gg 1,\hspace{0.5em}p\ll 1,\hspace{0.5em}q\ll 1,\hspace{0.5em}\text{and}\hspace{0.5em}r\ll 1.$$ (5)

The first two conditions allow us to employ the standard coalescent approximation (Kingman 1982). The first four conditions allow us to neglect events involving simultaneous changes of population size and coalescence. Similarly, as a consequence of combining the first two conditions with the fifth one, we may omit events involving simultaneous coalescence and recombination. Finally, combining conditions three to five allows us to neglect simultaneous occurrences of population-size changes and recombination. Assuming large population sizes allows us to approximate the discrete generation index τ = 0, 1, 2, … by a continuous-time variable t. As mentioned in the Introduction, we choose the units of time such that τ = ⌊tN₀⌋. We denote the population size at time t by N(t).

Under the conditions summarized above, we find the following expression for the term 〈〈t_a(ij)|$\mathcal{D}$〉〈t_b(ij)|$\mathcal{D}$〉〉 ≡ 〈〈t_a(ij)|$\mathcal{D}$〉²〉 occurring in Equation 3:

$$\langle {\langle t_{a\left(ij\right)}|\mathcal{D}\rangle }^2\rangle =\frac{{\lambda }_{\text{B}}\left(\text{2}x\lambda +{\lambda }_{\text{B}}+3\right)+x\lambda \left(x\lambda +x+\text{2}\right)+\text{2}}{\left(\lambda +{\lambda }_{\text{B}}+1\right)\left(\lambda +{\lambda }_{\text{B}}+\text{2}\right)}.$$ (6)

This equation follows from Equation 20 in Eriksson et al. (2010). The parameters λ and λ_B in Equation 6 are given by λ = pN₀ and λ_B = qN_B.

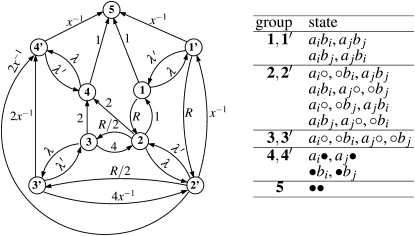
To evaluate the remaining term in Equation 3, 〈t_a(ij)t_b(ij)〉, we adapt the method described by Eriksson and Mehlig (2004) for calculating the covariance of the times to the MRCA at two loci. As can be seen in Figure 2, C and D, there are only a small number of possible combinations of ancestral lines in gene genealogies of two loci for two chromosomes. Thus, we can write down a Markov process for how states of the ancestral lines change along a gene genealogy. The corresponding graph is shown in Figure 3, where the vertices represent states (combinations of ancestral lines), and the edges represent transitions between the states (the transition rates are shown along the edges. The vertices labeled by a prime correspond to states with population size N_B (bottlenecks). The expected value 〈t_a(ij)t_b(ij)〉 is determined by a subgraph of the graph shown in Figure 3, consisting of the vertices 1, 2, 3, 1′, 2′, and 3′. Let M be the corresponding 6 × 6 transition matrix. Its off-diagonal elements M_mn, m ≠ n, are given by the transition rates w_mn. The diagonal elements M_nn are equal to the negative sum of the rates of all edges leaving node n in the graph, $M_{nn}=-{\displaystyle {\sum }_{m\ne n}{M}_{mn}}$. In terms of M we can write

$$\langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}\rangle ={\displaystyle {\int }_0^{\mathrm{\infty }}d{t}_1 t_1^2\mathbf{u} e^{\mathbf{M}\hspace{0.17em}{t}_1}\mathbf{v}+{\int }_0^{\mathrm{\infty }}d{t}_1{\displaystyle {\int }_{t_1}^{\mathrm{\infty }}d}{t}_2 t_1 t_2 \mathbf{c}{e}^{\mathbf{K}\left(t_2-t_1\right)}\mathbf{Q} e^{\mathbf{M}\hspace{0.17em}{t}_1}\mathbf{v}}$$ (7)

(Eriksson and Mehlig 2004). The vectors u, v, and c and the matrices Q and K in Equation 7 are given by

$$\begin{array}{l}\begin{array}{ll}\mathbf{v}={\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\end{array}\right]}^{\mathsf{T}},\hfill & \mathbf{u}=\left[\begin{array}{cccccc}1& 0& 0& x^{-1}& 0& 0\end{array}\right],\hfill \end{array}\\ \mathbf{c}=\left[\begin{array}{cc}1& x^{-1}\end{array}\right],\\ \begin{array}{l}\mathbf{Q}=\left[\begin{array}{cccccc}0& 2& 2& 0& 0& 0\\ 0& 0& 0& 0& 2x^{-1}& 2x^{-1}\end{array}\right],\hfill \end{array}\\ \mathbf{K}=\left[\begin{array}{cc}-(\lambda +1)& {\lambda }_{\text{B}}{x}^{-1}\\ \lambda & -({\lambda }_{\text{B}}+1)x^{-1}\end{array}\right].\end{array}$$

Here T denotes the transpose, while t₁ = min(t_a(ij), t_b(ij)) and t₂ = max(t_a(ij), t_b(ij)) are the times to the first and second coalescent events, respectively. The first term in Equation 7 corresponds to a common MRCA of the loci a and b (i.e., to a transition from state 1 or 1′ to state 5). The second term in Equation 7 corresponds to a different MRCA (transition from state 2 or 3 to state 4 or from state 2′ or 3′ to state 4′, followed by a transition to state 5). At the present time the system is assumed to be in state 1, represented by the vector v. The elements of the vector u correspond to the transition rates from the states 1, 2, 3, 1′, 2′, and 3′ to 5. The two rows in the matrix Q contain the transition rates from 1, 2, 3 and 1′, 2′, 3′ to 4 and 4′, respectively. The matrix K contains the transition rates between states 4 and 4′, whereas the vector c contains the coalescent rates in each population-size regime. Both M and K have negative real eigenvalues. Hence, the integrals in Equation 7 can be evaluated in terms of matrix inverses (Eriksson and Mehlig 2004). We find

$$\begin{array}{l}\langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}\rangle =2\mathbf{u}{\left(-\mathbf{M}\right)}^{-3} \mathbf{v}\\ +2\mathbf{c}{\left(-\mathbf{K}\right)}^{-2}\left\{{\left(-\mathbf{K}\right)}^{-1}\mathbf{Q}+\mathbf{Q}{\left(-\mathbf{M}\right)}^{-1}\right\}{\left(-\mathbf{M}\right)}^{-2} \mathbf{v}.\end{array}$$ (8)

Combining Equations 6 and 8 yields

$$\langle {\text{cov}}_{\mathcal{D}}\left[t_{a(ij)},t_{b(ij)}\right]\rangle =\frac{R^3{C}_3+R^2{C}_2+R{C}_1+C_0}{R^4{D}_4+R^3{D}_3+R^2{D}_2+R{D}_1+D_0}$$. (9)

The coefficients C₀, … , C₃, and D₀, … , D₄, are functions of the parameters x, λ, and λ_B. They are given in Appendix A.

Figure 3.

(Left) Graph showing the states and transition rates determining the ancestral history of two loci in a sample of two chromosomes, under the population model introduced in the Model section. States where the population is in a bottleneck are marked with a prime. The final state is denoted by 5 (in this state it does not matter whether the population is in a bottleneck or not). Arrows indicate transitions between states. The corresponding transition rates from state n to m, w_mn, are displayed next to the lines. For notational convenience we have used the abbreviations x = N_B/N₀, λ = pN₀, and λ′ = qN₀. While x and λ are referred to in the main text, λ′ is not. (Right) Table of possible states of the system. The two loci are denoted by a and b, and the corresponding chromosomes by i and j. Open circles denote genetic material not ancestral to sampled loci, and solid circles denote the MRCA.

We now discuss three special cases of this result. First, we consider the case when the time to the first bottleneck is much longer than the expected time to the MRCA in the large population-size regime. Second, we discuss the case when the population-size fluctuations are much faster than all other processes. Third, we analyze the case of severe reductions of population size during bottlenecks.

In the first case one has $p\ll N_0^{-1}$. This implies that the time to the first bottleneck is much larger than the time to the MRCA, and as a consequence all bottlenecks are irrelevant to the mean covariance of the times to the MRCA. Formally, this case is obtained from Equation 9 by taking the limit λ → 0. In this limit we obtain Equation 2 with x_eff = 1, which is the expression that is valid in the case of constant population size.

The second case is described by the conditions $p\gg N_0^{-1}$ and $q\gg N_{\text{B}}^{-1}$. Formally, this case corresponds to taking the limit λ → ∞, and λ_B → ∞ in Equation 9, in such a way that the ratio λ/λ_B is kept constant. In this limit we obtain Equation 2, with x_eff = (x + λ_B/λ)/(1 + λ_B/λ). This demonstrates that in this limit the resulting two-locus gene genealogies are described by the effective population-size approximation.

Third is the case of severe reductions of population size during bottlenecks, described by the condition N_B ≪ N₀. Such demographic histories can occur during range expansions, where small groups of animals repeatedly colonize new areas [as mentioned in the Introduction, examples are the human out-of-Africa scenario (Ramachandran et al. 2005; Liu et al. 2006), the accompanying expansion of the parasite P. falciparum causing severe malaria (Tanabe et al. 2010), and the recolonization by the marine snail L. saxatilis of Sweden's west coast archipelago (Johannesson 2003)]. This case can be treated analytically by taking the limit x → 0 in Equation 9, keeping λ and λ_B fixed. In this limit we find

$$\langle {\text{cov}}_{\mathcal{D}}[t_{a(ij)},t_{b(ij)}]\rangle \approx \frac{R^2{A}_2+R{A}_1+A_0}{R^2{B}_2+R{B}_1+B_0}.$$ (10)

Here the coefficients A₀, A₁, A₂, B₀, B₁, and B₂ are functions of the parameters λ and λ_B. They are given in Appendix A. Note that Equation 10 reaches a plateau for large values of R:

$$\begin{array}{l}\langle {\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]\rangle \\ \hspace{1em}\approx \frac{2{\lambda }_{\text{B}}\left(1+{\lambda }_{\text{B}}\right)\lambda }{\left(1+{\lambda }_{\text{B}}+\lambda \right)\left(2+{\lambda }_{\text{B}}+\lambda \right)\left(9\left(2+\lambda \right)+{\lambda }_{\text{B}}\left(27+8\lambda +{\lambda }_{\text{B}}\left(10+{\lambda }_{\text{B}}+\lambda \right)\right)\right)}.\end{array}$$ (11)

This expression implies long-range association between the two loci.

Comparison of the Coalescent Calculations to the Wright–Fisher Simulations

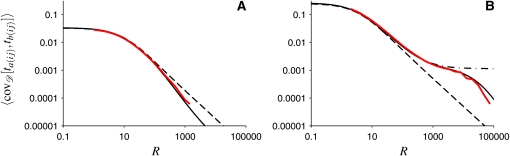
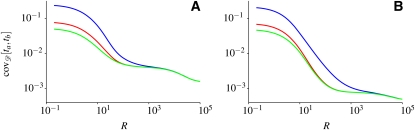
To further illustrate the role of the relevant timescales of genetic drift and recombination in shaping genetic association between two loci, we compare the full coalescent result, Equation 9, and the different limiting cases considered in Covariance of the Times to the MRCA, to the average covariance calculated from the Wright–Fisher simulations. These comparisons are shown in Figure 4.

Figure 4.

Covariance of the times to the MRCA of two loci averaged over random population-size histories. (A) The red line shows the average covariance corresponding to p = 10⁻³, q = 10⁻³, N₀ = 10⁵, and N_B = 10⁴, determined numerically from Wright–Fisher simulations (same as in Figure 1A). The solid line shows our exact result (Equation 9), and the dashed line shows the effective population-size approximation (Equation 2). The numerical result deviates from the effective population-size approximation when the recombination timescale is the smallest (R > 100). (B) The same as in A, but for the case of severe reductions of population size during bottlenecks: p = 10⁻⁵, q = 2 × 10⁻², N₀ = 10⁶, and N_B = 5 × 10². The dashed-dotted line denotes the result of Equation 10, corresponding to the Xi-coalescent approximation.

The parameters used in Figure 4A correspond to rapid population-size fluctuations (the second case described in the previous section). As can be seen in Figure 4A, the agreement between the numerical result (red line) and the approximation (Equation 2) (dashed line) is good for a wide range of recombination rates. A small disagreement appears at large values of R, more precisely at R ≈ 100 for the parameters chosen in Figure 4A. This discrepancy is expected, as at such large recombination rates the population-size fluctuations are no longer rapid compared to the process of recombination. But the corresponding deviations from the effective population-size approximation are very small. In summary, in the case of rapid population-size fluctuations, the results of the Wright–Fisher simulations are well approximated by the effective population-size approximation.

Figure 4B shows results for parameters corresponding to the third case analyzed in the previous section, the case of severe reductions of population size during bottlenecks. As we noted already in the Introduction, this case exhibits long-range association (between the two loci in question) that cannot be accurately described by the effective population-size approximation (Equation 2). The average covariance curve obtained by computer simulations (Figure 4B) can be divided into three regions in which the curve behaves qualitatively differently. First, at very small recombination rates, for the parameters chosen in Figure 4B, the covariance can be approximated using the effective population-size approximation. This is expected since in this region the population-size fluctuations are fast compared to the process of recombination. Second, the effective population-size approximation breaks down when R ≈ pN₀ = 10 for the parameters chosen in Figure 4B. At recombination rates larger than this value, such that recombination occurs frequently between bottlenecks but rarely within, we find long-range association between the two loci. Hence, in this region the effective population-size approximation fails to describe the covariance of the times to the MRCA. However, Equation 10 agrees well with the resulting covariance in this region. We show in Appendix B that Equation 10 can be derived using the Xi-coalescent approximation, which allows for simultaneous multiple coalescences of lines. Third, the agreement between Equation 10 and the full coalescent result breaks down when recombination events in bottlenecks can no longer be ignored (i.e., when R ≈ qN₀, where qN₀ is the rate of leaving a bottleneck). For still larger recombination rates, only the full coalescent result agrees with the Wright–Fisher simulations. The slight deviations between the Wright–Fisher simulations and Equation 9, visible in Figure 4B at large values of R, are discussed in the concluding section.

The Effect of Recurrent Bottlenecks upon ${\sigma }_{\text{d}}^2$

In the previous sections we showed how sustained population-size fluctuations in the form of recurrent bottlenecks can give rise to long-range association between loci, measured by the covariance of the times to the MRCA, Equation 3. An important question is how such population-size fluctuations affect common measures of linkage disequilibrium such as, for example, ${\widehat{r}}^2$, and its closely related measure, ${\sigma }_{\text{d}}^2$, on the basis of a sample of n chromosomes (Ohta and Kimura 1971; McVean 2002). In this section, we discuss the effect of recurrent bottlenecks upon ${\sigma }_{\text{d}}^2$ in the case n ≫ 1. In this case, Equation 9 in McVean (2002) becomes

$${\sigma }_{\text{d}}^2=\langle \frac{{\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]-2{\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ik\right)}\right]+{\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(kl\right)}\right]}{{\langle t_{a(ij)}|\mathcal{D}\rangle }^2+{\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(kl\right)}\right]}\rangle .$$ (12)

As before, a and b denote two loci, and i, j, k, and l denote four different chromosomes in the sample. The main properties of this measure are determined by how the numerator depends on the recombination rate (McVean 2002). To simplify the analysis, we therefore focus on the expected value of the numerator:

$$\langle {\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ij\right)}\right]\rangle -2\langle {\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(ik\right)}\right]\rangle +\langle {\text{cov}}_{\mathcal{D}}\left[t_{a\left(ij\right)},t_{b\left(kl\right)}\right]\rangle .$$ (13)

The mean of the conditional covariance 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉 is given by Equation 9. The covariances 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)]〉 and 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)]〉 can be calculated in the same way that Equation 9 was obtained, but starting from different initial conditions (McVean 2002; Eriksson and Mehlig 2004). In our Markov representation, this corresponds to taking v = [0 1 0 0 0 0]^T and v = [0 0 1 0 0 0]^T, respectively, in Equation 7.

Figure 5 shows how the covariances 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉 (blue lines), 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)]〉 (red lines), and 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)]〉 (green lines) depend on R. Figure 5 demonstrates that when R is small, each covariance is well approximated by the corresponding effective population-size approximation. In the case shown in Figure 5B, all three covariances exhibit a plateau at the same level, in approximately the same range of R values. This demonstrates that all three covariances show long-range association between loci. But, in the linear combination (Equation 13) these enhancements cancel. We have checked that this conclusion also holds for ${\sigma }_{\text{d}}^2$ given by Equation 12. In Figure 6 we show for two random demographic histories how the covariances ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)] (blue lines), ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)] (red lines), and ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)] (green lines) depend on R. Figure 6, A and B, shows results of two different demographic histories, but in both cases the parameters p, q, N₀, and N_B are chosen to correspond to the case shown in Figures 4B and 5B. In both examples in Figure 6, a plateau appears in all three covariances of the times to the MRCA, as expected. These plateaus cancel in the same way as the three contributions to Equation 13.

Figure 5.

Average covariances 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉 (blue lines), 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)]〉 (red lines), and 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)]〉 (green lines). (A and B) Values of the parameters p, q, N₀, and N_B are the same as in Figures 1A and 4A. The parameters in B are the same as in Figures 1B and 4B. Exact results are shown as solid lines, whereas results obtained within the effective population-size approximation are shown as dashed lines.

Figure 6.

Covariances ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)] (blue lines), ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)] (red lines), and ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)] (green lines) for two random realizations of population-size history. In both A and B the parameters are p = 10⁻⁴, q = 0.2, N₀ = 10⁵, and N_B = 50, resulting in the same values of x, λ, and λ_B, as in Figures 4B and 5B.

Discussion

The aim of this article was to provide an understanding of how sustained population-size fluctuations influence the degree of association between two loci. Our conclusions are based on both analytical and numerical calculations, which we find to agree well. Using the population-size model depicted in Figure 2A, and assuming Wright–Fisher dynamics, we have derived a coalescent result for the covariance of the times to the MRCA of two loci, Equation 9. We have discussed three particular cases of our result. First, if the expected times to the MRCA are much smaller than the expected time to the most recent bottleneck, our model reduces to a constant population-size model with effective population size equal to the population size at the present time. Second, if the population size fluctuates much faster than the remaining two processes (coalescence and recombination), the effective population-size approximation works well with an effective population size given by Equation 1. Third, if the population size is severely reduced during bottlenecks, the results of our computer simulations depend on the relation between the timescales of recombination and of population-size changes. For the parameters chosen in Figure 4B, we find that when recombination is the slowest process, that is, at very small values of recombination rates, the effective population-size approximation works well. By contrast, when recombination is frequent between bottlenecks but rare within bottlenecks, the effective population-size approximation fails to describe the covariance of the times to the MRCA. In this region the covariance is not only enhanced with respect to the result of the effective population-size approximation, but also approximately independent of R. In this case we say that pairs of distant loci exhibit long-range association.

These conclusions rely on analyzing covariances averaged over different demographic histories. This raises the question of how typical such averages are. In other words, how large are the fluctuations around the average? We observe that in the case shown in Figure 1B the fluctuations around the mean covariance are much higher than in the case shown in Figure 1A. However, in both cases shown, the averages represent the qualitative behavior of individual realizations.

The coalescent approximations employed in this article assume large population sizes. While we generally find very good agreement between the coalescent approximations and the Wright–Fisher simulations, we observe some deviations, in particular for large recombination rates in the case shown in Figure 1B. As expected, when we increase the parameter N₀ in our computer simulations, the deviations become smaller (results not shown).

In the remainder of this section, we discuss our result (Equation 10) in terms of the so-called Xi-coalescent approximation. Xi coalescents form a broad family of gene-genealogical models allowing for simultaneous multiple mergers. The Kingman coalescent is a special case, allowing only for pairwise mergers. See Schweinsberg (2000) and Möhle and Sagitov (2001) for detailed descriptions of the family of Xi coalescents. We show in Appendix B how a Markov process with simultaneous multiple mergers is obtained in the case of severe reductions of population size during bottlenecks and compute the corresponding transition rates. This not only gives an alternative way of deriving Equation 10, it also provides insight into why a plateau forms. It turns out that the plateau arises as a direct consequence of simultaneous multiple mergers. This implies that long-range associations between two loci are also expected in other situations where simultaneous multiple mergers are important: Durrett and Schweinsberg (2004) have studied populations subject to selective sweeps, and Eldon and Wakeley (2008) have demonstrated the importance of multiple mergers in shaping ${\sigma }_{\text{d}}^2$ in populations with skewed offspring distributions.

We note that there is a particular case where we can find a precise correspondence between the model of Eldon and Wakeley (2008) and the model analyzed in this article. This is the case of extreme reproductive success where one parent alone gives rise to the next generation. This case is obtained by setting ω = 1 in the notation of Eldon and Wakeley (2008). In our model this corresponds to a population subject to one severe and infinitely strong bottleneck, that is, to the limit x → 0 and λ_B → 0. In this limit we find (averaging numerator and denominator in Equation 12 separately)

$${\sigma }_{\text{d}}^2\approx \frac{10+R+2\lambda }{22+R^2+16\lambda +2{\lambda }^2+13R+3\lambda R}.$$ (14)

This result is equivalent to the equation for Y₂ on p. 1522 in Eldon and Wakeley (2008), identifying ${\sigma }_{\text{d}}^2$ = Y₂, λ = φ, R = 2η, and setting ω = 1, α = 1, and β = 1 in the notation of Eldon and Wakeley (2008). We remark that for a population subject to a bottleneck, ${\sigma }_{\text{d}}^2$ was calculated explicitly by Eriksson and Mehlig (2004). Eriksson et al. (2009) discuss corresponding results within the sequential Markov coalescent approximation (McVean and Cardin 2005; Marjoram and Wall 2006).

We conclude with the observation that ${\sigma }_{\text{d}}^2$, which is a function of the covariances ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)], ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ik)], and ${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(kl)], fails to show the plateaus observed in these covariances in Figure 6. This was observed already in Eriksson and Mehlig (2004) for the case of a single, recent bottleneck. Because of the close link between ${\sigma }_{\text{d}}^2$ and ${\widehat{r}}^2$, a common measure of linkage disequilibrium (McVean 2002), this casts doubt on the suitability of such measures for characterizing the degree of association between two loci [another example is the measure HR² (Sabatti and Risch 2002)], in populations that may have been subject to recent population bottlenecks and range expansions. A more accurate approach, especially for detecting long-range association between two loci, may be to estimate the covariance of the times to the MRCA directly. For example, simulations show that the covariance of the number of mutations in small windows (e.g., a few hundred nucleotides long) can be used to estimate the covariance of the times to the MRCA (Eriksson and Mehlig 2004). However, it remains to investigate which observables are most suitable for detecting long-range dependencies in the underlying gene genealogies for more general demographic histories.

Appendix A: Coefficients Appearing in Equations 9 and 10

In this Appendix we list the coefficients appearing in Equations 9 and 10.

The coefficients in Equation 9 are

$$\begin{array}{l}{C}_0=36x^5\left({\lambda }_{\text{B}}+\lambda +3\right)\left({\lambda }_{\text{B}}+\lambda +6\right)({\lambda }_{\text{B}}({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}+2x\lambda +\lambda +4\right)\\ +\lambda (x((x+2)\lambda +x+6)+1)+5)+x\lambda (x(\lambda +1)(\lambda +3)+2)+2),\\ C_1=2x^5({\lambda }_{\text{B}}({\lambda }_{\text{B}}({\lambda }_{\text{B}}({\lambda }_{\text{B}}({\lambda }_{\text{B}}+3x(\lambda +9)+2\lambda +13)+(3x(x+2)+1){\lambda }^2\\ +(x(55x+76)+29)\lambda +252x+59)+x^3\lambda (\lambda +1)(\lambda +27)\\ +2x^2\lambda (\lambda (3\lambda +58)+213)+x(\lambda (\lambda (3\lambda +80)+370)+801)+2\lambda (8\lambda +55)+119)\\ +x^3\lambda (\lambda +1)(\lambda +21)(2\lambda +9)+x^2\lambda (\lambda (\lambda (3\lambda +76)+452)+903)\\ +x(\lambda (\lambda (31\lambda +226)+647)+1044)+(3\lambda +4)(5\lambda +27))\\ +x(\lambda (x^2(\lambda +1)(\lambda +3)(\lambda +6)(\lambda +15)+x(5\lambda +18)(\lambda (3\lambda +16)+33)\\ +44\lambda +270)+468)+18(\lambda +2)),\\ C_2=x^5({\lambda }_{\text{B}}({\lambda }_{\text{B}}(x{\lambda }_{\text{B}}(3{\lambda }_{\text{B}}+2x(4\lambda +9)+4(\lambda +7))+x(x^2\lambda (7\lambda +39)\\ +10x(\lambda (\lambda +7)+9)+\lambda (\lambda +25)+89)+4\lambda )\\ +x(2x^3\lambda (\lambda +1)(\lambda +9)+x^2\lambda (\lambda (8\lambda +65)+129)\\ +2^x{(\lambda +2)}^2(\lambda +18)+\lambda (9\lambda +55)+116)+4\lambda )\\ +x(x(\lambda (2x^2(\lambda +1)(\lambda +3)(\lambda +6)+x(\lambda (\lambda (\lambda +22)+83)+102)\\ +4{\lambda }^2+42\lambda +96)+72)+26(\lambda +2))),\\ C_3=x^7\left({\lambda }_{\text{B}}+\lambda +2\right)\left({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}+2x\lambda +3\right)+x\lambda (x\lambda +x+2)+2\right),\end{array}$$ (A1)

$$\begin{array}{l}{D}_0=36x^5{\left({\lambda }_{\text{B}}+\lambda +1\right)}^2\left({\lambda }_{\text{B}}+\lambda +2\right)\left({\lambda }_{\text{B}}+\lambda +3\right)\left({\lambda }_{\text{B}}+\lambda +6\right),\\ D_1=2x^5({\lambda }_{\text{B}}+\lambda +1)({\lambda }_{\text{B}}+\lambda +2)({\lambda }_{\text{B}}({\lambda }_{\text{B}}(13{\lambda }_{\text{B}}+13(x+2)\lambda +27x+130)\\ +13(2x+1){\lambda }^2+157(x+1)\lambda +9(19x+39))\\ +13x(\lambda +1)(\lambda +3)(\lambda +6)+9(\lambda +2)(3\lambda +13)),\\ D_2=x^5({\lambda }_{\text{B}}+\lambda +1)({\lambda }_{\text{B}}+\lambda +2)({\lambda }_{\text{B}}({\lambda }_{\text{B}}(2{\lambda }_{\text{B}}+4x\lambda +39x+2\lambda +20)\\ +x(2x(\lambda (\lambda +8)+9)+4{\lambda }^2+86\lambda +247)+16\lambda +54)\\ +2x^2(\lambda +1)(\lambda +3)(\lambda +6)+13x(\lambda +2)(3\lambda +13)+18(\lambda +2)),\\ D_3=x^6\left({\lambda }_{\text{B}}+\lambda +1\right){\left({\lambda }_{\text{B}}+\lambda +2\right)}^2\left(3{\lambda }_{\text{B}}+x(3\lambda +13)+13\right),\\ D_4=x^7\left({\lambda }_{\text{B}}+\lambda +1\right){\left({\lambda }_{\text{B}}+\lambda +2\right)}^2.\end{array}$$ (A2)

The coefficients in Equation 10 are

$$\begin{array}{l}{A}_0=18\left({\lambda }_{\text{B}}+1\right)\left({\lambda }_{\text{B}}+\lambda +3\right)\left({\lambda }_{\text{B}}+\lambda +6\right)\left({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}+\lambda +3\right)+2\right),\\ A_1=\left({\lambda }_{\text{B}}+1\right)\left({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}({\lambda }_{\text{B}}^2+2\left(\lambda +6\right){\lambda }_{\text{B}}+\lambda \left(\lambda +27\right)+47)+\lambda (15\lambda +83)+72\right)+18(\lambda +2)\right),\\ A_2=2{\lambda }_{\text{B}}({\lambda }_{\text{B}}+1)\lambda ,\\ B_0=18{\left({\lambda }_{\text{B}}+\lambda +1\right)}^2\left({\lambda }_{\text{B}}+\lambda +2\right)\left({\lambda }_{\text{B}}+\lambda +3\right)\left({\lambda }_{\text{B}}+\lambda +6\right),\\ B_1=\left({\lambda }_{\text{B}}+\lambda +1\right)\left({\lambda }_{\text{B}}+\lambda +2\right)\left({\lambda }_{\text{B}}\left(13{\lambda }_{\text{B}}\left({\lambda }_{\text{B}}+2(\lambda +5)\right)+\lambda (13\lambda +157)+351\right)+9(\lambda +2)(3\lambda +13)\right),\\ B_2=\left({\lambda }_{\text{B}}+\lambda +1\right)\left({\lambda }_{\text{B}}+\lambda +2\right)\left({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}\left({\lambda }_{\text{B}}+\lambda +10\right)+8\lambda +27\right)+9(\lambda +2)\right).\end{array}$$ (A3)

Appendix B: Severe Reductions of Population Size During Bottlenecks: Connection to the Xi coalescent

In this Appendix, we turn our attention to the case of severe reductions of population size during bottlenecks, the third case discussed in Covariance of the Times to the MRCA. Formally, we describe this case by the following limit: N₀ → ∞, N_B → ∞, N_B/N₀ → 0, while λ = pN₀ and λ_B = qN_B are kept constant. This limit implies the following. First, it is possible that a bottleneck may host more than one coalescence. How frequently this occurs is determined by the rates λ, and λ_B. We remark that the probability for two lines to coalesce between two successive bottlenecks is (1 + λ)⁻¹ and the probability for two lines to coalesce within a single bottleneck is (1 + λ_B)⁻¹. Second, this limit implies that the duration of a single bottleneck is negligible compared to the time between two successive bottlenecks, because in this limit one has p/q → 0. This not only allows for neglecting the durations of bottlenecks, but also implies that possible coalescences within a single bottleneck can be considered as a single simultaneous multiple merger. This allows for employing the Xi-coalescent approximation in this case (as was also suggested by Birkner et al. 2009). The corresponding coalescent rates for our Xi-coalescent approximation show, in terms of the parameters λ and λ_B, how important multiple mergers are for shaping the resulting gene genealogies in this case.

In what follows we demonstrate how the Xi-coalescent approximation yields Equation 10 for the mean covariance 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉. Our method for calculating the term 〈t_a(ij)t_b(ij)〉 is described in the main text (Covariance of the Times to the MRCA). But in the Xi-coalescent approximation employed here, the Markov process differs from the one described in Covariance of the Times to the MRCA. The corresponding graph is shown in Figure B1. It consists of the same five states 1, … , 5 shown in Figure 3, but in Figure B1 the states in bottlenecks are omitted, since the time spent in a bottleneck is short compared to the time between two successive bottlenecks.

The remainder of this Appendix is organized as follows. First, we show how the transition rates w_mn are derived using the Xi-coalescent approximation. Second, using the Xi-coalescent transition rates we demonstrate how to derive Equation 10.

Formulas for w_mn Under the Xi-Coalescent Approximation

Assume that l ancestral lines enter a bottleneck, and that b lines leave this bottleneck. In our Xi-coalescent approximation, we assume that the l − b coalescent events in the bottleneck happen instantaneously.

In what follows we derive the coalescent rates for our Xi-coalescent approximation. Let l lines be partitioned into b families (b ≤ l), such that k_i families are of sizes i = 1, … , l. By construction, the following conditions must be satisfied:

$$l={\displaystyle \sum _{i=1}^{l}i}{k}_i,b={\displaystyle \sum _{i=1}^l{k}_i}\hspace{0.17em}\hspace{0.17em}.$$ (B1)

In our model, the collision rate ${\phi }_{\{l;k_1,\dots ,k_l\}}$ of l lines colliding into a particular partition {l; k₁, … , k_l}, such that Equation B1 is satisfied, is given by

$${\phi }_{\{l;k_1,\dots ,k_l\}}=1_{\{b=l-1\}}+\lambda {\Xi }_{\{l;k_1,\dots ,k_l\}}.$$ (B2)

Here the first term stands for the Kingman coalescent outside bottlenecks, and the second term corresponds to the contribution from (multiple) coalescences during bottlenecks (multiple mergers are obtained in the case b < l−1). Bottlenecks occur at a rate λ. Given the probability C_lb that during a bottleneck l lines collide into b lines, ${\Xi }_{\{l;k_1,\dots ,k_l\}}$ can be calculated according to

$${\Xi }_{\{l;k_1,\dots ,k_l\}}=C_{lb}{p}_{\{l;k_1,\dots ,k_l\}}\hspace{0.17em},$$ (B3)

where

$$C_{lb}=\frac{{\lambda }_{\text{B}}}{\left(\begin{array}{c}b\\ 2\end{array}\right)+{\lambda }_{\text{B}}}{\displaystyle \prod _{i=b+1}^l\frac{\left(\begin{array}{c}i\\ 2\end{array}\right)}{\left(\begin{array}{c}i\\ 2\end{array}\right)+{\lambda }_{\text{B}}}},$$ (B4)

and $p_{\{l;k_1,\dots ,k_l\}}$ is the probability of observing a particular partition {l; k₁, … , k_l} of l lines. As shown by Kingman (1982), it is given by

$$p_{\{l;k_1,\dots ,k_l\}}=\frac{(l-b)!b!(b-1)!}{l!(l-1)!}{\displaystyle \prod _{i=1}^l}{(i!)}^{k_i}.$$ (B5)

The rate ${\phi }_{\{l;k_1,\dots ,k_l\}}$ appearing in Equation B2 is conditional on a particular partition. Thus the total collision rate of l lines into any of partitions of type {l; k₁, … , k_l} is given by

$${\phi }_{\{l;k_1,\dots ,k_l\}}^{\text{tot}}=\left(\begin{array}{l}l\\ 2\end{array}\right)1_{\{b=l-1\}}+\lambda C_{lb}{p}_{\{l;k_1,\dots ,k_l\}}{S}_{\{l;k_1,\dots ,k_l\}}.$$ (B6)

Here

$$S_{\{l;k_1,\dots ,k_l\}}=\frac{l!}{{\displaystyle {\prod }_{i=1}^l{\left(i!\right)}^{k_i}{k}_i!}}$$ (B7)

denotes the number of possible ways of collisions of l lines into a partition {l; k₁, … , k_l}, such that restrictions in Equation B1 hold.

The graph corresponding to the Markov process in the limit described in this Appendix consists of five states 1, … , 5 (see Figure B1). We now show how the corresponding transition rates between the states 1, … , 5 can be derived from Equation B6.

We observe that a collision of type {2; 0, 1} describes a transition from either state 1 or 4 to 5. It follows that

$$w_{51}=w_{54}={\mathit{\phi }}_{\left\{2;0,1\right\}}^{\text{tot}}.$$ (B8)

State 2 consists of three lines. A collision of one particular pair of lines, among the three lines, results in a transition from 2 to 1, while a collision of either of the two remaining pairs of lines results in a transition from 2 to 4. Because a collision of a pair of lines among three lines is of type {3; 1, 1, 0}, we obtain the following transition rates:

$$w_{12}=\frac{1}{3}{\phi }_{\left\{3;1,1,0\right\}}^{\text{tot}},\hspace{1em}{w}_{42}=\frac{2}{3}{\phi }_{\left\{3;1,1,0\right\}}^{\text{tot}}.$$ (B9)

A collision of all three lines of state 2 leads to a transition from state 2 to 5 at the rate

$$w_{52}={\mathit{\phi }}_{\left\{3;0,0,1\right\}}^{\text{tot}}.$$ (B10)

Now consider transitions from state 3, consisting of four ancestral lines. We analyze first a collision of a single pair of lines, that is, a collision of type {4; 2, 1, 0, 0}. There are in total six different ways to pair the four lines entering the bottleneck: four choices describe a transition from state 3 to 2, and the remaining two lead to a transition from 3 to 4. Thus, we have

$$w_{23}=\frac{2}{3}{\phi }_{\left\{4;2,1,0,0\right\}}^{\text{tot}}.$$ (B11)

Further, there are three possibilities for simultaneous collisions of two pairs of lines. Two possibilities result in a transition from 3 to 1, and one leads to a transition from 3 to 5 (see Figure 2D). It is also possible to obtain a collision of three lines, in which case the transition from 3 to 4 is obtained. Further, a collision of all four lines results in a transition from 3 to 5. Thus, we obtain the following transition rates:

$$w_{13}=\frac{2}{3}{\phi }_{\left\{4;0,2,0,0\right\}}^{\text{tot}},\hspace{1em}{w}_{43}=\frac{1}{3}{\phi }_{\left\{4;2,1,0,0\right\}}^{\text{tot}}+{\phi }_{\left\{4;1,0,1,0\right\}}^{\text{tot}},\hspace{1em}{w}_{53}=\frac{1}{3}{\phi }_{\left\{4;0,2,0,0\right\}}^{\text{tot}}+{\phi }_{\left\{4;0,0,0,1\right\}}^{\text{tot}}.$$ (B12)

The remaining nonvanishing rates, w₂₁ = R, and w₃₂ = R/2, describe recombination transitions from state 1 to 2 and from 2 to 3. This shows how the transition rates w_mn are expressed in terms of the collision rates of the Xi coalescent. Explicit formulas for the rates w_mn in terms of λ and λ_B are given in Figure B1.

Figure 1.

(Left) Graph showing the states and possible transitions corresponding to the limit of severe reductions of population size during bottlenecks. The states 1, … , 5 are explained in Figure 3. The three red arrows in this graph correspond to simultaneous multiple mergers. (Right) Transition rates, w_mn, from state n to m, in terms of the parameters λ = pN₀ and λ_B = qN_B.

Obtaining Equation 10 Under the Xi-Coalescent Approximation

Given the rates w_mn, the mean covariance 〈${\text{cov}}_{\mathcal{D}}$[t_a(ij), t_b(ij)]〉 is computed from

$$\langle t_{a\left(ij\right)}{t}_{b\left(ij\right)}\rangle ={\displaystyle {\int }_0^{\mathrm{\infty }}d}{t}_1 t_1^2 u{e}^{\mathbf{M}\hspace{0.17em}{t}_1}v+{\displaystyle {\int }_0^{\mathrm{\infty }}d}{t}_1{\displaystyle {\int }_{t_1}^{\mathrm{\infty }}d}{t}_2 t_1{t}_2 c e^{K\left(t_2-t_1\right)}Q e^{\mathbf{M}\hspace{0.17em}{t}_1}v.$$ (B13)

This equation corresponds to Equation 7 given in Covariance of the Times to the MRCA. But the dimensions of the matrices and vectors in Equation B13 differ from those in Equation 7 because states in the bottleneck are omitted. Here M is a 3 × 3 matrix. Its off-diagonal elements correspond to the rates w_mn:

$$M_{12}=1+\lambda {\lambda }_{\text{B}}{\left(\left(1+{\lambda }_{\text{B}}\right)\left(3+{\lambda }_{\text{B}}\right)\right)}^{-1},M_{13}=4\lambda {\lambda }_{\text{B}}{\left(\left(1+{\lambda }_{\text{B}}\right)\left(3+{\lambda }_{\text{B}}\right)\left(6+{\lambda }_{\text{B}}\right)\right)}^{-1},M_{21}=2M_{32}=R,M_{23}=4+4\lambda {\lambda }_{\text{B}}{\left(\left(3+{\lambda }_{\text{B}}\right)\left(6+{\lambda }_{\text{B}}\right)\right)}^{-1}.$$ (B14)

The diagonal elements of M are given by $M_{nn}=-{\displaystyle {\sum }_{m\ne n}{M}_{mn}}$ for n = 1, 2, 3. The remaining quantities appearing in Equation B13 are K = −1, c = 1, v = [1, 0, 0]^T, and

$$u={\left[\begin{array}{c}1+\lambda {\left(1+{\lambda }_{\text{B}}\right)}^{-1}\\ 3\lambda {\left(\left(1+{\lambda }_{\text{B}}\right)\left(3+{\lambda }_{\text{B}}\right)\right)}^{-1}\\ 2\lambda \left(9+{\lambda }_{\text{B}}\right){\left(\left(1+{\lambda }_{\text{B}}\right)\left(3+{\lambda }_{\text{B}}\right)\left(6+{\lambda }_{\text{B}}\right)\right)}^{-1}\end{array}\right]}^{\mathsf{T}},\mathbf{Q}={\left[\begin{array}{c}0\\ 2\left(1+\lambda {\lambda }_{\text{B}}{\left((1+{\lambda }_{\text{B}})(3+{\lambda }_{\text{B}})\right)}^{-1}\right)\\ 2\left(1+\lambda {\lambda }_{\text{B}}\left(7+{\lambda }_{\text{B}}\right){\left(\left(1+{\lambda }_{\text{B}}\right)\left(3+{\lambda }_{\text{B}}\right)\left(6+{\lambda }_{\text{B}}\right)\right)}^{-1}\right)\end{array}\right]}^{\mathsf{T}}.$$ (B15)

Combining Equation B13 with Equations B14 and B15 results in Equation 10. This shows that the covariance of the times to the MRCA in the case of severe reductions of population size can be derived within the Xi-coalescent approximation.