Measuring Selection Coefficients Below 10⁻³: Method, Questions, and Prospects

Abstract

Measuring fitness with precision is a key issue in evolutionary biology, particularly in studying mutations of small effects. It is usually thought that sampling error and drift prevent precise measurement of very small fitness effects. We circumvented these limits by using a new combined approach to measuring and analyzing fitness. We estimated the mutational fitness effect (MFE) of three independent mini-Tn10 transposon insertion mutations by conducting competition experiments in large populations of Escherichia coli under controlled laboratory conditions. Using flow cytometry to assess genotype frequencies from very large samples alleviated the problem of sampling error, while the effect of drift was controlled by using large populations and massive replication of fitness measures. Furthermore, with a set of four competition experiments between ancestral and mutant genotypes, we were able to decompose fitness measures into four estimated parameters that account for fitness effects of our fluorescent marker (α), the mutation (β), epistasis between the mutation and the marker (γ), and departure from transitivity (τ). Our method allowed us to estimate mean selection coefficients to a precision of 2 × 10⁻⁴. We also found small, but significant, epistatic interactions between the allelic effects of mutations and markers and confirmed that fitness effects were transitive in most cases. Unexpectedly, we also detected variation in measures of s that were significantly bigger than expected due to drift alone, indicating the existence of cryptic variation, even in fully controlled experiments. Overall our results indicate that selection coefficients are best understood as being distributed, representing a limit on the precision with which selection can be measured, even under controlled laboratory conditions.

MUTATIONS of small effect can play an important role in evolution, but they are difficult to measure experimentally because the precision with which fitness effects can be measured is relatively low. For this reason, it remains unclear to what extent mutations with small beneficial effects contribute to fitness improvements (Orr 2005). It is also unclear how much deleterious mutations of small effect contribute to the genetic load and inbreeding depression (Charlesworth and Charlesworth 1998; Bataillon and Kirkpatrick 2000). More generally, the existence and influence of mutations of small effect is at the heart of the neutralist–selectionist controversy (e.g., Nei 2005). This debate can be addressed experimentally only if the precision of fitness measurements is lower than the inverse of effective population size, which seems beyond reach for large populations (Kreitman 1996). Finally, a low precision in fitness measures limits the ability to determine whether the fitness effect of a mutation varies across different environmental or genetic contexts and adds to other sources of stochasticity (Lenormand et al. 2009) to make it difficult to reliably predict evolutionary trajectories.

Precisely measuring fitness poses technical, conceptual, and statistical challenges. The technical challenge is to set up a technique that allows experiments to be carried out efficiently. The first major advance was to use “population cages” with Drosophila or other small animals (starting in the 1930s with the work of L’Heritier and Teissier 1937a,b). With such devices, environmental conditions are relatively controlled and gene flow can be eliminated. However, drift and indirect selection caused by loci under selection in linkage disequilibrium with the focal locus are difficult to account for. The same approach was applied to microorganisms (Dykhuizen and Hartl 1980), which can be made isogenic save for a focal gene, thereby reducing indirect selection due to initial linkage disequilibrium (e.g., Carrasco et al. 2007; Domingo-Calap et al. 2009 for distribution of mutation fitness effects; Elena et al. 1998; Sanjuan et al. 2004; Peris et al. 2010) and can be propagated as large populations, minimizing the effect of drift relative to selection. They can also be followed over many generations (Dykhuizen and Hartl 1983; Thatcher et al. 1998; Lunzer et al. 2002). Long-term monitoring increases the ability to detect small differences in fitness between competing genotypes, but adds the complication that newly arising mutations may perturb the assay (Dykhuizen and Hartl 1983). An important technical issue in all competition experiments is to determine the frequency of competing genotypes reliably and quickly. In many cases the idea is to link an easily recognized marker with the gene under scrutiny. It is, however, important to recognize that a marker can confer a selective difference (a marker “cost”), which might vary with the genetic background (epistasis) or external environment (G × E interactions). Finally, inferring allelic selection coefficients against a common reference strain requires that genotypic fitness is transitive. These potential complications require adding proper controls to competition experiments.

A key conceptual difficulty in measuring the fitness effects of mutations is to distinguish selection from drift (Beatty 1984; Millstein 2008), which is at the heart of several population cage experiments with Drosophila (Dobzhansky and Pavlovsky 1957). To account for the effect of drift, a selection coefficient can be defined from the expected change in allele frequency over one generation (e.g., Rousset 2004), which can be estimated from the mean frequency change in independent competition experiments. Because of drift, replication is fundamentally necessary to estimate fitness, and the precision of a given fitness measure must account for the interreplicate variance. Indeed, it is possible to count all organisms in an experimental population, so that the genotype frequencies are known without sampling error. Such an experiment would allow frequency variation to be determined “exactly,” but would clearly not account for the possibility that drift will cause different outcomes in different replicates. A further complication is that fitness may vary because of changing environmental conditions. Fluctuating selection during the course of a competition experiment or varying selection across replicates of a competition assay can mimic drift (Felsenstein 1976; Lynch 1987; O'hara 2005). If selection varies, and it probably always does to some extent (Bell 2008; Bell 2010), measuring selection requires measuring both a mean and a variance (the latter not including sampling error). The remaining variance can be caused by drift or by heterogeneity in selection, which are difficult to disentangle without extra information on the effective population size. In summary, measuring selection with precision requires estimating an expectation over several replicates, so that its variance can be decomposed into components due to sampling error, drift, and variable selection.

From a statistical point of view, selection coefficients in the field or in the laboratory are best estimated by using a fully specified selection model in a likelihood framework (e.g., Clark 1979; Wilson et al. 1982; Oakeshott et al. 1983; Manly 1985; Arnason and Lewontin 1991; Lenormand and Raymond 2000; Saccheri et al. 2008; Labbe et al. 2009), which can include drift if longitudinal data are available (Manly 1985; O'hara 2005; Bollback et al. 2008). When selection can be approximated by a continuous process through time in an isolated population, a simple approach is to regress Log(p/q) (where p and q represent the frequencies of the two competitors) over time expressed in units of generations (Fisher 1930). The connection with logistic regression and general linear models is then straightforward (Arnason and Barker 1999) and more appropriate than the use of least squares. However, complications arise in the analysis of time series and correlated error in repeated measurement through time (Arnason and Barker 1999; O'hara 2005), especially when both drift and fluctuating selection cause frequency variation. The latter problems can be important, particularly when analyzing multiple time point series (e.g., arising in long-term population cage or chemostat experiments), although they are rarely taken into account. Often, replicated experiments are simply pooled, even if significantly different, and not analyzed to consider variance in the estimates of selection. The development of mixed models offers an attractive alternative to circumvent this problem and to measure selection and its variation.

We present an approach combining several features to improve and quantify the precision of fitness measures. First, we use techniques that have proved to be among the most efficient to measure fitness: competition assay between large populations of Escherichia coli strains to minimize drift and engineered mutations to avoid the problem of indirect selection. Specifically, we used three genotypes, each carrying a single mutation introduced by the integration of a mini-Tn10 transposon. These mutations were considered neutral, relative to a common progenitor genotype, in a previous experiment (Elena et al. 1998). We use two fluorescent markers (Rosenfeld et al. 2005) combined with flow cytometry (Lunzer et al. 2002) to measure frequency variation with great precision, and thus minimize sampling error. Other studies have shown the utility of these approaches in measuring genotype fitness (Lunzer et al. 2002; Zhu et al. 2005; Lee et al. 2009). Key aspects of our approach are as follows:

1. A comprehensive set of four competition assays enables us to separately estimate mutational selection coefficients (α), the cost of the marker (β), epistasis between mutation and marker (γ), and transitivity (τ).

2. We use short-term batch culture to facilitate massive replication and to reduce the possibility that de novo beneficial mutations will occur.

3. We analyze the data in an integrated likelihood framework with random effects to partition sources of variation in our estimates (sampling error vs. drift vs. variable selection).

Our approach allowed us to estimate both mean and variance in selection coefficients at a precision of 0.02%. This precision allowed us to detect variation in measures of some mutation selection coefficients that were significantly larger than expected due to drift alone, indicating the action of some kind of cryptic variation during our competitions. This finding implies that, in practice, selection coefficients should be considered as being distributed and that precise measures require evaluating both the mean and the variance of this distribution. Furthermore, the variance in s indicates that some uncontrolled processes occur in these experiments (cryptic environmental or genetic variation), which impose a limit to further dissecting the differences seen across replicates. We discuss implications of these findings and the prospects of this high-throughput method for fitness measurement.

Materials and Methods

Strain construction

The E. coli B strain used in this study, REL4548, was evolved in Davis minimal medium supplemented with 25 μg/ml glucose (DM25) for 10,000 generations as part of a long-term evolution experiment (Elena et al. 1998).

Insertions of the chromosomal fluorescent markers:

The YFP and CFP genes (provided by the Yeast Resource Center of the University of Washington) were inserted at the rhaA locus of REL4548 using a technique developed by Datsenko and Wanner (2000). Table 1 gives a description of this method as applied to our experiments. A full description of the method is given in supporting information, File S1.

Table 1. Strain construction description.

Step	Experiment	Description	Achievement
1	PCR	PA1 promoter was introduced in front of the CFP and YFP genes.	PCR products called PA1-CFP and PA1-YFP
2	Cloning	PA1-CFP and PA1-YFP were cloned in pKD4.a	plasmids called pKD4-CFP and pKD4-YFP
3	PCR	pKD4-CFP and pKD4-YFP were used as templates. Primers with 50 bases sequences homologous to the E. coli rhaA gene at their 5′ ends were used.	PCR products called rhaA-CFP-Kan and rhaA-YFP-Kan
4	Transformation	The plasmid pKD46a was electroporated into the REL4548 recipient cells.	REL4548 carrying pKD46
5	Transformation and homologous recombination	PCR products rhaA-CFP-Kan and rhaA-YFP-Kan were electroporated in REL4548 carrying pKD46.	REL4548 CFP-KanR and REL4548 YFP-KanR
6	Transformation	The plasmid pCP20a was electroporated into REL4548 CFP-KanR and REL4548 YFP-KanR.	REL4548 CFP-KanR pCP20 and REL4548 YFP-KanR pCP20
7	Heat Shock	KanR cassette were excised from the REL4548 CFP-KanR and REL4548 YFP-KanR genomes.	REL4548/CFP and REL4548/YFP

^aFrom Datsenko and Wanner (2000).

Mutant construction:

The three mutants studied here were constructed by Elena et al. (1998) and were obtained by random single insertions of mini-Tn10 derivative 104—which contains a tetracycline resistance cassette (Kleckner et al. 1991)—into REL4548. We chose mutations T63, T103, and T121 from this original collection because they were identified as neutral using the standard plating method. These mutations were transduced into REL4548/CFP and REL4548/YFP by P1 transduction to have each mutation associated with each fluorescent marker. Since P1 transductions were performed between isogenic strains (except for the marker and the mobilized mutation), the risk of secondary mutations was low. Transductants were selected on LBA-Tet plates (LB agar plates supplemented 10 μg/ml tetracycline). We denote the wild-type genotype with CFP marker wc (wc for wild-type cyan), wy for wild-type YFP, mc for mutant CFP, my for mutant YFP.

Competition experiments

Media:

Lysogeny broth (LB) was used for routine molecular work and for reviving strains from storage (10 g/liter NaCl, 10 g/liter tryptone, 5 g/liter yeast extract; LB Agar LB + 15 g/liter agar). Davis minimal (DM) medium supplemented with 250 μg/ml glucose (DM250) was used for all competition assays (KH₂PO₄·3H₂0 7 g/liter, KH₂PO₄ 2 g/liter, (NH₄)₂SO₄ 1 g/liter, sodium citrate 0.5 g/liter; pH was adjusted to 7.0 with HCl or NaOH as necessary). Bottles were weighed before and after autoclaving and sterile milliQ water was added to compensate for evaporation. After autoclaving, DM was supplemented with: 2.5 ml glucose 10%, 1 ml MgSO₄²⁻ 10%, 1 ml thiamine (vitamin B1) 0.2%. We call this medium DM250, which is equivalent to the one used by Lenski et al. (1991), in which the strain REL4548 grew for 10,000 generations, but with 10 times more glucose.

Glycerol stocks:

All strains were grown overnight and a sample of 750 μl of each culture was mixed to 250 μl of 60% glycerol and kept at −80° for storage.

Culture:

The relative fitness, W, of each mutant was estimated by measuring the change in its relative frequency in competition experiments. To measure the mutation fitness effect (MFE) and to control for potential marker effects and epistasis between the mutation and the marker, we performed four competition types for each mutant: (a) wc/wy, (b) mc/my, (c) my/wc, and (d) mc/wy. The rationale for performing all these competitions is presented below. Competitions were begun by growing the strains to be competed at 37° overnight with shaking at 250 rpm in 24-well microtiter plates (Greiner Bio—one 662102—suspension culture plates) containing 1 ml/well of DM250. We used DM250 as the growth medium to obtain large population sizes, which limit the effect of drift, and to facilitate the measurement of hundreds of thousands of cells without having to sample large volumes. To limit evaporation, each 24-well plate was placed in a 2-liter plastic box containing paper towels soaked with 100 ml water (at the bottom of the box). The next day, 10 μl (100-fold dilution) of each culture was transferred to a fresh plate and incubated for 24 hr under identical conditions. On the third day, competitors were mixed at a 1:1 ratio (5 μl of each competitor) and transferred to a fresh plate under identical conditions. On day 4, 20 μl of each competition was transferred into 10 replicate wells containing 1980 μl of DM250. After mixing, 1 ml was removed from each well and placed in a plastic test tube at 4° for a subsequent flow cytometry measurement (performed 1 hr later), while the remaining 1 ml was kept in the microtiter plate to be cultivated under the conditions described above. Finally, on the fifth day, a 100-μl sample was taken from each competition, diluted in DM (not containing glucose, thiamine, or MgSO₄²⁻), and placed in a plastic test tube at 4° for a subsequent flow cytometry measurement (performed 1 hr later). Ten different types of competitions were performed: wc vs. wy, m_T63c vs. m_T63y, m_T63c vs. wy, wc vs. m_T63y, m_T103c vs. m_T103y, m_T103c vs. wy, wc vs. m_T103y, m_T121c vs. m_T121y, m_T121c vs. wy, wc vs. m_T121y. Each experimental block consisted of each of these 10 competitions replicated 10-fold. Each experimental block was repeated at four different dates.

Flow cytometry:

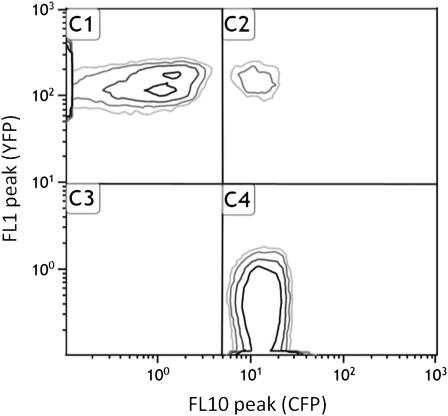
The relative frequency of competitors marked with CFP or YFP was measured using a Gallios Beckman Coulter flow cytometer at 0 and 24 hr following mixing of competing genotypes. We decided to separate competitor populations only on the basis of their fluorescent markers, because CFP and YFP cell populations did not have the same distribution pattern on forward vs. side scatter plots. Thresholds were applied manually (since clustering algorithms often introduce more noise) on the CFP–YFP plots to determine the boundaries of each population (CFP, YFP, unmarked cells, and doubled marked objects) as shown on Figure 1. These thresholds were the same for all competition plots because in such a constant environment, cell clusters were always localized in the same areas of the plot. The frequency of each marker type was calculated using CFP and YFP population counts only. Unmarked and double-marked populations represented approximately 0.2 and 1% of the total population, respectively. For simplicity, “doublets” (objects composed of two cells) were excluded from our frequency estimates. CC, YY, and CY doublets occur, but only the latter are detected in the C2 population (Figure 1). Furthermore, doublets may not form at random; doublets with the same color were often overrepresented (data not shown). Nevertheless, even considering these complications, ignoring doublets only introduces a bias on s measures proportional to sε, where ε is the fraction of the CY population (C2 in Figure 1). Under our conditions, ε ≈ 1% making this bias negligible compared to s (see File S1 and File S2 for details).

Figure 1.

Measuring genotype frequencies with flow cytometry. The fluorescence of each bacterium was measured in the FL1 (YFP) and FL10 (CFP) channels. Here we show a representative contour plot. Quadrants represent thresholds delimiting the YFP (C1), CFP (C4), doubled marked (C2), and unmarked (C3) populations. In this example, populations are composed of YFP, 110718 (51.03%); CFP, 103996 (47.93%); doubled-marked, 2110 (0.97%); Unmarked 151 (0.07%) individuals.

Precision of frequency measures with cytometry

Our method is based on measuring the relative frequency p of two competing genotypes at different time points by counting C = 200000 cells. This large figure, however, still represents a small fraction of the total population and, therefore, we estimate frequencies with sampling error. The theoretical expectation for this sampling error is

$${\sigma }_{\text{e}}^2=p(1-p)/C.$$

If nothing else contributes to measurement error, we should obtain this variance when measuring repeatedly the frequency in a given test tube. Preliminary experiments (not shown) indicated that much larger error could occur, in particular when test tubes were insufficiently mixed. This is an important technical issue and comparing actual measurement error to ${\sigma }_{\text{e}}^{\text{2}}$ provides an internal check that measurement error is not inflated above the sampling error expectation. In the experiments presented here, we used measures of initial frequencies (p₀) in our replicated competitions to estimate the variance of frequency measures performed with cytometry${\sigma }_{\text{obs}}^2$. We found that ${\sigma }_{\text{obs}}^2/{\sigma }_{\text{e}}^{\text{2}}$ was 0.94, 1.83, 1.07, and 0.95 for the four different dates where all the competitions were performed. Except for date 2, measurement error was very close to that inherent to sampling only. However, as shown by ${\sigma }_{\text{obs}}^{\text{2}}$ at date 2 (and other preliminary assays showing more dramatic results), using cytometry does not guarantee that measurement error will be low. In particular, thorough mixing of test tubes throughout the growth cycle limits cell aggregation and is a crucial step in taking advantage of the advantages offered by the cytometric approach (or any other approach based on frequency variation).

Measure of genotypic fitness

We measured fitness on the basis of a continuous time model $dp/dt=sp(1-p)$, which defines selection coefficient (s) on the basis of frequency (p) variation. This frequency variation was measured in the competition experiments described above. For a given competition assay k, the data are a vector ${\mathbf{n}}_k=\left\{n_{1k}^0,n_{2k}^0,n_{1k}^t,n_{2k}^t\right\}$ giving the number of genotypes 1 and 2 counted at time 0 (beginning) and t (end of the competition). The log-likelihood of this data given initial frequency of genotype 1 $p_{1k}^0$ and selection coefficient s_k is computed as

$$\text{ln Pr}\left({\mathbf{n}}_k\text{|}{p}_{1k}^0,s_k\right)\hspace{0.17em}=\sum _{i=1,2}{\sum }_{j=0,t}\left(n_{ik}^j\ln p_{ik}^j\right),$$ (1)

where $p_{2k}^j=1\hspace{0.17em}-\hspace{0.17em}{p}_{1k}^j$ and

$$p_{1k}^t=e^{s_{k}t}{p}_{1k}^0/\left(p_{2k}^0+e^{s_{k}t}{p}_{1k}^0\right).$$ (2)

The frequency variation is measured over 24 hr. To scale fitness measurements per generation, we used the number of cell generations as the time unit. This measure is an average over the duration of the competition, which does not contradict the fact that conditions change with time in a given assay (e.g., the glucose becomes limiting) because it does so similarly in all replicates. Because populations expand by binary fission, we have t = ln(100)/ln(2) = 6.6 in Equation 2. Across replicates of the same competition, s_k might vary for reasons other than sampling error, owing, for example, to drift or to cryptic environmental variation. To measure this variation, we used the same logistic regression approach (Equations 1 and 2), but including the assumption that s was normally distributed $s\hspace{0.17em}\sim \hspace{0.17em}N(\stackrel{-}{s},{\sigma }_s)$ among replicates. The log-likelihood of this logistic regression with random slope is then

$$\text{ln Pr}\left(n|{\mathbf{p}}_1^0,\stackrel{-}{s},{\sigma }_s\right)={\sum }_k\text{ln}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}N\left(\stackrel{-}{s},{\sigma }_s;s\right){\prod }_{i=1,2}{\prod }_{j=0,t}{n}_{ik}^j\text{ln}{p}_{ik}^{j}ds,$$ (3)

where n is the data matrix {${\text{n}}_1,{\text{n}}_2,{\text{n}}_3,\dots$}, ${\text{p}}_1^0$ the vector of all initial frequencies, and $N(\mu ,\sigma ;x)$ denotes the probability density function of the Normal distribution with mean μ and standard deviation σ. In all cases, parameters were estimated by maximizing the log-likelihood. Support limits for a given estimate were computed within 2 units of log-likelihood from the maximum with all other parameters being freely fitted. An equivalent of standard error SE_eq was computed as a quarter of the support range (similarly, 95% confidence intervals are ± 1.96 SE). Computations were performed with Mathematica (Wolfram Research 2008).

Fitness transitivity, allelic fitness, and epistasis

To test whether a constant fitness can be attributed to a genotype irrespective of its competitor, we performed all possible combinations of competition assays for a given mutant. At a first locus we have the wild-type (w) and mutant (m) alleles. At a second locus we have two alleles c and y (corresponding to the CFP and YFP marker proteins, respectively). Each competition assay requires competing genotypes to have different alleles at the marker locus. There are thus four possible combinations: (a) wc/wy, (b) mc/my, (c) my/wc, and (d) mc/wy. Table 2 indicates the selection coefficient expected in each of these cases if we assume that the fitness of genotypes wc, wy, mc, and my are constant and equal to W_wc, W_wy, W_mc, and W_my, respectively. When measuring the marker effect in the same background (competitions a and b), we measured the selection coefficient of the CFP genotype. Otherwise, we measured the selection coefficient of the mutant genotype against the wild type (competitions c and d).

Table 2. Selection coefficient expected in the different combinations of competition assays: wc/wy, mc/my, my/wc, and mc/wy.

Genotypes	Wild-type CFP (wc)	Wild-type YFP (wy)	Mutant CFP (mc)
Wild-type YFP (wy)	sa = Wwc/Wwy − 1
Mutant CFP (mc)		sd = Wmc/Wwy – 1 + τ
Mutant YFP (my)	sc = Wmy/Wwc − 1		sb = Wmc/Wmy − 1

Each combination was performed for each mutant strain.

Population genetics models usually assume that fitness effects are transitive, i.e., that they could be deduced from some absolute value ranking of the different genotypes. However, this is an assumption that requires evaluation before attributing a selection coefficient to genotypes. Since competitions a, b, and c are sufficient to estimate all fitness if they are transitive, competition d can be used to measure departure from transitivity. Specifically, we introduce a parameter τ measuring this departure (see Table 2). Further reparameterization allows decomposing genotypic fitness into allelic effects and their interaction (epistasis). We note that W_wc = W_wy + α, W_my = W_wy + β, W_mc = W_wy + α + β + γ. α is the “cost” of the CFP marker, β is the selective effect of the mini-Tn10 mutation, and γ is the epistasis between the two loci.

To fit this model, for each mutant, we used Equation 1 summed over the four competition assays and their replicates, with the parameterization indicated above. Support limits for estimates were computed within 2 units of log-likelihood, all other parameters being freely fitted.

Expected amount of drift

In our experiments, population size increases by binary fission. To compute the variance in frequency introduced by drift, we first determine that each bacteria division increases this variance by a quantity$pq/n^2$, where n is the population size at the time of this division. We then sum this variance to the end of population growth:

$${\sum }_{n=n_i}^{n_f}\frac{pq}{n^2}=pq\left(\frac{1}{n_i}-\frac{1}{n_f}\right)+O{\left(\frac{1}{n_i}\right)}^2.$$ (4)

We thus expect the variance of selection coefficients contributed by drift to be

$${\sigma }_s^2=\frac{n_f-n_i}{g^2{n}_f{n}_{i}pq},$$ (5)

where g is the number of generations (6.6 as explained above, over the time course of the competition experiment). The variance in frequency change caused by selective differences among replicates is var(sgpq) = ${\sigma }_s^2{(gpq)}^2$. In our experiments we have $n_f$ in the range ${10}^8-{10}^9$ and $n_i$ 100 times less. These population sizes were estimated by serial dilution and plating (not shown), and these numbers represent the extreme cases. Thus we expect ${\sigma }_s$ to be between ${10}^{-4}$and $3\times {10}^{-4}$. Significantly larger ${\sigma }_s$ would indicate that a source of variation, in addition to sampling error and drift, contributed to differences among replicate competitions (e.g., such as random fluctuations in selection coefficients among replicates).

Results

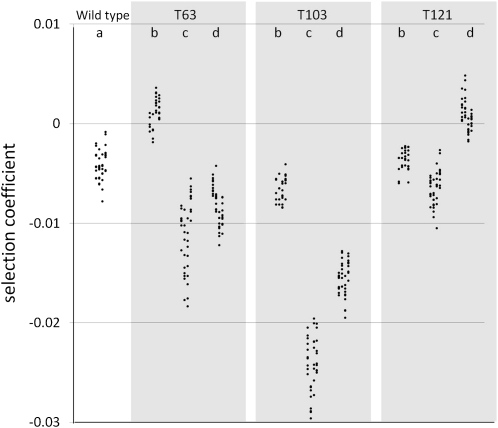
We used a flow cytometric approach to measure the fitness of three mutants, each carrying a single mutation, that were classified as being neutral with conventional methods (Elena et al. 1998). We performed 10 types of competition assays, each replicated 10-fold at each of 4 weeks, giving a total of 400 fitness measures (Figure 2). A standard analysis of deviance (Equations 1 and 2) revealed that 96.6% of the deviance was among competition assay types. There were significant week (0.6% of the total deviance), week × competition (1.3%), and replicate (1.4%) effects, although they accounted for a very small fraction of the total deviance. In particular, although detectable, the week effect was smaller than the replicate effect (well-to-well variation for the same competition during the same week), indicating that the experiments were repeatable from one week to another. We also used a simple one-way ANOVA to test whether the standard deviation in s measures among replicates was consistent when measured at different weeks. This was the case, although the repeatability was not extremely high. Specifically, we found that 53% of the variance in this standard deviation was among competitions and 47% within competition between weeks. This variation among competitions is significantly larger than across dates for the same competition (F_9,30 = 3.7, P = 0.003). Repeatability of means and variance at different weeks is crucial for measuring fitness with precision: it is fairly easy to obtain a very precise measure of frequency change in a single assay (or even an exact measure if all individuals in the competition are counted at the beginning and the end), but this is not equivalent to obtaining an accurate measure of fitness, which must account for inter-replicate variance. As this example shows, analyzing a very large data set also provides sufficient statistical power for detecting very small biological effects, but it can also reveal “nuisance” effects (almost anything tested becoming “significant”). To cope with these issues, we used an approach quantifying variance components in a mixed model (Equation 3 in Materials and Methods).

Figure 2.

Selection coefficients (s) of the wild-type (REL4548) and mutant strains (REL4548 T63, T103, or T121) measured in the (a) wc/wy, (b) mc/my, (c) my/wc, and (d) mc/wy competitions. Each point represents an s measure estimated from a single competition experiment. s measures are grouped in lines to show the variance between experiments performed at different dates.

Precision of fitness measures

Competition assays provide a direct measure of the fitness of one genotype relative to a competing genotype. To determine if the differences we observed in fitness estimates between replicate competitions was biologically meaningful, as opposed to a sampling effect, we used a mixed model to directly estimate the amount of variation in s (σ_s) beyond sampling error (Equation 3). This approach provides an estimate of average selection intensity ($\stackrel{-}{s}$), a measure of biological heterogeneity in selection among replicates (σ_s), and standard errors associated with these two parameters. Beyond estimating average selection ($\stackrel{-}{s}$) with some precision, it is important to indicate the magnitude of variation in s (σ_s) and the precision reached to estimate it. Table 3 presents these estimates for our 10 competition assays. Estimates of $\stackrel{-}{s}$ (Table 3) range from 0.00088 (T121 YFP) to −0.024 (T103 CFP). Estimates of σ_s range from 0 to 0.0035, with 7 of 10 estimates being greater than zero. In all cases the precision of these estimates is about ±0.0002.

Table 3. Estimation of the mean ($\stackrel{-}{s}$) and standard deviation (σ_s) of genotypic selection coefficients per generation in the different competition assays (code in first column).

$(\times {10}^{-3})$	$\stackrel{-}{s}$	Inf	Sup	SEeq	σs	Inf	Sup	SEeq
Wild type (a)	−4.13	−3.74	−4.53	0.20	0.80	0.25	1.27	0.26
T63 (b)	1.16	1.58	0.74	0.21	0.59	0.00	1.18	0.29
T63 CFP (c)	−12.23	−11.93	−12.63	0.18	3.51	3.20	3.82	0.16
T63 YFP (d)	−8.28	−7.28	−6.28	0.29	1.49	1.02	1.94	0.23
T103 (b)	−6.48	−6.14	−6.81	0.17	0.00	0.00	0.60	0.15
T103 CFP (c)	−24.26	−24.10	−24.82	0.19	2.84	2.52	3.13	0.15
T103 YFP (d)	−15.55	−14.55	−13.55	0.24	1.11	0.71	1.60	0.22
T121 (b)	−3.60	−3.39	−3.80	0.10	0.00	0.00	0.44	0.11
T121 CFP (c)	−6.40	−5.92	−6.87	0.24	1.15	0.75	1.65	0.23
T121 YFP (d)	0.88	1.88	2.88	0.21	0.87	0.35	1.33	0.25

Inf and Sup indicate the inferior and superior support limits of the estimates, respectively. SE_eq gives a measure analogous to standard error and equals (sup − inf)/4. All figures are multiplied by 1000.

The origin of variation in s among replicates

There are four nonexclusive reasons that changes in the frequency of reference and mutant genotypes during competitions could be truly different among replicates: (1) experimental error unrelated to sampling (e.g., pipeting), (2) new mutations occurring in some replicated competitions, (3) drift, and (4) variation in selection intensity among replicates (e.g., due to cryptic environmental variations). We consider each possibility in turn.

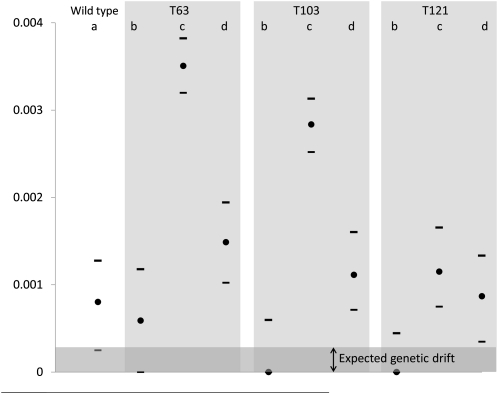
Experimental error is unlikely to be the source of the variation in s in our experiment. We repeated each competition type at four dates and σ_s was consistently low and comparable to the drift expectation in competitions a and b (Figure 3). It is unlikely that systematic error would occur only for some competition types and even more unlikely that this pattern would be repeatable at different dates. The second hypothesis is that new deleterious or beneficial mutations, unrelated to the mutation of interest, may occur during the competition and influence the outcome. The case of deleterious mutations is not really problematic, because they are unlikely to reach high frequency in a large population and because, if many occur, they will occur equally in the two competing genotypes. The case of beneficial mutations may, at first sight, seem trickier. Let us consider a worst-case scenario of the early occurrence of a beneficial mutation providing a growth advantage of 10% per division. If we consider the appearance of this mutant at the very start of the preculture (i.e., ∼17 generations before the start of the competition assay), its frequency at the end of the competition will be <10⁻⁵ (assuming a competition of 6.6 generations and an effective population size of 10⁶ as used in this study), which is too low to have any impact on our measures. Significant frequency variation (above ∼0.02% in our case) would require a mutation to confer a benefit greater than ∼30% (see File S1 for details), which is very unlikely in a strain that has been adapted to the environment for 10,000 generations and for which no such mutations have been identified during the early stages of this adaptation, when fitness increases were most rapid (Barrick et al. 2009). Moreover, even if such large-effect mutations were available to our strains, they would have to occur repeatedly in many competitions because our observed var(s) is not due to isolated outliers (Figure 2). We note that some mutation types, notably genomic amplifications, have been observed to occur at high frequencies and may sometimes confer beneficial effects either directly or indirectly by increasing the mutational target for new mutations to occur. However, if these mutations occur at a very high rate, they would occur in both competitors and thus have a limited effect on var(s). Furthermore, if the occurrence of de novo genomic amplifications were increasing var(s) in our experiments, they should do so in all competition types, and not only in competitions c and d (Figure 3). In summary, we conclude that the rise and spread of new mutations is very unlikely to explain our results.

Figure 3.

Variance in selection coefficients (σ_s estimate bold point ± support limits indicated by bars) of the wild-type (REL4548) and mutant strains (REL4548 T63, T103, or T121) measured in the (a) wc/wy, (b) mc/my, (c) my/wc, and (d) mc/wy competitions. The predicted variation expected by genetic drift alone is represented by the shaded line at the bottom of the figure.

Drift can also cause variation in genotype frequency changes in the different replicates. This process scales with the inverse of population size and should effectively vanish in very large populations. In our experiments, we expect σ_s to be between ${10}^{-4}$and $3\times {10}^{-4}$ if it was due to drift alone (see Materials and Methods). Our estimates of σ_s (Table 3) varied among the competition assays. In competitions a and b, estimates of σ_s were not different from the maximum value that would be expected because of drift ($3\times {10}^{-4}$, Figure 3). These competition assays correspond to CFP vs. YFP competitions within the same genetic background. We thus conclude that the cost of expressing the different fluorescent proteins is not significantly affected by uncontrolled cryptic environmental variation in our experiments. Other estimates of σ_s (in competitions c and d) are much larger than the drift expectation (Figure 3). One possibility is that the effect of drift is greater than expected from consideration of population size alone. This may be the case if there was substantial phenotypic diversity in the competing populations so that a subset of the population contributed disproportionately to population growth. In fact, this explanation seems unlikely. We find a typical value of σ_s of about 0.001, which would require that N_e was reduced to ∼9% of the actual population (from Equation 5) (Figure 3). This means that drift can explain our observed σ_s only if more than 90% of the sampled population is not growing. (In the most extreme case, <1% of the population would have to be growing (T63, competition c). Studies performed on E. coli populations showing that only a few percent of the total population were in an “atypical” nongrowing physiological state during exponential population growth (Balaban et al. 2004; Levin and Rozen 2006) support the conclusion that phenotypic variation is not sufficient to account for variance among replicates in some of our competitions.

In cases where variation is too high to be explained by drift (competitions c and d), variation necessarily implies that selection intensity changes slightly among replicates, perhaps due to environmental variation among replicates. Furthermore, σ_s estimates were larger for large $\left|\stackrel{-}{s}\right|$(Pearson r = 0.69), a situation that would be expected when different competitors have environmental tolerance curves with different slopes (i.e., a G × E effect). In this case environmental variation will not necessary affect both competitors with the same intensity. Thus, small environmental variations across replicated competitions can have a nonnegligible impact on σ_s. Both the high values of σ_s (compared to the drift expectation) and its pattern of variation (larger in assays with large fitness differences) support the conclusion that, even under very controlled and standardized conditions, cryptic environmental variation has a detectable impact on fitness measures.

Fitness transitivity

Population genetic models of selection usually consider fitness effects to be transitive between competing genotypes. In this view, fitness can be associated with a given genotype rather than being defined locally relative to particular competitors. [There are, of course, particular frequency-dependent selection schemes that can generate nontransitive fitness measures (e.g., Sinervo and Lively 1996).] Methodologically, transitivity is also an important assumption in inferring allelic from genotypic fitness effects, as when using a marker to infer the effect of a mutation. Our experimental design allows us to test for departures from transitivity because we measured relative fitness in four combinations of genotypes pairs (see Materials and Methods). Specifically, to test for transitivity, we need to make three estimates for a mutation: (1) the allelic cost of the marker, (2) the allelic effect of the mutation, and (3) the epistasis between both. With three competitions, we have three equations and three unknowns. Thus, adding one competition adds one equation and provides a means to estimate a departure from consistency (i.e., transitivity) among competition types. We found that τ, a parameter measuring deviations from transitivity, was not significantly different from zero for competitions involving the T63 and T121 mutants (LRT; Table 4), meaning that fitness was transitive. By contrast, τ was significantly different from zero for T103, but this departure was quite small (τ = −0.00171 ± 0.0003) and, more importantly, very small compared to the fitness differences measured in those competition assays (Table 4).

Table 4. Estimation of allelic selection coefficients per generation in the different competition assays (the subscript refers to the mutant T63, T103, or T121).

Parameter	Estimate$(\times {10}^{-3})$	SEeq $(\times {10}^{-3})$	Sign.
α	−4.13	0.14	***
β63	−12.27	0.22	***
γ63	5.28	0.22	***
τ63	−0.13	0.30	NS
β103	−17.89	0.22	***
γ103	−2.23	0.22	***
τ103	−1.71	0.30	**
β121	−2.81	0.22	***
γ121	0.55	0.22	*
τ121	−0.48	0.30	NS

α is the cost of the marker (bacteria expressing the fluorescent proteins CFP having a 0.4% cost relative to those expressing YFP). β are the allelic effects of the three random mutations. γ are the epistasis between the random mutations and the marker. τ measures departure from transitive genotypic fitness. SE_eq gives a measure analogous to standard error and is a quarter of the support range. Sign. (significance) indicates whether the estimates are different from zero (LRT). NS, nonsignificant. All figures are multiplied by 1000. *** P-value <0.001; ** P -value <0.01.

Allelic fitness and epistasis

To test for epistasis between our markers and the focal mutations, we decomposed genotypic fitness into the allelic effects of the marker and the mutation and their interaction (epistasis). The expression of CFP was more costly than YFP (a 0.4% difference in the wild type) and the allelic effect of mutations was −1.2%, −1.7%, and −0.3% for T63, T103, and T121, respectively (Table 4). However, we detected significant differences between fitness effects of the same mutations when measured in the CFP and YFP backgrounds, indicating the existence of epistasis between the marker and the three individual mutations. Even though the strength of epistatic interactions was quite small, it could represent an important part of the genotypic selection coefficients. For instance, for T63, epistasis was larger than the cost of the marker and represented 43% of the allelic mutational effect. For the two other mutations, the quantitative importance of epistasis was much smaller. A caveat to our interpretation of epistasis is that it is possible that we inadvertently introduced secondary mutations into genotypes during some step required for strain construction (see Materials and Methods). Since we observed fitness differences with the three mutants we tested, the hypothesis of secondary mutation introduction supposes a very high rate of such mutations during P1 transduction.

Discussion

In a large population, even mutations with very small fitness effects can play a role in the process of adaptation. However, studying them empirically is a significant practical challenge. Measurement error and drift obviously limit the precision of fitness measures that can be obtained experimentally. Is it possible to measure selection up to a limit imposed by the noise produced by sampling error and drift? If not, how close to this limit can we go? We addressed these questions by performing competition experiments in large E. coli populations (to minimize drift) and by tracking frequency changes using flow cytometry to count marked cells (to minimize sampling error).

Our experiments are based on short-term batch cultures (6.6 generations). This design has several convenient features. First, it is a relatively simple experimental set-up that can be massively replicated. Second, it reduces, although does not eliminate, the complication of newly arising mutations. Third, it entirely accounts for the effect of the marker. Finally, it avoids the complication of using time series data.

Cryptic variation in s

A surprising, and we think important, result was that, for some competitions types, selection was variable across replicates, probably because of cryptic environmental variation to which the competing genotypes had different sensitivity. Although not empirically excluded, the alternative hypothesis that variation in estimates of s was caused by beneficial mutations spreading in a large number of the batch cultures, seems unlikely for two reasons: (1) such mutations would have to confer a very large benefit (unlikely to appear in a strain that has evolved in the same environment for 10,000 generations) and (2) adaptive mutations would increase var(s) in all competition types, not only in competitions c and d. Such variation arose despite considerable effort to perform all competitions in precisely controlled conditions. In an absolute sense, this variation was not large (although much larger than our precision), but it supports the idea that the effect of mutations can be strongly context dependent. For instance, it is possible that if our experiment was performed in a different lab, the $\stackrel{-}{s}$ and σ_s might be slightly different (because of differences in the average environment or in the magnitude of microenvironmental fluctuations, respectively). A fortiori, we expect σ_s to be even larger under environmentally heterogeneous natural conditions. These observations raise the question of whether selection coefficients should be described by only their mean values $\stackrel{-}{s}$, or more appropriately by distributions (with two parameters $\stackrel{-}{s}$ and σ_s), and consequently if mutations are appropriately described as beneficial, neutral, or deleterious, since their effects are context dependent, even within controlled laboratory environments. So far, population genetic models do not typically consider that s values are distributed, such that one mutation can have very different fates depending on its σ_s. For instance, the probability of fixation of a mutation with $\stackrel{-}{s}$ = 0 and σ_s > 0 will not be driven by drift only, as described by the neutral theory, but will depend on the environmental pattern responsible for σ_s > 0 (see, e.g., Ewens 1979). In any case, much more attention should be paid to variable selection coefficients and their evolutionary impact. The experimental design and statistical analysis we propose here offers an efficient and new approach to doing that.

Epistasis with the marker

In competition experiments with microbes, the neutrality of the marker is always verified; however, the potential epistatic interactions between the marker and mutations is not usually systematically investigated. Controlling for this issue requires switching the markers between backgrounds [to perform complementary competition assays (Dykhuizen and Hartl 1980)] and a high level of precision. We found epistatic interactions between the inserted mutations and the fluorescent marker in all cases, suggesting that epistatic effects, although perhaps very small, may be common. Such interactions complicate measures of s because they require separating the MFE from the marker cost and the epistatic interactions between them. We note that if we had found that epistatic effects were of a similar size to (or larger than) the allelic effects it would have raised the concern that the compared strains may not have been isogenic. This was not the case in our experiment; nevertheless, we cannot formally exclude the possibility that transformation and P1 transduction manipulations did not introduce any secondary mutations.

Transitivity

The assumption of fitness transitivity is made in most population genetic models that do not specifically include social effects or frequency dependence. This assumption has been evaluated on several occasions and in different organisms (Richmond et al. 1975; Goodman 1979; Paquin and Adams 1983; De Visser and Lenski 2002; Bell 2008). The main conclusion is that fitness tends to be transitive unless special social interactions are present. Like for any “null hypothesis,” it is, however, important to realize that the statistical power of an experiment gives an inherent limit to the detectable departure of transitivity. In our experiment, we tested this hypothesis and did not find consequential departures from transitivity in the genotypic fitness measures (Table 4). Given our high statistical power, this finding represents a strong internal check that our experimental results are robust. The fact that fitness effects are transitive is also an important result in simplifying experiments: without the need to check for transitivity, only three types of competition need to be performed to estimate allelic effects and epistasis (instead of four in our design).

Precision of fitness measures and the statistics of selection

Although sampling error and drift can make it difficult to measure small fitness effects, replicated measures will tend not to significantly differ from each other. Consequently, a single fitness value can be legitimately attributed to a given genotype in a given environment and the precision of this estimate can be determined as the standard error of the mean fitness effect across replicates. New high-throughput counting methods alleviate limits due to sampling error and drift. Here, we show that such methods can reveal that replicated measures differ from one another for a given genotype in a given environment—i.e., that var(s) is significantly greater than the value expected by drift and sampling error alone. This situation challenges the simple concept of precision mentioned above. When confronted with this problem, one approach is to do “as usual” and neglect the observation that replicates differ. In this case, providing only a mean fitness effect and its standard error do not reflect the actual precision of the experiment. In particular, it fails to acknowledge that replicates may differ beyond this standard error. The second approach is to admit that replicates actually differ and represent different draws in a distribution of fitness effects, even if the environment is supposed constant. If selection coefficients are distributed, it is thus necessary to measure the mean effect, but also the variance, and possibly higher moments (skewness, kurtosis, etc.) of the distribution of s values. The concept of precision in this case must incorporate estimates of these moments and their standard errors. This is the approach we have taken, introducing the use of a mixed model that allowed us to decompose sources of variation in frequency change (sampling error, drift, environmental variation of s).

We measure fitness on the basis of frequency change as in classical population genetics (Dykhuizen and Hartl 1980; Arnason and Barker 1999), which differs from common practices in experimental evolution (Chevin 2010), where fitness is measured as a ratio of growth rates (e.g., Lenski et al. 1991). We also fully use the information on the individual precision of fitness estimates (determined by the sampling effort: the number of colonies counted when plating, or the number of cells counted with flow cytometry), which is not usually reported with fitness competition experiments. Thus, we can discriminate between sampling error and other sources of variance across replicates (due to drift, variance in s, etc.), which greatly enhances the information that can be extracted from the data. By considering these factors, we were able to measure mean and variance in selection coefficients down to a precision of 0.02% (Tables 3 and 4). Regarding mean selection, this precision represents a ∼10-fold improvement over typical studies using flow cytometry (Lunzer et al. 2002; Ali and Yang 2006; Lee et al. 2009) and is comparable to the precision reached in Zhu et al. (2005). More importantly, as explained above, the massive replication we used also provides a precise measure of the variance of selection coefficient σ_s (±0.02%).

Neutralist vs. selectionist

The neutral theory of molecular evolution proposes that the fate of many mutations is governed by the effect of drift (Kimura 1983). The development of precise fitness measures was used in the neutralist/selectionist controversy on proteins to determine if allozymes differed in terms of selection (Dykhuizen and Hartl 1980). Today, this debate has shifted toward smaller fitness effects at the molecular level (Kreitman 1996; Nei 2005). The analysis of sequence polymorphism provides different indirect ways to confront neutralist vs. selectionist expectations. For most mutations, it is usually thought that there is no alternative to resolving this question. Measuring s with ever-increasing precision may start to change this perspective and may help to answer some of the key questions fueling this debate. As we have already seen in our study, mutations formerly considered as neutral (albeit in a slightly different medium, DM25 in Elena et al. 1998) actually confer small, but significant, fitness effects. Importantly, even in an apparently constant environment, their effect is best understood as being distributed, which complicates straightforward application of discrete classifications (deleterious/neutral/beneficial), and which would have to be accounted for in theoretical expectations, e.g., for the analysis of sequence polymorphism.

Sampling error, de novo beneficial mutations, and drift introduce elements of chance into fitness competitions, which can limit our ability to measure very small fitness effects. The effect of these factors can, however, be reduced. Sampling error can be dramatically decreased using flow cytometry, and the problem of the occurrence of new beneficial mutations and of drift is reduced by using very short-term batch cultures and high replication. However, a remaining issue is the variation in selection due to microenvironmental variation across replicated cultures. While this would not be surprising if replicate measurements had been obtained from different environments (e.g., Remold and Lenski 2001), that was not the case in our experiment in which all competitions were carried out in an environment that was kept as consistent as possible. Increased sampling effort, larger population sizes, or longer lasting experiments are not likely to resolve this issue. It is thus unclear how far precision in fitness measurement can be improved. It all relies on understanding the sources of variation, and controlling them, whenever possible. Would it be possible to measure the fitness effects of synonymous mutations or mutations occurring in noncoding sequences? We cannot answer these questions yet; however, our method is a step in that direction and it will certainly help to bridge the gap between studies measuring s experimentally and studies inferring s from genetic sequences (see Eyre-Walker and Keightley 2007 for review).