Stochastic Model of an Influenza Epidemic with Drug Resistance

Abstract

A continuous-time Markov chain (CTMC) model is formulated for an influenza epidemic with drug resistance. This stochastic model is based on an influenza epidemic model, expressed in terms of a system of ordinary differential equations (ODE), developed by Stilianakis et al. (1998). Three different treatments - chemoprophylaxis, treatment after exposure but before symptoms, and treatment after symptoms appear, are considered. The basic reproduction number, , is calculated for the deterministic model under different treatment strategies. It is shown that chemoprophylaxis always reduces the basic reproduction number. In addition, numerical simulations illustrate that the basic reproduction number is generally reduced with realistic treatment rates. Comparisons are made among the different models and the different treatment strategies with respect to the number of infected indivduals during an outbreak. The final size distribution is computed for the CTMC model and, in some cases, it is shown to have a bimodal distribution corresponding to two situations: when there is no outbreak and when an outbreak occurs. Given an outbreak occurs, the total number of cases for the CTMC model is in good agreement with the ODE model. The greatest number of drug resistant cases occurs if treatment is delayed or if only symptomatic individuals are treated.

1 Introduction

Antiviral drug resistance is an important concern in public health. The emergence and spread of drug resistance leads to treatment failure, limits the effectiveness of subsequent treatments, and results in the evolution of more virulent strains. In the past few years, many studies have focused on this topic (Austin and Anderson, 1999; Blower and Volberding, 2002; Blower and Chou, 2004; Blower et al., 1998; Blower and Gerberding, 1998; Blower et al., 2005; Ferguson et al., 2003; Hayden, 2001; Hayden, 2006; Levin et al., 1999; Levin et al., 2004; Longini Jr. et al., 2005; Moscona, 2005; Regoes and Bonhoeffer, 2006; Sánchez et al., 2005; Stilianakis et al., 1998). Some of these studies investigated drug resistance in tuberculosis (Blower and Chou, 2004; Blower and Gerberding, 1998), some in HIV (Blower and Volberding, 2002; Blower et al., 2005; Sánchez et al., 2005), and some in HSV-2 (Blower et al., 1998). In addition, there have been studies on the development of drug resistance during influenza epidemics (Ferguson et al., 2003; Hayden, 2001; Hayden, 2006; Longini Jr. et al., 2005; Moscona, 2005; Regoes and Bonhoeffer, 2006; Stilianakis et al., 1998). Much of this work has emphasized the importance of mathematical models to gain further insight into the development of drug resistance.

Antiviral drugs such as amantadine and rimantadine (M2 protein inhibitors) have been used for influenza A prevention and control. Such treatments are about 80% to 90% effective at preventing infection, and can reduce the duration of the flu by about one to five days, if given within 48 hours of infection (Bright et al., 2005). However, drug-treated persons infected with influenza may shed resistant viruses within five to seven days after treatment (CDC, 2005). Recently, high levels of resistance to amantadine and rimantadine have been detected among influenza A viruses. It has been shown that resistance to amantadine and rimantadine increased from 0.4% in 1994–1995 to 12.3% in 2003–2004 among circulating influenza viruses collected worldwide between October 1994 and March 2005 (Bright et al., 2005; CDC, 2006). In another U.S. study conducted from October through December 2006, 92.3% of influenza A (H3N2) viruses isolated from 209 patients showed a change in an amino acid known to be correlated with adamantine resistance (Bright et al., 2006). Currently, both of these drugs are not recommended (CDC, 2006). Other antiviral drugs, such as the neuraminidase inhibitors zanamivir and oseltamivir, are currently recommended (CDC, 2006). Only oseltamivir has been approved for prophylaxis but both zanamivir and oseltamivir are effective (84% and 82%, respectively) at preventing infection (Harper et al., 2005). However, recent studies have shown development of drug resistance in patients infected with influenza A when treated with oseltamivir, 18% of children infected with the H3N2 virus (Kiso et al., 2004) and 2 out of 8 patients infected with the H5N1 virus (de Jong et al., 2005). Studies on oseltamivir resistance are under investigation (CDC, 2006; Moscona, 2005).

Vaccination is a major preventive strategy in the control of influenza A but is not considered in this investigation. Instead we concentrate on the effectiveness of antiviral treatment and the development of drug resistance in a small community of susceptible individuals.

There are three major antiviral treatment strategies for influenza classified according to the time at which the treatments are given. These three strategies are chemoprophylaxis, drug treatment after exposure but before symptoms appear, and drug treatment after symptoms appear. Chemoprophylaxis is treatment with a drug to prevent the development of the disease and is given prior to exposure. The effectiveness of these three treatment strategies are studied using a susceptible-infected-recovered (SIR) model for an influenza epidemic.

A variety of models have been developed to study the dynamics of an influenza epidemic or pandemic (Ferguson et al., 2005; Ferguson et al., 2006; Ferguson et al., 2003; Germann et al., 2006; Levin et al., 2004; Longini Jr. et al., 2005; Regoes and Bonhoeffer, 2006; Stilianakis et al., 1998). Some of these models consider drug resistance as a major factor in the epidemic process (Ferguson et al., 2003; Regoes and Bonhoeffer, 2006; Stilianakis et al., 1998). Other models have been applied to large scale pandemics with spatially explicit dynamics and require extensive computer simulations (Ferguson et al., 2005; Ferguson et al., 2006; Germann et al., 2006; Longini Jr. et al., 2005). These latter models are either fully stochastic (Germann et al., 2006; Longini Jr. et al., 2005) or include random contacts (Ferguson et al., 2005; Ferguson et al., 2006). The small scale stochastic dynamics of an influenza epidemic have not been studied in these models.

In this investigation, we apply the deterministic SIR model developed by Stilianakis, Perelson, and Hayden (1998) and a continuous-time Markov chain (CTMC) model, to study how the epidemic progresses under different treatment strategies. The effectiveness of the three antiviral treatment strategies are compared in the deterministic and stochastic models. The basic reproduction number, , is computed when there is no treatment and compared to the reproduction numbers when there is treatment. In the numerical examples, we show that the basic reproduction number is reduced with treatment. Because the general form of with treatment involves a large number of parameters, it is difficult to determine whether all treatment strategies reduce . Extensive numerical examples illustrate some of the differences between the deterministic and stochastic models. The final size distribution is computed for the CTMC model. In some cases, it is shown to have a bimodal distribution corresponding to two situations: outbreak or no outbreak. Given an outbreak occurs, the total number of cases for the CTMC model are compared to the deterministic model.

2 Description of Models

Two models, a deterministic model and a stochastic model are described. The deterministic model is a system of ordinary differential equations (ODE) originally developed by Stilianakis et al. (1998) for the development of drug resistance during treatment for influenza during an outbreak. This deterministic model serves as the basis for development of a stochastic model, a CTMC model. The CTMC model includes variability due to birth, death, transmission, and recovery processes.

2.1 Deterministic Model

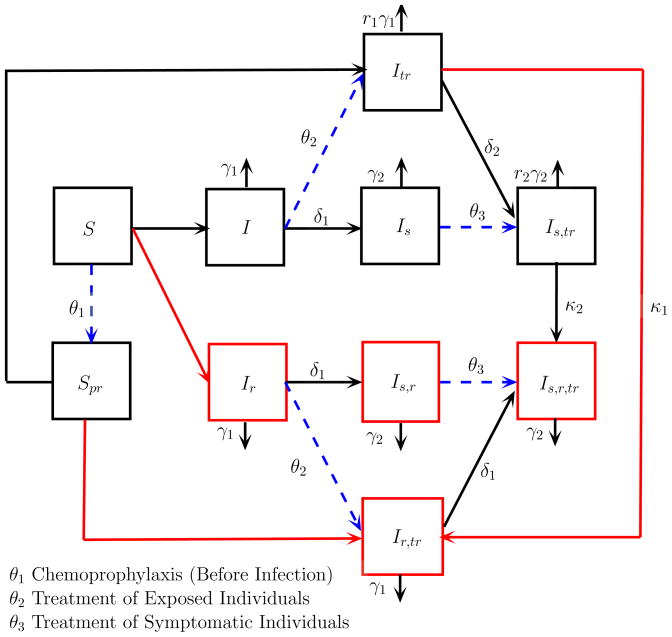
The influenza model developed by Stilianakis et al. (1998) is an SIR model, where the total population size is assumed to be constant. Figure 1 is a compartmental diagram illustrating the transmission dynamics among the susceptible and infected states. The recovered state is not included in this diagram.

Figure 1.

A Compartmental Diagram of an SIR Influenza Model with Drug Therapy

The model includes two susceptible states, eight infected states, and one recovered state. The susceptible and infected states are further subdivided according to whether individuals are asymptotic or symptomatic, treated or untreated, and resistant or sensitive to the drugs. Subscripts on the variables identify the particular subtype. The susceptible individuals are divided into S = susceptible persons not taking drugs and S_pr = susceptible persons taking drugs prophylactically. The infected individuals are divided into I = infected untreated persons, I_s = infected untreated persons who develop clinical symptoms, I_r = infected untreated asymptomatic persons who shed drug-resistant virus, I_s,r = infected untreated persons with clinical symptoms who shed drug-resistant virus, I_tr = infected treated asymptomatic persons, I_s,tr = infected treated persons who develop clinical symptoms, I_r,tr = infected treated asymptomatic persons who shed drug-resistant virus, and I_s,r,tr = infected treated persons with clinical symptoms who shed drug-resistant virus.

The parameters in this diagram indicate transition rates between compartments. For example, γ_i is the recovery rate for asymptomatic (i = 1) and symptomatic (i = 2) individuals. Recovery is faster for drug-sensitive individuals after treatment, r₁γ₁ and r₂γ₂, where

$$r_i>1,i=1,2.$$ (2.1)

The transmission rate depends on the type of infection. The rate of transmission from an asymptomatic infected person to a susceptible person is β₁SI and the rate of transmission from a symptomatic infected person to a susceptible person is β₂SI_s. A mass action transmission rate is assumed. However, because the population size is constant (≡ N), this assumption is equivalent to the more commonly used standard transmission rate, where β₁ and β₂ are replaced by λ₁/N and λ₂/N, respectively. Transmission is reduced if either susceptible or infected individuals have been treated. If the susceptible individuals have been given prophylaxis, then the transmission rate is p₂β₁S_prI and p₂β₂S_prI_s, 0 < p₂ < 1. If the infected individuals have been treated, then the transmission rate is p₁β₁SI_tr and p₁β₂I_s,tr, 0 < p₁ < 1. Finally, if both susceptible and infected individuals have been treated, then the transmission rate is p₃β₁S_prI_tr and p₃β₂S_prI_s,tr, 0 < p₃ < 1. In general, p₃ < p₂ < p₁. Furthermore, β_1,r and β_2,r are transmission rates between susceptible and infected individuals that are drug resistant. Generally, due to a “cost of resistance”,

$${\beta }_{1,r}\le {\beta }_1\text{and}{\beta }_{2,r}\le {\beta }_2.$$ (2.2)

The parameter δ₁ describes the rate at which symptoms develop, I becomes I_s, I_r becomes I_s,r, and I_r,tr becomes I_s,r,tr, whereas the transition rate from I_tr to I_s,tr is δ₂. It takes a longer period of time to develop symptoms after treatment; therefore,

$${\delta }_1>{\delta }_2.$$ (2.3)

Parameters κ₁ and κ₂ are the rates of developing drug resistance during treatment (due to treatment failure) either before (κ₁) or after symptoms develop (κ₂), κ₁ < κ₂. Three different types of treatment strategies are considered, chemoprophylaxis (treatment of susceptible individuals prior to exposure), treatment after exposure but before symptoms, and treatment after symptoms appear. The per capita rate of these three treatment strategies is θ_i, i = 1, 2, 3.

Stilianakis et al. (1998) state that for small closed populations, treatment of individuals who show clinical symptoms would not have an important effect on the epidemic process (third treatment strategy). They argued that chemoprophylaxis reduces the risk of infection and therefore, emergence of drug resistance was expected to be low in this case. They also concluded that if chemoprophylaxis was combined with the treatment after symptoms appear, then this combination would lead to a result similar to chemoprophylaxis treatment itself.

Stilianakis et al. (1998) analyzed a flu outbreak in a closed population, such as a school or nursing home in which the total population size remains constant; and thus assumed that there are no births and deaths during the epidemic. But for the pandemic situation, which could be longer and include more individuals, the assumption of a closed population is not applicable. In addition to births and deaths, there may be immigration and emigration. Based on this consideration, we include births (immigration) and deaths (emigration) in the SIR epidemic model. Births are assumed to occur at a constant rate Λ and deaths at a per capita rate μ. If Λ and μ are small relative to the time scale, then these demographic parameters have little effect on the outcome. The SIR model with births and deaths takes the following form:

$$\begin{array}{l}\frac{ds}{dt}=\mathrm{\Lambda }-({\beta }_{1}I+{\beta }_2{I}_s+{\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S-({\theta }_1+\mu )S\\ \frac{{dS}_{pr}}{dt}=-(p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+{\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}+{\theta }_{1}S-\mu S_{pr}\\ \frac{dI}{dt}=({\beta }_{1}I+p_1{\beta }_1{I}_{tr}+{\beta }_2{I}_s+p_1{\beta }_2{I}_{s,tr})S-({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I\\ \frac{{dI}_s}{dt}={\delta }_{1}I-({\gamma }_2+{\theta }_3+\mu )I_s\\ \frac{{dI}_r}{dt}=({\beta }_{1,r}{I}_r+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r}+{\beta }_{2,r}{I}_{s,r,tr})S+({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}-({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I_r\\ \frac{{dI}_{s,r}}{dt}={\delta }_1{I}_r-({\gamma }_2+{\theta }_3+\mu )I_{s,r}\\ \frac{{dI}_{tr}}{dt}=(p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr})S_{pr}-(r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu )I_{tr}+{\theta }_{2}I\\ \frac{{dI}_{s,tr}}{dt}={\delta }_2{I}_{tr}-(r_2{\gamma }_2+{\kappa }_2+\mu )I_{s,tr}+{\theta }_3{I}_s\\ \frac{{dI}_{r,tr}}{dt}=({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}-({\gamma }_1+{\delta }_1+\mu )I_{r,tr}+{\kappa }_1{I}_{tr}+{\theta }_2{I}_r\\ \frac{{dI}_{s,r,tr}}{dt}={\delta }_1{I}_{r,tr}-({\gamma }_2+\mu )I_{s,r,tr}+{\kappa }_2{I}_{s,tr}+{\theta }_3{I}_{s,r}\\ \frac{dR}{dt}={\gamma }_1(I+I_r+I_{r,tr})+{\gamma }_2(I_s+I_{s,r}+I_{s,r,tr})+r_1{\gamma }_1{I}_{tr}+r_2{\gamma }_2{I}_{s,tr}-\mu R\end{array}$$

This model is used as a basis for formulating the stochastic model.

2.2 Continuous-Time Markov Chain Model

Based on the preceding deterministic model, we develop a CTMC model, where time is continuous and the class variables are discrete. Considering time t as a continuous variable, where t ∈ [0, ∞), and according to the population classification in the deterministic model, we define the random vector

$$\overrightarrow{X}(t)={(S(t),S_{pr}(t),I(t),I_s(t),I_r(t),I_{s,r}(t),I_{tr}(t),I_{s,tr}(t),I_{r,tr}(t),I_{s,r,tr}(t),R(t))}^T$$

and ΔX⃗(t) = X⃗(t + Δt) − X⃗(t). The probability of a transition is

$$\text{Prob}\{\mathrm{\Delta }\overrightarrow{X}(t)=(a,b,c,d,e,f,g,h,i,j,l)\mid \overrightarrow{X}(t)\}.$$ (2.4)

We assume that Δt is sufficiently small so that the values of a, b, c, …, l take on the values ±1 or 0. At most one change occurs during the time interval Δt. There are 36 possible changes in states, where at least one of the a, b, c, …, l is nonzero. From the deterministic model, it is straightforward to write down the infinitesimal transition probabilities. The transition probabilities (2.4) are described according to the changes in each of the states, ΔS(t), ΔS_pr(t), ΔI(t), etc. We assume the change in state is zero unless otherwise indicated and, for simplicity, the t dependence in the functions is omitted, e.g., S and I instead of S(t), I(t). For example, a change in the susceptible class, ΔS = a, can be due to a birth, a = 1, an infection from contact with infected drug-sensitive individuals, a = −1 and ΔI = c = 1, an infection from contact with infected resistant individuals, a = −1 and ΔI_r = e = 1, chemoprophylaxis, a = −1 and ΔS_pr = b = 1, or a death, a = −1. The corresponding probabilities associated with these changes are

$$\begin{array}{l}\text{Prob}\{\mathrm{\Delta }S=1\mid \overrightarrow{X}\}=\mathrm{\Lambda }\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ \text{Prob}\{(\mathrm{\Delta }S,\mathrm{\Delta }I)=(-1,1)\mid \overrightarrow{X}\}=({\beta }_{1}I+{\beta }_2{I}_s+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ \text{Prob}\{(\mathrm{\Delta }S,\mathrm{\Delta }{I}_r)=(-1,1)\mid \overrightarrow{X}\}=({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ \text{Prob}\{(\mathrm{\Delta }S,\mathrm{\Delta }{S}_{pr})=(-1,1)\mid \overrightarrow{X}\}={\theta }_{1}S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ \text{Prob}\{\mathrm{\Delta }S=-1\mid \overrightarrow{X}\}=\mu S\mathrm{\Delta }t+o(\mathrm{\Delta }t).\end{array}$$

The transition probabilities for the 36 possible changes in state are defined below:

$$\{\begin{array}{ll}\mathrm{\Lambda }\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & a=1\hfill \\ ({\beta }_{1}I+{\beta }_2{I}_s+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & a=-1,c=1\hfill \\ ({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & a=-1,e=1\hfill \\ {\theta }_{1}S\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & a=-1,b=1\hfill \\ \mu S\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & a=-1\hfill \\ (p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & b=-1,g=1\hfill \\ ({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & b=-1,e=1\hfill \\ ({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & b=-1,i=1\hfill \\ \mu S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & b=-1\hfill \\ {\gamma }_{1}I\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & c=-1,l=1\hfill \\ {\delta }_{1}I\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & c=-1,d=1\hfill \\ {\theta }_{2}I\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & c=-1,g=1\hfill \\ \mu I\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & c=-1\hfill \\ {\gamma }_2{I}_s\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & d=-1,l=1\hfill \\ {\theta }_3{I}_s\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & d=-1,h=1\hfill \\ \mu I_s\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & d=1\hfill \\ {\gamma }_1{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & e=-1,l=1\hfill \\ {\delta }_1{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & e=-1,f=1\hfill \\ {\theta }_2{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & e=-1,i=1\hfill \\ \mu I_r\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & e=-1\hfill \\ {\gamma }_2{I}_{s,r}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & f=-1,l=1\hfill \\ {\theta }_3{I}_{s,r}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & f=-1,j=1\hfill \\ \mu I_{s,r}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & f=-1\hfill \\ r_1{\gamma }_1{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & g=-1,l=1\hfill \\ {\delta }_2{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & g=-1,h=1\hfill \\ {\kappa }_1{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & g=-1,i=1\hfill \\ \mu I_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & g=-1\hfill \\ r_2{\gamma }_2{I}_{s,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & h=-1,l=1\hfill \\ {\kappa }_2{I}_{s,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & h=-1,j=1\hfill \\ \mu I_{s,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & h=-1\hfill \\ {\gamma }_1{I}_{r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & i=-1,l=1\hfill \\ {\delta }_1{I}_{r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & i=-1,j=1\hfill \\ \mu I_{r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & i=-1\hfill \\ {\gamma }_2{I}_{s,r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & j=-1,l=1\hfill \\ \mu I_{s,r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & j=-1\hfill \\ \mu R\mathrm{\Delta }t+o(\mathrm{\Delta }t),\hfill & l=-1\hfill \end{array}$$

These transition probabilities completely define the CTMC model. Sample paths, mean values, and the final size distribution of the CTMC model are compared to the solution of the ODE model in section 4.

An Itô stochastic differential equation (SDE) model can be formulated based on the transition probabilities defined for the CTMC model (Allen, 2007; Allen, 1999; Allen, 2003; Kirupaharan and Allen, 2004), e.g.,

$$d\overrightarrow{X}(t)=\overrightarrow{f}(\overrightarrow{X}(t))dt+D(\overrightarrow{X}(t))d\overrightarrow{W}(t),$$ (2.5)

where f⃗(X⃗(t)) is the drift vector, D(X⃗(t)) is the diffusion matrix, and W⃗(t) is a vector of independent Wiener processes. For large population sizes and large number of infected individuals, the dynamics of the SDE model follow closely those of the CTMC model. The SDE formulation is described briefly in the Appendix. We do not apply the SDE model here because in most of the numerical simulations, only one initial infected individual is introduced into a population of size 400. However, we found that the mean of the SDE model agrees well with the mean of the CTMC model and the ODE model (< 3% difference in number of symptomatic cases with no treatment) when the initial number of infected individuals is ≥ 10 in a population of size 400 or ≥ 5 in a population of size 800.

3 Basic Reproduction Number

In the study of infectious diseases, one of the most interesting questions is whether the disease will invade the population. The basic reproduction number, generally denoted , is a parameter used to determine whether the disease will invade. The basic reproduction number is defined as the number of secondary infections caused by one infected individual in an entirely susceptible population (Hethcote, 2000). It is one of the most important parameters in epidemiology. If < 1, then the disease-free equilibrium (DFE) is locally asymptotically stable and there is no disease outbreak, but if > 1, then the DFE is unstable and an outbreak occurs.

The basic reproduction number is useful in predicting outbreaks in stochastic models as well. For example, in the case of a simple CTMC SIR epidemic model with I(0) initial infected individuals, the basic reproduction number provides an estimate for the probability of an outbreak (Allen, 2003; Bailey, 1975),

$$1-{\left(\frac{1}{{\mathcal{R}}_0}\right)}^{I(0)}.$$ (3.6)

There is no outbreak with probability (1/ )^I(0). Hence, the final size distribution of the epidemic may be bimodal, with one mode at zero when there is no outbreak and the other mode centered at the average number of cases when there is an outbreak (Bailey, 1953; Ludwig, 1975). Eventually, however, the epidemic dies out because I ≡ 0 is an absorbing state.

The basic reproduction number is calculated for the deterministic model under various treatment strategies. Although extensive numerical simulations were performed in Stilianakis et al. (1998), the basic reproduction number and treatment reproduction numbers were not computed. The effect of treatment, θ_i > 0, on the reduction of is examined in section 4.

To compute the basic reproduction number we apply a method known as the next generation approach (Diekmann et al., 1990; van den Driessche and Watmough, 2002). In this method it is necessary to compute the DFE. For the deterministic model, it is straightforward to verify that there are two disease-free equilibria for this system. If θ₁ = 0, i.e., no prophylaxis, then the DFE is S̄ = Λ/μ with all other states zero, and if θ₁ ≠ 0, then the DFE is

$$\overline{S}=\frac{\mathrm{\Lambda }}{\mu +{\theta }_1},{\overline{S}}_{pr}=\frac{\mathrm{\Lambda }{\theta }_1}{\mu (\mu +{\theta }_1)},$$ (3.7)

and all other states zero. If Λ = 0 = μ as in the original model of Stilinakis et al. (1998), the DFE depends on the initial population size. If the initial population size is K, Λ = 0 = μ, and θ₁ = 0, then the DFE is S̄ = K with all other states zero, but if θ₁ ≠ 0, the DFE is S̄ = 0, S̄_pr = K, and all other states zero.

In the next generation approach, the system of ODEs is decomposed into two vector components 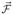and 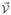, with only the eight infective states included. The element 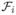is 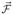is the rate of appearance of new infections in infective state i. For vector 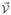, let ${\mathcal{V}}_{\text{i}}^{+}$ be the rate of transfer of individuals into infective state i by methods other than transmission and ${\mathcal{V}}_i^{-}$ be the rate of transfer of individuals out of infective state i. Then the element 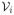in 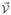is defined as ${\mathcal{V}}_i^{-}-{\mathcal{V}}_{\text{i}}^{+}$ (van den Driessche and Watmough, 2002). Next, the Jacobian matrices for 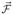and 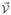are calculated and evaluated at the DFE. Jacobian matrices F and V are obtained,

$$F=\left(\frac{\partial {\mathcal{F}}_i}{\partial x_j}\right)\text{and}V=\left(\frac{\partial {\mathcal{V}}_i}{\partial x_j}\right).$$

Then is the spectral radius of the matrix FV⁻¹, denoted as

$${\mathcal{R}}_0=\rho ({FV}^{-1}).$$

In the next section, the value of is computed in the general case when all three treatments are applied.

3.1 General Form for

The expression for is related to the treatment parameters θ_i, i = 1, 2, 3. Suppose θ_i ≠ 0, i = 1, 2, 3, and the DFE for the case Λ ≠ 0 ≠ μ is given by (3.7), where, for simplicitly, we let K₁ and K₂ denote

$$\overline{S}=K_1=\frac{\mathrm{\Lambda }}{\mu +{\theta }_1},{\overline{S}}_{pr}=K_2=\frac{\mathrm{\Lambda }{\theta }_1}{\mu (\mu +{\theta }_1)}$$ (3.8)

and K₁ + K₂ = K = Λ/μ. If Λ= 0 = μ, then K₁ = 0 and K₂ = K.

To simplify the computation, we rearrange the order of the eight infected states in the ODE system as follows: I, I_r, I_tr, I_r,tr, I_s, I_s,r, I_s,tr, and I_s,r,tr. The vectors 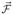and 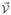corresponding to these eight states are

$$\overrightarrow{\mathcal{F}}=\left(\begin{array}{c}({\beta }_{1}I+p_1{\beta }_1{I}_{tr}+{\beta }_2{I}_s+p_1{\beta }_2{I}_{s,tr})S\\ ({\beta }_{1,r}{I}_r+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r}+{\beta }_{2,r}{I}_{s,r,tr})S+({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}\\ (p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr})S_{pr}\\ ({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}\\ 0\\ 0\\ 0\\ 0\end{array}\right)$$ (3.9)

and

$$\overrightarrow{\mathcal{V}}=\left(\begin{array}{c}({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I\\ ({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I_r\\ (r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu )I_{tr}-{\theta }_{2}I\\ ({\gamma }_1+{\delta }_1+\mu )I_{r,tr}-{\kappa }_1{I}_{tr}-{\theta }_2{I}_r\\ ({\gamma }_2+{\theta }_3+\mu )I_s-{\delta }_{1}I\\ ({\gamma }_2+{\theta }_3+\mu )I_{s,r}-{\delta }_1{I}_r\\ (r_2{\gamma }_2+{\kappa }_2+\mu )I_{s,tr}-{\delta }_2{I}_{tr}-{\theta }_3{I}_s\\ ({\gamma }_2+\mu )I_{s,r,tr}-{\delta }_1{I}_{r,tr}-{\kappa }_2{I}_{s,tr}-{\theta }_3{I}_{s,r}\end{array}\right).$$ (3.10)

Jacobian matrices F and V are given in the Appendix. Because of the zeros in 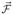, matrix FV⁻¹ simplifies. The last four rows are all zeros and the spectral radius of FV⁻¹ can be computed from a 4 × 4 submatrix, M₄, defined in the Appendix. Hence,

$${\mathcal{R}}_0=\rho ({FV}^{-1})=\rho (M_4).$$

3.2 No Treatment

When there is no treatment, θ_i = 0 (i = 1, 2, 3) in the deterministic model. In this case, the DFE is S̄ = K with all other states zero, and the rates of generating new infections only appear in compartments I and I_r since S̄_pr = 0. Vectors 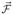and 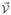include the transfer rates from the eight infective states. In this case, only the first two rows of 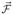are nonzero (see (3.9)) and 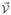is given by (3.10). Computing Jacobian matrices F and V lead to a matrix F with only the first two rows nonzero and a matrix V with the same form as in the general formulation given in the Appendix. Therefore, the spectral radius of FV⁻¹ is determined by the following 2×2 submatrix,

$$M_2=\left(\begin{array}{cc}\frac{{\beta }_{1}K}{{\gamma }_1+{\delta }_1+\mu }+\frac{{\beta }_{2}K{\delta }_1}{({\gamma }_1+{\delta }_1+\mu )({\gamma }_2+\mu )}& 0\\ 0& \frac{{\beta }_{1,r}K}{{\gamma }_1+{\delta }_1+\mu }+\frac{{\beta }_{2,r}K{\delta }_1}{({\gamma }_1+{\delta }_1+\mu )({\gamma }_2+\mu )}\end{array}\right)$$

so that = ρ(FV⁻¹) = ρ (M₂). Because of the relations given in (2.2), it follows that

$${\mathcal{R}}_0=\frac{{\beta }_{1}K}{{\gamma }_1+{\delta }_1+\mu }+\frac{{\beta }_{2}K{\delta }_1}{({\gamma }_1+{\delta }_1+\mu )({\gamma }_2+\mu )}.$$ (3.11)

The basic reproduction number is the sum of two terms. The first term is due to infections from the asymptotic class I and the second term from infections in the symptomatic class I_s. If there are no births nor deaths, Λ = 0 = μ, then the basic reproduction number is given by (3.11), where μ = 0.

3.3 Treatment Given After Exposure

Assume treatment is given after exposure, θ ₂ ≠ 0 and θ₁ = 0 = θ_3. The DFE is S̄ = K with all other states zero. Since θ₁ = 0, the spectral radius of FV⁻¹ can be determined by a 2×2 matrix M₂. Denote the reproduction number with treatment θ₂ as ${\mathcal{R}}_0^{[2]}$. (In the remaining discussion, we shall refer to , defined in (3.11), as the “basic reproduction number” and ${\mathcal{R}}_0^{[i]}$ as the “reproduction number” with treatment θ_i.) Then

$$\begin{array}{l}{\mathcal{R}}_0^{[2]}=\frac{K}{{\gamma }_1+{\delta }_1+{\theta }_2+\mu }max\{{\beta }_1\left[1+\frac{p_1{\theta }_2}{r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu }\right]+\frac{{\beta }_2}{{\gamma }_2+\mu }[{\delta }_1\\ +\frac{p_1{\theta }_2{\delta }_2({\gamma }_2+\mu )}{(r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu )(r_2{\gamma }_2+{\kappa }_2+\mu )}],{\beta }_{1,r}\left[1+\frac{{\theta }_2}{{\gamma }_1+{\delta }_1+\mu }\right]\\ +\frac{{\beta }_{2,r}}{{\gamma }_2+\mu }\left[{\delta }_1+\frac{{\theta }_2{\delta }_1({\gamma }_2+\mu )}{({\gamma }_1+{\delta }_1+\mu )({\gamma }_2+\mu )}\right]\}.\end{array}$$ (3.12)

The reproduction number is the sum of four terms that depend on drug-sensitive infected individuals, I, I_tr, I_s, I_s,tr, or on resistant infected individuals I_r, I_r,tr, I_s,r, I_s,r,tr (whichever sum is larger). If there are no births nor deaths, Λ = 0 = μ, then the reproduction number is given by (3.12), where μ = 0. If θ₂= 0, then the expression (3.12) simplifies to (3.11). Also, if p₁ ≈ 0 (treatment reduces transmission rate almost to zero) and β_1,r and β_2,r are sufficiently small, then ${\mathcal{R}}_0^{[2]}\le {\mathcal{R}}_0$. However, if p₁ is not sufficiently small, then it is not clear whether treatment θ₂ reduces the basic reproduction number.

3.4 Treatment Given After Infection

Assume drug treatment is given after infection, θ₃ ≠ 0 and θ₁ = 0 = θ₂. The DFE is S̄ = K with all other states zero. In this case, the spectral radius of FV⁻¹ can also be determined by a 2×2 matrix M₂, ${\mathcal{R}}_0^{[3]}=\rho (M_2)$, where

$${\mathcal{R}}_0^{[3]}=\frac{K}{{\gamma }_1+{\delta }_1+\mu }max\left\{{\beta }_1+\frac{{\beta }_{2,r}{\delta }_1}{{\gamma }_2+{\theta }_3+\mu }\left[1+\frac{p_1{\theta }_3}{r_2{\gamma }_2+{\kappa }_2+\mu }\right],{\beta }_{1,r}+\frac{{\beta }_{2,r}{\delta }_1}{{\gamma }_2+{\theta }_3+\mu }\left[1+\frac{{\theta }_3}{{\gamma }_2+\mu }\right]\right\}.$$ (3.13)

The reproduction number is the sum of three terms which in turn depend on the drug-sensitive cases, I, I_s, I_s,tr, or on the resistant cases, I_r, I_s,r, I_s,r,tr, whichever sum is larger. If there are no births nor deaths, Λ = 0 = μ, then the reproduction number is given by (3.13), where μ = 0. If θ₂= 0, the expression (3.13) simplifies to (3.11). Also if p₁ ≈ 0 and β_1,r and β_2,r are sufficiently small, then ${\mathcal{R}}_0^{[3]}\le {\mathcal{R}}_0$.

3.5 Prophylaxis

Assume chemoprophylaxis of susceptible individuals, θ₁ ≠ 0 and θ₂ = 0 = θ₃. The DFE is given by (3.7), where we let K₁ and K₂ be the values of S̄ and S̄_pr, respectively, as in (3.8). Since θ₁ ≠ 0, ${\mathcal{R}}_0^{[1]}=\rho (M_4)$, where M₄ is given in (6.17). However, in the simpler case where there are no births and deaths, Λ = 0 = μ, with the DFE S̄ = 0 and S̄_pr = K, the reproduction number simplifies to

$${\mathcal{R}}_0^{[1]}=Kmax\left\{p_3\left[\frac{{\beta }_1}{r_1{\gamma }_1+{\delta }_2+{\kappa }_1}+\frac{{\beta }_2{\delta }_2}{(r_1{\gamma }_1+{\delta }_2+{\kappa }_1)(r_2{\gamma }_2+{\kappa }_2)}\right],\frac{{\beta }_{1,r}}{{\gamma }_1+{\delta }_1}+\frac{{\beta }_{2,r}{\delta }_1}{{\gamma }_2({\gamma }_1+{\delta }_1)}\right\}.$$ (3.14)

The reproduction number is the sum of two terms that depend on drug-sensitive cases, I_tr, I_s,tr or on resistant cases, I_r,tr, I_s,r,tr. For chemoprophylaxis, it is always the case that ${\mathcal{R}}_0^{[1]}\le {\mathcal{R}}_0$ because of the relations (2.1), (2.2), and (2.3).

It is important to note that ${\mathcal{R}}_0^{[1]}$ does not depend on the treatment rate θ₁. However, the DFE (3.7) does depend on θ₁. For θ₁ ≫ μ, the DFE (3.7) is very close to S̄ ≈ 0 and S̄_pr ≈ K. In this case, if prophylaxis is begun in advance of the epidemic, as a preventive strategy, most individuals will have been treated (in state S_pr). Then ${\mathcal{R}}_0^{[1]}<1$ predicts local stability of this equilibrium.

3.6 Combined Strategies

Assume the treatment strategies given after exposure θ₂ and after infection θ₃ are combined (θ₁ = 0). The DFE in this case is S̄ = K with all other states zero. Similar to the previous cases, ${\mathcal{R}}_0^{[2,3]}$ can be computed from a 2×2 matrix M₂. Then

$${\mathcal{R}}_0^{[2,3]}=Kmax\left\{\frac{{\beta }_1}{v_{11}}\left[1+\frac{p_1{\theta }_2}{v_{33}}\right]+\frac{{\beta }_2}{v_{11}{v}_{55}}\left[{\delta }_1+\frac{p_1({\theta }_3{\delta }_1{v}_{33}+{\theta }_2{\delta }_2{v}_{55})}{v_{33}{v}_{77}}\right],\frac{{\beta }_{1,r}}{v_{11}}\left[1+\frac{{\theta }_2}{v_{44}}\right]+\frac{{\beta }_{2,r}{\delta }_1}{v_{11}{v}_{55}}\left[1+\frac{{\theta }_3{v}_{44}+{\theta }_2{v}_{55}}{v_{44}{v}_{88}}\right]\right\},$$ (3.15)

where the values of v_ii are the diagonal elements of matrix V defined in (6.16). The reproduction number is the sum of four terms which depend on sensitive cases, I, I_tr, I_s, I_s,tr or on resistant cases, I_r, I_s,r, I_r,tr, I_s,r,tr. Combining other treatment strategies, the values of the reproduction numbers, ${\mathcal{R}}_0^{[1,3]}$ or ${\mathcal{R}}_0^{[1,2]}$, can be computed from a 4 × 4 matrix.

The effectiveness of the treatment strategies is difficult to assess from the various formulas for the reproduction number because of the large number of parameters. Treatment after infection or after exposure may even increase the basic reproduction number , given in (3.11), if some of the parameters related to drug resistance are not sufficiently small, e.g., p_i, β_i,r. However, it is interesting to note that chemoprophylaxis always results in a reduction of . The reproduction numbers will be computed for the numerical examples studied in the next section.

4 Numerical Simulations

For the numerical simulations, basic parameter values are chosen for the epidemic situation discussed in Stilianakis et al. (1998), but we use the more general model with births and deaths. In their study, the parameter values were chosen to fit an epidemic that occurred in a boarding school for boys with treatment based on the antiviral drug amantadine. Two different population sizes are assumed, K = 400 and K = 800. In addition, a population size of K = 358 is assumed, as in the cases studied in Stilianakis et al. (1998). The results 1 of the ODE model are compared to the CTMC model. We choose $\mu =\frac{1}{80.365}/\text{day}$ so that the average life expectancy is 80 years. If the birth rate $\mathrm{\Lambda }=\frac{5}{365}/\text{day}$, then K = Λ/μ= 400. If the birth rate Λ is changed to $\mathrm{\Lambda }=\frac{10}{365}/\text{day}$, then K = 800. The dynamics are graphed over a thirty-day time period; an epidemic occurs when there is no treatment. Because the values of Λ and μ are small, the numerical results for the ODE model when Λ ≠ 0 ≠ μ are very close to the results when Λ = 0 = μ

The initial number of infected individuals is assumed to be either I_s(0) = 1 or I_s(0) = 5; one or five individuals exhibit symptoms of the disease. In addition, the initial number of susceptible individuals is S(0) = K − I_s(0) and S_pr(0) = 0. All other initial states are zero. Unless specified otherwise, treatment is started immediately (at t = 0). In one example, treatment begins at day seven. The basic parameter values for the epidemic case are given in Table 1.

Table 1.

Basic Parameter Values (Stilianakis et al., 1998)

Parameter	Basic Values	Parameter	Basic Values
β1	6 × 10−4/day	γ1	0.50/day
β1,r	β1/5 = 1.2 × 10−4/day	γ2	0.25/day
β2	6 × 10−3/day	r1	2.0/day
β2,r	β2/5 = 1.2 × 10−3/day	r2	1.33/day
p1	0.67/day	κ1	0.25 × 0.02 = 0.005/day
p2	0.33/day	κ2	0.25 × 0.20 = 0.05/day
p3	0.10/day	θ1	0.70/day
δ1	0.50/day	θ2	0.70/day
δ2	0.10/day	θ3	0.70/day

4.1 Comparison of the ODE and the CTMC Models: No Treatment

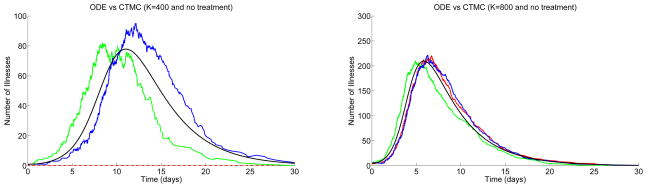
First, the CTMC model is compared to the ODE model when there is no treatment, θ_i = 0, i = 1, 2, 3. Figure 2 graphs a solution of the ODE model and three sample paths of the CTMC model when the population sizes are K = 400 and K = 800 and the initial number of symptomatic individuals are I_s(0) = 1 and I_s(0) = 5, respectively. The graphs show the total number of sick individuals (those exhibiting symptoms) versus time. These individuals are easily identifiable during an epidemic because of their symptoms. In particular, I_s(t) + I_s,tr(t) + I_s,r(t) + I_s,r,tr(t) is graphed for each model for a period of thirty days. Each of the figures contains plots of three sample paths for the stochastic model when K = 400 and I_s(0) = 1 and when K = 800 and I_s(0) = 5.

Figure 2.

Comparison of the ODE model (smooth curve) to the CTMC model, where θ_i= 0, i = 1, 2, 3, $\mathrm{\Lambda }=\frac{5}{365}$ and where either K = 400 and I_s(0) = 1 ( = 5.04) (left) or K = 800 and I_s(0) = 5 ( = 10.08) (right). Three sample paths are illustrated.

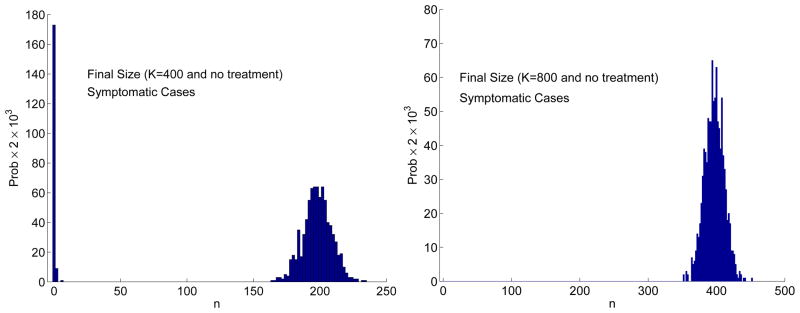
In Figure 2, an outbreak does not occur for one of the three sample paths. This is due to the fact that the final size distribution is bimodal (see Figure 3). When the final size is zero or very small there is no outbreak but when the number of cases is relatively large there is an outbreak. Applying the estimate in (3.6) for the CTMC model, when = 5.04 and I_s(0) = 1, the probability of an outbreak is ≈ 0.8 and the probability of no outbreak is ≈ 0.2. For = 10.08 and I_s(0) = 5, the probability of an outbreak is very close to one. These estimates are in good agreement with the approximate final size distribution based on 1000 sample paths (Figure 3). The final size distribution is clearly bimodal when K = 400 and I_s(0) = 1 (an outbreak occurs with probability 0.82 and no outbreak with probability 0.18). The bimodality is not evident when K = 800 and I_s(0) = 5 because for all 1000 sample paths there is an outbreak. Given an outbreak occurs, the average number of symptomatic cases after 30 days is ≈ 199 when K = 400 and I_s(0) = 1 and ≈ 397 when K = 800 and I_s(0) = 5. These values are in good agreement with the ODE model, where the total number of symptomatic cases after 30 days is 198 when K = 400 and I_s(0) = 1 and is 400 when K = 800 and I_s(0) = 5 (the initial number of symptomatic cases is not included in these estimates).

Figure 3.

Approximate final size distribution Prob{Final Size = n} for the CTMC model when K = 400 and I_s(0) = 1 (left) and when K = 800 and I_s(0) = 5 (right) based on 1000 sample paths and no treatment. The bar width in the frequency histogram equals 2. Hence, for 1000 sample paths, the probability of the final size is multiplied by 2 × 10³.

Due to the mass action assumption, when θ ₁ = 0, is proportional to K. For the examples in Figures 2 and 3, when K = 400, = 5.04 and when K = 800, = 10.4. These values are larger than estimates of for influenza pandemics which range between 1 and 2 (Gani et al., 2005).

4.2 Comparison of the ODE and the CTMC Models: Treatment Begins at Day Seven

In Stilianakis et al. (1998) it was assumed that the population size included 358 susceptible individuals with 220 people immune. All of the treatments were given at day seven and I_s(0) = 1. Some examples in Stilianakis et al. (1998) are simulated using the ODE and the the CTMC models. However, in our simulations, we assume $\mathrm{\Lambda }=\frac{4.475}{365}/\text{day}$ and $\mu =\frac{1}{80.365}/\text{day}$. For a thirty-day period, there are few births and deaths. Thus, the simulations in the ODE model for Λ ≠ 0 ≠ μ are very close to those when Λ = 0 = μ. Treatment begins at day seven, seven days after the initial case of one symptomatic individual.

In the examples, we compare no treatment with treatment of symptomatic individuals (θ₃ = 0.7, θ₁ = 0 = θ₂) and with prophylaxis and treatment of symptomatic individuals (θ₃= 0.7 = θ₃, θ₂ = 0) for the ODE and the CTMC models. At a treatment rate of θ₃ = 0.7, approximately half of the population is treated in one day. Table 2 gives the total number of symptomatic individuals (S cases), the total number of symptomatic and resistant individuals (S&R cases), the total number of infected individuals (T cases), and the total number of resistant individuals (TR cases) after 30 days. In the CTMC model, approximately 22–23% of the sample paths (out of 1000 sample paths) do not generate an outbreak. Therefore, given there is an outbreak in the CTMC model, the mean number of cases are recorded in Table 2. Notice that with treatment of symptomatic individuals, the number of cases is twice that of combined treatment of symptomatic individuals and prophylaxis. In addition, the number of symptomatic and resistant cases is much greater if there is only treatment of symptomatic individuals rather than combined treatment.

Table 2.

Total number of cases, total number of resistant cases, total number of symptomatic individuals and total number of symptomatic and resistant individuals when treatment begins at day 7, K = 358 and I_s(0) = 1, S=Symptomatic, S&R=Symptomatic and Resistant, T=Total Cases, TR=Total Resistant Cases, PO= Probability of an Outbreak.

Treatment Day 7	ODE		CTMC
	S Cases (T Cases)	S&R Cases (TR Cases)	Mean S Cases (T Cases)	Mean S&R Cases (TR Cases)	PO
θi = 0, i = 1, 2, 3	176 (353)	0 (0)	176 (352)	0 (0)	0.78
θ3 = 0.7, θ1 = 0 = θ2	167 (333)	16.6 (18.5)	166 (332)	16.3 (18.2)	0.77
θ1 = 0.7 = θ3, θ2 = 0	81.2 (189)	10.9 (15.5)	80.8 (183)	10.0 (14.0)	0.78

The reproduction numbers for these two cases are ${\mathcal{R}}_0^{[3]}=2.73$ and ${\mathcal{R}}_0^{[1,3]}=0.90$. However, these values only apply if treatment is given immediately (at t = 0) and when initial values are close to the DFE given by (3.7). A better descriptor of the dynamics in these cases is = 4.51 (when K = 358); delaying treatment causes an outbreak because >1. Applying the estimate (3.6) to compute the probability of an outbreak, PO= 0.78, which agrees with the values given in Table 2.

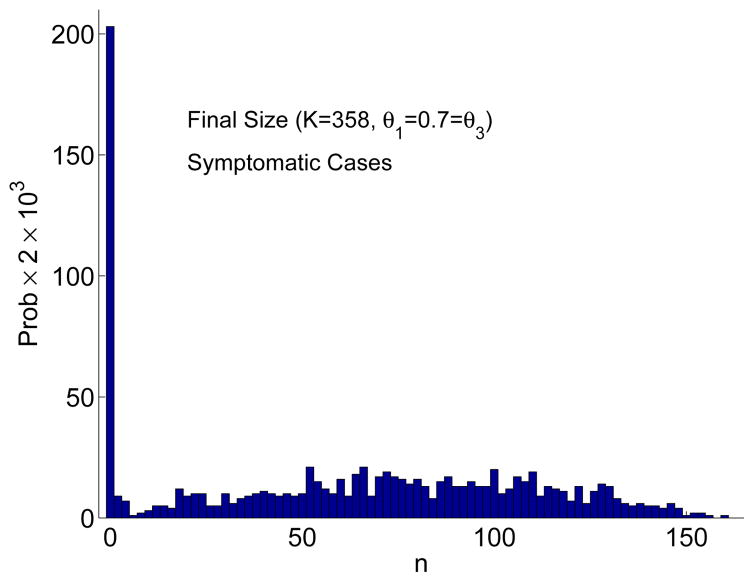
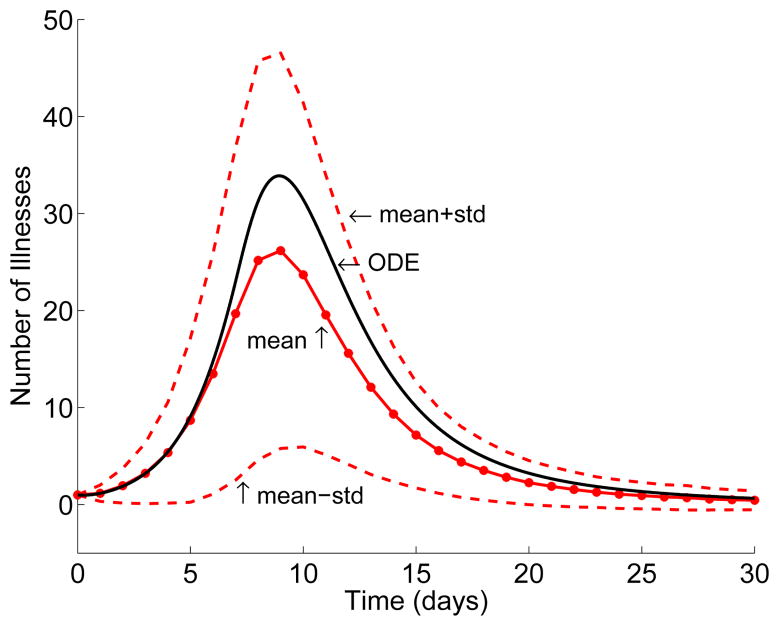
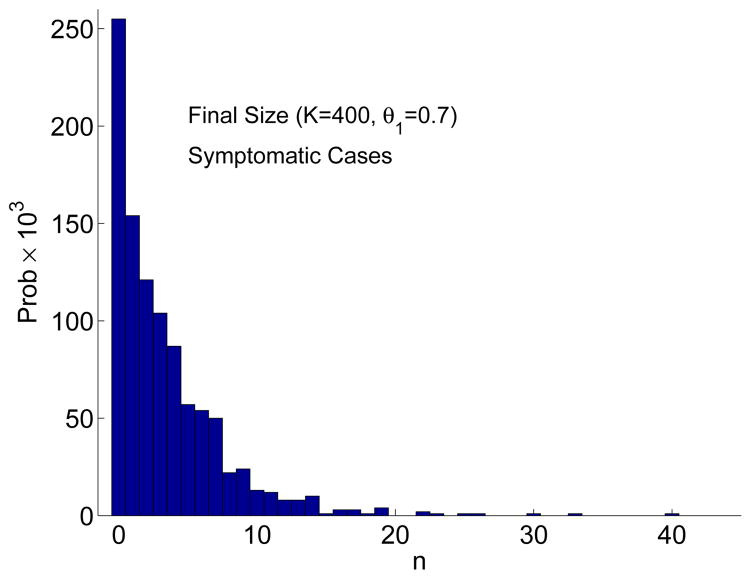
The final size distributions are bimodal when there is no treatment or when there is treatment of only symptomatic individuals (similar to the graph on the left in Figure 3). However, the bimodality is not as evident when there is combined treatment (Figure 4). Chemoprophylaxis does not change the probability of an outbreak (PO) but does reduce the number of cases and results in a large variation in the number of cases. Graphs of the solution to the ODE model and the mean of the CTMC model (± one standard deviation) in Figure 5 illustrate the dynamics of the two models. In these graphs, the mean number of symptomatic individuals for the CTMC is less than the ODE solution because the mean includes those few cases where there is no outbreak.

Figure 4.

Approximate final size distribution for the CTMC model based on 1000 sample paths when K = 358 and I_s(0) = 1. Combined treatment of symptomatic individuals and prophylaxis begins at day 7 (θ₁ = 0.7 = θ₃, θ₂ = 0). The bar width in the frequency histogram equals 2. Hence, for 1000 sample paths, the probability of the final size is multiplied by 2 × 10³.

Figure 5.

Solution to the ODE and mean of the CTMC model (± one standard deviation). Number of symptomatic individuals is graphed, K = 358 and I_s(0) = 1. Treatment begins at day 7 with treatment of symptomatic individuals and prophylaxis (θ₁ = 0.7 = θ₃, θ₂ = 0).

4.3 Comparison of the ODE and the CTMC Models: Single and Combined Treatment Strategies

Next, we use the ODE and the CTMC models to compare treatment with one drug versus combined treatment strategies (1000 sample paths are generated in the CTMC model). We assume the population size is K = 400 with initial conditions I_s(0) = 1 and S(0) = 399. There is no outbreak or a very minor outbreak with prophylaxis, θ₁ = 0.7 and θ₂ = 0 = θ₃ ( ${\mathcal{R}}_0^{[1]}=1.01$), but an outbreak occurs with treatment after exposure, θ₂ = 0.7 and θ₁ = 0 = θ₃ ( ${\mathcal{R}}_0^{[2]}=3.18$, Probability of an outbreak=PO= 0.71, see Table 3). With prophylaxis and treatment after exposure, again there is no outbreak, θ₁ = 0.35 = θ₂ and θ₃ = 0 ( ${\mathcal{R}}_0^{[1,2]}=1.01$). However, an outbreak occurs, if treatment is given after symptoms appear, θ₃ = 0.7 and θ₁ = 0 = θ₂ ( ${\mathcal{R}}_0^{[3]}=3.05$, Probability of an Outbreak=PO= 0.76). Note that the treatment reproduction numbers applied to formula (3.6) may not in general provide a good estimate for the probability of an outbreak. When treatment is applied early, our model is more complex than a simple SIR epidemic model for which the formula (3.6) was derived. In the two cases with prophylaxis treatment, there is no outbreak and the final size distribution has the shape of an exponential distribution, PO ≈ 0; it is not bimodal (see Figure 6). Thus, as expected, chemoprophylaxis or chemoprophylaxis combined with treatment prior to symptoms is a better strategy than treatment after symptoms appear.

Table 3.

Total number of cases, total number of resistance cases, total number of symptomatic individuals and total number of symptomatic and resistant individuals when treatment begins at day 0, K = 400 and I_s(0) = 1, S=Symptomatic, S&R=Symptomatic and Resistant, T=Total Cases, TR=Total Resistant Cases, PO= Probability of an Outbreak. There is no outbreak with chemoprophylaxis.

Treatment Day 0	ODE		CTMC
	S Cases (T Cases)	S&R Cases (TR Cases)	Mean S Cases (T Cases)	Mean S&R Cases (TR Cases)	PO
θi = 0, i = 1, 2, 3	198 (396)	0 (0)	199 (396)	0 (0)	0.82
θ1 = 0.7, θ2 = 0 = θ3	3.5 (14.8)	0.6 (1.2)	3.5 (14.3)	0.6 (1.1)	0
θ2 = 0.7, θ1 = 0 = θ3	126 (379)	2.7 (3.5)	125 (377)	2.7 (3.6)	0.71
θ3 = 0.7, θ1 = 0 = θ2	189 (378)	21.0 (24.1)	190 (377)	21.4 (24.7)	0.76
θ1 = 0.35 = θ2, θ3 = 0	6.2 (25.6)	1.0 (1.8)	5.8 (24.3)	0.7 (1.3)	0

Figure 6.

Approximate final size distribution for the CTMC model based on 1000 sample paths when K = 400 and I_s(0) = 1. Chemoprophylaxis begins at day 0 (θ₁ = 0.7, θ₂ = 0 =θ₃). The bar width in the frequency histogram equals 1. Hence, for 1000 sample paths, the probability of the final size is multiplied by 10³.

The CTMC model predicts the same number of symptomatic individuals as in the ODE model given there is an outbreak. But the CTMC model often predicts a positive probability of no outbreak. For the strategies treatment after exposure, θ₂ = 0.7, θ₁ = 0 = θ₃, and treatment after symptoms appear, θ₃ = 0.7, θ₂ = 0 = θ₁, the probability of no outbreak is 0.29 and 0.24, respectively.

It is interesting to note that the reproduction number ${\mathcal{R}}_0^{[1]}=1.01$ calculated for θ₁ = 0.7 and θ₂ = 0 = θ₃ in Table 3 is based on the resistant cases, e.g., see formula (3.14). A few resistant cases develop but an outbreak is averted. The treatment reproduction numbers ${\mathcal{R}}_0^{[2]}=3.18$ and ${\mathcal{R}}_0^{[3]}=3.15$ for the examples θ₂ = 0.7, θ₁ = 0 = θ₃ and θ₃ = 0.7, θ₁ = 0 = θ₂ in Table 3 (calculated formulas (3.12) and (3.13)) depend on the sensitive cases.

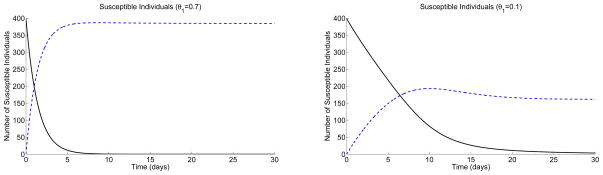
It should be noted that the reproduction number for chemoprophylaxis assumes the disease-free equilibrium is given by (3.7). Thus, the reproduction number is useful in prediction of an outbreak only if the population size is initially close to the disease-free equilibrium. That is, individuals need to be successfully prophylaxed prior to introduction of any infective individual for the reproduction number to be applied. For example, for the parameter values in the previous simulations with K = 400 and with θ₁ as low as θ₁ = 0.1, the disease-free equilibrium in (3.7) is S̄_pr = 399.86 and S̄ = 0.14.

In the last example, we compare the dynamics of chemoprophylaxis given before or after introduction of infectives and the level of treatment. If chemoprophylaxis is given at levels of θ₁ = 0.1 or θ₁ = 0.7 for a sufficiently long period of time, then the class S_pr builds up to a level close to K (=400) in both cases. If, after chemoprophylaxis, an infective is introduced, there is no outbreak (or a very minor outbreak) because the reproduction number is very close to one in both cases. If, however, an infective is introduced at the same time chemoprophylaxis is begun (S(0) = 399 and S_pr(0) = 0, and I_s(0) = 1), the level of treatment θ₁ has a big effect on the number of cases that occur. In this case ${\mathcal{R}}_0^{[1]}$ is a good predictor of the dynamics only at high treatment levels (e.g., θ₁ = 0.7). Graphs of the susceptible individuals in Figure 7 for the ODE model illustrate that with a treatment level of θ₁ = 0.7, the DFE is reached very quickly; S_pr is close to 400 after a short period of time. But with low levels of treatment θ₁ = 0.1, S_pr approaches a value less than 200 because individuals are getting infected faster than being treated. For the ODE model, when θ₁ = 0.1 the total number of symptomatic cases after 30 days is 76 with 2.3 symptomatic and resistant cases (232 total cases and 3.6 total resistant cases), whereas with θ₁ = 0.7, the total number of symptomatic cases is 3.5 with 0.6 symptomatic and resistant cases (13.8 total cases and 1.2 total resistant cases). These estimates agree with the CTMC model given that an outbreak occurs. The final size distribution for the case θ₁ = 0.7 has a shape similar to that given in Figure 4.

Figure 7.

Graphs of the susceptible individuals, S(t) (solid curve) and S_pr(t) (dashed curve), for the ODE model with K = 400; θ₁ = 0.7, θ₂ = 0 = θ₃ (left) and θ₁ = 0.1, θ₂ = 0 = θ₃ (right); S(0) = 399 and S_pr(0) = 0.

5 Summary

We formulated a CTMC model for an influenza epidemic with drug resistance and computed reproduction numbers for the ODE model under different treatment strategies. We also compared the number of cases predicted by the ODE model to the CTMC model and studied the effects of different treatment strategies through numerical simulations.

Treatment, especially with amantadine or rimantadine, can lead to the shedding of drug resistant virus. Formulas (3.11)–(3.15) for the reproduction numbers clearly show the contributions from the resistant cases and the sensitive cases. Under particular treatment strategies it is possible that the resistant cases rather than the sensitive cases will determine the magnitude of the reproduction number. Resistant cases that arise due to treatment may cause a minor outbreak in an epidemic situation or result in disease persistence in a pandemic situation.

Based on the numerical examples, the basic reproduction number decreased with all of three of the treatments considered: chemoprophylaxis, treatment of exposed individuals before symptoms appear, and treatment of symptomatic individuals. In all cases, chemoprophylaxis was the most effective treatment strategy. This was also shown by Stilianakis et al. (1998). In addition, we have shown that chemoprophylaxis will always reduce the basic reproduction number. Combining treatment strategies, the same or greater reduction in cases can be achieved as with a single strategy but the combined treatment rates can be lower than a single treatment rate (compare θ₁ = 0.7, θ₂ = 0 = θ₃ with θ₁ = 0.35 = θ₂, θ₃ = 0 in Table 3).

Caution is needed when the reproduction numbers calculated for various treatment strategies are used to predict an outbreak. With chemoprophylaxis, calculation of the reproduction number assumes that the population has already been treated at a level θ₁ so that initial number of susceptible individuals is reduced and is close to the disease-free equilibrium (DFE) (3.7). If this is not the case, for example, if chemoprophylaxis is started at the same time symptomatic individuals are introduced into the population, then a high level of chemoprophylaxis is needed to reach the DFE rapidly to prevent further infection.

In our numerical examples, drug resistance contributed to the overall number of cases. But in the epidemic situation considered here, they represented a small proportion of the cases. The small number of resistant cases is due to the assumed lower transmission rates for resistant cases than sensitive cases. However, even though the number of resistant cases is small, they may still impact the basic reproduction number and lead to minor outbreaks. They also represent a danger in that they might set off a second drug resistant wave of the epidemic (Stilianakis et al., 1998).

We have shown for small population sizes and for small initial number of infected individuals, variability in the epidemic process may result in no outbreak (probability 1–PO). Therefore, treatment applied to a small population may be more effective than predicted by the ODE model. In addition, the final size distribution for the CTMC model shows that there may be a large variability in number of cases (Figure 4).

In all cases, chemoprophylaxis was the most effective strategy. This work thus supports the conclusions of the recent large scale simulations of influenza A outbreaks that suggest that prophylaxis, targeted to regions where influenza infections are occurring, should be the backbone of any strategy to contain influenza (Ferguson et al., 2005; Ferguson et al., 2006; Germann et al., 2006; Longini Jr. et al., 2005). While the parameters used in our simulations apply to amantadine treatment they can be modified to the case of treatment with neuraminidase inhibitors as recently shown by Regoes and Bonhoeffer (2006).

Our models assume a single well-mixed population. They need to be generalized to more realistic situations that contain age and spatial structure and which relax the well-mixed assumption for contacts between individuals. These more general models will be especially important in pandemic planning for an H5N1 outbreak.

6 Appendix

6.1 SDE Model

We assume the changes ΔS(t), ΔS_pr(t), etc. (±1 or 0) are small relative to the total population size. To compute the drift vector f⃗(X⃗(t)) in (2.5), we apply the transition probabilities for the CTMC model and compute the expectations. The expectation of ΔS(t) is

$$\begin{array}{l}E(\mathrm{\Delta }S(t))=[\mathrm{\Lambda }-({\beta }_{1}I+{\beta }_2{I}_s+{\beta }_{2,r}{I}_{s,r}+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S-({\theta }_1+\mu )S]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ =f_1(\overrightarrow{X}(t))\mathrm{\Delta }t+o(\mathrm{\Delta }t,)\end{array}$$

where the right side equals the values of the random variables at time t. In particular,

$$E(\mathrm{\Delta }\overrightarrow{X}(t))=E\left(\begin{array}{c}\mathrm{\Delta }S(t)\\ \mathrm{\Delta }{S}_{pr}(t)\\ ⋮\\ \mathrm{\Delta }R(t)\end{array}\right)=\left(\begin{array}{c}{f}_1(\overrightarrow{X}(t))\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ f_2(\overrightarrow{X}(t))\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ ⋮\\ f_{11}(\overrightarrow{X}(t))\mathrm{\Delta }t+o(\mathrm{\Delta }t)\end{array}\right)=\overrightarrow{f}(\overrightarrow{X}(t))\mathrm{\Delta }t+\mathbf{o}(\mathrm{\Delta }t),$$

where the drift vector f⃗(X⃗(t)) has the same form as the right side of the ODE model.

To compute the diffusion matrix D(X⃗(t)) in (2.5), we find the covariance matrix Σ(X⃗(t)) = E(ΔX⃗[ΔX⃗]^T) − E(ΔX⃗)[E(ΔX⃗)]^T = E(ΔX⃗(ΔX⃗)^T) + o(Δt). Then Σ(X⃗(t)) = D(X⃗(t))D^T (X⃗(t)) Δt + o(Δt). Matrix ΔX⃗(ΔX⃗)^T is an 11×11 symmetric positive definite matrix of the form

$$\left(\begin{array}{ccccc}{(\mathrm{\Delta }S)}^2& \mathrm{\Delta }S\mathrm{\Delta }{S}_{pr}& \mathrm{\Delta }S\mathrm{\Delta }I& \cdots & \mathrm{\Delta }S\mathrm{\Delta }R\\ \mathrm{\Delta }S\mathrm{\Delta }{S}_{pr}& {(\mathrm{\Delta }{S}_{pr})}^2& \mathrm{\Delta }{S}_{pr}\mathrm{\Delta }I& \cdots & \mathrm{\Delta }{S}_{pr}\mathrm{\Delta }R\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ \mathrm{\Delta }S\mathrm{\Delta }R& \mathrm{\Delta }R\mathrm{\Delta }{S}_{pr}& \mathrm{\Delta }R\mathrm{\Delta }I& \cdots & {(\mathrm{\Delta }R)}^2\end{array}\right).$$

Applying the 36 transition probabilities defined for the CTMC model, the nonzero entries in E(ΔX⃗(ΔX⃗)^T) are given as follows:

$$\begin{array}{l}E({(\mathrm{\Delta }S)}^2)=[\mathrm{\Lambda }+({\beta }_{1}I+{\beta }_2{I}_s+{\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S+({\theta }_1+\mu )S]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }S\mathrm{\Delta }{S}_{pr})=-{\theta }_{1}S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }S\mathrm{\Delta }I)=-({\beta }_{1}I+{\beta }_2{I}_s+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }S\mathrm{\Delta }{I}_r)=-({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{S}_{pr})}^2)=[(p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+{\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr}+\mu )S_{pr}+{\theta }_{1}S]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{S}_{pr}\mathrm{\Delta }{I}_r)=-({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{S}_{pr}\mathrm{\Delta }{I}_{tr})=-(p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{S}_{pr}\mathrm{\Delta }{I}_{r,tr})=-({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }I)}^2)=[({\beta }_{1}I+{\beta }_2{I}_s+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr})S+({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }I\mathrm{\Delta }{I}_s)=-{\delta }_{1}I\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }I\mathrm{\Delta }{I}_{tr})=-{\theta }_{2}I\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }I\mathrm{\Delta }R)=-{\gamma }_{1}I\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_s)}^2)=[{\delta }_{1}I+({\gamma }_2+{\theta }_3+\mu )I_s]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_s\mathrm{\Delta }{I}_{s,tr})=-{\theta }_3{I}_s\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_s\mathrm{\Delta }R)=-{\gamma }_2{I}_s\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_r)}^2)=[({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S+({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}+({\gamma }_1+{\delta }_1+{\theta }_2+\mu )I_r]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_r\mathrm{\Delta }{I}_{s,r})=-{\delta }_1{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_r\mathrm{\Delta }{I}_{r,tr})=-{\theta }_2{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_r\mathrm{\Delta }R)=-{\gamma }_1{I}_r\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_{s,r})}^2)=[{\delta }_1{I}_r+({\gamma }_2+{\theta }_3+\mu )I_{s,tr}]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{s,r}\mathrm{\Delta }{I}_{s,r,tr})=-{\theta }_3{I}_{s,r}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{s,r}\mathrm{\Delta }R)=-{\gamma }_2{I}_{s,r}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_{tr})}^2)=[(p_2{\beta }_{1}I+p_2{\beta }_2{I}_s+p_3{\beta }_1{I}_{tr}+p_3{\beta }_2{I}_{s,tr})S_{pr}+(r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu )I_{tr}+{\theta }_{2}I]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{tr}\mathrm{\Delta }{I}_{s,tr})=-{\delta }_2{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{tr}\mathrm{\Delta }{I}_{r,tr})=-{\kappa }_1{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{tr}\mathrm{\Delta }R)=-r_1{\gamma }_1{I}_{tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_{s,tr})}^2)=[{\theta }_3{I}_s+{\delta }_2{I}_{tr}+(r_2{\gamma }_2+{\kappa }_2+\mu )I_{s,tr}]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{s,tr}\mathrm{\Delta }{I}_{s,r,tr})=-{\kappa }_2{I}_{s,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{s,tr}\mathrm{\Delta }R)=-r_2{\gamma }_2{I}_{s,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_{r,tr})}^2)=[({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}+{\theta }_2{I}_r+{\kappa }_1{I}_{tr}+({\gamma }_1+{\delta }_1+\mu )I_{r,tr}]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{r,tr}{\mathrm{\Delta }I}_{s,r,tr})=-{\delta }_1{I}_{r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{r,tr}\mathrm{\Delta }R)=-{\gamma }_1{I}_{r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }{I}_{s,r,tr})}^2)=[{\theta }_3{I}_{s,r}+{\kappa }_2{I}_{s,tr}+{\delta }_1{I}_{r,tr}+({\gamma }_2+\mu )I_{s,r,tr}]\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E(\mathrm{\Delta }{I}_{s,r,tr}\mathrm{\Delta }R)=-{\gamma }_2{I}_{s,r,tr}\mathrm{\Delta }t+o(\mathrm{\Delta }t)\\ E({(\mathrm{\Delta }R)}^2)=[{\gamma }_1(I+I_r+I_{r,tr})+{\gamma }_2(I_s+I_{s,r}+I_{s,r,tr})+r_1{\gamma }_1{I}_{tr}+r_2{\gamma }_2{I}_{s,tr}-\mu R]\mathrm{\Delta }t+o(\mathrm{\Delta }t).\end{array}$$

The diffusion matrix D can be defined so that it has dimension 11 × 36. Entries in the matrix D consist of the square root of the births, the deaths, and the transitions. The nonzero entries in the first three rows and first eight columns of D are defined explicitly as follows:

$$D(\overrightarrow{X}(t))=\left(\begin{array}{ccccccccc}\sqrt{\mathrm{\Lambda }}& -\sqrt{\mu S}& d_{1,3}& d_{1,4}& -\sqrt{{\theta }_{1}S}& 0& 0& 0& \cdots \\ 0& 0& 0& 0& \sqrt{{\theta }_{1}S}& d_{2,6}& d_{2,7}& d_{2,8}& \cdots \\ 0& 0& -d_{1,3}& 0& 0& 0& 0& 0& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \cdots \end{array}\right),$$

where

$$\begin{array}{l}{d}_{1,3}=-\sqrt{({\beta }_{1}I+{\beta }_2{I}_s+p_1{\beta }_1{I}_{tr}+p_1{\beta }_2{I}_{s,tr})S}\\ d_{1,4}=-\sqrt{({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r}+{\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S}\\ d_{2,6}=-\sqrt{\mu S_{pr}}\\ d_{2,7}=-\sqrt{({\beta }_{1,r}{I}_r+{\beta }_{2,r}{I}_{s,r})S_{pr}}\\ d_{2,8}=-\sqrt{({\beta }_{1,r}{I}_{r,tr}+{\beta }_{2,r}{I}_{s,r,tr})S_{pr}}.\end{array}$$

The dependence on time, e.g., S ≡ S(t), is omitted for simplicity. Vector W⃗(t) in (2.5) equals (W₁(t), W₂(t), …, W₃₆(t))^T, a vector of 36 independent Wiener processes. Other SDE formulations and more details may be found in the references (Allen, 2007; Xu, 2006).

6.2 Basic Reproduction Number

To compute the basic reproduction number for the ODE system, where θ_i ≠ 0, i = 1, 2, 3, the Jacobian matrices F and V are computed from the vectors 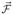and 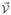, defined in (3.9) and (3.10), respectively. Computing F and V and evaluating at the DFE, S̄ = K₁, S̄_pr = K₂, lead to

$$F=\left(\begin{array}{cccccccc}{\beta }_1{K}_1& 0& p_1{\beta }_1{K}_1& 0& {\beta }_2{K}_1& 0& p_1{\beta }_2{K}_1& 0\\ 0& {\beta }_{1,r}(K_1+K_2)& 0& {\beta }_{1,r}{K}_1& 0& {\beta }_{2,r}(K_1+K_2)& 0& {\beta }_{2,r}{K}_1\\ p_2{\beta }_1{K}_2& 0& p_3{\beta }_1{K}_2& 0& p_2{\beta }_2{K}_2& 0& p_3{\beta }_2{K}_2& 0\\ 0& 0& 0& {\beta }_{1,r}{K}_2& 0& 0& 0& {\beta }_{2,r}{K}_2\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

and

$$V=\left(\begin{array}{cccccccc}{v}_{11}& 0& 0& 0& 0& 0& 0& 0\\ 0& v_{11}& 0& 0& 0& 0& 0& 0\\ -{\theta }_2& 0& v_{33}& 0& 0& 0& 0& 0\\ 0& -{\theta }_2& -{\kappa }_1& v_{44}& 0& 0& 0& 0\\ -{\delta }_1& 0& 0& 0& v_{55}& 0& 0& 0\\ 0& -{\delta }_1& 0& 0& 0& v_{55}& 0& 0\\ 0& 0& -{\delta }_2& 0& -{\theta }_3& 0& v_{77}& 0\\ 0& 0& 0& -{\delta }_1& 0& -{\theta }_3& -{\kappa }_2& v_{88}\end{array}\right),$$ (6.16)

where

$$\begin{array}{l}{v}_{11}={\gamma }_1+{\delta }_1+{\theta }_2+\mu \\ v_{33}=r_1{\gamma }_1+{\delta }_2+{\kappa }_1+\mu \\ v_{44}={\gamma }_1+{\delta }_1+\mu \\ v_{55}={\gamma }_2+{\theta }_3+\mu \\ v_{77}=r_2{\gamma }_2+{\kappa }_2+\mu \\ v_{88}={\gamma }_2+\mu .\end{array}$$

We then compute FV⁻¹. Since in FV⁻¹, the last four rows are all zeros, the spectral radius is determined by the following 4×4 submatrix of FV⁻¹,

$$M_4=\left(\begin{array}{cccc}{m}_{11}& 0& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& m_{24}\\ m_{31}& 0& m_{33}& 0\\ m_{41}& m_{42}& m_{43}& m_{44}\end{array}\right)$$ (6.17)

where

$$\begin{array}{l}{m}_{11}=\frac{{\beta }_1{K}_1}{v_{11}}+\frac{{\beta }_2{K}_1{\delta }_1}{v_{11}{v}_{55}}+\frac{p_1{\beta }_1{K}_1{\theta }_2}{v_{11}{v}_{33}}+\frac{p_1{\beta }_2{K}_1({\theta }_3{\delta }_1{v}_{33}+{\delta }_2{\theta }_2{v}_{55})}{v_{11}{v}_{33}{v}_{55}{v}_{77}}\\ m_{13}=\frac{p_1{\beta }_1{K}_1}{v_{33}}+\frac{p_1{\beta }_2{K}_1{\delta }_2}{v_{33}{v}_{77}}\\ m_{21}=\frac{{\beta }_{1,r}{K}_1{\kappa }_1{\theta }_2}{v_{11}{v}_{33}{v}_{44}}+\frac{{\beta }_{2,r}{K}_1({\kappa }_2{\theta }_3{\delta }_1{v}_{33}{v}_{44}+{\kappa }_2{\delta }_2{\theta }_2{v}_{44}{v}_{55}+{\delta }_1{\kappa }_1{\theta }_2{v}_{55}{v}_{77})}{v_{11}{v}_{33}{v}_{44}{v}_{55}{v}_{77}{v}_{88}}\\ m_{22}=\frac{{\beta }_{1,r}(K_1+K_2)}{v_{11}}+\frac{{\beta }_{1,r}{K}_1{\theta }_2}{v_{11}{v}_{44}}+\frac{{\beta }_{2,r}(K_1+K_2){\delta }_1}{v_{11}{v}_{55}}+\frac{{\beta }_{2,r}{K}_1{\delta }_1({\theta }_3{v}_{44}+{\theta }_2{v}_{55})}{v_{11}{v}_{44}{v}_{55}{v}_{88}}\\ m_{23}=\frac{{\beta }_{1,r}{K}_1{\kappa }_1}{v_{33}{v}_{44}}+\frac{{\beta }_{2,r}{K}_1({\kappa }_2{\delta }_2{v}_{44}+{\delta }_1{\kappa }_1{v}_{77})}{v_{33}{v}_{44}{v}_{77}{v}_{88}}\\ m_{24}=\frac{{\beta }_{1,r}{K}_1}{v_{44}}+\frac{{\beta }_{2,r}{K}_1{\delta }_1}{v_{44}{v}_{88}}\\ m_{31}=\frac{p_2{\beta }_1{K}_2}{v_{11}}+\frac{p_3{\beta }_1{K}_2{\theta }_2}{v_{11}{v}_{33}}+\frac{p_2{\beta }_2{K}_2{\delta }_1}{v_{11}{v}_{55}}+\frac{p_3{\beta }_2{K}_2({\theta }_3{\delta }_1{v}_{33}+{\theta }_2{\delta }_2{v}_{55})}{v_{11}{v}_{33}{v}_{55}{v}_{77}}\\ m_{33}=\frac{p_3{\beta }_1{K}_2}{v_{33}}+\frac{p_3{\beta }_2{K}_2{\delta }_2}{v_{33}{v}_{77}}\\ m_{41}=\frac{{\beta }_{1,r}{K}_2{\kappa }_1{\theta }_2}{v_{11}{v}_{33}{v}_{44}}+\frac{{\beta }_{2,r}{K}_2({\kappa }_2{\theta }_3{\delta }_1{v}_{33}{v}_{44}+{\kappa }_2{\delta }_2{\theta }_2{v}_{44}{v}_{55}+{\delta }_1{\kappa }_1{\theta }_2{v}_{55}{v}_{77})}{v_{11}{v}_{33}{v}_{44}{v}_{55}{v}_{77}{v}_{88}}\\ m_{42}=\frac{{\beta }_{1,r}{K}_2{\theta }_2}{v_{11}{v}_{44}}+\frac{{\beta }_{2,r}{K}_2{\delta }_1({\theta }_3{v}_{44}+{\theta }_2{v}_{55})}{v_{11}{v}_{44}{v}_{55}{v}_{88}}\\ m_{43}=\frac{{\beta }_{1,r}{K}_2{\kappa }_1}{v_{33}{v}_{44}}+\frac{{\beta }_{2,r}{K}_2({\kappa }_2{\delta }_2{v}_{44}+{\delta }_1{\kappa }_1{v}_{77})}{v_{33}{v}_{44}{v}_{77}{v}_{88}}\\ m_{44}=\frac{{\beta }_{1,r}{K}_2}{v_{44}}+\frac{{\beta }_{2,r}{K}_2{\delta }_1}{v_{44}{v}_{88}}\end{array}$$

and v_ii is a diagonal element in matrix V. Then = ρ(FV⁻¹) = ρ(M₄).