Stochastic Models for Virus and Immune System Dynamics

Abstract

New stochastic models are developed for the dynamics of a viral infection and an immune response during the early stages of infection. The stochastic models are derived based on the dynamics of deterministic models. The simplest deterministic model is a well-known system of ordinary differential equations which consists of three populations: uninfected cells, actively infected cells, and virus particles. This basic model is extended to include some factors of the immune response related to Human Immunodeficiency Virus-1 (HIV-1) infection. For the deterministic models, the basic reproduction number, , is calculated and it is shown that if < 1, the disease-free equilibrium is locally asymptotically stable and is globally asymptotically stable in some special cases. The new stochastic models are systems of stochastic differential equations (SDEs) and continuous-time Markov chain (CTMC) models that account for the variability in cellular reproduction and death, the infection process, the immune system activation, and viral reproduction. Two viral release strategies are considered: budding and bursting. The CTMC model is used to estimate the probability of virus extinction during the early stages of infection. Numerical simulations are carried out using parameter values applicable to HIV-1 dynamics. The stochastic models provide new insights, distinct from the basic deterministic models. For the case > 1, the deterministic models predict the viral infection persists in the host. But for the stochastic models, there is a positive probability of viral extinction. It is shown that the probability of a successful invasion depends on the initial viral dose, whether the immune system is activated, and whether the release strategy is bursting or budding.

1. Introduction

Viruses invade almost any type of body tissue, from the brain to the skin [12]. In healthy individuals, the majority of viral infections are eliminated by the body’s innate or adaptive immune response. Although the immune response is one of the most important factors in viral elimination, other factors play a role, including the initial viral dose and the viral release strategy. The goal of this research is to apply deterministic and stochastic models to investigate the effect of three factors on viral establishment: the immune response, initial viral dose, and viral release strategy.

A well-known deterministic model for viral entry and release from a host cell, but with no immune response, serves as the starting point for our model development. This simple model consists of a system of three ordinary differential equations (ODEs) for the target cells, actively infected target cells, and virus particles [25, 29, 42]. We also consider a deterministic model with an immune response, applicable to Human Immunodeficiency Virus-1 (HIV-1) [6, 33]. New stochastic differential equations (SDEs) and continuous-time Markov chain (CTMC) models are derived based on the ODE models.

The stochastic models distinguish between two types of viral release strategies: budding and bursting. In the budding strategy, virus particles are produced throughout the life cycle of an infected cell, budding from the surface of the cell. This release strategy is often employed by enveloped viruses, e.g., influenza, HIV-1, rabies virus [23, 30, 35]. In the bursting strategy, viruses are reproduced within a cell and released only upon death of the infected cell, in a “burst” of new virus particles or virions. This latter strategy is often employed by nonenveloped viruses e.g., polioviruses [35, 37]. Parameter values estimated from HIV-1 clinical trials [6, 8] are used in the numerical simulations of the models. In HIV-1 infection, the predominant release strategy early in the infection is budding [30]. It is shown in the stochastic model with an immune response and parameter values appropriate for HIV-1 that budding is a more successful invasion strategy than bursting.

Numerous deterministic models have been developed to study various aspects of viral invasion and the initial immune response to HIV-1 infection (e.g., [5, 28, 29, 39, 42, 43] and references therein) but only a few stochastic models have been developed (e.g., [8, 18, 22, 27, 36, 38, 40]). Chao et al. used a stage-structured CTMC approach to model HIV-1 infection [8]. Tan et al. [36] and Lin et al. [22] applied Monte Carlo methods. Tuckwell et al. [38, 40] used SDEs to model early HIV-1 infection, a model with four populations but with no immune response: healthy, latent, and infected cell populations and virus particles. Their model was further studied by Kamina et al. [18]. Our SDE models are most closely related to the model of Tuckwell et al. [38], but our derivation is new. In addition to the SDE models, we formulate new CTMC models to investigate the probability of viral extinction during the early stages of infection. Komarova [20] applied a deterministic spatial model to study the optimal release strategies, budding versus bursting, in the presence of antibodies. Pearson et al. [27] applied stochastic theory, similar to the branching process theory applied here, to obtain estimates for the probability of viral extinction for the two release strategies in a virus-cell model with no immune response. Their results agree with ours for the model with no immune response.

In the next section, a well-known ODE model for viral infection in the absence of an immune response is described, then an ODE model for HIV-1 infection with an immune response [6, 33]. The basic reproduction number and the type reproduction number are calculated. In Section 4, new SDE and CTMC models for the early stages of infection are formulated. Applying branching processes theory, an expression is derived for the probability of viral extinction when > 1 (or > 1) which depends on initial viral dose, viral release strategy, and immune response. In Section 5, numerical examples illustrate and compare the results of the three model formulations, ODE, SDE, and CTMC models. In Section 6, the results are summarized and further research problems are suggested.

2. Deterministic Mathematical Models

A virus must successfully enter a target cell, then use the host machinery to reproduce multiple copies of itself and to assemble within the cell so that mature virus particles or virions can be released into the blood to begin a new cycle. The immune response, triggered by the infection, is a complex set of pathways consisting of the innate and the adaptive immune response. In this investigation, we concentrate on only three components of the immune response, amplification of the helper T cells after stimulation by infected cells, clearing of the infected cells by killer cells or cytotoxic lymphocytes (CTLs) and clearing of virus particles after immunoglobulin binding and engulfment by macrophages. These three responses are modeled in an HIV-1 infection. First, the simple model with no immune response is described, then a model formulated by Bagnoli et al. [6] and Sguanci et al. [33] for HIV-1 infection that includes the three components related to an immune response.

2.1. Model with No Immune Response

The most well-known model for intra-host viral invasion and reproduction consists of three ODEs representing the dynamics of the target cells, T, actively infected target cells, I, and virions, V (e.g., [25, 29]):

$$\frac{dT}{dt}=\lambda (1-T/K)-{\delta }_{T}T-\beta VT$$ (1)

$$\frac{dI}{dt}=\beta VT-{\delta }_{I}I$$ (2)

$$\frac{dV}{dt}=\pi I-cV-\beta VT.$$ (3)

Parameter λ is the production rate of new target cells with decreased production as their density increases. The amount of decrease depends on the parameter K. For the case K → ∞, the differential equation for T simplifies to

$$\frac{dT}{dt}=\lambda -{\delta }_{T}T-\beta VT.$$ (4)

Parameters δ_T, δ_I, and c are the death rates of target cells, infected target cells, and virus particles, respectively. Generally, δ_T ≤ δ_I ≤ c. Parameter β is the infection rate per healthy target cell upon interaction with the virus. Note that βVT appears in all three equations, representing a transition from a healthy T cell to an infected T cell and a loss of a virus particle. This term is often neglected from the virus equation (3) because the number of virions is large compared to this loss term (e.g., [25, 29]). The units for β differ between equations (3) and equations (1) and (2) because βVT is in units of virions in equation (3), whereas, in the other two equations, βVT is in units of cells. But the rate is often taken to be the same for all three equations [38]. Finally, the parameter π = Nδ_I is the production rate of new virus particles per infected cell. The value N is referred to as the “burst size”, the number of new virus particles produced during the lifetime of an infected cell. We assume N is an integer and N ≥ 2. All of the parameter values are positive.

2.2. HIV-1 Model with Immune Response

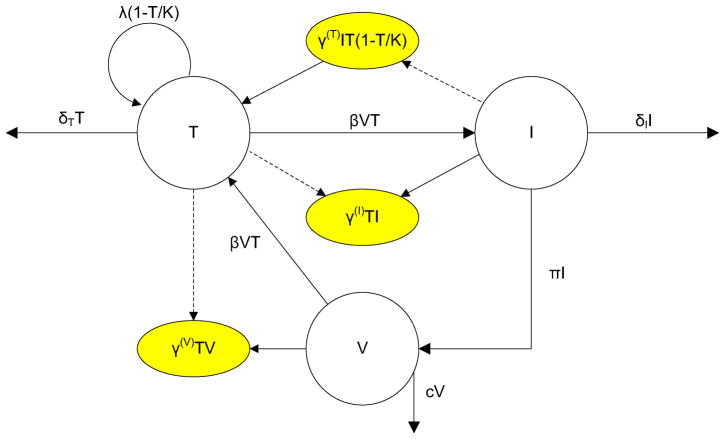
The preceding model (1)–(3) is extended to one that includes some factors related to an immune response, specifically for HIV-1 infection [6, 33]. In HIV-1, the target cells are the CD4⁺ T cells (T) which include primarily helper T cells but also macrophages and dendritic cells. When the healthy T cells become infected (I), the viral epitope presented on the cell surface triggers B cells and CTLs [33]. The B cells release antibodies that bind to the antigen while CTLs remove infected helper T cells. Although many HIV models emphasize different aspects of the intra-host virus and immune system dynamics (see e.g. [5, 7, 39, 42, 43]), our model is adapted from the one proposed by Bagnoli et al. [6] and Sguanci et al. [33]. Their model is a system of ordinary differential equations that only involves three variables, T, I, and V. The B cell and CTL responses are modeled through inclusion of parameters that represent receptor recognition and activation of helper T cells. Activation of helper T cells is via antigen presenting cells (APCs) that process the virus. APCs include macrophages, dendritic cells, and B cells. Unprocessed viral antigens, V, are not involved in activation of helper T cells. Thus, clonal amplification of the helper T cells in this simplified model, has a mass action form which is proportional to both helper T cells and infected T cells. The B cell and CTL responses are assumed to be proportional to the concentration of helper T cells. These assumptions simplify the model, restricting the number of variables to three, the same number as in the model (1)–(3). A compartmental diagram for the variables T, I and V with some factors related to immune control is graphed in Figure 1.

Figure 1.

Compartmental Diagram for the Model with Immune Response

The circles represent compartments T, I and V. The arrows indicate the direction of flow between the compartments. The terms δ_T T, δ_I I and cV are death rates. The terms with γ^(T), γ^(I) and γ^(V) are an interaction that involves two compartments but only affects one of them, either inflow or outflow. The dashed arrow indicates this type of interaction, but the compartment connected by a dashed line is not changed after the interaction.

In the model of Bagnoli et al. [6] and Sguanci et al. [33], three additional parameters and terms are added to model (1)–(3) to represent some of the important factors related to activation of the immune system. Parameter γ^(T) represents clonal amplification of the helper T cells after stimulation by infected T cells. The increase in helper T cells (also the target cells of the virus) through the γ^(T)IT term represents an increase in the immune response due to infection. The helper T cells in conjunction with either the infected T cells or virions V activate the CTLs or the B cells through the terms γ^(I)TI and γ^(V)TV, respectively. These latter expressions represent removal of infected T cells and clearance of virus particles. The model has the following form:

$$\frac{dT}{dt}=(\lambda +{\gamma }^{(T)}IT)(1-T/K)-{\delta }_{T}T-\beta VT$$ (5)

$$\frac{dI}{dt}=\beta VT-({\delta }_I+{\gamma }^{(I)}T)I$$ (6)

$$\frac{dV}{dt}=\pi I-(c+{\gamma }^{(V)}T)V-\beta VT.$$ (7)

Some of the parameter values applied to model (5)–(7) are given in Table 1 [6, 8]. The units of β in the equations (5) and (6) are (virions × day)⁻¹ but in equation (7), the units are (cell × day)⁻¹. Here, we include this term and assume it has the same magnitude in all three equations [38], assuming it takes one virus particle to successfully enter and infect a cell. The term −βVT in equation (7) is neglected in [6] and [33].

Table 1.

Parameters values for model (5), (6), and (7) taken from [6, 8] for total blood volume

Parameter	Value	Units
λ	105	cell × day−1
γ(T)	10−5	(cell × day)−1
K	1012	cell
δT	0.1	day−1
β	–	–
δI	0.8	day−1
γ(I)	10−5	(cell × day)−1
π = NδI	100	virions × (cell × day)−1
c	2.3	day−1
γ(V)	5 × 10−6	(cell × day)−1

3. Deterministic Model Analysis

The disease-free equilibrium (DFE) of models (1)–(3) and (5)–(7) is

$$(\overline{T},\overline{I},\overline{V})=\left(\frac{\lambda K}{\lambda +K{\delta }_T},0,0\right).$$ (8)

For the case K → ∞, T̄ = λ/δ_T. Calculation of the basic reproduction number and local stability of the DFE is verified for model (5)–(7) which also applies to the simpler model (1)–(3) when γ⁽ⁱ⁾ = 0, i = T, I, V.

The local stability of the DFE of model (5)–(7) can be determined by application of the next generation matrix approach [41]. (See Appendix A1.) The next generation matrix equals

$$\mathbb{K}=\left(\begin{array}{cc}0& \frac{\beta \overline{T}}{c+({\gamma }^V+\beta )\overline{T}}\\ \frac{\pi }{{\delta }_I+{\gamma }^{(I)}\overline{T}}& 0\end{array}\right).$$ (9)

The basic reproduction number is the spectral radius of :

$${\mathcal{R}}_0=\rho (\mathbb{K})=\sqrt{\frac{\pi \beta \overline{T}}{({\delta }_I+{\gamma }^{(I)}\overline{T})(c+({\gamma }^{(V)}+\beta )\overline{T})}}.$$ (10)

Hence, the DFE (8) is locally asymptotically stable if < 1. For the parameter values in Table 1 corresponding to model (1)–(3), = 1 if β ≈ 8.839 × 10⁻⁷.

Roberts and Heesterbeek [31] proposed an alternative method of calculating a threshold quantity, equivalent to . Based on the work of Heesterbeek and Roberts [17], a type reproduction number for controlling the infected cells is as follows:

$${\mathcal{T}}_1=e^{tr}\mathbb{K}{(\mathbb{I}-(\mathbb{I}-P)\mathbb{K})}^{-1}e,$$

where e is the first unit vector, tr refers to the transpose of the vector, is the next generation matrix (9), is the identity matrix, and P is the projection matrix for the infected cells or type 1 compartment (i.e. p₁₁ = 1, and p_ij = 0 for all other entries). Thus,

$${\mathcal{T}}_1=\frac{\pi \beta \overline{T}}{({\delta }_I+{\gamma }^{(I)}\overline{T})(c+({\gamma }^{(V)}+\beta )\overline{T})},$$ (11)

so that 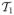= ( )². If the objective is to control the virus, instead of infected cells, the type reproduction number is denoted 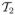. For this model, 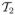= 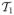. Since the type reproductions are equal, we denote the single type reproduction number as = = 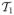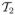. It is the type reproduction number that is often used as the definition of the basic reproduction number (e.g., [7, 25, 27, 29, 42, 43]).

For model (1)–(3) with γ⁽ⁱ⁾ = 0, i = T, I, V, the basic reproduction number and type reproduction numbers are

$${\mathcal{R}}_0=\sqrt{\frac{\pi \beta \overline{T}}{{\delta }_I(c+\beta \overline{T})}}$$ (12)

and

$$\mathcal{T}=\frac{\pi \beta \overline{T}}{{\delta }_I(c+\beta \overline{T})}=\frac{N\beta \overline{T}}{c+\beta \overline{T}}.$$ (13)

For the parameter values in Table 1 with γ⁽ⁱ⁾ = 0, i = T, I, V, it follows that = 1 if β ≈ 1.855 × 10⁻⁸. Infection occurs if > 1 ( > 1). It will be shown in the stochastic models as well, that the condition > 1 is required for occurrence of infection.

For models (1)–(3) and (5)–(7), a more complete analysis is summarized in Appendix A2.

4. Stochastic Mathematical Models

Itô SDE models can be derived by applying the modeling procedure in [1, 2, 3, 4]. In biochemical applications, the derived SDE system is referred to as the chemical Langevin equation [13, 14]. In addition, a CTMC model is derived based on the theory of branching processes [16, 19, 24]. The derivations distinguish between the two release strategies, bursting and budding. The bursting case assumes there is a coupling of the release of free virions and burst of infected cells. That is, π = Nδ_I and, therefore, the number of virions will not increase until the lysis of the infected cells and release of virions. The accumulation of virions, inside an infected cell, exhausts all the cell resources. For the budding case, the death of infected cells and release of virions are assumed to be independent processes; virus particles are being produced and released continuously during the entire life of the infected cells.

4.1. SDE: Bursting

Possible state changes in the stochastic process are based on the deterministic models. When Δt is small, these changes are given in Table 2. For ease of notation, the same notation is used as for the deterministic models, although for the SDE models, T, I, and V are continuous random variables. Let X⃗(t) = (I, V, T)^tr be a continuous random vector, ΔX⃗ = X⃗ (t + Δt) − X⃗ (t), and t ∈ [0, ∞).

Table 2.

Possible state changes during Δt: bursting case

i	State change ${(\mathrm{\Delta }\overrightarrow{X})}_i^{tr}$	Probability PiΔt	Description
1	(1, −1, −1)	βVTΔt	viral entry into a T cell
2	(−1, 0, 0)	γ(I)TIΔt	natural death or killing by CTLs of an infected T cell
3	(−1, N, 0)	δI IΔt	bursting of an infected T cell and release of virions
4	(0, −1, 0)	(c + γ(V)T)VΔt	natural death or removal of a virion
5	(0, 0, 1)	$(\lambda +{\gamma }^{(T)}IT)\left(1-\frac{T}{K}\right)\mathrm{\Delta }t$	production or clonal amplification of a T cell
6	(0, 0, −1)	δT TΔt	death of a T cell
7	(0, 0, 0)	$1-{\displaystyle \sum _{i=1}^6}{P}_i\mathrm{\Delta }t$	no change

When one infected cell dies, at the same time, N virions are released, (ΔX⃗)₃ = (−1, N, 0)^tr. In addition, it is assumed that a loss of one virus particle by entry into a healthy cell results in a new infected cell, (ΔX⃗)₁ = (1, −1, −1)^tr. Based on the state changes and their associated probabilities, we can compute the following expectations 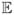(ΔX⃗) and 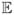((ΔX⃗)(ΔX⃗)^tr).

The expectation of ΔX⃗ is the drift vector f⃗ times Δt:

$$\mathbb{E}(\mathrm{\Delta }\overrightarrow{X})=\sum _{i=1}^6{P}_i\mathrm{\Delta }t{(\mathrm{\Delta }\overrightarrow{X})}_i=\overrightarrow{f}(I,V,T)\mathrm{\Delta }t,$$

where

$$\overrightarrow{f}=\left(\begin{array}{c}\beta VT-({\delta }_I+{\gamma }^{(I)}T)I\\ \pi I-(c+{\gamma }^{(V)}T)V-\beta VT\\ (\lambda +{\gamma }^{T}IT)(1-T/K)-({\delta }_T+\beta V)T\end{array}\right).$$

Note that f⃗ is the same as the right side of the ODE system. An approximation of the covariance matrix of ΔX⃗ to order Δt leads to the diffusion matrix Σ times Δt:

$$\mathbb{E}((\mathrm{\Delta }\overrightarrow{X}){(\mathrm{\Delta }\overrightarrow{X})}^{tr})\approx \sum _{i=1}^6{P}_i\mathrm{\Delta }t{(\mathrm{\Delta }\overrightarrow{X})}_i{(\mathrm{\Delta }\overrightarrow{X})}_i^{tr}=\mathrm{\sum }(I,V,T)\mathrm{\Delta }t,$$

where

$$\begin{array}{l}\mathrm{\sum }=\left(\begin{array}{ccc}{P}_1+P_2+P_3& -P_1-{NP}_3& -P_1\\ -P_1-{NP}_3& P_1+N^2{P}_3+P_4& P_1\\ -P_1& P_1& P_1+P_5+P_6\end{array}\right)\\ =\left(\begin{array}{ccc}\beta VT+({\delta }_I+{\gamma }^{(I)}T)I& -\beta VT-N{\delta }_{I}I& -\beta VT\\ -\beta VT-N{\delta }_{I}I& \beta VT+N^2{\delta }_{I}I+(c+{\gamma }^{(V)}T)V& \beta VT\\ -\beta VT& \beta VT& {\mathrm{\Gamma }}^{(T)}+({\delta }_T+\beta V)T\end{array}\right)\end{array}$$

and Γ^(T) = (λ + γ^(T)IT)(1 − T/K). The term (ΔX⃗)[ (ΔX⃗)]^tr in the covariance matrix is dropped since it is of order (Δt)².

Since a 3 × 3 square matrix S = Σ^1/2 is difficult to find in practice, we use an equivalent matrix H such that HH^tr = Σ as in [3], where matrix H is of dimension 3 × 5:

$$H=\left(\begin{array}{ccccc}\sqrt{\beta VT}& \sqrt{{\gamma }^{(I)}TI}& -\sqrt{{\delta }_{I}I}& 0& 0\\ -\sqrt{\beta VT}& 0& N\sqrt{{\delta }_{I}I}& -\sqrt{(c+{\gamma }^{(V)}T)V}& 0\\ -\sqrt{\beta VT}& 0& 0& 0& \sqrt{{\mathrm{\Gamma }}^{(T)}+{\delta }_{T}T}\end{array}\right)$$

and Γ ^(T) = (λ + γ^(T)IT)(1 −T/K). The Itô SDE model for the bursting case has the following form:

$$\{\begin{array}{lll}d\overrightarrow{X}(t)\hfill & =\hfill & \overrightarrow{f}(I,V,T)dt+H(I,V,T)d\overrightarrow{W}(t)\hfill \\ \overrightarrow{X}(0)\hfill & =\hfill & {(I(0),V(0),T(0))}^{tr},\hfill \end{array}$$ (14)

where W⃗ (t) = (W₁(t), W₂(t), · · ·, W₅(t))^tr is a vector of five independent Wiener processes. In the absence of infection, V (0) = 0, I(0) = 0, and T (0) = T̄ with γ⁽ⁱ⁾ = 0 for i = T, I, V. The Itô SDE for the target cells, T (t), can be computed from Table 2 with state changes i = 5, 6, 7, leading to

$$dT=\left[\lambda \left(1-\frac{T}{K}\right)-{\delta }_{T}T\right]dt+\sqrt{\lambda \left(1-\frac{T}{K}\right)+{\delta }_{T}T}dW.$$ (15)

ODEs for the mean, variance, and higher-order moments corresponding to each of the random variables can be computed by applying the multivariate Itô’s formula [26]. However, these ODEs do not form a closed system; they depend on successively higher-order moments so that approximation methods for the higher-order moments are needed to form a finite system of ODEs [11]. For the case of the scalar equation (15), the moment differential equations form a closed system that can be solved. Applying Itô’s formula [26] to equation (15), the mean and variance of T (t) can be shown to equal

$$\mathbb{E}(T(t))=\overline{T}$$

and

$$\mathit{Var}(T(t))=\frac{{\delta }_T}{\lambda }{(\overline{T})}^2(1-e^{-2\lambda t/\overline{T}}).$$

For large K ≫ 1 and t → ∞, Var(T (t)) ≈ T̄. In the examples in Section 5, the mean and variance of the random variables for models (1)–(3) and (5)–(7) will be computed numerically.

4.2. SDE: Budding

For the budding case, the expectation matrix and the drift vector are the same as the ones for the bursting case. The covariance matrix and diffusion matrix differ from the previous case. Table 3 lists the possible state changes. There are no “N” terms and δ_I and π are only related through the definition Nδ_I = π. Release of virions occurs continuously throughout the life of the infected cell.

Table 3.

Possible state change during Δt: budding case

i	State change ${(\mathrm{\Delta }\overrightarrow{X})}_i^{tr}$	Probability PiΔt	Description
1	(1, −1, −1)	βVTΔt	viral entry into a T cell
2	(−1, 0, 0)	(γ(I) T + δI)IΔt	natural death or killing by CTLs of an infected T cell
3	(0, 1, 0)	πIΔt	budding of a virion
4	(0, −1, 0)	(c + γ(V) T)VΔt	natural death or removal of a virion
5	(0, 0, 1)	$$(\lambda +{\gamma }^{(T)}IT)\left(1-\frac{T}{K}\right)\mathrm{\Delta }t$$	production or clonal
6	(0, 0, −1)	δT TΔt	amplification of a T cell death of a T cell
7	(0, 0, 0)	$$1-{\displaystyle \sum _{i=1}^6}{P}_i\mathrm{\Delta }t$$	no change

The diffusion matrix Σ has the form

$$\begin{array}{l}\mathrm{\sum }=\left(\begin{array}{ccc}{P}_1+P_2& -P_1& -P_1\\ -P_1& P_1+P_3+P_4& P_1\\ -P_1& P_1& P_1+P_5+P_6\end{array}\right)\\ =\left(\begin{array}{ccc}\beta VT+({\delta }_I+{\gamma }^{(I)}T)I& -\beta VT& -\beta VT\\ -\beta VT& \beta VT+\pi I+(c+{\gamma }^{(V)}T)V& \beta VT\\ -\beta VT& \beta VT& {\mathrm{\Gamma }}^{(T)}+({\delta }_T+\beta V)T\end{array}\right).\end{array}$$

where Γ^(T) = (λ + γ^(T)IT)(1 − T/K). Applying a similar approach to the bursting case, we can find a matrix G which satisfies GG^tr = Σ [3]:

$$G=\left(\begin{array}{cccc}\sqrt{\beta VT}& -\sqrt{{\gamma }^{(I)}TI+{\delta }_{I}I}& 0& 0\\ -\sqrt{\beta VT}& 0& \sqrt{\pi I+(c+{\gamma }^{(V)}T)V}& 0\\ -\sqrt{\beta VT}& 0& 0& \sqrt{{\mathrm{\Gamma }}^{(T)}+{\delta }_{T}T}\end{array}\right),$$

where Γ^(T) = (λ + γ^(I)IT)(1 − T/K). The Itô SDE model for budding has the following form:

$$\{\begin{array}{lll}d\overrightarrow{X}(t)\hfill & =\hfill & \overrightarrow{f}(I,V,T)dt+G(I,V,T)d\overrightarrow{W}(t)\hfill \\ \overrightarrow{X}(0)\hfill & =\hfill & {(I(0),V(0),T(0))}^{tr}\hfill \end{array},$$ (16)

where W⃗ (t) = (W₁(t), W₂(t), W₃(t), W₄(t))^tr is a vector of four independent Wiener processes. In the absence of the infection, the SDE for the target cells is given by equation (15).

4.3. CTMC Model

To gain an understanding of the probability of virus extinction, a time-homogenous CTMC model can be formulated based on the infinitesimal probabilities. After an initial viral invasion, the target cells are assumed to be at steady-state, T (t) = T̄. Then a simplified CTMC model can be expressed in terms of the disease states, I(t) and V (t). For γ^(T) and I(t) small, the healthy target cell population size is approximately T̄, that is, we assume that the immune system has been activated and the T cell levels are at normal levels, T̄. For the CTMC model, let I(t) and V (t) be discrete random variables with values in the set of nonnegative integers for t ∈ [0, ∞) and Y⃗ (t) = (I(t), V (t)). Assume that each infected cell or virion acts independently from each other and the dynamics do not depend on past history. Theory from branching processes, applied to the probability generating functions (p.g.f.s) of I(t) and V (t), can be used to obtain estimates for the probability of virus extinction, that is, $\underset{t\to \infty }{lim}\overrightarrow{Y}(t)=\overrightarrow{0}$ at the outset of infection.

The p.g.f.s of I(t) and V (t) are used to write the backward Kolmogorov equation whose steady-state solution yields the probability of extinction. If Y⃗ (0) = (1, 0), then the p.g.f. of I(t) is

$${\phi }_1(t;x,y)=\sum _{k,j}\text{Prob}\{\overrightarrow{Y}(t)=(k,j)\mid \overrightarrow{Y}(0)=(1,0)\}{x}^k{y}^j.$$

If Y⃗ (0) = (0, 1), then the p.g.f. of V (t) is

$${\phi }_2(t;x,y)=\sum _{k,j}\text{Prob}\{\overrightarrow{Y}(t)=(k,j)\mid \overrightarrow{Y}(0)=(0,1)\}{x}^k{y}^j.$$

The infinitesimal probabilities in Tables 2 and 3 can be used to write the backward Kolmogorov differential equations for φ_i(t; x, y) [19]:

$$\frac{\partial {\phi }_i}{\partial t}=g_i({\phi }_1(t;x,y),{\phi }_2(t;x,y)),i=1,2,$$ (17)

with initial conditions φ_i(0; x, y) = x and φ₂(0; x, y) = y. At t = 0, the functions $g_1(x,y)={\displaystyle \sum _{j,k=0}^{\infty }}{a}_{j,k}{x}^j{y}^k$ and $g_2(x,y)={\displaystyle \sum _{j,k=0}^{\infty }}{b}_{j,k}{x}^j{y}^k$, where the terms a_j,k and b_j,k are the infinitesimal probabilities in Tables 2 and 3. That is, the expression δ_1,j δ_0,k + a_j,kΔt + o(Δt) is the probability that a single infected cell, I(0) = 1, will produce j infected cells and k virions, where δ_j,k is the Kronecker delta symbol, i.e., δ_j,k = 0 if j ≠ k and δ_j,j = 1. Similarly δ_0,j δ_1,k + b_j,kΔt + o(Δt) is the probability that a single virion, V (0) = 1, will produce j infected cells and k virions. The process is time-homogeneous; a_j,k and b_j,k are independent of time t. To find the probability of virus extinction, we are interested in steady-state solutions of (17). Setting the right side of the differential equations (17) to zero, the roots (q₁, q₂) of g_i(q₁, q₂) = 0, i = 1, 2, such that 0 < q_i ≤ 1 can be used to estimate the probability of virus extinction when Y⃗ (0) = (1, 0) or Y⃗ (0) = (0, 1) [16, 19, 24]. The properties of g_i imply that there always exists a solution g_i(1, 1) = 0. But there may exist another positive solution (q₁, q₂), 0 < q_i < 1, i = 1, 2 [16, 19, 24].

Let Y⃗ (0) = (I(0), V (0)) = (m, n), T (0) = T̄ and q_i be the smallest positive solutions of the equation g_i(q₁, q₂) = 0, i = 1, 2, 0 < q_i ≤ 1. Then, assuming independence of events, it follows from Galton-Watson branching theory [16, 19, 24] that the probability of virus extinction $\underset{t\to \infty }{lim}\overrightarrow{Y}(0)=\overrightarrow{0}$ for the CTMC model is

$$q_1^m{q}_2^n.$$

4.3.1. CTMC: Bursting

For the bursting case, the expressions for the infinitesimal probabilities can be obtained from Table 2. Only the following state changes, (ΔX⃗)_i, i = 1, 2, 3, 4, 7, in Table 2, affect I and V. Assuming Y⃗ (0) = (1, 0), then a_0,0 = γ^(I)T̄, a_0,N = δ_I, and a_1,0 = −(γ ^(I)T̄ +δ_I). Next, assuming Y⃗ (0) = (0, 1), b_0,0 = c + γ^(V)T̄, b_1,0 = βT̄, and b_0,1 = −(c +γ^(V)T̄ + βT̄). Thus,

$$g_1(x,y)={\gamma }^{(I)}\overline{T}+{\delta }_I{y}^N-({\gamma }^{(I)}\overline{T}+{\delta }_I)x$$ (18)

and

$$g_2(x,y)=c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}x-(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})y.$$ (19)

To estimate the probability of extinction, the smallest positive solution (q₁, q₂) of g_i(q₁, q₂) = 0 are calculated. Alternately, the roots (q₁, q₂) are solutions of the time-homogeneous “offspring” p.g.f.s, denoted as f_i(x, y), i = 1, 2. That is, the solutions (q₁, q₂) of f_i(q₁, q₂) = q_i, i = 1, 2. In the case of bursting, the offspring p.g.f.s are given by

$$\begin{array}{l}{f}_1(x,y)=\frac{{\gamma }^{(I)}\overline{T}+{\delta }_I{y}^N}{{\gamma }^{(I)}+{\delta }_I}\\ f_2(x,y)=\frac{c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}x}{c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}}.\end{array}$$

It is easy to check that there always exists a solution x = 1 = y to g_i(x, y) = 0, i = 1, 2. Another solution of equations (18)–(19) exists, (x, y) = (q₁, q₂), where 0 < q_i < 1 iff > 1 (or > 1). This can be shown by solving g₂(x, y) = 0 for x and substituting the value of x into g₁(x, y) = 0:

$$p(y)=y^N-c_{1}y+c_2=0,$$ (20)

where

$$c_1=\frac{({\delta }_I+{\gamma }^{(I)}\overline{T})(c+\beta \overline{T}+{\gamma }^{(V)}\overline{T})}{{\delta }_I\beta \overline{T}}=\frac{N}{\mathcal{T}}$$

and c₂ = c₁ − 1 > 0. By Descarte’s rule of signs and the fact that y = 1 is a solution of p(y) = 0, it follows that the polynomial p(y) has exactly two positive real roots. If ≤ 1, there is no solution of p(y) = 0 on the interval (0, 1), which follows from the facts that p(0) > 0, p(1) = 1, and dp(y)/dy < 0 for y ∈ (0, 1). In addition, there is a positive root q₂, 0 < q₂ < 1 iff > 1. If 0 < q₂ < 1, then the solution x = q₁ of g₂(x, q₂) = 0 also satisfies 0 < q₁ < 1.

Theorem 1

The probability of virus extinction with bursting, T (t) = T̄, and Y⃗ (0) = (I(0), V (0)) = (m, n) is approximately one, if ≤ 1 ( ≤ 1) and is approximately $q_1^m{q}_2^n$, if > 1 ( > 1), where (q₁, q₂) is the smallest positive root such that 0 < q_i < 1, i = 1, 2 of (18) and (19).

For the model with no immune system activation, γ^(I) = 0 = γ^(T), the probabilities (q₁, q₂) agree with those calculated by Pearson et al. [27]. In the numerical examples, the roots q₁ and q₂ of equations (18) and (19) will be calculated numerically.

4.3.2. CTMC: Budding

For the budding case, the same method as in the previous section can be applied to the infinitesimal probabilities from Table 3. Given Y⃗ = (1, 0), a_0,0 = δ_I + γ^(V)T̄, a_1,1 = π, and a_1,0 = −(δ_I + γ^(V)T̄ + π). Also, given Y⃗ = (0, 1), b_0,1 = βT̄, b_0,0 = c + γ^(V)T̄, and b_0,1 = −(βT̄ + c + γ^(V)T̄. Thus,

$$g_1(x,y)={\delta }_I+{\gamma }^{(I)}\overline{T}+\pi xy-({\delta }_I+{\gamma }^{(I)}\overline{T}+\pi )x$$ (21)

and

$$g_2(x,y)=c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}x-(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})y.$$ (22)

The time-homogeneous offspring p.g.f.s in the case of budding are given by

$$\begin{array}{l}{f}_1(x,y)=\frac{{\delta }_I+{\gamma }^{(I)}\overline{T}+\pi xy}{{\delta }_I+{\gamma }^{(I)}\overline{T}+\pi }\\ f_2(x,y)=\frac{c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}x}{c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}}.\end{array}$$

It can be shown that there is a solution (q₁, q₂), 0 < q_i < 1, to equations (21) and (22) iff > 1 (or > 1). To verify this assertion, solve for y in g₂(x, y) = 0, then substitute y into g₁(x, y) = 0:

$$p(x)=x^2-d_{1}x+d_2=0,$$

where

$$d_2=\frac{({\delta }_I+{\gamma }^{(I)}\overline{T})(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})}{\pi \beta \overline{T}}=\frac{1}{\mathcal{T}}$$

and d₁ = d₂ + 1. The solutions to the quadratic equation p(x) = 0 are x = 1, 1/ . Thus, q₁ = 1/ < 1 iff > 1. But if q₁ = 1/ < 1, then

$$q_2=\frac{c+{\gamma }^{(V)}\overline{T}}{c+{\gamma }^{(V)}\overline{T}+\beta \overline{T}}+\frac{{\delta }_I+{\gamma }^{(I)}\overline{T}}{\pi }<1.$$ (23)

Theorem 2

The probability of virus extinction with budding, T (t) = T̄, and Y⃗ (0) = (I(0), V (0)) = (m, n) is approximately one, if ≤ 1 ( ≤ 1) and is approximately ${(1/\mathcal{T})}^m{q}_2^n$, if > 1 ( > 1), where q₂ is defined in equation (23).

In the case γ^(I) = 0 = γ^(T), the probabilities

$$(q_1,q_2)=\left(\frac{1}{\mathcal{T}},\frac{c}{c+\beta \overline{T}}+\frac{1}{N}\right).$$ (24)

Applying a similar technique, Pearson et al. [27] obtained these same probabilities of extinction.

5. Numerical Examples

Two sets of numerical examples illustrate the dynamics of the SDE and CTMC models for the budding and bursting cases with and without the immune response. Hypothetical but reasonable values for the transmission rate β are chosen so that > 1 in each case. Estimates for the probability of virus extinction are obtained based on the analysis in the preceding section. In addition, in the case of virus persistence, simulations of the SDE models are used to illustrate an approximate stationary probability distribution, obtained after a sufficiently long period of time. Estimates are given for the expectation and variance of the distributions.

5.1. No Immune Response

In the first set of examples, γ⁽ⁱ⁾ = 0, i = T, I, V. All other parameter values are given in Table 1. In addition, β = 1 × 10⁻⁷ so that > 1. In particular, = 2.28 and = 5.21.

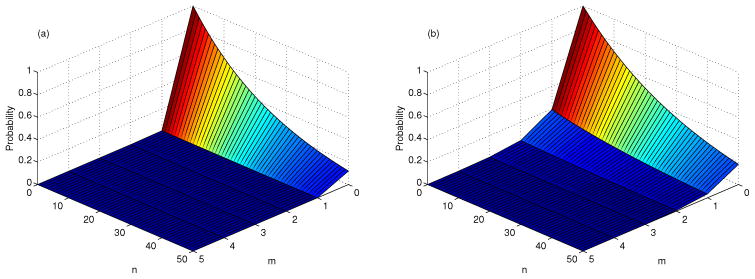
For the CTMC model, estimates for the probability of extinction are calculated. Estimates for (q₁, q₂) in the bursting case are: (0.005029, 0.9585) and in the budding case are (1/ , q₂), where q₂ is defined in (23): (0.1920, 0.9663). (See Table 4 and Figure 2.) A viral invasion is initiated with Y⃗ (0) = (I(0), V (0)) = (0, n). For this initial condition, there is a slight difference in the probability of virus extinction, $q_2^n$, between the two release strategies, although q_2,burst < q_2,bud. But there is a significant difference in probability of virus extinction if a cell is initially infected, I(0) = m, q_1,burst ≪ q_1,bud; the probability of extinction is close to zero in the bursting model, m ≥ 1.

Table 4.

Estimates of (q₁, q₂) for the CTMC model with no immune response

β			bursting, (q1, q2)	budding, (q1, q2)
1 × 10−7	2.28	5.21	(0.005029, 0.9585)	(0.1920, 0.9663)
2 × 10−7	3.16	10.0	(0.00002976, 0.9200)	(0.1000, 0.9280)
1 × 10−6	6.15	37.9	(0.0, 0.6970)	(0.0264, 0.7050)
2 × 10−6	7.62	58.1	(0.0, 0.5349)	(0.0172 0.5429)

Figure 2.

Probability of virus extinction, given T (t) = T̄, I(0) = m, V (0) = n, β = 1 × 10⁻⁷, = 2.28, and = 5.21, (a) bursting, (b) budding.

Pearson et al. [27] obtained the same estimates for q₁ and q₂ and showed that q_2,burst < q_2,bud for burst sizes N ≥ 2. In addition, they showed that if βT̄/(c + βT̄) ≈ 1, then q_2,burst ≈ 0 and q_2,bud ≈ 1/N and if the burst size approaches infinity, N → ∞, then q₂ → c/(c + βT̄) for both budding and bursting (follows from equations (20) and (24) and Figure 2, p. 5, [27]).

In the absence of infection, equation (15), the probability density of the healthy target cells T (t) has an expectation and a variance that are approximately equal. For the parameter values in Table 1, the probability density of T (t), based on equation (15) has an expectation (T (t)) = T̄ = 10⁶ and variance Var(T (t)) ≈ 10⁶. An approximation to the probability density function is graphed in Figure 3. The distribution is approximately normally distributed.

Figure 3.

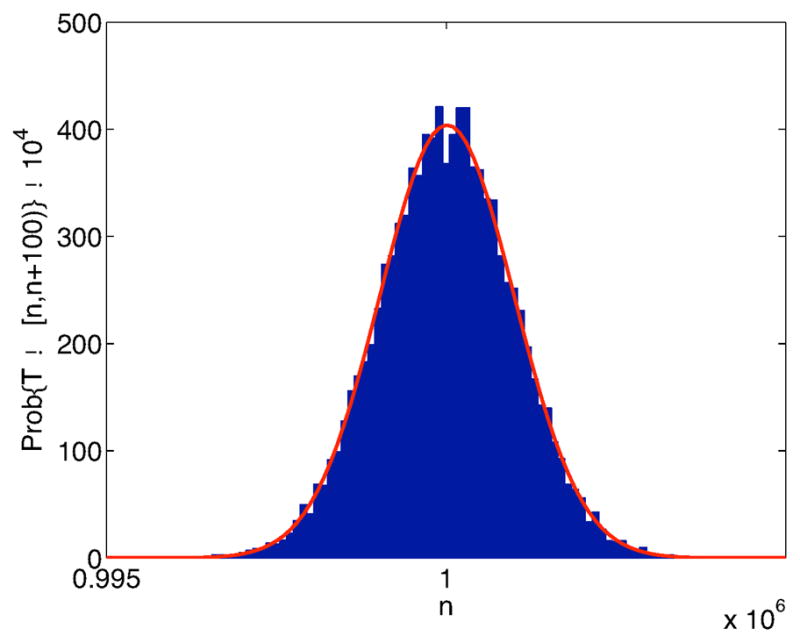
Approximate stationary probability density function for healthy target cells T (t) in the absence of infection, equation (15). The solid curve is the normal approximation to the density.

If V (0) = 1000, then the probability of virus extinction is approximately zero, that is, the virus will persist in the host. In this case, the solutions approach a stationary distribution. The expectation of the stationary solution of the SDE models for bursting (14) and budding (16) are approximately equal to each other and equal to the EE of the ODE model, equilibrium (A.2) (Appendix A2). (See Figure 4.) Based on 10,000 sample path solutions to (14) (or 16), the expectations are

Figure 4.

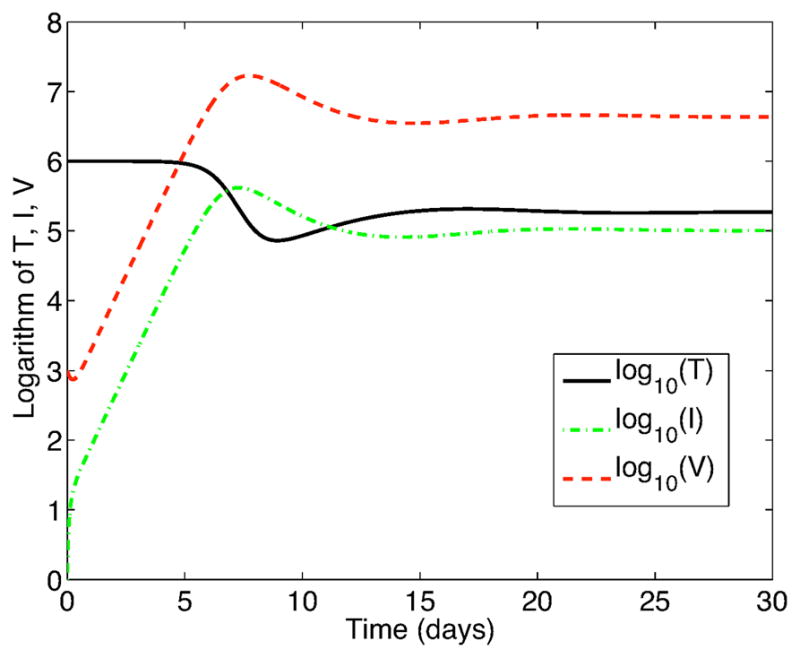
Expectation of 10,000 sample paths of the SDE models, systems (14) and (16), with no immune response, γ⁽ⁱ⁾ = 0, i = T, I, V, = 2.28.

$$\mathbb{E}(T)=1.86\times {10}^5,\mathbb{E}(I)=1.01\times {10}^5,\mathbb{E}(V)=4.35\times {10}^6.$$

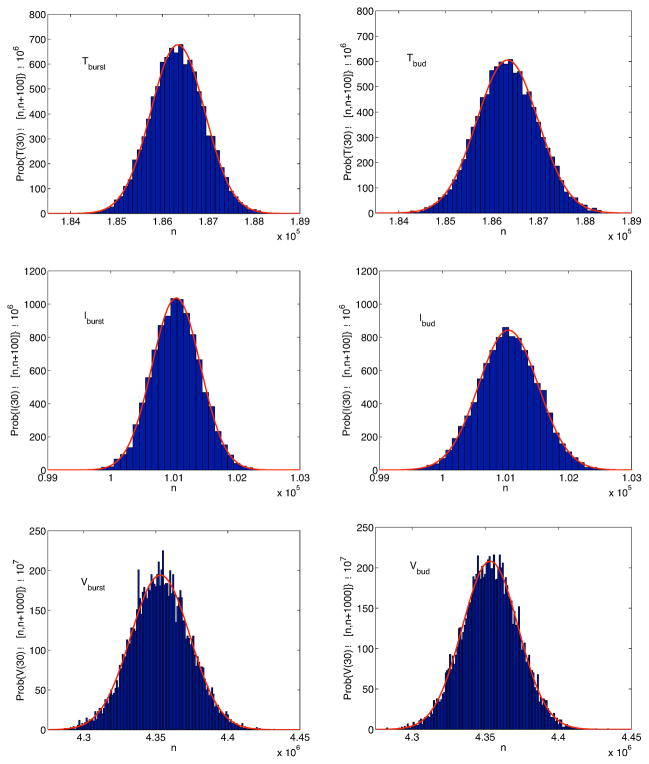
Approximate stationary distributions for each of the random variables are attained by t = 30 days. The distributions are graphed in Figure 5.

Figure 5.

Approximate stationary distribution for T, I and V for systems (14) and (16) at t = 30 days with no immune response, γ⁽ⁱ⁾ = 0, i = T, I, V and = 2.28. Each distribution is fit to a normal curve (solid curve). The standard deviations σ_burst and σ_bud for each of the distributions are σ_burst(T) = 600, σ_burst(I) = 380, σ_burst(V) = 2.06 × 10⁴, and σ_bud(T) ≈ 660, σ_bud(I) ≈ 470, σ_bud(V) ≈ 1.90 × 10⁴.

5.2. HIV-1 with Immune Response

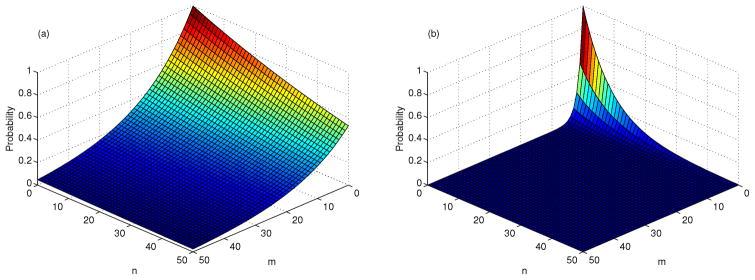
For the model with γ⁽ⁱ⁾ > 0, the parameter values are given in Table 1. Let β = 2 ×10⁻⁶ so that > 1. In particular, = 1.41 and = 1.99. For the CTMC model, estimates for (q₁, q₂) in the bursting case are: (0.9409, 0.9873) and in the budding case are (0.5022, 0.8929). (See Table 5.) The probability of extinction $q_1^m{q}_2^n$ is graphed in Figure 6.

Table 5.

Estimates of (q₁, q₂) for the CTMC model with immune response.

β			bursting, (q1, q2)	budding, (q1, q2)
1 × 10−6	1.06	1.12	(0.9851, 0.9982)	(0.8964, 0.9875)
2 × 10−6	1.41	1.99	(0.9409,0.9873)	(0.5022, 0.8929)
1 × 10−5	2.32	5.35	(0.9262, 0.9574)	(0.1868, 0.5300)
2 × 10−5	2.60	6.78	(0.9260, 0.9458)	(0.1474, 0.3754)

Figure 6.

Probability of virus extinction, given T (t) = T̄, I(0) = m, V (0) = n, β = 2 × 10⁻⁶, = 1.41, and = 1.99, (a) bursting, (b) budding.

The values of (q₁, q₂) are computed for various values of β in Table 5. Given the explicit expression for q₂ in (23), it can be seen that as the transmission rate β or the burst size N increases, the value of q₂ decreases, resulting in a smaller probability of virus extinction. With immune system activation and parameter values appropriate for HIV-1, there is a distinct difference between the success of a viral invasion with bursting versus budding. With the budding strategy, there is a much lower probability of virus extinction than with bursting.

For V (0) = 1000, the viral invasion is successful, independent of the strategy; solutions to the SDEs approach an approximate stationary distribution by time t = 30 days. The expectation of these distributions for the SDE models for bursting (14) and budding (16) are approximately equal to each other and equal to a locally stable EE of the ODE model. (See Figures 7 and 8.) Based on 10,000 stochastic realizations of model (14) (or (16)), the expectations are

Figure 7.

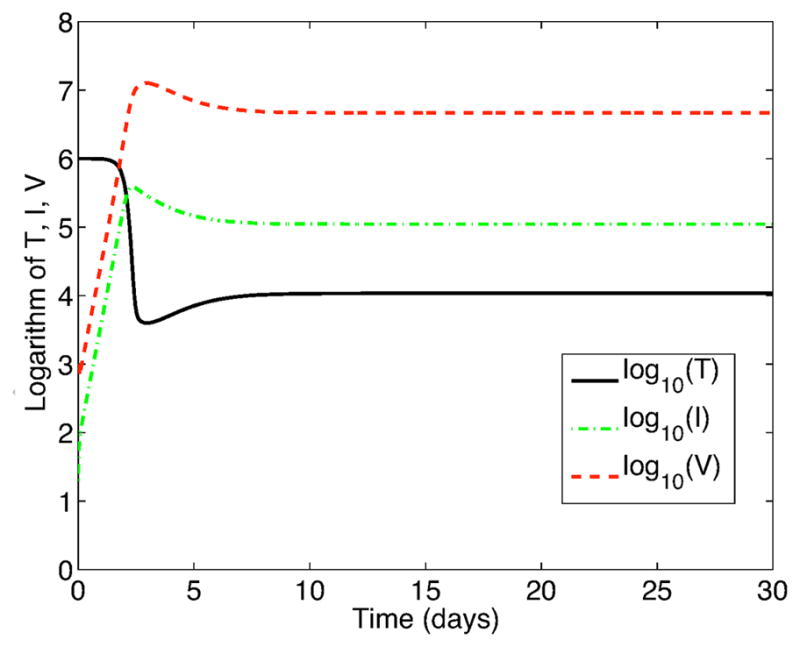
Expectation of 10,000 sample paths of the SDE models, systems (14) and (16), with immune system activation, = 1.41.

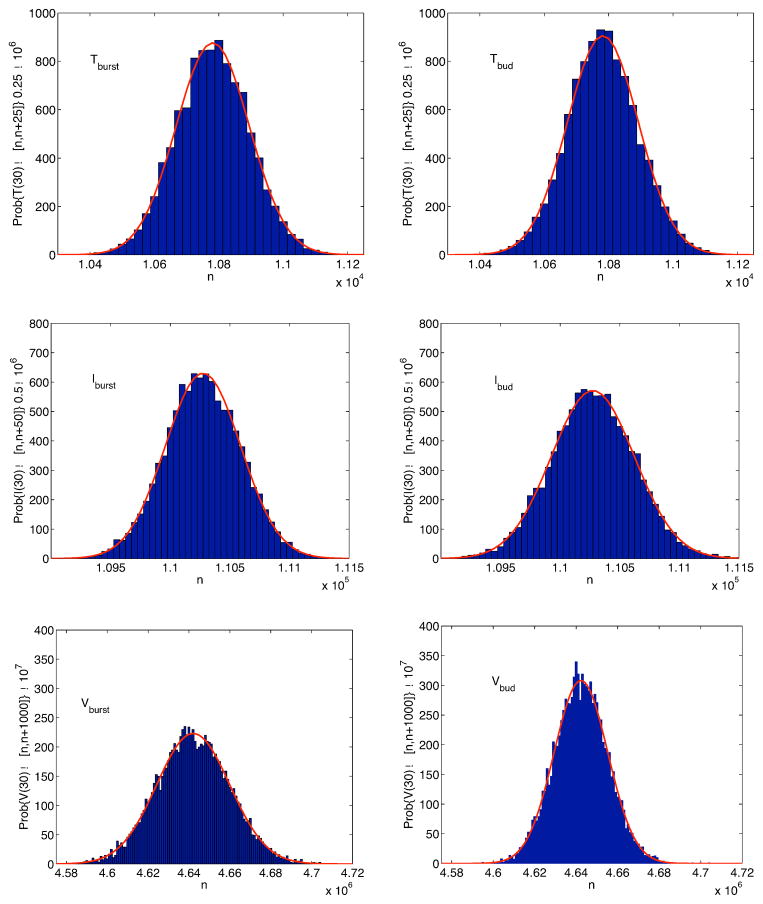
Figure 8.

Approximate stationary distribution for T, I and V for systems (14) and (16) at t = 30 days with an immune response. Each stationary distribution is fit to a normal curve (solid curve). The standard deviations σ_burst and σ_bud for each of the distributions are σ_burst(T) = 112, σ_burst(I) = 316, σ_burst(V) = 1.80 × 10⁴, and σ_bud(T) ≈ 111, σ_bud(I) ≈ 344, σ_bud(V) ≈ 1.30 × 10⁴.

$$\mathbb{E}(T)=1.08\times {10}^5,\mathbb{E}(I)=1.10\times {10}^5,\mathbb{E}(V)=4.64\times {10}^6.$$

As might be expected the variance in the virions is larger in the bursting strategy than in the budding strategy.

6. Summary and Discussion

Our goal in this investigation was to apply stochastic techniques that can be used in conjunction with ODE models to assess the importance of viral release strategy, viral dose, and the immune response in viral invasion and persistence. ODE models for intra-host viral infection with and without an immune response, models (1)–(3) and (5)–(7), provided the motivation for our stochastic model development. Explicit expressions for the basic reproduction number and the type reproduction number were obtained for the ODE models.

New stochastic models, SDE models and CTMC models, were derived based on the assumptions in the ODE models. It was shown for the CTMC models that if ≤ 1, then with probability one, there is virus extinction. But if > 1, the probability of virus extinction is less than one. The success of the viral invasion was studied with respect to the immune response, viral dose, and release strategy, either bursting or budding.

In the CTMC model with no immune response, it was found that the bursting strategy is more successful at viral invasion than the budding strategy. This result was demonstrated with parameter values applicable to HIV-1 but it is independent of the choice of parameter values, as shown by Pearson et al. [27]. The difference in extinction for the two strategies is slight if the infection is initiated with a low viral load, V (0) = n, and no infected cells I(0) = 0 but is much greater if the infection is initiated with V (0) = 0 and I(0) = m (see Table 4 and Figure 2).

In the CTMC with an immune response, applicable to HIV-1, with the helper T cells at normal levels and for parameter values appropriate for HIV-1, it was found that the budding strategy rather than bursting is more successful at viral invasion. The more successful strategy switches from bursting when there is no immune response to budding when there is an immune response. The differences in the probabilities of extinction for these two strategies are much greater in the presence of an immune response. A possible reason for the more successful strategy to be budding rather than bursting is that small numbers of virions may bud off and invade an infected cell without being detected by the immune system. The implicit delay before bursting of new virions may allow the CTLs to detect and destroy infected cells. Pearson et al. [27] showed that even without an immune response, with bursting, the infection takes longer to establish than with budding. However, it must be noted that model (5)–(7) is a simplified characterization of the immune response applicable to HIV-1 and does not account for the many complex chemical and cellular interactions typical of an immune response. Whether the more successful budding strategy is the preferred strategy of HIV-1 infection when CTLs and B cells have been activated remains to be tested.

When the viral invasion is successful, V (0) ≫ 0 and > 1, the ODE and SDE models predict that the virus persists. The expectation of the random variables in the SDE models agree with the endemic equilibrium of the ODE models. The SDE models provide additional information about the distribution associated with the target cells, infected target cells, and virions. At the chronic infection level, with or without the immune response, the coefficient of variation, the ratio of standard deviation to mean, is on the order of 1 ×10⁻³ to 5 ×10⁻³. The small values for the coefficient of variation indicate a low level of variation in T, I and V after the infection becomes established. The largest variation is present in the viral load for the bursting strategy. Therefore, these SDE models for HIV-1 infection indicate that after viral establishment, the stochastic fluctuations in viral levels are less significant than during the early stages of infection. But it must be noted that there may be additional variability in the immune response not accounted for in the CTMC and SDE models due to more complex cellular interactions or to the variability between individuals as a result of past history, behavior, co-infection, sex, or genetics.

Although the models studied in this investigation are simple and apply parameter values appropriate to HIV-1, the techniques applied in this investigation can be used to investigate more general models of virus and immune system dynamics. In the model (5)–(7), the immune system is already activated; there are no delays, no spatial variation and no explicit modeling of some of the important immune system components. In a more general spatial, virus-antibody model, analyzed by Komarova [20], some of the same findings were obtained as in this investigation. That is, if the virus replication rate and the antibody responses are the same for both the budding and bursting strategies, then the budding strategy is more successful because it enables the virus to spread faster. But in some cases the bursting strategy may be advantageous for the virus. For example, if the diffusion coefficient of the antibodies is small, with the bursting strategy, new virions can flood the antibodies allowing a greater number of viruses to escape and infect new cells [20].

Further detailed modeling efforts are needed to accurately describe mechanisms involved in the release of viruses from infected cells. Enveloped viruses are generally released by budding from intracellular membranes, whereas, nonenveloped viruses are generally cytolytic, that is, the virus is released following cell lysis [9, 32, 34]. Some exceptions occur. For example, simian virus 40, a nonenveloped virus, is released from epithelial cells without cell lysis [9]. Both release strategies have been observed in HIV-1, an enveloped virus [15]. Therefore, the importance of the viral envelope to the release strategy is unclear. Modeling and analysis of the patterns of behavior of the virus under various assumptions about its release from the host cell will provide valuable insights for control and treatment of viral diseases.

Research Highlights.

• New stochastic virus-cell models distinguish between two viral release strategies.

• In the absence of an immune response, bursting is more successful than budding.

• With an immune response, in a model for HIV-1, budding is more successful

Appendix A. Appendix

Appendix A.1. Next Generation Matrix

To define the basic reproduction number and to verify local stability, denote the vectors 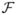and 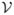, the inflow and outflow from disease compartments I and V as follows:

$$\mathcal{F}=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\end{array}\right)=\left(\begin{array}{c}\beta VT\\ \pi I\end{array}\right),\mathcal{V}=\left(\begin{array}{c}{\mathcal{V}}_1\\ {\mathcal{V}}_2\end{array}\right)=\left(\begin{array}{c}({\delta }_I+{\gamma }^{(I)}T)I\\ (c+({\gamma }^{(V)}+\beta )T)V\end{array}\right).$$

Let x = (x₁, x₂) = (I, V) and y = T so that 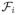≡ 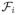(x, y) and 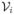≡ 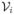(x, y), i = 1, 2. Five conditions are needed to verify local asymptotic stability of the DFE and to define a basic reproduction number [41].

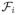1. (0, y) = 0 and 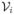(0, y) = 0 for y ≥ 0.

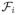2. (x, y) ≥ 0 for all nonnegative x and y.

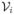3. (x, y) ≤ 0 if x_i = 0, i = 1, 2.

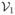4. (x, y) + 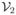(x, y) ≥ 0 for all nonnegative x and y.

5. The disease-free system ẏ = h(0, y) has a unique equilibrium that is asymptotically stable.

It is straightforward to verify that all five conditions are satisfied [44]. For example, condition (5) written in terms of T is

$$\stackrel{.}{T}=\lambda (1-T/K)-{\delta }_{T}T=\lambda \left(1-\frac{T}{\overline{T}}\right)$$

from which it follows that T = T̄ is globally asymptotically stable.

We compute the 2 × 2 Jacobian matrices, evaluated at the DFE,

$$\mathbb{F}=\left(\frac{\partial {\mathcal{F}}_i}{\partial x_j}(0,\overline{T})\right)\text{and}\mathbb{V}=\left(\frac{\partial {\mathcal{V}}_i}{\partial x_j}(0,\overline{T})\right),$$

that is,

$$\mathbb{F}=\left(\begin{array}{cc}0& \beta \overline{T}\\ \pi & 0\end{array}\right)\text{and}\mathbb{V}=\left(\begin{array}{cc}{\delta }_I+{\gamma }^{(I)}\overline{T}& 0\\ 0& c+({\gamma }^{(V)}+\beta )\overline{T}\end{array}\right).$$

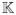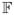
The next generation matrix is = 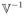defined in (9).

Appendix A.2. Stability of the DFE and EE

Model (1)–(3) and more general models with different growth rates for healthy T cells were analyzed by De Leenheer and Smith [10]. The definition of used by De Leenheer and Smith [10] differs from the definitions given in (12) and (13), but is equivalent to them in terms of being a threshold.

Assume the initial conditions are positive for T and V and nonnegative for I and, in addition,

$$T(0)+I(0)\in (0,\overline{T}].$$ (A.1)

De Leenheer and Smith [10] proved if < 1, then the DFE is globally asymptotically stable and if > 1, the DFE is unstable and there exists an EE, a chronic disease state. For our model, the chronic disease state is

$$(T_c,I_c,V_c)=\left(\frac{c{\delta }_I}{\beta (\pi -{\delta }_I)},\frac{\lambda }{{\delta }_I}\left[1-\frac{T_c}{\overline{T}}\right],\frac{\lambda }{\beta T_c}\left[1-\frac{T_c}{\overline{T}}\right]\right).$$ (A.2)

Note that T_c < T̄ < λ/δ_T and δ_I ≥ δ_T implies T_c + I_c < T̄. Sufficient conditions for global asymptotic stability of the EE require another condition

$$\beta \lambda -min\{{\delta }_T+\lambda /K,{\delta }_I\}{\delta }_I<0.$$ (A.3)

The following theorem summarizes the results for model (1)–(3), a special case of a more general model studied in [10].

Theorem 3

(Theorem 2.1, [10]) Assume the initial conditions satisfy condition (A.1).

1. If < 1 (or < 1), then the DFE (8) of model (1)–(3) is globally asymptotically stable.

2. If > 1 (or > 1) and if condition (A.3) is satisfied, then the EE (A.2) of model (1)–(3) is globally asymptotically stable.

Global asymptotic stability of the DFE (8) in model (5)–(7) can be verified under two restrictions:

$$T(t)\le \overline{T}=\frac{\lambda K}{\lambda +K{\delta }_T}$$ (A.4)

and

$${\mathcal{R}}_0^{\prime }=\sqrt{\frac{\pi \beta \overline{T}}{{\delta }_I(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})}}<1.$$ (A.5)

With the restriction γ^(T) = 0, ${\mathcal{R}}_0^{\prime }={\mathcal{R}}_0$. However, condition (A.5) is more restrictive than < 1, where is defined in (12) since ${\mathcal{R}}_0<{\mathcal{R}}_0^{\prime }$. In particular, it may be the case that ${\mathcal{R}}_0<1<{\mathcal{R}}_0^{\prime }$.

To verify global stability of the DFE for model (5)–(7), a Liapunov function is defined:

$$L(T,I,V)=(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})I+\beta \overline{T}V.$$

To show global asymptotic stability and apply Liapunov’s direct method [21], L(T, I, V) ≥ 0, L(T, I, V) = 0 only if I = 0 = V, and L̇ (T, I, V) ≤ 0 with L̇(T, I, V) = 0 only if I = 0 = V and T = T̄. The first conditions on L are easily satisfied.

Calculating the derivative of L along solution trajectories leads to

$$\stackrel{.}{L}(T,I,V)=\beta Vc(T-\overline{T})-[(c+{\gamma }^{(V)}\overline{T}+\beta \overline{T})({\delta }_I+{\gamma }^{(I)}T)-\beta \pi \overline{T}]I.$$

Thus, if (A.4) and (A.5) are satisfied, the conditions on L̇ required of a Liapunov function are satisfied. If I = 0 = V for model (5)–(7), then T (t) = T̄ is the only invariant set. The sufficient conditions for global stability of the DFE for model (5)–(7) are summarized in the following theorem.

Theorem 4

Assume the initial conditions (A.1) and conditions (A.4) and (A.5) are satisfied. Then the DFE (8) of model (5)–(7) is globally asymptotically stable.