Probabilistic Elastography: Estimating Lung Elasticity

Abstract

We formulate registration-based elastography in a probabilistic framework and apply it to study lung elasticity in the presence of emphysematous and fibrotic tissue. The elasticity calculations are based on a Finite Element discretization of a linear elastic biomechanical model. We marginalize over the boundary conditions (deformation) of the biomechanical model to determine the posterior distribution over elasticity parameters. Image similarity is included in the likelihood, an elastic prior is included to constrain the boundary conditions, while a Markov model is used to spatially smooth the inhomogeneous elasticity. We use a Markov Chain Monte Carlo (MCMC) technique to characterize the posterior distribution over elasticity from which we extract the most probable elasticity as well as the uncertainty of this estimate. Even though registration-based lung elastography with inhomogeneous elasticity is challenging due the problem's highly underdetermined nature and the sparse image information available in lung CT, we show promising preliminary results on estimating lung elasticity contrast in the presence of emphysematous and fibrotic tissue.

1 Introduction

Lung function is closely related to the mechanical properties of lung parenchyma which is in turn determined by the orientation and proportion of the elastin and collagen fibers in the tissue matrix. The disparate properties of these tissues provide both the natural lung elastic recoil necessary for passive exhalation as well as the structural support for the pulmonary vasculature and airways. Diseases of the lung that alter lung function often do so by altering amounts of elastin and collagen [12].

In clinical practice, lung function tests are used to assess the severity of chronic lung diseases such as chronic obstructive pulmonary disease (COPD) and pulmonary fibrosis. While these tests are simple and safe to do, they reflect aggregate lung function and are unable to differentiate the relative amounts of emphysema or scarring that may be found in the lung of a smoker. In these cases, clinicians often turn to CT to assess both the extent and distribution of lung disease. A common method employed for the detection and quantification of emphysema is based upon lung densitometry, i.e. voxels with values less than e.g. −950 HU are indicative of emphysematous tissue. A clear limitation to this observation is that the detection of abnormal tissue is not followed by an assessment of its mechanical properties.

In [5], image registration was proposed as a way of monitoring emphysema progression in lung CT. They align a baseline CT scan with a follow-up scan and relate intensity differences between the two images, corrected for intensity differences due to local tissue expansion and compression, to the disease progression. Yin et al. [13] propose a similar approach to handle differing intensity levels due to compression/expansion when matching inspiration to expiration images of the lung, however, their results do not significantly improve over using a standard sum of squared difference similarity measure.

Elastography is a non-invasive method to determine local elastic properties, e.g. Young's modulus. One approach to elastography imaging is to apply a low frequency oscillation to the tissue and measure the resulting deformations with ultrasound (US). The elasticity of the material can be extracted from the observed movement of the slowly oscillating tissue, e.g. to distinguish healthy from abnormal tissue. In Magnetic Resonance Elastography (MRE), a synchronized cyclic shear wave displacement is encoded into the phase of the MR signal. Because of the air in the lung, it has been difficult to perform elastography imaging of the lung. However, McGee et al. [6] recently showed it technically feasible to do MRE of the lung using hyperpolarized 3He. They present results on estimation of the shear modulus of an ex vivo porcine lung in 2D. The main challenges with using this method for estimation of elasticity in COPD patients are signal to noise ratio and relatively long acquisition times.

Another approach to elastography is taken by Miga et al. [7] who introduce modality independent registration-based elastography to estimate tissue stiffness. Given two, potentially multi-modal, images of an object undergoing an elastic deformation, they minimize a modality independent similarity measure with regards to the elastic parameters. The method uses a Finite Element (FE)-discretization of the solution domain and the linear elastic energy, and it requires as input the boundary conditions of the biomechanical model, i.e. the deformation of the boundary of the FE-mesh. In Ou et al. [8], the same group applies the method to study elasticity of breast lesions and shows that the estimates can be quite sensitive to the boundary conditions. In some cases, the linear elastic assumption, i.e. geometric linearity of the strain tensor and linear stress-strain response of the tissue, might not be reasonable. Gokhale et al. [4] use a hyperelastic model of soft tissue and minimize a cost function representing the difference between the measured and predicted displacement fields. However, their results are preliminary – they only apply the method to 2D synthetic images.

Among the most sophisticated current methods for registering intra-patient images are those based on biomechanical modeling of tissue deformation where specific material parameters that reflect the underlying tissue properties can be included. However, reported material parameters for many tissue types are estimated from in-vitro samples and quite divergent. Furthermore, it is unknown how medication and tissue pathologies might affect the material parameters. We have recently shown the feasibility of determining the posterior distribution over registration parameters restricted by a linear elastic biomechanical model discretized by a FE method [9, 10]. To avoid using point-estimates for the material parameters, we showed in [9] how the material parameters can be marginalized out of the posterior by modeling them as random variables with broad priors. The method was applied in the realm of intra-operative registration of brain images with a very coarse spatial distribution of the elastic parameters: a three compartment model (cerebrospinal fluid, white matter, gray matter).

In this paper we estimate the posterior distribution over the inhomogeneous elastic modulus without any prior information regarding the underlying tissue labels. To reduce the sensitivity of the approach to boundary conditions (deformation), we propose to marginalize over the boundary condition of the biomechanical model. An MCMC method, where marginalization over parameters is easily achieved, is designed to characterize the posterior distribution. We show how important application dependent estimates, such as the most probable elasticity parameters and their corresponding uncertainty, can be derived from our results. Preliminary lung elastography experiments are carried out on both synthetic and clinical lung inspiration/expiration CT data which shows the feasibility of the method.

2 Methods

The deformation u of an elastic object Ω, e.g. the lung, caused by a static loading, can be explained by a biomechanical model. It is common to separate the deformation into the boundary deformation u_b which occurs on ∂Ω and the internal deformation u_i in Ω \ ∂Ω. The parameters of a linear elastic biomechanical model are usually defined in terms of the Young's modulus E (stiffness) and Poisson's ratio v (compressibility). Suppose we are given the Dirichlet (deformation) boundary condition u_b, then the permissible elastic deformation u is parameterized by the unknown inhomogeneous elastic parameters. In this paper we label the unknown elastic parameters θ and note that they can be E, v, or both depending on the situation. In registration-based elastography, we maximize the similarity between two images of Ω acquired under different static loading by adjusting the elastic properties of the biomechanical model.

2.1 Probabilistic Elastography

We treat u_b and θ as unknown random variables and pose registration-based elastography in a Bayesian framework where we marginalize over u_b to get at the posterior distribution over θ:

$$p\left(\theta |I_i,I_e\right)\propto {\int }_{{\text{u}}_b}p\left(I_i,I_e|\theta ,{\mathbf{\text{u}}}_b\right)p\left({\mathbf{\text{u}}}_b|\theta \right)p\left(\theta \right).$$ (1)

Our likelihood model estimates the similarity between two images, I_i(x) (inspiration image) and I_e(x) (expiration image) for x ∈ Ω, given the elastic parameters θ(x), x ∈ Ω, and the boundary conditions u_b(x), x ∈ ∂Ω. A prior on u_b puts low probability on configurations with high elastic energies, and a spatial prior on the elastic parameters is included to constrain them to be relatively smoothly varying. We employ a Markov Chain Monte Carlo (MCMC) sampling approach to characterize the posterior distribution. An advantage of MCMC is that marginalization over random variables is easily carried out, and from the posterior distribution we can estimate the most probable estimate and assess the uncertainty of this estimate. In the following sections we describe the main components of the proposed elastography method.

Biomechanical Model

The linear elastic energy of an elastic body Ω with elastic material parameters θ and deformed by u is defined as:

$${\mathit{\text{E}}}_{\mathit{\text{elastic}}}\left(\mathbf{\text{u}},\theta \right)= {\int }_{\Omega }\epsilon {\left(\mathbf{\text{u}}\right)}^T\mathbf{\sigma }(\mathbf{\text{u}},\theta )d\mathbf{\text{x}},$$ (2)

where ε is the engineering strain vector and σ is the engineering stress vector [2]. We discretize Eq. (2) with a Finite Element (FE) model of the displacement field. The volumetric solid Ω is discretized into a tetrahedral FE mesh which consists of nodes n_b = {n_b¹,…n_b^B} on ∂Ω, nodes n_i = {n_i¹…n_i^I} on Ω \ ∂Ω and P tetrahedral finite elements Ω_e such that ∩_e=1…PΩ_e = ∅ and ∪_e=1…PΩ_e = Ω. The elastic parameters are defined per element, however, the space of unknown elastic parameters can be reduced by, e.g., grouping together elements or defining another lower dimensional material space and interpolating per element from this space. We discretize the elastic parameters per FE node and use the FE machinery to linearly interpolate these parameters to each element. Consequently, since u_i can be computed by minimizing Eq. (2) given u_b and θ, the unknowns in our biomechanical model are the B boundary deformation vectors u_b and the Q = B + I material parameters θ.

We construct a prior on the boundary deformation parameters u_b by including the elastic energy in a Boltzmann's distribution with a temperature T_e:

$$p\left({\mathbf{\text{u}}}_b|\theta \right)=\frac{1}{Z}exp(-E_{\mathit{\text{elastic}}}/T_e).$$ (3)

Similarity Model

We incorporate an intensity-based similarity measure to estimate the likelihood of observing the two images given the elastic parameters and the boundary deformation. From the elastic parameters and the boundary deformation, we can find the internal deformation u_i by minimizing Eq. (2). Any similarity measure that can be formulated as an energy function can be included in the framework, but in this paper we restrict ourselves to the Sum of Squared Differences (SSD) E_SSD = ∫_Ω(I_i(x) − I_e(x + u(x)))²dx. The energy function is converted into a probability by way of the Boltzmann distribution:

$$p\left(I_i,I_e|\theta ,{\mathbf{\text{u}}}_b\right)=\frac{1}{Z}\text{exp}(-E_{\mathit{\text{SSD}}}/T_s),$$ (4)

where Z_s is a normalizing constant and T_s is the temperature of the distribution. This is equivalent to modeling the similarity distribution with independent zero-mean Gaussian distributions with a variance of T_s/2 for each voxel.

Spatial Prior on Elasticity

Registration based elastography is an underdetermined problem which benefits from including prior knowledge into the estimation process. Furthermore, in areas where there is a lack of image information, the method will favor soft tissue because that will reduce the elastic energy. Our framework includes an elasticity prior which can be used to regularize elasticity at neighboring nodes. We incorporate a prior distribution on the elastic parameters in the form of a Markov model which penalizes the difference in the elastic parameters of neighboring nodes:

$$p\left(\theta \right)=\frac{1}{Z}\prod _{c}exp(-E_c({\theta }_c)/T_c),$$ (5)

where T_c is the temperature and c = {n_i, n_j} denotes a clique where n_i and n_j are nodes in the FE-mesh connected by an element. The clique energy is defined as E_c(θ_c) = (θ(n_i) − θ(n_j))². Many organs have relatively homogeneous tissue characteristics (e.g. liver and prostate), while others might have more heterogeneous tissue characteristics (e.g. an unhealthy lung which exhibits emphysema and fibrotic tissue), so the “temperature” T_c can be set according to the prior knowledge we have about tissue homogeneity.

2.2 Sampling the Posterior Distribution

We propose to fully characterize the posterior distribution over the elastic parameters by generating samples from the posterior. Unfortunately, because of the complexity of the posterior, it is not possible to draw samples directly from it. Instead, we use a Markov Chain Monte Carlo (MCMC) (Metropolis-Hastings) method to draw samples from the posterior [3]. It constructs a Markov chain that after a sufficient burn-in period has the posterior distribution as its stationary distribution. The necessary burn-in period is dependent on the initial parameters where a poor choice of starting values can require a long burn-in period. Finding optimal starting points for MCMC estimation is currently an area of much research, but the general advice is to initialize the chain with estimates as close to the center of the distribution's mode as possible [3].

The marginalization of the boundary deformation is easily achieved with a MCMC method by sampling (θ*, u_b*) ∼ p(θ, u_b | I_i, I_e) and “discarding” the u_b* samples. In practice, we start with an initial estimate of the parameters, τ⁰ = (θ⁰, u_b⁰), and generate candidate samples τ̂ from a proposal distribution q(τ | τ^t−1) which only depends on the previous sample τ^t−1. Candidate samples are accepted with probability

$$A\left(\widehat{\tau },{\tau }^t\right)=min(1,\frac{p\left(\widehat{\tau }|I_i,I_e\right)}{p\left({\tau }^t|I_i,I_e\right)}).$$ (6)

If a sample is accepted we set τ^t+1 = τ̂, otherwise τ_t+1 = τ^t.

To reduce the autocorrelation between subsequent samples from the chain and to reduce the memory/storage footprint, thinning of the chain is common procedure, i.e. to discard every k-th sample. After burn-in and thinning we have a set of statistically independent samples {τ⁰,…, τ^N} from the posterior distribution.

Proposal Distributions

Because the two parameter sets u_b and θ are different in nature, we split the parameters into two blocks from which proposal samples are generated independently: q(u_b, θ|u_b^t−1, θ^t−1) = q(u_b|u_b^t−1) q(θ|θ^t−1). A proposal boundary deformation is generated from a univariate normal distribution û_b ∼ q(u_b|u_b^t−1) = N(u_b; u_b^t−1, σ_d²) centered on the previous estimate u_b^t−1 and with σ_d² variance. The elastic parameters are sampled from a multivariate Gaussian θ̂ ∼ q(θ | θ^t−1) = N(θ; θ^t−1, σ_e²Σ) centered on θ^t−1 and with covariance σ_e²Σ. We assume that the material at node i is likely to vary closely with node j if they are in proximity of each other. We compute Σ_i,j, the element in the covariance matrix which relates the FE-nodes i and j, by a distance function Σ_i,j = exp(−dist(n_i, n_j)/D) where D is a constant.

Preventing Folding of Finite Elements

Folding of the tetrahedral elements should be prevented in our sampling scheme because it constitutes non-physical deformations. The boundary of the mesh consists of nodes and a set of triangles that span these nodes. If we can prevent the sampler from drawing samples which folds the boundary triangles, the minimization of Eq. (2) with respect to the elastic parameters will almost guarantee that the resulting deformation is free from folded elements. One exception may occur, however, when one side of the mesh is “pushed” through the opposite side of the mesh. We assume that the mesh is close to convex, that the two mesh sides are relatively far apart, and that there is enough image intensity information between two sides to restrict such a “collapse” of the mesh.

After sampling u_b, our method searches for folded boundary triangles. When a folded triangle is detected, the deformation of the nodes that span this triangle, as well as any neighboring triangles, are resampled, and this procedure is reiterated until no triangles are folded.

2.3 Summarizing the Posterior Distribution

The local marginal distribution over each random variable contains important information regarding the most probable value and its uncertainty, while the full posterior distribution is a high-dimensional complex object from which complex covariance information can be extracted. Even though we marginalize over the boundary deformations, we still retain the u_b samples so we can summarize both marginal statistics on θ and u_b as well as joint statistics.

A local marginal distribution over one component of θ or u_b is a 1D probability distribution. The mode of this distribution is the most probable estimate and the dispersion of the distribution can be interpreted as the uncertainty of the most probable estimate. We use the Inter Quartile Range (IQR), i.e. the difference between the third and first quartiles, to estimate the statistical dispersion of the samples.

3 Results

We have tested the proposed elastography method on both synthetic and clinical CT lung images, and in this section we report on these experiments and the corresponding results. Based on results from [1], we assume that the lung is somewhat compressible with a Poisson's ratio of 0.4 and restrict ourselves to estimate an inhomogeneous Young's modulus (θ = E).

3.1 Synthetic Experiments

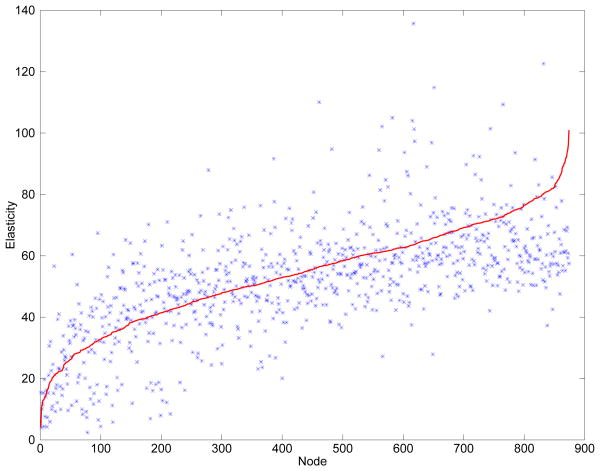
We constructed a synthetic dataset with known ground truth elasticity values and tested the ability of the method to recover them. Our inspiration dataset of size 512×512×419 and spacing (0.95, 0.95, 0.65) mm was acquired from a healthy patient. To reduce the computation time, we downsampled the images by a factor of 2 in each dimension and applied a Gaussian smoothing filter with σ² = 0.5. Slices can be seen in Fig. 1 (d) and (g). A boundary deformation was constructed based on observed deformations between inspiration and expiration datasets. From the geometric center of the right lung, we let the elasticity (Young's modulus) values increase continuously by a factor of 100 up to the part of the lung at the furthest distance from the center. Using the synthetic boundary deformation and the inhomogeneous elasticity, we could construct the full deformation u by minimizing Eq. (2) with regards to the deformation. Using the synthetic deformation, we deformed the inspiration lung into a synthetic “expiration” lung. Figure 1 (b) shows a slice of the synthetic elastography map and (a) shows the deformed “expiration” lung overlaid on the full inspiration dataset. From the inspiration label map we created a tetrahedral FE mesh with 874 nodes and 3603 elements. For the estimation we used parameters T_s = 0.5, T_e = 10⁷, T_c = 300, D = 10mm, σ_d² = 0.005 and σ_e = 0.1, where the temperatures are set so that the likelihood is the predominant term in the posterior. The initial Young's modulus was set to 50 and the boundary deformation was initialized to the ground truth. The sampler generated approximately 7 samples per second. We generated approximately 100 000 samples, discarded the first 50 000 to avoid burn-in effects, and used a thinning factor of 10 to end up with 5 000 independent samples. We computed the mode and IQR and show qualitative results in Fig. 1 and quantitative results in Fig. 2. The method is sensitive to stiffness, but the estimates are scattered around the ground truth value with a relatively high variance which can be explained by the fact that lung CT in some areas contain little image contrast (image information) which may make it difficult for the method to locally estimate a reliable stiffness value. In Fig. 1 we show that the method is able to detect major aspects of the stiffness patterns (the synthetic tissue stiffness increasingly goes from soft in the middle of the lung to stiff on the lung boundary).

Fig. 1.

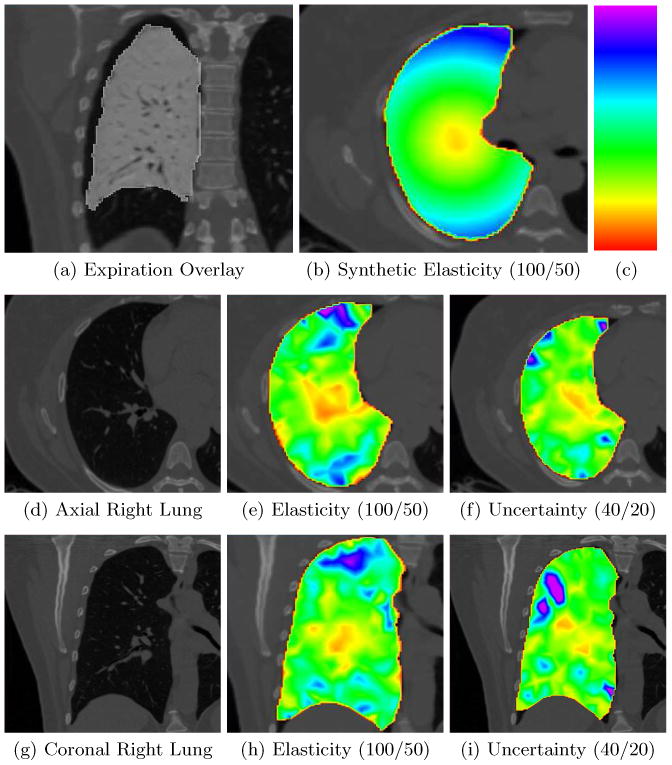
Synthetic data. All values in parentheses describe the window level setting we use to highlight tissue stiffness where the lower value of the window is colored red (softest) and the upper value is colored purple (stiffest) according to the rainbow color scheme included in (c). (a) Synthetic expiration lung with an inverted gray colormap overlaid on the inspiration volume. Notice the large deformations due to expiration. (b) The synthetic elasticity map corresponding to the slice in (d). (d) Axial slice of the inspiration lung volume. (e) Estimated elasticity. (f) The IQR uncertainty map. (g) Coronal slice of the inspiration lung volume. (h) Estimated elasticity. (i) The IQR uncertainty map. Notice that these results are consistent with the results in Fig. 2 where the general stiffness can be estimated, but with large outliers.

Fig. 2.

This figure includes quantitative results on estimating the stiffness (Young's modulus) for the synthetic case (qualitative results are included in Figure 1). The nodes in the plot have been sorted according to ground truth stiffness and plotted in red while the corresponding estimated stiffness is plotted in blue. It is clear from the plot that the method is sensitive to major differences in stiffness, but the estimates are scattered around the ground truth with a relatively high variance. It is also evident that the method does a better job of estimating the stiffness in the middle to the left of the graph than on the far right. The mean of the difference between the estimated values and the ground truth was 2.6 with a standard deviation of 14.5.

3.2 Clinical Experiments

We also tested the method on a clinical dataset which exhibits both fibrotic and emphysematous lung tissue. The original inspiration and expiration CT images have size 512×512×703 and spacing (0.75, 0.75, 0.5) mm, however, to reduce the computation time we downsampled the images by a factor of 2 in each dimension and applied a Gaussian smoothing filter with σ² = 0.5. Labelmasks of both the inspiration and expiration lungs were created using the segmentation method in [11]. From the inspiration labelmask we created a tetrahedral FE mesh with 867 nodes and 3670 elements. The elasticity (Young's modulus) estimates were homogeneously initialized to 1000. An initial deformation can be found e.g. by using a registration algorithm [13], or as we did, by minimizing the distance between u_b and the expiration lung labelmap by way of a distance field generated from the expiration labelmap.

The sampler generated approximately 4 samples per second while using the following parameters T_c = 10000, T_e = 10⁷, T_s = 3.0, σ_d² = 0.005, σ_e = 5 and D = 10mm. Because we wanted to detect local changes in stiffness in unhealthy lungs we used a high temperature for the T_c and T_e, while the similarity temperature was set relatively low to make it the predominant distribution in the posterior. Approximately 200 000 samples were generated, but after discarding the first half as “burn-in” samples and with a thinning factor of 10, we ended up with 10 000 statistically independent samples. Figure 3 shows elasticity results from parts of the lung where there is considerable fibrosis, while Fig. 4 shows elasticity results from an emphysematous part of the lung.

Fig. 3.

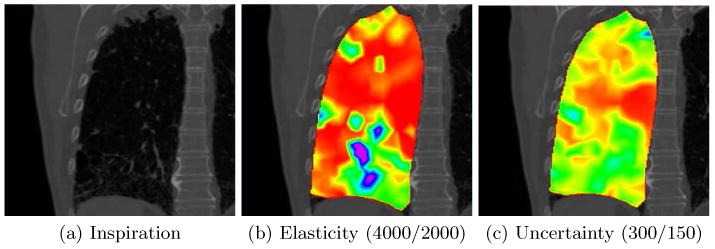
Fibrotic tissue. The elasticity and uncertainty maps are color coded using the rainbow colormap in Fig. 1 (red is soft, purple is stiff) (c) and the window level in parentheses. (a) A coronal slice of the inspiration dataset where the upper and lower part is identified as fibrotic by a physician. (b) Notice how the fibrotic areas in the lower and upper lung appear stiffer than the surrounding tissue, and also that the cyst in the lower left of the image is estimated as “soft” which could mean that it is ventilated and therefore collapses during expiration. (c) The IQR of the estimated elasticity map. The uncertainty is somewhat larger in the stiffer fibrotic area.

Fig. 4.

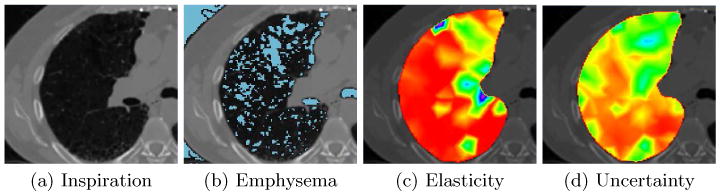
Emphysematous tissue. The elasticity and uncertainty maps are color coded using the rainbow colormap in Fig. 1 (c) and the window levels (4000/2000) and (300/150) for figures (c) and (d) respectively. (a) Axial slice of the inspiration CT dataset. (b) Thresholded image at −950Hu to identify emphysematous tissue and overlaid on the axial slice in (a). (c) Estimated elasticity map. Notice how the elasticity in the lower part of the image is relatively homogeneous, while in the upper area where the emphysema is most predominant it appears stiffer. The reason may be that this emphysematous region is not ventilated and the air filled emphysematous regions do not collapse during expiration. (d) Uncertainty map. We can see that because of the emphysematous regions and consequently the lack of image information, the uncertainty is larger in the area of emphysema compared to non-emphysematous regions.

4 Discussion

This paper has introduced a probabilistic elastography method which can estimate inhomogeneous tissue elasticity given two images of the same object under different external loading. The synthetic results indicate that the method can distinguish between major differences in tissue characteristics. Because expiration causes large deformations and compression of lung tissue, we can expect intensity differences between perfectly aligned inspiration and expiration images because of interpolation artifacts and the fact that compressed tissue in the expiration dataset will appear brighter then the corresponding image in the inspiration image. Lung images also contain regions of relatively homogeneous tissue and sparse image information/contrast which makes it difficult to match the images without prior information. Both the intensity differences and the lack of image information may explain the outliers we see in the synthetic experiments.

It is generally accepted that lung tissue can be modeled as an elastic material. Our method is very computationally intensive, and consequently we used a linear elastic FE-model with tetrahedral elements to limit computation times to approximately 14 hours. Linear elasticity is applicable when we expect infinitesimal strains or small deformations. However, lung deformations due to inspiration/expiration are large, thus the estimated elasticity can only be assumed to be approximate. Better elastography results may be achieved with lung images where the volume change is smaller. Furthermore, because no external or internal forces are used in the biomechanical calculations, we can only estimate elasticity contrast and not the real elasticity. Another limitation of the simple elastic model is that it assumes an isotropic material model which cannot be assumed to be accurate for the highly anisotropic blood vessels in the lung. Also, because some of the blood vessels are quite large and are connected to the exterior of the lung, they may induce external forces on the internal lung tissue. Consequently, the model may be inaccurate around large vessels.

In future work we will increase the number of FE elements to better discriminate between emphysematous, fibrotic and healthy tissue. However, because of the added degrees of freedom, additional prior information needs to be included e.g. through densitometry to identify regions with emphysema and fibrosis or by having additional correspondence information such as vessel or bronchial branches. FE-methods are known to be sensitive to boundary conditions. The covariance between elasticity and boundary estimates can be extracted from the posterior distribution and used to investigate this sensitivity. Even though registration-based elastography is a challenging under-determined problem, we have shown that it is feasible to estimate lung elasticity with a registration based approach. We believe that with better modeling, e.g. through the inclusion of more prior information and finer resolution meshes, the clinical impact of registration based elastography for studying lung function can be substantial, especially since traditional ultrasound and MR elastography is difficult because of the air filled lungs. However, further validation is required, e.g. by comparing our results with histology samples or MRE. A potential high-impact clinical application would be to study the mechanical nature of smoking related lung disease.