Molecular explanation for why talc surfaces can be both hydrophilic and hydrophobic

Abstract

While individual water molecules adsorb strongly on a talc surface (hydrophilic behavior), a droplet of water beads up on the same surface (hydrophobic behavior). To rationalize this dichotomy, we investigate the influence of the microscopic structure of the surface and the strength of adhesive (surface-water) interactions on surface hydrophobicity. We show that at low relative humidity, the competition between adhesion and the favorable entropy of being in the vapor phase determines the surface coverage. However, at saturation, it is the competition between adhesion and cohesion (water-water interactions) that determines surface hydrophobicity. The adhesive interactions in talc are strong enough to overcome the unfavorable entropy, and water adsorbs strongly on talc surfaces. However, they are too weak to overcome the cohesive interactions, and water thus beads up on talc surfaces. Surprisingly, even (talc-like) surfaces that are highly adhesive, do not fully wet at saturation. Instead, a water droplet forms on top of a strongly adsorbed monolayer of water. Our results imply that the interior of hydrophobic zeolites suspended in water may contain adsorbed water molecules at pressures much smaller than the intrusion pressure.

Introduction

Wetting properties of minerals in soils and rocks play a crucial role in the transport, and thus availability, of water and oil. Clay minerals are particularly interesting, not only due to their abundance in nature and in synthetic materials, but also because the existence of clays with different structures allows us to investigate the effect of surface microstructure on macroscopic properties. Clay surfaces can be either charge-neutral or have a net charge, which is balanced by counter-ions in solution. Molecular simulation has furthered our understanding of both these types of clays: uncharged clays have been studied using both abinitio^1,2 and classical simulations,^3,4 whereas simulations of charged clays have provided insights into interlayer properties,^5–8 swelling,^9–12 and cation exchange.^13–15 These studies have shown that the surface microstructure is expected to be more important in determining surface-water interactions in uncharged clays^16,17 and it is these surfaces that are the focus of the current work. Among uncharged clays, talc surfaces have attracted a lot of attention,^18–21 because of their peculiar behavior with respect to water. While chemically different surfaces of the same clay mineral, e.g. kaolinite, may display different affinities for water,^22,23 the fact that the same talc surface appears either as hydrophilic or hydrophobic depending on the relative humidity (RH) is rather surprising. Water adsorption at low RH indeed reveals the presence of strong binding sites on talc.²⁴ Such strong binding sites are absent in similar uncharged clays such as pyrophyllite and fluorotalc. Yet, experimental contact angles indicate that the surface of talc monocrystals is hydrophobic, similar to that of pyrophyllite.^25,26

To investigate this dichotomy, here we employ molecular dynamics simulations combined with recently developed algorithms.^27,28 In agreement with experiments, we find that at low RH, talc surfaces display hydrophilic behavior as water adsorbs strongly to the binding sites on the surface. However, at saturation, cohesive interactions dominate and the interaction between the surface binding sites and water is minimal, resulting in a hydrophobic surface.

To further explore the role of surface microstructure and the strength of the adhesive interactions on surface hydrophobicity, we also study similar clay minerals, pyrophyllite and fluorotalc, as well as modified talc surfaces with a range of binding site polarities, both at low relative humidity and at saturation. We find that the dual hydrophilic-hydrophobic behavior observed in talc, is generically expected to manifest for surfaces whose adhesive interaction energy lies in a special range. If the adhesion to water is strong enough to overcome the entropy of being in the vapor phase at low RH, water adsorbs strongly to the surface (hydrophilic behavior). At the same time, if adhesion is too weak to overcome the cohesive interactions in water, the surface is hydrophobic at saturation. For modified talc surfaces with strong enough adhesion to overcome the cohesive interactions, all surface binding sites are occupied by water molecules at saturation, as expected. Surprisingly, instead of observing complete wetting, we find that a water droplet sits atop the adsorbed water monolayer.

Microscopic Models

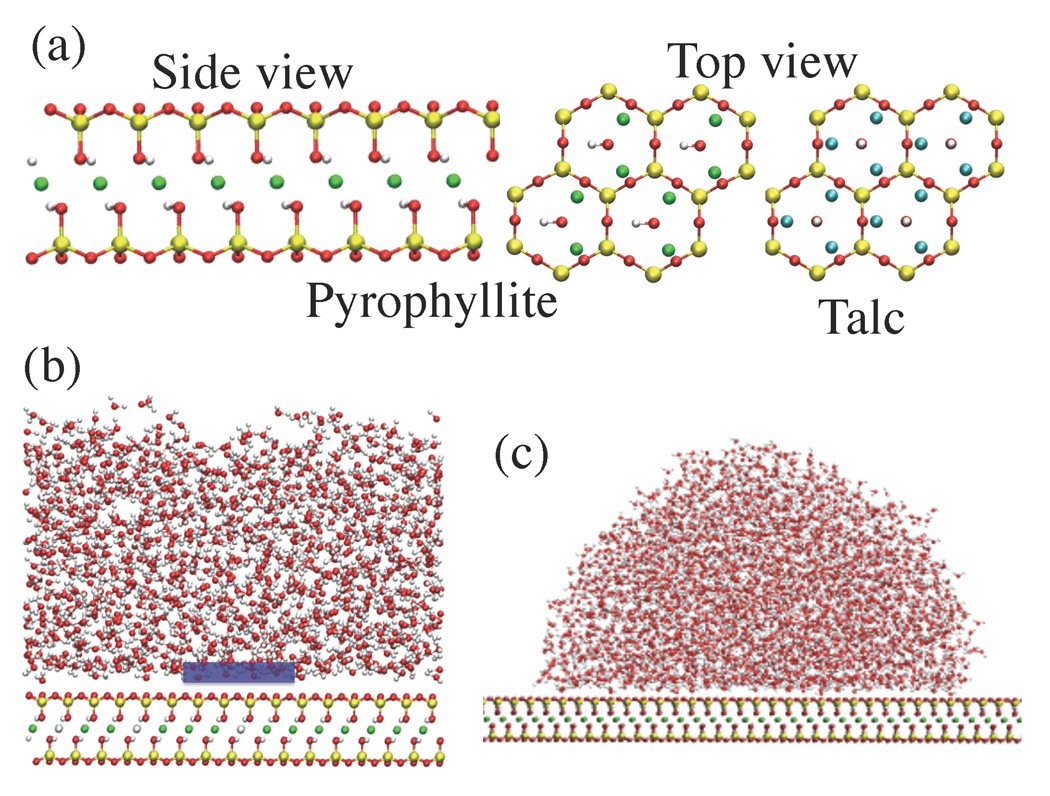
Talc, fluorotalc and pyrophyllite are uncharged clay minerals, i.e., layered silicates of magnesium (Mg) or aluminum (Al). They belong to the family of TOT clays: each clay sheet consists of a layer of octahedrally coordinated Mg or Al oxide between two layers of tetrahedral silicon oxide (see Figure 1(a) - side view). The surface of these sheets displays hexagonal rings of SiO₂ tetrahedra. In talc and fluorotalc, all octahedral sites are occupied by Mg atoms, while in pyrophyllite two third of these sites are occupied by Al atoms (see Figure 1(a) - top view). The charge on Mg and Al is balanced by hydroxyl groups in the center of the hexagonal cavities. In talc, these hydroxyl groups are oriented perpendicular to the surface, and can participate in hydrogen bonds with water. In pyrophyllite, the hydroxyl groups are oriented parallel to the surface, and in fluorotalc, they are replaced by fluorine atoms. The atomic coordinates for the unit cells of these clays have been included as Supplementary Information.

Figure 1.

(a) Microscopic clay structure (Red: O, White: H, Yellow: Si, Green: Al, Cyan: Mg atoms). The side and top views of the pyrophyllite clay sheet show the hydroxyl (−OH) groups that are parallel to the sheet. In talc (top view shown), the −OH groups are perpendicular to the sheet and can participate in hydrogen bonds with water. In fluorotalc (not shown), the talc −OH groups are replaced by F atoms. (b) Part of the simulation setup for studying the clay - water interface. The blue box is the observation volume, v, used to probe density fluctuations. (c) Simulation setup for determining contact angles.

We use the CLAYFF force field³ to model the interactions of the clay atoms and the SPC/E model to describe water.²⁹ Lorentz-Berthelot combination rules are used to determine the pair Lennard-Jones parameters and a rigid clay structure is assumed. As there are no parameters for fluorine in CLAYFF, we assigned it a charge equal to that of the -OH group in talc (−0.525) and Lennard-Jones parameters of the fluoride ion reported in Ref. 30. All simulations were performed in the NVT ensemble using the LAMMPS simulation package³¹ at a temperature, T = 300 K, maintained using a Nose-Hoover thermostat.³² SHAKE was used to integrate the motion of the rigid water molecules³³ and long-range electrostatic interactions were computed using Ewald summation.

Methods

Clay - water interface

A clay-water interface is representative of the situation at saturation. The setup shown in Figure 1(b) is used to calculate the local water density, ρ(z), as well as the water density fluctuations near the interface. The potential of mean force, ℱ, for bringing a water molecule from bulk to a distance z from the plane of the Mg atoms for talc and fluorotalc (and Al for pyrophyllite) is related to ρ(z) by ℱ(z) = −k_BT ln[ρ(z)/ρ_b], where k_B is the Boltzmann constant and ρ_b is the bulk water density. To quantify density fluctuations, we measure the probability distribution, P_v(N), of finding N water molecules in an observation volume v, adjacent to the clay surface, using the indirect umbrella sampling (INDUS) method.^27,28 We chose a rectangular parallelopiped of dimensions 15 × 15 × 3 ų placed near the surface [see Figure 1(b)], as the observation volume. The exact z-position of v was chosen so that the mean water density in v is equal to ρ_b. The simulation box also contained a fixed wall of repulsive WCA particles (not shown), placed at the top of the box (far from v) to nucleate a vapor-liquid buffering interface.

Contact angle

The simulation setup for contact angle measurements is shown in Figure 1(c). The contact angle is determined by computing water density maps in the plane of the center-of-mass of the drop. The curve with density equal to half of the bulk density is then fit to a circle and the angle between the tangent to this circle at z_S = 7 Å and the horizontal axis is taken to be the contact angle. While the exact quantitative value of the contact angle depends on the choice of z_S, our qualitative findings do not.

Water vapor adsorption

The adsorption of water vapor at low RH corresponds the interaction of an isolated water molecule with the surface. To determine the corresponding adsorption free energy, Δμ_ads, we compute ℱ(z) using umbrella sampling, with the weighted histogram analysis method (WHAM) ^34,35 being used to reconstruct ℱ(z) from the biased trajectories.

Hydrophobicity at low and high RH

Using the various molecular measures of hydrophobicity described above, we study talc, as well as fluorotalc and pyrophyllite surfaces, both at saturation and at low RH.

High RH

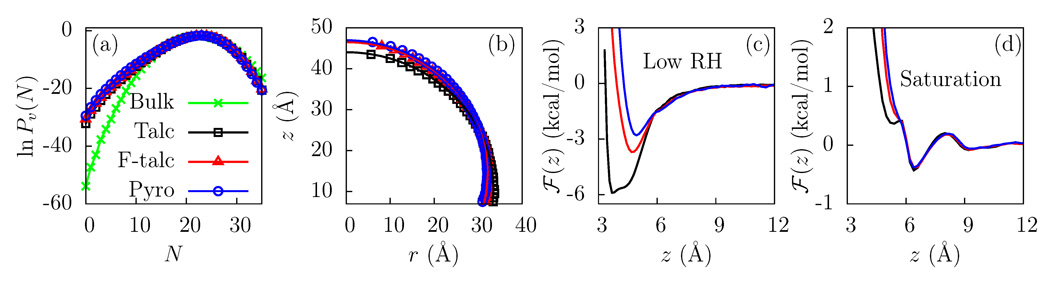
Theory^36–39 and simulations^27,40–43 have shown that the mean water density near a surface is not a good measure of its hydrophobicity. Instead, fluctuations away from the mean, and in particular, the rare fluctuations²⁷ indicating the cost of creating a cavity at the interface correlate quantitatively with the contact angle.⁴⁴ Patel et al. have shown that hydrophobic surfaces display an enhanced probability of density depletion or a low N fat tail in the P_v(N) distribution, while P_v(N) near hydrophilic surfaces is similar to that in bulk water.²⁷ As shown in Figure 2(a), P_v(N) near all three clay surfaces displays a low N fat tail, indicating that these surfaces are hydrophobic. A slight lifting of the fat tail from talc to fluorotalc and pyrophyllite suggests a corresponding marginal increase in hydrophobicity.

Figure 2.

(a) The probability, P_v(N), of observing N water molecules in a probe volume (v = 15 × 15 × 3 ų) displays a low N fat tail when v is near the surface of talc (black), fluorotalc (red), and pyrophyllite (blue), as compared to that when v is in bulk water (green). (b) Water droplet profiles corresponding to ρ(r, z) = 0.5ρ_b are shown for the clay surfaces. The contact angles for the surfaces are similar: 96° for talc, 103° for fluorotalc, and 105° for pyrophyllite (based on tangents drawn at z_S = 7Å). (c) Potential of mean force, ℱ(z), for the adsorption of an isolated water molecule (low RH) to the clay surfaces. The hydrogen atoms of the talc −OH groups are located at z = 2 Å and can participate in hydrogen bonds with water molecules. (d) ℱ(z) at the clay - liquid water interface (saturation). To maximize H-bonding with other waters, the binding site is no longer occupied.

Another way to probe surface hydrophobicity is by simulating a sufficiently large water droplet on the surface and estimating the corresponding contact angle. Figure 2(b) shows the average shape of droplets on the clay surfaces. The curve corresponding to ρ(r, z) = 0.5ρ_b is a circle in the (r, z) plane, where r is the distance from the axis that passes through the center of mass of the droplet. The contact angles obtained by tangents drawn at z_S = 7Å on the three surfaces are similar (talc: 96°, fluorotalc: 103° pyrophyllite: 105°), and clearly indicate hydrophobic behavior.

Reliable experimental estimates of the contact angle of water droplets on both talc and pyrophyllite monocrystals are between 80° and 85°.^25,26 The reported values for measurements on powders are usually smaller due to the presence of hydrophilic sites on the edges of finite clay particles.⁴⁵ To the best of our knowledge, no experimental contact angles have been reported for fluorotalc. For both talc and pyrophyllite, the contact angles obtained from our simulations (96° and 105° respectively) are somewhat larger than the experimental estimates, suggesting that surfaces modeled with the CLAYFF model are too hydrophobic. Nevertheless, amongst various commonly used clay force fields,^46–48 we find that the correspondence with experiments is closest for CLAYFF. A comparison of these force fields with experiments is provided in the Supplementary Information.

Low RH

To investigate the wetting behavior of clay surfaces at low RH, we calculate the potential of mean force, ℱ(z), for the adsorption of an isolated water molecule. ℱ(z) displays a minimum near all the clay surfaces [see Figure 2(c)], corresponding to an adsorption (or binding) free energy, Δμ_ads. For talc, Δμ_ads ≈ −5.9 kcal/mol, or 10 k_BT, consistent with the formation of a hydrogen bond between the water molecule and the hydroxyl group in talc. In fluorotalc, the hydroxyl group is replaced by fluorine, resulting in a reduction in Δμ_ads to −3.5 kcal/mol. It also shifts the location of the minimum out by ≈1 Å as the water is no longer strongly bound to the surface. Pyrophyllite, with the hydroxyl group parallel to the surface has an even smaller Δμ_ads ≈ −2.8 kcal/mol, and the minimum is shifted out even more.

To compare our estimate of Δμ_ads from simulations to experimental data, we analyzed the data of Michot et al.²⁴ using a Langmuir model. This model assumes that there are no interactions between the adsorbed molecules and predicts a surface coverage, Θ = (P/P^*)/(1 + P/P^*). P^* is the pressure at which half of the surface sites are occupied and is related to Δμ_ads through

$$P^{*}=\frac{{\sigma }_{\text{max}}{k}_{\mathrm{B}}T}{\delta }{e}^{\beta \mathrm{\Delta }{\mu }_{\text{ads}}},$$ (1)

where σ_max ≈ 4.2 nm⁻² is the surface site density, δ ≈ 1 – 2 Å is the width of the surface layer, i.e. the width of the PMF well in Figure 2(c), and 1/β = k_BT is the thermal energy.

In the very low RH limit, corresponding to single water adsorption, we can safely assume that water molecules do not interact with each other. In this regime, Θ ≈ P/P* and the data in Figure 11 of Ref. 24, allow us to obtain an experimental estimate of P* ≈ 0.056P_sat for the talc surface. Here, P_sat = 30 mbar is the saturation pressure of water. Using this value of P* in equation eq. (1), we get an experimental estimate of Δμ_ads ≈ −8 kcal/mol.⁴⁹ This somewhat stronger adsorption than that predicted from simulations using CLAYFF (−5.9 kcal/mol), is consistent with the overestimate of the CLAYFF talc contact angle.

If we further assume that the adsorbed water molecules do not interact with each other even at higher RH, the Langmuir model (with P* = 0.056P_sat) predicts that Θ ≈ 0.9 at 50% RH. As water coverage on the talc surface can be large even at moderate RH, interactions between water molecules may be important, consistent with suggestions that clustering needs to be considered.^24,50 In contrast, for fluorotalc Θ at saturation estimated from Δμ_ads is very small (≈ 1.5%), in agreement with the hydrophobic adsorption behavior reported in Figure 10 of Ref. 24.

Thus, the clay surfaces simulated using the CLAYFF force field are more hydrophobic than the real clay surfaces used in experiments. However, the interesting dichotomy of talc surfaces is also observed in the simulations and our findings are qualitatively consistent with the experiments, both at low RH (strong adsorption for talc and not the other clays) and at high RH (large contact angles for all clays).

Cohesion vs Adhesion

To investigate the disparate behavior of talc surfaces at low and high RH, we compare ℱ(z) for moving a water molecule away from the surface under both conditions. At saturation, ℱ(z) for the clay surfaces are similar [Figure 2(c)], consistent with similar droplet contact angle on the three surfaces [Figure 2(b)]. ℱ(z) for fluorotalc is nearly identical to that for pyrophyllite, and that for talc features an additional local minimum around z = 5 Å corresponding to water molecules above the binding site. However, the ℱ(z) curves at saturation are qualitatively different from those at low RH [see Figure 2(c–d)]. For all three clays, and especially so for talc, the depth of the minimum at saturation is smaller than that at low RH, suggesting a weakening of adhesive interactions at saturation. The average number of H-bonds donated by the surface hydroxyl groups of talc is Θ × N_HB, with N_HB the average number of H-bonds donated per occupied site. At low RH, N_HB ~ 0.83, while at saturation it drops to only 0.02, as a result of the H-bonding to other water molecules.

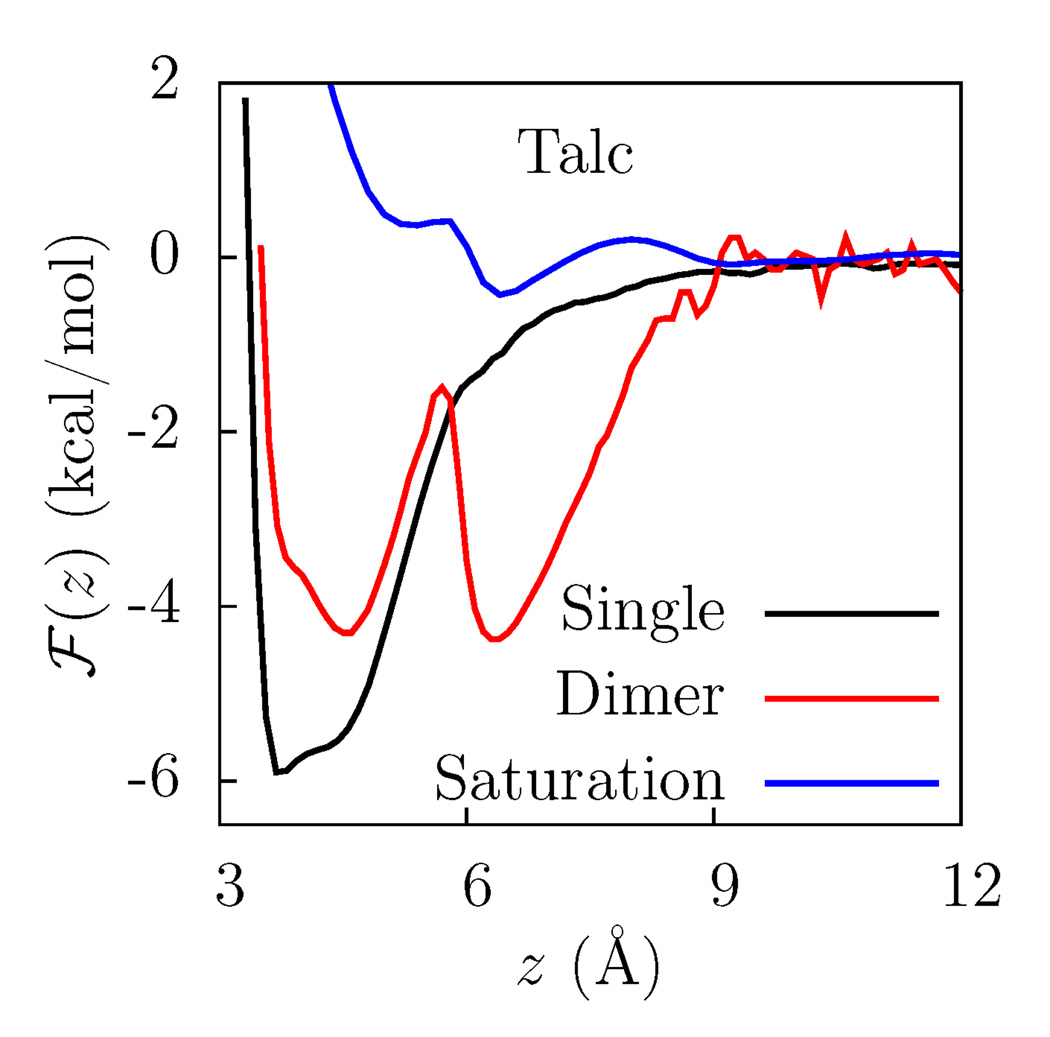
To explore the competition between adhesive and cohesive interactions in talc, in Figure 3, we compare ℱ(z) for an individually adsorbed water, with that for water in a dimer, and that for water at saturation. As shown in Figure 3, the ℱ(z) for the dimer displays two minima. The minimum corresponding to the molecule inside the cavity is shifted to slightly larger values compared to the minimum in the ℱ(z) for a single water. In addition, the depth of the minimum is smaller, and is comparable to that for a single water on the more hydrophobic fluorotalc surface [Figure 2(c) and Figure 3]. In other words, the presence of the second water weakens the adhesive surface-water interactions, which have to compete with the cohesive interactions between the waters. As the dimer is less tightly bound to the surface than a single water, it is easier for the water to escape the cavity in the presence of a second molecule. The dimer is in fact more mobile on the talc surface than isolated water molecules (not shown), confirming that the interaction of the surface with the dimer is weaker than with individual molecules. Finally, at saturation, cohesive interactions prevail, and water no longer occupies the binding site cavity as evidenced by the lack of a minimum in ℱ(z) for 3Å < z < 5Å.

Figure 3.

ℱ(z) for adsorbing a single water molecule on the talc surface, compared to that for a molecule in the dimer and a molecule at saturation.

Modified Talc Surfaces

While the H-bonding between binding sites on the talc surface and water leads to an interesting transition from hydrophilic at low RH to hydrophobic at high RH, the binding sites interact weakly with water in fluorotalc and pyrophyllite, which display hydrophobic behavior for all RH. To investigate the effect of the binding strength on the hydrophobicity of the surface, following Giovambattista et al.,⁵¹ we construct a series of modified talc surfaces. The only force field parameters that are changed are the charges on the oxygen (from q_O = −0.95 to q_O − δq) and the hydrogen (from q_H = 0.425 to q_H + δq) of the hydroxyl group. We study modified talc surfaces for δq ranging from −0.425 which corresponds to a non-polar binding site similar to that in fluorotalc, to +0.6 which corresponds to an ion-pair. δq = 0 is the talc surface, by definition.

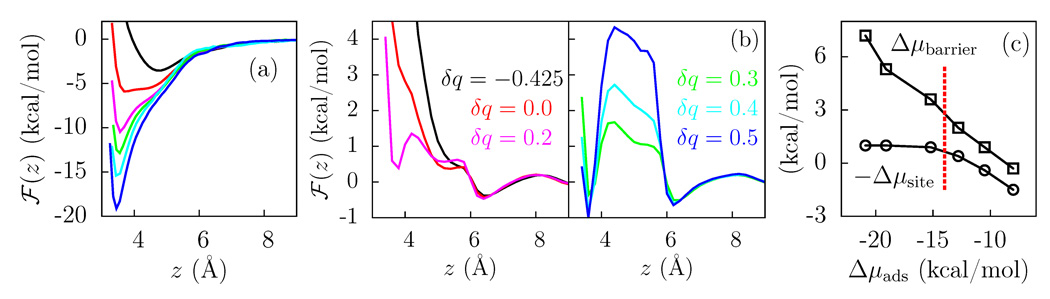
In Figure 4(a), we show ℱ(z) for an isolated water molecule on the modified talc surfaces. As the polarity of the −OH bond is increased, the magnitude of Δμ_ads also increases, providing us with surfaces that display a wide range of binding strengths. ℱ(z) at saturation, shown in Figure 4(b) for these surfaces is particularly interesting. For weakly adhesive surfaces (−0.425 ≤ δq < 0.1), there is only one stable basin at z ≈ 6.5 Å, corresponding to molecules outside the binding site cavity. For stronger adhesion (larger δq), a second basin develops at z ≈ 3.5 Å and is separated from the first basin by a barrier.

Figure 4.

(a) ℱ(z) for a single water on various talc surfaces modified to span a range of Δμ_ads-values. (b) The corresponding ℱ(z) curves at saturation. (c) The relative stability of water in the binding site compared to that in bulk, −Δμ_site, and the barrier to escape the binding site, Δμ_barrier, as a function of the binding strength, Δμ_ads. The dashed vertical line corresponds to μ_sat, the chemical potential at saturation.

Figure 4(c) shows the depth of this minimum relative to bulk, Δμ_site, as a function of Δμ_ads. As the surface becomes more adhesive, more waters occupy the binding site and the depth of this minimum increases. When adhesive interactions are large enough to overcome cohesive interactions, i.e., when −Δμ_ads becomes larger than the chemical potential at saturation, −μ_sat (for δq ≈ 0.4), every binding site is occupied by a water molecule, resulting in a plateau in Δμ_site. The average number of H-bonds donated by surface hydroxyl groups also behaves as Δμ_site and its dependence on Δμ_ads is provided in the Supplementary Information.

However, the height Δμ_barrier of the barrier to escape the cavity, also shown in Figure 4(c), continues to increase approximately linearly with the binding strength. Thus, for surfaces with strong binding, Δμ_barrier is large, and the exchange of molecules between the cavities and the liquid is expected to be very slow, with possible consequences on the extent of stick/slip at such surfaces in the presence of a hydrodynamic flow.

Tuning cohesion/adhesion via RH/Δμ_ads

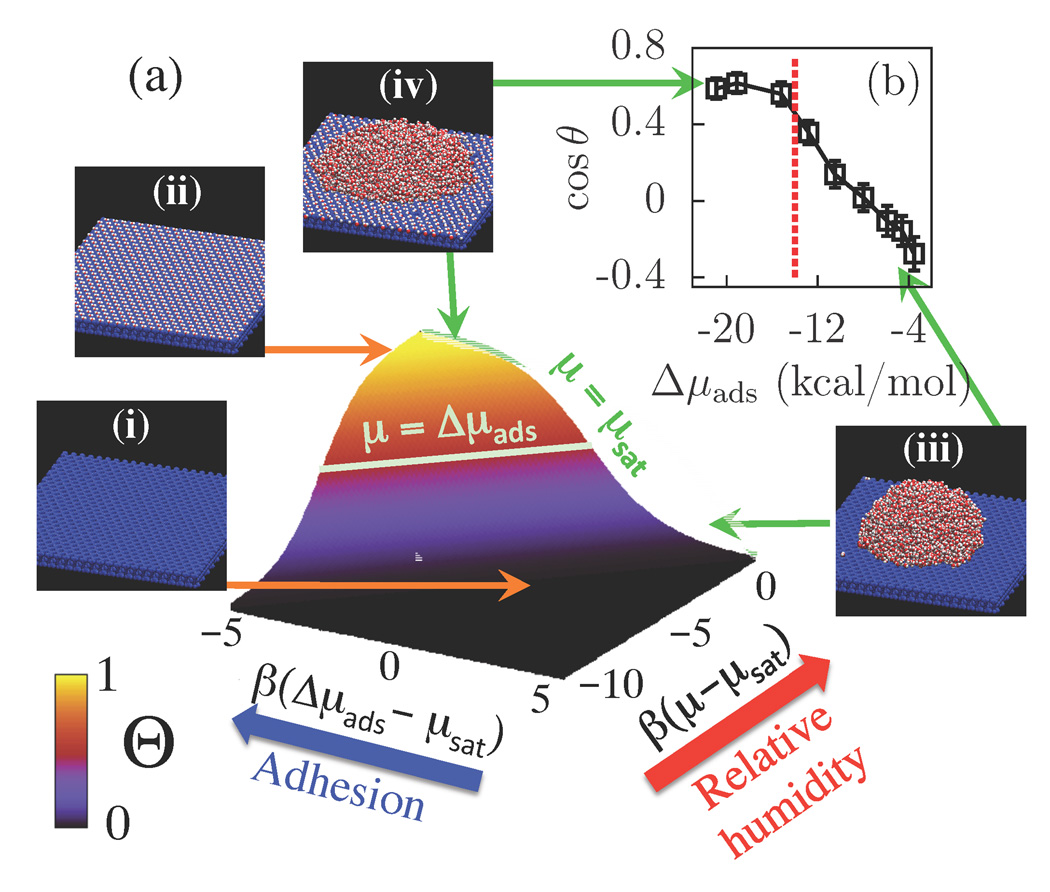
Collectively our results paint a comprehensive picture of how the experimentally measurable quantities, the surface coverage Θ, and the contact angle θ, respond to changes in relative humidity (or water chemical potential), and on the strength of the adhesive surface-water interactions. The surface coverage Θ, is defined as the fraction of binding sites occupied by water molecules, and its dependence on RH and Δμ_ads is shown schematically in Figure 5(a).

Figure 5.

(a) Schematic showing the surface coverage, Θ, over a wide range of relative humidities (RH≡P/P_sat ~ exp[β(μ – μ_sat)]) and adhesive interaction strengths (Δμ_ads). (b) Effect of Δμ_ads on surface hydrophobicity quantified by cos θ. The dashed vertical line corresponds to μ_sat. Snapshots indicating typical configurations of water molecules (red and white) on modified talc surfaces (blue) are also shown. As the adhesive interactions (Δμ_ads) overcome the cohesive interactions (μ), there is a transition from a dry surface [snapshots (i) and (iii)] to one covered with a monolayer of water [snapshots (ii) and (iv)].

At low RH (≡ P/P_sat), the competition between the adhesive interactions and the entropy of being in the vapor determines the surface coverage, Θ. At very low RH, there are no interactions between adsorbed waters and Θ can be approximated as:

$$\mathrm{\Theta }\approx P/P^{*}=0.1(P/P_{\text{sat}})e^{-\beta \mathrm{\Delta }{\mu }_{\text{ads}}-8.3},$$ (2)

where the second part of the equation is obtained by substituting for P* using Equation (1), and using appropriate values of the constants that depend on the surface geometry, σ_max and δ, and those that depend on thermodynamic conditions, T and P_sat.

For surfaces with small adhesive interactions, i.e., −Δμ_ads < 5 kcal/mol (or −βΔμ_ads < 8.3), the coverage remains small (Θ < 0.1) even at saturation [snapshot (i) in Figure 5]. Thus, no appreciable interactions between waters are expected over the entire range of RH-values. Both pyrophyllite and fluorotalc fall in this regime.

Since Θ increases exponentially with βΔμ_ads, for values of −Δμ_ads > 5 kcal/mol, there can be substantial coverage even at modest RH [snapshot (ii) in Figure 5]. Equation (2) is then valid only for small RH-values for which the predicted Θ-values are small. Talc lies in this regime.

For larger RH values, there are appreciable interactions between the waters, and it is the competition between adhesive and cohesive interactions that determines surface properties. For surfaces such as talc, for which −Δμ_ads < −μ_sat, cohesion prevails at saturation, and the adsorbed waters bead up into a droplet, while the rest of the binding sites on the surface are devoid of waters [snapshot (iii) in Figure 5]. Thus, the interesting crossover from hydrophobic to hydrophilic behavior in talc is a result of its adhesive interactions being strong enough to overcome vapor phase entropy at low RH, but not strong enough to overcome cohesive interactions at saturation. In this regime, with increasing polarity of the binding site, the surface gradually shifts from hydrophobic to hydrophilic, and cos θ increases approximately linearly as shown in Figure 5(b).

Finally, for surfaces with even larger values of −Δμ_ads that are greater than −μ_sat, adhesion dominates. Surprisingly, water does not fully wet the surface at saturation. Instead, all binding sites are occupied by water molecules and only this first layer of water wets the surface. This water is strongly bound to the surface and the microstructure of the surface dictates the relative positions of the waters. In the present case, the arrangement of waters on the surface is not commensurate with the hydrogen bonding network of water, so that water beads up on the monolayer [snapshot (iv) in Figure 5]. For the modified talc surfaces with −Δμ_ads > −μ_sat, the surface has a strongly adsorbed water monolayer with a droplet on it that makes a contact angle of about 50°.

Concluding remarks: Surface details matter

Similar behavior was reported by Ohler et al. for titanium dioxide surfaces, with droplet contact angles of 32 – 34° on top of roughly two monolayers of water⁵² and by Wang et al. who studied model polar surfaces with hexagonal charge patterns and observed a water droplet atop an ice-like water monolayer.⁵³ However, other simulation studies investigating the effects of surface polarity on hydrophobicity,^54,55 do not observe a plateau with non-zero contact angle at large polarities, seen in our results [Figure 5(b)]. Our modified talc surfaces are different from these previous studies in that the variation in polarity was achieved by changing the charges on atoms in recessed binding sites, while the remaining surface atoms remained the same. In contrast, in ref. 54, the surface was modified by changing dipoles that protrude from the surface, while leaving the remaining surface atoms unchanged; whereas in ref. 55, the charges on all atoms in the top two layers of an FCC crystal (111 facet) were changed to tune the polarity. Thus, our results indicate that the microstructure of the surface is important in determining the effect of polarity on its wetting properties.

In contrast to the wetting properties of the model FCC surfaces used in ref. 55, experimental measurements indicate that the FCC crystals of platinum (Pt), palladium (Pd), and gold (Au) are hydrophobic. Kimmel et al. observed a hydrophobic water monolayer on both Pt(111) and Pd(111) crystals.^56,57 Similarly, water has been shown to bead up on Au surfaces⁵⁸ with a contact angle of 100° and Au surfaces have also been shown to adsorb, and facilitate the unfolding of proteins;⁵⁹ behavior that is typically associated with hydrophobic surfaces.⁴⁴ We speculate that the hydrophobicity of these metal surfaces arises from the presence of a monolayer of water, which binds strongly to the surface in a geometry that inhibits hydrogen bonding to the subsequent liquid water molecules.

Our results also have implications on the wetting properties of nanoporous silicates such as hydrophobic zeolites^60–62 and metal-organic frameworks.⁶³ These hydrophobic pores are thought to be devoid of water at ambient conditions, with water intrusion into the pores occurring only at sufficiently high water pressures. Our results suggest that in the presence of strong binding sites, these nanoporous materials may contain strongly adsorbed water molecules, even at lower pressures. If the resulting water-covered surface is hydrophobic, no further filling of the pores (analogous to wetting for planar surfaces) would be observed at ambient pressures, and intrusion would occur only at higher pressures.