Abstract
Neurons in the early stages of visual processing are often thought of as edge detectors for different orientations. Here we investigate the existence of detectors for specific combinations of edges—detectors for specific curvatures. Previous attempts to demonstrate such detectors through aftereffects have ultimately been explained by adaptation to local orientation rather than curvature per se. To control for local aftereffects, we adapted one patch of visual field to two adjacent gratings presented as an obtuse contour (compound patch), and another patch to the same component gratings presented alternately (component patch). In this way both patches are adapted equally to the local orientation components of the stimuli, but only the compound patch is adapted to the global contour. Thus any difference in adaptation between the patches must result from the presence of the contour as a global figure. We found that perceived contrast of probe stimuli was not differentially altered in the two patches. However, apparent curvature of the probes was consistently greater in the compound patch than in the component patch. This effect was considerably reduced by increasing the spatial separation of the component gratings. The results are consistent with curvature detectors involved in the perceptual grouping of edges.
Keywords: contours, perceptual organization, adaptation
Introduction
One of the general principles of visual processing is that, at each stage in the processing stream, signals from previous stages are combined to create a more complex and sparse representation of the stimulus. Firstly, outputs from retinal photoreceptors are combined to form the center-surround antagonistic receptive fields of retinal ganglion cells. Then, in primary visual cortex (V1) the outputs of retinal ganglion cells are combined to create elongated receptive fields that typically respond to spatiotemporal contrast of a particular orientation and spatial frequency (DeValois & DeValois, 1988; Hubel & Wiesel, 1968). These are thought of by many as suitable detectors for edges or lines; locations in visual space where chromatic or luminance contrast is high. Higher in the visual system, in ventral visual regions, cells appear to respond to complex stimuli such as faces (e.g. Desimone, 1991; Desimone, Albright, Gross, & Bruce, 1984). Little is known about how the low level orientation signals are organized and combined into these complex representations. One logical extension of the general principle is an intermediate stage where conjunctions of local orientation signals in the form of curves or corners would be detected.
The Gabor path paradigm, where subjects must detect a contour formed from a series of Gabor patches within a larger array, is one approach used to study how features are integrated into a contour (Field, Hayes, & Hess, 1993). Other studies have also investigated visual contour processing through detection and discrimination thresholds for various curved stimuli, from simple curves to more complex radial frequency patterns (Loffler, Wilson, & Wilkinson, 2003; Watt & Andrews, 1982; Wilkinson, Wilson, & Habak, 1998; Wilson, 1985; Wilson & Richards, 1989).
The selectivity of the mechanisms that underlie curve and contour processing can be studied using aftereffects, whereby prolonged exposure to a shape (adapter) alters perception of a subsequent shape. Such aftereffects are believed to reflect a change in the activity of neurons that code for the adapted feature and thus imply the existence of neurons that act as detectors for that feature. Exposure to a curved stimulus can generate a range of aftereffects including chromatic aftereffects, curvature shape aftereffects, and threshold elevation aftereffects. Riggs (1973) reported that adaptation to green convex lines and red concave lines generated a chromatic aftereffect whereby convex lines appeared pink and concave lines appeared green. Test lines with greater curvature than the adapting pattern produced a stronger aftereffect. He concluded that this effect reflected adaptation of specific curvature detectors with a preference for strong curvature.
However, the results may also be explained by adaptation of linear orientation detectors that respond to the tangents of the curve. This is supported by evidence that the curvature aftereffect can be abolished by making eye movements along the chord of the curve so that each location of the retina was equally exposed to all tangent orientations (Sigel & Nachmias, 1975; Stromeyer & Riggs, 1974).
Similar findings have been reported for the curvature shape aftereffect (Blakemore & Over, 1974), whereby a straight line appears convex after exposure to a concave stimulus (Gibson, 1933), although there are some reports, from curvature specific threshold elevation aftereffects, of data consistent with independent processing of local orientation and curvature (Timney & MacDonald, 1978).
From these early studies it appears that curvature aftereffects can generally be explained by the combination of aftereffects caused by adaptation of local orientation detectors, rather than curvature detectors. More recently, shape aftereffects have been reported that do appear to have a basis in global shape processing rather than local orientation (Gheorghiu & Kingdom, 2006, 2007; Suzuki, 2001, 2003). The shape-frequency aftereffect (SFAE) and the shape-amplitude aftereffect (SAAE) (Gheorghiu & Kingdom, 2006, 2007) occur when exposure to a sine-wave-shaped contour causes a perceived shift in the frequency or amplitude of a subsequently presented contour. To control for local orientation the effect was tested using a sine wave adapting stimulus and a square wave test pattern so that any local tilt aftereffects (TAEs) generated by the positive and negative sides of the wave would cancel out. Although this provides a convincing argument for TAEs not being the basis of the SFAE there were some differences in the results generated with a square wave test pattern and those in the original demonstration with sine wave test stimuli.
A global aftereffect for convexity generated by an hourglass shaped adapting figure has also been reported (Suzuki, 2001, 2003). In this case, a local orientation basis for the effect was rejected as the aftereffect transferred across different sized stimuli and was dependent on attention, which suggests a high-level basis.
In the current experiments we developed a compound adaptation paradigm (Peirce & Taylor, 2006) that is based on adapting one location to a contour and another location to the components of that contour in isolation. In this way both patches are adapted equally to the local orientation components of the stimuli, but only the compound patch is adapted to the global contour. Thus any difference in adaptation between the two patches must logically result from the presence of the contour as a global figure. This has allowed us to stringently control for adaptation to local orientation and demonstrate a global aftereffect over and above that generated by the parts of the contour. This effect is demonstrated in Movie 1 below. The results provide evidence for the existence of detectors for conjunctions of oriented features in the human visual system.
General methods
Methods
Participants
Five healthy volunteers (three experienced observers, including the two authors, and two naïve participants), with normal or corrected-to-normal vision, gave their informed consent and participated in this study. All procedures were approved by the School of Psychology Ethics Committee, University of Nottingham, UK. The three experienced observers took part in both experiments and the naïve observers took part in Experiment 2 only.
Apparatus
Stimuli were presented on a computer-controlled CRT monitor (Vision Master Pro 454, Iiyama) at a resolution of 1024 × 768 pixels and at a refresh rate of 85 Hz with a mean luminance of 112.5 cd/m2. The monitor was driven by 14-bit digital-to-analog converters (DACs) (Bits++, Cambridge Research Systems, Cambridge, UK http://www.crsltd.com). It was calibrated using a photo-spectrometer (PR650, Photo Research, Chatsworth, CA, USA) and the gamma correction was verified psychophysically using a 2nd-order motion-nulling procedure (Ledgeway & Smith, 1994). Stimuli were presented and data collected using the PsychoPy stimulus generation library (Peirce, 2007a). The observer’s head was stabilized in a chin-rest 57 cm from the monitor with the viewable area subtending 36.5° of visual angle horizontally.
Stimuli
Stimuli were constructed from 2 luminance modulated sinusoidal gratings, with different orientations (Figure 1). Both gratings had spatial frequency (SF) of 1.75 cpd. Grating A had an orientation of 10.5° and Grating B had an orientation of −10.5°. All stimuli were presented in a Gaussian envelope with a standard deviation of 0.33° (such that the stimuli had a diameter of 2° at the point at which it fell below 1% contrast). The adapter stimuli were presented with a jittered spatial phase (randomly selected every 100 ms) to prevent the formation of luminance afterimages on the retina. The phase was the same for both components.
Figure 1.
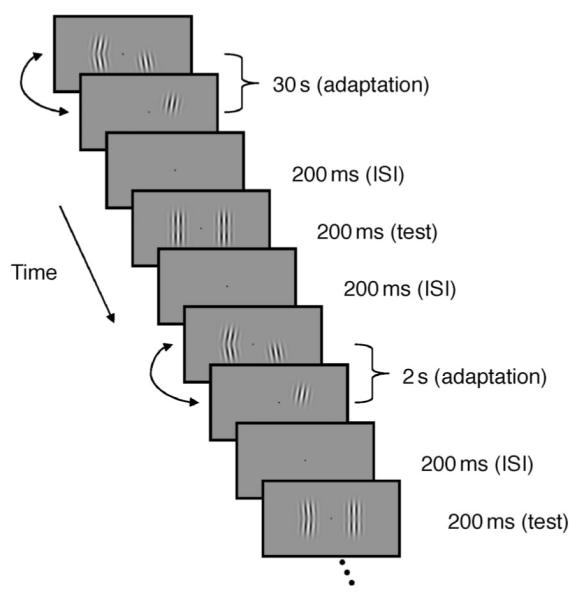
Schematic of the procedure for Experiment 2. For this experiment the reference probe orientation (component side) was held constant at 0° and the test probe orientation (compound side) was varied according to a staircase procedure to find the PSE. All stimuli were presented at maximum contrast. On each trial observers indicated which probe stimulus appeared to point more to the left. Each observer performed a minimum of 4 staircases for each adapting configuration.
Procedure
The basic procedure is shown schematically in Figure 1. Participants were adapted to pairs of component gratings at different locations on the retina (centered 2° either side of the fovea on the horizontal meridian). In the baseline conditions Gratings A and B overlapped spatially so that they gave the perception of a continuous contour when presented simultaneously in a Gaussian envelope. During adaptation A and B were presented simultaneously as a compound contour (AB) at maximum contrast in one visual hemi-field and the individual gratings were presented at maximum contrast in the other field alternating between A and B every second (see Movie 1 for a demonstration). The compound stimulus was alternated with a blank field every second to equate the duration each grating was presented for in each visual field. The temporal phases of the alternations in each hemi-field were independently randomized. Throughout this paper the hemi-field receiving both stimuli simultaneously will be referred to as the compound field, and the hemi-field with the alternating gratings will be referred to as the component field. After adaptation participants were probed with a compound stimulus in both locations.
The initial period of adaptation lasted 30 s and was ‘topped up’ with another 2 s of adaptation prior to each trial. This was followed by a 200 ms ISI, consisting of a mean gray field, before presentation of the probe stimuli for a further 300 ms. The fixation spot was visible for the entire trial. Observer’s pressed one of two keys to make a 2AFC response indicating the side on which the stimulus appeared to have higher contrast (Experiment 1) or was most convex to the left (Experiment 2), triggering the next trial to commence with another ‘top-up’ adaptation period.
Test probe contrast (Experiment 1) and orientation (Experiment 2) were varied according to a staircase procedure based on the observers’ responses. Each observer collected a minimum of four staircases with the compound adapter in the left hemi-field and four staircases with the compound adapter in the right hemi-field. Each staircase contained 50 trials (and typically generated around 30–40 reversals). Within any session all trials had the compound adapter on the same side and a minimum time of 1 h was left between sessions to prevent crossover adaptation between conditions.
Data analysis
The aim of the experiments was to determine the amount of adaptation to the compound adapter over and above adaptation to the components. Since exposure to the components was equivalent in both hemi-fields any remaining difference in adaptation between the patches must reflect adaptation to the compound stimulus as a whole.
We quantified the effect of this compound adaptation as the amount of additional contrast (Experiment 1) or tilt (Experiment 2) required in the compound adapted hemifield for the probes to appear equal (point of subjective equality, PSE). For each probe stimulus intensity level (either contrast difference in Experiment 1 or orientation difference in Experiment 2), responses were averaged for each observer. Logistic functions were then fit to this psychometric data. The PSE was derived from this fit as the point at which the observer was at 50% probability of responding on the compound side. Using this method of binning, all data contribute to the calculation of the PSE, rather than only the trials on which reversals occur, and a full psychometric function can be recovered. It should be noted that data points near the PSE have more trials contributing to each point, as a result of the staircase procedure itself. The PSE values for each presentation side are averaged to account for any side bias in responding to give a single PSE value derived from a total of 400 trials (200 on each side of presentation).
Logistic functions were also fit to 5000 within-subject bootstrap resamples from the 200 individual responses for each presentation side so that, for each resample, a whole new pair of psychometric functions could be derived (one for each side on which the compound was adapted). The PSE values for each pair of functions were averaged to account for side bias then used to derive 95% confidence intervals of the PSE for each observer.
Experiment 1: Contrast aftereffects
Adaptation to a stimulus often results in decreased apparent contrast for a similar test stimulus. The first experiment here examined the effect of adaptation on the apparent contrast of probes in the component and compound hemi-fields. If adaptation only occurs to the individual component gratings (local orientation) then the perceived contrast for the probe stimuli should be raised equally in each hemi-field, so the point at which the two probe stimuli appear equal in contrast (PSE) should be the point at which they were physically identical. In contrast, if there were a neural mechanism responding and adapting to the conjunction of the two component gratings into compound AB, we might expect greater adaptation to occur in the compound hemi-field leading to a greater reduction in perceived contrast in the compound field. This would result in the probe stimuli appearing equal when the contrast was higher in the compound hemi-field than in the component hemi-field (a positive shift in the PSE).
In this experiment, the reference probe (in the component hemi-field) consisted of the compound stimulus at a constant Michelson contrast of 30%. For the test probe (in the compound hemi-field) the grating contrasts were variable and controlled by a staircase procedure designed to home in on the point of subjective equality (PSE) starting at a contrast of 50%.
Results
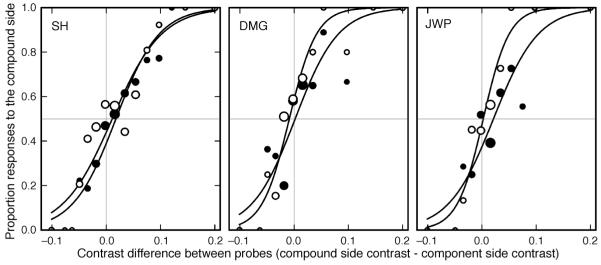
The psychometric functions for three observers are shown in Figure 2. The PSE is the mean shift of the two functions from zero. There is minimal shift in the PSE for any of the observers, indicating that little or no difference in the contrast of the test stimuli was required for them to appear equal.
Figure 2.
Psychometric functions for Experiment 1 for trials where the compound stimulus was presented on the right (open symbols) and on the left (filled symbols). Symbol size indicates the relative number of responses underlying each data point (actual numbers vary from 1 to 92, 1 to 49, and 1 to 55 responses per point for observers SH, DMG and JWP respectively). The horizontal gray line represents the point of 50% probability of responding on the compound side. Zero on the x-axis gives the point of veridical equality (indicated by the vertical gray line). Only very small shifts from zero are seen for any observer.
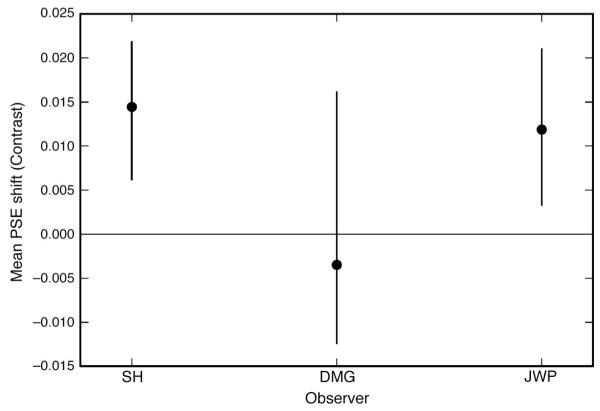
The magnitude of the compound adaptation effect is shown for each observer in Figure 3. The effect magnitude is the average PSE shift and is calculated by (PSER + PSEL)/2. For the three observers the average effect was 0.8%, meaning that the stimuli appeared to have equal contrast when the test probe in the compound hemi-field had a contrast of 30.8% compared to a reference contrast of 30.0% in the component hemi-field. The effect was very small and only significant for 2 of the three observers (zero PSE shift predicted by the null hypothesis of local orientation adaptation fell outside the 95% confidence intervals).
Figure 3.
Magnitude of the compound adaptation effect (Mean PSE shift) for Experiment 1. The gray horizontal line represents the point of veridical equality as predicted by the null hypothesis. Error bars indicate 95% confidence intervals based on 5000 bootstrap resamples. Two of the three observers show a small positive effect of ~1.5% contrast.
Experiment 2: Contour shape aftereffects
Experiment 1 found no evidence for differential adaptation to contrast in the two hemi-fields. We wondered, however, whether adaptation might alter the perceived form of subsequently presented stimuli rather than their apparent contrast, making them appear differently curved, for instance. The aim of this experiment was to determine whether we could generate a curvature aftereffect (CAE) that could not be explained in terms of local tilt aftereffects (TAEs).
The logic of the experiment is similar to that of Experiment 1. Two fields are adapted to either the components of a curved contour in isolation or to the components presented together. A pair of vertical stimuli is then presented (reference and test stimuli) underlying the positions of the adapters. Local tilt aftereffects should be equivalent in the two locations and cause the straight probe stimuli to appear curved in the opposite direction to the adapters. The question is whether this apparent curvature is greater in the compound-adapted field.
Methods
The procedure and stimuli for this experiment were as for Experiment 1 except that the probe stimuli varied in orientation rather than contrast. Five observers took part in this experiment. The reference probe (in the component hemi-field) consisted of two vertical grating components (0°-tilt). For the test probe (in the compound hemi-field) the grating orientations were variable and controlled by a staircase procedure designed to home in on the point of subjective equality (PSE) starting at a tilt of 10° in the same direction as the adapting stimuli. As in the adapting stimuli, the two gratings comprising each probe always had equal but opposite orientation. All stimuli in this experiment were presented at maximum contrast. The observer’s task was to report whether the left or right stimulus appeared to point more to the left (the orientation of the adapting stimulus).
When adapted to a stimulus tilted in one direction and tested with a vertical stimulus the TAE induces apparent tilt in the opposite direction to the adapting stimulus. In this experiment exposure to the two component gratings was equal in the two hemi-fields so the TAEs generated should also be equal. If only local TAEs occurred, the PSE would be at the point where the two probe stimuli were physically identical in their component orientations. In contrast, neural mechanisms selectively responding to the compound AB might produce greater adaptation in the compound hemi-field, resulting in a greater apparent curvature in that location after adaptation. This could be nulled by introducing a curvature in the opposite (adapted) direction, resulting in a shift of the PSE.
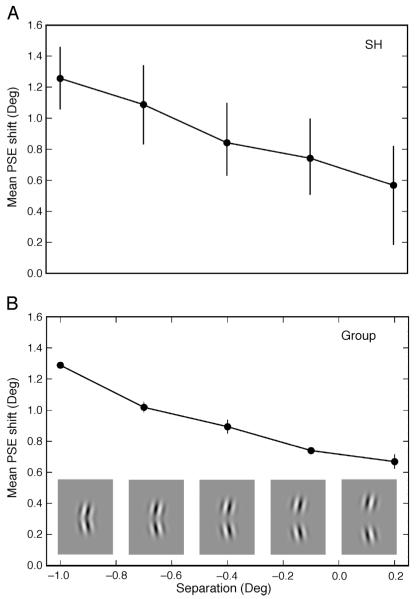
For three of the observers, we also varied the spatial separation of the two gratings within both the adapting and probe stimuli. In Experiment 1 the overlap of A and B was 1.2°. In Experiment 2 we used component stimuli which; overlapped by 1.0, 0.7, 0.4 and 0.1° or were separated by a gap of 0.2°. With an overlap of around 0.7° the components actually appear separate due to the lower contrast at the extremities of the Gaussian envelope in which they were presented (sample separated stimuli are shown in Figure 5).
Figure 5.
Mean magnitude of the compound adaptation effect for different separations in Experiment 2 for (A) a sample observer (SH, error bars represent 95% confidence intervals based on 5000 bootstrap resamples) and (B) the group data averaged across three observers (error bars represent ±SEM across observers). Examples of the separated stimuli are given along the x-axis. Negative separation values indicate that the stimuli overlapped. All observers show a consistent decrease in the effect magnitude with increased component separation.
Each observer conducted a minimum of 4 staircases for each stimulus condition (compound adapter side × spatial separation) in a random order.
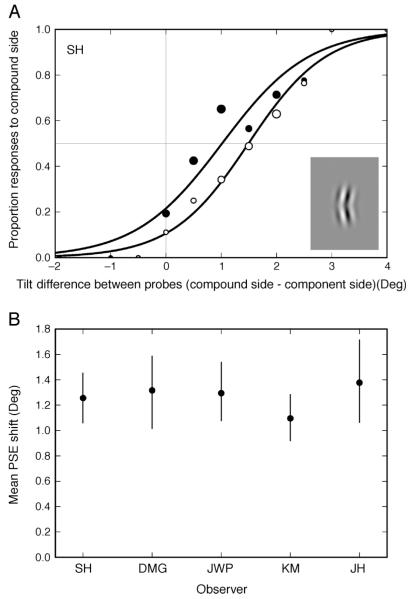
Results
Figure 4 shows the effect of compound adaptation effect in the baseline condition (1.0° overlap). Psychometric functions are presented for one observer (SH) (Figure 4A) and are summarized as PSE values for all five observers (Figure 4B). For each observer the 95% confidence interval from a bootstrapping procedure is presented. From these it is clear that all observers show a significant shift in their PSE (the 95% CI does not include zero). The average effect for the five observers was 1.3°, meaning that the stimuli appeared equal when the test probe in the compound hemi-field had a tilt of 1.3 (A = +1.3, B = −1.3), relative to the vertical reference probe. This shift results from a greater adaptation in the compound hemi-field than the component hemi-field—an effect consistent with adaptation to the compound stimulus as a whole and the existence of neural mechanisms for simple contours. Readers can see the effect for themselves in Movie 1.
Figure 4.
Effect of compound adaptation for the baseline condition in Experiment 2 (components overlap by 1.0°). (A) Psychometric functions for a sample observer (SH), for trials where the compound stimulus was presented on the right (open symbols) and on the left (filled symbols). Symbol size indicates the relative number of responses underlying each data point (actual numbers vary from 1 to 54 responses per point. The horizontal gray line represents the point of 50% probability of responding on the compound side. Zero on the x-axis gives the point of veridical equality (indicated by the vertical gray line). (B) Magnitude of the compound adaptation effect (Mean PSE shift). Zero on the y-axis represents the point of veridical equality as predicted by the null hypothesis. Error bars indicate 95% confidence intervals based on 5000 bootstrap resamples. All observers show a clear PSE shift in the predicted direction (compare with the effects on perceived contrast in Figure 3).
The compound effect we have observed here could be due to a change in the tuning or response of the orientation filters, dependent on the context of another simultaneously presented grating (that is, the presence of the additional grating is affecting the TAE itself), Alternatively, it could be due to adaptation of detectors for a particular conjunction of oriented components, occurring in different (higher level) neurons. In order to differentiate between these possibilities, three observers completed a further condition whereby adaptation was the same as in the above experiment, but the probe stimuli consisted of only one of the two components. If the adaptation to the compound were somehow feeding back and affecting the component detectors themselves then we should see an equivalent adaptation under these conditions. In fact we found a small and variable shift in the PSE for the component probes (the average PSE across observers was 0.624° with a standard error of 0.316°). This effect is too small to account for the compound aftereffect we have observed, which appears to result, at least partially, from adaptation at a level subsequent to the local feature detectors.
We also examined the effect of spatially separating the component gratings. If the neural mechanisms involved in the compound adaptation effect are responding to the stimulus as a contour with good continuity then separating the components should reduce the adaptation effect. If the effect is not reduced then the mechanisms may be responding simply to the simultaneous presence of any two gratings.
Figure 5 shows the magnitude of the compound adaptation effect as a function of spatial separation for a single observer (SH, Figure 5A) and the average across all three observers (Figure 5B). 95% confidence intervals from the bootstrapping procedure are shown in Figure 5A, while the error bars in Figure 5B show the standard error between observers. As spatial separation increased the magnitude of the compound adaptation effect decreased significantly from 1.3° at 1.0° overlap to only 0.7° at 0.2° separation (comparison of the 95% confidence intervals for 1.0° and 0.2° separations show no overlap for any observer). However even with a separation of 0.2° of visual angle there was significant compound adaptation (0 PSE shift fell outside the 95% confidence intervals). Interestingly, at this separation the magnitude of the effect was similar to that found when the probes consisted of only one of the two components.
General discussion
Although we have known for over 30 years about the oriented-edge-detecting properties of V1 neurons, we still know relatively little about how the outputs of those cells are combined into more meaningful complex representations. Here we propose a mid-level mechanism capable of grouping together local oriented components in the form of small curved contours, and demonstrate it using a selective adaptation paradigm.
Support for specialized curve and angle detectors has been suggested by studies demonstrating better acuity for angle and curve perception than would be expected by line orientation acuity (Andrews, Butcher, & Buckley, 1973; Chen & Levi, 1996; Heeley & Buchanan-Smith, 1996; Regan, Gray, & Hamstra, 1996; Watt & Andrews, 1982; Wilson, Wilkinson, & Asaad, 1997). These studies have all used sensitivity measures, however, and don’t allow us to understand the selectivity of the mechanisms. The shape aftereffects of Gheorghiu and Kingdom (2006, 2007) and the hourglass illusion (Suzuki, 2001, 2003) have both implied the existence of curvature-selective mechanisms that might be affected by adaptation.
Previous psychophysical attempts to show the existence of curvature detectors directly (e.g. Riggs, 1973) have generally been explained simply by local tilt aftereffects (see Blakemore & Over, 1974; Sigel & Nachmias, 1975; Stromeyer & Riggs, 1974) or have had rather mixed results (Timney & MacDonald, 1978). We aimed to generate a curvature aftereffect that could not be explained by such effects using an adaptation method that directly titrates a field adapted to a particular compound stimulus against one adapted to identical components presented independently.
In Experiment 1 we examined the effect of this compound adaptation on perceived contrast. Little or no difference in the perceived contrast between the test stimuli in the two adapting patches was found. In Experiment 2, however, we found that adaptation to the compound adapter did result in a greater apparent curvature of our probe stimuli than could be explained by adaptation to the components alone. This is an effect consistent with a compound specific aftereffect and the existence of detectors for simple contours. Such mechanisms seem likely candidates to underpin the SFAE and SAAE found by Gheorghiu and Kingdom (2006, 2007).
The fact that there was no effect on apparent contrast but a change in the apparent form of the stimuli, is an interesting departure from many lower level adaptation effects typically found using psychophysics (e.g. Blakemore, Muncey, & Ridley, 1973; Snowden & Hammett, 1996) and electrophysiology (e.g. Bonds, 1991; Ohzawa, Sclar, & Freeman, 1982, 1985; Sclar, Lennie, & DePriest, 1989). It may result from a mechanism in which the contrast response function saturates very strongly at low contrast approximating a step function.
Earlier papers which found curvature aftereffects to be caused wholly or predominantly by TAEs (Blakemore & Over, 1974; Sigel & Nachmias, 1975; Stromeyer & Riggs, 1974) may have done so because they were not comparing directly and simultaneously the two fields in which adaptation to the components or the compound had occurred. Comparing the fields directly would appear to be a rather more sensitive technique.
The aftereffect in the current study was decreased, but not completely abolished, by separating the two components in space. As such it appears that good apparent grouping of the components is required for the adapting mechanisms. So the mechanism could be involved with the perceptual binding of component features into a contour.
The remaining aftereffect found with separated component stimuli had a similar magnitude to that of the effect found when we tested probe stimuli consisting of only a single component grating. This residual effect could indicate that, as well as a contour specific adaptation effect, there is also an effect of compound adaptation on the perceived local orientation, so that adapting to two simultaneous gratings generates bigger tilt aftereffects than adaptation to the individual components. However, unlike the contour specific effect, this local effect does not appear to depend on the compound adapter being perceived as a contour so it seems unlikely to be related to a contour integration mechanism per se.
The data we have reported here demonstrate that the contour mechanism can combine at least two components into a contour, but we do not know how many components these mechanisms might integrate in a single step. We also don’t know whether multiple changes in the direction of curvature could be encoded by a single cell.
Precisely how such curvature detectors might generate their selectivity and where they lie anatomically is not clear. End-stopped complex cells in V1 may be capable of directly detecting curvature (Dobbins, Zucker, & Cynader, 1987, 1989). Additionally the combination of the output from neurons, responding preferentially to different orientations, might be used (Poirier & Wilson, 2006). To create an appropriate AND gate a mechanism need only actually sum the outputs of V1, thanks to the nonlinear output properties of those units (Peirce, 2007b). The result is a cell for which the whole stimulus is substantially greater than the sum of its parts. In V2, some neurons do show non-uniform tuning to orientation across their receptive fields, indicative of tuning to curvature (Anzai, Peng, & Van Essen, 2007) and, in V4, neurons are responsive to moderately complex stimuli including curved contours (Gallant, Braun, & Van Essen, 1993; Gallant, Connor, Rakshit, Lewis, & Van Essen, 1996; Pasupathy & Connor, 1999, 2001, 2002).
Conclusions
Here we show psychophysically a curvature aftereffect whereby a straight vertical pattern is perceived as having a curvature after prolonged exposure to a pattern curved in the opposite direction. This apparent curvature is greater than that in a similar control field in which the components of the curve are presented in an isolated fashion. As such the effect cannot be explained by local tilt aftereffects and appears more likely to arise from the existence of curvature detectors. Since good continuity of the contour is required for the effect, these mechanisms appear to be critically involved in the segmentation and grouping of visual edges.
Supplementary Material
A demonstration of the curvature aftereffect. Keep the eyes fixated carefully on the point in the center of the screen, ignoring the stimuli flashing on and off to either side. After a period of adaptation two (identical) static probes will appear on either side of fixation. If adaptation has been equal in the two hemifields, resulting purely from the tilt of the components, then the probe stimuli will appear to bend equally to the right. If the adaptation is not equal in the two fields (because of additional adaptation to the global figure of the curve), then the probe stimuli will appear to differ in their degree of curvature.
Acknowledgments
This research was supported by a grant from the BBSRC (BB/C50289X/1), United Kingdom. The authors would like to thank David McGovern for his help and comments, and an anonymous reviewer for some very constructive suggestions.
Footnotes
Commercial relationships: none.
Contributor Information
Sarah Hancock, Nottingham Visual Neuroscience, School of Psychology, University of Nottingham, Nottingham, UK.
Jonathan W. Peirce, Nottingham Visual Neuroscience, School of Psychology, University of Nottingham, Nottingham, UK
References
- Andrews DP, Butcher AK, Buckley BR. Acuities for spatial arrangement in line figures: Human and ideal observers compared. Vision Research. 1973;13:599–620. doi: 10.1016/0042-6989(73)90026-6. [DOI] [PubMed] [Google Scholar]
- Anzai A, Peng X, Van Essen DC. Neurons in monkey visual area V2 encode combinations of orientations. Nature Neuroscience. 2007;10:1313–1321. doi: 10.1038/nn1975. [DOI] [PubMed] [Google Scholar]
- Blakemore C, Muncey JP, Ridley RM. Stimulus specificity in the human visual system. Vision Research. 1973;13:1915–1931. doi: 10.1016/0042-6989(73)90063-1. [DOI] [PubMed] [Google Scholar]
- Blakemore C, Over R. Curvature detectors in human vision? Perception. 1974;3:3–7. doi: 10.1068/p030003. [DOI] [PubMed] [Google Scholar]
- Bonds AB. Temporal dynamics of contrast gain in single cells of the cat striate cortex. Visual Neuroscience. 1991;6:239–255. doi: 10.1017/s0952523800006258. [DOI] [PubMed] [Google Scholar]
- Chen S, Levi DM. Angle judgment: Is the whole the sum of its parts? Vision Research. 1996;36:1721–1735. doi: 10.1016/0042-6989(95)00245-6. [DOI] [PubMed] [Google Scholar]
- Desimone R. Face selective cells in the temporal cortex of monkeys. Journal of Cognitive Neuroscience. 1991;3:1–8. doi: 10.1162/jocn.1991.3.1.1. [DOI] [PubMed] [Google Scholar]
- Desimone R, Albright TD, Gross CG, Bruce C. Stimulus-selective properties of inferior temporal neurons in the macaque. Journal of Neuroscience. 1984;4:2051–2062. doi: 10.1523/JNEUROSCI.04-08-02051.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeValois RL, DeValois KK. Spatial Vision. Oxford University Press; Oxford, UK: 1988. [Google Scholar]
- Dobbins A, Zucker SW, Cynader MS. Endstopped neurons in the visual cortex as a substrate for calculating curvature. Nature. 1987;329:438–441. doi: 10.1038/329438a0. [DOI] [PubMed] [Google Scholar]
- Dobbins A, Zucker SW, Cynader MS. Endstopping and curvature. Vision Research. 1989;29:1371–1387. doi: 10.1016/0042-6989(89)90193-4. [DOI] [PubMed] [Google Scholar]
- Field DJ, Hayes A, Hess RF. Contour integration by the human visual system: Evidence for a local “association field.”. Vision Research. 1993;33:173–193. doi: 10.1016/0042-6989(93)90156-q. [DOI] [PubMed] [Google Scholar]
- Gallant JL, Braun J, Van Essen DC. Selectivity for polar, hyperbolic, and Cartesian gratings in macaque visual cortex. Science. 1993;259:100–103. doi: 10.1126/science.8418487. [DOI] [PubMed] [Google Scholar]
- Gallant JL, Connor CE, Rakshit S, Lewis JW, Van Essen DC. Neural responses to polar, hyperbolic, and Cartesian gratings in area V4 of the macaque monkey. Journal of Neurophysiology. 1996;76:2718–2739. doi: 10.1152/jn.1996.76.4.2718. [DOI] [PubMed] [Google Scholar]
- Gheorghiu E, Kingdom FA. Luminance-contrast properties of contour-shape processing revealed through the shape-frequency after-effect. Vision Research. 2006;46:3603–3615. doi: 10.1016/j.visres.2006.04.021. [DOI] [PubMed] [Google Scholar]
- Gheorghiu E, Kingdom FA. The spatial feature underlying the shape-frequency and shape-amplitude after-effects. Vision Research. 2007;47:834–844. doi: 10.1016/j.visres.2006.11.023. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. Adaptation, after-effect and contrast in the perception of curved lines. Journal of Experimental Psychology. 1933;16:1–31. [Google Scholar]
- Heeley DW, Buchanan-Smith HM. Mechanisms specialized for the perception of image geometry. Vision Research. 1996;36:3607–3627. doi: 10.1016/0042-6989(96)00077-6. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. The Journal of Physiology. 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledgeway T, Smith AT. Evidence for separate motion-detecting mechanisms for first- and second-order motion in human vision. Vision Research. 1994;34:2727–2740. doi: 10.1016/0042-6989(94)90229-1. [DOI] [PubMed] [Google Scholar]
- Loffler G, Wilson HR, Wilkinson F. Local and global contributions to shape discrimination. Vision Research. 2003;43:519–530. doi: 10.1016/s0042-6989(02)00686-7. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat visual cortex. Nature. 1982;298:266–268. doi: 10.1038/298266a0. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat’s visual system. Journal of Neurophysiology. 1985;54:651–667. doi: 10.1152/jn.1985.54.3.651. [DOI] [PubMed] [Google Scholar]
- Pasupathy A, Connor CE. Responses to contour features in macaque area V4. Journal of Neurophysiology. 1999;82:2490–2502. doi: 10.1152/jn.1999.82.5.2490. [DOI] [PubMed] [Google Scholar]
- Pasupathy A, Connor CE. Shape representation in area V4: Position-specific tuning for boundary conformation. Journal of Neurophysiology. 2001;86:2505–2519. doi: 10.1152/jn.2001.86.5.2505. [DOI] [PubMed] [Google Scholar]
- Pasupathy A, Connor CE. Population coding of shape in area V4. Nature Neuroscience. 2002;5:1332–1338. doi: 10.1038/nn972. [DOI] [PubMed] [Google Scholar]
- Peirce JW. PsychoPy—Psychophysics software in Python. Journal of Neuroscience Methods. 2007a;162:8–13. doi: 10.1016/j.jneumeth.2006.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JW. The potential importance of saturating and supersaturating contrast response functions in visual cortex. Journal of Vision. 2007b;7(6):13, 1–10. doi: 10.1167/7.6.13. http://journalofvision.org/7/6/13/, doi:10.1167/7.6.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JW, Taylor LJ. Selective mechanisms for complex visual patterns revealed by adaptation. Neuroscience. 2006;141:15–18. doi: 10.1016/j.neuroscience.2006.04.039. [DOI] [PubMed] [Google Scholar]
- Poirier FJ, Wilson HR. A biologically plausible model of human radial frequency perception. Vision Research. 2006;46:2443–2455. doi: 10.1016/j.visres.2006.01.026. [DOI] [PubMed] [Google Scholar]
- Regan D, Gray R, Hamstra SJ. Evidence for a neural mechanism that encodes angles. Vision Research. 1996;36:323–330. doi: 10.1016/0042-6989(95)00113-e. [DOI] [PubMed] [Google Scholar]
- Riggs LA. Curvature as a feature of pattern vision. Science. 1973;181:1070–1072. doi: 10.1126/science.181.4104.1070. [DOI] [PubMed] [Google Scholar]
- Sclar G, Lennie P, DePriest DD. Contrast adaptation in striate cortex of macaque. Vision Research. 1989;29:747–755. doi: 10.1016/0042-6989(89)90087-4. [DOI] [PubMed] [Google Scholar]
- Sigel C, Nachmias J. A re-evaluation of curvature-specific chromatic aftereffects. Vision Research. 1975;15:829–836. doi: 10.1016/0042-6989(75)90262-x. [DOI] [PubMed] [Google Scholar]
- Snowden RJ, Hammett ST. Spatial frequency adaptation: Threshold elevation and perceived contrast. Vision Research. 1996;36:1797–1809. doi: 10.1016/0042-6989(95)00263-4. [DOI] [PubMed] [Google Scholar]
- Stromeyer CF, 3rd, Riggs LA. Curvature detectors in human vision? Science. 1974;184:1199–1201. doi: 10.1126/science.184.4142.1199. [DOI] [PubMed] [Google Scholar]
- Suzuki S. Attention-dependent brief adaptation to contour orientation: A high-level aftereffect for convexity. Vision Research. 2001;41:3883–3902. doi: 10.1016/s0042-6989(01)00249-8. [DOI] [PubMed] [Google Scholar]
- Suzuki S. Attentional selection of overlapped shapes: A study using brief shape aftereffects. Vision Research. 2003;43:549–561. doi: 10.1016/s0042-6989(02)00683-1. [DOI] [PubMed] [Google Scholar]
- Timney BN, MacDonald C. Are curves detected by ‘curvature detectors’? Perception. 1978;7:51–64. doi: 10.1068/p070051. [DOI] [PubMed] [Google Scholar]
- Watt RJ, Andrews DP. Contour curvature analysis: Hyperacuities in the discrimination of detailed shape. Vision Research. 1982;22:449–460. doi: 10.1016/0042-6989(82)90193-6. [DOI] [PubMed] [Google Scholar]
- Wilkinson F, Wilson HR, Habak C. Detection and recognition of radial frequency patterns. Vision Research. 1998;38:3555–3568. doi: 10.1016/s0042-6989(98)00039-x. [DOI] [PubMed] [Google Scholar]
- Wilson H,R. Discrimination of contour curvature: Data and theory. Journal of the Optical Society of America A, Optics, and Image Science. 1985;2:1191–1199. doi: 10.1364/josaa.2.001191. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Richards WA. Mechanisms of contour curvature discrimination. Journal of the Optical Society of America A, Optics, and Image Science. 1989;6:106–115. doi: 10.1364/josaa.6.000106. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Wilkinson F, Asaad W. Concentric orientation summation in human form vision. Vision Research. 1997;37:2325–2330. doi: 10.1016/s0042-6989(97)00104-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A demonstration of the curvature aftereffect. Keep the eyes fixated carefully on the point in the center of the screen, ignoring the stimuli flashing on and off to either side. After a period of adaptation two (identical) static probes will appear on either side of fixation. If adaptation has been equal in the two hemifields, resulting purely from the tilt of the components, then the probe stimuli will appear to bend equally to the right. If the adaptation is not equal in the two fields (because of additional adaptation to the global figure of the curve), then the probe stimuli will appear to differ in their degree of curvature.