Abstract
In three N-Back experiments, we investigated components of the process of working memory (WM) updating, more specifically access to items stored outside the focus of attention and transfer from the focus to the region of WM outside the focus. We used stimulus complexity as a marker. We found that when WM transfer occurred under full attention, it was slow and highly sensitive to stimulus complexity, much more so than WM access. When transfer occurred in conjunction with access, however, it was fast and no longer sensitive to stimulus complexity. Thus the updating context altered the nature of WM processing: The dual-task situation (transfer in conjunction with access) drove memory transfer into a more efficient mode, indifferent to stimulus complexity. In contrast, access times consistently increased with complexity, unaffected by the processing context. This study reinforces recent reports that retrieval is a (perhaps the) key component of working memory functioning.
Working memory (WM) is the workplace of the mind. It refers to a temporary memory buffer – lasting for a few seconds at most – which is able to passively store and actively manipulate information (Baddeley & Hitch, 1974; Kane, Bleckley, Conway, & Engle, 2001; Miyake & Shah, 1999). Working memory is typically considered to consist of a set of domain-specific stores for storage, along with a domain-general supervisory attentional mechanism. A crucial feature of this system is its limited capacity, which forces resources to be shared between storage and processing. Given ongoing changes in information content, working memory needs to be updated constantly. The accuracy and/or efficiency with which this updating requirement is performed is reliably associated with fluid intelligence (Friedman et al., 2006; Kane, Conway, Miura, & Colflesh, 2007; Shelton, Elliott, Matthews, Hill, & Gouvier, 2010; Schmiedek, Hildebrandt, Lövdén, Wilhelm, & Lindenberger, 2009; Unsworth & Engle, 2007), making it an important source of individual (and age-related; Chen & Li, 2007) differences.
In our own work (e.g., Verhaeghen & Basak, 2005; Verhaeghen, Cerella, & Basak, 2004; Zhang & Verhaeghen, 2009), we have investigated working memory updating from a structural point of view. This work was inspired by theories that posit a hierarchy of availability within working memory. For instance, Cowan (1995, 2001) proposes a hierarchical two-tier structure, distinguishing a zone of immediate access, labeled the focus of attention, from a larger, “activated” portion of long term memory (not capacity-limited, but subject to interference and decay) where memory representations are available but not immediately accessible (We have labeled this ‘the outer store’; Verhaeghen et al., 2004). Most paradigms purporting to measure WM updating (such as keep-track, memory updating, N-Back, running count, and running span; e.g. Friedman et al., 2006; Garavan, 1998; McElree, 2001; Oberauer, 2002) create demonstrable overflow of the focus of attention, so that in practice, a typical WM updating task implicates the following constituent processes: (a) access to items previously stored in the outer store, bringing them into the focus of attention in the service of the task at hand, and (b) transfer of currently active items from the focus of attention to the outer store for storage and later access (Ecker, Lewandowsky, Oberauer, & Chee, 2010; Kessler & Meiran, 2006; McElree, 2001; Oberauer, 2002; Verhaeghen & Basak, 2005; Voigt & Hagendorf, 2002). We will label these two processes WM access and WM transfer, respectively.
What is the evidence for the involvement of these processes in the updating cost? The literature suggests that WM access is a clear contributor to updating costs. For instance, Voigt and Hagendorf (2002) compared a running-count task, which requires both memory access and memory transfer, with an otherwise identical task in which no memory access was required. They found that latencies were longer for the running-count task, and the difference between tasks was larger when WM access was involved, that is, when items needed to be retrieved from the outer store rather than remained in the focus of attention. Related to this result, Ecker et al. (2010) found that memory access accuracy was correlated with both working memory capacity and general memory updating accuracy.
The role of WM transfer in updating, however, is less clear. Our own previous work is relevant here. We have used an N-Back task in which participants indicate with a button press whether the currently presented item matches the item presented N instances back or not. In this particular task, the focus of attention seems to be able to hold only a single item, as indicated by a jump in response time between N = 1 and N > 1 (Verhaeghen & Basak, 2005; Verhaeghen, Cerella, & Basak, 2004; see also McElree, 2001, and Oberauer, 2006). For any value of N larger than 1, then, the memory representation needs to be accessed from the outer store. One fortuitous side-effect of this task is that WM transfer is (presumable, and we check on this assumption in one of the present experiments) only necessary when the item currently on screen differs from the memory representation (a mismatch stimulus); no new transfer is needed when the two items are identical (a match stimulus). Therefore, the latency difference between match and mismatch stimuli can be taken as a proxy for the time needed to transfer an item to the outer store. (Other factors, including a potential response bias towards a match response, are likely to increase response time in mismatch trials as well, see Luce, 1986, but there is no reason to believe those would covary with the focus-switching requirement.) In all of our previous experiments, we obtained a significant latency difference between match and mismatch trials (mismatch trials were reliably longer), and in six out of seven cases (Vaughan, Basak, Hartman. & Verhaeghen, 2008, Expts 1–2; Verhaeghen & Basak, 2005, Expt 2; Verhaeghen et al., 2004; Zhang & Verhaeghen, 2009, Expts 1–2), the match/mismatch difference was no smaller when items could be accommodated within the focus of attention (i.e., for N = 1) than when they needed to be transferred to the outer store (N > 1). These findings strongly – and surprisingly -- suggest that WM transfer does not add to the time needed to update the content of WM outside the focus of attention.
The striking hypothesis that emerges from this set of results is that WM access is an important determinant of updating, whereas WM transfer contributes little or nothing to the updating cost. This was the hypothesis we investigated in the present set of studies, using a modified version of the N-Back task that allowed us to independently manipulate WM transfer and WM access. We pitted this hypothesis against two alternatives. The first alternative was that the latency difference between match and mismatch stimuli found in our previous studies may not be a proxy for memory transfer after all. Perhaps transferring an item into the outer store occurs not only with mismatch stimuli, but with match stimuli as well. That is, memory transfer may be engaged not only when needed or advantageous for the task, but may be a default process, occurring with every stimulus, necessary or not, unless prohibited by the task. If WM transfer were the default case, the match/mismatch latency difference would come from some other process that was unaffected by the need for memory updating.
The second alternative hypothesis took into account that the updating process as implemented during mismatch trials occurs in a dual-task context, that is, updating requires both WM transfer and WM access. (We do not know whether these processes chain in an additive fashion or can partially occur in parallel; the first scenario is a task-switching situation, the second a true dual-task situation. We use the term ‘dual-task context’ here to describe either possibility – they both require dual-task-set maintenance and selection of the appropriate task.) Dual-task contexts often lead to trade-offs, in this case perhaps to the prioritization of access over transfer. This would then imply that the memory transfer process that gets engaged when working memory is truly ‘working’ is qualitatively distinguishable from the same nominal process when executed in isolation – an intriguing conclusion indeed.
The paradigm we used (as in most of our previous work) was an identity-judgment N-Back task, with N = 3. In this task, participants are presented with a set of stimuli, shown one at a time, and are required to indicate whether the stimulus currently on screen matches the one presented three positions back. (The first three stimuli are presented without the matching requirement.) We present the stimuli in three columns, filled from left to right, so that in practice participants indicate whether the stimulus on screen matches the one previously shown in the same column. The columnized display serves to facilitate item-to-position binding, thus maximizing the item-memory aspect of the task and minimizing the keeping-track demand. To disentangle the contributions of memory transfer and memory access to WM updating, we need a tracer or marker -- an independent stimulus manipulation that reliably affects the size of the updating cost and can then be used to trace the influence of isolated transfer and access processes on the updating operation. Our manipulation of choice is stimulus complexity: Increasing stimulus complexity has been shown to reliably lead to increased updating costs in N-back and related paradigms (Leonards, Ibanez, & Giannakopoulos, 2002; Vaughan et al., 2008; Zhang & Verhaeghen, 2009). The stimuli we used were random checkerboards that differed systematically in the number of filled squares (see Method for details of stimulus complexity manipulation).
The manipulations used to separate the role of WM transfer and WM access was simple: We presented the stimuli in two (Expt. 1) or three (Expts. 2 and 3) rows of three stimuli, and examined the effects of complexity on each row. In Experiment 1, the first row was for study only; participants committed each checkerboard pattern to memory. The second row was a test row; participants accessed the WM representation in the same column and decided whether or not it matched the current stimulus. Thus only WM transfer should be involved in the first row, and only WM access in the second row (assuming WM transfer is not a default process, an assumption we investigated in Experiment 3). This experiment provided us with an estimate of the size of the stimulus complexity effect (if any) for WM transfer and WM access as they occur in isolation, without the dual-task access-and-transfer context imposed by the updating situation.
Experiment 2 used three rows. In this case, row 1 involved only WM transfer. Row 2 was an updating situation, where both WM transfer and WM access processes were engaged, and row 3 involved only WM access (again, assuming transfer is not a default process). This experiment tested the second alternative explanation for the lack of transfer effects on the updating process, namely the hypothesis of dual-task-context trade-offs, by comparing results for row 1 (transfer only) and row 2 (transfer plus access). Experiment 3 again used three rows, but required participants to compare stimuli in both row 2 and row 3 with those in row 1. Under these instructions, transfer of the stimuli in row 2 was not necessary (and if undertaken, would hurt performance). Experiment 3 assessed the first of the alternative hypotheses, namely that memory transfer is engaged by default, even when only access is necessary. By comparing performance in row 2 of Experiment 3 (access only) with performance in row 3 of Expt. 2 or Expt. 3 (access plus possibly default transfer), we could test the default-transfer hypothesis.
Method
Participants
All participants were recruited from an introductory psychology course and received course credit for their participation. Different samples of younger adults participated in the three experiments: Experiment 1, N = 36 (Mage=18.75, SDage=1.2; Meducation=12.28, SDeducation=1.4); Experiment 2, N = 29 (Mage=19.89, SDage=2.1; Meducation=14.09, SDeducation=1.8); Experiment 3, N = 25 (Mage=20.58, SDage=1.5; Meducation=13.61, SDeducation=2.4). No participant reported being colorblind.
Stimuli and Complexity-Effect Pilot Experiment
Stimuli were black and white checkerboard patterns created by blackening C cells of an invisible 3 × 3 matrix in a pseudo-random fashion. We used C values of 1, 2, 4, 5, 7, and 8 filled cells. The number of possible stimuli is large; in this and the subsequent experiments, only nine patterns were prepared for each value of C, in analogy with the nine digits used in the standard digit versions of the N-Back task. (We also piloted checkerboards with 3 and 6 filled cells. Reponses to these particular stimuli were not monotonic with the other C values, and these stimulus sets were dropped from the final experiments.) Figure 1 depicts the final set of stimuli in black and white. From the geometry we can see that stimulus complexity should increase from 1-cell to 2-cells and from 2-cells to 4-cells, and then decrease from 5 to 7, and from 7 to 8, given that the latter patterns are contrast reversals of the former.
Figure 1.
The checkerboard stimuli as used in all four experiments. Each row represents all nine stimuli within each C value; row 1 represents the stimuli with C =1, row 2 the stimuli with C = 2, and so on.
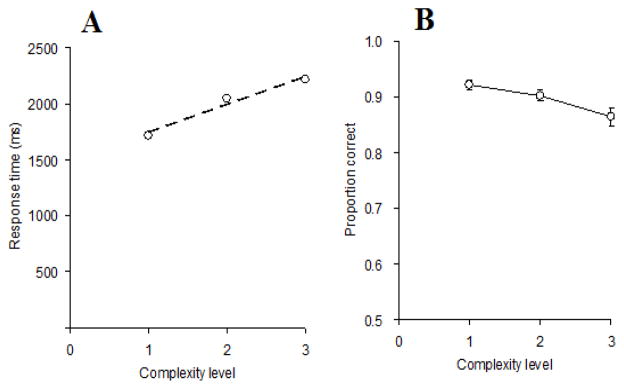
To formally test the effective complexity of these stimuli, we conducted a pilot experiment using the stimuli in a visual search task (see Alvarez & Cavanagh, 2004, and Eng, Chen, & Jiang, 2005, for similar tests; more information-rich stimuli are found to lead to longer search times). Data from 24 participants are presented in Figure 2. Participants searched for a specified target among eight distractors with the same number of cells. The target was precued for 500 ms, followed by a 1000 ms blank screen. The search display was then presented until a response was given. In half of the trials, the search display included the target. Participants pressed the “/” key to signify presence of the target; the “z” key signified target absence. Feedback indicating RT and accuracy was given for 1000 ms following each response. We scheduled 12 trials for each value of C; C values were blocked and presented in ascending order. The checkerboards were presented in nine randomly selected locations from a 4 × 3 invisible matrix spanning the screen. To avoid perfectly aligned rows and columns, we displaced each checkerboard by a few pixels horizontally or vertically.
Figure 2.
Results from the visual search task used to assess complexity effects. Panel A represents RT as a function of stimulus complexity, along with the best fitting regression lines; Panel B shows accuracy as a function of stimulus complexity. Error bars represent standard errors. RT and accuracy are both sensitive to complexity. Complexity level 1 includes conditions with C = 1 and C = 8, level 2 with C = 2 and C = 7, and level 3 with C = 4 and C = 5. Error bars represent SE.
As we anticipated, the effect of C in the pilot experiment (and all further experiments reported in this paper) was nearly symmetrical around the midpoint of its range. Therefore we combined the data from C values that differed only in contrast, that is, 1- and 8-cell patterns (complexity level 1), 2- and 7-cell patterns (complexity level 2), and 4- and 5-cell patterns (complexity level 3). Figure 2A shows search latencies as a function of complexity level. ANOVA results showed a significant complexity effect on RT, F (2, 46) = 99.67, MSE = 15,297.30, p < 0.001, with a significant linear component; the slope was 248 ms/level (F (1, 23) = 178.29, MSE = 16,560.99, p < 0.001). (Slopes are presented here and in the following experiments for ease of comparison between conditions; we do not assume that the underlying effect is exactly linear in C). Accuracies are shown in Figure 2B. An ANOVA on complexity level revealed a significant complexity effect, F (2, 46) = 14.27, MSE = 0.00, p < 0.001, with a significant linear component, indicating that accuracy decreased monotonically with complexity, (F (1, 23) =21.24, MSE = 0.00, p <0.01).
Procedure
The WM task was an identity-judgment 3-Back procedure (Verhaeghen & Basak, 2005), with items presented in two (Expt. 1) or three (Expts. 2 and 3) rows of three columns. The first row was study-only. From the second row on, participants in Experiments 1 and 2 indicated whether the current item was identical to the item presented three positions back. In practice, this meant that participants indicated whether the item currently on screen matched the item presented in the same column as the current item but in the previous row. In Experiment 3, they decided whether the item matched the one presented in the same column in the initial row. Each column was depicted in a different color. (The column/color scheme was meant to aid participants in keeping track, to emphasize the memory aspect of the task over the executive-control aspect.) Figure 3 shows a black-and-white rendition of a sample stimulus set for a single trial in each of the three experiments as it would appear on the computer screen if all the items remained visible. The size of each checkerboard was 3.2 cm × 3.6 cm; the checkerboards were separated by a horizontal gap of 4.7 cm, and a vertical gap of 1.3 cm. In practice, only one pattern was shown at any time; the order of presentation was the conventional reading pattern for the English language: left to right, top to bottom. Presentation of successive stimuli in the top row was self-paced, initiated by pressing the space bar; from the second row on, participants pressed one of two keys to indicate their answer. The “/” key signified a match; the “z” key signified a mismatch. As soon as a key was pressed, the next stimulus appeared. Viewing distance was not fixed; participants were allowed to choose the distance they felt most comfortable with. Participants were instructed to be both fast and accurate. All participants were tested in a single session of about 60 – 90 minutes in duration. Participants were encouraged to take breaks between blocks.
Figure 3.

A sample trial from each of the experiments, at complexity level 2, if all the stimuli were to remain onscreen, with the correct answer added. Stimuli were shown one at a time, in a reading pattern (left to right, then on the next line, etc.); each column was depicted in a different color. Presentation times were subject-paced. In Experiment 1 (panel A), stimuli in row 2 were compared to those in row 1; in Experiment 2 (panel B), stimuli for rows 2 and row 3 were compared to those in the row above it; in Experiment 3 (panel C), stimuli in rows 2 and 3 were compared to those in row 1.
For Experiment 1, we used a two-row task. A total of 180 trials were presented (30 trials for each of the six C values), yielding 1080 responses (540 responses from the first row recording the time participants took to transfer the stimuli, because study was self-paced; 540 from the second row recording the time to make match/mismatch judgments). Half the participants received C values in increasing order; the other half received them in decreasing order. Experiment 2 used a three-row task. A total of 120 trials were presented, 20 trials for each C value, yielding 1080 responses (360 from the first row, 360 from the second row and 360 from the third row). Experiment 3 was identical to Experiment 2, with one exception: Comparisons in row 3 were made to the stimuli from row 1 (just like the row 2 comparisons), instead of to the immediately preceding row (Thus the row 2 stimuli did not need be transferred into the outer store; transfer would in fact interfere with row 3 judgments).
Results
Experiment 1: Two-row 3-Back task
As part of the design, responses from the first stimulus in each row were omitted from the data analysis, given their contamination by task-switching effects (i.e., switching from study to test, and from the right side of the screen to the left side). For the first row, RT analyses were conducted on all responses; for the second row, RT analyses were conducted on correct responses only. To remove outliers, RT distributions were truncated at three interquartile ranges above or below the median, to remove potential high-leverage points from the calculation of the mean RT. This procedure removed 2.5% of the eligible RTs.
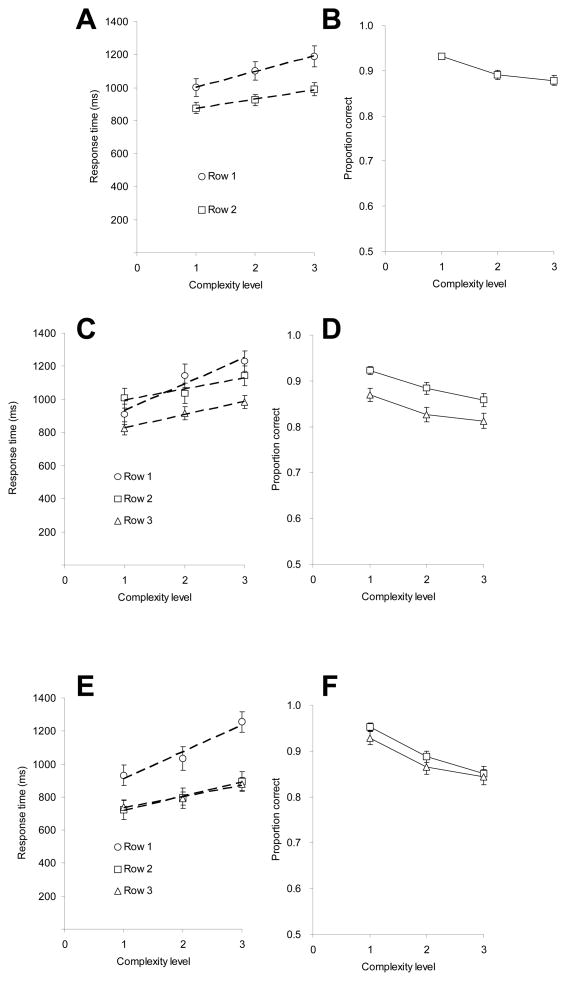
Figure 4A shows the mean RT as a function of complexity and row. The complexity effect appears to be larger in row 1 than in row 2. An ANOVA revealed a significant main effect of row, F (1, 35) = 33.63, MSE = 45,115.98, p < 0.001 (row 1 yielded slower responses than row 2), and of complexity, F (2, 70) = 13.39, MSE = 30,611.27, p < 0.001 (more complex shapes yielded longer RTs). The complexity by row interaction was also significant, F (2, 70) = 3.16, MSE = 8,333.18, p < .05. To assess the latter effect, we calculated slopes and intercepts for the RT by complexity regression (intercepts were evaluated at complexity level 1). The slope and the intercept for the first row were 94 ms/level and 910 ms respectively, and for the second row, 57 ms/level and 816 ms. An ANOVA was also conducted with trial type (match vs. mismatch) and complexity as within-subject factors for row 2 (there was no trial type for row 1). The results showed a significant main effect of trial type (mismatch responses were on average 75 ms slower than match responses), F (1, 35) = 9.20, MSE = 32,587.60, p < 0.01, and a significant effect of complexity, F (2, 70) =11.35, MSE = 22,088.15, p < .0001; trial type did not interact with complexity, F (2, 70) = 0.31, MSE = 4,438.67.
Figure 4.
Panel A represents response time (RT) as a function of stimulus complexity and stimulus row for Experiment 1 (row 1 = transfer; row 2 = retrieval of row 1), along with the best fitting regression lines; Panel B represents accuracy for row 2 as a function of stimulus complexity (Experiment 1). Row 1 is slower and more sensitive to complexity than row 2. Panel C: RT as a function of stimulus complexity and stimulus row for Experiment 2 (row 1 = transfer; row 2 = transfer and retrieval of row 1; row 3 = retrieval of row 2), along with the best fitting regression lines; Panel D shows accuracy for rows 2 and 3 as a function of stimulus complexity (Experiment 2). Row 1 is slower and more sensitive to complexity than rows 2 and 3, which have identical RT-by-complexity slopes. Panel E: RT as a function of stimulus complexity and stimulus row in Experiment 3 (row 1 = transfer; row 2 = retrieval of row 1; row 3 = retrieval of row 1), along with the best fitting regression lines; Panel F: accuracy for rows 2 and 3 as a function of stimulus complexity (Experiment 3). Row 1 is slower and more sensitive to complexity than row 2 and 3, which do not reliably differ in RT. Error bars represent standard errors. Complexity level 1 includes conditions with C = 1 and C = 8, level 2 with C = 2 and C = 7, level 3 with C = 4 and C = 5. Error bars represent SE.
Figure 4B shows complexity effects on accuracy for row 2 (there was no right or wrong response for the first row). There was a significant main effect of complexity, F (2, 70) = 13.34, MSE < 0.01, p < 0.001 (more complex shapes yielded lower accuracy). There was a significant difference in accuracy between match and mismatch responses (mismatch responses were on average 2.4 % less accurate than match responses), F (1, 35) = 4.49, MSE = 0.01, p < 0.05. Trial type interacted with complexity, F (2, 70) = 6.46, MSE < 0.01, p < 0.01. Accuracy for match responses was lower than for mismatch responses at complexity level 1, and accuracy for mismatch responses was lower than for match responses at complexity levels 2 and 3.
Experiment 2: Three-row 3-Back task
The proportion of RTs removed as outliers was 2.1%. Inspection of Figure 4C shows that the complexity effect is larger in row 1 than in rows 2 and 3, which appear to show a similar-sized effect. Additionally, row 2 RTs are generally slower than row 3 RTs. These observations were confirmed in an ANOVA with stimulus complexity (1 – 3) and row (1, 2, 3) as within-subject factors. There was a significant main effect of row, F (2, 56) = 16.29, MSE = 52,402.90, p < 0.001, and of complexity, F (2, 56) = 23.12, MSE = 40,011.45, p < 0.001, as well as a significant complexity by row interaction, F (4, 112) = 8.24, MSE = 12,624.63, p < 0.001. The slope and the intercept for row 1 were 161 ms/level and 772 ms, respectively; the slope and the intercept for row 2 were 68 ms/level and 926 ms; the slope and the intercept for row 3 were 80 ms/level and 749 ms. The slope difference between row 1 and row 2 was significant, as evidenced by a significant interaction between complexity and row for an analysis including rows 1 and 2 only, F (2, 56) = 14.38, MSE = 12,823.83, p < 0.001. The slope difference between row 1 and row 3 was also significant, signaled by a significant interaction between complexity and rows 1 and 3, F (2, 56) = 5.94, MSE = 19,176.08, p < 0.01. The slope difference between row 2 and row 3 was not significant, indicated by a non-significant interaction between complexity and rows 2 and 3, F (2, 56) = 2.34, MSE = 5,873.96. Turning from slope differences in the complexity functions to intercept differences, we analyzed response times at complexity level 1 as a surrogate for the intercepts. On this measure, the intercept difference between row 1 (908 ms) and row 2 (1006 ms) was significant, t (29) = 2.40, p <0.05; the difference between row 2 (1006 ms) and row 3 (825 ms) was significant, t (29) = 4.54, p < 0.001, and the difference between row 1 (908 ms) and row 3 (825 ms) approached significance, t (29) = 1.76, p = 0.09.
Additionally, an ANOVA was conducted on the three factors of trial type (match vs. mismatch), row (row 2 vs. row 3) and complexity (1 – 3). There was a main effect of row (responses in row 2 were slower than responses in row 3, F (1, 28) = 25.21, MSE = 85,489.90, p < 0.001), and a main effect of trial type (mismatch responses were slower than match responses, F (1, 28) = 70.05, MSE = 39,690.91, p < 0.001); trial type interacted with row, F (1, 28) = 11.73, MSE = 20,911.23, p < 0.01, but not with complexity, F (2, 56) = 0.17, MSE = 9,204.19. The three-way interaction was also not significant, F (2, 56) = 0.09, MSE = 7,974.77. Thus the difference between match and mismatch response times was larger in row 2 (232 ms) than in row 3 (126 ms).
Accuracy results are presented in Figure 4D. An ANOVA based on complexity (1 – 3) and row (row 2 vs. row 3) revealed a significant effect of row, F (1, 28) = 13.53, MSE = 0.01, p = 0.001 (accuracy in row 2 was higher than that in row 3), and of complexity level, F (2, 56) = 20.77, MSE < 0.01, p < 0.001 (accuracy was less for more complex shapes), but the interaction of complexity by row was not significant, F (2, 56) = 0.29, MSE < 0.01. Analysis of the accuracy of match and mismatch responses indicated that there was no difference between the two trial types, F (1, 29) = 1.55, MSE = 0.02. Trial type interacted neither with row, F (1, 28) = 1.14, MSE = 0.01, nor with complexity, F (2, 56) = 2.39, MSE < 0.01. The three-way interaction was not significant either, F (2, 56) = 0.21, MSE < 0.01.
Experiment 3: Three-row, no transfer 3-Back task
The percentage of RTs which were removed as outliers was 1.5%. Inspection of Figure 4E shows that the complexity effect in RT was larger in row 1 than in rows 2 and 3, which appear to not differ. These observations were tested in an ANOVA with stimulus complexity and row as the within-subject factors. There was a significant main effect of row, F (2, 48) = 34.05, MSE = 53,305.09, p < 0.001, and of complexity, F (2, 48) = 13.30, MSE = 64,626.45, p < 0.001, as well as a significant complexity by row interaction, F (4, 96) = 7.29, MSE = 9,224.83, p < 0.001. The slope and the intercept for row 1 were 162 ms/level and 749 ms, respectively; for row 2 they were 86 ms/level and 633 ms; and for row 3 they were 69 ms/level and 666 ms. The slope difference between row 1 and row 2 was significant, F (2, 48) = 7.05, MSE = 81,737.66, p =0.002, as was the slope difference between row 1 and row 3, F (2, 48) = 8.24, MSE = 14,087.15, p =0.001. The slope difference between row 2 and row 3 was not significant, F (2, 48) = 1.88, MSE = 1,989.30. We used the response times at complexity level 1 to estimate intercepts. The intercept difference between row 1 (749 ms) and row 2 (633 ms) was significant, t (24) = 4.51, p < 0.001, as was the difference between row 1 (749 ms) and row 3 (666 ms), t (24) = 4.20, p < 0.001. The intercept difference between row 2 (633 ms) and row 3 (666 ms) was not significant, t (24) = −1.72, p =0.098.
An additional ANOVA was conducted on the three factors of trial type (match vs. mismatch), row (row 2 and row 3) and complexity (1 – 3). The results showed that response time in row 2 was equal to response time in row 3, F (1, 24) = 0.10, MSE = 8,677.81, and that mismatch responses were slower than match responses, F (1, 24) = 33.99, MSE = 12,272.77, p < 0.001. Trial type did not interact with row, F (1, 24) = 0.54, MSE = 3,288.15, nor with complexity, F (2, 48) = 0.61, MSE = 6,433.26. The three-way interaction was not significant either, F (2, 48) = 0.28, MSE = 4,466.61.
Accuracy results are presented in Figure 4F. An ANOVA on complexity (1 – 3) and row (row 2 and row 3) revealed a significant effect of row, F (1, 24) = 8.26, MSE < 0.01, p = 0.008, and of complexity level, F (2, 48) = 20.74, MSE = 0.01, p < 0.001; the interaction between complexity and row was not significant, F (2, 48) = 0.61, MSE < 0.01. Match trials were more accurate than non-match trials, F (1, 24) = 4.95, MSE = 0.02, p < .05; trial type did not interact with row, F (1, 24) = 0.24, MSE < 0.01; it did, however, interact with complexity, F (2, 48) = 6.24, MSE = 0.01, p < 0.01. The three-way interaction was not significant, F (2, 48) = 0.29, MSE < 0.01. To further explore the trial type by complexity interaction, we analyzed each row separately. For row 2, the main effect of trial type was significant, F (1, 24) = 5.86, MSE = 0.01, p < 0.05 (accuracy was higher in match trials than on mismatch trials); trial type interacted with complexity, F (2, 48) = 4.32, MSE = 0.01, p < 0.05. For row 3, the main effect of trial type was not significant, F (1, 24) = 2.47, MSE = 0.01, and the trial type by complexity interaction approached significance, F (2, 48) = 2.57, MSE = 0.01, p = 0.087.
Discussion
In three experiments, we investigated components of the process of working memory updating, more specifically the speed and accuracy of access to representations stored outside the focus of attention, in the outer store, as well as speed and accuracy of transfer from the focus to the outer store. Our stimuli were series of checkerboard patterns; the task was a 3-Back same-different working-memory task. Presentations and instructions were varied to create either single-task (either access or transfer) or dual-task (both access and transfer) processing contexts. We used checkerboard complexity as a marker for WM effects. The RT by complexity slope for the first row of each experiment (the study row) measured the complexity effect for WM transfer in a single-task context. Similarly, the RT by complexity slope for the final row of each experiment, as well as for the second row in Expt. 3, measured the complexity effect for WM access in a single-task context (i.e., there was no need to transfer the stimuli from the final row into WM; we argue below that in such cases participants did not in fact engage in WM transfer).
In all three experiments the same pattern emerged: We obtained a significant complexity effect for both transfer (in isolation) and access (in isolation), and the effect for WM transfer was consistently and considerably larger than that for WM access. The complexity slope for transfer varied from 94 ms/complexity level (Expt. 1) to 161 ms/complexity level (Expt. 2) and 162 ms/complexity level (Expt. 3); the complexity slope for access varied from 57 ms/complexity level (Expt. 1) to 80 ms/complexity level (Expt. 2) and 69 ms/complexity level (Expt. 3). Within each experiment, the transfer slope was about double the access slope; the ratio varied from 1.6 (Expt. 1) to 2.0 (Expt. 2) and 2.3 (Expt. 3).
These findings, a large effect of stimulus complexity on WM transfer and a lesser effect on WM access, pertained to simple, single-task conditions, where each process was measured in isolation from the other. What about dual-task conditions, when both access and transfer were required in a full-blown WM updating situation? Were complexity effects altered? This situation arose in the second row of Experiment 2. In row 2 a WM representation had to be accessed for comparison with the stimulus on screen; then a representation of the on-screen stimulus had to be transferred into the outer store in preparation for row 3. The empirical result in this case was clear: The complexity slope of this dual-task access-and-transfer row was statistically identical to that of the final row of the same experiment, where only access was implicated. Rather than increasing the slope of the row 2 regression line, the dual-task access-and-transfer requirement increased its intercept. This indicates that in the dual-task access-and-transfer context transfer lost its single-task sensitivity to stimulus complexity, taking instead a constant amount of time regardless of the complexity of the stimulus.
This result was further refined by separating responses to match stimuli and mismatch stimuli in row 2, estimating a separate regression line for each stimulus type. Mismatch responses were longer, and at least some of the excess can be attributed to the transfer process entailed by mismatch stimuli and not required by match stimuli (although other processes are likely to contribute to negative penalties as well, Luce, 1986). In these more highly resolved data we again found that the transfer requirement increased the intercept of the mismatch line without increasing its slope, compared to the match line.1 Again the conclusion follows that in the dual-task access-and-transfer context, the transfer operation lost its sensitivity to stimulus complexity.
This conclusion, although surprising at first blush, agrees with those from other of our experiments. As mentioned in the Introduction, we have regularly found a latency difference between match stimuli and mismatch stimuli attributable at least in part to the added transfer requirement, and in a large majority of those cases the latency difference was found not to interact with the focus-switching requirement (Vaughan et al, 2008, Expts 1–2; Verhaeghen & Basak, 2005, Expt 2; Verhaeghen et al., 2004; Zhang & Verhaeghen, 2009, Expts 1–2). This suggests that transfer was not a significant contributor to the focus-switching cost in those cases, paralleling our conclusion here.
We can be certain that the first-row transfer slopes were not contaminated with WM access – there were simply no stimuli to access. It is less certain that the last-row access slopes were uncontaminated by WM transfer. Possibly participants did transfer the stimuli in the final row to the outer store, at least to some extent, even though only memory access was needed. If that were the case, final row slopes would reflect the combined effects of transfer and access. Experiment 3 offered evidence against this possibility. Participants in Experiment 3 were instructed to access but not to ‘remember’ (i.e., transfer) the stimuli in row 2 (because both row 2 and row 3 had to be compared to row 1). The RT by complexity function for row 3 coincided with the function for row 2, which carried only an access requirement. The Experiment 3 result strongly suggests that slopes for the final rows reflected memory access and only memory access.2
In Experiment 3 no transfer was required in either row 2 or row 3; transfer in row 2 would in fact ruin performance. Under those circumstances, we would expect the mismatch-match difference to be constant across rows, and this is just what we found. In Experiment 2, on the other hand, the mismatch-match difference did interact with row. In row 2 of Experiment 2 (a 232 ms mismatch-match difference), transfer was crucial for success in row 3; in row 3 (a 126 ms mismatch-match difference), transfer was unnecessary. If we assume additivity between transfer and other more generic processes underlying negative penalties, the duration of the transfer process in Experiment 2 can be estimated at 106 ms (232 ms – 126 ms).
The reason for the steeper slope and the slow RTs in the first row of all the experiments is uncertain. Perhaps this slope reflects the default mode of WM transfer, that is, transfer might generally be sensitive to stimulus characteristics such as complexity. This makes sense – more complex stimuli require more complex representations, and this would likely be reflected in longer transfer times. The additional dual-task access-and-transfer context of true updating as introduced in row 2 of Experiment 2 may drive a participant away from this default mode into faster and less complexity-sensitive processing. One reason for this could be metacognitive -- a subjective feeling on the part of the participant that time is running out and that items would decay from the outer store if the subject does not respond as fast as she can. Another or additional reason could be that access, which is necessary for providing a correct answer, takes subjective precedence over transfer. This interpretation is supported by the large drop in accuracy from row 2 to row 3 in this experiment. Alternately, the row 1/row 2 difference may signal a strategy shift from an overly cautious mode of processing to an efficient mode of processing. Participants may spend more time on row 1 than is needed, and then revert to a more efficient pace in the dual-task access-and-transfer setting of row 2. One indication of possible over-caution in row 1 is the lack of interaction between row and complexity in the accuracy data of Experiment 2. Accuracy for the third row is determined (in part) by the complexity-insensitive transfer in row 2, whereas accuracy for the second row is determined (in part) by the complexity-sensitive transfer in row 1. If the longer transfer times for more complex stimuli observed in row 1 mattered, we would expect an accuracy drop for higher levels of complexity in row 3 compared to row 2. We did not observe this drop.
In sum, our experiments suggest that an updating requirement altered the nature of processing in working memory. When transfer occurred in the absence of a requirement for WM access, it was slow and highly sensitive to stimulus complexity, much more so than access – the RT by complexity slopes for the initial, transfer-only rows in the three experiments were considerably steeper than the slopes for the final, access-only rows. When transfer occurred within the context of WM updating, however, it was fast (taking around 106 ms) and no longer sensitive to stimulus complexity. Thus the updating operation altered the nature of processing: The dual-task context (transfer in the presence of access) drove transfer into a different, perhaps more automatic mode. Surprisingly, this different mode was no less efficacious. In Experiment 2, we found no interaction between stimulus complexity and type of transfer (in isolation vs. in the updating context). This in turn suggests some form of over-cautiousness while processing the initial row, rather than deficient transfer of the second row under updating conditions.
Our analysis recalls the oft-made distinction between a “passive” short-term or primary memory store and an “active” working memory store (e.g., Miyake & Shah, 1999), Our study is (as far as we know) the first to show that pushing the system from passive into active mode seems to fundamentally alter the nature of transfer, be it by necessity or by strategic choice. Specifically, the requirement to transfer items into the outer store in the context of WM updating (i.e., while access is also required) speeds up memory transfer and makes it indifferent to stimulus quality (at least within the bounds of the present stimulus set). This result fits well with current evidence that accurate access to the outer store (in this literature often labeled ‘secondary memory’) is an essential contributor to working memory capacity and/or tests of fluid intelligence (Ecker et al., 2010; Mogle, Lovett, Stawski, & Sliwinski, 2008; Rose, Myerson, Roediger, & Hale, 2010; Shelton, et, al., 2010; Unsworth & Engle, 2007) – access appears to bear the brunt of stimulus-specific processing.
Acknowledgments
Yanmin Zhang, Department of Psychology, Yale University; Paul Verhaeghen, School of Psychology, Georgia Institute of Technology; John Cerella, Department of Psychology and Center for Health and Behavior, Syracuse University. This research was supported by a grant from the National Institute on Aging (AG-16201); parts of the research were conducted in partial fulfillment of the requirements for Yanmin Zhang’s Master of Sciences degree.
Footnotes
This finding of parallel lines for match and mismatch stimuli also argues against one alternative interpretation of the access slope as formulated by one reviewer, namely that correct answers on mismatch trials can be based on partial mismatches, that is, as soon as enough information accumulates to indicate a mismatch, a response can be emitted. If partial mismatch information is available quicker for more complex stimuli (which is likely, on statistical grounds), then this could explain why access trials (rows 2-3) have lower slopes than transfer trials (row 1). If this were true, however, mismatch trials should show shallower slopes than match trials (because all information needs to be available before a match can be indentified as such); and this is not what was found.
One of the reviewers suggested that subjects may transfer stimuli to the outer store under all circumstances, and that the slope of the complexity functions may be due to slower transfer times for the more complex stimuli; access would then be complexity-insensitive. This would explain why all slopes are identical in all rows past Row 1 – they would reflect the mixture of complexity-sensitive access and complexity-insensitive transfer. This alternative interpretation of the data, however, would leave the intercept difference between row 2 and row 3 in Experiment 2 unexplained.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final cigf form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Yanmin Zhang, Yale University.
Paul Verhaeghen, Georgia Institute of Technology.
John Cerella, Syracuse University.
References
- Alvarez GA, Cavanagh P. The capacity of visual short-term memory is set both by total information load and by number of objects. Psychological Science. 2004;15:106–111. doi: 10.1111/j.0963-7214.2004.01502006.x. [DOI] [PubMed] [Google Scholar]
- Baddeley AD, Hitch G. Working memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 8. New York: Academic Press; 1974. pp. 47–89. [Google Scholar]
- Chen T, Li D. The roles of working memory updating and processing speed in mediating age-related differences in fluid intelligence. Aging, Neuropsychology, and Cognition. 2007;14:631–646. doi: 10.1080/13825580600987660. [DOI] [PubMed] [Google Scholar]
- Cowan N. Memory theories from A to Z. Contemporary Psychology. 1995;40:552–555. [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24:87–185. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Ecker UKH, Lewandowsky S, Oberauer K, Chee AEH. The components of working memory updating: An experimental decomposition and individual differences. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:170–189. doi: 10.1037/a0017891. [DOI] [PubMed] [Google Scholar]
- Eng HY, Chen D, Jiang Y. Visual working memory for simple and complex visual stimuli. Psychonomic Bulletin & Review. 2005;12:1127–1133. doi: 10.3758/bf03206454. [DOI] [PubMed] [Google Scholar]
- Friedman NP, Miyake A, Corley RP, Young SE, DeFries JC, Hewitt JK. Not all executive functions are related to intelligence. Psychological Science. 2006;17:172–179. doi: 10.1111/j.1467-9280.2006.01681.x. [DOI] [PubMed] [Google Scholar]
- Garavan H. Serial attention within working memory. Memory and Cognition. 1998;26:263–276. doi: 10.3758/bf03201138. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Bleckley MK, Conway ARA, Engle RW. A controlled-attention view of working-memory capacity. Journal of Experimental Psychology: General. 2001;130:169–183. doi: 10.1037//0096-3445.130.2.169. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Conway ARA, Miura TK, Colflesh GJH. Working memory, attention control, and the N-back task: A cautionary tale of construct validity. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:615–622. doi: 10.1037/0278-7393.33.3.615. [DOI] [PubMed] [Google Scholar]
- Kessler Y, Meiran N. All updateable objects in working memory are updated whenever any of them is modified: Evidence from the memory updating paradigm. Journal of Experimental Psychology: Learning, Memory and Cognition. 2006;32:570–585. doi: 10.1037/0278-7393.32.3.570. [DOI] [PubMed] [Google Scholar]
- Leonards U, Ibanez V, Giannakopoulos P. The role of stimulus type in age-related changes of visual working memory. Experimental Brain Research. 2002;146:172–183. doi: 10.1007/s00221-002-1175-9. [DOI] [PubMed] [Google Scholar]
- Luce RD. Response Times: Their Role in Inferring Elementary Mental Organization. Oxford University Press; New York: 1986. [Google Scholar]
- McElree B. Working memory and focal attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:817–835. [PMC free article] [PubMed] [Google Scholar]
- Miyake A, Shah P, editors. Models of working memory: Mechanisms of active maintenance and executive control. New York: Cambridge University Press; 1999. [Google Scholar]
- Mogle JA, Lovett BJ, Stawski RS, Sliwinski MJ. What’s so special about working memory? An examination of the relationships among working memory, secondary memory, and fluid intelligence. Psychological Science. 2008;19:1071–1077. doi: 10.1111/j.1467-9280.2008.02202.x. [DOI] [PubMed] [Google Scholar]
- Oberauer K. Access to information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:411–421. [PubMed] [Google Scholar]
- Oberauer K. Is the focus of attention in working memory expanded through practice? Journal of Experimental Psychology: Learning, Memory & Cognition. 2006;32:197–214. doi: 10.1037/0278-7393.32.2.197. [DOI] [PubMed] [Google Scholar]
- Rose NS, Myerson J, Roediger HL, Hale S. Similarities and differences between working memory and long-term memory: Evidence from the levels-of-processing span task. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:471–483. doi: 10.1037/a0018405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedek F, Hildebrandt A, Lövdén M, Wilhelm O, Lindenberger U. Complex span versus updating tasks of working memory: The gap is not that deep. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35:1089–1096. doi: 10.1037/a0015730. [DOI] [PubMed] [Google Scholar]
- Shelton JT, Elliott EM, Matthews RA, Hill BD, Gouvier WD. The relationships of working memory, secondary memory, and general fluid intelligence: Working memory is special. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:813–820. doi: 10.1037/a0019046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unsworth N, Engle RW. The nature of individual differences in working memory capacity: Active maintenance in primary memory and controlled search from secondary memory. Psychological Review. 2007;114:104–132. doi: 10.1037/0033-295X.114.1.104. [DOI] [PubMed] [Google Scholar]
- Vaughan L, Basak C, Hartman M, Verhaeghen P. Aging and working memory inside and outside the focus of attention: Dissociations of availability and accessibility. Aging, Neuropsychology, and Cognition. 2008;15:703–724. doi: 10.1080/13825580802061645. [DOI] [PubMed] [Google Scholar]
- Verhaeghen P, Basak C. Aging and switching of the focus of attention in working memory: Results from a modified N-Back task. Quarterly Journal of Experimental Psychology (A) 2005;58:134–154. doi: 10.1080/02724980443000241. [DOI] [PubMed] [Google Scholar]
- Verhaeghen P, Cerella J, Basak C. A working memory workout: How to change to size of the focus of attention from one to four in ten hours or less. Journals of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:1322–1337. doi: 10.1037/0278-7393.30.6.1322. [DOI] [PubMed] [Google Scholar]
- Voigt S, Hagendorf H. The role of task context for component processes in focus switching. Psychologische Beiträge. 2002;44(S):248–274. [Google Scholar]
- Zhang Y, Verhaeghen P. Glimpses of a One-Speed Mind: Focus-Switching and Search for Verbal and Visual, and Easy and Difficult Items in Working Memory. Acta Psychologica. 2009;131:235–244. doi: 10.1016/j.actpsy.2009.05.009. [DOI] [PubMed] [Google Scholar]