DETERMINING CONFIDENCE OF PREDICTED INTERACTIONS BETWEEN HIV-1 AND HUMAN PROTEINS USING CONFORMAL METHOD

Abstract

Identifying protein-protein interactions (PPI’s) is critical for understanding virtually all cellular molecular mechanisms. Previously, predicting PPI’s was treated as a binary classification task and has commonly been solved in a supervised setting which requires a positive labeled set of known PPI’s and a negative labeled set of non-interacting protein pairs. In those methods, the learner provides the likelihood of the predicted interaction, but without a confidence level associated with each prediction. Here, we apply a conformal prediction framework to make predictions and estimate confidence of the predictions. The conformal predictor uses a function measuring relative ’strangeness’ interacting pairs to check whether prediction of a new example added to the sequence of already known PPI’s would conform to the ’exchangeability’ assumption: distribution of interacting pairs is invariant with any permutations of the pairs. In fact, this is the only assumption we make about the data. Another advantage is that the user can control a number of errors by providing a desirable confidence level. This feature of CP is very useful for a ranking list of possible interactive pairs. In this paper, the conformal method has been developed to deal with just one class - class interactive proteins - while there is not clearly defined of ’non-interactive’ pairs. The confidence level helps the biologist in the interpretation of the results, and better assists the choices of pairs for experimental validation. We apply the proposed conformal framework to improve the identification of interacting pairs between HIV-1 and human proteins.

1. Introduction

1.1. Protein-protein interactions

Protein-protein interactions (PPI’s)^1,2 are fundamental building blocks of communication within and across cells: cells responding to signals in the environment and pathogens interacting with host cells do so via complex networks of PPI’s. Identification of the full sets of PPI’s (interactomes), for individual species is an important general problem in biology. Experimental, computational and combined efforts are underway^1,4,5 to identify such interactomes in the form of lists of pairs of proteins that are labeled as one of two classes: interacting and not interacting. However, this binary label is a simplification of the problem, as for most PPI labels we are not absolutely certain if the proteins interact or not. This is because experimental data is noisy and the confidence placed in a label vastly depends on the type and number of experiments carried out that support a particular interaction. Furthermore, there are no negative labels at all. Negative results in experiments designed to test for PPI do not provide ultimate proof that two proteins don’t interact, because not all of the criteria necessary for an interaction to occur may have been fulfilled. These parameters will vary for different proteins and their interactions. Therefore, we avoid using terms sensitivity/specificity and precision/recall as they are related to the case when there are both positives and negatives for validation. The identification of protein interactomes has been focused on the positive (interacting) pairs. Prediction output may be presented as a sorted list of protein pairs. Pairs in its beginning are considered more likely to be interacting. Thus, a reasonable choice which pair to experimentally validate by a biological experiment, is to choose pairs that are ranked high in the list. Typically, biological intuition or interest is further used in selecting pairs from this top-ranking list for experimental validation. This interest varies with the potential application area for studying an interaction. For example, a structural biologist is interested in those pairs that are well characterized, from a biological as well as biophysical perspective. Biological characterization of a protein pair (for example co-crystallization trials) can require a large amount of time and effort. Thus it is useful to have an estimate for likelihood of success to decide whether structural studies are meaningful. On the other hand, a biomedical researcher might be more interested in identification of truly novel interactions, for which no prior evidence was reported in the literature. Such pairs could provide novel drug targets or biomarkers of disease. This divergence in biological interest in PPI’s is an important consideration for experimentalists to use computational predictions, but it has not been addressed previously.

One biomedical application area for PPI prediction is the study of host-pathogen interactions such as between human and human immunodeficiency virus type 1 (HIV-1) proteins. HIV-1 is the causative agent for the AIDS epidemic that has affected more than 33 million people across the world. Currently, for treating HIV-1 infection therapeutic agents use reverse transcriptase, protease, and envelope. However, drug resistance, poor compliance and side effects pose problems in efficient antiviral therapy justifying the search for alternative approaches to viral inhibition. One avenue is to target interactions between HIV-1 and host proteins. HIV-1 depends on its host for virtually every aspect of its life cycle, and the communication between virus and host is via PPI’s. Targeting such PPI’s therefore has great promise for anti-HIV-1 drug design. However, more than 2500 putative interactions involving some 1440 human proteins have been reported.² Selecting a pair from this large list to pursue for further studies is not trivial, while at the same time the list is likely not complete. The analysis of such data would greatly benefit from being able to quantify a required level of confidence in the data.

In this paper we approach this current gap in PPI research by incorporating a pre-determined level of confidence rather than relying on empirical performance such as precision/recall curves given by prediction scores. This allows the biological user to specify their required level of confidence in an interaction and the need to recover known interactions in the list of predicted interactions. This approach is based on a machine learning method called conformal predictors,^3,8 a new technique for ’hedging’ predictions. We ’hedge’ our predictions by quantitative measure of the accuracy and reliability of predictions. In particular, each individual prediction is supplied by its confidence measure. The problem of hedged prediction is connected with the problem of testing randomness. The hedged predictions include quantitative measures of the confidence and reliability of the predictions. These measures are provably valid under the assumption of exchangeability. One of the major advantages is that the method allows us to control the reliability of prediction by selecting a suitable confidence level.

The utility of this new approach is demonstrated for the HIV-1, human PPI case. We used the protein interaction dataset studied previously.⁶ This dataset contains labels of interaction derived from the NIAID database² by defining critera for interaction related to physical contact between the proteins and 35 features collected from various databases, used to predict potential PPI’s between the 17 HIV-1 and the full human proteome consisting of 20873 human proteins. Description of these features and other details can be found in supplementary materials⁷ to our previous work.⁶ There are 1063 interactions in this dataset. The rest of the 353778 pairs are to be labeled as interacting or not. In the previous work,⁶ we randomly sampled from this pool examples taken as negative pairs for training of the classifier. In this work, we do not define a negative set, but rather consider their labels to be unknown.

The aim here is to look for interactions between these HIV-1 and human proteins. Some of the interactions (1063 ones) are already known and the tasks are (1) to find additional new pairs that are also likely to interact and (2) to report how confident we are in the predicted interaction. Here, we will demonstrate the application of conformal predictors to these tasks. In the evaluation, we will use two performance measures to check our framework: validity that guarantees that a true interaction is covered by a list of predictions with certain confidence, and efficiency is characterized by how often interaction hypotheses are rejected (i.e. how many known interactions are not included in the list of interactions).

1.2. Background: conformal prediction

Originally, the conformal prediction approach^3,8 was introduced for the supervised machine learning problem: to predict a label for a new example from a given training set and estimate confidence of the prediction.

The advantage of the conformal predictor is that it has a proven validity: if we set up a confidence level, say, 95%, then we can guarantee that in the long run our prediction would contain the true label with probability at least 95%. To prove this property of validity, the only assumption we make is the i.i.d. assumption (data examples are generated from identical distribution independently on each other) or weaker exchangeability one (data examples appear in random order).

The main idea is to check each possible hypothesis about the label of a new example, and to the label of new example would conform the assumption of exchangeability, or with which label the example ’fits well’ into the training set?

There are two ways to present the results. Either we can provide the prediction of a new label together with measures of its individual confidence. Alternatively, if we set up a pre-determined confidence level γ (or significance level 1 − γ) we present a prediction region: a list of classifications which meet this confidence requirement. The correspondence between two types of output is following: individual confidence is the highest confidence level at which prediction region consists of only one value. In terms of p-values assigned to different labels, it is a complement to 1 of the second highest p-value. As we said before the only requirement for this approach to be applicable is that the data follows the exchangeability assumption, no matter what probability distribution the examples follow and no matter what nonconformity measure is used to construct the conformal prediction region. Supposing the examples in the data sequence z₁,…, z_l,…, z_N where z_i = (x_i, y_i) are generated in random order, if the N! different orderings of this sequence are equally likely, then we say that z₁,…, z_l,…, z_N are exchangeable.

The calculations of prediction regions are based on a special function called non-conformity measure (NCM) that basically reflects how strange an example is with respest to others. The validity property implies that the probability of error (in the sense of a true value being outside the prediction region) is at most 1 − γ whenever the exchangeability (or i.i.d.) assumption is true.

1.3. Problem setting: prediction of interactions between proteins

Suppose, there is a pool of examples (protein pairs); in this pool some examples (a subset) have a specific property: they are known to interact. Our task is to select more examples that are likely to have this property.

Let us introduce the following notation.

• x₁,…, x_l are known to interact;

• x_l+1 is a new example from the pool being classified;

• U = {x_l+2,…, x_l+s+1} is a random selection from other examples in the pool (’background’ set);

• the labels are used to denote examples having property of interaction: y_i = 1 for interactions y_i = 0 for non-interactions; so y_i = 1 for i = 1,…, l and y_i ∈ {0, 1} for i > l.

The conformal prediction method needs some modifications in order to be applied to the PPI prediction task. In particular, there is the unique characteristic in PPI’s that just one class is clearly defined, namely the class of interactions; there are no clear examples of non-interactions. Thus, our aim becomes to test the hypothesis that the example is an interaction and see if we can reject this hypothesis. In general, conformal prediction deals with 2 or more classes, with second largest p-value as individual confidence. However, here we deal with one clearly defined class and our p-values are related to the hypothesis that the label is positive. So small p-value assigned to an example means that this example is unlikely to be an interaction. This may be opposite to usual use of p-values when a null hypothesis is rejected if p-value is small.

The ’background’ set contains unlabelled examples and we can expect that at least some of them represent protein pairs that do not interact, although we do not know which of them.

We shall make the reasonable assumption (’exchangeability’) about the mechanism of discovery: any of the undiscovered interactions has equal chance to be discovered next.

2. Conformal approach for protein interaction search

2.1. The algorithm

The conformal approach to the protein interaction search presented here is given by Algorithm 2.1.

X is the set of possible objects. In the PPI problem, each protein pair is presented as a vector

$$x_i=(x_i(1),\dots ,x_i(k))$$

of k numeric attributes measuring within-pair similarities and other properties of the pair, so X is a k-dimensional linear space, in the considered dataset k = 35.⁶

The paramater γ corresponds to the confidence level γ. Due to the validity property, if this level is pre-selected, then a true interaction will be predicted at this level as interactions with probability at least γ. Usually in statistics a selected confidence level is close to 1, such as γ = 95% or γ = 99%.

Algorithm 2.1 Unlabelled Conformal Predictor in search of interactions
Input: training examples (known interactions) x1, x2,…, xl ∈ X
Input: a new example xl+1 ∈ X
Input: unlabelled examples U = {xl+2, xr+2,…, xl+s+1} ⊂ X
Input: a confidence level γ
Input: a NCM A
for j in 1, 2,…, l + 1 do
αj = A(xj, {x1,…, xl, xl+1},U)
end for $$p=\frac{\#\{j=1,\dots ,l+1:{\alpha }_j\ge {\alpha }_{l+1}\}}{l+1}$$
Output: xl+1 is predicted as a suspected interaction if p > 1 − γ.

2.2. Non-conformity measure

As stated, our aim is to test the hypothesis that a given example is an interaction. For a new example x_l+1, the conformal predictor checks whether the hypothesis that x₁,…, x_l, x_l+1 is generated by an exchangeable distribution can be rejected, and assigns an individual p-value to x_l+1. Note that individual p-value does not depend on the selected confidence level γ. So if the program outputs individual p-value for each pair, it allows users to select appropriate confidence level later, and cut the list, leaving only pairs with individual p-values at least 1 − γ.

This is being done by an NCM that is a function of an element x ∈ X and two subsets T ⊂ X and U ⊂ X, defined whenever x ∈ T. Its aim is to measure how strange is X relatively to other elements of T; U plays an auxiliary role. By defintion, NCM can be any function of this type, but performance depence on its choice and relevence for a specific problem. Usually in supervised learning the NCM is constructed on the basis of a prediction algorithm. We can use an underlying method such as SVM or k-Nearest-Neighbours for separation of two or several classes. However the PPI problem really requires a one-class NCM applied to unlabelled objects.

2.3. Example of one-class NCM

The described conformal prediction framework requires that we first choose an NCM. In the supervised classification case, NCMs are based on underlying algorithms, and applied to sets of example and label pairs (x_i, y_i), where y_i is usually taken from a finite set. However, in this work, the NCM will be defined on sets of unlabelled examples x_i instead of pairs, and may optionally depend on an additional ’background’ set U - a random selection of examples other than examples known to interact.

Algorithm 2.2 formalizes the following concepts of non-conformity (’strangeness’):

• a pair is ’strange’ with respect to the interaction set if one of its features has a value either too large or too small; it is even ’stranger’ if there are several such features;

• since we expect that the background set mainly consists of non-interactions, additional value is added to NCM if the example is not ’strange’ with respect to the background set.

We shall call this approach a feature-wise NCM. Although the last point is indirectly using the second class (in the form of the background set), the NCM itself is still a one-class one, as its scores are finally assigned only to x₁,…, x_l+1.

Algorithm 2.2 Feature-wise NCM
Input: data examples T = {x1,…, xl+1} ⊂ X = Rk
Input: xj ∈ T (one of examples above)
Input: Background set U = {xl+2,…, xl+s+1} ⊂ X.
for i in 1, 2,…, k do
let ai be percentage of x1(i),…, xl+1(i) larger or equal than xj(i), or percentage of x1(i),…, xl+1(i) smaller or equal than xj(i), (the smallest one of two, taking values from 1/(l + 1) to 1/2);
let $a_i^{\prime }$ be percentage of xl+2(i),…, xl+s+1(i); xj(i) larger or equal than xj(i), or percentage of xl+2(i),…, xl+s+1(i) smaller or equal than xj(i), (the smallest one of two);
end for
Output: a NCM (ranged is from −k log(l + 1) to + k log(l + 1)) $${\alpha }_j=-\sum _{i=1}^k\text{log}(a_j/a_i^{\prime })$$

3. Results

We applied our approach to the HIV-1, human PPI prediction task. The full list of individual predictions sorted by p-value will be presented in the Supplementary website http://www.clrc.rhul.ac.uk/people/alex/HIVpsb12/.

Each protein pair (for example: POL-PROTEASE and MYH7) is assigned an individual p-value (0.100564 in this example). A small p-value means the interaction hypothesis can be rejected.

Table 1 summarizes the results for the whole dataset in order to assess the overall quality of prediction with the selected NCM. The first column lists confidence level γ. As mentioned above, γ determines the confidence that a true interaction will be predicted as interaction The second and third columns show how many examples are predicted as interactions at different confidence levels γ. An example is predicted as interaction if its p-value is at least 1 − γ. We ask the question how many examples have such p-values. Since there were two types of examples, namely the 1063 known interacting protein pairs and the remaining 353778 pairs with unknown labels, we consider them separately. Column 2 is related to individual p-values assigned to pairs already known to interact. These figures illustrate validity: 90% of these interactions are really reported as interactions at confidence level 90% when the algorithm is applied to them in leave-one-out mode.

Table 1.

Size of prediction lists

confidence level	pred.interactions (amongst known interactions)	pred.interactions (amongst other pairs)
0%	1/1063(0.1%)	4/353778(0%)
1%	11/1063(1%)	37/353778(0%)
5%	54/1063(5.1%)	241/353778(0.1%)
10%	107/1063(10.1%)	604/353778(0.2%)
20%	213/1063(20%)	2185/353778(0.6%)
30%	320/1063(30.1%)	5446/353778(1.5%)
40%	426/1063(40.1%)	10380/353778(2.9%)
50%	533/1063(50.1%)	18988/353778(5.4%)
60%	639/1063(60.1%)	31412/353778(8.9%)
70%	745/1063(70.1%)	49019/353778(13.9%)
80%	852/1063(80.2%)	72743/353778(20.6%)
90%	957/1063(90%)	121091/353778(34.2%)
95%	1010/1063(95%)	150711/353778(42.6%)
99%	1053/1063(99.1%)	189432/353778(53.5%)
100%	1063/1063(100%)	353778/353778(100%)

As mentioned, we assume that all the other examples can be either true interactions or not, so we need to deal with all of them. Column 3 shows how many of these examples are predicted as possible interactions.

Consider a yet unknown interacation. To be confident at level 90% that the prediction list covers it, we need to include into it all predictions with individual p-value at least 10%. Table 1 shows that in our experiment 34.2% of all pairs do have such p-values.

This is related to efficiency: the smaller this percentage is, the more interaction hypotheses are rejected and the more efficient is a conformal predictor with selected NCM.

4. Biological interpretation

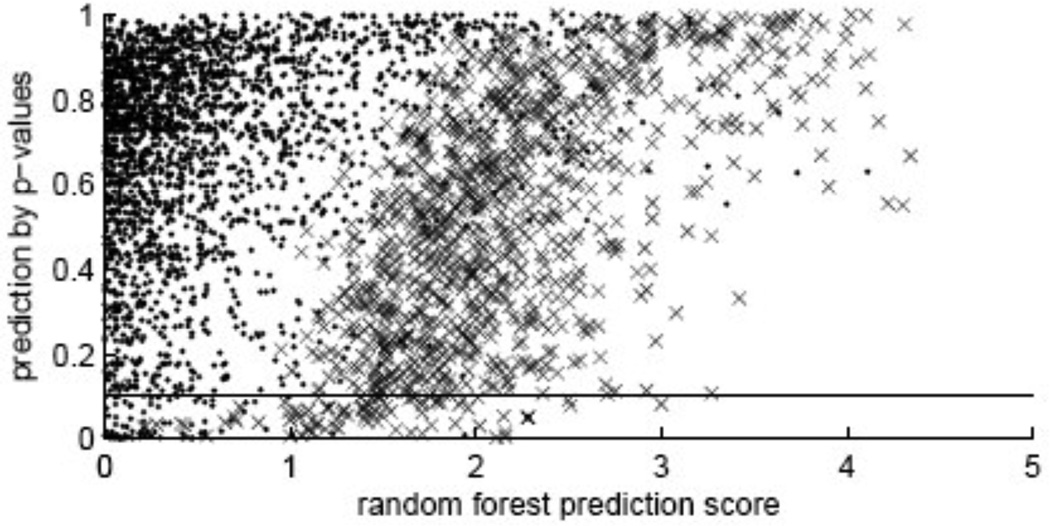
The full list of rank-ordered interactions sorted by p-value of the conformal predictor are provided in the supplement, together with additional information, including the random forest (RF) score of the previous classifier.⁶ Fig. 1 shows a comparison of the predictions made by the RF classifier and the conformal predictor with the known interactions. One can see that both methods agree on many of the top-ranked predicted interactions. The known interactions are given a particularly high RF score, especially when the p-value of the conformal predictor is high. The trend is towards lower RF scores as the p-value decreases.

Fig. 1.

Random Forest (RF) prediction scores⁶ (where they are positive) and p-values obtained by the conformal predictor for the same pairs. Crosses (interactions) are known interactions, other examples are represented as points. Examples with RF prediction score less than zero are not included. The horizontal line corresponds to 10% cut-off for p-value (significance level), or confidence level 90% (for a true interaction, we are 90% sure that it is above this line).

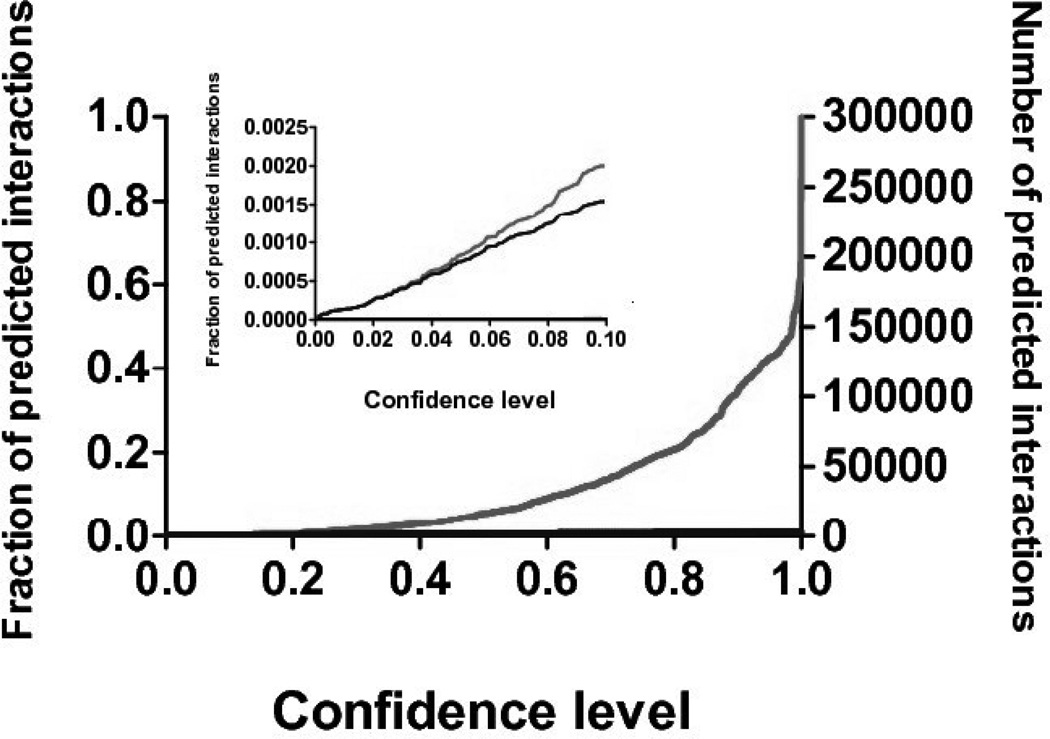
Because of the guaranteed number of known interactions at a given confidence level, an informative way to compare the previous RF classifier with the conformal prediction is by plotting the number of predicted interactions at a given p-value for each prediction method, shown in Fig. 2.

Fig. 2.

Dependence of the size of conformal prediction list on the confidence level. Lower line corresponds to the percentage of pairs predicted as interactions both by conformal prediction and by positive random forest score.

Of the 354,848 possible interactions, there is a total of 1063 interacting pairs in the NIAID dataset. Thus, as expected at a confidence level of 0.5 there are 532 known interactions, corresponding to 50% of the known interactions. At this confidence level there are 19,460 interactions suspected by the conformal predictor. Only 2376 of these have RF scores greater than zero. For 7424 of these suspected interactions there is some additional evidence of interaction (see Section 4.4, below). 1678 of these have RF scores greater than 0 (see Supplement). The comparison shows that the RF classifier may miss many potential interactions, but there are a larger number of interactions suspected by the conformal predictor, indicating the chance for false interactions. Because the false interaction rate is not known, this is to be expected, but does mean that potentially more experiments need to be carried out to find novel interactions, especially when looking at low p-values.

Below, we discuss some of the specific characteristics of the predictions made.

4.1. Top-ranked predictions

When resources are limited or the interaction to be pursued should be very likely (e.g. as a candidate for structural biology), one would look at the top-group of predicted interactions. For example, for p-values greater than 0.95, there are 295 interactions, with 54 interactions being already known. 267 have RF scores greater than 0. As we will see in section 4.4, more than half (117) of the 242 novel predictions have some evidence from ’siRNA’, ’in virion’ or other interactors supporting that these interactions may be true.

When looking at the top-ranked predictions, the first disagreement is ranked interaction 105 between tat and thyroid hormone receptor interactor 13, TRIP13. This interaction is not predicted by the RF classifier, but is ranked with a p-value of 0.98. Similarly ranked and not predicted by the classifier are interactions of tat with CHD4, EZH2, DYNLL1, Stat4 and Stat5B. All of these proteins except DYNLL1 are involved in regulation of transcription and may well interact with tat because the function of tat is to increase the level of transcription of the HIV-1 dsRNA. In addition, HIV-1 tat targets microtubules to induce apoptosis,⁹ thus making the predicted interaction with DYNLL1 plausible. In many of the suspected interactions, there is additional evidence supporting the interactions. For example, ranked at a p-value of 0.97 is the interaction between tat and IRS1, insulin receptor substrate 1. There are several publications that implicate the interaction between early insulin signaling, including phosphorylation of IRS1 with HIV-1 infection and treatment, discussion and links to them can be found in the previous work.¹⁰

4.2. Intermediate and low p-values

Statistically, we would normally reject the hypothesis that two proteins interact if their p-value is less than 10%. However, many of the known interactions will be found at such lower values and it may be of interest to a biologist to look at putative pairs amongst lower values, in particular when novelty in the new pairs is a criterion. Looking at the extreme - the interaction with the lowest p-value - is actually a known interaction, gp160 with PRMT6, protein arginine methyltransferase 6. This interaction is also not predicted by the RF. However, the evidence is rather strong for this interaction to be true: rev, tat and gp160 are all methylated by this protein.^11–13 Just above are interactions of almost every single HIV-1 protein predicted by the RF with CLCA3, chloride channel, calcium activated, family member 3, which is known to interact with gp120.¹⁴ The actual interaction between CLCA3 and gp120 has an RF score of 1.00 and a p-value of 0.0056. Although the conformal predictor uses the same features, it appears to be better able to differentiate between such non-specifically predicted HIV-1 interactions.

4.3. Tat predictions

Because of the nature of the dataset, many of the predicted interactions are with tat. This is simply because the dataset from which both methods learned the features characterizing true interactions contained tat interactors in excess over the other HIV-1 proteins. However, because of this relatively unspecific spectrum of tat interactors already known, newly predicted interactions are not biologically as interesting as those involving other HIV-1 proteins. In the case of the conformal predictor, there are more non-tat predictions ranked highly. This becomes particularly apparent, when going to slightly lower p-values. For example, there are 712 interactions with p-value greater than 0.9, of these 646 are for tat (91%). Amongst these are 107 known interactions and 549 have RF scores greater than 0. In contrast, when looking at p-values between 0.8 and 0.9, there are 1687 interactions, including 106 known interactions. Here, 608 have RF scores greater than 0. Of these only, 726 are tat (43%). 255 of these tat interactors have RF scores greater than 0. Thus, in addition to the observation that the top-ranked predicted interactions not previously known make sense and would be very reasonable to validate experimentally (Section 4.1 above), there may be an additional advantage of the conformal predictor over the RF classifier, in being less affected by artifacts produced through an imbalanced representation of some HIV-1 proteins (especially tat) in the dataset.

4.4. Comparison to in virion and siRNA human gene lists

As can be seen for individual predictions in the Supplement, for many predicted human binding partners there is evidence for a relationship with HIV-1 function, even when a direct interaction has not yet been experimentally established. We quantified this observation by quantifying how many of the top ranked predicted HIV-1, human pairs contain human proteins that are also part of the following two human gene list: ’in virion’, representing 316 human proteins that are highjacked by HIV-1 in its virion¹⁶ and ’siRNA’, 282 human genes that have been reported in the siRNA screen to have an effect on HIV-1 infection upon silencing.¹⁵ These lists can be accessed at www.cs.cmu.edu/˜qyj/HIVsemi/validateHumanGeneLists/ and are summarized in Table 2.

Table 2.

Overlap with in virion and siRNA lists.

Conf.level	novel interactions	overlap with in virion	overlap with siRNA.
10%	604	38	11
20%	2185	78	26
30%	5446	111	57
40%	10380	140	68
50%	18988	173	85
60%	31412	187	103
70%	49019	217	124
80%	72743	239	142
90%	121091	264	165

The ’virion’ and ’siRNA’ datasets are not directly evidence about virus-protein interactions. They are functional related evidence though. Thus the comparison of our predictions to them is not a direct ’validation’ experiment, but a ’functional validation’.

In this table, we compare how many of the human genes involved in top-ranked novel interactions, listed in the last column of Table 1, are also present in the siRNA and in virion lists. Note that these lists contain only human proteins, so we consider every predicted pair a hit, if the human protein is predicted to be involved in an interaction, regardless of the identity of the HIV-1 protein. This results in a very high overlap: for example, at confidence level 90% our prediction list involves 264 of 316 (83.5%) human genes from the in virion list and 165 of 282 (58.5%) human genes from the siRNA list. This high overlap further supports the functional relevance of the predictions made.

5. Conclusion and discussion

In this paper, we have developed a new framework for the prediction and quantitative ranking of suspected and known PPI’s, referred to as conformal predictors. In contrast to the typical classification approach integrating multiple feature evidences or the commonly used simpler predictions based on single features such as sequence homology, this approach allows the user to specify the required confidence in predicted interactions. Inspection of the predictions made by the conformal predictor for HIV-1, human interactions indicates that the predicted novel pairs are excellent candidates for experimental validation; for many of them, there is indirect evidence from various databases and publications supporting the interaction, which was not used in the prediction and thus independently validates the predictions made.

Comparison with the previously developed RF based classifier on the same data indicates that the conformal prediction may be less prone to artifacts related to some of the unspecific aspects of the features used in the prediction (e.g. if one HIV-1 protein interacts with a human protein, the classifier tends to predict a large number of additional HIV-1 proteins to interact with the same protein) or the relative abundance of HIV-1 proteins in pairs used for training, such as tat. On the other hand, the number of suspected interactions is larger compared to those obtained by the RF, potentially affecting the false interaction rate.

This is of particular note in the PPI prediction problem because proving experimentally a negative interaction is not possible. Another major advantage of the conformal predictor approach is the quantitative treatment of the ranking of suspected pairs. The biologist can use the p-value as a guide to inspect the predictions because it guarantees a given number of known interactions to be present amongst the predictions. Thus, biologists with different interests can decide on the range of interactions to study because novel interactions are ranked quantitatively with respect to known interactions. Thus, a structural biologist interested in high-confidence interactions would chose a different range of p-values than a virologist interested in discovery of novel interactions that may represent new, yet potentially risky drug targets.

The conformal predictor approach described here presents the first application of its kind to a problem in computational biology and is general. Thus, it is likely that the good results achieved here with the HIV-1, human PPI task would translate to other PPI predictions and potentially other tasks in computational biology.

A possible direction of research to improve on the proposed framework is to find other NCMs with better performance. On the current dataset, the NCM based on SVM shows slightly less efficiency as compared to feature-wise NCM. This may change with improvements in the methodology. However, in the PPI prediction task we assumed true percentage of interactions between all pairs to be unknown; thus, we cannot say what will be the ’ideal’ result. Especially interesting extensions of the approach may be based on support vector machines. This method can be kernelized, equivalent to mapping the original vector into a high-dimensional space.

In this work we use exchangeability assumption as a basic model, although in fact some kinds of interactions may be not presented in the training set. Testing of exchangeability and its possible replacement with another assumption is also a subject for our future work.