Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM)

Abstract

We propose a compressive sensing approach for multi-energy computed tomography (CT), namely the prior rank, intensity and sparsity model (PRISM). To further compress the multi-energy image for allowing the reconstruction with fewer CT data and less radiation dose, the PRISM models a multi-energy image as the superposition of a low-rank matrix and a sparse matrix (with row dimension in space and column dimension in energy), where the low-rank matrix corresponds to the stationary background over energy that has a low matrix rank, and the sparse matrix represents the rest of distinct spectral features that are often sparse. Distinct from previous methods, the PRISM utilizes the generalized rank, e.g., the matrix rank of tight-frame transform of a multi-energy image, which offers a way to characterize the multi-level and multi-filtered image coherence across the energy spectrum. Besides, the energy-dependent intensity information can be incorporated into the PRISM in terms of the spectral curves for base materials, with which the restoration of the multi-energy image becomes the reconstruction of the energy-independent material composition matrix. In other words, the PRISM utilizes prior knowledge on the generalized rank and sparsity of a multi-energy image, and intensity/spectral characteristics of base materials. Furthermore, we develop an accurate and fast split Bregman method for the PRISM and demonstrate the superior performance of the PRISM relative to several competing methods in simulations.

1. Introduction

Since Hounsfield’s Nobel-Prize-winning breakthrough, x-ray computed tomography (CT) has been widely applied in clinical and preclinical applications and produces a huge amount of tomographic grayscale images. Currently, more than 100 million medical CT scans are performed in the USA alone annually, and a huge number of micro-CT scans are performed in research institutions and pharmaceutical companies worldwide. However, the images are often insufficient to distinguish diagnostically crucial shading differences due to poor tissue contrast, inherent quantum noise and involved radiation dosage. Physically, the x-ray spectrum contains much information, and CT images need not be only in grayscale. Just as television technology is now in true color, as a natural extension of dual-energy CT [1], the future of CT will be multi-energy, generating much richer information. The multi-energy CT is also referred to as spectral, spectroscopic, energy-selective or energy-sensitive CT. To convey the power of multi-energy CT vividly, we can also call it ‘true-color CT’ occasionally although x-rays cannot be directly perceived at either soft or hard energies.

The x-ray detection technology is the key to achieve multi-energy CT. Roughly speaking, x-ray detectors can be categorized into two groups: energy integrating and energy discriminating. Almost exclusively, all current x-ray scanners use energy-integrating detectors, where the interactions between an x-ray beam and materials are accumulated over an entire energy spectrum. In typical energy-discriminating detectors [2–4], each photon above some minimum energy is counted, regardless of its energy. This capability can be utilized in a sophisticated way for energy discrimination. A primary example is the Medipix detector family. Particularly, a Medipix3 detector recognizes each x-ray photon along with its energy range effectively and efficiently [2]. Clearly, such multi-energy detectors give full spectral information, support novel contrast-enhanced studies [5, 6] and open new possibilities for functional, cellular and molecular imaging [7–10]. It is recognized that data collected in different spectral channels are not totally independent. For example, in the high-energy region of the x-ray spectrum, the Compton scattering is dominant and the attenuation coefficient is mainly proportional to the density of material. However, given the complexity of biological tissues, this dependence does not mean the complete redundancy (e.g. due to the Doppler broadening or electron binding energy and momentum). More importantly, the use of contrast agents of various K-edges (figure 2) makes multi-energy CT definitely necessary and clearly superior to dual-energy CT [6].

Figure 2.

Multi-energy CT phantom. (a) The geometric setting of the phantom with 14 objects (table 1) and (b) plots of the linear attenuation coefficients of the employed eight base materials with respect to energies. (The x-axis unit is keV and the y-axis unit is cm⁻¹.)

Parallel to the development of energy-discriminating detectors, an emerging theory—compressive sensing (CS)—was recently developed to capture compressible signals at a sampling rate much below the Nyquist rate and allow accurate reconstruction of these signals from sparse samples [11, 12]. Typically, CS starts by taking a limited number of samples, using a least correlated measurement matrix, and then the signal is exactly recovered with an overwhelming probability from the limited data via the L₁ norm minimization [11, 12]. The major motivation for CS is that most signals are sparse under an appropriate basis. That is, a majority of their expansion coefficients with respect to the basis are equal to or close to zero. Through CS, it is sufficient to precisely reconstruct the image using undersampled data with roughly the same cardinality as the image sparsity. Consequently, the sparser image representation allows accurate reconstruction with fewer data. Besides L₁ sparsity (L1) [13], other popular choices for the sparsity representation include the total variation (TV) [14], combination of L1 and TV (L1+TV) [15, 16], wavelet [17, 18] and tight frame or framelet (TF) [19, 20]. As a generalization of L1+TV and wavelet, the TF usually offers a sparser representation due to its redundant basis and multi-resolution structure [19, 20]. We will use the TF for the sparser representation.

In this paper, we propose a CS approach for multi-energy CT, namely the prior rank, intensity and sparsity model (PRISM). To further compress the multi-energy image for allowing the reconstruction with fewer CT data and less radiation dose, the PRISM models a multi-energy image as the superposition of a low-rank matrix and a sparse matrix (with row dimension in space and column dimension in energy), where the low-rank matrix corresponds to the stationary background over energy that has a low matrix rank, and the sparse matrix represents the rest of distinct spectral features that is often sparse. Distinct from previous methods, the PRISM utilizes the generalized rank, e.g., the matrix rank of TF transform of a multi-energy image, which offers away to characterize the multi-level and multi-filtered image coherence across the energy spectrum. Besides, the energy-dependent intensity information can be incorporated into the PRISM in terms of the spectral curves for base materials, with which the restoration of the multi-energy image becomes the reconstruction of the energy-independent material composition matrix. (Depending on specific applications, the optimal selection of energies or spectral channels must be done to avoid matrix singularities and maximize the image quality. However, in this feasibility study, sufficiently many energy bins have been arbitrarily selected to keep all of the intrinsic information.) In other words, the PRISM utilizes prior knowledge on the generalized rank and sparsity of a multi-energy image, and intensity/spectral characteristics of base materials. Furthermore, we develop an accurate and fast split Bregman method for the PRISM and demonstrate the superior performance of the PRISM relative to several competing methods in simulations.

The PRISM is motivated by the recent work on rank–sparsity incoherence [21], robust principle component analysis (RPCA) [22] and RPCA-4DCT model [23]. In the rank–sparsity decomposition [21] and RPCA [22], the data matrix is decomposed into a low-rank part and a sparse part, and both parts can be recovered by minimizing the sum of the nuclear norm of the low-rank component and the L₁ norm of the sparse component (subject to certain incoherence conditions). Similar models have been considered in various applications [24–30]. In the RPCA-4DCT model [23], a 4D spatiotemporal object is modeled as a summation of a low-rank matrix and a sparse matrix with the generalized sparsity in the TF. Another difference of the RPCA-4DCT model is that the CT data are the Radon transform or x-ray transform of an image through some ill-posed system matrix rather than directly from the image. In this paper, the PRISM generalizes the previous methods and is pertinent to multi-energy CT for using spectral priors. A distinct feature of the PRISM is that the image rank under consideration is generalized from the matrix rank of the multi-energy image to the matrix rank of the TF transform of the multi-energy image to characterize multi-level and multi-filtered image coherence.

2. Methodology

2.1. Multi-energy CT

Consider a multi-energy image X with N_E spectral channels, i.e. a spectral sequence of spatial images:

$$X=\{X_i,i\le N_E\}.$$ (2.1)

In the 2D case with N_x pixels along the x-axis and N_y pixels along the y-axis,

$$\begin{array}{cc}\hfill X_i=\{x_{i,\mathit{\text{jk}}},j\le N_x,k\le N_y\}\hfill & \hfill \text{or\hspace{1em}}{X}_i=\{x_{i,j},j\le N_S\},\hfill \end{array}$$ (2.2)

where the second j is a double index for convenience and N_S = N_x × N_y.

In order to compute the image rank of X, we form X as a spatial spectral matrix with row dimension in space indexed by j and column dimension in energy indexed by i.

Let A be the system matrix [31] for a monochromatic x-ray transform in the CT scanning geometry under consideration, which implies the energy-discriminating detection within a sufficiently narrow energy bin [32–35]. Assuming additive Gaussian noise N, without downsampling, the acquired multi-energy data are

$$Y=\{Y_i={\mathit{\text{AX}}}_i+N_i,i\le N_E\}.$$ (2.3)

The objective of multi-energy CT is to recover X from Y. From a practical point of view in terms of radiation dose, the imaging by acquiring the least amount of CT data is favorable. That is, we consider the undersampled problem

$$Y=\{Y_i=P_i({\mathit{\text{AX}}}_i)+N_i,i\le N_E\},$$ (2.4)

where P_i denotes the undersampling pattern at the ith energy bin. In this study, we adopt the dynamic undersampling strategy [23]. To simplify the notation, we abbreviate (2.3) or (2.4) as

$$Y=\mathit{\text{AX}}+N.$$ (2.5)

2.2. Prior work related to the PRISM

The original problems similar to the PRISM were considered for rank–sparsity incoherence [21] and RPCA [22]. The problem of recovering the principle component X_L (modeled as a low-rank matrix) from data Y with outliers X_S (modeled as a sparse matrix) is converted to the following minimization problem:

$$\begin{array}{c}\hfill (X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}r{\Vert X_L\Vert }_{*}+{\Vert X_S\Vert }_1\hfill \\ \hfill \text{subject to}{X}_L+X_S=Y.\hfill \end{array}$$ (2.6)

When certain incoherence conditions are satisfied, both X_L and X_S can be uniquely recovered. Here, the value of r (for the matrix with n₁ rows and n₂ columns) [22] is suggested to be

$$r=\sqrt{\text{max}(n_1,n_2)}.$$ (2.7)

Inspired by the above idea, the RPCA-4DCT model was proposed for 4D CT [23]

$$(X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}{\Vert A(X_L+X_S)-Y\Vert }^2+{\lambda }_{*}{\Vert X_L\Vert }_{*}+{\lambda }_1{\Vert T_S(X_S)\Vert }_1,$$ (2.8)

where T_S was chosen to be the TF transform [19, 20].

Two major differences between RPCA-4DCT (2.8) and (2.6) are: (1) data Y for RPCA-4DCT is the Radon transform or x-ray transform of X rather than a subset of X, and consequently, the reconstruction of X is more challenging and (2) the sparsity of X_S is generalized in RPCA-4DCT under the proper sparsifying transform, such as the TF.

2.3. PRISM: rank and sparsity decomposition

Inspired by CS theory, where the sparser image representation allows the reconstruction with fewer data, we will choose the TF as the sparsifying basis since it is a generalization of several popular sparsity transforms, such as L1+TV and the wavelet [19, 20].

On the other hand, the structural similarity shared by images within different energy bins can be utilized to further compress their representation. This spectral coherence can be mathematically characterized by the matrix rank of X over the spectral dimension. The lower the rank, the more coherent the images. Theories suggest that the amount of data required for exact recovery of the images only needs to match their rank [35, 36].

However, the representation can be further sparsified by considering the rank-and-sparsity decomposition [21–23]. Therefore, a further reduction of CT data, that are proportionally correlated to the radiation dose, can be expected for multi-energy CT. In figure 1, for example, despite the matrix being full rank and nonzero everywhere, it can be decomposed into a low-rank component and a sparse component. This simple observation (figure 1) suggests an alternative view of the multi-energy image: X can be abstracted as the superposition of the background component, which is spectrally coherent, and the variation component, which is spatially sparse. Now, we generalize previous models into a coherence-and-variation decomposition model, namely the PRISM, aiming for the sparser representation of the multi-energy image to allow a higher undersampling factor or better image quality with the same data.

Figure 1.

Rank-and-sparsity decomposition: R(X) is the matrix rank and #(X) is the number of nonzeros.

That is, we model X as the sum of two matrices X_L and X_S

$$X=X_L+X_S$$ (2.9)

and enforce the following regularization:

$$R(X_L,X_S)={\lambda }_{*}{\Vert T_L(X_L)\Vert }_{*}+{\lambda }_1{\Vert T_S(X_S)\Vert }_1+{\lambda }_t\Vert X\Vert$$ (2.10)

in the PRISM

$$(X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}{\Vert A(X_L+X_S)-Y\Vert }^2+R(X_L,X_S).$$ (2.11)

In (2.10), ‖ • ‖* is the nuclear norm for the rank regularization on X_L with the parameter λ*. Let {σ_i} be the singular values of X. Then

$${\Vert X\Vert }_{*}={\displaystyle \sum _i}{\sigma }_i.$$ (2.12)

‖ • ‖₁ is the L₁ norm for the sparsity regularization on X_S with the parameter λ₁. Let {x_i} be the entries of X. Then

$${\Vert X\Vert }_1={\displaystyle \sum _i}|x_i|.$$ (2.13)

‖ • ‖ is a regularizing norm on the total image X to preserve its smoothness and contrast, with the parameter λ_t. Since we regularize the image rank of X_L and the image sparsity of X_S, we name X_L the low-rank component and X_S the sparse component. In multi-energy CT, X_L often corresponds to stationary background or slow variation, while X_S characterizes spectral jumps, such as K-edges.

More importantly, we consider the generalized rank and sparsity in the PRISM: T_L (resp. T_S) represents a transform for the strengthened rank regularization (resp. sparsity regularization). In particular, we consider the rank of the TF transform of X_L and the sparsity of X_S under the TF.

2.4. PRISM: sparsity

In this study, we choose the piecewise-constant B-spline TF transform W that can be constructed from two refinement masks: the averaging mask and the differencing mask. Consequently, the 2D refinement masks constructed from the tensor product are

$$\begin{array}{cc}{w}_{0,0}=\frac{1}{4}\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right],\hfill & w_{0,1}=\frac{1}{4}\left[\begin{array}{cc}\hfill 1\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill -1\hfill \end{array}\right],\hfill \\ w_{1,0}=\frac{1}{4}\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill -1\hfill & \hfill -1\hfill \end{array}\right]\hfill & \begin{array}{cc}\hfill \text{and}\hfill & \hfill w_{1,1}=\frac{1}{4}\left[\begin{array}{cc}\hfill 1\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 1\hfill \end{array}\right].\end{array}\hfill \end{array}$$ (2.14)

Let x be a 2D image with the standard 2D indices, i.e. x = {x_jk, j≤N_x, k≤N_y}. The multilevel TF transform of x up to L levels is

$$\mathit{\text{Wx}}=\left[\underset{\text{Level}:1}{\underbrace{\begin{array}{ccc}\hfill {[\mathit{\text{Wx}}]}_{0,1}^1\hfill & \hfill {[\mathit{\text{Wx}}]}_{1,0}^1\hfill & \hfill {[\mathit{\text{Wx}}]}_{1,1}^1\hfill \end{array}}}\cdots \underset{\text{Level}:l}{\underbrace{\begin{array}{ccc}\hfill {[\mathit{\text{Wx}}]}_{0,1}^l\hfill & \hfill {[\mathit{\text{Wx}}]}_{1,0}^l\hfill & \hfill {[\mathit{\text{Wx}}]}_{1,1}^l\hfill \end{array}}}\cdots \underset{\text{Level}:L}{\underbrace{{[\mathit{\text{Wx}}]}_{0,1}^L{[\mathit{\text{Wx}}]}_{1,0}^L{[\mathit{\text{Wx}}]}_{1,1}^L}}{x}^L\right],$$ (2.15)

with x⁰ = x and the following convolutions:

$$\begin{array}{ccc}{x}^l=w_{0,0}^l*x^{l-1},\hfill & {[\mathit{\text{Wx}}]}_{0,1}^l=w_{0,1}^l\times x^l,\hfill & {[\mathit{\text{Wx}}]}_{1,0}^l=w_{1,0}^l\times x^l,\hfill \\ {[\mathit{\text{Wx}}]}_{1,1}^l=w_{1,1}^l\times x^l,\hfill & \hfill 1\le l\le L.\hfill & \hfill \end{array}$$ (2.16)

Here, the dependence of the mask on the level comes from the choice of TF without downsampling x^l. That is, instead of downsampling x^l, we dilute the masks (2.14) so that

$$\begin{array}{cc}\hfill w_{i_1,i_2}^l=D^l{w}_{i_1,i_2},\hfill & \hfill 0\le i_1,i_2\le 1,\hfill \end{array}$$ (2.17)

where D^lw’s are (2^l + 1) × (2^l + 1) matrices with four nonzero entries defined by

$$\begin{array}{cc}\hfill D^{l}w=\left[\begin{array}{ccc}\hfill w(1,1)\hfill & \hfill \cdots \hfill & \hfill w(1,2)\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill w(2,1)\hfill & \hfill \cdots \hfill & \hfill w(2,2)\hfill \end{array}\right]\hfill & \hfill \text{for\hspace{1em}}w=\left[\begin{array}{cc}w(1,1)\hfill & w(1,2)\hfill \\ w(2,1)\hfill & w(2,2)\hfill \end{array}\right].\hfill \end{array}$$ (2.18)

On the other hand, the transpose of TF is defined by

$$W^T(\mathit{\text{Wx}})=x^L+{\displaystyle \sum _{l=1}^L}({[\mathit{\text{Wx}}]}_{0,1}^l+{[\mathit{\text{Wx}}]}_{1,0}^l+{[\mathit{\text{Wx}}]}_{1,1}^l).$$ (2.19)

One can show that the TF has a left inverse [37]

$$W^T(\mathit{\text{Wx}})=x.$$ (2.20)

Now, let us define the TF norm of a single 2D image as

$${\Vert \mathit{\text{Wx}}\Vert }_1={\Vert x^L\Vert }_1+{\displaystyle \sum _{l=1}^L}\{{\Vert {[\mathit{\text{Wx}}]}_1^l\Vert }_1+{\Vert {[\mathit{\text{Wx}}]}_2^l\Vert }_1\},$$ (2.21)

with

$$\begin{array}{ccc}\hfill {[\mathit{\text{Wx}}]}_1^l=\sqrt{{({[\mathit{\text{Wx}}]}_{0,1}^l)}^2+{({[\mathit{\text{Wx}}]}_{1,0}^l)}^2}\hfill & \hfill \text{and}\hfill & \hfill {[\mathit{\text{Wx}}]}_2^l={[\mathit{\text{Wx}}]}_{1,1}^l.\hfill \end{array}$$ (2.22)

Here, the second term of (2.21) is to make the regularization isotropic with respect to x–y coordinate that has the same spirit as the isotropic TV norm.

Note that TF (2.21) generalizes TV in the sense that its second term corresponds to TV; it generalizes L1+TV since the first term corresponds to L1; it also generalizes the wavelet transform since the TF often forms the redundant basis rather than the orthonormal basis. On the other hand, due to property (2.20), the algorithm with the TF regularization is in general faster than using the transform without left inverse, such as TV, since it would then require additional computation of W^TW. We will further clarify this advantage of TF in the solution algorithm.

Consequently, we define the TF norm of the multi-energy image X (2.1) by

$${\Vert \mathit{\text{WX}}\Vert }_1={\displaystyle \sum _{i=1}^{N_E}}{\Vert {\mathit{\text{WX}}}_i\Vert }_1.$$ (2.23)

Here, we select the regularization on both X_S and X in (2.10) to be the TF norm (2.23):

$$\begin{array}{ccc}\hfill {\Vert T_L(X_S)\Vert }_1={\Vert {\mathit{\text{WX}}}_S\Vert }_1\hfill & \hfill \text{and}\hfill & \hfill \Vert X\Vert ={\Vert \mathit{\text{WX}}\Vert }_1.\hfill \end{array}$$ (2.24)

2.5. PRISM: rank

Distinct from previous work, the PRISM considers the rank regularization in the transform domain as well. In this study, we regularize the rank of the TF transform of X:

$${\Vert T_L(X_L)\Vert }_{*}={\Vert {\mathit{\text{WX}}}_L\Vert }_{*},$$ (2.25)

with the nuclear norm in the TF basis defined as

$${\Vert \mathit{\text{WX}}\Vert }_{*}={\Vert X^L\Vert }_{*}+{\displaystyle \sum _{\mathrm{l}=1}^{\mathrm{L}}}({\Vert {[\mathit{\text{WX}}]}_1^l\Vert }_{*}+{\Vert {[\mathit{\text{WX}}]}_2^l\Vert }_{*}).$$ (2.26)

That is, we compute the TF transform (2.15) of X_i from X_L and reorganize them into groups of matrices corresponding to different TF levels and masks:

$$\begin{array}{ccc}{[\mathit{\text{WX}}]}_1^l=[\sqrt{{({[{\mathit{\text{WX}}}_1]}_{0,1}^l)}^2+{({[{\mathit{\text{WX}}}_1]}_{1,0}^l)}^2}\hfill & \dots \hfill & \sqrt{{({[{\mathit{\text{WX}}}_{N_E}]}_{0,1}^l)}^2+{({[{\mathit{\text{WX}}}_{N_E}]}_{1,0}^l)}^2}]\hfill \\ {[\mathit{\text{WX}}]}_2^l=[\begin{array}{ccc}{[{\mathit{\text{WX}}}_1]}_{1,1}^l\hfill & \dots \hfill & {[{\mathit{\text{WX}}}_{N_E}]}_{1,1}^l\hfill \end{array}]\hfill & \text{and}\hfill & X^L=[\begin{array}{ccc}{X}_1^L\hfill & \dots \hfill & X_{N_E}^L\hfill \end{array}],l\le L.\hfill \end{array}$$ (2.27)

This generalized rank allows more freedom in applications. For example, in multi-energy CT, the similarity across spectral channels is more in structures (boundaries, contours, and edges) rather than in images (grayscale shading). On the other hand, the rank of the multi-energy image after the TF transform focuses on the structural features, while the rank of the image itself correlates energy-dependent gray-shading variations. Clearly, it is more appropriate to regularize the rank of the structures through the TF transform. Besides, the TF transform offers a way to characterize the multi-level and multi-filtered image coherence through (2.26).

2.6. PRISM: intensity/spectral priors

Spectral knowledge can be incorporated in the PRISM for better performance. Suppose that we know the intensity (linear attenuation coefficient) curves of base materials with respect to the energy:

$$B=\{b_{\mathit{\text{mi}}},m\le N_B,i\le N_E\},$$ (2.28)

where N_B is the number of base materials and b_mi is the attenuation coefficient of the mth material at the ith energy. Using the intensity/spectral priors B, we have an alternative representation of X. That is, the attenuation at the jth pixel for the ith energy is a linear combination of b_mi:

$$x_{\mathit{\text{ji}}}={\displaystyle \sum _m}{z}_{\mathit{\text{jm}}}{b}_{\mathit{\text{mi}}},$$ (2.29)

or in the matrix form

$$X=ZB,$$ (2.30)

where Z is now a material composition matrix with its row dimension in a spatial variable and column dimension in a material variable:

$$Z=\{z_{\mathit{\text{jm}}},j\le N_S,m\le N_B\}.$$ (2.31)

With intensity/spectral priors, the reconstruction of X is a consequence of the reconstruction of Z. The most apparent benefit of (2.30) is that Z is independent of energy. Moreover, all z_ik are between 0 and 1, and therefore, the image representation in Z is robust in terms of image contrast. In contrast, X is spectrally dependent; the values of x_ij may differ greatly due to the spectral dependence.

Similarly, we have the rank-and-sparsity decomposition for Z:

$$Z=Z_L+Z_S.$$ (2.32)

Again, Z_L (resp. Z_S) is the low-rank (resp. sparse) component with respect to the proper basis.

However, we still regularize Z in the image domain

$$R(Z_L,Z_S)={\lambda }_{*}{\Vert T_L(Z_{L}B)\Vert }_{*}+{\lambda }_1{\Vert T_S(Z_{S}B)\Vert }_1+{\lambda }_t\Vert X\Vert .$$ (2.33)

With the aforementioned equation, we have transformed the original PRISM into an enhanced PRISM with the reconstruction of the spectrally independent variable Z.

More generally, if the base materials are partially known, we have a hybrid representation of X as follows:

$$X=(X_L+Z_{L}B)+(X_S+Z_{S}B),$$ (2.34)

where B represents the partial intensity/spectral priors, X_L (resp. Z_L) corresponds to the known materials (resp. the remaining portion) of the low-rank component, and X_S (resp. Z_S) corresponds to the known materials (resp. the remaining portion) of the sparse component. Consequently, the regularization with the partial priors is

$$R(X_L,Z_L,X_S,Z_S)={\lambda }_{*}{\Vert T_L(X_L+Z_{L}B)\Vert }_{*}+{\lambda }_1{\Vert T_S(X_S+Z_{S}B)\Vert }_1+{\lambda }_t\Vert X\Vert ,$$ (2.35)

where X is related to X_L, X_S, Z_L and Z_S through (2.34).

In summary, we have proposed three variants of the generic PRISM: (1) the PRISM without intensity/spectral priors defined by (2.10); (2) the PRISM with intensity/spectral priors of all the base materials as defined by (2.33); and (3) the PRISM with intensity/spectral priors for only part of the base materials as defined by (2.35). Other variants of the PRISM can be similarly defined. For example, when we have statistical knowledge of spatial and/or spectral characteristics of classes under investigation, which can be learned from a training data set, we can define the corresponding PRISM-based inverse problems.

2.7. Methods for comparison

To show the superiority of the PRISM over several other methods for the multi-energy CT, we will first compare the following PRISM:

$$(X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+{\lambda }_{*}{\Vert X_L\Vert }_{*}+{\lambda }_1{\Vert {\mathit{\text{WX}}}_S\Vert }_1+{\lambda }_t{\Vert \mathit{\text{WX}}\Vert }_1,$$ (2.36)

with L₂ regularization (L2)

$$X=\underset{X}{\text{arg min}}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+\lambda {\Vert X\Vert }_2^2,$$ (2.37)

TF regularization (TF)

$$X=\underset{X}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+\lambda {\Vert \mathit{\text{WX}}\Vert }_1,$$ (2.38)

rank regularization (LR)

$$X=\underset{X}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+\lambda {\Vert X\Vert }_{*}$$ (2.39)

and simultaneous TF and rank regularization (TFLR)

$$X=\underset{X}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+{\lambda }_1{\Vert \mathit{\text{WX}}\Vert }_1+{\lambda }_{*}{\Vert X\Vert }_{*}.$$ (2.40)

Second, to show the superiority of the PRISM with generalized rank, we will compare (2.36) with

$$(X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+{\lambda }_{*}{\Vert {\mathit{\text{WX}}}_L\Vert }_{*}+{\lambda }_1{\Vert {\mathit{\text{WX}}}_S\Vert }_1+{\lambda }_t{\Vert \mathit{\text{WX}}\Vert }_1.$$ (2.41)

Last, we will compare the PRISM without priors (2.36) with the PRISM with partial spectral priors

$$(X_L,Z_L,X_S,Z_S)=\underset{(X_L,Z_L,X_S,Z_S)}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+{\lambda }_{*}{\Vert X_L+Z_{L}B\Vert }_{*}+{\lambda }_1{\Vert W(X_S+Z_{S}B)\Vert }_1+{\lambda }_t{\Vert \mathit{\text{WX}}\Vert }_1$$ (2.42)

and the PRISM with full spectral priors

$$(Z_L,Z_S)=\underset{(Z_L,Z_S)}{\text{arg min}}\frac{1}{2}{\Vert \mathit{\text{AX}}-Y\Vert }_2^2+{\lambda }_{*}{\Vert Z_{L}B\Vert }_{*}+{\lambda }_1{\Vert W(Z_{S}B)\Vert }_1+{\lambda }_t{\Vert \mathit{\text{WX}}\Vert }_1.$$ (2.43)

2.8. PRISM: solution algorithm by the split Bregman method

Here, we consider the solution algorithm for the following convex minimization problem:

$$(X_L,X_S)=\underset{(X_L,X_S)}{\text{arg min}}\frac{1}{2}{\Vert A(X_L+X_S)-Y\Vert }_2^2+{\lambda }_{*}{\Vert {\mathit{\text{WX}}}_L\Vert }_{*}+{\lambda }_1{\Vert {\mathit{\text{WX}}}_S\Vert }_1,$$ (2.44)

based on the split Bregman method [38–40], which is simple-to-implement, yet particularly accurate and efficient for L1-type optimization problems [23, 41], such as (2.44). The solution algorithms for other variants of the PRISM and other models can be developed in a similar fashion.

For improved accuracy, we minimize (2.44) with the regularization term replaced by its Bregman distance and simplify it to the add-residual-back iterative scheme by introducing a dummy variable f. To efficiently handle non-differentiable TF norms, we first change TF norms into L1 norms by introducing the dummy variables d_L = WX_L and d_S = WX_S and relax the constrained optimization into an unconstrained optimization. Then, we use the similar add-residual-back iterative scheme to relax L1 norms into L2 norms by introducing the dummy variables v_L and v_S. That is, with zero initial guesses (i.e. X⁰_L = X⁰_R = 0, f⁰ = 0 and d⁰_L = υ⁰_L = d⁰_S = υ⁰_S = 0), the solution algorithm for (2.44) consists of a single-iteration loop with the following three steps:

$$(X_L^{n+1},X_S^{n+1})=\underset{(X_L,X_S)}{\text{arg min}}{\Vert A(X_L+X_S)-Y+f^n\Vert }_2^2+{\mu }_{*}{\Vert {\mathit{\text{WX}}}_L-d_L^n+{\upsilon }_L^n\Vert }_2^2+{\mu }_1{\Vert {\mathit{\text{WX}}}_S-d_S^n+{\upsilon }_S^n\Vert }_2^2,f^{n+1}=f^n+A(X_L^{n+1}+X_S^{n+1})-Y;$$ (2.45)

$$d_S^{n+1}=\underset{d_S}{\text{arg min}}\frac{1}{2}{\Vert {\mathit{\text{WX}}}_S^{n+1}+{\upsilon }_S^n-d_S\Vert }_2^2+\frac{{\lambda }_1}{{\mu }_1}{\Vert d_S\Vert }_1,{\upsilon }_S^{n+1}={\upsilon }_S^n+{\mathit{\text{WX}}}_S^{n+1}-d_S^{n+1};$$ (2.46)

and

$$d_L^{n+1}=\underset{d_L}{\text{arg min}}\frac{1}{2}{\Vert {\mathit{\text{WX}}}_L^{n+1}+{\upsilon }_L^n-d_L\Vert }_2^2+\frac{{\lambda }_{*}}{{\mu }_{*}}{\Vert d_L\Vert }_{*},{\upsilon }_L^{n+1}={\upsilon }_L^n+{\mathit{\text{WX}}}_L^{n+1}-d_L^{n+1}.$$ (2.47)

The convergence of this iterative scheme can be established by mimicking the proofs in [40].

The first step (2.45) is equivalent to an iteration step in a typical L₂ minimization problem, and its solution can be derived from the optimal condition:

$$\begin{array}{c}{A}^{T}A(X_L+X_S)+{\mu }_{*}{X}_L=A^T(Y-f^n)+{\mu }_{*}{W}^T(d_L^n-{\upsilon }_L^n)\hfill \\ A^{T}A(X_L+X_S)+{\mu }_1{X}_S=A^T(Y-f^n)+{\mu }_1{W}^T(d_S^n-{\upsilon }_S^n).\hfill \end{array}$$ (2.48)

Note that if it were not the TF transform with W^TW = 1, we may need to add W^TW in front of the second terms on the left-hand side of (2.48). Here, we use the conjugate gradient (CG) method for solving the resultant linear system without explicitly formulating the linear system matrix, for which A^TAX often dominates the computational cost. Since the linear system is symmetric positive definite, CG gives the exact solution after a few iterations. Again, if it were not the TF norm with W^TW = 1, one may have to compute W^TWX during each CG inner iteration.

The second step (2.46) consists of the following scalar subproblems according to (2.21) for each i ≤ N_E × N_S:

$$({[d]}_{0,1,i}^l,{[d]}_{1,0,i}^l)=\underset{({[d]}_{0,1,i}^l,{[d]}_{1,0,i}^l)}{\text{arg min}}\frac{1}{2}{({[Y]}_{0,1,i}^l-{[d]}_{0,1,i}^l)}^2+\frac{1}{2}{({[Y]}_{1,0,i}^l-{[d]}_{1,0,i}^l)}^2+{\lambda }^l|{[d]}_{1,i}^l|,l\le L,$$ (2.49)

$$\begin{array}{cc}{[d]}_{1,1,i}^l=\underset{{[d]}_{1,1,i}^l}{\text{arg min}}\frac{1}{2}{({[Y]}_{1,1,i}^l-{[d]}_{1,1,i}^l)}^2+{\lambda }^l|{[d]}_{2,i}^l|,\hfill & l\le L,\hfill \end{array}$$ (2.50)

$$d_i^L=\underset{d_i^L}{\text{arg min}}\frac{1}{2}{(Y_i^L-d_i^L)}^2+{\lambda }^L|d_i^L|,$$ (2.51)

where the subscript ‘S’ is neglected for clarity, λ = λ₁/μ₁, Y = WX_Sⁿ⁺¹+v_Sⁿ, and the dependence of λ on the level is to balance the shrinkage at different levels, i.e. λ^l = λ⁰/2^l. The solution of (2.49)–(2.51) can be solved by considering the following problem with the scalars x and y:

$$\{x_i,i\le D\}=\underset{(\{x_i,i\le D\})}{\text{arg min}}\frac{1}{2}{\displaystyle \sum _{i=1}^D}{(x_i-y_i)}^2+\lambda \sqrt{{\displaystyle \sum _{i=1}^D}{x}_i^2}.$$ (2.52)

Its solution is given by the so-called generalized shrinkage formula [39]

$$\begin{array}{cc}\hfill x_i=S_{\lambda }(y_i)=\text{max}(y^{*}-\lambda ,0)\frac{y_i}{y^{*}},\hfill & \hfill i\le D,\hfill \end{array}$$ (2.53)

with y* defined as

$$y^{*}=\sqrt{{\displaystyle \sum _{i=1}^D}{y}_i^2}.$$ (2.54)

The third step (2.47) consists of the following matrix subproblems according to (2.25)

$$({[d]}_{0,1}^l,{[d]}_{1,0}^l)=\underset{({[d]}_{0,1}^l,{[d]}_{1,0}^l)}{\text{arg min}}\frac{1}{2}{\Vert {[Y]}_{0,1}^l-{[d]}_{0,1}^l\Vert }_2^2+\frac{1}{2}{\Vert {[Y]}_{1,0}^l-{[d]}_{1,0}^l\Vert }_2^2+{\lambda }_l{\Vert {[d]}_1^l\Vert }_{*},l\le L,$$ (2.55)

$$\begin{array}{cc}\hfill {[d]}_{1,1}^l=\underset{{[d]}_{1,1}^l}{\text{arg min}}\frac{1}{2}{\Vert {[Y]}_{1,1}^l-{[d]}_{1,1}^l\Vert }_2^2+{\lambda }_l{\Vert {[d]}_2^l\Vert }_{*},\hfill & \hfill l\le L,\hfill \end{array}$$ (2.56)

$$d^L=\underset{d^L}{\text{arg min}}\frac{1}{2}{\Vert Y^L-d^L\Vert }_2^2+{\lambda }_L{\Vert d^L\Vert }_{*},$$ (2.57)

where the subscript ‘L’ is neglected for clarity, λ = λ_*/μ_* and Y = WX_Lⁿ⁺¹+v_Lⁿ. The solution of (2.55)–(2.57) can be solved by considering the following problem with the matrices x and y:

$$\{x_i,i\le D\}=\underset{(\{x_i,i\le D\})}{\text{arg min}}\frac{1}{2}{\displaystyle \sum _{i=1}^D}{\Vert x_i-y_i\Vert }_2^2+\lambda {\Vert \sqrt{{\displaystyle \sum _{i=1}^D}{x}_i^2}\Vert }_{*}.$$ (2.58)

The proof in appendix A shows that the solution of (2.58) is given by the following generalized singular value thresholding (G-SVT) formula:

$$\begin{array}{cc}\hfill x_i=T_{\lambda }(y_i)=[U·\text{diag}(\text{max}(\sigma -\lambda ,0))·V^T]\frac{y_i}{y^{*}},\hfill & \hfill i\le D,\hfill \end{array}$$ (2.59)

with y* from the following point-wise operation, and U, V and σ as its orthonormal vectors and singular values:

$$\begin{array}{ccc}{y}^{*}=\sqrt{{\displaystyle \sum _{i=1}^D}{y}_i^2}\hfill & \text{and}\hfill & y^{*}=U·\text{diag}(\sigma )\hfill \end{array}·V^T.$$ (2.60)

In the aforementioned equation, the operation with respect to y_i (resp. y*) is the point-wise multiplication (resp. division), and the convention is that y_i/y* is zero, whenever y* is zero. Here, the G-SVT step is computationally negligible compared with (2.48) since the number of the spectral dimension is usually only a few, which is much less than that of the spatial dimension.

Now, we summarize the solution algorithm as follows:

$$\begin{array}{c}(X_L^{n+1},X_S^{n+1})=\mathit{\text{CG}}(A,Y,f^n,d^n,{\upsilon }^n),\hfill \\ f^{n+1}=f^n+{\mathit{\text{AX}}}^{n+1}-Y;\hfill \\ d_S^{n+1}=S_{{\lambda }_1/{\mu }_1}({\mathit{\text{WX}}}_S^{n+1}+{\upsilon }_S^n),\hfill \\ {\upsilon }_S^{n+1}={\upsilon }_S^n+{\mathit{\text{WX}}}_S^{n+1}-d_S^{n+1};\hfill \\ d_L=T_{{\lambda }_{*}/{\mu }_{*}}({\mathit{\text{WX}}}_L^{n+1}+{\upsilon }_L^n),\hfill \\ {\upsilon }_L^{n+1}={\upsilon }_L^n+{\mathit{\text{WX}}}_L^{n+1}-d_L^{n+1}.\hfill \end{array}$$ (2.61)

Here, CG represents the solution to the L₂ subproblem (2.45); the generalized shrinkage formula S is given by (2.53); and the G-SVT solution T is given by (2.59). Note that the step by G-SVT (2.59) is computationally negligible since the number of columns of the matrix considered here is only a few. The dominant step is the first one for solving the L₂ subproblem. Due to its iterative nature, empirically it is not necessary to solve each CG step with very high accuracy in order for the whole loop to achieve fast convergence. In our study, CG with ten inner iterations is adequate for (2.61) to reach an acceptable reconstruction accuracy within 30 outer iterations.

Regarding the regularization parameters, the following formulas are recommended:

$$\begin{array}{ccc}r=\sqrt{\text{max}(n_1,n_2)},\hfill & {\lambda }_{*}=r{\lambda }_1,\hfill & {\mu }_{*}={\mu }_1={\lambda }_1,\hfill \end{array}$$ (2.62)

where n₁ (n₂) is the number of rows (columns) of the image matrix X and the choice of r is suggested by [22]. Moreover, the proper scaling is recommended for energy-dependent regularization since the scale of X may vary substantially across different energies. That is, we weight r by the L₂ norm of the measurement Y at different energies:

$$\begin{array}{cc}{r}_i=r\frac{{\Vert Y_i\Vert }_2}{\underset{i}{\text{max}}{\Vert Y_i\Vert }_2},\hfill & i\le N_E,\hfill \end{array}$$ (2.63)

where r_i is the regularizing parameter for the ith energy bin. Therefore, the only parameters to be determined are λ₁. Empirically, it was found that λ₁∈[0.1, 1] provides satisfactory performance in terms of both accuracy and speed.

3. Results

In this proof-of-concept study, for simplicity, we simulated in 2D, rather than in 3D, on a 256 × 256 spatial grid. Projection data were acquired in the equidistant fan-beam scanning geometry with a scanning trajectory of a 10 cm radius, being similar to a typical micro-CT setting. Only 16 views of data per energy bin were simulated using the dynamic undersampling strategy [23]. Then, the data were contaminated with 1% Gaussian noise. Here, L = 2 in the TF regularization.

We first compared the PRISM (2.36) with L2 (2.37), TF (2.38), LR (2.39) and TFLR (2.40). We also compared the PRISM (2.36) with λ_t = 0 to show the difference due to the regularization on the entire image. See figures 3 and 4 for the results. Here, we did not compare with the direct reconstruction by the filtered back projection (FBP), which generally gives worse accuracy than L2 when reconstructing with undersampled data. Then, we evaluated the effect of generalized rank in the PRISM by comparing (2.36) and (2.41). See figures 5 and 6 for the results. Finally, we evaluated the effect of specific intensity/spectral priors by comparing (2.36), (2.42) and (2.43). See figures 7 and 8 for the results.

Figure 3.

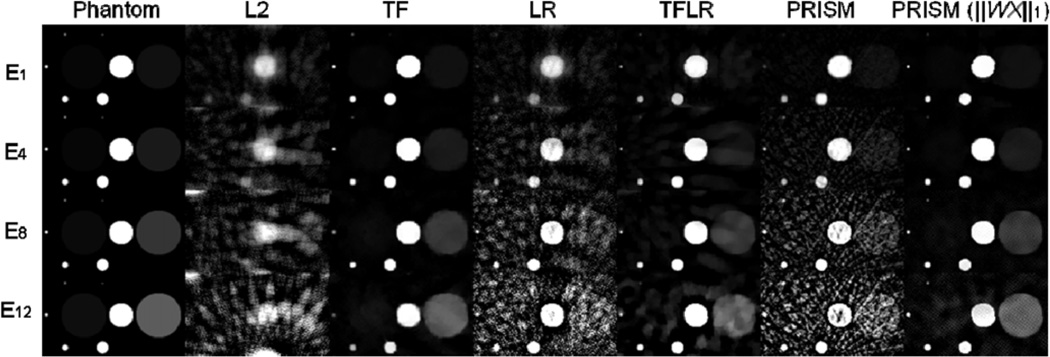
PRISM versus other methods. Columns 1–7 correspond to the multi-energy phantom (Phantom), L2 regularization (L2), tight frame regularization (TF), rank regularization (LR), tight frame and rank regularization (TFLR), PRISM without regularizing the total image (PRISM), and PRISM with TF regularization of the total image (PRISM ‖WX‖₁), respectively. Rows 1–4 are from the first, fourth, eighth and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row. (See figure 4 for the zoom-in image details inside the red squares.)

Figure 4.

PRISM versus other methods. The images are the zoom-in details inside the red squares in figure 3. Columns 1–7 correspond to the multi-energy phantom (Phantom), L2 regularization (L2), tight-frame regularization (TF), rank regularization (LR), tight frame and rank regularization (TFLR), PRISM without regularizing the total image (PRISM), and PRISM with TF regularization of the total image (PRISM ‖WX‖₁), respectively. Rows 1–4 are from the first, fourth, eighth and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row.

Figure 5.

Image rank versus generalized rank in the PRISM. Column 1 is the multi-energy phantom (Phantom). Columns 2–4 are from the PRISM with image rank regularization (PRISM ‖·‖*): the total image, the low-rank background component (X_L) and the sparse variation component (X_S). Columns 5–7 are from the PRISM with transformed rank regularization (PRISM ‖W·‖*): the total image, the low-rank background component (X_L) and the sparse variation component (X_S). Rows 1–4 are from the first, fourth, eighth, and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row. (See figure 6 for the zoom-in image details inside the red squares.)

Figure 6.

Image rank versus generalized rank in the PRISM. The images are the zoom-in details inside the red squares in figure 5. Column 1 is the multi-energy phantom (Phantom). Columns 2–4 are from the PRISM with image rank regularization (PRISM ‖·‖*): the total image, the low-rank background component (X_L) and the sparse variation component (X_S). Columns 5–7 are from the PRISM with transformed rank regularization (PRISM ‖W·‖*): the total image, the low-rank background component (X_L) and the sparse variation component (X_S). Rows 1–4 are from the first, fourth, eighth and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row.

Figure 7.

PRISM with intensity/spectral priors for multi-energy CT. Columns 1–4 correspond to the multi-energy phantom (Phantom), PRISM without spectral priors (PRISM (X)), PRISM with partial spectral priors (PRISM (X, Z)) and PRISM with full spectral priors (PRISM (Z)), respectively. Rows 1–4 are from the first, fourth, eighth and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row. (See figure 8 for the zoom-in image details inside the red squares.)

Figure 8.

PRISM with intensity/spectral priors for multi-energy CT. The images are the zoom-in details inside the red squares in figure 7. Columns 1–4 correspond to the multi-energy phantom (Phantom), PRISM without spectral priors (PRISM (X)), PRISM with partial spectral priors (PRISM (X, Z)) and PRISM with full spectral priors (PRISM (Z)), respectively. Rows 1–4 are from the first, fourth, eighth, and twelfth energy bins, respectively. The images in each row have the same display window as the first image in that row.

Except L2, which is differentiable and therefore can be solved with iterations with a single step that is similar to (2.45), all the other aforementioned models can be solved through split Bregman iterations similar to (2.61). Since the major computational cost with all of the models is from the L₂ subproblem (2.45), the total computational time is approximately proportional to the number of iterations. It was found that roughly 30 iterations together with the parameters specified by (2.62) and (2.63) were sufficient, with each reconstruction that took 1–2 min on the MATLAB platform on a desktop with Intel CPU E6850 3 GHz. In other words, all of the models except L2 were similar in terms of computational cost, but L2 failed to provide satisfactory image quality regardless of the number of iterations.

3.1. Phantom

A circular phantom of a 2 cm diameter (figure 2(a)) was designed to simulate a mouse, and it contained 14 circular inclusions each of which was made of a different material (table 1). While objects 1–8 were used to simulate the unique biologically relevant spectral characteristics, objects 9–14 were intended to quantify the image resolution.

Table 1.

Parameters of the objects in the phantom (figure 2) and the names of the associated materials.

Object	Center (cm)	Radius (cm)	Base material
1	(0.0000, 0.0000)	1.0000	Soft tissue
2	(0.0000, 0.0000)	0.1667	Water
3	(0.5556, 0.0000)	0.1667	Blood
4	(0.2778, −0.4811)	0.1667	0.2% gold+99.8% blood
5	(−0.2778, −0.4811)	0.1667	0.3% iodine+99.7% blood
6	(−0.5556, 0.0000)	0.1667	1.0% barium+99.0% water
7	(−0.2778, 0.4811)	0.1667	0.3% gadolinium+99.7% blood
8	(0.2778, 0.4811)	0.1667	10% calcium+90% water
9	(0.2778, 0.0000)	0.0899	10% calcium+90% water
10	(0.1389, −0.2406)	0.0444	10% calcium+90% water
11	(−0.1389, −0.2406)	0.0222	10% calcium+90% water
12	(0.1389, 0.0000)	0.0111	10% calcium+90% water
13	(−0.1389, 0.2406)	0.0056	10% calcium+90% water
14	(0.1389, 0.2406)	0.0028	10% calcium+90% water

The NIST Report 5632 by Hubbell and Seltzer provided tables of x-ray mass attenuation coefficients and mass energy-absorption coefficients from 1 keV to 20 MeV for elements Z = 1–92 and 48 additional substances of dosimetric interest (http://www.nist.gov/pml/data/xraycoef/index.cfm). Based on these tables, Tuszynski published an open source package (http://www.mathworks.com/matlabcentral/fileexchange/12092-photonattenuation-2) to interpolate the attenuation and energy absorption coefficients for x-rays and gamma-rays in various materials including mixtures and compounds, with additional functions that provided x-ray attenuation and absorption mean free paths and x-ray fractional transmission and absorption coefficients in these 140 materials, homogenous mixtures and chemical compounds based on these materials. The attenuation coefficients used in this study were interpolated using Tuszynski’s open source package. The spectral curves of the attenuation coefficients of eight typical materials are plotted in figure 2(b). In particular, in this proof-of-concept study, we assumed there were 12 energy channels centering at 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84 and 90 keV, respectively. We also assumed that each channel was strictly selective around its central energy. Therefore, it was not necessary to specify the x-ray spectrum. Figures 3–8 show the attenuation maps at the first, fourth, eighth and twelfth energy bins, where the images in each row have the same display window as the first phantom image in that row.

3.2. PRISM versus other methods

The reconstruction results with various methods are shown in figure 3 with regional zoom-in details in figure 4. As shown in these two figures, the result from L2 was blurred and full of artifacts; the TF improved the image quality significantly for this piecewise-constant phantom by reducing its blurring and artifacts, however failed to resolve object 13 and blurred object 12; despite the alleviated blurring, strong artifacts still presented for LR that prevented it from visualizing objects 12 and 13; the improvement from TFLR was between TF and LR; the PRISM with λ_t = 0 resolved object 13, but still with some artifacts that are particularly notable in figure 4; finally, the PRISM with the total image regularization offered the best image quality with much fewer artifacts, the best contrast for object 12 and clearly resolved object 13.

3.3. PRISM with generalized rank

The comparison of the PRISM with generalized rank and the PRISM with image rank is shown in figure 5 with regional zoom-in details in figure 6. As shown in these two figures, the use of the rank of the TF transform of the multi-energy image (2.26) indeed improved the image quality with much fewer artifacts, better contrast for object 13 and better resolution for object 14. Besides, the use of generalized rank offered a better decomposition into the low-rank component and the sparse component.

3.4. PRISM with intensity/spectral priors

The comparison of the PRISM with no, partial, and full priors is shown in figure 7 with regional zoom-in details in figure 8. For clarity, the image rank was used instead of the generalized rank. Here, the full intensity/spectral prior matrix B defined by (2.28) was directly obtained from the spectral curves in figure 2(b), and the partial prior matrix consisted of five known mixed materials as listed in table 1 (i.e. objects 4–14). As shown in these two figures, the use of the priors clearly improved the image quality, such as the clearly resolved object 14; with full spectral priors, the PRISM reconstructed almost the same image as the phantom.

4. Discussions and conclusion

A natural extension of the PRISM for multi-energy CT and 4D CT is the development for 5D CT, i.e. spatial, temporal and spectral CT. A similar matrix decomposition model can be established, for example, with the row dimension in a spatial variable (3D) and the column dimension in a temporal spectral variable (2D). That is, the stationary background over time and across energy can be extracted as the low-rank component, while the distinct spectral features and temporal changes can be captured as the sparse component. Again, both components can be with respect to the proper transform and additional spectral and temporal priors can be utilized as well.

Most interestingly, we can and should view a 5D object as a spatial, temporal and spectral tensor, which should be more appropriate for 5D CT (and for 4D CT and multi-energy CT as well). However, this may require advanced tensor-based mathematical tools and next-generation algorithms that could be fundamentally different from that for matrix algebra. This is an exciting direction for applied mathematical research.

Moreover, the PRISM and the aforementioned ideas can be translated for interior tomography [42–45], a theoretically justified methodology with which an interior region of interest (ROI) can be theoretically exactly reconstructed only from local projection data directly associated with paths through this ROI. While solving such an interior problem would conventionally require the whole-body x-ray illumination, by its nature interior tomography promises to reduce the radiation dose, handle large objects, and accelerate imaging speed. The robustness of interior tomography is an active research area. Newer types of algorithms are needed and can be developed based on the work reported here. For example, similar models and algorithms can be carried over for interior multi-energy CT or interior 5D CT.

In conclusion, we have proposed a novel rank-and-sparsity decomposition model, namely the PRISM, for multi-energy CT. The PRISM approach synergistically utilizes prior knowledge on the sparsity and rank of the multi-energy image up to the proper transform and energy-dependent intensity characteristics of structures and/or base materials. Also, we have developed an accurate and fast solution algorithm based on the split Bregman method and numerically demonstrated the merits of our approach. Further work is under way, including algorithmic optimization and experimental validation.

Appendix A

Solution of (2.58)

Theorem 1. The solution of the following minimization problem:

$$\{X_i,i\le D\}=\underset{(\{X_i,i\le D\})}{\text{arg min}}\frac{1}{2}{\displaystyle \sum _{i=1}^D}{\Vert X_i-Y_i\Vert }_2^2+\lambda \Vert \sqrt{{\displaystyle \sum _{i=1}^D}{X}_i^2}{\Vert }_{*},\lambda >0$$ (A.1)

is uniquely determined by the G-SVT formula

$$X_i=T_{\lambda }(Y_i)=[U·\text{diag}(\text{max}(\sigma -\lambda ,0)).V^T]\frac{Y_i}{Y^{*}},i\le D,$$ (A.2)

with Y* defined by the following point-wise operation, and U, V and σ as its orthonormal vectors and singular values:

$$Y^{*}=\sqrt{{\displaystyle \sum _{i=1}^D}{Y}_i^2}\text{and}{Y}^{*}=U·\text{diag}(\sigma )·V^T.$$ (A.3)

Proof. Since (A.1) is strictly convex, its solution must be unique. That is, we only need to show that (A.2) is a solution of (A.1).

Recall that X_i minimizes (A.1) if and only if 0 is a subgradient of (A.1) at X_i:

$$0\in X_i-Y_i+\lambda \partial {\Vert X^{*}\Vert }_{*}\frac{X_i}{X^{*}},i\le D,$$ (A.4)

with ∂ being a subgradient of the nuclear norm that can be characterized by [22, 46]

$$\partial {\Vert X^{*}\Vert }_{*}=\{{\mathit{\text{UV}}}^T+W:X^{*}=U\mathrm{\Sigma }{V}^T,U^{T}W=0,\mathit{\text{WV}}=0,{\Vert W\Vert }_2\le 1\}.$$ (A.5)

On the other hand, let Σ₀ (resp. Σ₁) be the singular values of Y* larger (resp. smaller) than l, and U₀ and V₀ (resp. U₁ and V₁) be the associated singular vectors; then, we have

$$Y^{*}=U_0{\mathrm{\Sigma }}_0{V}_0^T+U_1{\mathrm{\Sigma }}_1{V}_1^T,$$ (A.6)

and from (A.2),

$$\begin{array}{cc}{T}_{\lambda }(Y_i)=[U_0({\mathrm{\Sigma }}_0-\lambda I)V_0^T]\frac{Y_i}{Y^{*}},\hfill & i\le D.\hfill \end{array}$$ (A.7)

Therefore,

$$T_{\lambda }{(Y)}^{*}=[U_0({\mathrm{\Sigma }}_0-\sigma I)V_0^T].$$ (A.8)

From (A.7) and (A.8), we have

$$\begin{array}{cc}\frac{T_{\lambda }(Y_i)}{T_{\lambda }{(Y)}^{*}}=\frac{Y_i}{Y^{*}},\hfill & i\le D.\hfill \end{array}$$ (A.9)

Combining (A.6), (A.7) and (A.9),

$$Y_i-T_{\lambda }(Y_i)=\frac{Y_i}{Y^{*}}\{Y^{*}-[U_0({\mathrm{\Sigma }}_0-\lambda I)V_0^T]\}=\frac{T_{\lambda }(Y_i)}{T_{\lambda }{(Y)}^{*}}\lambda [U_0{V}_0^T+U_1({\lambda }^{-1}{\mathrm{\Sigma }}_1)V_1^T].$$ (A.10)

That is,

$$\begin{array}{cc}{Y}_i-T_{\lambda }(Y_i)=\frac{T_{\lambda }(Y_i)}{T_{\lambda }{(Y)}^{*}}\lambda (U_0{V}_0^T+W)\hfill & \text{with\hspace{1em}}W=U_1({\lambda }^{-1}{\mathrm{\Sigma }}_1)V_1^T.\hfill \end{array}$$ (A.11)

Next, by the facts that (i) U₀ and V₀ are the singular vectors of T_λ(Y)* from (A.8), (ii) ‖W‖₂≤1 since ‖λ⁻¹σ₁‖₂22641, and (iii) U₀^TW = 0 and WV₀ = 0, we conclude from (A.5)

$$\begin{array}{cc}{Y}_i-T_{\lambda }(Y_i)\in \lambda \partial {\Vert T_{\lambda }{(Y)}^{*}\Vert }_{*}\frac{T_{\lambda }(Y_i)}{T_{\lambda }{(Y)}^{*}},\hfill & i\le D.\hfill \end{array}$$ (A.12)

Therefore, T_λ(Y_i) satisfies (A.4), and theorem 1 is proved.

Appendix B

It is well known that an x-ray projection is generated in two steps: first modulated by chemical components and their density distributions, and then transformed by the imaging components. Under the ideal imaging conditions that (1) x-ray energy is monochromatic, (2) there is neither scattering nor noise, and (3) the imaging components are linear, the x-ray signal is modeled by the Lambert–Beer law

$$I(E_0)=I_0(E_0)D(E_0)\text{exp}(-\int \mu (E_0,l)\mathrm{d}l),$$ (B.1)

where E₀ is a monochromatic energy, I₀(E₀) is the photon intensity emitting from an x-ray source, D(E₀) is a detector efficiency, I₀(E₀) is a photon intensity received by the detector, l is the x-ray path, and μ(E₀, l) is an attenuation map depending on the energy E₀. After a logarithm operation on (B.1), we obtain

$$P(E_0)-\text{ln}(I_0(E_0)D(E_0)/I(E_0))=\int \mu (E_0,l)\mathrm{d}l.$$ (B.2)

The aforementioned equation is the well-accepted imaging model—the Radon transfom in the CT field. However, in practial applications, the x-ray source is polychromatic instead of monochromatic, which is defined by the spectrum I₀(E) for E∈ [0, ∞). As a result, (B.1) is now

$$I=\int I_0(E)D(E)\text{exp}\left(-\int \mu (E,l)\mathrm{d}l\right)\mathrm{d}E,$$ (B.3)

where I is the photon intensity received by the detector over all the energy range. Although μ(E, l) depends on the energy E in (B.3), the Radon tranfrom model is still well accepted and suceeded with beam-hardening correction. As a simple example,

$$P=\text{ln}\left(\int I_0(E)D(E)\mathrm{d}E/I\right)=\int \overline{\mu }(l)\mathrm{d}l,$$ (B.4)

where μ(l) is a weighted average of the attenuation map independent of the energy. When the energy spectrum of an x-ray tube is wide in a photon integrating detection mode, the inconsistency between data at different energies can generate significant errors from the approximation (B.4). Consequently, beam-hardening correction is needed [50, 51]. It is a major merit of multi-energy CT that when the energy bin is small in the spectral detection mode, the beam-hardening artifact is essentially negligible without a need for correction [47–49]. Using the energy-sensitive technology, for a given energy bin, the photon intensity can be modeled as

$$I(E_1,E_2)={\displaystyle {\int }_{E_1}^{E_2}}{I}_0(E)D(E)\text{exp}\left(-\int \mu (E,l)\mathrm{d}l\right)\mathrm{d}E,$$ (B.5)

where 0 < E₁ < E₂ are two energy thresholds [47]. Similar to convertional CT, the Radon transform model can be applied to (B.5):

$$P(E_1,E_2)=\text{ln}\left({\displaystyle {\int }_{E_1}^{E_2}}{I}_0(E)D(E)\mathrm{d}E/I(E_1,E_2)\right)=\int \mu (E_c(l),l)\mathrm{d}l,$$ (B.6)

where E₁ < E_c (l) < E₂, and P is dependent on the x-ray path l. When E₂−E₁ is negligable, (B.5) becomes (B.1), and (B.6) becomes (B.2). This is the Radon transfom model that has been well accepted in the CT field [48, 49].