A Study of the Hydration of the Alkali Metal Ions in Aqueous Solution

Abstract

The hydration of the alkali metal ions in aqueous solution has been studied by large angle X-ray scattering (LAXS) and double difference infrared spectroscopy (DDIR). The structures of the dimethyl sulfoxide solvated alkali metal ions in solution have been determined to support the studies in aqueous solution. The results of the LAXS and DDIR measurements show that the sodium, potassium, rubidium and cesium ions all are weakly hydrated with only a single shell of water molecules. The smaller lithium ion is more strongly hydrated, most probably with a second hydration shell present. The influence of the rubidium and cesium ions on the water structure was found to be very weak, and it was not possible to quantify this effect in a reliable way due to insufficient separation of the O–D stretching bands of partially deuterated water bound to these metal ions and the O–D stretching bands of the bulk water. Aqueous solutions of sodium, potassium and cesium iodide and cesium and lithium hydroxide have been studied by LAXS and M–O bond distances have been determined fairly accurately except for lithium. However, the number of water molecules binding to the alkali metal ions is very difficult to determine from the LAXS measurements as the number of distances and the temperature factor are strongly correlated. A thorough analysis of M–O bond distances in solid alkali metal compounds with ligands binding through oxygen has been made from available structure databases. There is relatively strong correlation between M–O bond distances and coordination numbers also for the alkali metal ions even though the M–O interactions are weak and the number of complexes of potassium, rubidium and cesium with well-defined coordination geometry is very small. The mean M–O bond distance in the hydrated sodium, potassium, rubidium and cesium ions in aqueous solution have been determined to be 2.43(2), 2.81(1), 2.98(1) and 3.07(1) Å, which corresponds to six-, seven-, eight- and eight-coordination. These coordination numbers are supported by the linear relationship of the hydration enthalpies and the M–O bond distances. This correlation indicates that the hydrated lithium ion is four-coordinate in aqueous solution. New ionic radii are proposed for four- and six-coordinate lithium(I), 0.60 and 0.79 Å, respectively, as well as for five- and six-coordinate sodium(I), 1.02 and 1.07 Å, respectively. The ionic radii for six- and seven-coordinate K⁺, 1.38 and 1.46 Å, respectively, and eight-coordinate Rb⁺ and Cs⁺, 1.64 and 1.73 Å, respectively, are confirmed from previous studies. The M–O bond distances in dimethyl sulfoxide solvated sodium, potassium, rubidium and cesium ions in solution are very similar to those observed in aqueous solution.

Short abstract

The hydration of alkali metal ions has been studied by large angle X-ray scattering, LAXS, and double difference infrared spectroscopy. The obtained M−O bond distances from LAXS have been compared to relevant crystal structures, conclusions about hydration numbers in aqueous solution have been made, and new ionic radii have been proposed. Hydration numbers of six, seven, eight and eight are proposed for the sodium, potassium, rubidium and cesium ions in aqueous solution.

Introduction

The sodium and potassium ions are among the most important metal ions in biology as well as industry. Aqueous solutions in living systems contain appreciable amounts of these ions, and their concentrations in living cells are regulated by intricate control systems, such as the sodium–potassium pump, which also play an important role in transmitting nerve signals.¹ Their importance in biology is reflected by their high abundance in living systems and in nature in general. Sodium and potassium ions are key constituents of many minerals, and their general high solubility is responsible for the composition of marine water. Abundance, high solubility and reaction inertness are desirable properties in industrial processes where they are frequently used as counterions for anions with desirable properties. The importance of lithium in the society is steadily increasing, especially in the area of rechargeable batteries.² Other industrial applications to be mentioned are lithium stearates for grease production, metallic lithium for high strength low weight alloys, lithium carbonate in the glass and porcelain industry, and applications in psychiatric medicine.³ On the other hand, the use of rubidium and cesium is presently more limited in society. Accidental and intentional emissions of radioactive cesium isotopes from nuclear industry and testing of weapons have caused an environmental problem.⁴ In spite of many conducted studies the knowledge of the structures and bonding properties of the hydrated alkali metal ions in aqueous solution is scarce and deviating. The structures of hydrated metal ions in aqueous solution have been reviewed by several authors.⁵⁻⁹

The frequently high solubility of alkali metal salts in water is due to large entropies of solution while heats of solution often are endothermic, as for example sodium chloride.¹⁰ This shows that the alkali metals are weakly hydrated, the heats of hydration are small,¹¹ and they have a tendency to disrupt the aqueous bulk structure without ordering the water molecules as the highly charged metal ions do through strong hydration. Hydrogen bonding is very important at the description of the hydration of chemical species. It is well-known that ions affect the network of hydrogen bonds making up the bulk structure of water. In order to systematize the way ions affect the hydrogen bonds in the aqueous bulk, the concept of structure making and structure breaking ions has been introduced.¹² Originally referring to increased or decreased viscosity in the vicinity of ions,¹² the concept has been interpreted in somewhat different ways. Marcus reviews the subject considering e.g. reorientation times, and thermodynamic as well as spectroscopic parameters as indicators.⁶A common view of the structure making and breaking properties is the difference in hydrogen bonding around the ion under study.⁶ The structure of liquid water can be viewed either as a mixture of hydrogen bound and interstitial water molecules⁶or as primarily hydrogen bound structure with hydrogen bonds of varying strength.¹³ The latter view is supported by the fact that the broad distribution of angles and distances in bulk water can only be compared to arbitrary definitions of hydrogen bonds.¹³ It can be concluded that small highly charged ions are structure makers while large ions with low charge density, such as the perchlorate ion, are definite structure breakers.⁶ Soper et al. have pointed out that the structure maker/breaker concept is unfortunate in the sense that small highly charged ions are considered structure makers while they are actually breaking the hydrogen bonds of the aqueous bulk to form even stronger ones in the close vicinity of the ion.¹⁴

It is proposed that the double difference infrared (DDIR) spectroscopy method offers a possibility to study the structure making or breaking properties of solvated ions as defined by whether hydration shell molecules interact more strongly or more weakly with water molecules than bulk water molecules interact with each other.¹⁵ By comparing the O–D oscillation energy of HDO molecules in the hydration shell of an ion or molecule with those in the aqueous bulk, the relative behavior of the hydration shell molecule can be investigated. An O–D stretching frequency lower than in bulk water has been interpreted as belonging to structure making ions, as defined above, while ions or molecules which increase the O–D stretching frequency in their hydration shell are considered as structure breakers.¹⁵ The concept of negative hydration is equivalent or closely related to the term structure breaker.¹⁶

The DDIR method was introduced by the Lindgren group¹⁷⁻²⁶ and further developed and applied by the Stangret group.^15,27−35 The foundation for this method is the rule of Badger and Bauer,³⁶ stating that the position of the O–D stretching vibration in monodeuterated water is affected proportionally to the energy of hydrogen bonds. By taking a series of differences between experimental infrared spectra of a solute dissolved in pure water, and in water containing ca. 8% HDO, a spectrum representing the O–D stretching vibrations of water molecules in the hydration shells is obtained.¹⁷ This spectrum, representing the water molecules affected in such a way that it is significantly different from the spectrum of pure water, is divided into contributions from waters binding to one or several solutes. One conclusion from the experiments performed so far has been that anions affect the peak position of the O–D stretching vibration in HDO in a continuous manner, while the same vibration of the water molecules hydrating cations tends to group at certain levels.^15,31 The position of the O–D stretching vibration of HDO molecules in the second hydration shell of di-, tri- and tetravalent metal ions is thought to approximately coincide with the values of the first hydration shell water molecules of alkali metal ions.¹⁵ In the hydration shell of ions or molecules, HDO molecules whose O–D stretching vibration is located at lower wavenumbers than 2509 cm^–1 form stronger hydrogen bonds than those within the aqueous bulk. The opposite is assumed for hydrated species where HDO molecules show an O–D stretching vibration at wavenumbers higher than 2509 cm^–1. The general view so far is that most cations and anions with high charge density are structure makers, while monovalent anions are structure breakers. Exceptions to this rule of thumb are for example alkali metal ions such as potassium, rubidium and cesium as well as anions such as fluoride and hydroxide.^15,33

The sodium ion crystallizes with full hydration shell with large low-symmetrical counterions, Table S1b in the Supporting Information (SI), while in salts with small and symmetric anions the lattice energies favor crystallization with the anhydrous sodium ion. The hydrated disodium ion, [Na₂(H₂O)₁₀]²⁺, is observed in several solid compounds, as well as other hydrated polysodium ions, Table S1b in the SI. However, these di- and polysodium ions have never been observed in aqueous solution. The hydrated sodium and polysodium ions have octahedral configuration in a vast majority of the structures reported in the solid state, Table S1b in the SI. In the same way the vast majority of the compounds containing hydrated lithium ions in the solid state are tetrahydrates with tetrahedral configuration. However, there are also examples of structures with six-coordinate lithium ions in endless chains of shared water molecules, Table S1a in the SI.

The strong relationship between ionic radius and coordination number was established in a thorough investigation by Shannon.³⁷ At the determination of structures in solution, independent of method used, the mean bond distances can be determined accurately, while the coordination numbers are less reliable due to the very strong correlation with the temperature factor/Debye–Waller coefficient. The mean bond distance in homoleptic complexes, e.g. pure hydrates or solvates, gives therefore a strong indication of the coordination number knowing the relationship between ionic radius and coordination number for the metal ion under study.

The alkali metal ions are spheres with low charge density forming mainly electrostatic interactions. As the alkali metal ions, except lithium, are large, the charge densities are low and the electrostatic interactions formed are weak as well as their ability to form covalent interactions due to filled outer electron shells. The inability of the potassium, rubidium and cesium ions to form well-defined hydrate and solvate complexes in the solid state is a clear sign of the weak hydration, and their hydrate structures must be determined in aqueous solution. The ionic radii of the lithium and sodium ions in different configurations can be accurately determined from the number of homoleptic complexes reported in the literature (ICSD and CSD).^38,39 On the other hand, the ionic radii of the potassium, rubidium and cesium ions are much more difficult to extract as the number of complexes with a well-defined configuration and a nondistorted structure is very limited (ICSD and CSD).^38,39 Only compounds as oxides, where the lattice energies are strong and the preferred coordination of the alkali metal ion can be suppressed, have been used so far to estimate the ionic radii of the alkali metal ions.

A large number of X-ray and neutron scattering studies and theoretical simulations have been performed on the hydrated lithium ion in aqueous solution. The spread in the data is very large, and the interpretation of especially X-ray data is difficult, almost impossible, due to the very weak scattering effect of lithium in such experiments. We have performed LAXS experiments on the hydrated lithium ion in this study, but concluded that the contribution from the electron-poor lithium ion is too small to obtain any significant information. Experimentally reported values of the Li–O distance in the hydrated lithium ion are e.g. 1.90,⁴⁰ 1.98⁴¹ and 2.17 Å,⁴² of which ref (40) is a neutron scattering study while the other two used X-rays. Smirnov and Trostin have been reviewing available experimental data for the lithium ion,⁴³ and more information is available in general reviews.^6,7,44,45 It is not possible from the present knowledge to unambiguously decide the coordination number of the hydrated lithium ion in aqueous solution based on present experimental data. Neither do the reported simulation studies on the hydrated lithium ion in aqueous solution give a conclusive picture. Simulation studies have reported Li–O bond distances of 1.95,⁴⁶ 1.97,⁴¹ 1.971⁴⁷ and 2.03 Å.⁴⁸ For the lithium ion, the suggested hydration number is usually four.^40,42,46,49 The review article by Smirnov and Trostin gives a thorough collection of hydration studies of the lithium ion, whereof some suggest the coordination number six.⁴³

The experimentally determined Na–O distance in the hydrated sodium ion in aqueous solution is in a wide range as well, e.g. 2.34,⁵⁰ 2.40,⁵¹ 2.42⁴² and 2.50 Å.⁵² A recent computer simulation by Azam et al. predicts a Na–O distance of 2.34/2.36 Å,⁵³ and older simulations have reported values in the same order.^54,55 For the sodium ion, the hydration number has been suggested to be four,^41,51,56 4.6,⁵⁷ 5.3,⁵⁰ 5.5,⁵³ 5.6/6.5,⁵⁴ six,⁵⁸ 6.5⁵⁵ and eight.⁵² The available experimental data for the hydrated sodium ion in aqueous solution has been reviewed.⁵⁹

Experimental values of the K–O bond distance in the hydrated potassium ion in aqueous solution are in the range 2.65–2.97 Å.^{14,42,50,52,57,60} A computer simulation by Azam et al. predicts a K–O distance of 2.80 Å,⁵³ and a previous investigation from the same laboratory came to a similar conclusion, 2.78–2.81 Å.⁵⁴ The hydration number of the potassium ion in aqueous solution has been suggested to be 5.6/3.3,⁵⁷ six,^14,50 6.2/6.8⁵³ and 7.8/8.3.⁵⁴

A combined LAXS and EXAFS study of the hydrated rubidium ion determined the Rb–O bond distance in the hydrated rubidium ion in aqueous solution to 2.98 Å.⁶¹ Other Rb–O bond distances reported from experimental studies are 2.83,⁶² 2.90⁶³ and 3.05 Å.⁶⁴ In a QM/MM simulation study the Rb–O bond distance of the hydrated rubidium ion was predicted to 2.9 Å⁶⁵ and in a study with ab initio based model potentials to be 2.95.⁶⁶ The hydration number of the hydrated rubidium ion is reported to be six,⁶² 6.9,^64,65 7.1⁶⁶ and eight.^58,61

The reported Cs–O bond distances in the hydrated cesium ion from experimental studies are in the range 2.95–3.21 Å;^40,42,57,67 the value 2.95 Å of ref (40) has been misquoted in review references.^42,44,57,59 In a QM/MM simulation study three different simulation approaches were utilized, with the one yielding a Cs–O bond distance of 3.20 Å being regarded as the most reliable one,⁶⁸ while another simulation study suggests 3.10 Å.⁶⁹ The cesium ion is the alkali metal ion with lowest charge density and is therefore expected to affect the water matrix less than the other ions. At the same time its larger size opens up the geometrical possibility of a higher coordination number than eight.⁴⁴ The coordination number of the hydrated cesium ion has been suggested to be eight,^40,49,58 8–9⁶⁸ and 8/6.5,⁶⁹ while the low value 3.6⁵⁷ seems unrealistic. Smirnov and Trostin have reviewed available experimental structure data in aqueous solution for the potassium, rubidium and cesium ions.⁷⁰

There is a general agreement that the potassium, rubidium and cesium ions are structure breakers, and that the lithium ion is a structure maker.⁶ Opinions on whether the sodium ion decreases or increases the amount of hydrogen bonding differs somewhat, and Marcus assigns it as a borderline ion.⁶ Scientists working with computer simulations frequently report second and third hydration shells, as well as hydration shells even further from the central atom, utilizing the next-neighbor approach. However, in our context a hydration shell is only present if the included water molecules are structurally or spectroscopically distinguishable from bulk water. There is a general agreement that the potassium, rubidium and cesium ions are lacking a second hydration sphere due to their low charge density.^6,59For the lithium ion, a second hydration sphere has been reported by some authors but not by others.⁴³ Even though the existence of a second hydration sphere of the lithium ion has been considered likely, there is yet no consensus regarding its composition.^43,44 Whether a second hydration shell around the sodium ion is present or not is a difficult task to solve, but some authors propose that such a second hydration sphere should be present.^5,70 The reorientation times of water molecules in the first hydration shell decrease down the alkali metal group, with the hydrated lithium and sodium ions having longer reorientation times than in bulk water, supporting structure maker properties, while the opposite is true for the hydrated potassium, rubidium and cesium ions.^16,70,71 These data are consistent with the assignment of structure makers and breakers according to Marcus,⁶ also indicating that the sodium ion should be a weak structure maker.

Structural studies of the hydrated alkali metal ions in aqueous solution are difficult due to the weak hydration causing weak metal ion–water bonds. This makes EXAFS as a method less suitable due to the low sensitivity for long distances with large Debye–Waller factors. On the other hand, large angle X-ray scattering, LAXS, easily detects such distances.⁷² The drawback with LAXS is that all distances in the studied sample are included in the experimental data which in reality implicate that high concentrations are required, and that distances within the solvent may hide other relevant distances such as those between solute and water. The K–O, Rb–O and Cs–O bond distances are similar to the O···(H−)O distances in the aqueous bulk making data analysis challenging. In order to support the studies in aqueous solution, LAXS studies have been performed in the aprotic solvent dimethyl sulfoxide, Me₂SO. The advantage with this system is that it lacks such intermolecular solvent distances in the region of the K–O, Rb–O and Cs–O bond distances. The coordination numbers of hydrated and Me₂SO solvated metal ions are often the same, or at least very similar.⁷³ The coordination number is normally difficult to determine from measurements in solution, where the primary structure information is one-dimensional, as the correlation between temperature factor coefficient and number of distances is strong and cannot the be determined accurately without putting one of these parameters to a fixed value. On the other hand, distances are accurately determined by these methods, and as the correlation between ionic radius and coordination number is strong, very good predictions of the coordination number can be made from the obtained M–O bond distance. The ionic radius of a metal ion is preferably evaluated from homoleptic complexes of neutral ligands as discussed in detail below.

The aim of the present study is to determine the M–O bond lengths in the hydrated alkali metal ions in aqueous solution by means of LAXS measurements, as this is the experimental method most suitable to determine long distances with broad bond distance distribution.⁷² Complementary studies have been performed on dimethyl sulfoxide solvated alkali metal ions as dimethyl sulfoxide is expected to form solvate complexes similar to the hydrates, but as dimethyl sulfoxide is aprotic, no solvent–solvent distances are present close to the M–O ones, as in water. Crystallographic data of alkali metal ion complexes with oxygen donor ligands have been collected from structure databases,^38,39 and the relationship between M–O bond length and coordination number/configuration has been analyzed. With this as a basis, coordination numbers of hydrated alkali metal ions can be estimated from experimentally obtained M–O bond distances. This material also makes it possible to predict more accurate ionic radii of the alkali metal ions with different coordination numbers than before. The O–D stretching vibrations of the monodeuterated water molecules different from the bulk water have been determined by the DDIR method in order to describe the bonding properties of the water molecules binding to the alkali metal ions in as great detail as possible.

Experimental Section

Chemicals

The following chemicals have been used in the experiments: Milli-Q filtered deionized water, heavy water, D₂O, (99.96 atom % D₂O, Aldrich), sodium iodide, NaI (99.99%, Aldrich), potassium iodide, KI (99.5%, Merck), rubidium iodide, RbI (99.9%, Aldrich), cesium iodide, CsI (99.9%, Aldrich), lithium hydroxide, LiOH (99.9%, Aldrich), cesium hydroxide, CsOH (99.95%, Aldrich), lithium perchlorate, LiClO₄ (99.99%, Aldrich), sodium perchlorate, NaClO₄ (99.99%, Aldrich), and dimethyl sulfoxide, (CH₃)₂SO, (99.8%, Aldrich). All chemicals were used as purchased. Composition, concentration and density of the prepared solutions are summarized in Table S2 in the SI. Zero point solutions of deionized water containing ∼8% HDO were obtained by mixing water and heavy water. In order to minimize conversion of iodide to triiodide, exposure to daylight was minimized during the preparation and storage of the cesium and rubidium iodide solutions.

Large Angle X-ray Scattering

The scattering of Mo Kα X-ray radiation (λ = 0.7107 Å) from the free surface of the studied solutions was measured by means of a large angle θ–θ diffractometer at ca. 450 discrete points in the range 1 < θ < 65°; the scattering angle is 2θ. The solutions were contained in a Teflon cup inside an airtight radiation shield with beryllium windows. The scattered radiation was monochromatized in a focusing LiF crystal monochromator. At each preset angle 100,000 counts were accumulated and the entire angular range was scanned twice, which corresponds to a statistical error of about 0.3%. The divergence of the primary X-ray beam was limited by 1 or 1/4° slits for different θ regions, with partially overlapping data for scaling purposes. The experimental setup and the theory of the data treatment and modeling have been described elsewhere.⁷⁴ The data treatment was carried out by means of the KURVLR program.⁷⁵ The experimental intensities were normalized to a stoichiometric unit of volume containing one alkali metal atom, using the scattering factors f for neutral atoms, including corrections for anomalous dispersion, Δf′ and Δf′′, and for Compton scattering.^76,77 Least-squares refinements of the model parameters were carried out by means of the STEPLR program,⁷⁸ where the expression U = ∑w(s)[s·i_exp(s) – s·i_calc(s)]² is minimized; the scattering variable s = (4π/λ)sin θ and w(s) a weighting factor. The refinement of the model parameters was made for data in the high s region, 4.0–16.0 Å^–1, for which the intensity contribution from the long-range distances can be neglected. A Fourier back-transformation procedure was used to improve the alignment of the experimental structure-dependent intensity function i_exp(s) before the refinements, by removing spurious nonphysical peaks below 1.2 Å in the radial distribution function.⁷⁹

Double Difference Infrared (DDIR) Spectroscopy

The infrared spectroscopy measurements were performed on a Perkin-Elmer Spectrum 100 FT-IR spectrometer. The sample was kept between CaF₂ windows separated by a Teflon spacer. Path lengths were determined interferometrically to 32.8, 33.2, 32.9, 33.1, and 32.6 μm for the aqueous solutions of LiClO₄, NaI, NaClO₄, KI, RbI and CsI, respectively. The temperature was kept at 298.2 ± 0.1 K by an electrically heated liquid cell temperature controller from Pike Technologies. The beam diameter was set to 3 mm, and 256 scans were collected in the range 3500–900 cm^–1 with a resolution of 4 cm^–1. Spectral treatment was performed in accordance with the method developed by Lindgren et al.¹⁷ Removal of bulk water was performed in accordance with an algorithm developed by the Stangret group.^27,29 This algorithm utilizes measurements at several concentrations to obtain a derivative of absorbance with respect to concentration. The affected spectrum extrapolated to infinite dilution (ε_a) is obtained from the derivative, the bulk water spectrum (ε_b), the mean molar mass of the solvent, ca. 8% HDO in water (M) and the affected number of water molecules (N):

1

The way the number of affected water molecules is calculated is described elsewhere.^27,29 The absorption bands related to the water molecules affected by the ions are compared to the band of pure water, and their relative positions implicate how the aqueous structure is affected. In Figure 1 it can be seen that a strong energy rich O–D bond (Figure 1c), corresponding to a high wavenumber, causes a weak O···D–O bond. The spectral treatment has been performed with the spectroscopy software program GRAMS/AI 8.0 from Thermo Electron Corporation and its add-in Razortools from SpectrumSquare. The additional add-in program Yanuz from the Stangret group has also been used to obtain the derivative with respect to concentration.

Figure 1.

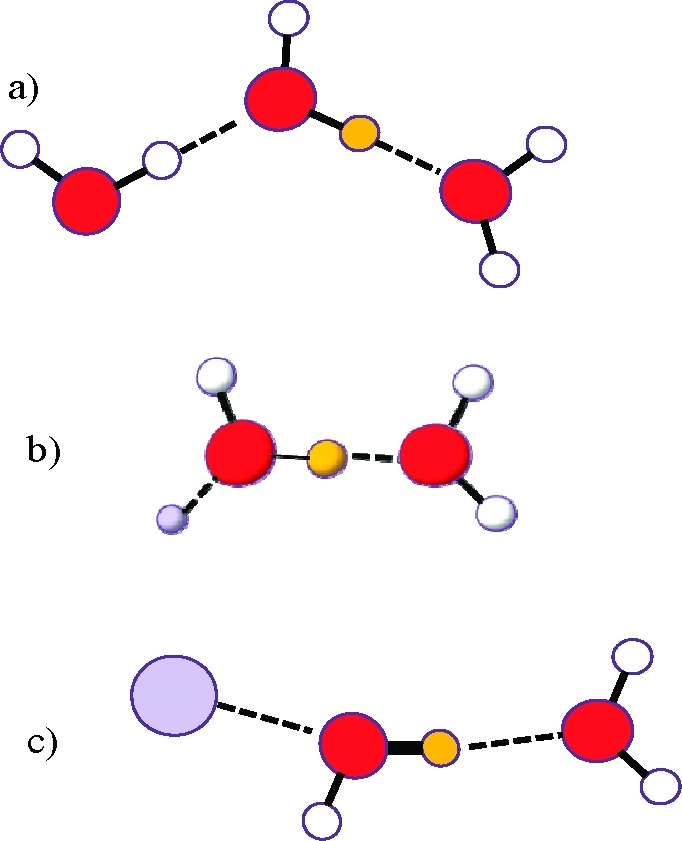
(a) HDO in bulk water, ν_O–D = 2509 cm^–1, d_{O(···D)–O} = 2.89 Å. (b) HDO affected by a structure making cation, ν_O–D < 2509 cm^–1, d_{O(···D)–O} < 2.89 Å. (c) HDO affected by a structure breaking cation, ν_O–D > 2509 cm^–1, d_{O(···D)–O} > 2.89 Å. O–D bond strength is indicated by the line thickness, and orange color represent a D atom.

Structure Databases and the Evaluation of Ionic Radii

In the search for relevant solid state structures, the databases Inorganic Crystal Structure Database³⁸ and Cambridge Crystallographic Data Centre³⁹ were used. As the collection of structures was diverse, it was found necessary to categorize them before judging their relevance. This categorization is described in Appendix 3 in the SI.

Results and Discussion

Analysis of Most Reliable Ionic Radii of the Alkali Metal Ions for Different Coordination Numbers

For the lithium and sodium ions, the available crystal structure material is sufficient for an accurate determination of the ionic radii in several configurations. In order to get a fair view of the ionic radii of the alkali metal ions it is important to select structures where the influence from lattice energies is as small as possible. Previously proposed ionic radii are based on oxide and fluoride structures,³⁷ where the close-packing of the anions is a strong driving force for their structures, while the preferred configuration of especially ions with low charge density, as the alkali metal ions, is suppressed. A number of structures of alkali metal compounds have in the present study been discarded due to repetitive measurements (R), suspicion of nonoxygen bonding (N), shackled structure (S) or failure of passing Grubbs statistical test (G), Appendix 1 in the SI. It has been assumed that structures, where the longest bond is no more than 10% longer than the shortest one, have a sufficient low constraint and are representative for a certain configuration. These structures are hereafter referred to as approved structures, and are given in Tables S1a–S1e in the SI together with considered but nonapproved structures of the various classes.

Considering the lithium ion, two groups of complexes with oxygen donor ligands have been identified as relevant: (i) neutral homoleptic hydrates, Figure 2, and (ii) complexes with neutral non-ether monodentate ligands, Figure 3. A summary for coordination numbers four and six is given in Table S4 in the SI, and the influence of data selection on average M–O bond distances is shown as well. Classification has been made in accordance with the system presented in Appendix 3 in the SI. It can be noted that the M–O distances does not differ appreciably between the 36 four-coordinated complexes, 1.942 Å, belonging to group (i) and the 80 four-coordinated complexes of the expanded group (ii),1.941 Å. By subtracting the radius of the oxygen atom in coordinated water, 1.34 Å,⁸⁰ an ionic radius of 0.60 Å is obtained for the lithium ion in four-coordination, tetrahedral fashion. The mean Li–O bond distance in four-coordinated homoleptic tetrahydrofuran solvated lithium ions is 1.918 Å. By subtracting the ionic radius of the lithium ion obtained from hydrates, the radius of the oxygen in tetrahydrofuran coordinated to an alkali metal ion is estimated to 1.32 Å for the investigated complexes, Table S1a. A large number of 1,2-dimethoxymethane solvated lithium ions has been reported in the solid state, almost all being six-coordinate in octahedral fashion. In total 75 structures with a mean Li–O bond distance of 2.134 Å remain as approved with respect to bond length distribution. In a limited number of compounds containing hydrated lithium ion in endless chains with bridging water molecules the lithium ion is six-coordinate with a mean bond distance of 2.132 Å, Table S4 in the SI and Figures 2 and 3. This gives, assuming an oxygen radius of 1.34 Å also in these oxygen donor ligands, an ionic radius of the lithium ion in octahedral configuration of 0.79 Å. This is slightly longer than reported by Shannon, 0.76 Å.³⁷

Figure 2.

Crystal structures of neutral, homoleptic, Li⁺ hydrates. The dashed line is drawn between mean values for four- and six-coordination (geometrically approved atoms). Error bars correspond to two standard deviations. The sums of the radii given by Shannon and the oxygen radius are shown as orange crosses.

Figure 3.

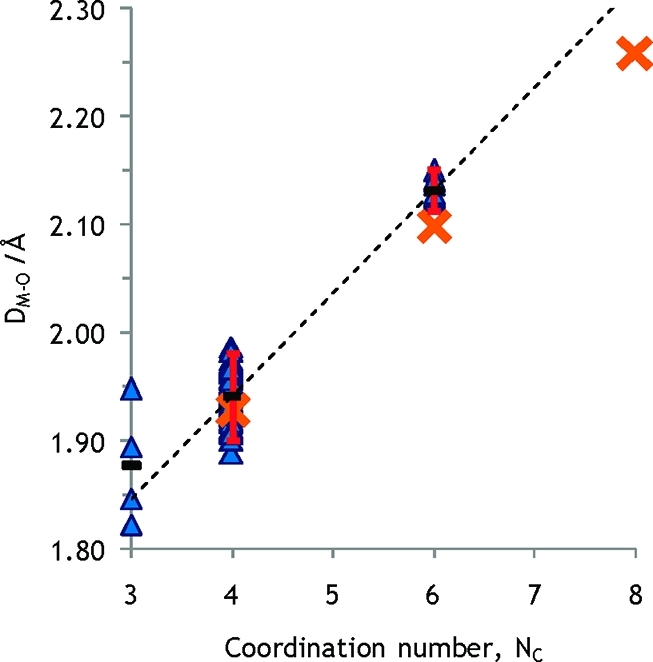
Crystal structures of neutral, monodentate non-ether Li⁺ complexes. The dashed line is drawn between mean values for four- and six-coordination (geometrically approved atoms). Error bars correspond to two standard deviations. The sums of the radii given by Shannon and the oxygen radius are shown as orange crosses.

The mean Na–O bond distance in five- and six-coordinate neutral homoleptic sodium complexes is 2.358 and 2.412 Å, respectively, Figures 4 and 5, Table S5 in the SI. This gives ionic radii of the sodium ion of 1.02 and 1.07 Å in five- and six-coordination, respectively. These ionic radii for the sodium ion are significantly larger than those proposed by Shannon.³⁷ This is probably due to large lattice effects in the oxide and fluoride compounds Shannon used in his analysis. The average Na–O distances in the THF solvates are 2.324 and 2.395 Å in five- and six-coordination respectively, and an oxygen radius for THF of 1.32 Å, as described above, gives the very same ionic radii of the sodium ion as other oxygen donor ligands.

Figure 4.

Crystal structures of neutral, homoleptic, Na⁺ hydrates. The dashed line is drawn between mean values for five- and six-coordination (geometrically approved atoms). Error bars correspond to ±2 standard deviations. The sums of the radii given by Shannon and the oxygen radius are shown as orange crosses. A green circle represents the experimental M–O distance determined by LAXS for six-coordination in this study.

Figure 5.

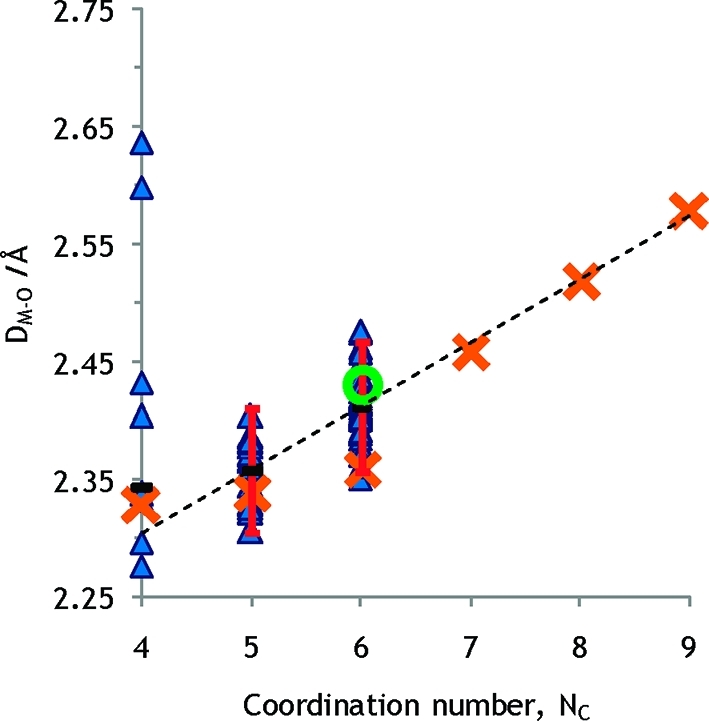
Crystal structures of neutral, non-ether, monodentate Na⁺ complexes. The dashed line is drawn between mean values for five- and six-coordination (geometrically approved atoms). Error bars correspond to ±2 standard deviations. The sums of the radii given by Shannon and the oxygen radius are shown as orange crosses. A green circle represents the experimental M–O distance determined by LAXS for six-coordination in this study.

In an attempt to follow the order of priority it was found that no relevant homoleptic hydrates was found for the potassium, rubidium and cesium ions, with the exception of the unreasonably short K–O bonding in the hexaaquapotassium dihydroxy-(2-guanidino-1-benzimidazole-N,N′)borate monohydrate.⁸¹ Therefore, it is necessary to rely on structures with less desirable features such as anionic ligands, heteroleptic complexes or multidentate ligands for the larger alkali metal ions. For the heavier alkali metal ions the lack of homoleptic hydrates is well in line with these ions' low charge density. If one would accept anionic, heteroleptic and multidentate ligands, they are still so few that it is difficult to make a proper analysis, as illustrated in Figures S2–S4 in the SI, and any safe conclusions cannot be drawn. Still, two features should be noted. First, the absence of homoleptic hydrates in the solid state underlines the weak hydration of the larger alkali metal ions. Second, the deviation from the ionic radii proposed by Shannon is noticeable. As Shannon used highly charged oxides for radius determination, the lattice energies are much stronger than M–O bond energies, and the alkali metal ions get a coordination environment controlled by close-packing and lattice energies, which has little significance at the discussion of ionic radii in a nonlattice environment as complexes in solution. Ions in an oxide matrix may have an increased or reduced size relative to the unconstrained species in solution, in order to fill available holes in a close-packed oxide matrix. Cations too large to reside in holes of a close-packed anionic matrix seek alternative arrangements, and this is the case of Rb⁺ and Cs⁺, which in fact are larger than the monatomic anions. The radius of six-coordinate K⁺ is in the same range as water oxygen and oxide oxygen, while the radius of K⁺ in seven-coordination exceeds both slightly. For six- and seven-coordinate K⁺, the radii proposed in this work are in agreement with those of Shannon,³⁷ Figures 6 and S2 in the SI. Values based on Shannon’s oxide and fluoride compounds are lower than those found in the crystal structure investigation for Rb⁺, and even more so for Cs⁺, Figures S3–S4 in the SI. This could be explained by an energetical driving force toward an equalized ionic size, suitable for stable non-close-packed crystal structures. From geometrical calculations it is found that the ratio between the radii of hypothetical hard-sphere cations and equally hypothetical hard-sphere anions must be below 0.732 for the former to fit into octahedral holes in a close-packed matrix of the latter.⁸² Deviations from this principle occur as ions are in reality not hard spheres, and that close-packing of water molecules around an ion is merely an approximation of varying validity.

Figure 6.

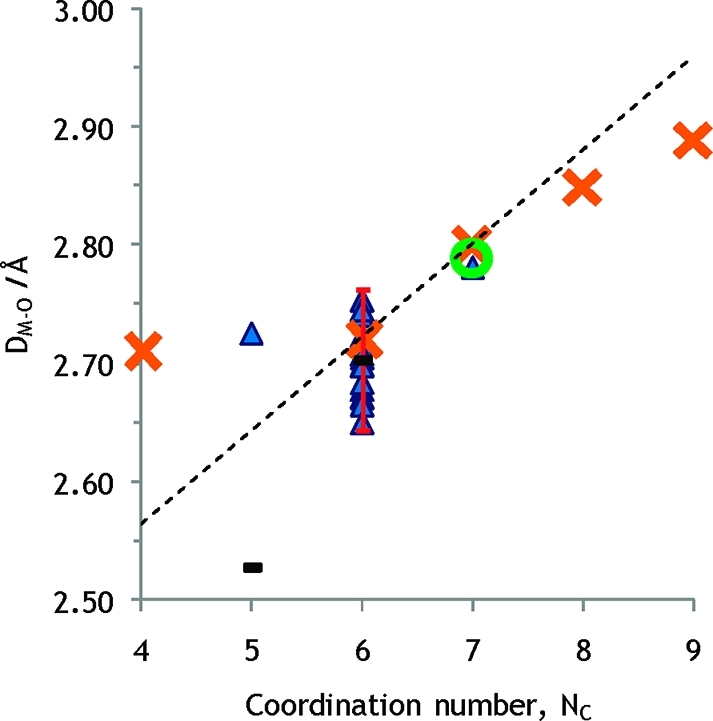
Crystal structures of potassium THF solvates. The error bar corresponds to ±2 standard deviations. The sums of the radii given by Shannon and the oxygen radius are shown as orange crosses. The dashed line is drawn 0.02 Å above average values for six- and seven-coordination in order to correct for the smaller size of THF oxygen relative to water oxygen (see text). A green circle represents the experimental M–O distance determined by LAXS for seven-coordination in this study.

Despite the objections regarding the cyclic ether tetrahydrofuran (THF) previously brought up, this compound may be useful in the study of potassium. The disadvantages found by Lundberg et al.,⁸³ concerning small highly charged hard ions, should be less severe in this study of cations with lower charge density. The mean K–O bond distance for the tetrahydrofuran solvated potassium ion in six-coordination was determined to 2.70 ± 0.06 Å (17 structures), Figure 6, Table S1c in the SI, giving an ionic radius of 1.38 Å using an oxygen radius of 1.32 Å in THF, see above. Utilizing the known radius of coordinated water oxygen radius the expected K–O bond distance for a six-coordinate hydrated potassium ion is 2.72 Å. The only crystal structure of a seven-coordinate potassium tetrahydrofuran solvate has a mean K–O bond distance of 2.78 Å, corresponding to an ionic radius of the potassium ion of 1.46 Å,⁸⁴ giving an expected K–O bond distance in a seven-coordinate potassium hydrate of about 2.80 Å. Proposed ionic radii are summarized in Table 1.

Table 1. New Proposed Ionic Radii in Å of the Alkali Metal Ions.

	4-coord	5-coord	6-coord	7-coord	8-coord
Li+	0.60		0.79
Na+		1.02	1.07
K+			1.38	1.46
Rb+					∼1.64
Cs+					∼1.73

Structure Determination of the Hydrated Alkali Metal Ions in Aqueous Solution

The radial distribution functions (RDFs) from the LAXS experiments on the aqueous sodium, potassium and cesium iodide solutions reveal two peaks, two peaks and one peak below 4 Å, see Figures 7–9. The peak or shoulder at 3.5 Å corresponds to the I–O bond distance in the hydrated iodide ion, which is full agreement with previous reports.⁸ The peak at 2.9 Å corresponds to an intermolecular O···O distance in the aqueous bulk, and to Cs–O and K–O bond distances in the hydrated cesium and potassium ions, respectively, Figures 7 and 8. The Na–O bond distance in the hydrated sodium ion is seen as a weak shoulder at ca. 2.4 Å, Figure 9. The RDF of the aqueous cesium hydroxide solution displays only one peak containing intramolecular O···O distances in the aqueous bulk, and the Cs–O bond distances in the hydrated cesium ion, Figure S5 in the SI. The obtained Na–O, K–O and Cs–O bond distances of 2.43, 2.80, and 3.07 Å, respectively, support six-, seven- and eight-coordination, respectively. These coordination numbers have been applied as fixed parameters in the final refinement of the structure parameters in the LAXS data. The refined M–O, I–O and O···O distances and the corresponding temperature factor coefficients are summarized in Table 2, and the fits of the experimental intensity functions are given in Figures 7–9 and S5 in the SI. The structure of the hydrated hydroxide ion indicates that it accepts strong hydrogen bonds from surrounding water molecules, which is in agreement with previous DDIR studies.³³

Figure 7.

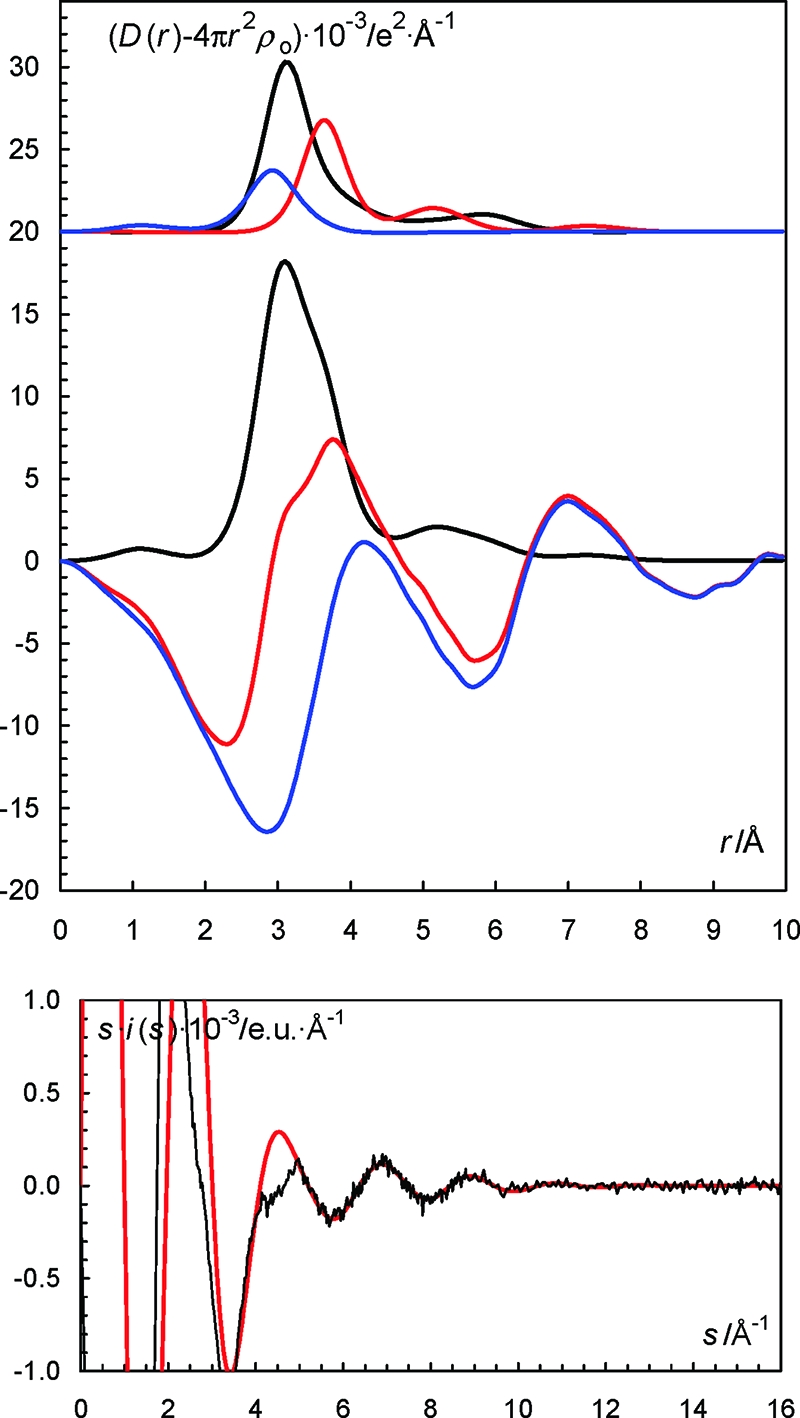
(Top) LAXS radial distribution curves for a 2.001 mol·dm^–3 aqueous solution of cesium iodide. Upper part: Separate model contributions (offset: 20) of the hydrated cesium ion (black line), the hydrated iodide ion (red line) and the aqueous bulk (blue line). (Middle) Experimental RDF: D(r) – 4πr²ρ_o (red line), sum of model contributions (black line) and the difference between experimental and calculated functions (blue line). (Bottom) Reduced LAXS intensity functions s·i(s) (solid line); model s·i_calc(s) (dashed line).

Figure 9.

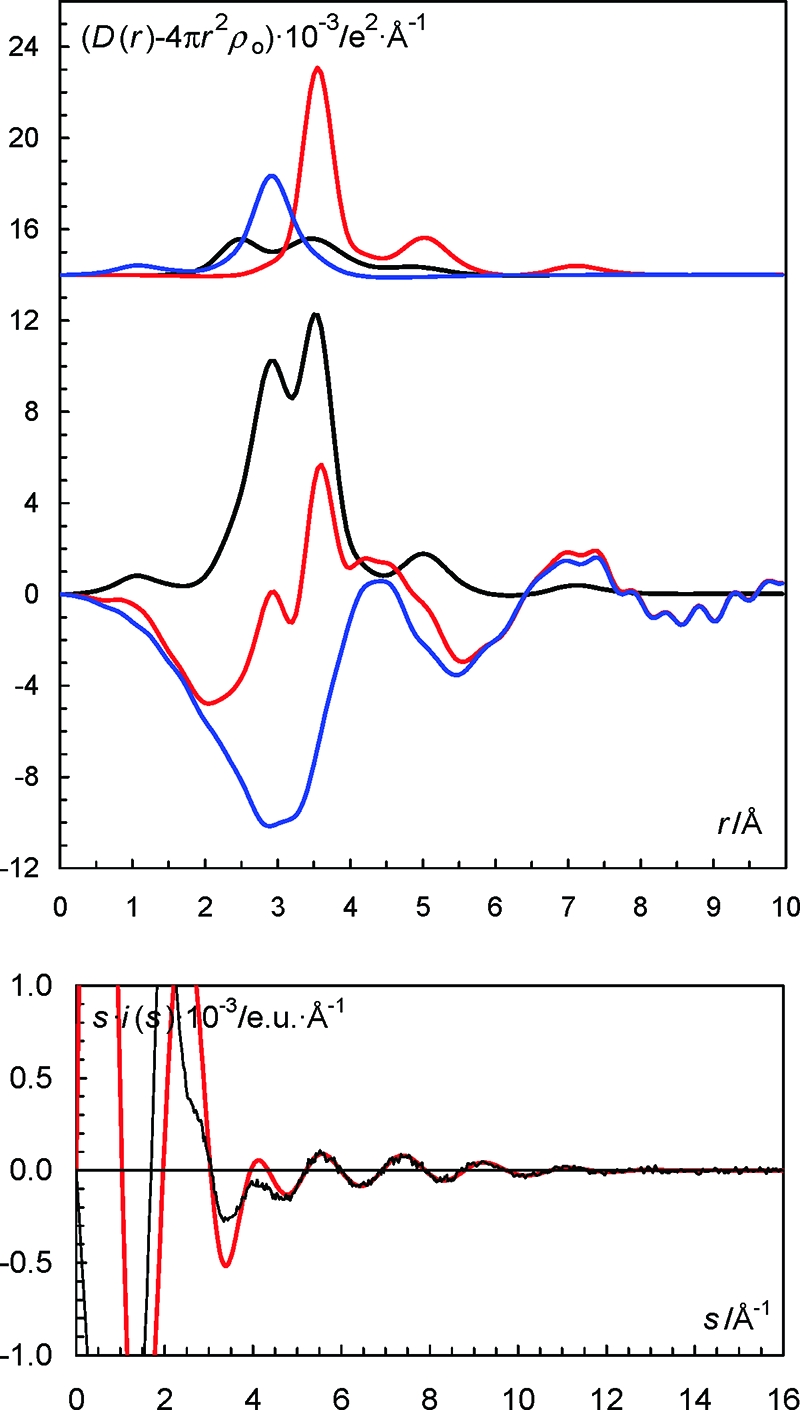
(Top) LAXS radial distribution curves for a 2.007 mol·dm^–3 aqueous solution of sodium iodide. Upper part: Separate model contributions (offset: 14) of the hydrated sodium ion (black line), the hydrated iodide ion (red line) and the aqueous bulk (blue line). (Middle) Experimental RDF: D(r) – 4πr²ρ_o (red line), sum of model contributions (black line) and the difference between experimental and calculated functions (blue line). (Bottom) Reduced LAXS intensity functions s·i(s) (solid line); model s·i_calc(s) (dashed line).

Figure 8.

(Top) LAXS radial distribution curves for a 2.007 mol·dm^–3 aqueous solution of potassium iodide. Upper part: Separate model contributions (offset: 12) of the hydrated potassium ion (black line), the hydrated iodide ion (red line) and the aqueous bulk (blue line). (Middle) Experimental RDF: D(r) – 4πr²ρ_o (red line), sum of model contributions (black line) and the difference between experimental and calculated functions (blue line). (Bottom) Reduced LAXS intensity functions s·i(s) (solid line); model s·i_calc(s) (dashed line).

Table 2. Mean Bond Distances, d/Å, Number of Distances, N, Temperature Coefficients, b/Ų, and the Half-Height Full Width, l/Å, in the LAXS Studies of the Hydrated Alkali Metal Ions in Aqueous Solution at Room Temperature.

species	interaction	N	d	b	l
Sodium Iodide in Water, 2.007 mol·dm–3
Na(OH2)6+	Na–O	6	2.43(2)	0.025(2)	0.22(1)
I– (aq)	I–O	6	3.549(9)	0.0180(8)	0.19(1)
water bulk	O···O	2	2.902(6)	0.0220(10)	0.21(1)
Potassium Iodide in Water, 2.002 mol·dm–3
K(OH2)7+	K–O	7	2.81(1)	0.027(2)	0.23(1)
I– (aq)	I–O	6	3.539(7)	0.0186(7)	0.19(1)
water bulk	O···O	2	2.889(7)	0.0219(8)	0.21(1)
Cesium Iodide in Water, 2.001 mol·dm–3
Cs(OH2)8+	Cs–O	8	3.081(1)	0.031(2)	0.25(1)
I– (aq)	I–O	6	3.555(7)	0.0191(7)	0.19(1)
water bulk	O···O	2	2.889(7)	0.0212(8)	0.21(1)
Cesium Hydoxide in Water, 1.802 mol·dm–3
Cs(OH2)8+	Cs–O	8	3.074(1)	0.031(2)	0.25(1)
OH– (aq)	O···O	5	2.73(2)	0.008(2)	0.13(1)
	O···O	1	2.95	0.0225	0.21
water bulk	O···O	2	2.898(7)	0.0202(8)	0.21(1)

Structure of the Dimethyl Sulfoxide Solvated Alkali Metal Ions in Solution

The RDFs from the LAXS experiments on the dimethyl sulfoxide solutions of sodium, potassium and cesium iodide solutions reveal three peaks or two peaks and a shoulder (potassium) respectively at 1.5, 2.4–3.0 and 3.5–4.5 Å (Figures S6–S8 in the SI). The peaks at 1.5 and 2.5 Å correspond to intramolecular S–O, S–C and O–C bond distances in dimethyl sulfoxide. The peak at 2.4–3.0 Å has also a significant contribution from the M–O bond distance in the dimethyl sulfoxide solvated alkali metal ions. The peak or shoulder in the region 3.5–4.5 Å corresponds to M···S distances. There are no peaks or shoulders in the RDF which correspond to the dimethyl sulfoxide solvated iodide ion showing that there is no well-defined structure of dimethyl sulfoxide molecules around this ion. The obtained Na–O, K–O and Cs–O bond distances of 2.43, 2.80, and 3.06 Å support six-, seven- and eight-coordination, respectively. This is consistent with the results in aqueous solution, see above. These coordination numbers have been applied as fixed parameters in the final refinement of the LAXS data. The refined M–O and M···S distances, and the corresponding temperature factor coefficients are summarized in Table 3, and the fit of the experimental intensity functions are given in Figures S6–S8 in the SI. The M–O–S bond angles of 136.3, 137.4, and 134.2° for sodium, potassium and cesium, respectively, are typical for metal ions binding to dimethyl sulfoxide through mainly electrostatic interactions.⁷³

Table 3. Mean Bond Distances, d/Å, Number of Distances, N, Temperature Coefficients, b/Ų, and the Half-Height Full Width, l/Å, in the LAXS Studies of the Dimethyl Sulfoxide Solvated Alkali Metal Ions in Solution at Room Temperature.

species	interaction	N	d	b	l
Sodium Iodide in Me2SO, 1.017 mol·dm–3
Na(OSMe2)6+	Na–O	6	2.43(2)	0.020(2)	0.20(1)
	Na···S	6	3.70(2)	0.040(2)	0.28(1)
Potassium Iodide in Me2SO, 1.017 mol·dm–3
K(OSMe2)7+	K–O	7	2.790(7)	0.0200(13)	0.200(6)
	K···S	7	4.060(8)	0.042(2)	0.29(1)
Cesium Iodide in Me2SO, 1.000 mol·dm–3
Cs(OSMe2)8+	Cs–O	8	3.061(8)	0.0234(8)	0.216(4)
	Cs···S	8	4.279(7)	0.056(2)	0.33(1)

Analysis of Bonding Characteristics of Hydrated the Alkali Metal Ions in Aqueous Solution Using Double Difference IR

The affected spectra, obtained as outlined in the Experimental Section, were obtained for NaI (N = 9.6), KI (N = 10.6), RbI (N = 8.9), CsI (N = 7.4), LiClO₄ (N = 10.3) and NaClO₄ (N = 11.6). Each spectrum can be modeled from Gaussian peaks, which are supposed to represent anion and cation affected HDO. Two peaks are required to represent the cationic contribution of NaI, LiClO₄ and NaClO₄. The affected spectra for the investigated iodide salts are given in Figure 10 and for the perchlorate salts in Figure 11, and the peak positions are summarized in Table 4.

Figure 10.

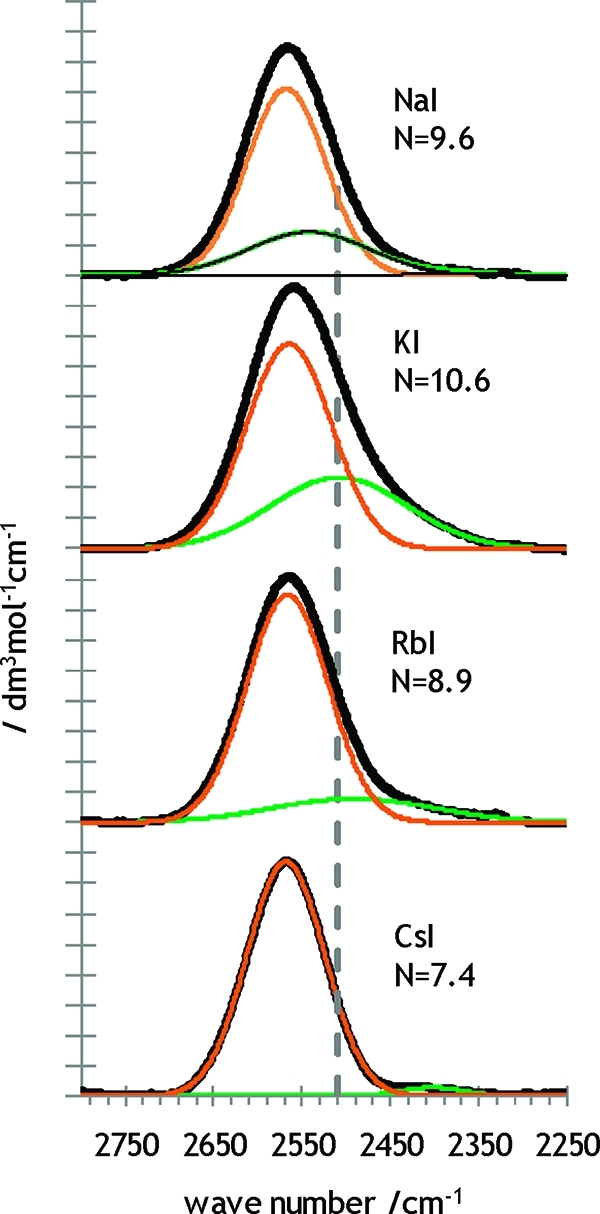
Affected spectrum for NaI(aq), KI(aq), RbI(aq) and CsI(aq). The spectrum can be divided into two main contributions, both of which are discussed in the text. The dashed line shows the position of the wavenumber 2509 cm^–1 where bulk water HDO is located.

Figure 11.

Affected spectrum for NaClO₄(aq) and LiClO₄(aq). The orange line represents the contribution from the anion (iodide) and the green line the contribution from the alkali metal cation. The dashed line shows the position of the wavenumber 2509 cm^–1 where bulk water affected HDO is located. Thin black lines show the Gaussian peaks that are combined to produce the cationic contribution.

Table 4. Affected Spectra Peaks Are Linear Combinations of Gaussian Peaks^a.

	center (cm–1)	weighted (cm–1)	assignment
CsI (N = 7.4)	2567	2567	affected spect.
	2568		I–
	2402		noise
RbI (N = 8.9)	2565	2560	affected spect.
	2566		I–
	2491		noise
KI (N = 10.6)	2559	2549	affected spect.
	2564		I–
	2508		K+/noise
NaI (N = 9.6)	2566	2563	affected spect.
	2568		I–
	2542	2539	Na+
	2542		Na+, main
	2374		Na+, assym
NaClO4(N = 11.6)	2544	2559	affected spect.
	2633		ClO4–
	2544	2540	Na+
	2544		Na+, main
	2398		Na+, assym
LiClO4(N = 10.3)	2626	2536	affected spect.
	2630		ClO4–
	2558		Li+
	2564		Li+, second shell
	2490		Li+, first shell
	2449		not explained

^aFor NaI, NaClO₄ and LiClO₄, the cationic contribution is also a linear combination of Gaussian peaks (given in italics).

The iodide peaks in Figure 10 are located at 2564–2568 cm^–1, while the perchlorate peaks in Figure 11 are found at 2630–2633 cm^–1, both in agreement with literature values.²³

In order to model the contribution of the hydrated lithium ion, using the perchlorate salt, two peaks are required. The peak at 2490 cm^–1 is assigned to the first hydration shell of Li⁺ while the higher wavenumber peak at 2564 cm^–1 is assigned to the second hydration shell. This is in line with the reasoning in Figure 1, that lower wavenumber HDO vibrations correspond to participation in stronger hydrogen bonds. The second hydration shell peak deviates from 2509 cm^–1 more than the first hydration shell peak, indicating that second hydration shell molecules participate in hydrogen bonds that are not only weaker than those of the first hydration shell but also weaker than hydrogen bonds in bulk water. This somewhat counterintuitive finding could possibly be explained by an unsatisfactory angle distribution resulting from difficulties of a hydrated lithium to fit into the network of hydrogen bonded bulk water with approximately tetrahedral bond arrangement on average. In Śmiechowski's alkali metal ion investigation³¹ an additional peak was found at around 2630 cm^–1. As this wavenumber coincides with the peak of the anion in this investigation, it is not possible to observe such a peak in this study. The authors of the previously mentioned work assigned the extra peak to the outermost IR-detectable shell of the cation. If the main peak of the lithium ion does in fact represent the second hydration shell, the interpretation of the peak at 2630 cm^–1 peak seems unlikely. It is reasonable to believe that, outside the well-defined first shell, each consecutive hydration sphere should approach the value of bulk water behavior (2509 cm^–1). A molecule in a possible third hydration shell should be more similar to bulk water than a molecule in the second hydration shell. The authors of that report consider the alternative interpretation that the main peak represents six-coordinate lithium coexisting with four-coordinate. If this is correct, their interpretation of the discovered 2630 cm^–1 band could hold true as the outermost shell would be the same as the second hydration shell. The coexisting coordination number hypothesis that the 2564 cm^–1 band would represent six-coordinate lithium does not find any support in this investigation when studying the measured spectra at different concentrations. A possible copresence of four- and six-coordinate hydrated lithium ions should result in a concentration dependent distribution with the six-coordinate hydrate species increasing in relative concentration with increasing dilution. This study shows that there is no such change in the DDIR spectra in the concentration range 0.1 to 1.0 mol·dm^–3; Figure S9 in the SI shows the difference spectra in the studies concentration range. This observation supports that the hydrated lithium ion has only one predominating configuration in the studied concentration range, tetrahedral. It shall also be emphasized that no isolated hexaaqualithium ion has been observed in the solid state, Table S1a in the SI. The actual location of the 2564 cm^–1 band deviates somewhat from previous investigations (2543 cm^–1 and 2530 cm^–1 respectively).^15,31 As the peak separation in this work is smaller than in the previous study,³¹ our results may have been affected. The results in ref (15) may have been affected by the use of asymmetric peak contributions and by the suspiciously low N value of 2.0 for the aqueous solution of lithium trifluoroacetate.

In the case of the hydrated sodium ion in perchlorate solution, the main peak is observed at 2544 cm^–1, which is in agreement with the result from the previous double difference IR study of alkali metal ions, 2543 cm^–1.³¹ It was however not possible to model the NaClO₄ spectra with only these two bands, but a third one was needed as well. This peak, located at 2398 cm^–1, will be regarded as an asymmetry contribution to the cationic peak. It would be unreasonable to take this peak for a first hydration shell, due to its low intensity and its location at much lower wavenumber than the first hydration shell of the lithium ion, which has higher charge density.

While an iodide peak can be found at the expected position, defining the cationic contribution of the iodide solutions presented in Figure 10 is not straightforward. For all ions, and especially for rubidium and cesium, the remaining part of the spectra is very small. As the sodium peak is easily recognized in the aqueous sodium perchlorate solution, Figure 11, it is reasonable to believe that the affected spectra of the sodium iodide solution, Figure 10, would be affected in a similar way. However, the separation of the alkali iodide spectra into two peaks probably does not represent anionic and cationic contribution respectively, as the supposed cationic peak has a much lower intensity than expected. Otherwise it would be tempting to interpret the spectra of the aqueous solutions of rubidium and cesium iodide as having negligible cationic contribution to the water structure. Iodide salts were chosen for the double difference IR experiments as these were the ions used in the LAXS study, but in effect, the peak separation is not sufficiently good to obtain nonoverlapping anionic and cationic peaks with these salts. On the other hand, the solubility of the perchlorate salts of these cations is too low to allow accurate measurements. Modeling the spectra with more Gaussian peaks than necessary for fitting serves no purpose but increases uncertainty markedly. Despite the setbacks of the DDIR alkali iodide experiments, from Figure 10 it can still be seen that the affected spectra of sodium, potassium, rubidium and cesium are quite similar to each other, underlining the similar hydration pattern showed by these ions. One must consider the possibility that a cation contribution with a peak shape and position similar to that of the bulk solvent could be accidentally removed in the previously mentioned water extinction process of finding the affected spectrum. Perhaps this is mostly a semantic problem since hydration shell molecules that behave like bulk water are in fact not affected.

Previous results for potassium show a cation peak location at 2541 cm^–1 with a small asymmetry contribution at lower wavelengths.³¹ Those results were obtained with the more structure breaking counterion, hexafluorophosphate, PF₆^–, and allowed for a good peak separation. While going down the group from K⁺ via Rb⁺ to Cs⁺, the affected DDIR spectrum gets narrower, consistent with the decrease in affected number of water molecules, N. To summarize the discussions above, the best lessons to be learned from the double difference IR experiments are not to be found within the differences of spectra, but in the similarities. It seems that the weak hydration behaviors among the larger alkali metal ions are quite similar, and this does not contradict the present knowledge.^6,44,65

The energetical driving force for a salt to refrain from solvation is the lattice energy of the solid phase, as well as the energetical cost of breaking interactions between solvent molecules. Working in the opposite direction is the enthalpy decrease associated with new ionic and molecular interactions between solvent and solute, and between solvent molecules. A solvation reaction, where the latter contribution exceeds the energy requirements for breaking existing bonds in the solid and the solvent, is an exothermic reaction. Endothermic reactions, in which energy released by formation of new bonds falls short of the energy required for breaking old bonds, occur spontaneously due to entropy effects. Considering the equation ΔG = ΔH – TΔS it can be seen that for an endothermic reaction (positive ΔH) the entropy change must be positive and of sufficient magnitude. Positive entropy is caused by the breakdown of a lattice but also by a decrease in the aqueous bulk order due to fewer or less well-defined hydrogen bonds. It can also be seen that if the entropy of the system decreases, representing a substantial increase in hydrogen bonding, the dissolution reaction must be sufficiently exothermic in order to occur spontaneously. This would be the case for hydration of efficient structure making ions. For weakly positive entropy changes, the amount of hydrogen bonding could either increase somewhat, in which case the lattice breakdown is responsible for the positive value, or decrease slightly. We would like to illustrate a view on structure making and breaking in Figure 12.

Figure 12.

A two-dimensional approximation of the three-dimensional hydrogen bonded network of water: (a) bulk water, (b) around a structure making ion, (c) around a structure breaking ion. The limitations associated with showing a three-dimensional network in two dimensions, such as incomplete bond illustration, have to be accepted. The effects on water structure are exaggerated in the figure.

Consider Figure 12:

• (a)In bulk water, O–H···O angles are fairly close to 180°.
• (b)The structure maker does remove water molecules from their network, but also has enough charge density to rebuild a new stronger structured network around itself. As this matrix is even more structured than bulk water, O–H···O angles are even closer to 180°. If the effect is strong enough, the ion is considered to have a second hydration shell, or even a third one. Reorientation times tend to be long as a result of the strong electrostatic interactions. One prerequisite for this behavior is that a water molecule in the close vicinity of the ion is more affected by its environment than a water molecule in bulk water. This attraction can be measured by the location of the OD stretching vibration. If located at lower wavenumbers than 2509 cm^–1, the OD oscillator is affected more than one in a bulk water HDO molecule. The molecule is affected by the ion and by neighboring water molecules in its close vicinity.
• (c)As with all particles, when the structure breaker interacts with water, the latter molecule is removed from its network. Contrary to the structure maker, the structure breaking ion does not have enough charge density to rebuild a well structured new water network around itself. As the weakly interacting structure breaking ion is competing with the surrounding hydrogen bonded network, retention times tend to be short. This situation will most certainly occur if a water molecule in the close vicinity of an ion is less affected by its environment than a water molecule in the bulk, indicated by an OD stretching vibration >2509 cm^–1.

The claim that affected spectra OD-stretching peaks >2509 cm^–1 represent hydration shell molecules which are less affected by their environment than HDO molecules in bulk water is not equivalent to saying that the hydration shell interaction is weaker than bulk water interaction. The reason is that a molecule in the bulk may be affected from more directions than a molecule in the close vicinity of an ion. This may be a reason why water molecules in the hydration shell of a sodium ion have longer reorientation times than bulk water molecules^6,16,70 even though bands in DDIR spectra of the hydrated sodium ion are located at higher wavenumbers^{15,17,18,20,30,31,33,85} than the one of bulk water (2509 cm^–1): They form stronger bonds than water molecules in the bulk but are still less affected due to geometrical limitations preventing them from forming bonds in four directions. This is the case in predominantly tetrahedral bulk water. A second hydration shell can only form with hydrated ions where the first hydration sphere is affected more by its environment than equivalent molecules in bulk water. Molecules in the first hydration shell of such an ion can affect bulk water molecules sufficiently to perturb the surrounding aqueous hydrogen bond network. Hydrated species with an affected peak above 2509 cm^–1 cannot unanimously be claimed to have weaker interactions with water than bulk water interacting with itself. However, all hydrated species with an affected spectrum below 2509 cm^–1 should interact with water more strongly than does water in the bulk, based on the following reasoning: an OD-oscillator in the hydration shell cannot have more bonding directions than the four found in an OD-oscillator in the bulk, two acceptors, one donor and the covalent bond to the H in the HDO molecule, and hence, any increased influence from the environment must be due to stronger interactions with the solute. A species such as the sodium ion may be a structure breaker even though it interacts more strongly with water than bulk water molecules interact internally. However any ion which is more affected by its environment, i.e., has an affected peak <2509 cm^–1, must be a structure maker. All such ions should have hydration shell reorientation times longer than those of bulk water molecules. It is convenient to define the borderline between structure makers and breakers for an affected spectrum peak at 2509 cm^–1, as this is a measure where the entire environmental impact is considered. The alternative definition based on the strength of the interactions with the solute normally coincides with a few exceptions, such as the sodium ion. Reorientation times are not proportional to interaction strength for highly hydrated species with several hydration shells, but should approximately be so for species where hydration occurs by weak electrostatic bonds. All discussion about structure making and breaking ions assumes sufficiently dilute solutions for bulk water to exist in reasonable amount, and is not applicable for solutions where extensive ion-pair formation exists. The effect from an ion on the solution structure could be divided into two contributions: one always occurring structure breaking action induced by the mere presence of a non-neutral particle close to the network, and one structure making action which in many cases is strong enough to reach beyond the first hydration shell in the direction along hydrogen bond axes.

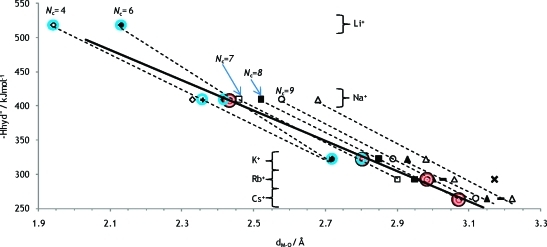
The heats of hydration have been plotted against the metal–oxygen distance, Figure 13. The heats of hydration are taken from the literature,¹¹ and the metal oxygen distances are the sum of Shannon radii,³⁷ and the water oxygen radius when bound to metal ions,⁸⁰/the three-coordinate oxide ion,³⁷ 1.34 Å, except for the cases where more reliable ionic radii have been derived, see above (Li⁺N_c 4 and 6, Na⁺N_c 5 and 6, K⁺N_c 6 and 7). The experimentally obtained values for aqueous solution are also shown in the plot. The position of the experimentally determined metal–oxygen distance can be compared with the positions of the linear regression lines for considered coordination numbers, and thereby the actual coordination number N_c can be estimated, Figure 13. It is assumed that deviation from linear dependence can be neglected. An alternative way to find the hydration number is to compare reliable crystal structure data directly with experimentally obtained values, Figures 4–6 and S2–S4 in the SI.

Figure 13.

Heats of hydration as a function of the inverse metal oxygen distance. Dashed trendlines are shown for the occurring hydration numbers 4, 6, 7, 8, 9, 10, and 12. Experimental values from this and a previous⁶¹ work are shown in red-white circles, and a possible linear relationship is shown with a solid line. Other values are based on crystal structures whereof values within blue circles are from the radii proposed in Table 1 and all other values are from Shannon radii of different coordination numbers, ref (37).

By comparing the regression lines for coordination numbers 6 and 7 in Figure 13, the experimentally obtained Na⁺–OH₂ distance gives a coordination number of 5.7. If the deviating slope of the N_c = 6 trend line is questioned, a similar comparison for N_c = 4 and 7 gives a hydration number of 6.2. The method is judged reliable enough to conclude that the hydration number for the Na⁺ ion is 6, as trend lines show a fair linear dependence. A direct comparison of the coordination number with crystal structure data, as in Figure 5, supports this conclusion with an indicated coordination number of 6.4. The same methodology for the potassium ion indicates a coordination number of 7.1 from comparing trends of heats of hydration, Figure 13, while directly comparing crystal structures in Figure 6 gives coordination number 6.9. Both methods make use of the available collection of THF solvates as well as the radius of tetrahydrofuran oxygen, 1.32 Å, as described above. As in the case of the sodium ion, the methods are judged reliable for the potassium ion as well and the coordination number 7 is proposed for the solvated K⁺ ion. The experimental value of Cs⁺ coincides with the trend line for coordination number 8, Figure 13. Crystal data is poor for the Cs⁺ ion, but the coordination number 8 is also indicated by Shannon data, Figure S4 in the SI. Hence we propose the coordination number 8 for the Cs⁺ ion. For Rb⁺ trends of enthalpy of hydration in Figure 13 suggest N_c = 8.6, but since the rubidium ion is unlikely to have a higher hydration number than the cesium ion, we suggest coordination number 8 for Rb⁺ as well. The quality of crystal structures is poor, and the hydration number of 7.1 indicated in Figure S3 in the SI can be questioned as it is based on ionic ligands. LAXS studies performed on solutions of lithium iodide and hydroxide did not give any conclusive results and are not reported in this paper. Extrapolation of a possible linear relationship for experimental data indicates a hydration number closer to 4 than 6 for the Li⁺ ion, and this is in agreement with the large number of four-coordinate crystal structures of lithium. The M–O distance value of 1.90 Å obtained by neutron scattering by Ohtomo and Arakawa⁴⁰ indicate four-coordination, Figure 3. Data obtained by X-ray scattering is considered less reliable as X-rays are scattered by electrons and Li⁺ have very few compared to the solvent. Furthermore, the relative change in radius for the alkali metal ions can be compared, and this is shown in Figure 14. A second degree function serves reasonably well to connect the proposed values for radii in aqueous solution, intersects the determined radius of four coordinated Li⁺ and extrapolates to approximately zero. We propose a coordination number of 4 for the Li⁺ ion in aqueous solution.

Figure 14.

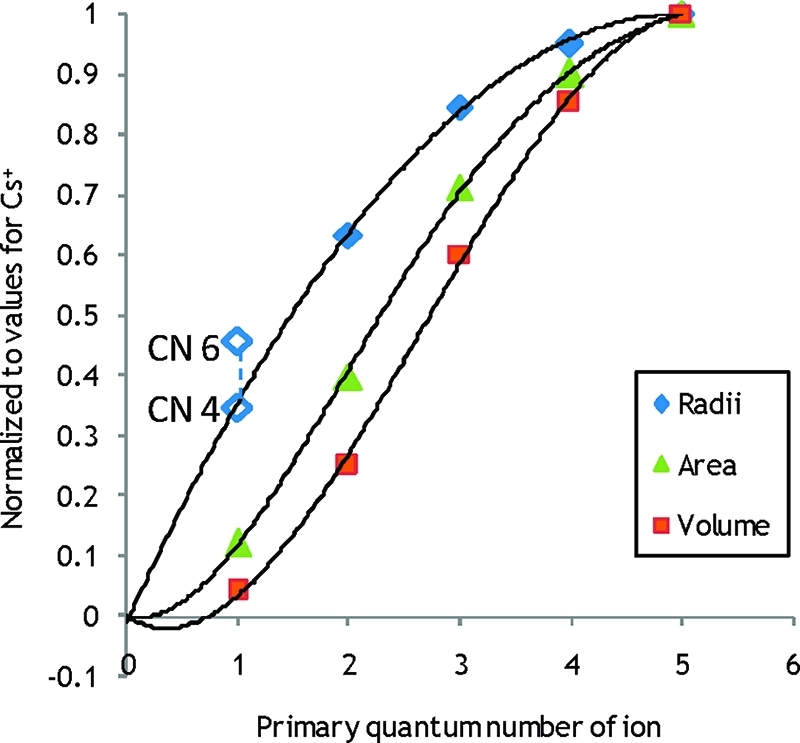
The relationship between determined ionic radii (diamonds), surface area (triangles) and volume (squares) for the alkali metal ions. Determined values for ionic radii are those proposed in this and previous papers based on experiments in aqueous solution. The radii for six- and four-coordinate Li⁺ respectively are also shown in open diamonds. Higher degree linear regression functions for volume and area have been forced through the origin while the second degree function for radii is unconstrained.

Considering Figure 14 again, it can be seen that, even while the ionic radius increase slows down considerably for the heavier alkali metal ions, the changes in volume and surface area are appreciable. Therefore the change in charge density will also be substantial.

Conclusions

A method for classification of atoms in crystal structures depending on their ligands was introduced, see Appendix 3 in the SI. It was found that the average Li–O distance in Li(H₂O)₄⁺ was 1.942 Å for 36 observed structures, and this number did not change noticeably if other neutral homo- or heteroleptic monodentate oxygen donor non-ether complexes were allowed. The Li–O distance of Li(H₂O)₆⁺ is 2.134 Å as an average for 10 observed structures. The average Na–O distance of Na(H₂O)₆⁺ is 2.415 Å as an average of 45 observed structures and does not change much when other neutral homo- or heteroleptic monodentate oxygen donor non-ether complexes are allowed. By subtracting the hydrate oxygen distance of 1.34 Å from the obtained distances, the ionic radii could be determined to 0.60 Å for the four-coordinate lithium ion and to 1.07 Å for the six-coordinate sodium ion. The latter value is well above the one proposed by Shannon.³⁷ The radius of tetrahydrofuran oxygen in the Li(THF)₄⁺ complex calculated from crystal structures was determined to 1.316 Å, and the same distance in the Na(THF)₆⁺ complex calculated from crystal structures was found to be 1.321 Å. By using the THF oxygen radius, the K–O distance of hypothetical K(H₂O)₆⁺ hydrates can be estimated to be 2.72 Å. For the only structure available an analogous calculation for the K(H₂O)₇⁺ ion has been estimated to be 2.80 Å. The actual lack of neutral hydrate crystal structures for the heavier alkali metal ions shows the weak H₂O binding abilities of K⁺, Rb⁺ and Cs⁺, and it is in line with their loosely formed hydration shells in aqueous solution.

Measurements with LAXS on solutions of alkali metal salts indicate M–O distances of 2.43 Å for Na⁺, 2.80 Å for K⁺ and 3.07 Å for Cs⁺, where the potassium value is an average from aqueous and dimethyl sulfoxide solution. The Rb–O distance has previously been determined to be 2.98 Å.⁶¹

From double difference IR, it can be seen that the affected spectra of NaClO₄ and LiClO₄ indicate a second hydration sphere for Li⁺ but not for Na⁺. It can be concluded that the hydration behavior for the heavier alkali metals is similar and there are indications that the heavier alkali ions affect surrounding water molecules too little to make them spectroscopically distinguishable. The moderately low charge density of the ions can explain their modest effect on surrounding water.

Supporting Information Available

Additional information as noted in the text. This material is available free of charge via the Internet at http://pubs.acs.org.