Abstract
The response of cone photoreceptors to light is stable and reproducible because of the exceptional regulation of the cascade of enzymatic reactions that link visual pigment (VP) excitation to the gating of cyclic GMP (cGMP)-gated ion channels (cyclic nucleotide–gated [CNG]) in the outer segment plasma membrane. Regulation is achieved in part through negative feedback control of some of these reactions by cytoplasmic free Ca2+. As part of the control process, Ca2+ regulates the phosphorylation of excited VP, the activity of guanylate cyclase, and the ligand sensitivity of the CNG ion channels. We measured photocurrents elicited by stimuli in the form of flashes, steps, and flashes superimposed on steps in voltage-clamped single bass cones isolated from striped bass retina. We also developed a computational model that comprises all the known molecular events of cone phototransduction, including all Ca-dependent controls. Constrained by available experimental data in bass cones and cone transduction biochemistry, we achieved an excellent match between experimental photocurrents and those simulated by the model. We used the model to explore the physiological role of CNG ion channel modulation. Control of CNG channel activity by both cGMP and Ca2+ causes the time course of the light-dependent currents to be faster than if only cGMP controlled their activity. Channel modulation also plays a critical role in the regulation of the light sensitivity and light adaptation of the cone photoresponse. In the absence of ion channel modulation, cone photocurrents would be unstable, oscillating during and at the offset of light stimuli.
INTRODUCTION
Cone photoreceptors in the vertebrate retina respond to light with high sensitivity over a large dynamic range. They respond to changes in luminance between darkness and the maximum radiance measured on earth’s surface under solar illumination, ∼1.6 × 109 cd/m2. At signal threshold, thoroughly dark-adapted cones respond to light flashes that excite as few as 4–12 visual pigment (VP) (cone opsin) molecules per cone, or a continuous stream of 30–60 excited VP molecules per second. Yet, they also adapt and respond to small percentage changes in intensity, even when background is a steady stream as large as 1010 excited VP/s (Burkhardt, 1994; Paupoo et al., 2000). Over the first six orders of magnitude above threshold, cones respond with constant contrast: flashes of a given intensity, measured as a percentage of the background intensity, generate the same amplitude response regardless of the absolute magnitude of the background luminance (Burkhardt, 1994; Normann and Werblin, 1974; Normann and Perlman, 1979).
The sensitivity, speed, and adaptation of the cone electrical response are stable and reproducible because of the exceptional regulation of the cascade of enzymatic reactions that couple the absorption of photons to changes in membrane current. Regulation arises both from the interaction of the enzymes of phototransduction with regulatory proteins and the effects of cytoplasmic Ca2+. In cones, Ca2+ controls the enzymatic activity of cone VP kinase (VPK) (Kawamura et al., 1996; Wada et al., 2006; Arinobu et al., 2010) and of guanylate cyclase (GC) (Lolley and Racz, 1982; Koch and Stryer, 1988; Duda et al., 1996; Baehr et al., 2007; Takemoto et al., 2009), as well as the cGMP sensitivity of the CNG ion channels (Rebrik and Korenbrot, 2004).
The regulatory function of Ca2+ in phototransduction is a feedback control mechanism because the output of phototransduction, a decrease in cytoplasmic Ca2+, influences the events that lead to the change in Ca2+ in the first place. It is a negative feedback because the output is fed back in such a way as to partially oppose the input. Signal stability is a serious challenge in the design of engineering systems that are controlled through negative feedback (Storey, 2004). Moriondo and Rispoli (2003) considered the instability (oscillations) that could occur in rod photocurrents in the absence of proper design of the regulatory Ca2+ negative feedback loop.
To better understand the highly regulated activity of the molecular events underlying transduction in cone photoreceptors, we develop and analyze a detailed computational model of this process. The pioneering mathematical modeling of phototransduction by Tranchina and Sneyd in cones (Sneyd and Tranchina, 1989; Tranchina et al., 1991) and Forti et al. (1989) in rods has been refined and renewed over time to yield contemporary computational models that, although not without controversy, have made our understanding of phototransduction more complete and exact (in rods: Pugh and Lamb, 1993; Hamer, 2000; Caruso et al., 2005; Hamer et al., 2005; Shen et al., 2010; in cones: Reingruber and Holcman, 2008; Soo et al., 2008). Here, we develop a model of cone phototransduction that explicitly includes Ca-dependent control of VP phosphorylation and CNG ion channel cGMP sensitivity, features that are not a part of previous models. The model is tested by fitting and predicting experimental photocurrents measured under voltage clamp in isolated photoreceptors. It is then used to investigate the physiological role of the Ca-dependent modulation of CNG channels; we find that CNG channel modulation is critically important to attain the time course, sensitivity, and stability characteristic of cone phototransduction.
MATERIALS AND METHODS
Materials and retinal cell dissociation
3–12-mo-old striped bass (Morone saxatilis) were received from The Center for Aquatic Biology and Aquaculture at UC Davis and maintained at 15°C in a small aquaculture facility under a 14:10 (L:D) light cycle. Animal upkeep and experimental protocols were approved by the UCSF Institutional Animal Care and Use Committee and met all requirements of the National Institutes of Health Office of Laboratory Animal Welfare and the Association for Assessment and Accreditation of Laboratory Animal Care International.
Fish were dark adapted for 30–40 min and then sacrificed in darkness. All of the following manipulations were performed under infrared (IR) illumination, aided by IR-sensitive video cameras and monitors. An eye was enucleated and hemisected, and the retina was then gently separated from the eyecup under glucose-Ringer’s solution. Square tissue pieces, ∼5 mm to a side, were recovered from the dorsal retina and incubated at room temperature for 3 min in 5 ml of glucose-Ringer’s solution containing 0.5 mg/ml of collagenase from Clostridium histolyticum and 1 mg/ml bovine hyaluronidase (Sigma-Aldrich), followed by 5 min in hyaluronidase alone. The tissue pieces were then rinsed extensively in pyruvate-Ringer’s solution to remove enzymes and exchange the glucose. They were suspended in 500 µl of pyruvate-Ringer’s solution and mechanically dissociated by teasing and tearing with fine forceps.
Voltage-clamped photocurrent recording in isolated bass single cones
The cell suspension was immediately deposited on a concanavalin A–coated glass coverslip that formed the transparent bottom of a recording chamber. The chamber was held on the stage of an inverted microscope equipped with differential interference contrast–enhancement optics and operated under IR illumination with the aid of IR-sensitive video cameras and monitors. After 10 min in darkness, the chamber was vigorously perfused with glucose-Ringer’s solution. Single and twin cones lacking their nuclear and synaptic regions (Miller and Korenbrot, 1993) remained firmly attached to the coverslip. The chamber was intermittently perfused throughout an experimental session, but not at the time photocurrents were measured.
Tight-seal electrodes were fabricated from aluminosilicate capillary glass (1.5 × 1.1 mm; 1724; Corning) and applied onto the side of the cone inner segment. After forming a giga-seal, whole cell mode was attained by sustained suction while holding membrane voltage at 0 mV. Membrane current drifted continuously toward an outward (positive) value. When this drifting ceased (5–15 s; +40 to +70 pA), holding voltage was shifted to −40 mV, where membrane current was near zero. This method yielded more stable recordings than attaining whole cell mode at −40 mV. Voltage-clamped membrane currents were measured with a patch-clamp amplifier (Axopatch 1D; Molecular Devices). Analogue signals were low-pass filtered below 50 Hz with an eight-pole Bessel filter (Frequency Devices) and digitally acquired at 1 KHz (Digidata 1322A and pClamp 9.2; Molecular Devices). All photocurrents reported and analyzed here were measured within 8 min of the moment whole cell mode was achieved.
Solutions composition
The Ringer’s solution was composed of 143 mM NaCl, 5 mM NaHCO3, 1 mM NaHPO4, 2.5 mM KCl, 1 mM CaCl2, 1 mM MgCl2, 10 mM glucose, 10 mM HEPES, and 1x MEM amino acids and vitamins, pH 7.5 (osmotic pressure of 309 mOsM). In pyruvate-Ringer’s solution, glucose was replaced with 5 mM Na pyruvate.
Tight-seal electrodes were filled with a solution composed of (in mM): 115 K gluconate, 20 K aspartate, 20 KCl, 4 MgCl2 (0.5 mM free), 1 GTPNa3, 3 ATPNa2, and 10 MOPS, pH 7.25 (osmotic pressure of 304 mOsM). The solution with all components except MgCl2 was first made free of multivalent cations by passing it over an ion exchange resin in its K+ form (Chelex 100; BioRad Laboratories). MgCl2 was then added.
Photostimulation
Two optical benches were assembled, each with narrow band interference (540 ± 5 nm) and neutral density filters to control light spectrum and intensity. Stimulation was timed with electromechanical shutters (Vincent Associates) controlled with a digital pulse generator slaved to the data acquisition system. Collimated light beams from each bench were combined in a cube beam splitter and then focused by a condenser lens assembly (0.4 numerical aperture [NA]) onto the end of a 2-mm diameter liquid light guide of similar NA. The other end of the light guide was positioned at the point source in an epi-illuminator attached to the inverted microscope. A circular aperture within the epi-illuminator was focused by the microscope objective (40×, oil, 1.3 NA; UV40; Nikon) to obtain a 40-µm diameter circle in the plane of the cells in the recording chamber. The outer segment of a cone under investigation was placed in the center of this circle. Light intensity was measured at the position of the recording chamber with a calibrated photodiode (UDT Sensors). Photon flux per unit area was converted to excited VP molecules (VP*) using 1.91 µm2 as the collecting area of the bass cone outer segment illuminated on its side with 540-nm wavelength light (Miller and Korenbrot, 1993).
Computational analysis
The system of simultaneous ordinary differential equations used to describe the molecular events of phototransduction was solved numerically using the Runge–Kutta method with integration time of 1 µs (20-Sim software v 4.2; Controllab Products BV). The software also allowed parameter optimization using the Newton–Raphson search method to reduce the difference between simulated and experimental data using Euler integral mean square error minimization. Optimized fitting of specified functions to experimental data were also executed using Origin software (version 8.1; OriginLab).
RESULTS
Photocurrents activated by flash and step photo stimulation of bass single cones
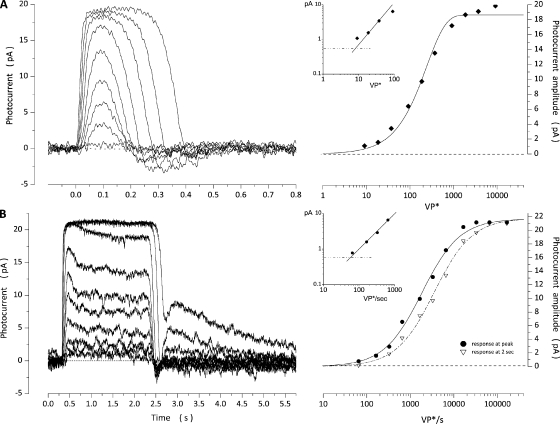
Bass single cones are large photoreceptors (outer segments are ∼15-µm long, 7 µm in diameter at their base, and 3 µm in diameter at their truncated distal end) that express a single visual pigment with peak absorbance at 542 nm (Miller and Korenbrot, 1993). Photocurrents measured at room temperature under voltage clamp in a thoroughly dark-adapted single cone in response to 10-msec flashes or 2-s light steps are illustrated in Fig. 1. Flash-elicited photocurrents reached a peak and then recovered with a distinct undershoot at the end (“off” response). Peak amplitude is a function of light intensity well described by an exponential saturation function,
| (1.1) |
where is the maximum value of the photocurrent, VP* is light intensity expressed as the number of excited VP molecules in the cell, and k is an adjustable parameter (σ = ln2k is the light intensity at which current amplitude is half its maximum value). We defined a signal threshold as the intensity that elicits a response of peak amplitude equal to twice the root mean square of the dark current noise. Mean values of , k, and signal threshold measured in 15 cones are listed in Table 1.
Figure 1.
Photocurrents measured under voltage clamp at −40 mV in a dark-adapted bass single cone in response to 10-msec flashes or 2-s steps of 540-nm light. (A) Responses elicited with flashes of intensities: 9, 18, 37, 91, 178, 372, 913, 1,933, 3,685, and 9,133 VP*. Peak amplitude increases with light intensity (right) in a manner well described by an exponential saturation function (Eq. 1.1; continuous line), with Ipeak = 18.8 pA and k = 260.1 VP*. The inset is a log–log plot to show that signal threshold was ∼8 VP*. (B) Responses elicited with step stimuli of intensities: 65, 327, 651, 1,635, 3,266, 6,513, 16,369, 65,131, and 163,687 VP*/s. The current at its peak (•) is more sensitive to light than in the stationary state (▽; right). Amplitude dependence on light intensity is well described by a Michaelis–Menten function (Eq. 1.2; continuous line), with Ipeak = 21.8 pA and σ = 1,844 VP*/s for the response at its peak, and Imax = 21.8 pA and σ = 3,522 VP*/s for the response at 2 s. The inset is a log–log plot of the peak amplitude of the step response to show that signal threshold was 56 VP*/s.
Table 1.
Light sensitivity of dark-adapted bass single cones
| Flash stimulation | Step stimulation | ||||||
| Threshold | σ | Threshold | σ at Peak | σ at 2 s | |||
| pA | VP* | VP* | pA | VP*/s | VP*/s | VP*/s | |
| Mean | 26.2 | 9.9 | 245.3 | 22.6 | 14.9 | 614.2 | 106.05 |
| SEM | 2.4 | 0.8 | 25.6 | 1.5 | 1.0 | 74.6 | 86.4 |
| Cell count (n) | 15 | 15 | 15 | 10 | 10 | 10 | 10 |
| Minimum | 16.5 | 4.6 | 101.9 | 12.4 | 11.1 | 315 | 607 |
| Maximum | 43.6 | 16.6 | 452.1 | 30 | 21.0 | 1,100 | 1,612 |
Steps of light 2 s in duration elicited photocurrents that reached an initial peak and then sagged over the next second or so to a steady-state value (Fig. 1). The steady state reached in the time scale shown, however, is only apparent; under continuing illumination, a much slower phase of current recovery follows in a time scale of tens of seconds (Perlman and Normann, 1998). At the termination of the light step, photocurrents rapidly recover and exhibit a brief “off” response. Photocurrents generated by very high intensity steps (over 104-fold above threshold) exhibit a distinct, slowly decaying rebound in the dark current after the light step ends (Fig. 1; response to 35,000 VP*/s and above). The peak and steady-state amplitudes of the step response are a function of light intensity well described by the Michaelis–Menten function,
| (1.2) |
where Imax is the maximum value of the photocurrent, VP* is the rate of excited VP molecules per second, and σ is the intensity at half-maximum response. Mean values of Ipeak, σ at the peak and in the steady state, and signal threshold for 11 cones are listed in Table 1. The photosensitivity of the cone decreases as the photocurrent sags from peak to steady state, a manifestation of light adaptation. The loss of photosensitivity is evident by the fact that the value of σ at the peak is about twice that at the stationary state (Table 1).
A model of the molecular mechanism of light transduction in bass single cones
We developed a computational model that successfully describes the outer segment dark current and its changes with flash and step illumination. The model is based on the currently known molecular events of the phototransduction cascade and is constrained, when possible, by experimental facts known specifically for the bass single cones or generalized from data for cones in other species. The model follows and refines concepts introduced in previous models of cone phototransduction (Sneyd and Tranchina, 1989; Tranchina et al., 1991; Reingruber and Holcman, 2008; Soo et al., 2008) but is novel in two major respects: (1) it develops in detail the inactivation of VP* by phosphorylation and its regulation by arrestin and Ca-dependent visinin (Kawamura, 1993; Kawamura et al., 1996), and (2) it introduces Ca-dependent modulation of ligand sensitivity in the CNG ion channels (Rebrik and Korenbrot, 1998; Rebrik et al., 2000).
Biophysical and biochemical processes in the dark
cGMP metabolic flux.
In the dark, the cytoplasmic concentration of cGMP is constant because the rates of its synthesis by GC and hydrolysis by phosphodiesterase (PDE) are the same. This unchanging nucleotide concentration determines the magnitude of the dark current.
The catalytic activity of GC and PDE in the dark in bass single cone is experimentally known (Holcman and Korenbrot, 2005):
| (2.1) |
This value was used in all simulations of dark current.
PDE activity in the dark.
The cone-specific PDE holoenzyme consists of two catalytic α subunits and two inhibitory γ subunits (PDE6; see Conti and Beavo, 2007). PDE enzymatic activity follows conventional Michaelis–Menten kinetics:
| (2.2) |
where is the PDE hydrolytic velocity, is the Michaelis–Menten constant for cGMP, is the catalytic turnover rate per active PDE molecule, is the number of active PDE molecules in the dark, and [cGMP]dark is the nucleotide concentration. To simulate dark current there is no need to independently know and because it is possible to determine experimentally the value of the parameter where
| (2.3) |
The value is known for cone PDE (Table 2) (Gillespie and Beavo, 1988; Huang et al., 2004), as is (Holcman and Korenbrot, 2005). For each cell, the dark current is measured, and from this value the concentration of cGMP in the dark can be computed (see below, Eqs. 2.5 and 2.6). Knowing these experimental quantities allows for calculation of the value of in each and every cone analyzed (Table 2).
Table 2.
Values of model parameters that best simulated dark current in bass single cones
| Parametersa | Category | Units | N | ||
| PDE | Statistical | µM/s | 6.5 ± 1.48b | 6 | |
| Km | Invariant | µM | 26c | ||
| Statistical | µM/s | 12.64 ± 0.89d | 18 | ||
| GC | Statistical | µM/s | 6.5 ± 1.48b | 6 | |
| Vmax | Invariant | µM/s | 110e | ||
| Invariant | µM | 0.1e | |||
| Invariant | 2e | ||||
| CNG ion channel | Statistical | pA | 27.3 ± 10.5 | 18 | |
| Invariant | 2.5f | ||||
| Invariant | µM | 172.3f | |||
| Dark Ca2+ influx | Statistical | µM/s | 14.2 ± 5.4g | 18 | |
| Pf | Invariant | 0.34h | |||
| Adjustable | µM | 20.9 ± 12.9i | 18 | ||
| Adjustable | µM | 0.052 ± 0.024 | 18 | ||
| B | Adjustable | 11.5 ± 3.9i | 18 | ||
| Dark Ca2+ efflux | Statistical | µM/s | 14.2 ± 5.4g | 18 | |
| Statistical | pA | 4.87 ± 1.88j | 18 | ||
| Adjustable | µM | 0.019 ± 0.009j | 18 |
Invariant parameters are taken from the literature, and their values are held constant in all cells and all simulations of dark and photocurrents. “Statistical” are parameters measured experimentally in each and every cone analyzed. “Adjustable” parameters are arrived at by optimized fit of simulated to experimental data and are constrained, when possible, by data in the literature. The values in this table are the mean ± SD.
Experimental data (Holcman and Korenbrot, 2005).
Experimental data (Huang et al., 2004).
Experimental data calculated in each cell from its measured dark current (and hence dark cGMP concentration), PDE Km, and dark PDE activity. See Eqs. 2.2 and 2.3.
Experimental data in carp cones (Takemoto et al., 2009), but calcium dependence as measured in rods (Koch and Stryer, 1988).
Experimental data (Picones and Korenbrot, 1992; Rebrik et al., 2000).
Computed from Eq. 2.8 since dark current is measured. Vcos is 0.19 pL, about one half of the geometrical outer segment volume. The outer segment is a truncated cone of approximate dimensions: base diameter, 7.5 µm; tip diameter, 3.5 µm; length, 17 µm (Miller and Korenbrot, 1993). Ca2+ influx and efflux are the same in the dark.
Experimental data (Ohyama et al., 2000).
Experimental values in aequorin-loaded rods are estimated to be CHA = 24 µM and B =10 (Lagnado et al., 1992).
The time constant of Ca2+ clearance from the bass cone outer segment determined from simulations with these values is 40.0 ± 15.4 msec, comparable to the experimental value of 43 ± 9.8 msec measured in the tiger salamander cone (Sampath et al., 1999). Time constant is the time it takes to reduce cytoplasmic free Ca2+ from 0.4 to 0.147 µM (1/e).
GC activity in the dark.
GC is a membrane-bound enzyme (GC-E and GC-F; Pugh et al., 1997; Koch et al., 2002, 2010), whose activity is controlled by Ca2+ concentration as mediated by the Ca2+-binding proteins GCAP1 and GCAP2 (Dizhoor et al., 1995; Gorczyca et al., 1995; Kachi et al., 1999; Koch, 2002; Baehr et al., 2007). The biochemical activity of GC in fish cones has been recently characterized (Takemoto et al., 2009), but we define its Ca dependence from biochemical studies of rod outer segments because cone GCAP is lost from the isolated fish cone outer segments (Takemoto et al., 2009). Electrophysiological studies in bass single cones suggest that the Ca2+ dependence of GC activity in these cells is similar to that in rods (Miller and Korenbrot, 1994):
| (2.4) |
where is the GC catalytic velocity in darkness, is the maximum catalytic activity, is the cytoplasmic free Ca2+ concentration in the dark, is the Ca2+ concentration at which the enzyme activity is half its maximum value, and is a dimensionless parameter that denotes cooperativity. The values of and are known experimentally (Table 2) (Koch and Stryer, 1988; Takemoto et al., 2009).
CNG ion channel activity.
The amplitude of the outer segment current is determined by the activity of cGMP-gated (CNG) ion channels and is given by:
| (2.5) |
where is the outer segment membrane current, is the maximum cGMP-dependent outer segment current, ∼2,500 pA in bass cones at −40 mV (Rebrik et al., 2000), [cGMP] is cGMP concentration, and nCNG is a dimensionless parameter that denotes cooperativity. In bass single cones, nCNG = 2.5 and the value of is Ca dependent (Picones and Korenbrot, 1992; Rebrik and Korenbrot, 1998; Rebrik et al., 2000):
| (2.6) |
where and are minimum and maximum values of Ca is cytoplasmic free Ca2+ concentration, and is the Ca2+ concentration at which
On average in bass single cones, the values of and are 105.5 and 316 µM, respectively, and = 0.86 µM (Rebrik and Korenbrot, 1998; Rebrik et al., 2000).
We assigned = 0.4 µM based on experimental measurements in tiger salamander cones (Sampath et al., 1999). Under this assignment, we used Eqs. 2.5 and 2.6 to compute free cGMP in each cone from its measured dark current (Table 2).
Ca2+ ionic flux.
It has long been established that Ca2+ ions flow into the photoreceptor outer segment via the CNG ion channels and flow out via Na+/Ca2+,K+ exchangers (Yau and Nakatani, 1985; Miller and Korenbrot, 1987). In the dark, Ca2+ influx and efflux are identical, and the outer segment free Ca2+ concentration is constant.
| (2.7) |
Dark Ca2+ influx.
Ca2+ ion influx, (µM/sec), is a constant fraction of the inward outer segment current at all voltages (Ohyama et al., 2002) and is given by:
| (2.8) |
where I (pA) is the membrane current, is the fraction of the current carried by Ca2+, z is the Ca2+ valence, F is Faraday’s constant, is the outer segment cytoplasmic volume, and is the cytoplasmic Ca2+-buffering capacity, defined below. The values = 0.34 and = 0.19 pL for the bass single cone are known from experimental determinations (Miller and Korenbrot, 1993; Ohyama et al., 2000). Dark Ca2+ influx is computed from Eq. 2.8 with current, I, set at the value of the dark current.
Dark Ca2+ efflux.
Ca2+ ion efflux, (µM/sec) depends on free cytoplasmic Ca2+ and is given by:
| (2.9) |
where (in pA) is the maximum exchanger-mediated efflux, and other terms are the same as in Eq. 2.8. The term in the square parenthesis is the Ca2+ dependence of the Na+/Ca2+,K+ exchanger transport rate, where Ca is free cytoplasmic Ca2+ in the dark and is the Ca2+ concentration at which the transport rate is half its maximum value (Sheng et al., 2000).
Because we measured the dark current in every cell we studied, we could calculate the magnitude of Ca2+ dark influx (Eq. 2.8) and, therefore, know Ca2+ dark efflux (Eq. 2.9). Assigning Ca = 0.4 µM in darkness (Sampath et al., 1999) allowed us to adjust the values of and (Tables 3–5). Although these two values are indeterminate if dark current alone is simulated, requiring that the same values simulate dark and photocurrents in the same photoreceptor constrained their values.
Table 3.
Values of model parameters that best simulated photocurrents in dark-adapted bass single cones: Response to 10-msec light flashes
| Parameters | Categorya | Units | Cone 1 | Cone 2 | Cone 3 | Mean ± SDb | ||||
| VP* | Intensity | Statistical | VP* | 167 | 17,443 | 174 | 17,136 | 173 | 7,720 | Fig. 4 |
| Adjustable | µM/s | 100c | 65 | 100 | 70 | 105 | 68 | |||
| Invariant | 1/s | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | — | ||
| Invariant | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | — | |||
| T* | Adjustable | 230d | 230d | 215 | 215 | 230 | 230 | 231 ± 19 | ||
| Invariant | 0.69e | 0.69e | 0.69e | 0.69e | 0.69e | 0.69e | — | |||
| PDE* | Adjustable | µM/s per molecule | 0.185 | 0.185 | 0.323 | 0.323 | 0.416 | 0.416 | 0.334 ± 0.091f | |
| Adjustable | 1/s | 17g | 47 | 7 | 19 | 14 | 28 | Fig. 4 | ||
| CNG ion channel | Statistical | pA | 22.2 | 22.2 | 18.8 | 18.8 | 42.3 | 42.3 | 27.3 ± 10.5 | |
| Ca2+ buffer | Adjustable | µM | 0.030 | 0.030 | 0.044 | 0.044 | 0.091 | 0.091 | 0.052 ± 0.025 | |
| Adjustable | µM | 21.4 | 21.4 | 4.6 | 4.6 | 66 | 66 | 20.9 ± 12.9 | ||
| B | Adjustable | 10.6 | 10.6 | 7 | 7 | 15 | 15 | 11.5 ± 3.9 | ||
| Ca2+ efflux | Statistical | pA | 4 | 4 | 3.23 | 3.23 | 7.63 | 7.63 | 4.87 ±1.88h | |
| Adjustable | µM | 0.025 | 0.025 | 0.005 | 0.005 | 0.025 | 0.025 | 0.019 ± 0.009h | ||
Values of invariant parameters first used to compute dark current are not repeated here. They have the same values listed in Table 2.
Mean ± SD; n = 18 single cones.
experimental value is 100–150 s−1 (Tachibanaki et al., 2005).
This value was initially constrained to 150 s−1 from experimental data (Leskov et al., 2000).
Experimental data (Gibson et al., 2000).
Experimental values of PDE* range from 2.2 to 8 × 103 s−1 (Dumke et al., 1994; D’Amours and Cote, 1999; Muradov et al., 2009). From the definition of (Eq. 3.11) and the highest value, the 0.334 value indicates the effective intracellular volume for cGMP is, on average, 0.08 pL, rather than the 0.19 pL used throughout these calculations. This factor of approximately two can probably be accounted for by the fact that the volume, in fact, changes some from cell to cell and is not the rigid assigned value of 0.19 pL. There is experimental uncertainty because the size of each and every cone recorded from was not measured. Also, the actual concentration of cGMP may be a little smaller than the computed value because there is intracellular cGMP binding (Olson and Pugh, 1993), a fact that would be revealed as a smaller apparent volume.
This value was initially constrained to 10 s−1 at dim lights from the analysis of dark current noise in bass single cones (Holcman and Korenbrot, 2005).
With these values, the computed time constant of Ca2+ clearance from bass cone outer segment is 40.0 ± 15.4 msec, similar to the experimental value of 43 ± 9.8 msec in the tiger salamander cone (Sampath et al, 1999).
Table 5.
Values of model parameters that best simulate photocurrents in dark-adapted bass single cones: Response to 2-s steps of light
| Parameter | Categorya | Units | Cone 4 | Mean ± SD | |||
| VP* | VP*/s | Statistical | VP*/s | 50 | 1,975 | 41,466 | Fig. 7 |
| Adjustable | µM/s | 95 | 95 | 40 | |||
| T* | Adjustable | 1/s | 250 | 250 | 250 | 237 ± 31 | |
| PDE* | Adjustable | µM/s per molecule | 0.239 | 0.239 | 0.239 | e0.366 ± 0.101 | |
| Adjustable | 1/s | 2.7 | 2.8 | — | Fig. 7 | ||
| 1/s | — | 7.8 | 55 | ||||
| 1/s | — | 10 | — | ||||
| Ca2+ influx | Adjustable | µM | 0.12 | 0.12 | 0.12 | 0.085 ± 0.024 | |
| Adjustable | µM | 31.4 | 31.4 | 31.4 | 26.4 ± 9.3 | ||
| B | Adjustable | 15 | 15 | 15 | 11 ± 3.3 | ||
| Ca2+ efflux | Statistical | pA | 3.89 | 3.89 | 3.89 | 3.96 ± 0.9 | |
| Adjustable | µM | 0.030 | 0.030 | 0.030 | 0.025 ± 0.006 | ||
Mean ± SD; n = 10 cones.
Values of invariant parameters first used to compute dark and flash photocurrents are not repeated here. They have the same values listed in Table 2.
Cytoplasmic Ca2+ buffer.
The molecular identity and physiological characteristics of the cone outer segment Ca2+ buffer are unknown, but studies in rod outer segments suggest that there exist two instantaneous buffer systems: one of high affinity and low capacity that operates below 1 µM free Ca2+, and another of low affinity and high capacity that operates at higher Ca2+ levels (Lagnado et al., 1992). Assuming that similar Ca2+ buffers exist in the cone outer segment cytoplasm, and following Lagnado et al. (1992):
| (2.10) |
where is the total exchangeable (bound) Ca2+, is the total capacity (concentration) of a high affinity buffer of Michaelis–Menten constant and B is the buffer capacity of the low affinity buffer.
Ca2+-buffering capacity, the ratio of bound to free Ca2+, in photoreceptor outer segments is not constant but changes with Ca2+ concentration. To calculate the Ca dependent Ca2+ buffer capacity, the derivative of Eq. 2.10, is computed (Berlin et al., 1994; Neher, 1995):
| (2.11) |
Simulations were very sensitive to the values of and To constrain these parameters, we assigned an initial value of 20 µM and B = 10, consistent with those measured in rods. We adjusted the value of to optimally fit simulated to experimental dark and photocurrents using a computer-aided least-square minimization search method (Raphson–Newton; tolerance, 0.001). We demanded the same optimized values of these parameters fit dark and light–dependent currents in the same cell. Mean values of these parameters arrived at by optimized fit of simulated to experimental membrane currents are listed in Tables 2–5.
Biophysical and biochemical processes in the light
Kinetics of VP activation and inactivation.
Photon absorption generates an active state of cone VP, VP*, one that interacts with the G protein transducin to initiate the phototransduction process (Hofmann et al., 2009).
VP* inactivates because it is phosphorylated, a process catalyzed by the activity of a cone-specific kinase (G protein–coupled receptor kinase 7; VPK; Hisatomi et al., 1998; Rinner et al., 2005; Tachibanaki et al., 2005). The time course of VP* inactivation is complex because VPK catalytic rate depends on the state of VP* phosphorylation: the rate of phosphorylation of additional sites depends on the number of sites already phosphorylated. The number of physiologically relevant VP* phosphorylation sites is controversial, as few as 2 and as many as 16. Hamer et al. (2005) have made a persuasive argument that six is a reasonable number for rhodopsin, which we have adopted. Kennedy et al. (2004) have demonstrated that light causes phosphorylation of up to five different sites per cone VP molecule in vivo.
The catalytic activity of VPK is regulated by its interaction with two different proteins: (1) arrestin, which quenches VP* lifetime by binding phosphorylated VP* and precluding further G protein activation (Craft and Whitmore, 1995; Gurevich and Gurevich, 2006; Nikonov et al., 2008); and (2) visinin (recoverin in rods), a Ca-binding protein that mediates Ca-dependent regulation of VPK activity (Kawamura, 1993; Kawamura et al., 1996).
VPK adds phosphates one at a time at a rate of which depends on the number of phosphorylated sites. Each phosphorylated state of VP* is identified as where When = 6, VP* is inactive. Arrestin binds to phosphorylated VP* with a rate and quenches the ability of VP* to activate transducin. Therefore, the rate of change in the number of VP* molecules with phosphorylated sites is given by:
| (3.1) |
| (3.2) |
| (3.3) |
where Phot(t) is the number of VP* molecules produced by stimulus photons, is the rate of phosphorylation of VP* with phosphorylated sites, and is the rate of arrestin-dependent quenching of VP*.
The rate of VP* phosphorylation decreases exponentially as the number of phosphorylated sites increases:
| (3.4) |
where is a constant. is assumed to increase linearly with the number of phosphorylated sites :
| (3.5) |
The Ca2+ dependence of cone VP* phosphorylation rate was taken to be the same as that of the rhodopsin kinase (our fit to the descriptive data) (Kawamura, 1993):
| (3.6) |
where is the maximum possible value of this rate, and = 0.9 µM.
cGMP metabolic flux
Time course of light-activated PDE activity.
VP* interacts with the G protein transducin and generates T*, an activated form of the G protein. The rate of T* creation is given by the encounter frequency between VP* and transducin in the plane of the membrane, a feature limited by the diffusion of the colliding molecules (Lamb, 1996). is a rate gain that specifies the number of T molecules activated per second by one VP*, a value that changes with the number of phosphorylated sites in VP* (Gibson et al., 2000). The affinity between of VP* and T declines exponentially with approximately twofold decrease per phosphorylation. Thus,
| (3.7) |
where, again, is the number of phosphorylated sites, between 0 and 6, and = 0.69 is the rate of exponential decay, an experimentally known value (Gibson et al., 2000) (Table 3).
T* activates PDE with a 1:1 stoichiometry (Leskov et al., 2000) to produce PDE*. PDE* inactivates at a rate Therefore,
| (3.8) |
T* disappears at a rate that is commonly thought to be the rate of GTP hydrolysis by GTPase activity inherent to Tα-GTP. This is not the case in rod photoreceptors. Disappearance of T* requires the interaction of Tα-GTP with several other proteins: RGS9, R9AP, Gβ5L, and γPDE (Wensel, 2008). Recent analysis has shown that the kinetics of this multi-molecular interaction is well represented by a simple “Michaelis module” in which the multiprotein complex behaves as though a single protein, “RGS9,” interacts with T*; the rate of formation of this T*–RGS9 complex is slower than the rate of GTP hydrolysis (Burns and Pugh, 2009). In such a scheme, then, the αPDE term of Eq. 3.8 is the rate of interaction of the RGS9 complex with T*, not the rate of GTP hydrolysis. An important consequence of this scheme is that the value of αPDE becomes dependent on RGS9 concentration, an experimental fact (Krispel et al., 2006).
Light-dependent changes in cytoplasmic free Ca2+ and the enhancement of GC activity.
Cytoplasmic free Ca2+ changes when its rate of influx is different than its rate of efflux (Yau and Nakatani, 1985; Miller and Korenbrot, 1987). Therefore, the light-dependent rate of change in Ca2+ concentration is given by the difference of Eqs. 2.8 and 2.9, as membrane current, I(t), changes with light:
| (3.9) |
Integration of Eq. 3.9 yields the magnitude and time course of light-dependent changes in free Ca2+ concentration. Light-dependent changes in GC activity simply track the changes in Ca2+ concentration, as defined in Eq. 2.4.
Time course of light-dependent changes in cytoplasmic cGMP concentration.
The light-dependent rate of cGMP hydrolysis is determined by PDE* catalytic activity, where:
| (3.10) |
PDE* is the number of active PDE (the integral of Eq. 3.8), is the nucleotide concentration, is the PDE Michaelis–Menten constant for cGMP, and
| (3.11) |
is used because PDE* is in units of number of molecules, is the enzymatic turnover rate per active PDE, and 2 reflects the fact that an active PDE* is a dimer. L is Avogadro’s number, and Vcos is the cone outer segment cytoplasmic volume. In simulations, the value of is adjusted.
In the course of the photoresponse, GC activity changes with time because cytoplasmic Ca2+ changes (the integral of Eq. 3.9):
| (3.12) |
The net rate of change of cGMP in the course of a light-elicited response is:
| (3.13) |
cGMP-gated, Ca-modulated membrane current.
Integration of Eq. 3.13 yields the time course of light-dependent changes in cGMP. The simultaneous changes in Ca2+ and cGMP concentration are then used to compute the light-dependent changes in membrane current (Eqs. 2.5 and 2.6).
Optimized fit of model simulations to experimental data
Selection of parametric values.
To fit simulated to experimental data, we divided model parameters into three categories: invariant, statistical, and adjustable. “Invariant” parameters were selected from the available literature, and their values were kept the same for all cells and all simulations. “Statistical” parameters were experimentally measured in the cell under analysis. “Adjustable” parameters were adjusted to optimize the fit between simulated and experimental currents in each cell under study. Adjustments were made with computer assistance to fit simulated to experimental data by least-square minimization (Raphson–Newton; tolerance, 0.001).
The values of adjustable parameters were not arbitrary; their initial values were constrained, whenever possible, by experimentally known values available for bass single cones specifically or from biochemical studies of cone phototransduction. Values of adjustable parameters are presented in Tables 2–5, and footnotes quote the constraining experimental values. Simulations were particularly sensitive to the following adjustable parameters: (a) The features of the Na+/Ca2+,K+ exchanger transport, and constrained by demanding their value be the same in the dark and the light for the same cell. Furthermore, their values in the dark were constrained in each cell because the dark Ca2+ efflux was known (from the dark current; Eqs 2.7 and 2.8), and cytoplasmic free Ca2+ in the dark was set at 0.4 µM (Sampath et al., 1999; Leung et al., 2007). (b) The features of cytoplasmic Ca2+ buffers, and constrained by demanding their value be the same in the dark and the light, and their initial values consistent with data available for Ca2+ buffering in rod outer segments (Lagnado et al., 1992). Furthermore, the values were constrained by the need to simulate the dark current measured in each cell with free Ca2+ set at 0.4 µM (Sampath et al., 1999). (c) the maximum rate of Ca-dependent VP* phosphorylation, with initial value 100 s−1 from measurements of VPK activity in fish cone outer segments (Tachibanaki et al., 2005). (d) αPDE, the rate of PDE* inactivation with initial value 10 s−1 from measurements of bass cone outer segment dark current noise (Holcman and Korenbrot, 2005).
Both VP* phosphorylation () and PDE* inactivation () contribute to the control PDE* lifetime, and there is no a priori mathematical argument to decide whether one is slower than the other and, therefore, the dominant rate constant that controls the duration of the photoresponse (Burns and Pugh, 2010). However, certain experimental facts are known for cones: (a) is 5–15 s−1 at dim lights, inferred from dark current noise (Holcman and Korenbrot, 2005), much slower than (100–150 s−1) measured biochemically (Tachibanaki et al., 2005). (b) is the dominant rate constant that controls photocurrent duration at high light levels that saturate cone photocurrent amplitude and above, as demonstrated by electrophysiological experiments (Matthews and Sampath, 2010). (c) At light levels that bleach 0.1% of the VP and above, cone photocurrent duration is controlled by the rate of decay of the cone-opsin photoproduct MetaII, shown by electrophysiological measurements combined with VP chromophore substitution experiments (Estevez et al., 2009). Because of this evidence, we adopted the postulate that at intensities below photocurrent amplitude saturation, was constant and only the value of was adjustable, whereas for intensities at and above amplitude saturation, was constant and only was adjustable. This hypothesis on the dual control of PDE* lifetime was not only consistent with available information but also proved critical for successful photocurrent simulations, as shown below.
Responses of dark-adapted cones to light flashes
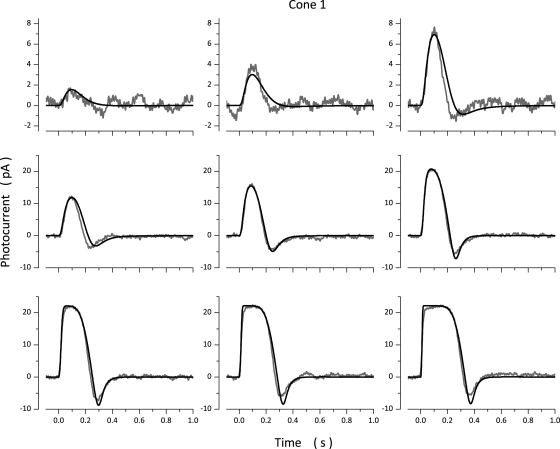
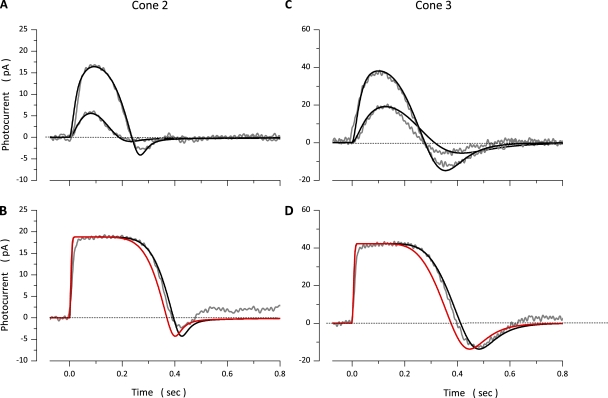
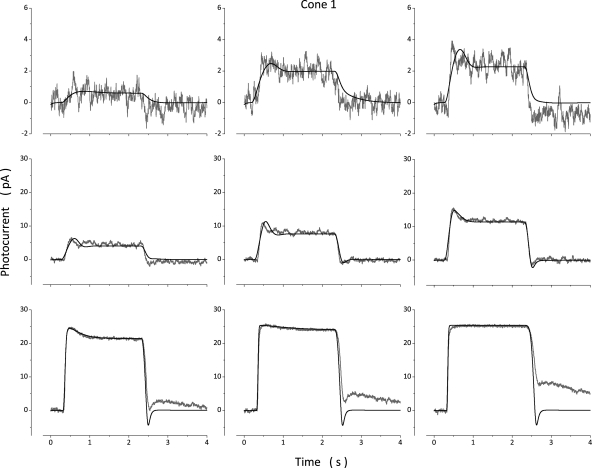
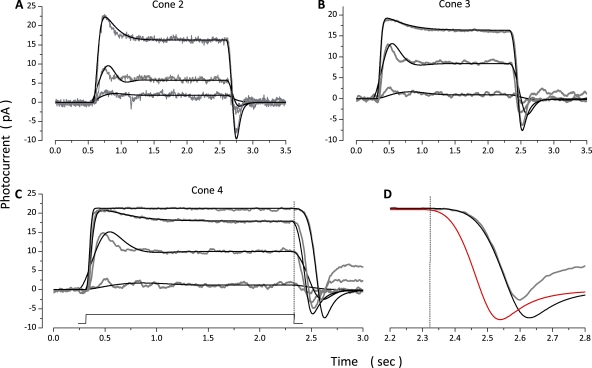
Photocurrents measured in a bass cone in response to 10-msec light flashes of varying intensity and simulated currents optimally fit to the experimental data are illustrated in Fig. 2. Values of the model parameters used in these computation are presented in Table 3 (Cone 1). Simulated photocurrents fit experimental data well, except they did not fit the small exponential component observed as photocurrent amplitude approached saturation. This component is generated by the electrogenic activity of the Na+/Ca2+,K+ exchanger (Nakatani and Yau, 1989; Perry and McNaughton, 1991), and the model does not specifically include simulation of this active transport system. To report the range of quality of fit between model and experimental data, Fig. 3 illustrates experimental and simulated data for two additional cones. Table 3 lists parametric values corresponding to simulations in Fig. 3, as well as the mean ± SD of values determined in a total of 18 cones.
Figure 2.
Experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents measured at −40 mV in a dark-adapted bass single cone. Photocurrents were elicited by 10-msec light flashes of intensity: 36, 71, 167, 356, 710, 1,744, 3,561, 7,106, and 17,443 VP*. The values of the parameters used to compute the simulated data are listed in Table 3 (Cone 1).
Figure 3.
Experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents measured at −40 mV in two different dark-adapted bass single cones. Data in A and B were measured in the same photoreceptor. Flash intensities tested were 174 and 1,747 VP* in A and 17,743 VP* in B. C and D were measured in the same cell. Flash intensities tested were 173 and 808 VP* in C and 7,720 VP* in D. The values of the parameters used to compute the simulated data are listed in Table 3. At intensities above amplitude saturation (B and D), simulations fit experimental data only if the VP* inactivation rate, was slower than for dim light responses (Table 3). The simulations illustrated in red were obtained when was kept at the same value used to fit the dim light responses.
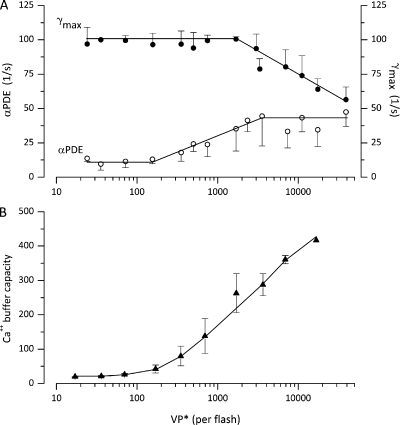
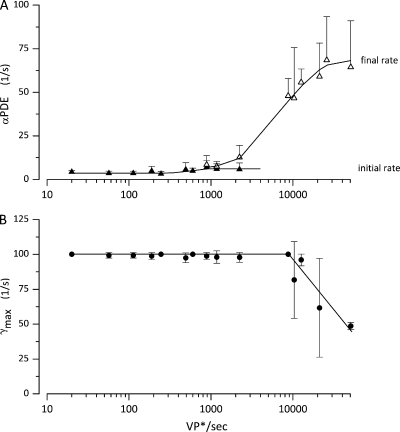
The values of the parameters and were found to be light dependent. Their mean value as a function of intensity arrived at by successful simulations in 18 cones is shown in Fig. 4 B. At all intensities below amplitude saturation, ∼2,000 VP* PDE inactivation, was the dominant rate constant in control of photocurrent duration. Its value changes little over the first ∼500 VP* and then rises up to a maximum value, where it remains over all intensities tested. At intensities above amplitude saturation, the rate of VP* inactivation by phosphorylation becomes the dominant rate constant. As is illustrated in Fig. 3 (B and D), simulations fit experimental data only if the value of was assigned a rate-limiting role and adjusted. If the value of was not adjusted, but kept at the value used to fit non-saturated photocurrents, simulations failed to fit experimental photoresponses (Fig. 3, B and D, red lines).
Figure 4.
Light dependence of the values of adjustable parameters inferred from successful simulations of flash photocurrents. Data points are the mean ± SD of values computed in 18 single cones. The light intensity shown on the graph is the mean of intensities binned within about plus or minus 10% of the mean. (A) PDE* inactivation rate () and VP* phosphorylation rate (). (B) Ca2+-buffering capacity ( Eq. 2.11). Continuous lines are drawn by eye to join the data points.
It is possible to adjust to fit the experimental photocurrents over all intensities tested. However, this would yield a biphasic dependence of on light, at first increasing with light intensity and then decreasing as the stimulus becomes brighter. Such biphasic behavior seems unreasonable and without a basis of fact. Thus, the hypothesis that PDE* lifetime is controlled by a dual mechanism, the rate of PDE inactivation at low intensities and VP* inactivation by phosphorylation at intensities above amplitude saturation, is consistent with experimental findings in other cones (Matthews and Sampath, 2010) and allows for successful simulation of experimental photocurrents in bass cones.
The Na+ /Ca2+,K+ exchanger transport rate determines the velocity at which Ca2+ is cleared from the outer segment when all light-sensitive channels are suddenly closed (Miller and Korenbrot, 1987). Experiments show the Ca2+ clearance time constant in tiger salamander cone outer segments is 43 ± 9.8 msec (±SD; n = 25) (Sampath et al., 1999). The Ca2+ clearance time constant computed from simulations using optimally adjusted values of and (Tables 2–5) is 40 ± 15.5.5 msec (±SD; n = 18), in good agreement with experiments.
Based on experimental findings in rods (Lagnado et al., 1992), we assumed the existence of both high and low affinity Ca2+ buffers. The features of this buffer system, its capacity and dissociation constant, were arrived at by computer-aided optimal fit of simulated to experimental data, constrained by the experimental values reported for rod outer segments (Tables 2–5) (Lagnado et al., 1992). Ca2+ buffer capacity is a function of Ca2+ (Eqs. 2.10 and 2.11), and because Ca2+ changes with light, buffer capacity is also light dependent. To illustrate this dependency, we measured the simulated free Ca2+ at the peak of the photocurrent at each intensity and calculated buffer capacity using the mean values of B, and in Table 2. Buffer capacity, increases with light intensity (Fig. 4), and its value is consistent with measurements of this quantity in many other cells, where values range between 40 and 480 (Neher, 1995).
Responses of dark-adapted cones to steps of light
In rods, photocurrents elicited by steps of dim lights are the temporal summation of individual dim flash responses (Baylor, 1987). Similarly, cone photocurrents elicited by light steps under ∼600–800 VP*/s (near the σ value of the initial peak of the step response) are well simulated by the temporal sum of dim flash photocurrents. Fig. 5 shows simulated and experimental voltage-clamped photocurrents measured in one dark-adapted single cone in response to 2-s light steps of varying intensity. Responses to stimuli under 1,177 VP*/s were well fit by simulations with the same parametric values (Table 4, Cone 1) inferred from the simulation of flash photocurrents in the very same cone. The sum of dim light flash photocurrents did not simulate the responses to light steps brighter than 1,177 VP*/s.
Figure 5.
Experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents measured at −40 mV in a dark-adapted bass single cone. Photocurrents were elicited with 2-s light steps of intensity: 21, 61, 120, 246, 601, 1,177, 12,614, 25,873, and 50,681 VP*/s. The values of the parameters used in the simulations shown are listed in Table 4 (Cone 1).
Table 4.
Values of model parameters that best simulate photocurrents in dark-adapted bass single cones: Response to 2-s steps of light
| Parameter | Categorya | Units | Cone 1 | Cone 2 | Cone 3 | |||||||
| VP* | Intensity | Statistical | VP*/s | 61 | 1,177 | 25,872 | 171 | 773 | 35,236 | 50 | 1,975 | 41,466 |
| Adjustable | µM/s | 100b | 100 | 90 | 100 | 100 | 63 | 100 | 100 | 55 | ||
| T* | Adjustable | 1/s | 250c | 250c | 250c | 250 | 250 | 250 | 220 | 220 | 220 | |
| PDE* | Adjustable | µM/s per molecule | 0.439d | 0.439d | 0.439d | 0.347 | 0.347 | 0.347 | 0.317 | 0.317 | 0.317 | |
| Adjustable | 1/s | 5e | 6.5 | 2 | 9 | 10 | — | 3 | 5 | — | ||
| 1/s | — | 9 | 97 | — | — | 55 | — | 8.4 | 42 | |||
| 1/s | — | 9 | 2 | — | — | — | — | 11 | — | |||
| Ca2+ influx | Adjustable | µM | 0.073 | 0.073 | 0.073 | 0.052 | 0.052 | 0.052 | 0.098 | 0.098 | 0.098 | |
| Adjustable | µM | 21.1 | 21.1 | 21.1 | 28.2 | 28.2 | 28.2 | 30.8 | 30.8 | 30.8 | ||
| B | Adjustable | 11.3 | 11.3 | 11.3 | 10 | 10 | 10 | 15 | 15 | 15 | ||
| Ca2+ efflux | Statistical | pA | 4.59 | 4.59 | 4.59 | 5 | 5 | 5 | 3.56 | 3.56 | 3.56 | |
| Adjustable | µM | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | ||
Values of invariant parameters first used to compute dark and flash photocurrents are not repeated here. They have the same values listed in Table 2.
experimental value is 100–150 s−1 (Tachibanaki et al., 2005).
This value was initially constrained to 150 s−1 from experimental data (Leskov et al., 2000).
Experimental values of PDE* range from 2.2 to 8 × 103 s−1 (Dumke et al., 1994; D’Amours and Cote, 1999; Muradov et al., 2009). From the definition of (Eq. 3.11) and the highest value, the mean value 0.334 (Table 5) indicates that the effective intracellular volume for cGMP is, on average, 0.08 pL, rather than the 0.19 pL used throughout these calculations. This factor of approximately two can probably be accounted for by the fact that the volume, in fact, changes some from cell to cell and is not the rigid assigned value of 0.19 pL. There is experimental uncertainty because the size of each and every cone recorded from was not measured. Also, the actual concentration of cGMP may be a little smaller than the computed value because there is intracellular cGMP binding (Olson and Pugh, 1993), a fact that would be revealed as a smaller apparent volume.
This value was initially constrained to 10 s−1 at dim lights from the analysis of dark current noise in bass single cones (Holcman and Korenbrot, 2005).
The need to evoke additional molecular processes to explain the sag in the step response from a peak to a stationary value was first recognized by Forti et al. (1989) in rods. They proposed that the sag arises from time-dependent changes in the concentration of a Ca2+-binding buffering molecule. This mechanism is improbable because it predicts light-dependent changes in cytoplasmic Ca2+ that are far different from what is observed experimentally. Nikonov et al. (2000) demonstrated that the sag in rods likely arises from a time-dependent increase in the PDE* inactivation rate. In cones, on the other hand, Soo et al. (2008) did not propose an a priori biochemical hypothesis to explain the sag in the step response; rather, they used simulations and found an optimal fit of simulated to experimental step responses by allowing an increase in PDE* inactivation rate (just as in rods), as well as changes in the Ca dependence of GC activity and the Na+/Ca2+,K+ exchanger transport rate.
In our simulation, in agreement with Nikonov et al. (2000), we assumed that when summation of dim light responses fails to fit experimental step photocurrents and up to intensities that saturate current amplitude, there is a time-dependent increase in PDE inactivation rate. Simulations successfully fit experimental photocurrents (Fig. 5) under the assumption that accelerates from an initial value to a final value along an exponential time course. Thus:
| (3.14) |
where is the exponential rate of change.
To report the range of quality of fit between model and experimental data, Fig. 6 illustrates a set of experimental and simulated currents measured in three additional photoreceptors, each stimulated at intensities just above threshold, near the σ value for the steady-state amplitude and near amplitude saturation. Tables 4 and 5 list parametric values corresponding to simulations in Figs. 5 and 6, as well as the mean ± SD of values determined in a total of 10 cones.
Figure 6.
Experimental (gray traces, noisy) and simulated (black traces, noiseless) step photocurrents measured at −40 mV in three different dark-adapted bass single cones. (A) Intensities tested were 171, 773, and 8,770 VP*/s. (B) Intensities tested were 50, 963, and 10,320 VP*/s. (C) Intensities tested were 50, 963, 10,320, and 41,466 VP*/s. The values of the parameters used in the simulations shown are listed in Table 4. (D) A time-expanded view of the end of the response to 41,466 VP*/s shown in C. At this intensity, photocurrent amplitude was saturated. The unsuccessful simulations illustrated in red were computed when was kept at the same value used to fit the responses to dim stimuli.
Increasing the intensity of light steps beyond that which saturates photocurrent amplitude prolongs the response duration, even though the stimulus duration is unchanged (Fig. 6 C). To simulate step photocurrents beyond amplitude saturation, we adjusted while keeping constant at its highest value. Fig. 6 D is a time-expanded view of the end of the amplitude-saturated step response in Fig. 6 C. Shown are simulated photocurrents that fit experimental data well by adjusting (Fig. 6 D, black traces), as well as a simulation that fails to fit the experimental data (Fig. 6 D, red trace) because was kept at the same value used to successfully fit the response to dim light steps. Thus, just as postulated in simulations of flash photocurrents, the rate-limiting reaction that controls PDE* lifetime changes from PDE* inactivation () to VP* phosphorylation () as a function of light is imperative to successfully match simulated to experimental photocurrents.
Under the assumptions detailed above, we successfully simulated step photocurrents elicited by intensities between 10 and ∼5 × 104 VP*/s, the intensity range tested here. The light dependence of the rates of PDE inactivation and VP* phosphorylation inferred from simulations in 10 cones is illustrated in Fig. 7 (A and B). Both and are light-independent at dim intensities. Above ∼1,000 VP*/s, increases exponentially from an initial value up to a final . is constant for all intensities below amplitude saturation; above that intensity, good fits were obtained keeping at its largest final value and progressively reducing
Figure 7.
Light dependence of the values of adjustable parameters inferred from successful simulations of step photocurrents. Data points are the mean ± SD of values computed in 10 single cones. The light intensity shown on the graph is the mean of intensities binned within plus or minus 10% of the mean. (A) Initial and final values of PDE* inactivation rate ( and Eq. 3.14). (B) VP* phosphorylation rate (). The continuous lines are drawn by eye to join the data points.
Examination of Figs. 5 and 6 shows that simulations failed to fit the large rebound in current observed in the dark after the end of very bright light steps (greater than ≈25,000 VP*/s). Hamer (2000; Hamer et al., 2005) succeeded in simulating a similar rebound in the dark observed in amphibian rods by assuming there is a back reaction that converts excited VP* back to VP, as first proposed by Forti et al. (1989). It is also possible that the light-like response in the dark at the end of very bright steps arises from the ability of bleached VP to activate the phototransduction cascade but with much lower efficiency than photo-excited VP*, a phenomenon proposed by Matthews et al. (1996) and referred to as “bleaching adaptation.” We do not find evidence to support or deny either hypothesis in bass cones, and, once photocurrents are saturated, simulations cannot be used to explore VP*, PDE*, or GC dynamics because changes in cGMP are no longer reflected by CNG channel activity.
Challenging the cone phototransduction model: Predicting the response to flashes superimposed on light steps
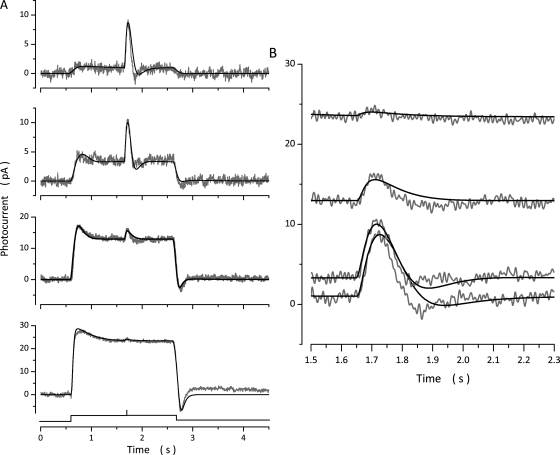
We tested the simulation model by its ability to predict experimental data. We investigated light adaptation, the observation that the response to a constant intensity flash superimposed on a light step becomes smaller and faster as the intensity of the step increases (Fig. 8). The flash responses are light adapted because, although small, they are larger than predicted from the light dependence of the amplitude of flash photocurrents measured in the same cone when it is thoroughly dark adapted. We first fit simulated currents to the responses elicited by the light steps alone, and then used the model to predict the response to a flash of the same intensity as the experimental one (Fig. 8 A). Fig. 8 B aligns the predicted and measured flash-elicited responses at various levels of background light intensity. There is good match between predicted and observed flash photocurrents at each of the various states of light adaptation tested.
Figure 8.
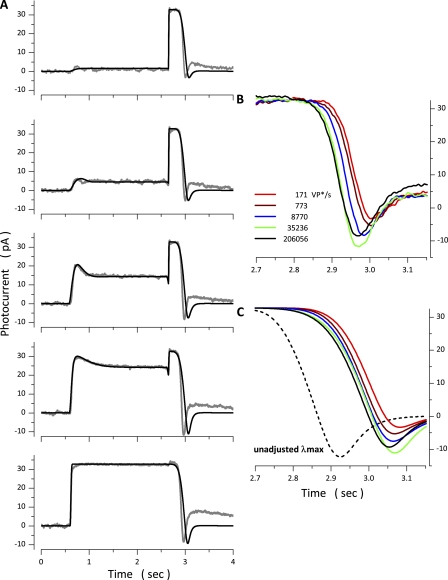
Experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents elicited by the same intensity flash superimposed on light steps of varying intensity. (A) Photocurrents generated by a 150-VP* flash delivered 1 s after the onset of light steps of intensities: 171, 773, 8,770, and 35,236 VP*/s. (B) Time-expanded view of the response to the constant intensity flash. Flash photocurrent on 171 VP*/s background was 7.3 pA in peak amplitude, 80 msec time to peak. On 773 VP*/s background it was 6.5 pA in peak amplitude, 77 msec time to peak. On 8,770 VP*/s background it was 2.9 pA in peak amplitude, 73 msec time to peak. On 35,236 VP*/s background it was 0.9 pA in peak amplitude, 63 msec time to peak.
We further tested the model by challenging its ability to match the response to a constant, bright flash presented at the end of step stimuli of varying intensity. Although the intensity of the bright test flash was constant and sufficient to saturate the photocurrent amplitude, the duration of the response to the flash shortened as the intensity of the conditioning light step increased (Fig. 9 A). The paradoxical observation that the duration of the flash-elicited photocurrent shortens as the step intensity increases reproduces similar observations by Matthews and Sampath (2010) in tiger salamander cones.
Figure 9.
Experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents elicited by the same intensity flash superimposed on light steps of varying intensity. (A) Photocurrents generated by the same flash, one that saturated photocurrent amplitude, delivered at the end of 2.5-s light steps of intensities: 171, 773, 8,770, 35,236, and 206,056 VP*/s. (B and C) Time-expanded views of experimental and simulated photocurrents, respectively. Shown are the ends of the saturated flash responses recorded at various step intensities, as labeled. Successful flash simulations were obtained by adjusting the value of from 90 s−1 during the step response to 90 s−1 at 171 VP*/s, 90 s−1 at 773 VP*/s, 52 s−1 at 8,770 VP*/s, 28 s−1 at 33,265 VP*/s, and 30 s−1 at 206,056 VP*/s. The dashed black line in C is the simulated response on a background of 206,056 VP*/s computed without adjusting keeping its value the same as that used to simulate the step response.
The simulation model successfully fit the paradoxical findings. Fig. 9 A presents simulated photocurrents optimally fit to the experimental photocurrents. Various experimental tests led Matthews and Sampath (2010) to propose that the rate-limiting reaction that controls the duration of the bright flash response is VP* inactivation (quenching). In agreement, we found that simulations fit experimental data only by assigning VP* phosphorylation a rate-limiting role and adjusting the value of during the flash response as a function of the intensity of the light step. Fig. 9 B illustrates the ends of the photocurrents activated by the same bright flash superimposed on the various light steps. The figure offers a time-expanded view to better illustrate the shortening of the flash-response duration as the step intensity increases. Fig. 9 C presents superimposed, time-expanded views of the ends of the simulated flash response that best fits the experimental data at each step intensity tested (the same data as in Fig. 9 A). The value of that fit the step responses was the same at all intensities. The simulated data shown as continuous traces in Fig. 9 C were computed by adjusting for the flash response at each step intensity. If is not adjusted but simply kept at the value used to compute the step response, simulations do not fit the experimental data (for example, dashed line in Fig. 8 C). The absolute need to adjust the value to simulate the experimental results affirms that the dominant rate constant that controls response duration at intensities that saturate photocurrent amplitude and up to ∼5 × 104 VP*/s (the range explored here) is the Ca-dependent rate of VP* inactivation by phosphorylation.
Computational gene knockout: The functional role of cone CNG ion channel modulation
The molecular model of cone phototransduction detailed here incorporates Ca-dependent modulation of the cGMP sensitivity of ion channels that sustain the photocurrent. The quantitative features of this modulation are known in detail in bass single cones (Rebrik and Korenbrot, 1998; Rebrik et al., 2000), as is the identity of a novel soluble Ca2+-binding protein named CNG-modulin that mediates this effect (unpublished data). The specific physiological role of channel modulation in the phototransduction process, however, is unknown. We investigated what this role might possibly be by examining with photocurrent simulations the consequence of deleting channel modulation, what might be called “computational gene knockout.”
We will refer to the model detailed above as “complete” and as “CNG channel modulation-minus” the model in all equations identical to the complete one, except Ca-dependent channel modulation is omitted by replacing Eqs. 2.5 and 2.6 by a single equation (Eq. 2.5) with unchanging KcGMP =172 µM, the value correspondent to Ca2+ = 0.4 µM. Figs. 10 and 11 show side-by-side comparisons of current simulations computed with the complete and the CNG channel modulation-minus models in response to flash or step stimuli of varying intensity. In each figure, the left panels illustrate simulations computed with the complete model, and the right panels illustrate those computed with the CNG channel modulation-minus one. Similar effects were observed in all other sets of experiment/computational data tested.
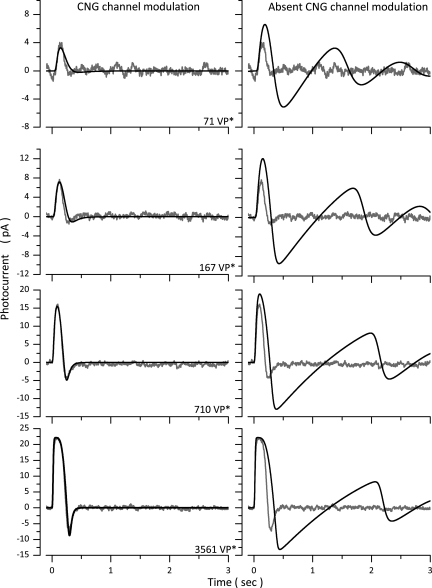
Figure 10.
The physiological role of Ca-dependent CNG channel modulation in flash photocurrents. Experimental photocurrents were measured at −40 mV in a dark-adapted bass single cone in response to 10-msec flashes of intensities: 71, 167, 710, and 3,561 VP*. The panels on the left illustrate experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents computed with the normal complete model (Table 3, Cone 1). The panels on the right reproduce the same experimental data (gray traces, noisy), now superimposed by simulated photocurrents (black traces, noiseless) computed with a model in which CNG channel modulation is omitted.
Figure 11.
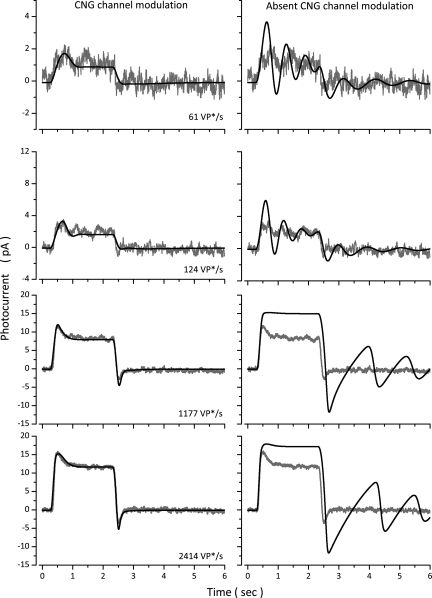
The physiological role of Ca-dependent CNG channel modulation in step photocurrents. Experimental photocurrents were measured in a dark-adapted bass single cone in response to steps of 61, 124, 1,177, and 2,414 VP*. The panels on the left illustrate experimental (gray traces, noisy) and simulated (black traces, noiseless) photocurrents computed with the normal complete model (Table 4, Cone 1). The panels on the right reproduce the same experimental data (gray traces, noisy), now superimposed by simulated photocurrents (black, noiseless traces) computed with a model in which CNG channel modulation is omitted.
The flash photocurrents and simulated data shown in Fig. 10 are a subset of the data measured in cone 1 of Fig. 2. In the absence of CNG channel modulation, the initial rate of rise of flash photocurrents is hardly affected because VP* and PDE* activation are not Ca dependent. But photocurrent peak sensitivity is enhanced and its time integral increased, and the “off” response is much larger in amplitude and the first one in a sequence of dampened oscillations at the end of the response at all light intensities.
Increased photosensitivity and oscillations in the photocurrent are experimentally observed when Ca2+-buffering molecules (BAPTA, for example) are loaded into the cone cytoplasm (Matthews et al., 1990; Holcman and Korenbrot, 2005), but the effects of deleting CNG modulation are not simply the same as those of “enhanced” buffering: Buffering prolongs response duration to a much larger extent than does deleting channel modulation, and the oscillations at “off” are much smaller than those anticipated by neglecting CNG channel modulation. It stands to reason that attenuating light-dependent changes in cytoplasmic Ca2+ by BAPTA would have overlapping effects with those anticipated when channel feedback is deleted; buffers attenuate by reducing the magnitude of Ca2+ concentration changes, whereas deleting the channel attenuates by removing a target of Ca2+ effect. Moreover, Ca2+ buffers affect more than channel modulation; they also affect the other Ca-dependent reactions in the phototransduction cascade (VP* phosphorylation and GC activity). Hence, buffers can affect functional features not affected when channel modulation is deleted.
The step photocurrent and simulated data shown in Fig. 11 are a subset of data measured in yet another cone, not illustrated in prior figures. In the absence of CNG modulation, the photocurrent initial rate of rise is hardly changed. More remarkable, the step response becomes much less stable. At dim light steps, prominent dampened oscillations are anticipated both during and after the light step. At brighter light steps, photocurrents are more light sensitive at both their peak and steady state, and light adaptation is compromised, as gauged by the lessened sag from peak to steady state. In summary, Ca-dependent CNG channel modulation in cones introduces a critical regulatory function, a quality control function, which assures that the complex sequence of chemical reactions underlying phototransduction yield the desired speed, light sensitivity, and light-adaptation features, and operate with great stability.
DISCUSSION
Mathematical models offer a succinct and precise expression of the state of understanding of a given physiological process at the time the model is developed. We present here new experimental data along with an explanatory model of cone phototransduction that expands prior cone transduction models to include explicit characterization of Ca-dependent VP phosphorylation and Ca-dependent CNG channel sensitivity modulation. Using the model, we simulate bass cone photocurrents elicited by light flashes, steps, and flashes superimposed on steps and fit the experimental results well.
We measured photocurrents in isolated bass single cones using tight-seal electrodes in the whole cell mode. Two technical details merit highlighting. First, this is the first study we know of to measure photocurrents elicited by light flashes, steps, and flashes superimposed on steps in the same cone under voltage clamp using tight-seal electrodes. This is important because in the absence of voltage clamp, the temporal dynamics of photocurrents measured in large cone outer segments are distorted because of the large membrane capacitance (in the range between 65 and 100 pF) (Miller and Korenbrot, 1993). Second, there is a serious disadvantage in the use of tight-seal electrodes in the whole cell mode because small-sized, soluble cytoplasmic molecules are lost by diffusion into the electrode lumen, and the cytoplasmic ionic composition may be different than in the intact cell, including the features of the cytoplasmic Ca2+ buffer. Indeed, in previous studies of bass single cones, we have noted the change in photocurrent kinetics upon attaining whole cell mode (Miller and Korenbrot, 1993) and the slow loss of Ca-dependent CNG ion channel modulation, which we attributed to the diffusion loss of the modulator molecule (Rebrik and Korenbrot, 1998, 2004). We mitigated this problem by limiting data reported here to photocurrents measured within the first 7–8 min after attaining whole cell mode, an interval over which photoresponse kinetics are stable and reproducible, although they can change thereafter.
The model makes explicit assumptions about the features of intracellular Ca2+ buffers in cone outer segments, about which very little is actually known. Two different models have been used previously to simulate the buffer in photoreceptors. The first one, most frequently used, assumes that buffer molecules bind Ca2+ instantaneously in the time scale of events in phototransduction, and the buffer is simply characterized by its capacity, the ratio of bound/free Ca2+ (Miller and Korenbrot, 1994; Soo et al., 2008). We found this assumption inadequate in the simulations reported here because it does not allow for time-dependent changes in buffer capacity. The second model was introduced by Forti et al. (1989) and assumes that buffering capacity is time dependent because Ca2+-binding molecules become available in a time-dependent manner. This model was developed to explain the sag in the step response of rod photoreceptors and has been extensively applied by Hamer and coworkers in their studies of rod phototransduction (Hamer, 2000; Hamer et al., 2005). Under this assumption, optimal fit of simulated data to experimental data in rods predicts that light causes rapid decreases in cytoplasmic free Ca2+, 50% of which are completed within tens of milliseconds from light onset. But this predicted fast component is not observed in experimental measurements in rods (Ratto et al., 1988; Gray-Keller and Detwiler, 1994) or cones (Sampath et al., 1999; Leung et al., 2007). For this reason, we elected not to adopt this assumption.
The model we adopted allows time dependency because the buffer capacity is not constant but a function of free Ca2+; buffer capacity changes in time as Ca2+ concentration changes. The quantitative features of a high affinity buffer inferred from simulations are close to values experimentally measured in other cells, including rods (Lagnado et al., 1992; Neher and Augustine, 1992; Berlin et al., 1994; Schwiening and Thomas, 1996; Xu et al., 1997; Trafford et al., 1999). The adequacy of the values of Ca2+-buffering parameters arrived at by simulation is best justified by the fact that the rate of Ca2+ clearance from bass cone outer segments, the time to reduce Ca2+ by 1/e when all CNG channels are closed by light, is, on average, 40 msec in simulations, essentially the same value measured experimentally (Sampath et al., 1999).
The duration of the photoresponse in cones is determined by the lifetime of light-excited PDE*, a feature dominated by the rate constant of one of three molecular events, depending on stimulus intensity: PDE* inactivation (), VP* inactivation by Ca-dependent phosphorylation (), and the rate of decay of the cone opsin photoproduct MetaII. The only hypothesis that allowed for successful simulation of all patterns of stimulation (flash, step, and flash superimposed on step) and all intensities postulates that the dominant rate constant that controls PDE* lifetime changes with light intensity: it is at intensities below amplitude saturation (less than ∼4,000 VP* in a flash; ∼0.001% VP bleached) and it is at intensities above that and up to ∼5 × 104 VP* (∼0.01% VP bleached). When intensities bleach 0.1% of the VP and above, the rate of MII decay is the dominant rate constant (Estevez et al., 2009).
The postulated light-dependent change in the dominant rate constant of photocurrent duration is consistent with findings in cone photoreceptors and is in contrast to the understanding of the dominant rate constant in rods (Burns and Pugh, 2009). For flashes activating up to ∼4,000 VP* in rods, the dominant rate constant is the rate of association of the RGS9 multiprotein complex with the T*–PDE* complex. For flashes activating 4,000–160,000 VP*, the dominant rate constant is the rate of association of RGS9 with T* alone, molecules activated by VP* but not forming a complex with PDE* (Burns and Pugh, 2010). In cones, and over this range intensity, in contrast, the dominant rate constant controlling photocurrent duration is , the rate of VP* phosphorylation.
A feature in our model, not included in any previous models, is the Ca-dependent modulation of the cGMP dependence of CNG channel gating. The most significant consequence of this modulation is that in cones, CNG ion channel activity is controlled by both cGMP and Ca2+. cGMP controls the probability of channel opening (gating) (Picones and Korenbrot, 1994), whereas Ca2+ controls the effectiveness of a given cGMP concentration to gate (Rebrik et al., 2000). Our computational simulations reveal that no one single specific feature of the phototransduction signal is controlled by the channel modulation. Rather, just as Ca2+ itself, ion channel modulation introduces one more regulatory tool to achieve the speed, light sensitivity, adaptation, and stability characteristic of the cone photoresponse.
CNG channel modulation is a not a prerequisite for stability in the phototransduction enzymatic cascade. It appears necessary only for the relatively fast dynamics of cone phototransduction. Rod photoresponses are stable, even though in these cells CNG channel modulation is very small in extent and occurs only at very low cytoplasmic Ca2+ levels (tens nanomolar) (Nakatani et al., 1995; Bauer, 1996; Sagoo and Lagnado, 1996). In fact, knocking out channel modulation in mammalian rods is of little functional consequence (Chen et al., 2010).
To understand why CNG ion channel modulation is of such functional importance, we illustrate with simulations some of the molecular events associated with flash and step responses in the complete and the CNG channel modulation-minus models. In both flash and step responses, the initial rate of change of the outer segment inward currents in flash and step photoresponses is essentially the same in the presence or absence of ion channel modulation (Fig. 12 A). This is because the activation of the VP* and PDE*, the feature that determines the initial rate of photocurrent rise, is not Ca dependent.
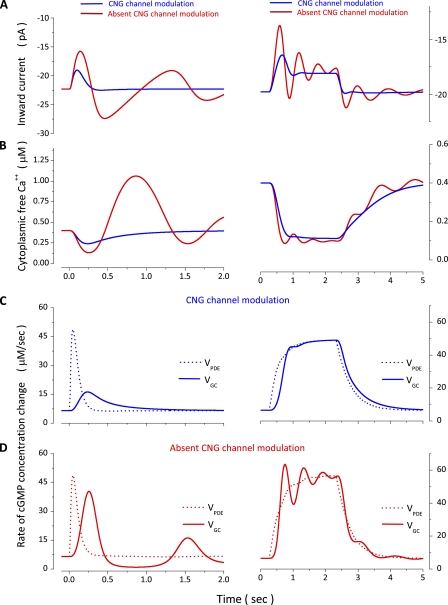
Figure 12.
Simulated dynamics of several molecular events underlying flash and step photoresponses in bass single cones. Left panels show various biochemical and biophysical events elicited by a 10-msec flash of 167 VP* intensity (Table 3, Cone 1). Right panels show the same events elicited by a 2-s step of 124 VP*/s in a different cone (Table 4, Cone 1). (A and B) The inward outer segment membrane current and the cytoplasmic free Ca2+ concentration. Superimposed in each panel are the results of simulations with the complete model (blue traces) and one in which CNG channel modulation is omitted (red traces). (C) Enzymatic activity of PDE (dashed line) and GC (solid line) and their change with light computed with the complete model. (D) Enzymatic activity of PDE (dashed line) and GC (solid line) computed with the model that omits CNG channel modulations.
Compared with the complete model, absence of channel modulation causes a larger change in current amplitude and a prolonged time integral in response to flash stimulation (Fig. 12 A). Because of these differences in the photocurrent, there is a difference in the light-dependent changes in cytoplasmic Ca2+. In the complete model, Ca2+ decreases and smoothly returns to its starting level, the same as is experimentally observed (Leung et al., 2007). In the absence of channel modulation, cytoplasmic Ca2+ falls to a lower level than normal and stays at that lower level for a longer period of time (Fig. 12 B). These seemingly small differences have enormous consequence because GC activity is so sensitive to free cytoplasmic Ca2+: GC activity is enhanced to a greater extent and over a longer time period in the absence of channel modulation than in its presence (compare GC activity in Fig. 12, C and D).
In the model of a normal cell, the dynamic balance between the Ca-enhanced GC activity and the light-enhanced PDE activity results in a properly controlled decrease and recovery of cGMP concentration. PDE activity initially exceeds that of GC and then lags behind it until the activity of both enzymes returns to the same initial dark value (Fig. 12 C, flash response). In the absence of channel modulation, this dynamic balance is lost (Fig. 12 D). PDE activity is essentially unchanged, but the enhanced GC activity causes a larger increase in cGMP concentration and, therefore, larger changes in the inward membrane current in the CNG modulation-minus model than the complete one (Fig. 12 A). This enhanced inward current results in cytoplasmic Ca2+ overload (Fig. 12 B), which, in turn, completely shuts down GC activity (D). Although the PDE activity is small because it has returned to its dark level, it is nonetheless higher than that of GC (Fig. 12 D). Hence, cGMP concentration decreases, channels close, and the anomalously enhanced inward current returns toward its starting value. As the inward current decreases, so does the cytoplasmic free Ca2+ (Fig. 12 B). The dynamic of the PDE–GC balance, however, is not at equilibrium; the iteration of over/under cGMP synthesis is repeated until a true equilibrium is reestablished, thus the oscillations in the membrane current.
In the complete model, the response to a steady light attains a stationary value because the activity of PDE and GC reach a new balance and are the same as long as light is present (Fig. 12 C). Again, the most dramatic consequence of the lack of channel modulation is a change in the extent and time course of Ca2+ concentration changes, which, in turn, change the time course and extent of changes in GC activity. Because PDE activity is little changed by the lack of channel modulation, the normal dynamic balance of the activity of the two enzymes is severely disturbed (Fig. 12, compare C and D, right column). The enzymatic activities are not in balance, and cycles of over/under cGMP synthesis are repeated, causing oscillation in membrane current both while the light is present and at the termination of the light step.
In brief, the simultaneous control of CNG ion channel activity by cGMP and Ca2+ causes the kinetics of light-dependent channel closing and reopening to be far different than they would be if controlled by cGMP alone. Under this dual control, the light-dependent changes in cytoplasmic free Ca2+ and, therefore, changes in GC activity are of appropriate amplitude and time course and in dynamic balance with PDE activity. If channels were controlled by cGMP alone, the light-dependent changes of Ca2+ would be far different, and the balance between light-dependent changes in GC and PDE activities would be lost.
Ca-dependent control of CNG channel ligand sensitivity and of VPK activity is an experimental fact that must be included in complete models of cone phototransduction. Yet, a contemporary model of cone phototransduction (Soo et al., 2008) that ignores Ca-dependent control of VP* phosphorylation and channel modulation can simulate photocurrents that well fit experimental data. In our own exploration, we find that even if the Ca-dependent regulation is ignored, judicious selection of values for the various adjustable parameters could simulate some experimental data, although for some parameters, their values are often different than the experimentally known value, and the models do not work nearly as well over the many stimulation paradigms and intensities reported here. This only indicates that what is gained by Ca-dependent controls is not the difference between transduction and the failure to transduce, but the ability to regulate the molecular events underlying phototransduction to attain the biological imperatives of time course, sensitivity, and light adaptation that sustain the visual process.
Acknowledgments
This work was completed with the immeasurable support of Dr. C. Korenbrot, J. Williams, and Dr. L.A. McNicol. Dr. J. Schnapf, an anonymous reviewer, and the editor offered insightful comments that improved the manuscript.
Funded by National Institutes of Health grant EY-05498.
Edward N. Pugh Jr. served as editor.
Footnotes
Abbreviations used in this paper:
- GC
- guanylate cyclase
- PDE
- phosphodiesterase
- VP
- visual pigment
- VPK
- VP kinase
References
- Arinobu D., Tachibanaki S., Kawamura S. 2010. Larger inhibition of visual pigment kinase in cones than in rods. J. Neurochem. 115:259–268 10.1111/j.1471-4159.2010.06925.x [DOI] [PubMed] [Google Scholar]
- Baehr W., Karan S., Maeda T., Luo D.G., Li S., Bronson J.D., Watt C.B., Yau K.W., Frederick J.M., Palczewski K. 2007. The function of guanylate cyclase 1 and guanylate cyclase 2 in rod and cone photoreceptors. J. Biol. Chem. 282:8837–8847 10.1074/jbc.M610369200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer P.J. 1996. Cyclic GMP-gated channels of bovine rod photoreceptors: affinity, density and stoichiometry of Ca(2+)-calmodulin binding sites. J. Physiol. 494:675–685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor D.A. 1987. Photoreceptor signals and vision. Proctor lecture. Invest. Ophthalmol. Vis. Sci. 28:34–49 [PubMed] [Google Scholar]
- Berlin J.R., Bassani J.W., Bers D.M. 1994. Intrinsic cytosolic calcium buffering properties of single rat cardiac myocytes. Biophys. J. 67:1775–1787 10.1016/S0006-3495(94)80652-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkhardt D.A. 1994. Light adaptation and photopigment bleaching in cone photoreceptors in situ in the retina of the turtle. J. Neurosci. 14:1091–1105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns M.E., Pugh E.N., Jr 2009. RGS9 concentration matters in rod phototransduction. Biophys. J. 97:1538–1547 10.1016/j.bpj.2009.06.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns M.E., Pugh E.N., Jr 2010. Lessons from photoreceptors: turning off G-protein signaling in living cells. Physiology (Bethesda). 25:72–84 10.1152/physiol.00001.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caruso G., Khanal H., Alexiades V., Rieke F., Hamm H.E., DiBenedetto E. 2005. Mathematical and computational modelling of spatio-temporal signalling in rod phototransduction. Syst. Biol. (Stevenage). 152:119–137 [DOI] [PubMed] [Google Scholar]
- Chen J., Woodruff M.L., Wang T., Concepcion F.A., Tranchina D., Fain G.L. 2010. Channel modulation and the mechanism of light adaptation in mouse rods. J. Neurosci. 30:16232–16240 10.1523/JNEUROSCI.2868-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti M., Beavo J. 2007. Biochemistry and physiology of cyclic nucleotide phosphodiesterases: essential components in cyclic nucleotide signaling. Annu. Rev. Biochem. 76:481–511 10.1146/annurev.biochem.76.060305.150444 [DOI] [PubMed] [Google Scholar]
- Craft C.M., Whitmore D.H. 1995. The arrestin superfamily: cone arrestins are a fourth family. FEBS Lett. 362:247–255 10.1016/0014-5793(95)00213-S [DOI] [PubMed] [Google Scholar]
- D’Amours M.R., Cote R.H. 1999. Regulation of photoreceptor phosphodiesterase catalysis by its non-catalytic cGMP-binding sites. Biochem. J. 340:863–869 10.1042/0264-6021:3400863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dizhoor A.M., Olshevskaya E.V., Henzel W.J., Wong S.C., Stults J.T., Ankoudinova I., Hurley J.B. 1995. Cloning, sequencing, and expression of a 24-kDa Ca(2+)-binding protein activating photoreceptor guanylyl cyclase. J. Biol. Chem. 270:25200–25206 10.1074/jbc.270.42.25200 [DOI] [PubMed] [Google Scholar]
- Duda T., Goraczniak R., Surgucheva I., Rudnicka-Nawrot M., Gorczyca W.A., Palczewski K., Sitaramayya A., Baehr W., Sharma R.K. 1996. Calcium modulation of bovine photoreceptor guanylate cyclase. Biochemistry. 35:8478–8482 10.1021/bi960752z [DOI] [PubMed] [Google Scholar]
- Dumke C.L., Arshavsky V.Y., Calvert P.D., Bownds M.D., Pugh E.N., Jr 1994. Rod outer segment structure influences the apparent kinetic parameters of cyclic GMP phosphodiesterase. J. Gen. Physiol. 103:1071–1098 10.1085/jgp.103.6.1071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estevez M.E., Kolesnikov A.V., Ala-Laurila P., Crouch R.K., Govardovskii V.I., Cornwall M.C. 2009. The 9-methyl group of retinal is essential for rapid Meta II decay and phototransduction quenching in red cones. J. Gen. Physiol. 134:137–150 10.1085/jgp.200910232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forti S., Menini A., Rispoli G., Torre V. 1989. Kinetics of phototransduction in retinal rods of the newt Triturus cristatus. J. Physiol. 419:265–295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson S.K., Parkes J.H., Liebman P.A. 2000. Phosphorylation modulates the affinity of light-activated rhodopsin for G protein and arrestin. Biochemistry. 39:5738–5749 10.1021/bi991857f [DOI] [PubMed] [Google Scholar]
- Gillespie P.G., Beavo J.A. 1988. Characterization of a bovine cone photoreceptor phosphodiesterase purified by cyclic GMP-sepharose chromatography. J. Biol. Chem. 263:8133–8141 [PubMed] [Google Scholar]
- Gorczyca W.A., Polans A.S., Surgucheva I.G., Subbaraya I., Baehr W., Palczewski K. 1995. Guanylyl cyclase activating protein. A calcium-sensitive regulator of phototransduction. J. Biol. Chem. 270:22029–22036 10.1074/jbc.270.37.22029 [DOI] [PubMed] [Google Scholar]
- Gray-Keller M.P., Detwiler P.B. 1994. The calcium feedback signal in the phototransduction cascade of vertebrate rods. Neuron. 13:849–861 10.1016/0896-6273(94)90251-8 [DOI] [PubMed] [Google Scholar]
- Gurevich V.V., Gurevich E.V. 2006. The structural basis of arrestin-mediated regulation of G-protein-coupled receptors. Pharmacol. Ther. 110:465–502 10.1016/j.pharmthera.2005.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamer R.D. 2000. Computational analysis of vertebrate phototransduction: combined quantitative and qualitative modeling of dark- and light-adapted responses in amphibian rods. Vis. Neurosci. 17:679–699 10.1017/S0952523800175030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamer R.D., Nicholas S.C., Tranchina D., Lamb T.D., Jarvinen J.L. 2005. Toward a unified model of vertebrate rod phototransduction. Vis. Neurosci. 22:417–436 10.1017/S0952523805224045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hisatomi O., Matsuda S., Satoh T., Kotaka S., Imanishi Y., Tokunaga F. 1998. A novel subtype of G-protein-coupled receptor kinase, GRK7, in teleost cone photoreceptors. FEBS Lett. 424:159–164 10.1016/S0014-5793(98)00162-8 [DOI] [PubMed] [Google Scholar]
- Hofmann K.P., Scheerer P., Hildebrand P.W., Choe H.W., Park J.H., Heck M., Ernst O.P. 2009. A G protein-coupled receptor at work: the rhodopsin model. Trends Biochem. Sci. 34:540–552 10.1016/j.tibs.2009.07.005 [DOI] [PubMed] [Google Scholar]
- Holcman D., Korenbrot J.I. 2005. The limit of photoreceptor sensitivity: molecular mechanisms of dark noise in retinal cones. J. Gen. Physiol. 125:641–660 10.1085/jgp.200509277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D., Hinds T.R., Martinez S.E., Doneanu C., Beavo J.A. 2004. Molecular determinants of cGMP binding to chicken cone photoreceptor phosphodiesterase. J. Biol. Chem. 279:48143–48151 10.1074/jbc.M404338200 [DOI] [PubMed] [Google Scholar]
- Kachi S., Nishizawa Y., Olshevskaya E., Yamazaki A., Miyake Y., Wakabayashi T., Dizhoor A., Usukura J. 1999. Detailed localization of photoreceptor guanylate cyclase activating protein-1 and -2 in mammalian retinas using light and electron microscopy. Exp. Eye Res. 68:465–473 10.1006/exer.1998.0629 [DOI] [PubMed] [Google Scholar]
- Kawamura S. 1993. Rhodopsin phosphorylation as a mechanism of cyclic GMP phosphodiesterase regulation by S-modulin. Nature. 362:855–857 10.1038/362855a0 [DOI] [PubMed] [Google Scholar]
- Kawamura S., Kuwata O., Yamada M., Matsuda S., Hisatomi O., Tokunaga F. 1996. Photoreceptor protein s26, a cone homologue of S-modulin in frog retina. J. Biol. Chem. 271:21359–21364 10.1074/jbc.271.35.21359 [DOI] [PubMed] [Google Scholar]
- Kennedy M.J., Dunn F.A., Hurley J.B. 2004. Visual pigment phosphorylation but not transducin translocation can contribute to light adaptation in zebrafish cones. Neuron. 41:915–928 [DOI] [PubMed] [Google Scholar]
- Koch K.W. 2002. Target recognition of guanylate cyclase by guanylate cyclase-activating proteins. Adv. Exp. Med. Biol. 514:349–360 10.1007/978-1-4615-0121-3_21 [DOI] [PubMed] [Google Scholar]
- Koch K.W., Stryer L. 1988. Highly cooperative feedback control of retinal rod guanylate cyclase by calcium ions. Nature. 334:64–66 10.1038/334064a0 [DOI] [PubMed] [Google Scholar]
- Koch K.W., Duda T., Sharma R.K. 2002. Photoreceptor specific guanylate cyclases in vertebrate phototransduction. Mol. Cell. Biochem. 230:97–106 10.1023/A:1014209711793 [DOI] [PubMed] [Google Scholar]
- Koch K.W., Duda T., Sharma R.K. 2010. Ca(2+)-modulated vision-linked ROS-GC guanylate cyclase transduction machinery. Mol. Cell. Biochem. 334:105–115 10.1007/s11010-009-0330-z [DOI] [PubMed] [Google Scholar]
- Krispel C.M., Chen D., Melling N., Chen Y.J., Martemyanov K.A., Quillinan N., Arshavsky V.Y., Wensel T.G., Chen C.K., Burns M.E. 2006. RGS expression rate-limits recovery of rod photoresponses. Neuron. 51:409–416 10.1016/j.neuron.2006.07.010 [DOI] [PubMed] [Google Scholar]
- Lagnado L., Cervetto L., McNaughton P.A. 1992. Calcium homeostasis in the outer segments of retinal rods from the tiger salamander. J. Physiol. 455:111–142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb T.D. 1996. Gain and kinetics of activation in the G-protein cascade of phototransduction. Proc. Natl. Acad. Sci. USA. 93:566–570 10.1073/pnas.93.2.566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leskov I.B., Klenchin V.A., Handy J.W., Whitlock G.G., Govardovskii V.I., Bownds M.D., Lamb T.D., Pugh E.N., Jr, Arshavsky V.Y. 2000. The gain of rod phototransduction: reconciliation of biochemical and electrophysiological measurements. Neuron. 27:525–537 10.1016/S0896-6273(00)00063-5 [DOI] [PubMed] [Google Scholar]
- Leung Y.T., Fain G.L., Matthews H.R. 2007. Simultaneous measurement of current and calcium in the ultraviolet-sensitive cones of zebrafish. J. Physiol. 579:15–27 10.1113/jphysiol.2006.120162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lolley R.N., Racz E. 1982. Calcium modulation of cyclic GMP synthesis in rat visual cells. Vision Res. 22:1481–1486 10.1016/0042-6989(82)90213-9 [DOI] [PubMed] [Google Scholar]
- Matthews H.R., Sampath A.P. 2010. Photopigment quenching is Ca2+ dependent and controls response duration in salamander L-cone photoreceptors. J. Gen. Physiol. 135:355–366 10.1085/jgp.200910394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews H.R., Fain G.L., Murphy R.L., Lamb T.D. 1990. Light adaptation in cone photoreceptors of the salamander: a role for cytoplasmic calcium. J. Physiol. 420:447–469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews H.R., Cornwall M.C., Fain G.L. 1996. Persistent activation of transducin by bleached rhodopsin in salamander rods. J. Gen. Physiol. 108:557–563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller D.L., Korenbrot J.I. 1987. Kinetics of light-dependent Ca fluxes across the plasma membrane of rod outer segments. A dynamic model of the regulation of the cytoplasmic Ca concentration. J. Gen. Physiol. 90:397–425 10.1085/jgp.90.3.397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J.L., Korenbrot J.I. 1993. Phototransduction and adaptation in rods, single cones, and twin cones of the striped bass retina: a comparative study. Vis. Neurosci. 10:653–667 10.1017/S0952523800005356 [DOI] [PubMed] [Google Scholar]
- Miller J.L., Korenbrot J.I. 1994. Differences in calcium homeostasis between retinal rod and cone photoreceptors revealed by the effects of voltage on the cGMP-gated conductance in intact cells. J. Gen. Physiol. 104:909–940 10.1085/jgp.104.5.909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moriondo A., Rispoli G. 2003. A step-by-step model of phototransduction cascade shows that Ca2+ regulation of guanylate cyclase accounts only for short-term changes of photoresponse. Photochem. Photobiol. Sci. 2:1292–1298 [DOI] [PubMed] [Google Scholar]
- Muradov H., Boyd K.K., Haeri M., Kerov V., Knox B.E., Artemyev N.O. 2009. Characterization of human cone phosphodiesterase-6 ectopically expressed in Xenopus laevis rods. J. Biol. Chem. 284:32662–32669 10.1074/jbc.M109.049916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatani K., Yau K.W. 1989. Sodium-dependent calcium extrusion and sensitivity regulation in retinal cones of the salamander. J. Physiol. 409:525–548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatani K., Koutalos Y., Yau K.W. 1995. Ca2+ modulation of the cGMP-gated channel of bullfrog retinal rod photoreceptors. J. Physiol. 484:69–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher E. 1995. The use of fura-2 for estimating Ca buffers and Ca fluxes. Neuropharmacology. 34:1423–1442 10.1016/0028-3908(95)00144-U [DOI] [PubMed] [Google Scholar]
- Neher E., Augustine G.J. 1992. Calcium gradients and buffers in bovine chromaffin cells. J. Physiol. 450:273–301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikonov S., Lamb T.D., Pugh E.N., Jr 2000. The role of steady phosphodiesterase activity in the kinetics and sensitivity of the light-adapted salamander rod photoresponse. J. Gen. Physiol. 116:795–824 10.1085/jgp.116.6.795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikonov S.S., Brown B.M., Davis J.A., Zuniga F.I., Bragin A., Pugh E.N., Jr, Craft C.M. 2008. Mouse cones require an arrestin for normal inactivation of phototransduction. Neuron. 59:462–474 10.1016/j.neuron.2008.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normann R.A., Perlman I. 1979. The effects of background illumination on the photoresponses of red and green cones. J. Physiol. 286:491–507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normann R.A., Werblin F.S. 1974. Control of retinal sensitivity. I. Light and dark adaptation of vertebrate rods and cones. J. Gen. Physiol. 63:37–61 10.1085/jgp.63.1.37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohyama T., Hackos D.H., Frings S., Hagen V., Kaupp U.B., Korenbrot J.I. 2000. Fraction of the dark current carried by Ca2+ through cGMP-gated ion channels of intact rod and cone photoreceptors. J. Gen. Physiol. 116:735–754 10.1085/jgp.116.6.735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohyama T., Picones A., Korenbrot J.I. 2002. Voltage-dependence of ion permeation in cyclic GMP-gated ion channels is optimized for cell function in rod and cone photoreceptors. J. Gen. Physiol. 119:341–354 10.1085/jgp.20028565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson A., Pugh E.N., Jr 1993. Diffusion coefficient of cyclic GMP in salamander rod outer segments estimated with two fluorescent probes. Biophys. J. 65:1335–1352 10.1016/S0006-3495(93)81177-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paupoo A.A., Mahroo O.A., Friedburg C., Lamb T.D. 2000. Human cone photoreceptor responses measured by the electroretinogram a-wave during and after exposure to intense illumination. J. Physiol. 529:469–482 10.1111/j.1469-7793.2000.00469.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlman I., Normann R.A. 1998. Light adaptation and sensitivity controlling mechanisms in vertebrate photoreceptors. Prog. Retin. Eye Res. 17:523–563 10.1016/S1350-9462(98)00005-6 [DOI] [PubMed] [Google Scholar]
- Perry R.J., McNaughton P.A. 1991. Response properties of cones from the retina of the tiger salamander. J. Physiol. 433:561–587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picones A., Korenbrot J.I. 1992. Permeation and interaction of monovalent cations with the cGMP-gated channel of cone photoreceptors. J. Gen. Physiol. 100:647–673 10.1085/jgp.100.4.647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picones A., Korenbrot J.I. 1994. Analysis of fluctuations in the cGMP-dependent currents of cone photoreceptor outer segments. Biophys. J. 66:360–365 10.1016/S0006-3495(94)80785-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pugh E.N., Jr, Lamb T.D. 1993. Amplification and kinetics of the activation steps in phototransduction. Biochim. Biophys. Acta. 1141:111–149 10.1016/0005-2728(93)90038-H [DOI] [PubMed] [Google Scholar]
- Pugh E.N., Jr, Duda T., Sitaramayya A., Sharma R.K. 1997. Photoreceptor guanylate cyclases: a review. Biosci. Rep. 17:429–473 10.1023/A:1027365520442 [DOI] [PubMed] [Google Scholar]
- Ratto G.M., Payne R., Owen W.G., Tsien R.Y. 1988. The concentration of cytosolic free calcium in vertebrate rod outer segments measured with fura-2. J. Neurosci. 8:3240–3246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebrik T.I., Korenbrot J.I. 1998. In intact cone photoreceptors, a Ca2+-dependent, diffusible factor modulates the cGMP-gated ion channels differently than in rods. J. Gen. Physiol. 112:537–548 10.1085/jgp.112.5.537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebrik T.I., Korenbrot J.I. 2004. In intact mammalian photoreceptors, Ca2+-dependent modulation of cGMP-gated ion channels is detectable in cones but not in rods. J. Gen. Physiol. 123:63–75 10.1085/jgp.200308952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebrik T.I., Kotelnikova E.A., Korenbrot J.I. 2000. Time course and Ca2+ dependence of sensitivity modulation in cyclic GMP-gated currents of intact cone photoreceptors. J. Gen. Physiol. 116:521–534 10.1085/jgp.116.4.521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reingruber J., Holcman D. 2008. The dynamics of phosphodiesterase activation in rods and cones. Biophys. J. 94:1954–1970 10.1529/biophysj.107.116202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinner O., Makhankov Y.V., Biehlmaier O., Neuhauss S.C. 2005. Knockdown of cone-specific kinase GRK7 in larval zebrafish leads to impaired cone response recovery and delayed dark adaptation. Neuron. 47:231–242 10.1016/j.neuron.2005.06.010 [DOI] [PubMed] [Google Scholar]
- Sagoo M.S., Lagnado L. 1996. The action of cytoplasmic calcium on the cGMP-activated channel in salamander rod photoreceptors. J. Physiol. 497:309–319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampath A.P., Matthews H.R., Cornwall M.C., Bandarchi J., Fain G.L. 1999. Light-dependent changes in outer segment free-Ca2+ concentration in salamander cone photoreceptors. J. Gen. Physiol. 113:267–277 10.1085/jgp.113.2.267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwiening C.J., Thomas R.C. 1996. Relationship between intracellular calcium and its muffling measured by calcium iontophoresis in snail neurones. J. Physiol. 491:621–633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen L., Caruso G., Bisegna P., Andreucci D., Gurevich V.V., Hamm H.E., DiBenedetto E. 2010. Dynamics of mouse rod phototransduction and its sensitivity to variation of key parameters. IET Syst. Biol. 4:12–32 10.1049/iet-syb.2008.0154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheng J.Z., Prinsen C.F., Clark R.B., Giles W.R., Schnetkamp P.P. 2000. Na(+)-Ca(2+)-K(+) currents measured in insect cells transfected with the retinal cone or rod Na(+)-Ca(2+)-K(+) exchanger cDNA. Biophys. J. 79:1945–1953 10.1016/S0006-3495(00)76443-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sneyd J., Tranchina D. 1989. Phototransduction in cones: an inverse problem in enzyme kinetics. Bull. Math. Biol. 51:749–784 [DOI] [PubMed] [Google Scholar]
- Soo F.S., Detwiler P.B., Rieke F. 2008. Light adaptation in salamander L-cone photoreceptors. J. Neurosci. 28:1331–1342 10.1523/JNEUROSCI.4121-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey N. 2004. Electrical and Electronic Systems. Pearson Education, London: 588 pp [Google Scholar]
- Tachibanaki S., Arinobu D., Shimauchi-Matsukawa Y., Tsushima S., Kawamura S. 2005. Highly effective phosphorylation by G protein-coupled receptor kinase 7 of light-activated visual pigment in cones. Proc. Natl. Acad. Sci. USA. 102:9329–9334 10.1073/pnas.0501875102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takemoto N., Tachibanaki S., Kawamura S. 2009. High cGMP synthetic activity in carp cones. Proc. Natl. Acad. Sci. USA. 106:11788–11793 10.1073/pnas.0812781106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trafford A.W., Diaz M.E., Eisner D.A. 1999. A novel, rapid and reversible method to measure Ca buffering and time-course of total sarcoplasmic reticulum Ca content in cardiac ventricular myocytes. Pflugers Arch. 437:501–503 [DOI] [PubMed] [Google Scholar]
- Tranchina D., Sneyd J., Cadenas I.D. 1991. Light adaptation in turtle cones. Testing and analysis of a model for phototransduction. Biophys. J. 60:217–237 10.1016/S0006-3495(91)82045-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wada Y., Sugiyama J., Okano T., Fukada Y. 2006. GRK1 and GRK7: unique cellular distribution and widely different activities of opsin phosphorylation in the zebrafish rods and cones. J. Neurochem. 98:824–837 10.1111/j.1471-4159.2006.03920.x [DOI] [PubMed] [Google Scholar]
- Wensel T.G. 2008. Signal transducing membrane complexes of photoreceptor outer segments. Vision Res. 48:2052–2061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T., Naraghi M., Kang H., Neher E. 1997. Kinetic studies of Ca2+ binding and Ca2+ clearance in the cytosol of adrenal chromaffin cells. Biophys. J. 73:532–545 10.1016/S0006-3495(97)78091-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yau K.W., Nakatani K. 1985. Light-induced reduction of cytoplasmic free calcium in retinal rod outer segment. Nature. 313:579–582 10.1038/313579a0 [DOI] [PubMed] [Google Scholar]