Theoretical analysis of the role of chromatin interactions in long-range action of enhancers and insulators

Abstract

Long-distance regulatory interactions between enhancers and their target genes are commonplace in higher eukaryotes. Interposed boundaries or insulators are able to block these long-distance regulatory interactions. The mechanistic basis for insulator activity and how it relates to enhancer action-at-a-distance remains unclear. Here we explore the idea that topological loops could simultaneously account for regulatory interactions of distal enhancers and the insulating activity of boundary elements. We show that while loop formation is not in itself sufficient to explain action at a distance, incorporating transient nonspecific and moderate attractive interactions between the chromatin fibers strongly enhances long-distance regulatory interactions and is sufficient to generate a euchromatin-like state. Under these same conditions, the subdivision of the loop into two topologically independent loops by insulators inhibits interdomain interactions. The underlying cause of this effect is a suppression of crossings in the contact map at intermediate distances. Thus our model simultaneously accounts for regulatory interactions at a distance and the insulator activity of boundary elements. This unified model of the regulatory roles of chromatin loops makes several testable predictions that could be confronted with in vitro experiments, as well as genomic chromatin conformation capture and fluorescent microscopic approaches.

Unlike most known cases of transcriptional regulation in prokaryotes and lower eukaryotes, metazoan genes are often regulated by enhancers placed tens to hundreds of kilobases away from the promoter (1–4). Facilitating mechanisms are necessary for such long-range enhancer action, as we shall explain below. Widespread distant regulation also requires additional mechanisms to ensure specificity. Enhancer-blocking DNA sequences, known as boundaries or insulators, define chromatin domains within which enhancer action is limited (5–11). While it is known that insulator elements bind to particular proteins (12) how these protein complexes manage to block enhancer action across domains remains controversial.

Several different models for long-range enhancer-promoter communication have been proposed, for review see refs. 5, 10. One model hypothesizes a tracking mechanism that involves the processive movement of regulatory machines launched from the enhancer towards the promoter. Another model hypothesizes that transcriptional up-regulation requires direct physical contact between proteins assembled at the enhancer and the transcriptional apparatus at promoter. This process necessarily leads to looping out the intervening chromatin. Looping model has received significant support in the context of the control of the beta-globin locus by the LCR (13, 14). For each of these models of enhancer-promoter communication, one needs a corresponding mechanism of action for insulators (9, 10, 15, 16). For the tracking model, insulators are assumed to work as barriers blocking the movement of the regulatory machine. In the looping model, insulators function by decoying promoters or other acting as sinks or traps for enhancer (17).

Yet another model for enhancer action is based on the idea that insulators subdivide the genome into topologically independent loops or domains (18). In this model, enhancer action at distance requires a mechanism that promotes intraloop enhancer-promoter contacts, while insulation requires that interloop contacts be disfavored. The topological loop model does seem to explain experiments that aim to contrast conjectured mechanisms of insulation (19–21); however, scant attention has been paid to the question of whether the topological loop model is plausible from a physical point of view. We redress this critical gap in our understanding of long-range gene regulation. Specifically, we resolve the following puzzles within the context of looping models—

• What are the ingredients necessary in a physical model of chromatin capable of producing efficient long-range enhancer-promoter communication?

• What are the signatures of such physical features on observable conformations of chromatin? What conformations are favored?

• What are the consequences of favored chromatin conformations on insulation by insulators arranging chromatin into topological loop domains?

Surprisingly, we discover that the same model that explains experimentally observed efficiency of long-range enhancer action is, paradoxically, capable of explaining the efficiency of insulator action; no added ingredients are needed.

Results

Our intention is to understand dynamics of large domains of chromatin ranging in size from tens to hundreds of kilobases of DNA. Ab initio molecular modeling of such large systems is hindered both by computational limitations and our lack of detailed knowledge of chromatin composition and structure. Moreover, keeping in mind that robust predictions can often be extracted from coarse-grained models, we use such an approach.

Long-Range Enhancer Action.

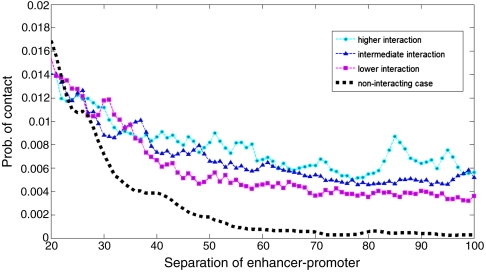
Distance dependence of contact probability between two points on a semiflexible polymer has been studied under many contexts (22). The contact probability is the highest for a separation of the order the persistence length and falls off rapidly as a power law for longer distances, see Fig. 1. If one takes the persistence length to be a few nucleosomes in the case of chromatin (23, 24), at separations of hundreds of kb, the contact probability should have fallen from its peak value to few orders of magnitude below, contrary to observations. Even for much larger estimates of persistence length, the problem of efficient communications over a 1 Mb remains a mystery (see SI Text for a more detailed discussion of the relevant length scales). Quite obviously, the semiflexible polymer properties of chromatin alone is incapable of reproducing such efficient long-range enhancer-promoter contacts. A plausible argument explaining the phenomenon is very strong enhancer-promoter interaction; the enhancer stays in contact with the promoter for a long time once (an otherwise improbable) contact is established. Had there been only one promoter, this mechanism could perhaps explain the enhanced level of average gene expression at long ranges. However, in this scenario, if the same enhancer has multiple competing promoters at different distances, the proximal promoters would always be favored for contact, contrary to experimental observations (25). Moreover, multiple enhancers activating the same promoter is difficult to arrange within this scenario (26).

Fig. 1.

Contact probability for fixed availability and different attraction, zoomed in on the tail of the distribution, against enhancer-promoter separation. The typical contact probability is peaked around a separation determined by the choice of persistence length, and is excluded from this plot. As expected, the tail of the distribution falls off as a power law for the noninteracting case, but has a much slower fall-off for our interaction model. We present data for three different values of effective interaction and show that higher interaction leads to better long-range communication.

Consequently, besides the semiflexible polymer features, we need to recognize some other feature of chromatin that might favor long-distance contacts. We argue that the new ingredient is chromatin-chromatin attractive interactions. There are many potential sources of such an interaction. One possibility that has been explored experimentally is histone-tail mediated internucleosome interaction (27–31). Another mechanism involving nucleosomes would be electrostatic interactions between histone cores (32–35). Alternatively, the many different DNA/chromatin binding proteins, known for promoting chromatin association and condensation, might mediate “nucleosome-nucleosome” interactions. Examples of such proteins include the linker histones H1 and H5 (36, 37), HMG proteins (38, 39), and HP1 (40). However, our conclusions do not depend upon the precise cause or causes of this postulated attractive chromatin-chromatin interaction. Rather we simply ask whether incorporating some type of transient and weak chromatin-chromatin attractions into our model is sufficient to generate efficient communication between distant enhancers and promoters.

What sort of attractive interactions should one consider? It is well known that polymer interactions with a static attraction potential (even if the potential is short range) can lead to polymer agglomeration for potentials with strength of the order of thermal fluctuation energy k_BT (which is about a tenth of a typical hydrogen bond). This phenomenon is known as the coil-globule transition. Many authors (41–45) have drawn analogies with the coil-globule transition and its relation to compaction of chromatin, including formation of heterochromatin. However, we are interested in the role of transient nucleosome-nucleosome interaction in euchromatin. Euchromatin conformations are known to be extended (46, 47). Motivated by the idea that an additional degree of freedom (tail configuration or protein binding) is the mediator, we set up our effective model of bead-to-bead interaction as follows: Instead of a uniformly attractive interaction, we introduce two discrete states for each nucleosome (inert and active) that it switches between stochastically. Only active nucleosomes can form an attractive bond within a short-interaction-range, see details in Materials and Methods.

Fig. 1 shows that when transient nucleosome-nucleosome interactions are incorporated into the model, enhancer-promoter interactions do not fall off rapidly with enhancer-promoter separation along the chromatin. Instead, the probability of enhancer-promoter contacts stays relatively constant over a wide range of distances, as is also seen in experimental studies (48). Moreover, with incremental increases in interactions, the probability of long-range contact is increased. We have verified this key result for a wide range of model parameters. This nearly flat tail of the contact probability is a robust feature of our model for intermediate separations of enhancer-promoter pairs, and is in striking contrast to the corresponding behavior of either noninteracting or collapsed polymers, see Fig. 1. Therefore, we identify unique aspects of chromatin polymer that are capable of explaining long-range action—

• Nucleosomes are only weakly and transiently mutually attractive.

• The nucleosome forming a pair-wise bond with another location does not interact attractively with anything else.

The bond saturation phenomenon limits our model to attractive pair-wise nucleosome interactions and repulsive higher-order interactions, as represented by large positive third and higher virial coefficients. This construction averts polymer collapse, see further discussion in Materials and Methods.

Analysis of Enhancer-Promoter Interaction.

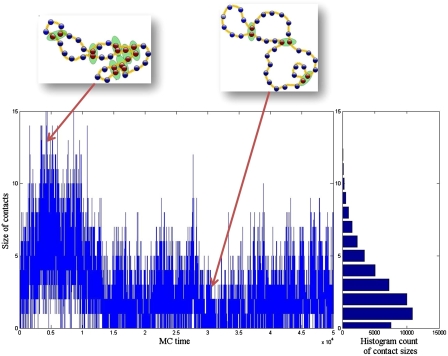
We have shown that it is possible to make efficient long-range contacts in our model of euchromatin without having to undergo a collapse transition. This result is attractive for the following reason. Experiments measuring typical physical distance in euchromatin as a function of genomic distance are consistent with Gaussian polymer statistics, at least for genomic distances between few kb and 1 Mb (41, 46, 47, 49). However, the probability of contact falls off fast as a function of distance for Gaussian polymers. Such a fall-off appears to be inconsistent with the phenomenon of efficient regulatory loop formation over large distances in euchromatin, requiring the probability of contact to remain almost constant over such distances. We resolve this puzzle by looking at the time dependence of number of contacts in our model, see Fig. 2. We observe that the configurations with many contacts are sporadic and relatively rare. The polymer goes through occasional compact configurations that are responsible for the enhancement of long-range contact probability; however, consistent with experimental measurements, the typical configuration statistics are roughly Gaussian. This situation is different from the regime in which there is well defined globule state where the typical polymer configuration has many long-range contacts (50) leading to a plateau in the probability of contact at long distance. We prove this claim by separating out the contact probabilities for configurations with low and high number of total instantaneous contacts, see Fig. 3. The key observation is that long-range contact probability is overwhelmingly contributed by high-contact configurations.

Fig. 2.

Time line plot (MC steps) of number of transient bonds formed in a window of a typical run. The red beads are the active beads that has formed transient bonds (green shadow) and the blue beads are inert. Portion of the 200 bead configuration shown. The box on the right shows the histogram of contact sizes, with the x-axis showing counts for different contact sizes.

Fig. 3.

Probability of contact as a function of separation, for low-contact configurations and for high-contact ones. In this particular case, configurations with more than 10 contacts were taken to be high-contact and those with less than five were classified as low-contact.

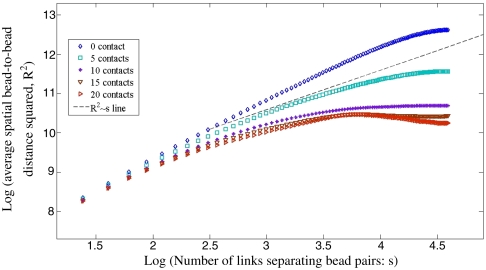
We unravel the Gaussian nature of configurations with low number of contacts more directly by measuring the root-mean-square (rms) bead-to-bead distance as a function of bead separation for configurations selected by their number of contacts. For a Gaussian polymer the rms distance should scale as the square root of separation, for separations beyond persistence length. Fig. 4 presents the log-log plot of the rms distance against separation. The plot shows that, for low number of contacts (e.g., five contacts), the behavior of the rms distance is indeed roughly Gaussian. The high-contact configurations are significantly more compact than what would be expected from Gaussian behavior. Because the high-contact configurations are rarer, the crucial conclusion from this analysis is that a typical configuration will exhibit Gaussian statistics, in agreement with experimental observations. Notice that the “zero contact” polymer is more “swollen” and the slope is in between that of a rigid polymer (slope 2) and of a self-avoiding walk (slope approximately 1.2).

Fig. 4.

Log-log plot of rms distance of bead pairs against separation for configurations selected by their number of contacts. The zero contact configurations are nearly Gaussian; deviation from the random walk scaling at short separations is owing to persistence of the polymer and at long separations owing to the finite size effect of the ring configuration studied here. For high number of contacts we see significant deviation from the random walk behavior; the polymer is more compact. However, these configurations are sporadic and rarer.

It turns out that the structure and sporadic behavior of these high-contact configurations is of crucial importance in understanding how insulators could potentially block enhancer action within this model. We emphasize that our model for long-range enhancer action is not augmented in any manner for our study of insulator action described below.

Insulator Action.

In the topological loop model the key function of insulators is to define the two end-points of each looped domain. How the insulators do so is a matter of conjecture. One idea is that insulators form loops by associating with the nuclear matrix or insulator bodies. Another idea is that insulators generate loops by pairing directly with each other.

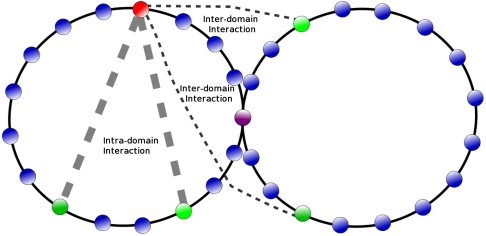
In order to study the simplest scenario for insulator dependent loop formation, we construct two equal domains by pinching a ring configuration of chromatin in the middle by a permanent bond between insulators. This arrangement would simulate insulator pairing, and of the possible mechanisms for insulator dependent loop formation, it is most exigent on the chromatin model. It is not at all obvious why in such a set-up, interdomain contacts could be suppressed in comparison to intradomain contacts (Fig. 5).

Fig. 5.

Set-up for studying insulator action: the green bead is an enhancer, red beads are insulators, magenta beads are equidistant intradomain promoters and cyan beads are equidistant interdomain promoters. Thick gray dashed lines correspond to intradomain interactions while thin black dashed lines correspond to interdomain interaction.

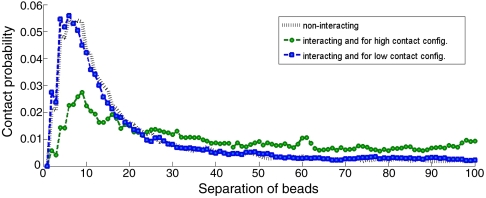
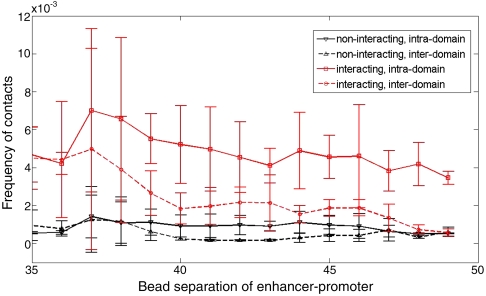
We simulate the same model used for studying enhancer-promoter communication, and vary the interaction strength in the same fashion. We query the probability of interdomain vs. intradomain contact by measuring the contact frequency between a bead (enhancer) and its four equidistant neighbors (promoters), two of which are inter- and two are intradomain, see Fig. 5. We measure these probabilities for various separations of these beads. Two findings are significant, see Fig. 6. First, as was the case for the simple ring, weak and transient nucleosome-nucleosome attraction promotes interdomain “enhancer-promoter” interactions, and the frequency of these long-distance “regulatory” interactions increases with increasing attraction. Second, while transient nucleosome-nucleosome attraction supports distant intradomain enhancer-promoter interactions, it also suppresses enhancer-promoter interactions between elements in different loop domains, see Fig. 6. Compared to the noninteracting case, the suppression factor can be quite large (Fig. 6), which, for the largest distances in our simulation, is about six to sevenfold. In many in vivo and in vitro experiments, the typical enhancement in gene expression in presence of an active distal enhancer activity is a factor of ten or less.

Fig. 6.

Efficiency of insulation for interacting polymer model. Interaction reduces long-range crossing of contacts as quantified in the graph by comparing inter- and intradomain contacts.

Apart from the presence of chromatin-chromatin attraction, the suppression also depends on how deep within a domain the enhancer is: deeper they are, the better the suppression factor. Note that when a short distance separates the enhancer-promoter pair, the looping interaction across an insulator is not particularly weaker than the interaction over a similar short distance inside the domain (Fig. 6). This phenomenon is in close agreement with the quality of insulation observed as a function of distance from the insulator in experiments (21, 51). In this context, it is worth noting that the barrier and the decoy insulator models of insulation cannot explain why the efficiency of insulation depends on the distance of the enhancer and promoter pair from the insulator pair bracketing it. In the topological loop model our data explains the phenomena as follows. When the enhancer and promoter are proximal to paired insulators (that create the loop domain), insulation is not as efficient because only further away from a certain proximity to insulators is insulation facilitated in our model. The origin of this length scale and the dependence of the efficiency of insulation on the interaction set-up are analyzed in the next section.

Understanding Insulator Action.

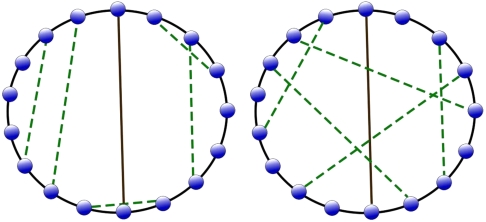
One seemingly paradoxical feature of our model is that weak transient nucleosome-nucleosome attraction on the one hand is able to promote long-distance intradomain enhancer-promoter communication and on the other hand is able to suppress enhancer-promoter communication across domains. In order to resolve this paradox, we analyzed the topological structure of the contact map. For any conformation of our model polymer, one can map the instantaneous contacts, formed during the sporadic events, into chords on a discrete circle where the end points of the chords are the beads in contact. For example, the permanent contact introduced between insulators is a diameter in this mapping. Interdomain/intradomain interactions correspond to chords that cross/do not cross this diameter (Fig. 7). We analyze the crossing of these chords in our model simulation for enhancer action to elucidate insulation action as follows.

Fig. 7.

The left box is a sketch of a typical contact map for the same number of contacts for random distribution of contacts and the right box, for our simulation of interacting nucleosomes. The solid line is the insulator contact (permanent) and dashed lines represent transient contacts between nucleosomes.

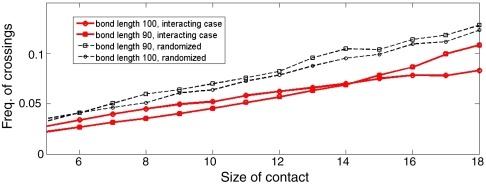
We select conformations by their number of instantaneous contacts (contact size). Because we are interested in long-range action, we only consider contacts between beads separated by more than a short-range cut-off. We pick this cut-off to be 20 beads which is the separation beyond which the probability of contact for noninteracting polymer begins to depart significantly from that of the interacting polymer (Fig. 3). For each contact size, we compute the statistics of number of crossings of all mapped chords with a single chord of fixed length. We perform this analysis for various lengths of the chosen chord. Note that each chord length corresponds to an arc length: namely, the number of links between the two beads along the shorter arc connecting them. We will call this number the bond length. As shown in Fig. 8, the central observation is that the frequency of crossing of a long-range contact is consistently lower in the interacting polymer, in comparison to when chords are randomly distributed on a circle. If the long-range contact linking the loop is permanent, as it is in the insulator simulation (Fig. 5), the observation immediately implies that interdomain contact is suppressed (Fig. 6). For random chords on a circle we do not expect any such suppression, and hence this acts as a benchmark for efficiency of insulation (Fig. 8). Note that suppression of crossing is poor for short-range contacts; i.e., an interaction dependent length-scale for efficient insulation emerges in this picture, as discussed earlier.

Fig. 8.

Frequency of crossing of chords (discussion of mapping of contacts to chords on a circle is in the text) with a chosen bond length, against contact sizes. Data shown for two bond lengths. The 100 bond length chord is a diameter in our 200 bead simulation, and therefore corresponds to the insulator set-up. For comparison we have randomized the chords and computed the frequency of crossing. No insulation is expected for random contacts between any two beads, therefore the randomized chords serves as a benchmark.

The contact map statistics also implies that the high-contact configurations are not just temporary appearance of a state of fully collapsed polymer. In polymer literature, pseudoknots in attractive polymers above the collapse transition have been explored, motivated mostly by RNA folding (52). Our results are consistent with the picture that a single contact usually does not form a pseudoknot by crossing a large number of other contacts. The entropic cost of a heavily crossed contact map makes such contact patterns less likely. We have verified that increasing nucleosome-nucleosome attraction does reduce the overall number of crossings of all long-range contacts for a given contact size. However this reduction, along with insulation, is nontrivially dependent on the effective interaction strength given by the combination of attraction and availability (see Materials and Methods). The subtle relationship between geometry of the double loop configuration and insulation is controlled by the typical contact size, which in turn is controlled by the effective interaction strength. This interaction strength sets the length scale beyond which contact crossing is suppressed. A detailed exploration of the putative reduction in pseudoknots of the contact map (and ensuing insulation) is beyond the scope of this paper, and will be presented elsewhere.

Discussion

Key Insights.

Long-distance regulatory control in higher eukaryotes has fascinated biologists for many decades by now (see SI Text for more background material). We have presented an attractive and unifying theory of two central facets of gene regulation in eukaryotes: enhancer action at distance and enhancer (silencer) blocking activity of insulators. We show that the topological loop model accounts not only for long-distance regulation by enhancers (silencers) but also for the ability of insulators to restrict the action of regulatory elements to the domain in which they reside. It is possible to reconstruct both of these regulatory phenomena in the context of the topological loop model with only one key but plausible assumption, namely that there are weak attractive interactions between nucleosomes or other generic chromatin components. By incorporating this feature into the properties of the chromatin polymer, the topological loop model not only explains the experimentally observed slow decay of long-range enhancer-promoter communication, but also the ability of insulators to block interdomain regulatory interactions.

One limitation of our model is that the chromatin fiber is simulated by a polymer whose structural properties approximate the nucleosomal beads-on-a-string configuration. In fact, chromatin in the cell has an as yet not fully understood higher-order structure that substantially condenses the chromatin fiber. In the context of a looped domain, this compaction would bring distant points in a loop in much closer contact than would be the case for a beads-on-a-string polymer. It remains to be seen, however, whether such compaction brings in a qualitative change in the nature of long-distance communication in chromatin.

Proposal for Experimental Investigation.

Our computational model not only expounds a possible mechanism for the hitherto unexplained efficacy of loop domains in long-range gene regulation, it offers concrete and testable predictions. Briefly, they are—

• Though euchromatin conformations are typically Gaussian polymer in nature, rare compact conformations appear sporadically, and these conformations predominantly contribute to long-range contact probability.

• In the presence of multiple insulators, the specific loop domains formed by insulator pairing/clustering determine the suppression of interdomain contacts and this suppression is dependent on the relative distances and positions of enhancers, promoters, and insulators.

Our model also offers a quantitative framework for investigating these predictions. Testing the first prediction is possible by direct visualization of chromatin conformation by in situ techniques like high-resolution multicolor three-dimensional (3D)-FISH (53) or multicolor 3D-SIM (54). Both of these techniques have the advantage of high-resolution; fluorescent probes can be used to tag tens of kilobases on chromatin where the total number of tags is limited by the total number of colors observable. A suitable genomic locus of length 100 Kb–1 Mb can be investigated in such techniques. Briefly, our model would predict that in a gene-poor region of euchromatin the statistics (averaged over many nuclei) of the 3D organization of the multicolor probe-signals would be approximately Gaussian. However, rare individual conformations would be observed where the colors are distributed in a compact conformation inexplicable by Gaussian statistics. We propose studying gene-poor region because the internucleosomal interactions that lead to such sporadic compaction is nonspecific in nature.

Testing the second prediction is possible by studying insulator-rich genomic loci using the same techniques. Knowledge of the genomic location of insulators (like CTCF) and the pairing/clustering interactions of insulator elements would allow one to resolve the statistics of interdomain and intradomain contacts using fluorescent microscopy. Another technique that can be used to complement such a quest is Chromatin Conformation Capture (3C/5C) (24, 55, 56), which map the pair-wise contact frequency between multiple regions of the chromatin. This technique has the advantage of being able to simultaneously query contacts between any number of “points” on chromatin, but the disadvantage that only average and pair-wise contacts are observable. The 3D conformation of chromatin cannot be extracted. Nevertheless, coupled with fluorescent microscopic techniques, 3C/5C can provide crucial information on the probable insulator pairing/clustering configurations, and the scope of inter and intradomain contacts within each of them.

We hope that the present work will inspire systematic experimental investigation of looping models in providing a robust physical mechanism of long-range gene regulation. Collaborative efforts on this front are already in progress.

Materials and Methods

Coarse-Grained Model of Chromatin.

We use a coarse-grained model of chromatin for our simulations; a bead-spring polymer where the nonoverlapping spherical beads represent nucleosomes and the springs connecting them represent the linker DNA and capture the overall flexibility of the nucleosomal packing. The spring is modeled by a version of the finite extensible nonlinear elastic (FENE) potential (57), which allows it finite extensibility, capturing chromatin’s stiffness to stretching. An energy cost to bending of the springs models the bending rigidity of chromatin. We also introduce phantom beads to ensure that the model polymer is non-self-crossing and all configurations preserve linking number. The polymer is also self-avoiding; we introduce a highly repulsive r^-12 potential (r is the center-to-center distance of beads) when beads overlap, effectively rejecting any Monte Carlo (MC) step that leads to overlap (guaranteeing no change in the linking number of the polymer configurations).

The transient interaction between nucleosomes is modeled as follows. As mentioned in the main text, the beads can be in two discrete states, active and inert, where the active state is of higher energy. Two active beads which happen to be within a short-interaction-range of each other (in any polymer configuration that the system explores) can form a temporary bond. This bond’s attractive potential is parametrized by the attraction parameter. The potential barrier to being active is parametrized by the availability parameter. In our simulations, we have used both a square well and a Gaussian well potential with a cut-off radius of twice the bead radius. Both of these potentials are a few k_BT in strength, where k_B is the Boltzmann constant and T is the temperature. The beads stochastically transition between the two states independent of the chromatin-polymer dynamics. We consider a range of values of attraction and availability parameter in our simulations. Both of them control effective interbead interactions and we have only presented robust features from many such parameter choices. We also disallow a nucleosome to make multiple bonds with other nucleosomes, a condition we refer to as bond saturation. Therefore, the higher-order interactions are repulsive in our model thereby disfavoring polymer collapse. It is known that the electrostatic-charge distribution on nucleosomes is highly complex (29), and uniformly attractive higher-order interactions seems unfeasible.

Simulation of the Model.

We simulate our model using MC method according to the standard Metropolis algorithm (57). In order to save computational cost, the slower processes of update of the state of the nucleosomes and the status of the bonds between them are done asynchronously with exponential waiting times between queries, where a single bead is chosen randomly at random query times to attempt the update steps. All beads are taken to be identical, and the raw data is the set of temporary bonds formed between beads at fixed sampling time intervals for the entire run. The bead-spring polymer is in a ring construction with 200 beads. We use a closed circle instead of linear molecule for two reasons. The first is to avoid potential boundary effects at the ends of the polymer. The second is to model a topologically independent chromatin loop domain. After an initial equilibration time, the equilibrated random configuration is used as the initial configuration for parallel runs to collect our data, which is of the order of fifty million accepted MC steps for each bead (where each MC attempted step length is 5% of bead size).