Low absorption losses of strongly coupled surface plasmons in nanoparticle assemblies

Abstract

Coupled surface plasmons in one-dimensional assemblies of metal nanoparticles have attracted significant attention because strong interparticle interactions lead to large electromagnetic field enhancements that can be exploited for localizing and amplifying electromagnetic radiation in nanoscale structures. Ohmic loss (i.e., absorption by the metal), however, limits the performance of any application due to nonradiative surface plasmon relaxation. While absorption losses have been studied theoretically, they have not been quantified experimentally for strongly coupled surface plasmons. Here, we report on the ohmic loss in one-dimensional assemblies of gold nanoparticles with small interparticle separations of only a few nanometers and hence strong plasmon coupling. Both the absorption and scattering cross-sections of coupled surface plasmons were determined and compared to electrodynamic simulations. A lower absorption and higher scattering cross-section for coupled surface plasmons compared to surface plasmons of isolated nanoparticles suggest that coupled surface plasmons suffer smaller ohmic losses and therefore act as better antennas. These experimental results provide important insight for the design of plasmonic devices.

Plasmonic antennas can convert optical radiation into intense local field distributions or enable coupling to guided modes that are confined to subwavelength dimensions (1–4). Strong surface plasmon (SP) coupling between neighboring nanoparticles (NPs) also leads to large enhancements of electromagnetic fields, which benefit various applications such as waveguides (5, 6), nano-antennas (7–9), field enhanced spectroscopies (10–12), and biological sensors (4, 13, 14). The interparticle coupling resulting from near-field interactions between closely spaced NPs is inversely proportional to d³ where d is the distance between the NPs (6). The largest local field enhancements are indeed found for the smallest interparticle distances (11, 15). Extremely small interparticle gaps of a few nanometers can be achieved in self-assembled nanostructures (16–19), opening up new paths for the design of plasmonic devices. With bottom-up assembly, precise periodic positioning of the NPs is more difficult and hence structures with a distribution of NP gaps are created. However, high throughput patterning for large area fabrication at reduced costs make NP assemblies attractive alternatives to structures made by conventional top-down approaches (20). For the system studied here, SI Appendix, Fig. S1 shows an example of a periodic array of rings assembled from a chloroform solution of 40 nm gold NPs. In addition, the recent use of correlated electron and optical microscopy on individual NP assemblies is making it possible to decipher the effects of local NP ordering and symmetry breaking on the collective optical response (21).

Independent of the plasmonic nanostructure, absorption by the metal is thought to be the main mechanism for plasmon energy dissipation due to nonradiative relaxation processes (3, 22–24). Substantial attenuation of electromagnetic waves due to ohmic loss is therefore the major issue for applications such as subwavelength plasmonic circuits (4, 5, 22–28). For example, the propagation distances of SP polaritons are significantly reduced because of absorption losses, limiting the effectiveness of plasmonic waveguides (22–28). Although a few theoretical studies have reported on absorption losses of SPs (22–24, 28), quantitative experimental studies are urgently needed. In particular, a deeper understanding of the field enhancements and absorption losses for coupled SPs in NP assemblies is required for the rational design of improved plasmonic NP devices.

The strength of near-field interactions between NPs is directly related to the red-shift of the coupled SP resonance as generally probed by scattering spectroscopy for small NP assemblies such as dimers and trimers (15, 29, 30). Higher order SP modes have also been observed for larger assemblies of closely spaced NPs (31). In addition, it has been shown that the spectral dependence of the electromagnetic field enhancement in these NP structures follows the collective scattering response (15, 32, 33). Because significantly larger electromagnetic field enhancements are encountered for coupled SPs (9, 11, 15, 33), more efficient plasmonic antennas can be realized for excitation at wavelengths corresponding to coupled SPs rather than the single NP SP resonance, unless the magnitude of ohmic loss also increases and absorption losses become prohibitive. Therefore, measuring both absorption (σ_ABS) and scattering cross-sections (σ_SCA) for coupled SPs in closely spaced NP assemblies is necessary to understand the interplay between electromagentic field enhancement and ohmic loss. While SP absorption of a single NP has been measured by photothermal heterodyne imaging (34–37), absorption of red-shifted coupled SPs has not been explored in detail.

In this work, we separately measured absorption and scattering of coupled SPs in individual self-assembled nanostructures. Micrometer large rings composed of polystyrene-functionalized gold NPs (31) served as quasi one-dimensional (1D) NP chains, whose structures were analyzed using electron microscopy (Fig. 1A and SI Appendix, Fig. S1). Experiments were complemented by detailed electrodynamic simulations. We found that, whereas σ_SCA increases for coupled SPs compared to isolated NPs, σ_ABS decreases for coupled SPs compared to the SP of the individual gold NPs.

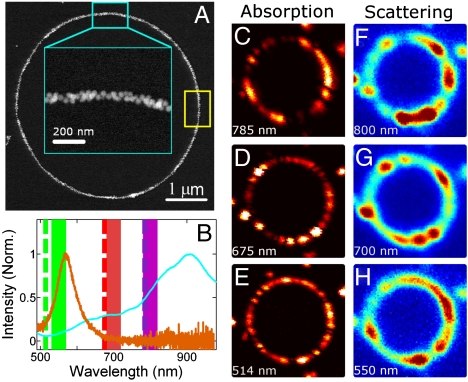
Fig. 1.

Absorption and scattering of coupled SPs in a self-assembled NP ring. (A) SEM image of a ring composed of 40-nm gold NPs. The diameter of this ring was 4.6 μm. (B) Scattering spectra of the ring segment (cyan) marked by the cyan rectangle in A and a single NP (orange). The purple, red, and green dashed lines represent the excitation wavelengths of 785, 675, and 514 nm that were used for photothermal heterodyne imaging. The purple, red, and green bars illustrate the spectral bandwidths of 800 ± 20, 700 ± 20, and 550 ± 20 nm that were used for wavelength selective scattering imaging. C, D, and E show the photothermal images of the NP ring with circularly polarized excitation at wavelengths of 785, 675, and 514 nm, respectively. F, G, and H are the unpolarized scattering images of the ring recorded at 800 ± 20, 700 ± 20, and 550 ± 20 nm, respectively. Note that the images are not scaled to each other as they were acquired adjusting the intensity of the incident or detected light so that the signal covered the full dynamic range for each experiment.

Results and Discussion

Rings of polystyrene-coated 40-nm gold NPs were fabricated on glass slides as described previously (31). Polyvinyl alcohol films with a refractive index of 1.5 were spin-cast on top of the rings to provide a homogenous surrounding medium. Fig. 1A shows a scanning electron microscopy (SEM) image of an NP ring with a diameter of 4.6 μm. Due to the large ring diameter compared to the NP size and hence small local curvature, a segment of the ring mimics a 1D NP chain.

The emergence of strongly coupled SP modes was visualized by acquiring scattering spectra for approximately 500-nm-long segments along the NP ring circumference. The length of the ring segment was determined by the size of a pinhole placed in the imaging plane of a home-built single particle microscope. Fig. 1B shows a scattering spectrum with multiple, broad peaks for the ring segment (cyan) that is marked by the cyan rectangle in Fig. 1A. The additional resonances at lower energies compared to the response of a single 40-nm gold NP (orange) result from strong near-field coupling between the NPs (19, 31).

Wavelength resolved imaging was used to investigate the absorption and scattering of coupled SPs for the NP ring. Fig. 1 C–E display the absorption images for the ring in Fig. 1A recorded by photothermal heterodyne imaging, which selectively measures only the absorption through heat-induced refractive index changes of the surrounding medium (34–39). Excitation was performed with lasers operating at 785, 675, and 514 nm as indicated by the dashed colored lines in Fig. 1B. Heating powers were kept below the threshold for laser mediated melting of the NPs as confirmed by the absence of a change in the scattering spectrum for the same local ring segment before and after photothermal imaging (SI Appendix, Fig. S2). Dark-field scattering images (Fig. 1 F–H) at corresponding wavelengths were obtained by placing 40-nm band pass filters centered at 800, 700, and 550 nm in front of the avalanche photodiode.

Excitations with 514 and 550 nm for absorption and scattering, respectively, are also resonant with the SP mode of the constituent 40-nm gold NPs (Fig. 1B) in addition to higher order coupled SP modes. On the other hand, at the two longer wavelengths only coupled SPs of the NP ring were excited as confirmed by measuring absorption images of single NPs with 785 and 675 nm (SI Appendix, Fig. S3). The coupled SP modes are more sensitive to the local arrangement of the NPs and several hot spots with large intensities that do not scale with the number of NPs per area are present in both absorption (Fig. 1 C and D) and scattering (Fig. 1 F and G) images. This result is characteristic of nonuniform electromagnetic field enhancements in strongly coupled NP clusters (40). Interestingly, at these longer wavelengths the absorption and scattering intensity distribution along the ring (i.e., the number and location of hot spots) do not correlate with each other. In contrast, at 514 nm the absorption intensity of the ring approximately scales with the number of NPs per area (SI Appendix, Figs. S4 and S5).

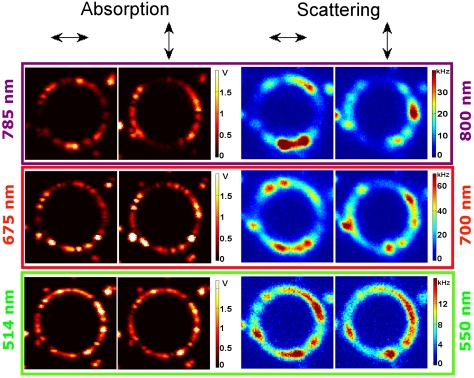
The coupled SP absorption modes for the NP ring were further investigated by polarization sensitive imaging. For wavelengths red-shifted from the single NP SP resonance, the absorption intensities were highly polarized along the direction of the local NP alignment. Fig. 2 presents wavelength resolved and polarization sensitive absorption (left) and scattering (right) images of the NP ring for two orthogonal polarizations. At the longest wavelength (785 nm for absorption and 800 nm for scattering), both absorption and scattering intensities increased when the polarization was parallel to the local ring segment. Minimum intensities were observed for polarization directions perpendicular to the local NP alignment. A similar trend, although with less contrast, was also observed for absorption at 675 nm and scattering at 700 nm. On the other hand, the absorption and scattering images taken at the shortest wavelength did not depend on the polarization.

Fig. 2.

Polarization sensitive and wavelength dependent photothermal and scattering images of an NP ring. Photothermal images of the same ring as shown in Fig. 1A excited with horizontal (first column) and vertical (second column) polarizations, and scattering images detected with horizontal (third column) and vertical (forth column) polarizations. The excitation and detection wavelengths for absorption and scattering are displayed next to the corresponding images.

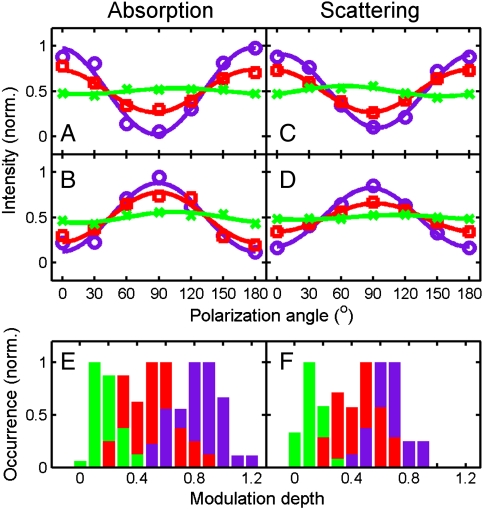
With increasing wavelength, the polarization dependence of coupled SP modes increases for both absorption and scattering. This was quantified by recording images as a function of polarization angle θ in 30° increments (SI Appendix, Figs. S6 and S7). Fig. 3 A and B show the polarization dependence of the absorption intensities for 785 nm (purple), 675 nm (red), and 514 nm (green) excitation analyzed at the ring locations marked by the yellow and cyan rectangles in Fig. 1A, respectively. The corresponding data for SP scattering at 800, 700, and 550 nm is given in Fig. 3 C and D. The polarization dependence was examined by fitting the intensities I to I(θ) = N(1 + M cos 2(θ - ϕ)) where N is a normalization constant (36). The modulation depth M represents the average in plane projection of a collection of dipoles describing the system. M = 1 for a single dipole or if all dipoles are aligned in parallel, while M = 0 if the dipoles are randomly distributed (SI Appendix, Fig. S8). The phase angle ϕ gives the orientation of the average dipole moment in the sample plane with respect to a reference axis. Consistent with a parallel orientation of the coupled SP oscillations and the local NP alignment, the polarization traces for the two highlighted ring locations are 90 ° out of phase.

Fig. 3.

Polarization of NP ring SPs for absorption and scattering intensities along an NP ring. (A and B) Polarization dependence of the photothermal intensity of the local ring segments marked by the yellow and cyan rectangles in Fig. 1A, respectively. Purple, red, and green symbols represent excitation wavelengths of 785, 675, and 514 nm. The lines are fits and yield modulation depths of M₇₈₅ = 0.93 and 0.76; M₆₇₅ = 0.47 and 0.55; M₅₁₄ = 0.06 and 0.12. (C and D) Polarization dependence of the corresponding scattering intensity for the same local ring segments. Purple, red, and green symbols represent the spectral windows of 800 ± 20, 700 ± 20, and 550 ± 20 nm. The lines are fits and yield modulation depths of M₈₀₀ = 0.82 and 0.65; M₇₀₀ = 0.47 and 0.31; M₅₅₀ = 0.11 and 0.05. (E and F) Histograms of the modulation depth obtained from the photothermal and scattering polarization traces, respectively. For this analysis, the ring was divided into 40 and 24 segments for the photothermal and scattering measurements, respectively. Note that the colors of the bars correspond to those of the polarization traces.

Oscillation of coupled SPs parallel to the local NP alignment direction was furthermore found to be independent of the specific ring location and mostly uniform around the entire ring. The absorption and scattering images were divided into 40 and 24 areas, respectively, which was based on the resolution of the two imaging techniques. Modulation depths M and angles ϕ for each of these areas were then determined. The distributions of M values for absorption and scattering are summarized in Fig. 3 E and F. 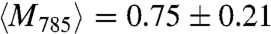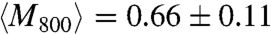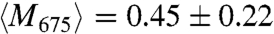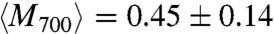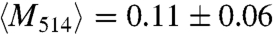The mean modulation depths are of comparable magnitude for absorption and scattering: and ; and ; and 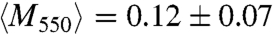. The error represents the standard deviation of M. The difference for the longest wavelength is most likely due to the larger wavelength interval of 40 nm probed by scattering in combination with the wavelength dependence of M. These results demonstrate how near-field interactions between isotropically shaped NPs lead to polarized collective nonradiative modes in addition to radiative modes.

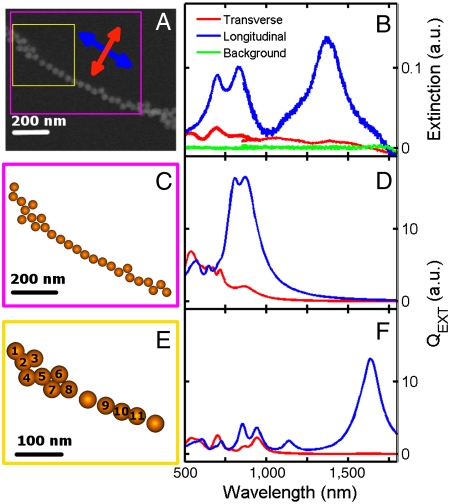
Electrodynamic simulations of local ring segments were carried out to validate and further interpret the experimental results. Because the scattering spectrum in Fig. 1A was cut off at low energies due to the limited spectral range of the Si CCD camera, we measured broadband extinction spectra covering a range of 500–1,800 nm in order to access the entire SP response of the NP ring. The SEM image in Fig. 4A shows the NP arrangement of a local ring segment. Extinction spectra recorded with linear polarization parallel and perpendicular to the local alignment of the NPs, as indicated by the blue and red arrows in Fig. 4A, are given in Fig. 4B and display a strong SP peak at 1,400 nm as well as multiple peaks between 500 and 1,000 nm. The longest wavelength SP modes are all highly polarized along the quasi 1D NP alignment. Although the relative intensities of these SP modes varied slightly from one ring area to another and for different NP rings having different diameters, all extinction spectra recorded shared similar spectral profiles (SI Appendix, Fig. S9).

Fig. 4.

Experimental and simulated extinction spectra for a segment of an NP ring. (A) SEM image of a ring segment composed of 40-nm gold NPs. (B) Extinction spectra of the ring segment in A recorded with excitation polarization parallel (blue) and perpendicular (red) to the 1D NP alignment direction. (C and D) GMT calculations for the ring segment marked by the magenta square in A. The modeled NP arrangement in C was taken from the SEM image keeping the minimum surface-to-surface separation between neighboring NPs greater than 1 nm. (E and F) FEM calculations for the ring segment marked by the yellow square in A. For the FEM calculations, the NPs labeled 1–8 and 9–11 were allowed to touch and hence coupled conductively.

Using the experimental NP arrangement, we calculated polarized extinction spectra using code developed based on generalized Mie theory (GMT) (41, 42). Fig. 4C shows the arrangement of 26 NPs that were all assumed to be 40-nm spheres and spaced at least 1 nm apart. Although this presents a simplification of the actual system where the NPs are highly faceted, GMT has the advantage of being able to compute the collective optical response of a large number of NPs while including many multipoles (42). The calculated polarized extinction spectra (Fig. 4D) show multiple SP resonances for wavelengths shorter than 1,000 nm, qualitatively reproducing the experimental results except for the SP resonance at 1,400 nm, which is absent in the GMT simulations. Increasing the number of NPs in the simulation did not push the longest wavelength SP resonance beyond 1,000 nm, consistent with previous results showing that the infinite chain limit is reached for about 10 NPs (42, 43).

The longest wavelength SP resonance can be explained by conductive plasmon coupling for touching NPs. Because GMT can only solve the optical response for nontouching NPs, we used the finite element method (FEM) to simulate the NP assembly shown in Fig. 4E containing only the first 13 NPs as these FEM calculations required significantly more computer resources. The calculated extinction spectrum with longitudinal polarization in Fig. 4F shows a strong SP resonance at 1,600 nm as well as several multipolar peaks with lower intensities. For this NP arrangement conductive contact for NPs 1–8 and 9–11 was assumed. However, because of the limited resolution of SEM it was not clear which NPs were actually touching. Therefore, different NP arrangements with varying numbers of touching NPs were simulated. The geometry in Fig. 4E resulted in the best qualitative agreement between the experimental (Fig. 4B) and calculated spectra (Fig. 4F). The simulation results for other NP arrangements are given in SI Appendix, Fig. S10. Further optimization of the NP shape and assembly geometry could in principle lead to better agreement between experiment and theory, but the main conclusion here is that it is necessary to consider touching NPs to explain the longest wavelength SP mode in these NP rings, which we assign to a charge transfer plasmon resonance (44–46). Because GMT matches the experimental results well for wavelengths below 1,000 nm the collective SP response in this wavelength range is assigned to mostly capacitive plasmon coupling between nontouching NPs.

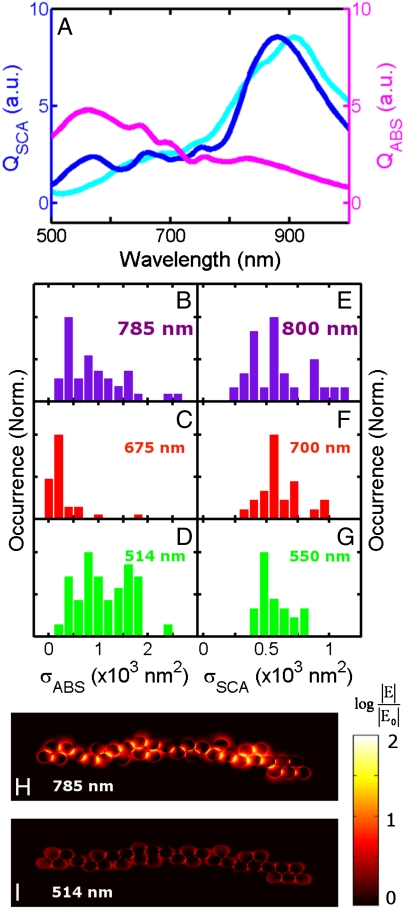
As all scattering and absorption measurements discussed earlier were also limited to the spectral range of 500–1,000 nm, we have chosen to use GMT to interpret the experimental results. Although this approach ignores the contribution from touching NPs, important physical insight can be gained. Fig. 5A shows unpolarized absorption (magenta) and scattering (blue) spectra simulated by GMT for the ring segment marked by the cyan rectangle in Fig. 1A. The experimental scattering spectrum (cyan) recorded with unpolarized excitation is also included. The excellent agreement between the experimental and calculated spectra confirms the validity of the GMT calculation and justifies our approach.

Fig. 5.

Absorption and scattering cross-sections of SPs in an NP ring. (A) Simulated absorption (magenta) and scattering (blue) spectra of the ring segment marked by the cyan rectangle in Fig. 1A. The experimental scattering spectrum (cyan) from Fig. 1A is also included for comparison. (B–D) Histograms of σ_ABS obtained from 40 ring segments of the photothermal images for 785, 675, and 514 nm excitation, respectively. (E–G) Histograms of σ_SCA obtained from 24 ring segments of the scattering images measured with band pass filters of 800 ± 20, 700 ± 20, and 550 ± 20 nm, respectively. (H and I) Electromagnetic-field enhancements of the same NP ring segment at 785 and 514 nm, respectively.

Based on the calculated spectra, the difference in modulation depths can now be explained more quantitatively. At 785/800 nm, because a combination of the SP dipole mode and the first higher-order mode was excited, the modulation depth was smaller than 1. At 675/700 nm, only higher-order SP modes were excited, which resulted in a smaller modulation depth. At 514/550 nm, both higher-order longitudinal as well as transverse SP modes were excited yielding the smallest modulation depth because of the orthogonal nature of these modes. Unpolarized interband transitions furthermore contributed to the reduced modulation depth at this wavelength.

Strongly coupled SPs at wavelengths red-shifted from the single NP SP response have smaller σ_ABS but larger σ_SCA. This can be directly seen from the simulated absorption and scattering spectra in Fig. 5A but can also be further quantified experimentally. We determined σ_ABS and σ_SCA of the NP ring by comparing the absorption and scattering intensities for the ring and individual NPs. We measured wavelength resolved photothermal and dark-field images for the NP ring and individual gold NPs under the same conditions. To cover the three wavelength regions of interest and yield strong scattering signals, we selected NP samples with mean sizes of 96 nm, 33 × 63 nm, and 22 × 70 nm as verified separately by TEM (SI Appendix, Fig. S11). FEM calculations of σ_ABS and σ_SCA for these NPs were performed assuming a homogenous surrounding medium with a refractive index of 1.5 (SI Appendix, Fig. S12). Experimentally, only NPs with a peak wavelength within ± 10 nm of the calculated value were selected based on their scattering spectra (SI Appendix, Fig. S13). The absorption and scattering intensity ratios between the individual NPs and areas along the ring were obtained and then multiplied by the calculated σ_ABS and σ_SCA of the single NPs. This procedure yields σ_ABS,ring and σ_SCA,ring for ring areas having a size that was limited by the optical resolution. To allow for comparisons independent of the detection area σ_ABS,ring and σ_SCA,ring were divided by the number of NPs per integration area to give σ_ABS and σ_SCA, which also include normalization constants that take the different spectral observation windows into consideration. Further details regarding the calculation of σ_ABS and σ_SCA are discussed in the supporting information (SI Appendix, Figs. S14—S16 and Tables S1–S4).

Fig. 5 B–D shows histograms of σ_ABS for the NP ring excited at 785, 675, and 514 nm, respectively. The median σ_ABS is significantly lower for the SPs at 785 and 675 nm compared to the SP at 514 nm. We determined values of σ_ABS = 736 nm² at 785 nm and σ_ABS = 163 nm² at 675 nm compared to σ_ABS = 1,048 nm² at 514 nm. The median is used here to exclude the effect of a few hot spots that are more dominant at longer wavelengths. On the other hand, the median σ_SCA calculated from the histograms given in Fig. 5 E–G increases slightly for 800 nm (σ_SCA = 576 nm²) and 700 nm (σ_SCA = 560 nm²) relative to 550 nm (σ_SCA = 521 nm²). The accuracy of this cross section analysis was verified by comparing the wavelength dependence of σ_SCA,ring for the area marked by the yellow rectangle in Fig. 1A with the scattering spectrum taken at the same location (SI Appendix, Fig. S17). The very good agreement between σ_SCA,ring and the scattering spectrum validates the procedure for the cross-section analysis. The observed trend for σ_ABS and σ_SCA in Fig. 5 B–G also agrees well with the simulated absorption and scattering spectra in Fig. 5A. These results lead us to conclude that in NP assemblies with small interparticle distances, smaller absorption, but larger scattering occurs for strongly coupled SP resonances at lower energies compared to the single NP SP. Because the scattering intensity is directly related to the electromagnetic field enhancement (15, 32, 33), the larger σ_SCA at red-shifted wavelengths should make coupled SPs better antennas. A larger electromagentic field enhancement at 785 nm compared to 514 nm was furthermore confirmed by calculating the field distributions (Fig. 5 H and I) using GMT for the local ring segment corresponding to the spectra in Fig. 5A.

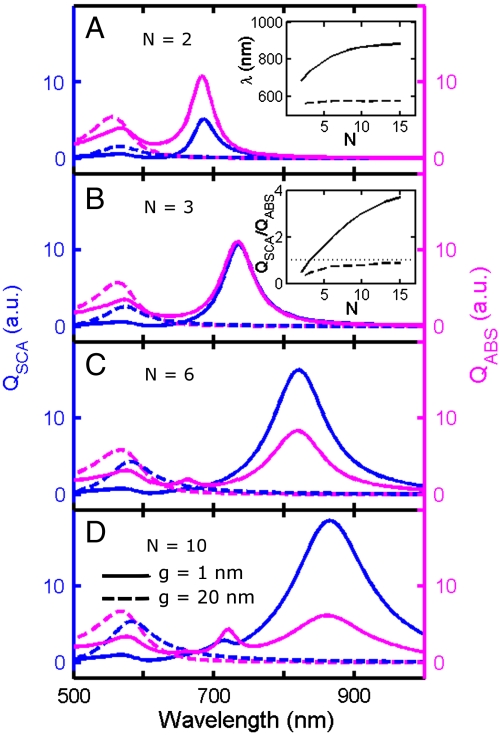
Small interparticle distances in assemblies of many NPs as investigated here in self-assembled NP rings are important to observe lower σ_ABS than σ_SCA for strongly coupled SPs. This is illustrated by GMT simulations of a simpler system of ordered linear chains with varying number of NPs. Fig. 6 shows scattering (blue) and absorption (magenta) efficiencies of NP chains with interparticle gaps of 1 nm (solid line) and 20 nm (dash line), composed of 2 (A), 3 (B), 6 (C), and 10 (D) NPs. For gaps of g = 1 nm, the dipole SP resonance red-shifted from 685 nm for a dimer to 862 nm for 10 NPs, while for 20 nm gaps because of reduced plasmon coupling the spectral shift was only 20 nm, which is further illustrated in the inset of Fig. 6A for chain length of up to N = 15. For both interparticle distances, the scattering efficiency of at the dipole SP resonance (superradiant mode) furthermore increases relative to the absorption efficiency with increasing number of NPs. This is shown in the inset of Fig. 6B where the ration of Q_SCA/Q_ABS is plotted vs. N. However, only for g = 1 nm scattering becomes more dominant than absorption for the ordered linear chains in Fig. 6. The stronger scattering results from an increased dipole of the collective SP response as more NPs contribute. The interparticle distances have to be small though to allow for strong coupling. Consistent with our results, calculations of NP dimers and heptamers have shown that radiation dominates the competition between scattering and absorption at the superradiant mode (47, 48). Interband absorption near the single NP resonance also contributed to the higher absorption cross section at 514 nm.

Fig. 6.

Absorption and scattering efficiency of ordered NP chains. (A–D) Scattering (Q_SCA, blue) and absorption (Q_ABS, magenta) efficiencies of linear chains composed of 2 (A), 3 (B), 6 (C), and 10 (D) 40-nm gold NPs. The efficiency Q is defined as the optical cross section normalized by the geometric cross-section of the total number of NPs. Spectra were calculated for gaps of g = 1 nm (solid line) and g = 20 nm (dashed line) between neighboring NPs. The insets in A and B show the resonance maximum and the ratio of scattering and absorption efficiencies at the dipole SP mode for gaps of 1 and 20 nm as a function of NP number, respectively. The dotted horizontal line in the inset in B, Q_SCA/Q_ABS = 1, is given as a reference to illustrate when scattering becomes more dominant than absorption.

Conclusions

In summary, we have measured σ_ABS and σ_SCA of coupled SPs in self-assembled quasi 1D structures composed of 40-nm gold NPs. Coupled absorption modes excited at longer wavelengths compared to the SP of the constituent single NPs were identified by polarization sensitive imaging and verified by electromagnetic calculations. Similar to scattering, the collective nonradiative SP modes are sensitive to the overall morphology of the NP assembly as the absorption intensities were enhanced when the polarization was parallel to the local ring segments. In addition, we found a lower σ_ABS in combination with a higher σ_SCA for the coupled SPs in these chemically prepared NP assemblies, implying smaller ohmic losses and larger local fields at red-shifted wavelengths, allowing one to minimize absorptive losses while maximizing electromagnetic field enhancements with coupled SPs for the design of efficient plasmonic nano-antennas.

Materials and Methods

Sample Preparation.

Polystyrene-functionalized gold NPs (MW_PS = 10,000 g/mol) were synthesized following the procedure described elsewhere (18). The diameter of the gold NPs was 40 ± 5 nm as confirmed by TEM (JEOL 1230 HC-TEM operated at 80 kV). By allowing a drop of the functionalized gold NPs solution to dry on a glass slide, rings were formed at the interface between the organic solvent and water droplets that condensed from the air due to evaporative cooling of chloroform. A gold pattern was evaporated onto glass slides using an indexed copper TEM grid (Ted Pella) that had no support layer, allowing us to locate the same structures in scanning electron and optical microscopy.

Dark-Field Spectroscopy.

Dark-field excitation was performed in a reflected light geometry using an inverted microscope (Zeiss) with a halogen lamp as the excitation source. Scattered light was collected using a Zeiss EC Epiplan-Neofluar objective (50×, N.A. = 0.8). After passing through a 50-μm pinhole, the signal was focused onto an avalanche photodiode (Perkin Elmer). A polarizer and a band pass filter were placed in the detection path after the pinhole to measure the polarization and wavelength dependence of the scattered light. The images were created by scanning the sample using a piezo scanning stage (Physik Instrumente) connected to a surface probe microscope controller (RHK Technology). Scattering spectra were acquired with a spectrometer and a Si CCD camera (Princeton Instruments).

Broadband Extinction Spectroscopy.

Extinction spectra were acquired using the same microscope setup. Light from a tungsten halogen lamp (Newport) was incident from above the sample to allow for excitation at normal incidence. The transmitted light was collected by a Zeiss EC Epiplan-Neofluar objective and directed either through the same 50-μm pinhole toward the Si CCD camera or focused into a 100-μm diameter fiber that was connected to a spectrometer (Andor Technology SR-163) equipped with an InGaAs array detector (Andor Technology DU491A-2.2). Broadband extinction spectra were then created by combining spectra from the Si CCD camera (500–1,000 nm) and the InGaAs array detector (900–1,800 nm).

Photothermal Heterodyne Imaging.

Photothermal heterodyne imaging was performed in transmission geometry (39) using the same microscope setup. A 514-nm Ar⁺ laser (Modu-Laser) and 675-nm or 785-nm diode lasers (Power Technology) were used as the heating beams. The polarization of the heating beams was controlled using half and quarter waveplates. A 633-nm He-Ne laser (JSD Uniphase) was employed as the probe beam. Each laser was focused independently to ensure best overlap at the focus between heating and probe beams for optimum resolution. The intensity of the heating beam was modulated at 400 kHz with an acousto-optic modulator (IntraAction). The laser beams were focused on the sample with a Zeiss Fluar objective (100×, N.A. = 1.3). The transmitted probe beam was collected by a Zeiss EC Epiplan-Neofluar objective (50×, N.A. = 0.8). The heating beam was rejected by a 633-nm band pass filter (Thorlabs). The photothermal signal was detected by an avalanche photodiode module (Hamamatsu) and fed into a lock-in amplifier (Princeton Applied Research), which was connected to the same surface probe microscope controller. Photothermal images were acquired by scanning the sample.

Electrodynamics Simulations.

GMT calculations were performed using a code that we have developed for modeling individual and multiple spherical metal NPs (42). For a single sphere, the electrodynamic solution for the optical cross-sections is the well-known Mie theory (49) in which the scattered and incident fields are represented as a complete expansion of vector spherical harmonics with appropriate weighting coefficients. By extending this solution to N NPs, whereby the incoming scattered fields from neighboring NPs act as further excitations, the scattering coefficients for each of the N NPs are solved, yielding analytical solutions for the electrodynamic fields and optical cross-sections. FEM calculations were carried out using the commercially available software COMSOL Multiphysics, which can simulate arbitrary NP geometries including overlapping spheres that mimic the conductive overlap of neighboring NPs. All calculations were carried using tabulated values for the complex dielectric response of gold (50) and an effective dielectric medium of 1.5.