Probability Machines: Consistent Probability Estimation Using Nonparametric Learning Machines

Summary

Background

Most machine learning approaches only provide a classification for binary responses. However, probabilities are required for risk estimation using individual patient characteristics. It has been shown recently that every statistical learning machine known to be consistent for a nonparametric regression problem is a probability machine that is provably consistent for this estimation problem.

Objectives

The aim of this paper is to show how random forests and nearest neighbors can be used for consistent estimation of individual probabilities.

Methods

Two random forest algorithms and two nearest neighbor algorithms are described in detail for estimation of individual probabilities. We discuss the consistency of random forests, nearest neighbors and other learning machines in detail. We conduct a simulation study to illustrate the validity of the methods. We exemplify the algorithms by analyzing two well-known data sets on the diagnosis of appendicitis and the diagnosis of diabetes in Pima Indians.

Results

Simulations demonstrate the validity of the method. With the real data application, we show the accuracy and practicality of this approach. We provide sample code from R packages in which the probability estimation is already available. This means that all calculations can be performed using existing software.

Conclusions

Random forest algorithms as well as nearest neighbor approaches are valid machine learning methods for estimating individual probabilities for binary responses. Freely available implementations are available in R and may be used for applications.

Introduction

The problem of making accurate binary classification, also termed pattern recognition has a long successful history. Statistical learning machines are often employed for this task because of their good discriminatory performance. A closely related problem is estimation of the probability of group membership, and this is very important in biomedical applications (1). Beyond a simple statement that a patient is in one group or another, they are better informed by having an estimated probability for belonging to one of the groups. The performance of such a probability estimation model is assessed in terms of calibration, which is defined as the degree to which estimated probabilities are accurate.

The model-free, nonparametric probability estimation problem has long been considered difficult (2), although the probability of group membership is just the conditional Bayes probability given a list of features, i.e., possible predictors. Classical parametric models, such as logistic regression, or semiparametric models, such as generalized additive models, have been widely used for probability estimation. Several assumptions underlying these methods are rather strict and limit its use in practice: all the important predictors and supposed interactions must be entered correctly in the model. Otherwise, important problems of model misspecification can arise. Such constraints do not support scalability in today’s very data-rich environments, where it is common to have data with up to a million potential predictors with unknown correlation structure. The application of logistic regression or generalized additive models therefore leave unsolved the more general question of nonparametric, nonlinear, robust estimation of individual probabilities, given arbitrarily large numbers of predictors, potentially of different types and having unknown interactions within the predictors.

A solution of this general probability estimation problem is obtained by treating it as a nonparametric regression problem, a task for which many learning machines are already available. We refer to learning machines which estimate the conditional probability function for a binary outcome as probability machines.

A key idea is that learning machines that perform well as nonparametric regression machines will also perform well as probability machines. The list of good regression machines is extensive and growing, and it includes nearest neighbors, neural networks, kernel methods and penalized least squares (3, 4). Bagged nearest neighbors (b-NN = k-nearest neighbors (k-NN) bagged regression), introduced by Breiman (5), and data partitioning methods, such as decision trees and random forests (RF; 6) are also among this group. However, some learning machines are known to be problematic and may not allow consistent estimation of probabilities, see, e.g., Mease et al. (7) and Mease and Wyner (8) for a discussion of logitboost and Adaboost. Furthermore, Bartlett and Tewari (9) consider the hazards of using the output of any support vector machine (SVM), or some transformation of it, as a direct estimate of the test subject probability; also see the erratum by Glasmachers (10) in which he withdraws his proof of consistency of multi-class SVM and states that multi-class SVM is not universally consistent.

Recent work on large-margin SVM classifiers have shown how they can be modified for solving the problem of estimating individual probabilities (11). Specifically, sophisticated computations are used as a solution path to bracket the probability for a given subject. This approach is not identical to the direct probability estimate we describe here because a practicably impossible infinite number of brackets, also termed bins is required for generating any desired level of accuracy. In summary, the consistency of parameter estimates from SVM can only be guaranteed for binning methods; other SVM schemes may be consistent but this has to be considered on a case-by-case basis. Still other approaches, such as those implemented in libSVM (12), have no proven theoretical basis for probability estimation.

It is important to emphasize that the probability machines considered here are fully nonparametric, make essentially no distributional assumptions for the vector of features, make no restrictions on the length of the feature list, and most importantly do not require a specified model as a starting point. As will be demonstrated below, these machines have one additional advantage when operated as regression machines: no additional coding or changes to the basic algorithms underlying these machines is required.

Critical readers might argue that estimating individual probabilities has been well studied in the field of machine learning or pattern recognition, even at a textbook level as soft classification. However, soft classification still is classification, not individual probability estimation. Another concern against our work might be that several software packages, such as the prob option in the randomForest package of R, already allow the estimation of individual probabilities. However, the availability of such an option does not mean that its output may be interpreted as a consistent estimate of a probability. The consistency still needs to be proven mathematically.

In this work, we focus on RF and b-NN, operating as probability machines. We demonstrate how RF, k-NN, and b-NN can be used for consistent estimation of individual probabilities. We illustrate the findings in a simulation study and the analysis of two biomedical data sets. The methods are also compared with logistic regression and logitboost which can give and claim to give, respectively, individual probability estimates conditional on the features.

Methods

Classification random forests (classRF) and regression random forests (regRF) as probability machines

As in Breiman (6) consider a training data set drawn from a sample of independently identically distributed random variables (x₁, y₁), (x₂, y₂), …, (x_n, y_n). Here, each subject i is a pair of a feature vector x_i taking values in IR^p and an outcome y_i with values 0 or 1. A test subject is dropped down the tree in the usual RF manner and soon resides in a terminal node. Under classification in random forests (classRF) a binary prognosis is made in each tree by taking a majority vote in this terminal node of the tree. Under regression in random forests (regRF), an estimate of the probability of y given the features x is obtained instead. This is done by taking the proportion of observations in the training data set with y-value being 1. We stress that the terms classRF and regRF are not related to the split criteria used for generating the RF although the split criterion might affect the performance of the RF. The general regRF procedure takes the following steps (modified from standard RF from Ref 13):

1. Consider a training data set of size n.

2. A bootstrap sample b consisting of n samples drawn with replacement is drawn from the original training data set. The samples left out due to the bootstrapping process are called ‘out-of-bag’ (OOB) data.

3. A regression tree is grown using the bootstrap data set. The tree is constructed by recursively splitting data into distinct subsets so that one parent node leaves two child nodes. For splitting data, all splits of a random subset of features are considered. If features are continuous, the optimal split of a feature is the one minimizing the mean square error (MSE) in the training data. The feature minimizing the MSE over all randomly selected features at this node is selected. The number of features selected at a node is termed mtry in many RF packages and might vary. In applications, it is held constant during the procedure, and the default setting is $\text{mtry}=\lceil \sqrt{p}\rceil$, where ⌈ · ⌉ denotes the next largest integer.

4. The tree is grown to the greatest extent possible but requiring a minimum nodesize of 10% of the sample. No pruning is performed. The final nodes in a tree are called terminal nodes.

5. The proportion of ‘1s’ in each terminal node of the tree is determined.

6. Steps 2 to 5 are repeated to grow a specific number of trees ntree.

7. To estimate the probability of a new subject, it is dropped down a tree until its final node. The proportion of ‘1s’ in this final node is determined. The probability estimate is the proportion of ‘1s’averaged over all ntree trees.

For classRF, only steps (3) and (5) in the algorithm are altered. Specifically, in (3) a dichotomous purity measure, such as the Gini index or the deviance is used instead of the MSE (for details, see, e.g., Ref. 14). In step (5), the majority vote is taken in a terminal node. Step (4) of the algorithm is different from current standard. In most RF implementations, tree growing is stopped when ≥ 5 observations are left in the terminal node, regardless of sample size, or they are grown to purity. The choice of 10% in step (4) is a practical decision only; theory guiding this choice is given in Devroye et al. (2).

k-nearest neighbors (k-NN) and bagged nearest neighbors (b-NN) as probability machines

The averaging idea described above can be directly used for bootstrap averaging (bagging) in the context of k-nearest neighbors, and the probability machine algorithm for k-NN bagged regression is as follows; also see Breiman (5):

1. Consider a training data set of size n.

2. A bootstrap sample b consisting of n samples drawn with replacement is drawn.

3. The distance in the feature space is determined for the samples in the bootstrap sample using a suitable metric.

4. The proportion of ‘1s’ of the k-nearest neighbors of a sample in the bootstrap sample is determined.

5. Steps 2 to 4 are repeated.

6. The probability estimate of the b-NN is the proportion of ‘1s’ averaged over all bootstrap samples.

Consistency of random forests and nearest neighbors

Informally, in the situation described above, the aim is to estimate the conditional probability η(x) = IP(y = 1|x) of an observation y being equal to 1 given the features x. By noting that IP(y = l|x) = IE(y|x) it can be seen that the probability estimation problem is identical to the nonparametric regression estimation problem f(x) = IE(y|x). Hence, any learning machine performing well on the nonparametric regression problem f(x) will also perform well on the probability estimation problem η(x).

Thus, we aim at building a prognostic rule f: IR^p → IR on the basis of the observations such that an estimate f̂(x) of the regression function f(x) is a “good approximation” to y. More formally, we say that a regression function estimate is consistent if the mean square error IE((f̂(x) – f(x))²) converges to 0 if n → ∞.

Consistency has been shown for many different nonparametric regression machines, such as nearest neighbors, neural networks, kernel methods and penalized least squares (3, 4). Recently, Biau et al. (15) have considered the simple randomized RF model of Breiman (6), where splits are done at random. Specifically, in a single tree of the forest a leaf is chosen at random in each step of its construction. A split feature is also chosen at random from the p candidates present in the feature vector. Furthermore, the selected leaf is randomly split using the selected feature. This procedure is performed k times in a tree. For this simple RF model, Biau et al. (15) considered the classRF mode. A related but slightly different RF model, where splits are done in the midpoint of the feature using the regRF approach has been investigated by Biau (16) recently. For both models, consistency of the classRF and regRF estimates f̂ of f has been proven. They also point out that one commonly applied version of RF, where splits are performed to purity, is not universally consistent. The last result is intuitively clear: If trees are grown to purity so that only a single observation resides in a terminal node, the probability estimate is based on only a sample of size n = 1. And averaging over a number of trees in an RF does not necessarily generate correct probabilities. Therefore, some impurity within the tree is required for consistency of RF; see Ref. (2) for more on terminal node size in trees. In contrast, bagging over trees split to purity does return consistency (15).

Biau and Devroye (17) have considered not only the random splitting and the midpoint splitting strategies of RF but also general splitting strategies, such as the one described in the RF algorithm above. They have been able to show that these RF models can be embedded into the theory of weighted layered nearest neighbors (18), and the RF models therefore inherit consistency properties of weighted layered nearest neighbors.

In these different articles, convergence rates are also discussed, showing that RF provably has the optimal rate under weak conditions.

Although these consistency and optimality results are quite general, we need to emphasize that RF has many moving parts, not all of which are being taken into account when these consistency results are obtained. The results also suggest that the convergence rates quoted in the current literature might be sharply improvable as more of the working properties of regRF are pulled into the story.

In simpler terms, the regression estimate tries to locate the expected value of the independent variable, which is the binary outcome when we start with classification data, given the feature vector. But this is exactly the best regression estimate of the true conditional probability, given the features. It follows that k-NN, single trees and other learning machines are consistent probability machines under exactly those conditions when they are known to be consistent as regression machines. Equally important is the fact that we do not have to worry about the probability estimate falling outside the interval [0, 1] with these methods: no postprocessing regularization or constrained optimization is required.

For b-NN, the recent papers by Biau and colleagues (15, 17, 19, 20) showed consistency under general conditions when operating as regression estimators. Therefore, these machines are also consistent when acting as probability machines. Optimality and convergence rates of k-NN are discussed in Györfi et al. (3, Chapter 6). Moreover, they have separate chapters on the consistency of neural nets and kernel methods, when they act as regression estimators.

Simulation study

The predictive performance of classRF, regRF and b-NN is compared using Monte-Carlo simulations against three competing learning machines which also provide probability estimates for the binary regression problem, i.e., logistic regression (logreg), LogitBoost (21; lboost), and k-NN.

We used two simulation models in this study. The first is from Mease et al. (7), where they considered a simple two-dimensional circle model. Let x be a two-dimensional random vector uniformly distributed on the square [0,50]², and let y be a dichotomous dependent variable with values 0 or 1 and conditional probabilities given x be defined as

$$\text{IP}(y=1\mid \mathit{x})=\{\begin{array}{ll}1\hfill & r(\mathit{x})<8\hfill \\ \frac{28-r(\mathit{x})}{20}\hfill & 8\le r(\mathit{x})\le 20,\hfill \\ 0\hfill & r(\mathit{x})>28\hfill \end{array}$$ (1)

where r(x) is the Euclidean distance of x from (25,25). We will refer to this as the Mease model. We generated 5000 observations for x for the Mease model and computed the conditional distribution of y|x. We then simulated 250 sets of y from this conditional distribution using a binomial random number generator. We set aside 20%, i.e., 1000 observations of (x, y) pairs for validation purposes, and we trained the probability machines on the remaining 4000 observations for each of the 250 simulated data sets.

The second model is generated from the Connectionist Bench (Sonar, Mines vs. Rocks) data set from the UCI machine learning repository (http://archive.ics.uci.edu/ml). This data set consists of 208 records with 60 numerical covariates originally intended to train networks to discriminate sonar signals bounced off a metal cylinder and a rock (22). We used the covariates in a logistic regression model, where the coefficients were generated from a normal distribution with mean 2 and variance 0.2. The linear function was centered using an intercept term, probabilities were generated using the expit function, and dichotomous outcomes y were obtained using a binomial random number generator with the corresponding probabilities. We will refer to this model as the Sonar model. We generated 250 simulated data sets from the Sonar model as well, and reserved 20% (41) covariate observations and the corresponding simulated outcomes as a validation set.

For evaluating the goodness-of-fit and comparing the different machines using the training data we used the following bootstrap approach: First, we drew a bootstrap sample and second, trained the machines on the identical in-bag samples. Third, we evaluated the performance of the machine using the OOB samples.

To evaluate predicted probabilities when we do not have the true probability available, we used the Brier score (BS), which is given by $\text{BS}=\frac{1}{n}{\sum }_{i=1}^n{(y_i\widehat{\text{IP}}(y_i=1))}^2$ for a sample of n data points. The Brier score is a proper score (23), can be estimated consistently if IP(y_i = 1) is estimated consistently, and therefore deemed suitable for this probability validation. We utilized the MSE which measures the squared difference between IP(y_i = 1) and $\widehat{\text{IP}}(y_i=1)$ when true probabilities were available. The sampling variances can also be determined for both BS and MSE (24) and used for construction of confidence intervals.

As a graphical display, the estimated probabilities were plotted against the true, i.e., simulated probabilities. A smooth local regression (loess) with a two degree polynomial and a span of 0.75 was used as graphical smoother.

Hosmer-Lemeshow type figures were created as described by Gillmann and Minder (25). For the dichotomous outcome and predicted 0/1 value, standard measures of diagnostic accuracy, i.e., sensitivity and specificity were calculated and used for creating a receiver operator characteristic (ROC) curve. Finally, the areas under the ROC curves (AUC) of different learning machines were estimated.

Simulations and analyses were performed in R version 2.12. The functions and machines used are provided in Tab. I. Example R code is provided in the Appendix. We ensured that the number of observations in the terminal nodes for the RF was ≥ 10%, and the number of neighbors used in k-NN and in b-NN was max {5% n, 20} to allow for efficient estimation. logreg was run using main effects without interactions. Default settings were used for the other machines.

Table I.

Summary of functions and packages in R used in the simulation study.

Machine	Function	R package
b-NN	bag, knn3	caret (v. 4.54)
classRF	randomForest	randomForest (v. 4.5)
Lboost	LogitBoost	Rweka (v. 0.4)
logreg	Glm	stats (core, v. 2.11)
k-NN	knn3	caret (v. 4.54)
regRF	randomForest	randomForest (v. 4.5)

Application I: Diabetes in Pima Indians

The diabetes in Pima Indians data set was obtained from the UCI Repository of Machine Learning Databases (http://archive.ics.uci.edu/ml). All patients in this data set are Pima-Indian women at least 21 years old and living near Phoenix, Arizona, USA. The response variable is dichotomous with values 1 = diabetes, and 0, otherwise. Among the 768 observations, there are 268 (34.9%) diabetic cases. Eight clinical variables are available: number of times pregnant, plasma glucose concentration at 2 hours in an oral glucose tolerance test, diastolic blood pressure (mm Hg), triceps skin fold thickness (mm), 2-hour serum insulin (mu U/ml), body mass index (kg/m2), diabetes pedigree function and age (years).

Application II: Appendicitis diagnosis

The appendicitis data set is from a published study on the assessment of 8 laboratory tests to confirm the diagnosis of appendicitis (26). Following surgery, only 85 out of 106 patients were confirmed by biopsy to have had appendicitis. Thus, the ability to discriminate the true appendicitis patients by lab tests prior to surgery would prove extremely valuable. Because one test had some missing values, for purposes of comparison, we excluded results from that test.

Results

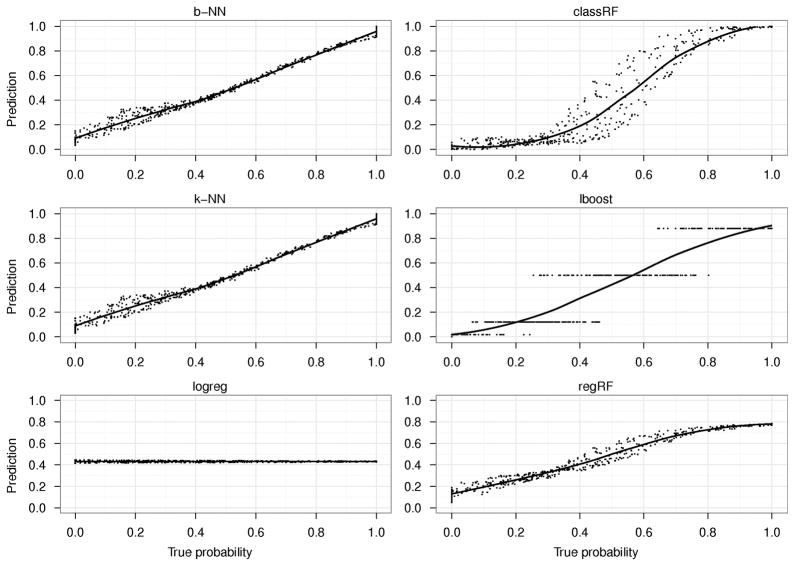
Fig. 1 shows the median probability predictions across simulations from the test data for each of the 6 machines against the true probabilities in the Mease model. regRF, b-NN and k-NN do the best on both the test and the training data (Supplementary Fig. 1). logreg is not able to correctly predict the probabilities. A better fitting logreg model on the Mease data could not be obtained using an interaction term of the form x₁ · x₂ because this interaction term does not allow a better fit of circular data. Instead, both quadratic terms of the form $x_1^2$ and $x_2^2$ would be required (for a detailed discussion, see Ref 27, Chapter 5). However, this points to a basic problem with any parametric model, namely the required complete and correct specification of interaction and higher order terms. And such specification is not required in the nonparametric methods such as regRF, k-NN, or b-NN. lboost has constant levels of predicted probabilities and does not do as well as the RF-based and the NN-based methods, either qualitatively or in terms of the MSE (Fig. 2, left, also see Supplementary Figs. 2–4; 24). For the Sonar model, both regRF and the NN-methods performed better than classRF (Supplementary Figs. 5–6). Note that classRF’s estimate is an average of vote-winners in the terminal nodes (“0” or “1”), whereas regRF’s estimate is an average of averages in the terminal nodes.

Figure 1.

Predicted versus true probabilities in the Mease model for the 6 learning machines using the test data. b-NN: k-nearest neighbor bagged regression, classRF: classification random forest, k-NN: k-nearest neighbors, lboost: logitboost, logreg: logistic regression, regRF: regression random forest.

Figure 2.

Boxplots of the MSE in the Mease model (left) and the Sonar model (right) for the 6 learning machines using the test data. b-NN: k-nearest neighbor bagged regression, classRF: classification random forest, k-NN: k-nearest neighbors, lboost: logitboost, logreg: logistic regression, regRF: regression random forest.

For the Sonar model, both the RF and the NN-methods performed well on both the training and the test data (Fig. 2, right; Supplementary Figs. 7–8), while lboost and logreg showed a poor fit (Fig. 2, right, and Supplementary Figures). We were surprised to see the bad performance of logreg on the Sonar data and therefore ran a second simulation with a substantially larger sample size (n = 40,000). The fit was substantially improved and better than regRF (results not shown).

regRF showed good performance on the two real datasets in terms of the Brier score and the ROC curves. The goodness-of-fit of the different models is depicted by Hosmer-Lemeshow-type plots in Supplementary Figs. 9–10. Both k-NN and b-NN performed well in terms of the Brier score but less well on ROC curves (Supplementary Fig. 11, Tab. II). classRF performs well on both datasets, but it is outperformed by regRF. Interestingly, lboost shows a similar AUC in the appendicitis data when compared with regRF, while it is substantially worse on the Pima Indians diabetes data set.

Table II.

Area under the ROC curves (AUC), Brier score, and nonparametric 95% bootstrap confidence intervals (in parenthesis) for the appendicitis and the Pima Indian diabetes data sets.

Machine	Appendicitis data		Pima Indian diabetes data
	AUC	Brier score	AUC	Brier score
b-NN	0.847 (0.672 – 1.000)	0.102 (0.066 – 0.145)	0.819 (0.779 – 0.858)	0.180 (0.167 – 0.197)
classRF	0.931 (0.846 – 0.900)	0.075 (0.038 – 0.121)	0.952 (0.853 – 0.913)	0.163 (0.147 – 0.184)
lboost	0.976 (0.928 – 0.900)	0.043 (0.023 – 0.073)	0.863 (0.825 – 0.897)	0.173 (0.155 – 0.198)
logreg	0.853 (0.672 – 0.900)	0.088 (0.050 – 0.136)	0.839 (0.802 – 0.875)	0.160 (0.145 – 0.181)
k-NN	0.844 (0.694 – 0.969)	0.106 (0.066 – 0.149)	0.843 (0.777 – 0.855)	0.182 (0.168 – 0.199)
regRF	0.976 (0.934 – 0.982)	0.061 (0.037 – 0.088)	0.971 (0.862 – 0.919)	0.163 (0.151 – 0.179)

Discussion

Probability estimation for individual subjects has a long-standing tradition in biomedicine. Applications include all areas of medicine, such as surgery (28), oncology (29), internal medicine (1), pathology (30), pediatrics (31), and human genetics (32).

Traditionally, the probability estimation problem is tackled by well-known statistical regression models, such as the logistic regression model, or density estimation approaches, such as linear discriminant analysis (33). Neural networks also belong to the class of model-based approaches, and the relationship between neural networks and regression analysis has been well established (34). However, model-based approaches impose important assumptions on the data, e.g., on the functional form of the probabilities or the underlying distribution of the features, to mention just two.

Nonparametric approaches avoid these assumptions. One such approach are SVMs. They are often used in bioinformatics applications and have also been considered for probability estimation (11, 33, 35). The SVM approaches are based on binning or bracketing and similar to nonparametric quantile regression estimators, as studied by Meinshausen (36). They repeatedly search for boundaries to weighted versions of the probability problem, starting from binary data. Approaches that use binning or bracketing the output probability interval appear to require rather extensive user input, calibration and the correct specification of the functional class containing the true conditional probability function. Most importantly, this line of research does not make the basic point that any regression consistent machine can provably do well, by directly estimating the individual test subject probability, often with much less need for computational resources or user input.

As an alternative to the model-based approaches and the bracketing methods, we have provided in this paper a general approach for probability estimation that is suitable for any binary outcome data. It builds on nonparametric regression methods and is thus model-free. It can use any kind of data, regardless of the structure of the predictors. Assumptions are not made about the distribution of the data, nor are specific functions or specification of interaction terms required. No pre-sifting or screening of features needs to be done. In fact, screening is discouraged to enable the learning machine to uncover hidden relationships or networks among the features. The importance, relevance or univariate predictive ability of a feature does not need to be assessed before including it in this approach. For some specific RF and NN machines, not only consistency but also sparseness has been shown (16, 19, 20).

To summarize, by viewing the conditional probability problem, given binary outcome data, as a regression problem we find that probability machines are already available, and they are fast and provably consistent. We expect this technique to be useful in any field in which probability estimation is important, such as credit scoring or weather forecasting. We have not considered here, by comparison, the many other provably consistent regression machines, such as specific forms of neural nets or SVMs. These also can provide probability estimates for each patient, though with possible computational limitations not present in regRF. Finally, we have also not considered some generalizations, such as the problem of multiclass probability estimation, where the training data are subjects having category or class outcomes. Other generalizations which will be considered in the near future include the analysis of matched data, right censored data, survival data, or data with dependent features.

Appendix: Example R code for estimating probabilities from random forests and k-nearest neighbors

In this section, we provide R code examples for estimating individual probabilities from regression random forests (regRF), classification random forests (classRF), k-nearest neighbors (k-NN) and k-nearest neighbors bagged regression (b-NN). First, the required packages need to be installed and loaded into the R workspace:

install.packages (‘randomForest’, repos=‘

http://cran.r-project.org

’)
install.packages (‘caret’, repos=‘

http://cran.r-project.org

’)
library (randomForest)
library (caret)

For illustration, we use a small example data set from the base R package.

data (infert)

The response variable is “case”; all other variables are features, indicates by the dot.

First, the regression RF method is shown. As an option, the nodesize needs to be declared. It indicates the minimum size of the terminal nodes, e.g., the minimum number or percentage of individuals that reside in a in the terminal node. In the example, the nodesize is set to 10% of the sample size of the applied data. It is important to note that case is not converted to a factor but is kept as a numeric variable for regression RF. Warnings on using a binary numerical variable in regression RF will be generated by the software and may be ignored.

regRF <- randomForest (case~., data=infert,
nodesize=floor (0.1*nrow (infert)))

ClassRF models can be generated by

classRF <- randomForest (factor (case) ~., data=infert,
nodesize=floor (0.1*nrow (infert))

Second, we apply k-NN method to the data. Here, the choice of the number of nearest neighbors k might be important. The option k controls the number of considered neighbors. In the example, the maximum number of neighbors is bounded by 5% of the sample size of the data.

knn <- knn3 (case~., data=infert, k=floor (0.05*nrow (infert)))

Third, b-NN is employed, and the calculations are slightly more complex for this learning machine. In the first step, the data frame infert is split into a data frame termed features here, which includes the features, and a vector class including the cases:

features <- infert [, names (infert) ! = “case”]
class <- infert$case

For b-NN in R, a fit, a prediction and an aggregate function must be declared. For a detailed description, see the manual.

baggedFit <- function (x, y, …) {
data <- as.data.frame (x); data$y <- y
knn3(y~., data = data, k=max (20, floor (0.05*nrow (data))))
}
baggedPred <- function (object, x) {
predict (object, x, type = “prob”) [, 2]
}
baggedAg <- function (x, type = “prob”) {
preds <- do.call (“cbind”, x); apply (preds, 1, mean)
}

After declaration of the bagged functions, b-NN is applied as follows:

bagKnn <- bag (features, class, B = 200, bagControl =
bagControl(fit =
baggedFit, predict = baggedPred, aggregate = baggedAg))

Here, the number of bootstraps is controlled by the parameter B.

Finally, the predictions are estimated for the single methods. Throughout, the estimation is done with the generic function predict, which has built-in versions for the different modeling methods. The main difference is the accumulation of the probability predictors. This depends on the architecture of the functions. Therefore each method needs a specific probability wrapper.

p.regRF <- predict (regRF, newdata=infert) # predict
random forest
p.classRF <- predict (classRF, newdata=infert, type=“prob”) [, 2]
p.knn <- predict (knn, newdata=infert) [, 2] # predict k-NN
p.bagKnn <- predict (bagKnn, newdata = infert, type = “prob”)