Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2012 Jan 4;102(1):144–151. doi: 10.1016/j.bpj.2011.11.4008

Discrete Molecular Dynamics Distinguishes Nativelike Binding Poses from Decoys in Difficult Targets

Elizabeth A Proctor †,‡, Shuangye Yin §, Alexander Tropsha †,‡,¶,‖, Nikolay V Dokholyan †,‡,§,¶,∗
PMCID: PMC3250674  PMID: 22225808

Abstract

Virtual screening is one of the major tools used in computer-aided drug discovery. In structure-based virtual screening, the scoring function is critical to identifying the correct docking pose and accurately predicting the binding affinities of compounds. However, the performance of existing scoring functions has been shown to be uneven for different targets, and some important drug targets have proven especially challenging. In these targets, scoring functions cannot accurately identify the native or near-native binding pose of the ligand from among decoy poses, which affects both the accuracy of the binding affinity prediction and the ability of virtual screening to identify true binders in chemical libraries. Here, we present an approach to discriminating native poses from decoys in difficult targets for which several scoring functions failed to correctly identify the native pose. Our approach employs Discrete Molecular Dynamics simulations to incorporate protein-ligand dynamics and the entropic effects of binding. We analyze a collection of poses generated by docking and find that the residence time of the ligand in the native and nativelike binding poses is distinctly longer than that in decoy poses. This finding suggests that molecular simulations offer a unique approach to distinguishing the native (or nativelike) binding pose from decoy poses that cannot be distinguished using scoring functions that evaluate static structures. The success of our method emphasizes the importance of protein-ligand dynamics in the accurate determination of the binding pose, an aspect that is not addressed in typical docking and scoring protocols.

Introduction

High-throughput screening has become a fundamental tool in the field of modern drug discovery. Despite technological advances, this technique is still very expensive and requires a large dedication of time and labor. In structure-based virtual screening methods, novel lead scaffolds are identified by docking a library of small molecules into a specific binding pocket in three-dimensional protein structures characterized by x-ray crystallography or NMR. Virtual screening is a fast and relatively inexpensive method of identifying lead drug candidates for a specific target from chemical libraries including millions of compounds, as compared to the libraries of hundreds of thousands used in high-throughput experimental screening (1). With the rapidly increasing availability of protein structures (2, 3), virtual screening has become an indispensable tool for drug discovery.

Virtual drug screening is limited by the accuracy of the scoring function used to evaluate ligand binding, which must compromise between full physical accuracy and computational efficiency. The accuracy and completeness of the scoring function have been identified as a bottleneck in the virtual screening procedure (4, 5). For some difficult targets, the docking algorithm generates nativelike binding poses, but the scoring functions cannot distinguish these poses from decoy poses. We hypothesize that scoring functions fail in difficult cases because they do not account for the entropic effects of binding or for protein-ligand dynamics. An ideal scoring function should be able to calculate the binding free energy of the ligand, which is a thermodynamic quantity that takes into account both entropic and enthalpic factors (6). In practice, however, only static structures are scored, and therefore, entropy and dynamics are not explicitly incorporated (7).

Recently, various methods have been explored for incorporating entropic effects into virtual drug screening. Structural ensembles created using simulation techniques can be used to explore multiple conformations of both the target and the ligands. Some docking methods attempt to incorporate the dynamic nature of protein-ligand binding by using multiple static target and ligand conformations (8, 9, 10, 11, 12) or accounting for coupled ligand and target flexibility (13, 14, 15, 16). However, despite the increased sampling and expanded conformational space explored using these innovations, these scoring functions are still based on static structural snapshots and cannot account for the coupled dynamics of protein-ligand interactions.

Alternatively, simulations of the target-ligand pair can be used to directly account for entropy and dynamics. Okimoto et al. performed molecular dynamics simulations of docked poses of ligands and found that their protocol of docking followed by molecular mechanics/Poisson Boltzmann surface area binding free energy estimation had enrichment of true binders superior to that of a protocol using docking alone (17). However, their method requires the use of a specialized computer built exclusively for molecular dynamics simulations, and it is therefore not available to most researchers. Colizzi et al. conducted single-molecule pulling simulations to compare the binding characteristics of ligand analogs in an antimalaria target (18), and found that they could differentiate binders from nonbinders by the profile of the potential of mean force. However, their method in its current form is not appropriate for large-scale screening because of the large amount of simulation time required for each ligand.

To conduct large-scale low-cost virtual screening studies that take into account entropic and dynamic conformational sampling information, we construct a streamlined protocol by performing discrete molecular dynamics (DMD) simulations on docking poses to extract the essential dynamic parameters. DMD uses discretized energy potentials and fast event-sorting techniques to speed up molecular dynamics simulation, which allows us to perform multiple molecular dynamics simulations to sample the conformational space of each pose. We apply the protocol on a test set that contains decoy poses that cannot be distinguished from native poses using conventional scoring functions. We extract the ligand residence time from the multiple simulation trajectories and find that the residence time of the ligand in its respective pose in the binding pocket is a distinguishing factor between native and decoy poses. Using this protocol, we successfully identify the native pose within the top 0.5% of poses for six out of eight cases in which static scoring functions fail. In addition, we observe that poses within the 2-Å root mean-squared deviation (RMSD) of the crystallographic pose also exhibit extended residence times in comparison to decoy poses, demonstrating that near-native poses sampled by docking programs will also be identified by measuring residence time. The success of our method confirms that explicitly incorporating protein-ligand dynamics into the analysis of docking poses should afford substantial improvement in virtual screening accuracy over current scoring functions that rely on static conformations of protein ligand complexes.

Methods

Selection of targets

We take all 85 targets from the Astex diverse docking benchmark set (19) and use MedusaDock (13) with the MedusaScore scoring function (20) to generate 1000 poses of each ligand with its target protein. For most targets, MedusaScore alone is able to distinguish the nativelike pose (the RMSD of the lowest-scoring pose is within 2 Å of the native ligand pose). However, for some targets, a number of decoy poses are scored more favorably than nativelike poses. We choose for testing those targets where the MedusaScore scoring function fails to rank the native (x-ray crystallographic) pose in the top 1% of generated poses (Fig. 1, Fig. S7, Fig. S8, Fig. S9, Fig. S10, Fig. S11, Fig. S12, and Fig. S13). We identify eight targets: acetylcholine esterase (AChE, Protein Data Bank (PDB) ID 1GPK), pantothenate synthetase (PDB ID 1N2J), C-Jun N-terminal kinase 3 (JNK3, PDB ID 1PMN), tuberculosis thymidylate kinase (PDB ID 1W2G), MAP kinase 14 (PDB ID 1YWR), colonic H(+)-K(+)-ATPase 1 (CHK1, PDB ID 2BR1), Pim-1 kinase (PDB ID 3BGQ), and LmrR (PDB ID 3F8C). To verify the difficulty of the chosen targets, we also generate and score docked poses using AutoDock (21) and Glide (22), with similar results (Fig. S1 and Fig. S2). We perform AutoDock scoring using the preparation and score computation scripts included in the AutoDockTools 4.1 package. We perform Glide scoring using the XGlide script provided by Schrodinger for preparation and optimization with the nativeonly (no cross-docking) scoring option.

Figure 1.

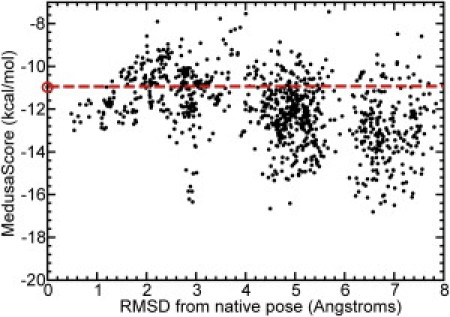
Figure 1

Open in a new tab

Native pose ranks poorly in scoring of 1000 decoy poses. MedusaScore of each of the 1000 poses generated for pantothenate synthetase, according to their RMSD from the native pose. The large open circle and the dashed line indicate the MedusaScore of the native pose.

Docking and creation of decoy poses

We employ the MedusaDock software (13) with the MedusaScore energy function (20) to dock and score the native ligands with their respective targets. Briefly, MedusaDock samples both ligand conformations and target side-chain rotamers simultaneously in a rapid flexible docking protocol. MedusaDock generates poses using the structural information in a supplied PDB file of the target and MOL2 file of the ligand. The program utilizes the atomic coordinates to identify rotatable bonds and build a stochastic library of ligand poses during docking simulations, but the initially supplied ligand conformer is not necessarily one of the output states. A benchmark of MedusaDock found substantial sampling of ligand conformational space, and the software was shown to perform well in both self-docking and cross-docking scenarios (13).

Selection of decoys for DMD simulation

For each target, we select those decoy poses that score better than the native pose for DMD simulation. Because most scoring functions compute only the enthalpic contribution to binding free energy, it is likely that the entropic factor, which is not explicitly accounted for by scoring functions applied to static structures, plays a critical role in the accurate prediction of the native ligand binding pose in these targets. These cases of top-ranking decoys are the most interesting for our study; we are not concerned with decoy poses that can be distinguished using enthalpic contributions alone, since fast and efficient methods already exist for determining these poses. Therefore, we eliminate from consideration those decoy poses whose scores are less favorable than the native pose.

We rank poses according to their MedusaScore without van der Waals repulsion (VDWR) energy to initially allow small steric clashes for sampling purposes. However, many of these 1000 poses can be clustered with multiple poses within 2 Å RMSD of one another. We observe in preliminary DMD simulations that once the RMSD of the ligand from its original pose exceeds 2 Å, the RMSD continues to increase rapidly, suggesting that an RMSD of >2 Å indicates pose exit. Conversely, poses could fluctuate within 2 Å RMSD from the original pose for an extended period of time, suggesting that they can be viewed as dynamically indistinguishable. To avoid simulation of dynamically indistinguishable poses and generate an unbiased representation of the poses, we cluster the poses using means-linkage hierarchical clustering in the OC suite (23). In means-linkage clustering, the distance between two clusters is defined as the average distance between all of their members. We include the native crystallographic pose in the clustering procedure to identify the near-native cluster. We employ a conservative intercluster distance cutoff of 2.5 Å, and select the pose with the most favorable MedusaScore (20) in each cluster as the representative of that cluster. We also eliminate those poses that score less favorably than the native pose when including the VDWR energy (indicating the existence of atomic clashes). In the end, we obtain a diverse set of decoy poses for DMD simulation.

We perform DMD simulations of the remaining structurally diverse ligand poses in complex with the target (Fig. 2, Fig. S7, Fig. S8, Fig. S9, Fig. S10, Fig. S11, Fig. S12, and Fig. S13) as well as the native crystallographic pose. In addition, we perform simulations of the poses in the native cluster that are within 2 Å RMSD of the crystallographic pose (near-native poses) to test the ability of our method to pick not only the crystallographic pose, but also near-native poses sampled by MedusaDock.

Figure 2.

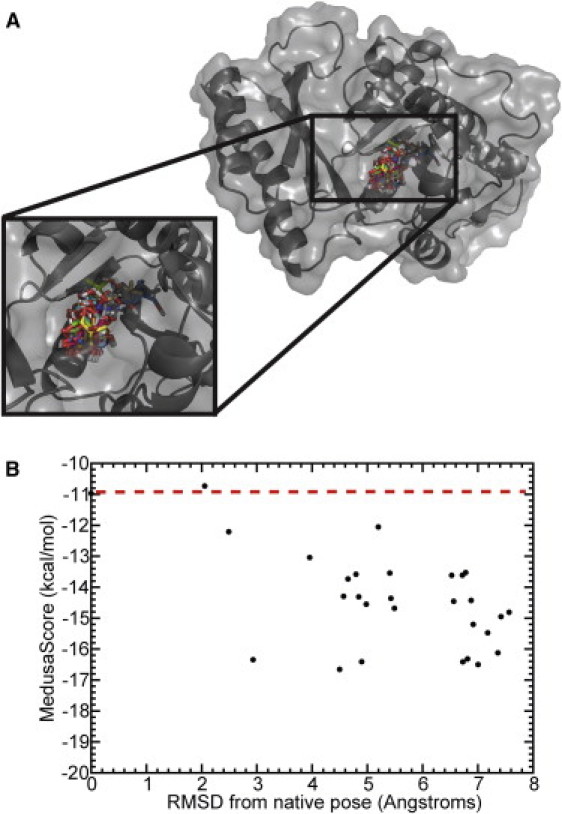
Figure 2

Open in a new tab

Representative decoy poses for pantothenate synthetase. (A) Decoy poses remaining after the application of the dual MedusaScore filter and clustering, in complex with the target. (B) MedusaScore of the remaining poses, according to their RMSD from the native pose. The dashed line indicates the MedusaScore of the native pose. We find that the poses are structurally diverse and have varied RMSD from the native pose.

Because in a real-world application of virtual screening we would not know in advance the score of the native pose, we also conduct a blind test of our method, removing the filtering steps that rely on this knowledge (Fig. S14, FILTER 1 and FILTER 2). We find that although the number of decoy poses that we test drastically increases from 29 to 118, the ranking of the native pose only changes from 1 to 4, whereas the significant separation of the native binding pose from the majority of decoy poses is maintained (see Fig. 6).

Figure 6.

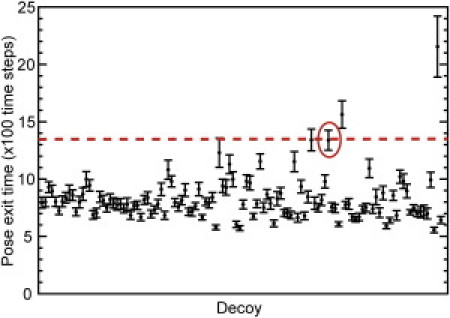
Figure 6

Open in a new tab

Average residence times for decoys with no imposed scoring criteria. We show that removal of the score-filtering steps has small effect on distinguishing the native pose. The average residence time of the native pose (in units of 100 time steps) is clearly separated from the majority of decoy poses in the target system of pantothenate synthetase. The native pose is circled, and the dashed line indicates the average residence time of the native pose.

DMD simulation

DMD uses discrete step function potentials to govern interatomic interactions, instead of the continuous potentials used in traditional MD simulation (24, 25). As a consequence, interactions can be described as collisions, where the velocities of the colliding atoms change instantaneously according to the laws of conservation of energy, momentum, and angular momentum. Having fewer and faster calculations without integration over Newton's equations allows DMD to achieve a significant increase in sampling over traditional MD.

We perform all simulations using the all-atom model for DMD developed by Ding et al. (26). We impose harmonic constraints on each atom of the target backbone, using a harmonic constant of 1.0 kcal/mol·Å2. A stiff harmonic constraint, while allowing limited adjustments of the backbone, more efficiently samples the protein conformations near the native structure and decreases the probability that a nonnative conformational sampling will dislodge the ligand. All side chains, as well as the ligand, are allowed to move freely. We use a simulation temperature of 0.6 kcal/mol·kB (∼300 K) and a heat-exchange coefficient of 1.

We perform 100 replica simulations of each pose in complex with the target. Each replica simulation has an identical starting structure, but the atoms have different randomly seeded starting velocities, thereby producing varying initial conditions for each replica simulation and allowing for a statistical description of each pose system.

Calculation of residence time

We write a snapshot of the system every 100 time steps, which corresponds to approximately every 5 ps of simulation time. For each snapshot, we calculate the RMSD of the ligand from its original pose. We find that, initially, ligands fluctuate in the binding pocket by <2 Å RMSD from their starting coordinates. Once a ligand crosses this 2 Å threshold, it begins a gradual increase in RMSD away from its initial position. Therefore, we consider a ligand as having exited its pose as soon as it deviates by >2 Å RMSD from its starting coordinates. We check simulations for pose exit every 104 time steps and terminate the simulation if the pose has exited. We record the frame at which the ligand exits its pose for each replica simulation of each decoy or native case and use the corresponding number of time steps as the residence time.

Results

Generation and evaluation of decoy poses

We start with 1000 ligand poses generated with MedusaDock (see Methods) and one native x-ray crystallographic pose (1001 poses total) for each target. All poses that score less favorably than the native pose are rapidly filtered using the MedusaScore static scoring function. For example, in pantothenate synthetase, MedusaScore ranks the native pose at position 741 out of 1001 poses (Fig. 1). We therefore discard the poses at ranks 742–1001, leaving 741 more favorably scoring poses for further filtering. After we apply the criteria of RMSD clustering and VDWR energy, only 29 poses remain for testing in DMD simulations. These poses have diverse geometry in the binding pocket (Fig. 2 A), being separated by at least 2.5 Å RMSD. The MedusaScores of the poses do not differentiate native and near-native poses from decoy poses (Fig. 2 B), emphasizing that a static scoring function is not effective in the case of this target-ligand system. For example, the MedusaScore of the native pose is −10.97 kcal/mol, whereas the MedusaScore for the best-scoring decoy pose, which is displaced by 4.5 Å from the native pose, is −16.66 kcal/mol, much better than the native pose. Notably, alternative scoring functions such as AutoDOCK and Glide also fail to discriminate native from decoy poses (Fig. S1 and Fig. S2).

Residence time metric

Direct calculation of the entropic and dynamic contribution to binding free energy is a formidable task (27). Likewise, simulation of the actual binding events is prohibitively time-consuming, involving exhaustive sampling to accurately measure the binding free energy. However, we can efficiently measure the time that the ligand stays in its respective pose in the binding pocket during simulation, which is directly related to the rate of dissociation from the enzyme, koff. We measure the residence time of the ligand pose as the number of DMD time steps (1 time step = ∼50 fs) that the ligand stays within 2 Å of the initial pose. We create a statistical description of each target-pose system by designing 100 replica simulations of each pose in complex with the target. For each replica simulation, particles in the system have different randomly seeded initial velocities (following Maxwell distribution (28, 29)), but identical initial spatial coordinates.

The distribution of replica residence times for each pose, regardless of the target, is Poissonian, despite differences in peak value and breadth of the distributions, so that the probability of the ligand exiting with a residence time t is P(t;μ)=μtt!e−μ, where the constant μ is the average residence time for that pose. Obtaining a Poissonian distribution of residence times for each decoy confirms sufficient sampling, since exit from ligand pose should follow the law of rare events, with each event discrete and independent. Early pose exits occur far more frequently than do late pose exits, with the standard deviation in general increasing with increasing mean. For each target, we average the residence times over all 100 replica simulations to report a mean residence time for each pose. We therefore examine the mean residence time of the ligand in its pose as the metric for distinguishing native and near-native from decoy poses, a task that cannot be accomplished with conventional static scoring functions. For most targets, all simulations finish within 10,000 DMD time steps, which with these system sizes equates to <3 h of CPU time per target.

Distinguishing the native binding pose

Upon performing simulations of the selected target-ligand complexes, we find that the native pose has a significantly longer residence time than all decoy poses (Fig. 3). For example, in the pantothenate synthetase system, the mean residence time for the native pose is 1100 time units. In contrast, the mean residence time of the best-scoring decoy pose is only 700 time units, even though the binding energy for that static pose (as measured using MedusaScore) is much stronger (Fig. 4). In fact, residence time and calculated binding energy do not appear to correlate. This observation is in agreement with the finding by Reynolds and Holloway (6) that binding free energy and binding enthalpy (the value calculated by most static scoring functions) are not correlated, and it highlights the importance of dynamics in properly evaluating the stability of protein-ligand binding. Using the average residence time of the ligand in its pose as a metric, we successfully identify the native binding pose from among 1000 decoys for the difficult target of pantothenate synthetase. We further observe that near-native binding poses (those within 2 Å of the crystallographic pose) exhibit a distribution of residence times that is approximately Gaussian-like and significantly higher than the distribution of decoy pose residence times. The distributions of residence times for decoy poses and near-native poses exhibit an overlap of <5% and separation in their mean values of ∼3 standard deviations (Fig. 5). The residence time for the native crystallographic pose is within the near-native distribution. Notably, the longest residence time observed is in a near-native pose, suggesting that our method could identify both the native and near-native poses from a collection of diverse poses generated by docking.

Figure 3.

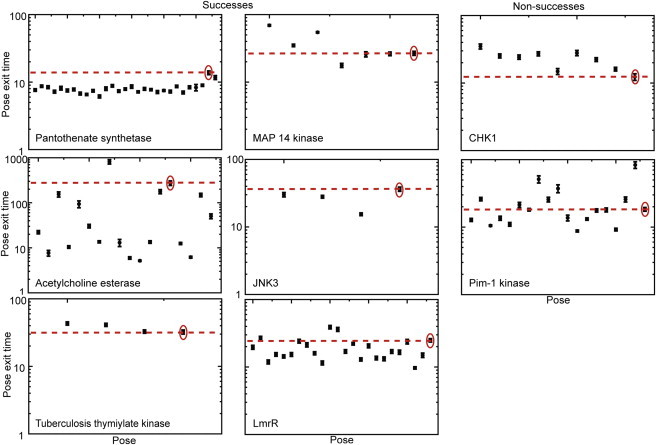
Figure 3

Open in a new tab

Residence times of ligand in the binding pocket. Average residence time for each decoy of each target tested, in units of 100 time steps. Each point represents the average residence time of the ligand in each pose over the 100 replica simulations for each pose. Error bars represent the standard error in residence time over the 100 replica simulations; in most cases, error is small enough that points and error bars cannot be distinguished. The native pose is circled, and the dashed line indicates the average residence time of the native pose.

Figure 4.

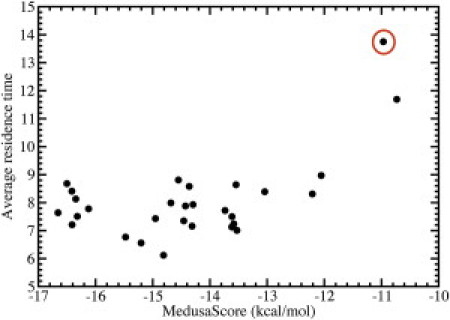
Figure 4

Open in a new tab

Residence time does not correlate with static energy scoring. The average residence times for each decoy of pantothenate synthetase, in units of 100 time steps, and their respective MedusaScores. The native pose is circled. The residence time does not correlate with the MedusaScore; similar results are obtained for other targets.

Figure 5.

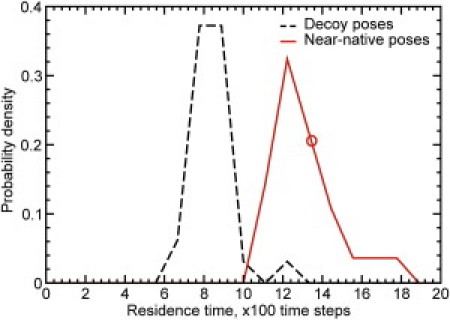
Figure 5

Open in a new tab

Near-native poses are distinguished from decoy poses by residence time. The distribution of near-native pose residence times (solid line) is significantly shifted toward longer times as compared to the distribution of decoy pose residence times (dashed line). The residence time of the native pose is indicated by an open circle on the distribution of near-native poses.

We count a case as successful when the average residence time of the native pose is in the top five out of all poses. The native pose is within the top five poses with the longest residence times in six of the eight targets tested (Fig. 3), placing the native pose in the top 0.5% of poses. We rank the native pose in the top two poses for three out of eight targets (acetylcholine esterase (AChE), pantothenate synthetase, and c-Jun N-terminal kinase (JNK3)), and in the top four poses for an additional three targets (tuberculosis thymidylate kinase, MAP kinase 14, and LmrR) (Fig. 3). In two cases, CHK1 and pim-1 kinase, we do not succeed in placing the native pose in the top 0.5% of poses. The native poses are ranked in the ninth and seventh positions, respectively, but these rankings still fall within the top 1% of all poses. Both of these targets are kinases, which are notorious for flexibility and allosteric conformational changes in the backbone upon ligand binding (30). It is possible that the harmonic constraints that we place on the backbone in our method overconstrain the dynamics of these targets for ligand binding. In the future, a smaller harmonic constant, or removal of the constraint, may be needed for targets with significant allostery.

Removing the native pose scoring criteria gives similar results, despite testing many more decoys (Fig. 6). Although only 259 decoys score less favorably than the native pose for pantothenate synthetase, including these decoys in the clustering analysis creates an additional 89 clusters (118 clusters from 1000 poses versus 29 clusters when only 742 poses were included). From these results, we conclude that, as expected, the region of conformational space occupied by less favorably scoring poses is more sparsely sampled by the MedusaDock algorithm, highlighting the efficiency of the docking protocol. Inclusion of these decoys results in the ranking of the native pose falling from 1/29 to 4/118, but a clear demarcation remains between the average residence time of the native pose and the majority of decoy poses (Fig. 6).

To further test the robustness of the method, we perform the same analysis with a different starting conformation of the target. We identify a structure of the same target, pantothenate synthetase, in complex with a different ligand in the same binding pocket. In this structure (PDB ID 1N2G), pantothenate synthetase is in complex with AMPCPP, a very bulky molecule in comparison to pantoate. Our decoy selection protocol identifies 60 decoy poses, the native pose, and one near-native pose for testing in DMD simulations. Because our protocol imposes harmonic constraints on the backbone of the target, we expect the native and near-native poses to decrease in ranking in a cross-docked system. However, we find that, while the native pose is ranked at 12/62, most of the higher-ranking decoy poses have residence times falling within error of that of the native pose (Fig. 7). In addition, the near-native pose is ranked 4/62, with error bars overlapping those of the top-ranked decoy pose. In this case, it is likely that the near-native pose represents a fine-tuning of the crystallographic pose for the cross-docked structure.

Figure 7.

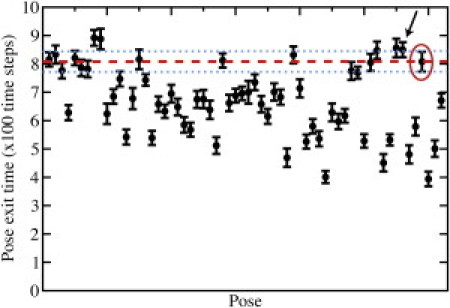
Figure 7

Open in a new tab

Average residence times for cross-docked system. We find that cross-docking of pantoate into pantothenate synthetase using the enzyme coordinates taken from its complex with a different ligand, the bulky AMPCPP molecule, causes the ranking of the native pose (red circle) to fall to 12/62. However, the average residence time of the native pose (dashed line) is within error of most of the higher-ranking decoys (error denoted by dotted lines), and a near-native pose (arrow) ranks 4/62, with error bars overlapping with the highest-scoring decoys.

Discussion

We demonstrate that we successfully distinguish the native pose from decoys using the average residence time of the ligand in the pose in the course of molecular simulations. In addition, poses within 2 Å RMSD of the native crystallographic pose also have significantly longer residence times than decoy poses, demonstrating that even if the native pose were unknown in this study, we would succeed in identifying a near-native pose. The latter observation is critical for practical application of our approach in those cases when the true binding pose is unknown, e.g., for new ligands. We conclude from these results that the entropic effects of binding and protein-ligand dynamics are crucial to the determination of the correct binding pose of the ligand in some difficult targets. In our method, we combine static scoring and molecular simulation, using traditional virtual screening methods as an initial filter to determine the most likely ligand poses, and then applying DMD simulation to identify the native or near-native (within 2 Å RMSD, dynamically indistinguishable) pose. In this way, our simulation method can be applied to the results of any traditional virtual screening protocol to incorporate the entropic and dynamic effects of binding into the ranking of binding poses. From among a set of poses generated by traditional docking procedures, we show that the most dynamically stable poses are the most nativelike.

Although simulation-based methods have the advantage of directly incorporating entropic and dynamic factors, they are significantly more computationally expensive than the enthalpic scoring of a static structure. Because of the cost in computer time, it would be beneficial to determine which targets and ligand types are routinely difficult to accurately identify with a traditional scoring function before applying this method in the screen of a large library. In this work, each target has on average ∼15 poses to be tested, with each pose having 100 replica simulations. Each replica simulation typically takes from 2 to 10 h of computer time on a single processor. Simulation time could be decreased in almost all target cases by changing the frequency of the pose exit verification step in our protocol from every 10,000 time steps to every 1000, since most targets have poses exiting between 2000 and 8000 time steps (Fig. 3).

As noted in the Results section, the two test cases in which our method failed are both kinases (31), which are known for their flexibility and allosteric conformational change upon ligand binding. The inclusion of harmonic constraints on the backbone of the target protein in our method may cause problems in some kinase cases where correlated motions between the binding pocket and the rest of the protein are necessary for native binding dynamics. We hypothesize that the failure of our method in these cases is due to the allostery of the kinase family, but when we examine unconstrained simulations of these targets compared with the success cases, we find that backbone RMSD over time, pairwise RMSD of the backbone and the binding pocket residues, number of ligand-target contacts, and various measures of correlated motion between the binding pocket and other sites in the protein, including the average minimal path, did not illuminate the differences between success and nonsuccess cases (Supplementary Protocols, Fig. S3, Fig. S4, Fig. S5, Fig. S6, Table S1, Table S2, Table S3, and Table S4). It is possible that we do not succeed in these two kinase cases because of additional complexities in ligand-protein interactions not yet accounted for in our force field. Further tuning of force-field parameters or adjustment of the protocol may be necessary for certain types of targets, and is an area for future improvement.

In addition to identification of the native binding pose, our method may also be applied to the screening of diverse chemical libraries. In a large-scale virtual screening procedure, active compounds may be missed if entropic contributions are ignored in the scoring and ranking of ligands. In target-ligand systems where entropy and dynamics make significant contributions to the binding energy, a scoring function based solely on enthalpic terms may over- or underestimate the binding affinity of any given pose or ligand, and as a result, native binding poses are not selected and decoy ligands may be ranked more favorably than native ligands. Using our method, we can take protein-ligand dynamics into account when selecting the most favorable pose of a potential ligand in the binding pocket. A traditional virtual screening protocol can be used as a filter for the individual ligands, and the top 1000 ligands selected for simulation. For each ligand, 100 replica simulations can be performed, and the average residence times evaluated. Using our method, one can conceivably screen a large library in a few weeks using computing resources available to most researchers. We plan to explore and optimize this two-step virtual screening protocol in future studies.

Conclusion

By conducting DMD simulations of the target-ligand system, we are able to account for the entropic effects of binding as well as dynamic interactions not observed in the static structures used in traditional scoring functions. We find that we can distinguish the native pose from decoys using the average residence time of the ligand in the pose; the ligand on average spends more time in the native pose than in other, decoy poses. From these results, we can conclude that small-scale protein dynamics play a significant role in protein-ligand binding. Using our method, we can identify the most stable poses among a collection of those generated by docking as the most nativelike, and we are able to correctly identify the nativelike pose in target-ligand systems where traditional methods fail.

Acknowledgments

The authors thank Dr. Feng Ding, Pradeep Kota, and Dr. Srinivas Ramachandran for helpful discussions.

This work is supported by National Institutes of Health grant R01GM080742 and its ARRA supplement, 3R01GM080742-03S1, to N.V.D., and GM066940 and its ARRA supplement, GM066940-06S1, to A.T. and N.V.D. E.A.P. was partially supported by the Curriculum in Bioinformatics and Computational Biology and National Institutes of Health Predoctoral Fellowship F31AG039266-01 from the National Institute on Aging.

Editor: George Makhatadze.

Footnotes

Additional discussion, 14 figures, and references (32, 33) are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(11)05359-8.

Supporting Material

Document S1. Additional discussion, 14 figures, and references (32,33)
mmc1.pdf (639.6KB, pdf)

References

  • 1.Schneider G., Böhm H.J. Virtual screening and fast automated docking methods. Drug Discov. Today. 2002;7:64–70. doi: 10.1016/s1359-6446(01)02091-8. [DOI] [PubMed] [Google Scholar]
  • 2.Terwilliger T.C., Stuart D., Yokoyama S. Lessons from structural genomics. Annu. Rev. Biophys. 2009;38:371–383. doi: 10.1146/annurev.biophys.050708.133740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Meslamani J., Rognan D., Kellenberger E. sc-PDB: a database for identifying variations and multiplicity of “druggable” binding sites in proteins. Bioinformatics. 2011;27:1324–1326. doi: 10.1093/bioinformatics/btr120. [DOI] [PubMed] [Google Scholar]
  • 4.Wang R., Lu Y., et al. Wang S. An extensive test of 14 scoring functions using the PDBbind refined set of 800 protein-ligand complexes. J. Chem. Inf. Comput. Sci. 2004;44:2114–2125. doi: 10.1021/ci049733j. [DOI] [PubMed] [Google Scholar]
  • 5.Warren G.L., Andrews C.W., et al. Head M.S. A critical assessment of docking programs and scoring functions. J. Med. Chem. 2006;49:5912–5931. doi: 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
  • 6.Reynolds C.H., Holloway M.K. Thermodynamics of ligand binding and efficiency. ACS Med. Chem. Lett. 2011;2:433–437. doi: 10.1021/ml200010k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Yuriev E., Agostino M., Ramsland P.A. Challenges and advances in computational docking. J. Mol. Recognit. 2009;24:149–164. doi: 10.1002/jmr.1077. [DOI] [PubMed] [Google Scholar]
  • 8.Koska J., Spassov V.Z., et al. Venkatachalam C.M. Fully automated molecular mechanics based induced fit protein-ligand docking method. J. Chem. Inf. Model. 2008;48:1965–1973. doi: 10.1021/ci800081s. [DOI] [PubMed] [Google Scholar]
  • 9.Rueda M., Bottegoni G., Abagyan R. Consistent improvement of cross-docking results using binding site ensembles generated with elastic network normal modes. J. Chem. Inf. Model. 2009;49:716–725. doi: 10.1021/ci8003732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Cheng L.S., Amaro R.E., et al. McCammon J.A. Ensemble-based virtual screening reveals potential novel antiviral compounds for avian influenza neuraminidase. J. Med. Chem. 2008;51:3878–3894. doi: 10.1021/jm8001197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Fan H., Irwin J.J., et al. Sali A. Molecular docking screens using comparative models of proteins. J. Chem. Inf. Model. 2009;49:2512–2527. doi: 10.1021/ci9003706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Soliva R., Gelpí J.L., et al. Orozco M. Dissection of the recognition properties of p38 MAP kinase. Determination of the binding mode of a new pyridinyl-heterocycle inhibitor family. J. Med. Chem. 2007;50:283–293. doi: 10.1021/jm061073h. [DOI] [PubMed] [Google Scholar]
  • 13.Ding F., Yin S., Dokholyan N.V. Rapid flexible docking using a stochastic rotamer library of ligands. J. Chem. Inf. Model. 2010;50:1623–1632. doi: 10.1021/ci100218t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Meiler J., Baker D. ROSETTALIGAND: protein-small molecule docking with full side-chain flexibility. Proteins. 2006;65:538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
  • 15.Davis I.W., Baker D. RosettaLigand docking with full ligand and receptor flexibility. J. Mol. Biol. 2009;385:381–392. doi: 10.1016/j.jmb.2008.11.010. [DOI] [PubMed] [Google Scholar]
  • 16.Anderson A.C., O'Neil R.H., et al. Stroud R.M. Approaches to solving the rigid receptor problem by identifying a minimal set of flexible residues during ligand docking. Chem. Biol. 2001;8:445–457. doi: 10.1016/s1074-5521(01)00023-0. [DOI] [PubMed] [Google Scholar]
  • 17.Okimoto N., Futatsugi N., et al. Taiji M. High-performance drug discovery: computational screening by combining docking and molecular dynamics simulations. PLOS Comput. Biol. 2009;5:e1000528. doi: 10.1371/journal.pcbi.1000528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Colizzi F., Perozzo R., et al. Cavalli A. Single-molecule pulling simulations can discern active from inactive enzyme inhibitors. J. Am. Chem. Soc. 2010;132:7361–7371. doi: 10.1021/ja100259r. [DOI] [PubMed] [Google Scholar]
  • 19.Hartshorn M.J., Verdonk M.L., et al. Murray C.W. Diverse, high-quality test set for the validation of protein-ligand docking performance. J. Med. Chem. 2007;50:726–741. doi: 10.1021/jm061277y. [DOI] [PubMed] [Google Scholar]
  • 20.Yin S., Biedermannova L., et al. Dokholyan N.V. MedusaScore: an accurate force field-based scoring function for virtual drug screening. J. Chem. Inf. Model. 2008;48:1656–1662. doi: 10.1021/ci8001167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Morris G.M., Huey R., et al. Olson A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Friesner R.A., Banks J.L., et al. Shenkin P.S. Glide: a new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004;47:1739–1749. doi: 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]
  • 23.Barton, G. J. 1993, 2002. OC: A Cluster Analysis Program. University of Dundee, Dundee, UK.
  • 24.Zhou Y., Karplus M. Folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. USA. 1997;94:14429–14432. doi: 10.1073/pnas.94.26.14429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Dokholyan N.V., Buldyrev S.V., et al. Shakhnovich E.I. Discrete molecular dynamics studies of the folding of a protein-like model. Fold. Des. 1998;3:577–587. doi: 10.1016/S1359-0278(98)00072-8. [DOI] [PubMed] [Google Scholar]
  • 26.Ding F., Tsao D., et al. Dokholyan N.V. Ab initio folding of proteins with all-atom discrete molecular dynamics. Structure. 2008;16:1010–1018. doi: 10.1016/j.str.2008.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Kollman P. Free energy calculations: applications to chemical and biochemical phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]
  • 28.Dokholyan N.V., Buldyrev S.V., et al. Shakhnovich E.I. Identifying the protein folding nucleus using molecular dynamics. J. Mol. Biol. 2000;296:1183–1188. doi: 10.1006/jmbi.1999.3534. [DOI] [PubMed] [Google Scholar]
  • 29.Ding F., Dokholyan N.V., et al. Shakhnovich E.I. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 2002;83:3525–3532. doi: 10.1016/S0006-3495(02)75352-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Brooijmans N., Chang Y.W., et al. Humblet C. An enriched structural kinase database to enable kinome-wide structure-based analyses and drug discovery. Protein Sci. 2010;19:763–774. doi: 10.1002/pro.355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.May A., Zacharias M. Protein-ligand docking accounting for receptor side chain and global flexibility in normal modes: evaluation on kinase inhibitor cross docking. J. Med. Chem. 2008;51:3499–3506. doi: 10.1021/jm800071v. [DOI] [PubMed] [Google Scholar]
  • 32.Nayal M., Honig B. On the nature of cavities on protein surfaces: application to the identification of drug-binding sites. Proteins. 2006;63:892–906. doi: 10.1002/prot.20897. [DOI] [PubMed] [Google Scholar]
  • 33.Sharma S., Ding F., Dokholyan N.V. Multiscale modeling of nucleosome dynamics. Biophys. J. 2007;92:1457–1470. doi: 10.1529/biophysj.106.094805. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Additional discussion, 14 figures, and references (32,33)
mmc1.pdf (639.6KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES