Energy Landscape of the Prion Protein Helix 1 Probed by Metadynamics and NMR

Abstract

The characterization of the structural dynamics of proteins, including those that present a substantial degree of disorder, is currently a major scientific challenge. These dynamics are biologically relevant and govern the majority of functional and pathological processes. We exploited a combination of enhanced molecular simulations of metadynamics and NMR measurements to study heterogeneous states of proteins and peptides. In this way, we determined the structural ensemble and free-energy landscape of the highly dynamic helix 1 of the prion protein (PrP-H1), whose misfolding and aggregation are intimately connected to a group of neurodegenerative disorders known as transmissible spongiform encephalopathies. Our combined approach allowed us to dissect the factors that govern the conformational states of PrP-H1 in solution, and the implications of these factors for prion protein misfolding and aggregation. The results underline the importance of adopting novel integrated approaches that take advantage of experiments and theory to achieve a comprehensive characterization of the structure and dynamics of biological macromolecules.

Introduction

It is crucial to obtain a detailed characterization of the structures and dynamics of proteins and peptides in solution to address the biomolecular processes that occur in cells. Protein backbone dynamics ranging from the subnanosecond to milliseconds (and beyond) are relevant for the majority of the biological processes, including peptide synthesis, enzyme catalysis, and macromolecular interactions (1, 2, 3). The general principle underlying functional dynamics is that proteins have been evolutionary optimized not only to attain a defined three- dimensional structure in their native states but also to gain access to a complex free-energy surface (FES) that allows for conformations with different physicochemical and biological properties to be simultaneously populated within the native-state ensemble (4). Conformational dynamics are particularly relevant in the case of intrinsically disordered proteins, whose ensemble properties are primarily defined by the distribution of states adopted in solution, as well as in the rare events that drive the occasional conversion of normally soluble proteins into insoluble amyloid aggregates. Such aggregates are connected to more than 20 pathological conditions, including severe neurodegenerative diseases such as Parkinson's, Alzheimer's, and prion diseases (5).

Several experimental techniques, including NMR (6), Raman spectroscopy (7), and fluorescence resonance energy transfer (8), have been optimized to probe protein dynamics. Although such approaches often provide information at a limited resolution, a view is emerging in which experimental data are complemented with molecular simulations to provide an atomic-resolution picture of the protein dynamics (9, 10). The constant improvement of first-principles force fields has allowed investigators to use molecular-dynamics (MD) simulations of proteins to successfully tackle a variety of problems in protein science, including those that are difficult to address experimentally (11). This framework, however, requires innovative sampling techniques to assist the exploration of the enormous phase space of protein conformations. Some methods have been proposed on the basis of a coarse representation of a peptide's side chains and main chains (12, 13); however, the general exploitation of such methods may be limited by the level of description of the system. Enhanced sampling methods (i.e., accelerated MD) have been proposed on the basis of a boost energy term (14, 15). Whereas accelerated MD requires a tuning based on a comparison with experimental data, an alternative approach, metadynamics, provides enhanced conformational samplings without employing experimental data to assess the convergence (16). Metadynamics samples the conformational phase space by means of collective variables (CVs). This method can be efficiently coupled with all-atom force fields and explicit-solvent models in such a way as to achieve enhanced samplings while maintaining a detailed description of the system. Recently, parallel tempering metadynamics (PT-MetaD) were introduced to allow highly effective conformational samplings that do not require a priori knowledge of the relevant slow degrees of freedom of the system (17, 18). PT-MetaD has proved to be efficient in overcoming the limitations of classical MD simulations by accurately sampling the equilibrium Boltzmann distributions of conformational states, as evidenced by a comparison of reweighted and experimental NMR scalar couplings (19).

In this work, we performed a multidisciplinary investigation of metadynamics simulations, with a full representation of the protein atoms and solvent molecules, and NMR measurements to exhaustively reconstruct the conformational free energy of proteins and peptides. In this way, we addressed the conformational properties of helix 1 of the prion protein (PrP-H1), whose misfolding and aggregation are inherently connected to a group of neurological diseases known as transmissible spongiform encephalopathies (TSEs) (20, 21). This investigation allowed us to reconstruct the FES of PrP-H1 with high accuracy and agreement with experimental data. We used a recently described reweighting method (22) to dissect the contributions of various parameters to the conformational preferences of PrP-H1. The results underline the importance of accurately determining the conformational FES to account for the ensemble properties of proteins and peptides, which we exemplify by linking the conformational properties of PrP-H1 to possible implications for PrP misfolding.

Materials and Methods

Simulations setup

We performed PT-MetaD (16, 17) of the fragment spanning the human PrP sequence 143–157 (Ac-ADYEDRYYRENMHRY-NH₂) by using the all-atom OPLS force field (23) and TIP3P explicit waters. The system was accommodated in a dodecahedron box of 101 nm³ with periodic boundary conditions and solvated with 3183 water molecules. We accounted for van der Waals interactions with a cutoff of 1.4 nm, and calculated the long-range electrostatics using the particle mesh Ewald algorithm with a grid spacing of 0.109 nm. The system sampled the canonical ensemble coupled with a Nosé-Hoover thermal bath.

Initially, we minimized the energy of the system and then allowed the solvent to relax with 100 ps of MD simulation at 283 K by keeping the heavy atoms of the peptide constrained with springs of strength 1000 kJ/(nm² mol). Subsequently, a thermal equilibration of the whole system was reached with a 100 ps MD simulation at 283 K and constant volume, followed by a density equilibration of 100 ps at 283 K and constant pressure (1 atm). The sampling was performed by starting from random conformations extracted from a 5 ns MD simulation at 500 K. This simulation allowed us to explore conformations significantly distant from the helix structure. We equilibrated 50 random conformations from this simulation by means of a replica exchange MD simulation performed with 50 replicas and extended for 10 ns in a temperature range of 283–471 K (swapping attempts performed at 0.2 ps frequency led to probabilities of exchange ranging from 20% to 30%).

We performed PT-MetaD sampling of PrP-H1 with 50 replicas by using CVs to explore the number of i-i+4 backbone hydrogen (H)-bonds and the radius of gyration, r_gyr, as described previously (18). The calculations were extended for 48 ns and the reconstructed FES was averaged over the converged part of the simulation. A detailed description of the employed probability of exchange is provided elsewhere (17), and additional details on the PT-MetaD setup are given in the Supporting Material.

Back-calculation of NMR chemical shifts from the PT-MetaD sampling

We calculated the ¹³C^α, ¹³C^β, and ¹H^α chemical shifts from the structural ensemble using the program SPARTA (24). To recover the unbiased distributions of variables not included in the CVs from a MetaD simulation (i.e., chemical shifts, exposed surface, and salt bridges), we saved the trajectories' snapshots with a 0.1 ps frequency and applied a recent method (19) that was shown to be effective in combination with PT-MetaD (22). It is worth noting that the original implementation of the reweighting algorithm was based on the well-tempered formulation of MetaD, which improves the convergence of the reweighting observables because of the decreasing contribution of the Gaussians along the simulation. Because we employed very small Gaussian heights in this work, we were able to achieve similar convergence properties by means of the PT-MetaD, as also shown by the simultaneous convergence of the reweighted NMR observables and the FES (Fig. S1).

PrP-H1 NMR sample

A peptide corresponding to the fragment spanning the human PrP sequence 143–157 (PrP-H1: Ac-ADYEDRYYRENMHRY-NH₂) with a leading alanine residue was purchased as high-performance liquid chromatography-purified and lyophilized powder from PANAtecs (Tübingen, Germany). To avoid charge effects from the free termini, the peptide was N-terminally acetylated and C-terminally amidated. The NMR sample was dissolved in 500 μl buffer containing 10 mM sodium phosphate buffer, pH 6.5, 0.1% azide to prevent microbial growth, and 10% D₂O as a lock substance. We determined the final concentration by measuring the A₂₈₀ (ε₂₈₀ = 5960 M⁻¹ cm⁻¹) to be 1 mM. Additional details on the NMR measurements and structure determination by means of nuclear Overhauser effects (NOEs) are provided in the Supporting Material.

Spectra assignment

NMR spectra for assignment were measured on a Bruker (Rheinstetten, Germany) AVANCE II+ 600 MHz spectrometer equipped with a triple-resonance probe head for inverse detection (DQF-COSY), and on a Bruker AVANCE II 700 spectrometer equipped with an inverse triple-resonance cryogenic probe head (TOCSY and NOESY), respectively. ¹³C- and ¹⁵N-HSQC spectra were collected at natural abundance. For structure calculation, additional NOESY spectra with mixing times of 100 ms, 200 ms, and 300 ms, respectively, were collected on a Bruker AVANCE II 800 MHz equipped with an inverse triple-resonance cryogenic probe head. All measurements were carried out at 283 K. Spectra were processed using NMRPipe and analyzed using NMRViewJ. Secondary chemical shifts were corrected for effects from the local amino acid sequence (25). ¹³C^α-secondary chemical shifts were used to estimate the helix content assuming a secondary shift of 3.1 ppm for a fully populated α-helix (26).

Results

Convergence of the metadynamics sampling

The solution conformations of the fragment spanning helix H1 of human PrP were sampled by means of PT-MetaD using 50 replicas, starting from random conformations, and extended for 48 ns. We performed metadynamics simulations by biasing the CVs, a set of functions of the system coordinates s(x) that are defined to properly explore the FES conformational phase space. We assessed the convergence of the metadynamics simulations by checking that all the accessible space in the CVs was sampled. This condition was satisfied within the initial 16 ns of sampling (Fig. S2). However, the time evolution of the difference between the free-energy values of the two main minima of the FES shows that the PT-MetaD sampling converged after 32 ns (Fig. S1). For internal consistency with the NMR experiments, which were performed at 283 K, all analyses of the PT-MetaD sampling were performed on the first replica.

FES of PrP H1

The general picture that arises from our investigation is that the solution state of PrP-H1 is characterized by α-helical conformations in equilibrium with random coil (RC) structures (Fig. 1; details of the PT-MetaD simulations and NMR experiments are reported in the Supporting Material). The sampled helical conformations present a variable degree of secondary structure, with the most stable helical basin (basin b1; Fig. 1 and Table 1) featuring three main-chain H-bonds between residues i and i+4. Basin b2 presents a higher number of main-chain H-bonds “i, i+4” (i5-6, i.e., six in the lobe designated as basin b2′). At 283 K, the free-energy values of basins b1 and b2 are −28.5 kJ/mol and −28 kJ/mol, respectively. Yet, a less populated basin (−20.0 kJ/mol), b3, adopts a complete helical fold with 9–10 main-chain H-bonds (i, i+4). Although the free-energy basins b1, b2, and b3 are indicative of helical propensity, the structured conformations of the peptide PrP-H1 represent only a minor portion of the ensemble (see reweighted secondary structures profiles in Fig. S3), whereas the majority of sampled conformations adopt an RC state (RC basin in Fig. 1) with the number of main-chain H-bonds (i, i+4) ranging from zero to two.

Figure 1.

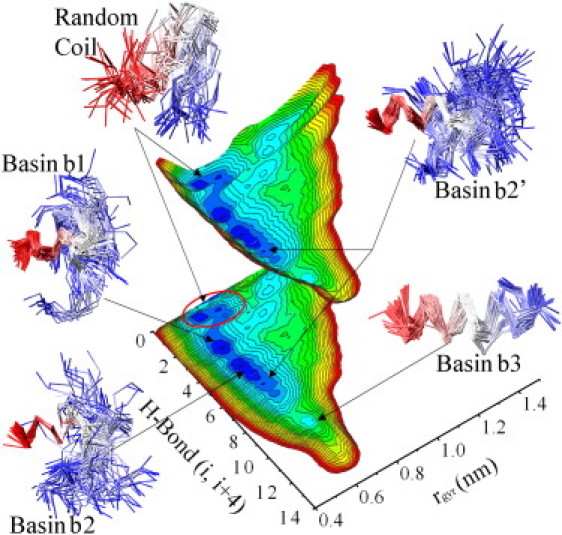
Free-energy landscape of PrP-H1. The surface is drawn as a 3D curve as well as a projection on the CV plane. For each basin, representative conformations are drawn by means of the C^α trace (red, N-terminus; blue, C-terminus). The energy isolines are plotted with 1 kJ/mol of spacing and color-coded for better visibility, with the lowest level (blue) corresponding to −28 kJ/mol. This is the case of a significantly populated basin among the RC conformations that is centered at H-bond values of ∼0 and r_gyr-values of ∼0.8 nm. This basin, which is very narrow in this projection, hosts the 13.4% of the reweighted population of the sampling and has a free-energy value of −35.6 kJ/mol. The sampling was performed by means of PT-MetaD (17), using the PLUMED (59) plugin interfaced with GROMACS (60). The PT-MetaD sampling involved 50 replicas ranging from 283 K to 471 K. The calculations were extended for 48 ns, and the reconstructed FES was averaged over the converged part of the simulation.

Table 1.

Characteristics of the FES principal basins

	RC	Basin 1	Basin 2	Basin 3
Free energy∗(kJ/mol)	−35.6	−28.5	−28.0	−20.0
H-bonds (i, i+4)	0.12	3.02	5.36	10.35
rgyr (nm)	0.77	0.64	0.64	0.71
Number of residues in α-helix	0	6	8	13
Number of salt bridges	2.81	1.82	1.76	1.81
Salt-bridge configurations	55	37	22 (17†)	4
Hydrophobic SASA (nm2)	9.04	8.45	8.60	8.78

^∗Refers to the free-energy value of the minimum of the basin.

^†Basin b2′.

Although our PT-MetaD ensemble is not based on CVs directly connected to the β-sheet structure, the resulting FES was shown to be effective for exploring β-sheet conformations. In the FES reported in Fig. 1, the β-sheet conformations accumulate in the RC basin; however, it is possible to infer their structures and Boltzmann weights by either reweighting the secondary structure content (Fig. S3 A) or reprojecting the FES onto specific β-sheet CVs (Fig. S3 B). The latter analysis shows that our sampling, owing to effective CVs and the enhanced parallel tempering, explored β-sheet conformations by a total population of 3.5% of the ensemble (Fig. S3, B and C). A chemical shift analysis allowed us to assess the level of accuracy of the β-sheet population as explored in the PT-MetaD ensemble. The analysis shows that the sampled β-sheet content (i.e., 3.5%) corresponds to the best agreement between experimental and simulated C^α and C^β chemical shifts, and deviates by only 1% from the best agreement on H^α chemical shifts (Fig. S3 D).

Conformational properties probed by chemical shifts

A combination of COSY, TOCSY, and NOESY spectra (mixing time: 300 ms) allowed the sequential assignment of PrP-H1. Signals for the respective side-chain positions could not be stereospecifically assigned due to the lack of differences in the corresponding crosspeak intensities. The assignment obtained for ¹H^α is in agreement with previous results (27). We extracted additional chemical shifts for the backbone amide nitrogen and the ¹³C^α and ¹³C^β nuclei by transferring the corresponding proton assignments from the ¹⁵N- and ¹³C-HSQC spectra, respectively. The chemical shifts of the backbone nuclei are summarized in Table 2. The sequence used here contains an additional amino-terminal alanine residue that is not present in the wild-type sequence. A comparison of the proton's chemical shifts and binding properties with those of a monoclonal antibody that recognizes helix H1 of PrP indicated that the addition of an alanine residue at the N-terminus does not alter the helix population and conformational properties of PrP-H1 (28).

Table 2.

Experimental backbone chemical shifts (ppm) from H1 NMR spectra

Sequence position	Amino acid	13Cα	13Cβ	1Hα	1HN	15NH
143	A	52.72	19.11	4.21	8.40	130.02
144	D	54.24	40.68	4.51	8.44	118.74
145	Y	58.61	38.43	4.38	8.04	120.18
146	E	57.15	29.99	4.15	8.25	121.39
147	D	54.98	41.28	4.55	8.30	121.33
148	R	58.03	30.05	4.04	8.27	121.23
149	Y	59.29	38.08	4.37	8.20	119.61
150	Y	59.73	38.35	4.30	8.04	120.80
151	R	57.46	30.52	4.06	8.14	120.78
152	E	57.57	29.70	4.10	8.30	119.67
153	N	53.91	38.60	4.57	8.15	117.70
154	M	56.21	32.08	4.28	8.04	119.33
155	H	55.82	28.89	4.55	8.30	118.59
156	R	56.47	30.57	4.18	8.08	121.36
157	Y	57.48	38.67	4.55	8.20	121.11

We used ¹³C^α-secondary chemical shifts to obtain an experimental estimate of the helix content by assuming a secondary shift of 3.1 ppm for a fully populated α-helix (26). The results indicate a population of 34% helical conformation, which is in agreement with previously published circular dichroism (CD) data (27) and the conformational FES explored in our PT-MetaD sampling. We compared experimental chemical-shift data with ensemble-averaged chemical shifts from the PT-MetaD ensemble (i.e., by adapting a recent analysis method (22) to reweight the chemical shifts calculated by the SPARTA program (24) on individual conformations of the sampling) and found an agreement that is largely within the standard error of SPARTA (24) (Fig. 2). Excellent agreement was found for ¹³C^α, ¹³C^β, and ¹H^α atoms (Fig. 2, A, C, and E, respectively), which are generally recognized as the principal probes for secondary structures by chemical shifts. Yet, secondary chemical shifts of ¹³C^α and ¹H^α atoms (Fig. 2, B and D) are consistent with the calculated helix content in the PT-MetaD sampling (Fig. 2 F), indicating that the N-terminal region of the peptide exhibits a significant propensity toward helical conformations, whereas the C-terminal part is mainly RC.

Figure 2.

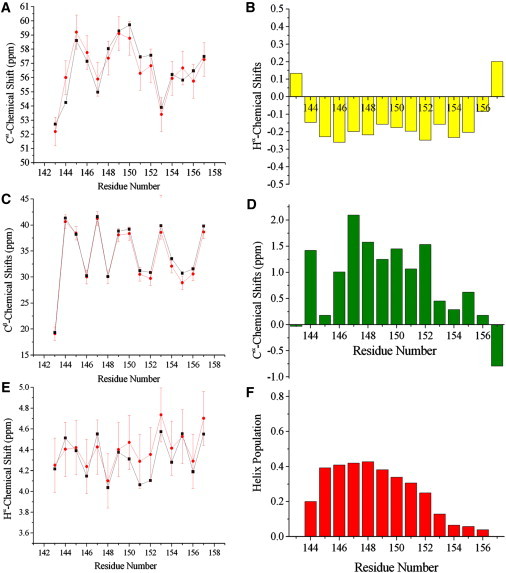
Chemical shifts of the PrP-H1 peptide. (A, C, and E) Comparison of the measured (black) and back-calculated (red) chemical shifts. The error bars for the back-calculated shifts report the standard error of SPARTA (24). (A) ¹³C^α atoms. (C) ¹³C^β atoms. (E) ¹H^α atoms. (B and D) Secondary shifts from the RC reference (25, 61). (B) ¹H^α secondary shifts. (D) ¹³C^α secondary shifts. (F) Overall helical content in the sampling, calculated as the sum of the reweighted occurrences of α-helix and 3₁₀-helix, which are both associated with positive ¹³C^α and negative ¹H^α secondary shifts.

By reweighting the PT-MetaD sampling, we were able to generate surfaces that described the relevant properties of the system. We therefore could infer in detail how NMR observables depend on the Boltzmann populations of different conformational species within the solution ensemble. The secondary shifts of three residues (one from each turn of the fully helical conformation) are shown in Fig. 3. The resulting general trend is that regions of the FES with high values of H-bonds (i, i+4) are featured by secondary shifts that are typical of α-helices (positive for ¹³C^α and negative for ¹H^α and ¹³C^β). This trend, however, is not uniform along the PrP-H1 sequence. Indeed, for amino-terminal residues (i.e., Y146 in Fig. 3), the secondary shifts assume values indicative of a helix conformation already at low H-bond values (i, i+4), which is in line with a high helix propensity at the amino-terminus of the peptide (Fig. 1). A different situation emerges in the case of residues in the carboxy-terminal region (i.e., N154 in Fig. 3). For these residues, secondary shifts are indicative of a helix conformation only at high values of H-bonds (i, i+4), in line with the fact that the terminal region of the peptide folds into the helix conformation only in the case of basin b3 and assumes RC conformations for the remainder of the sampling, including the other helical basins b1 and b2 (see Fig. 1). An intermediate situation occurs in the case of the residues belonging to the central turn of the fully helical conformation (Y150 in Fig. 3). Overall, this analysis points out the detailed dependence of the NMR observables on the conformations and Boltzmann weights adopted in solution.

Figure 3.

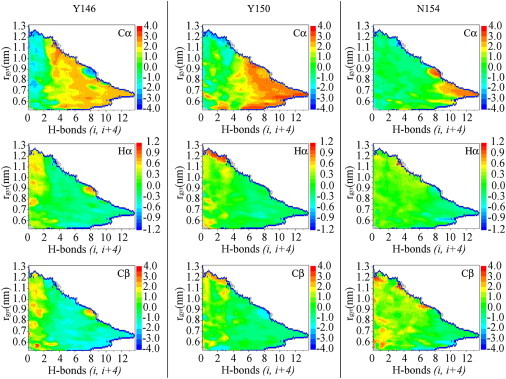
Surfaces of secondary shifts for three residues of the peptide. These are selected from the first (Y146), second (Y150), and third (N154) turns of the fully helical conformation of PrP-H1. The secondary shifts are calculated for each conformation by using the program SPARTA to predict chemical shifts from structures and subtracting the RC standard chemical shift values (25, 61). The calculated secondary shifts are then reweighted in the 2D space of the sampling.

The NOE-based NMR structural ensemble of PrP-H1 overrepresents helical conformations

Chemical shifts represent an ensemble property of the system, as does the NOE, which provides a powerful tool to calculate NMR structures (29, 30). It was recently shown that it is possible to convert NOE parameters into exact distances while simultaneously deriving dynamic information about a system (31). However, the applicability of this novel approach, which was tested on human ubiquitin, may be limited to stably folded proteins. Conversely, in the case of heterogeneous states of proteins and peptides, a structural determination by NOEs (32) can be ineffective owing to the strong influence that conformational averaging and dynamics exert on the experimental data. To demonstrate these problems, it is assumed that two helical turns, each of which is present only 34% of the time, are formed in an alternating manner (i.e., if helix turn one is formed, the other one is disordered, and vice versa). However, the NOE signatures thus obtained show only the presence of helical structure in both turns in this example, and do not allow one to distinguish time-dependent fluctuations and transient populations of different conformational states. Yet, although the crosspeak patterns in NOESY spectra are all compatible with the α-helical structure, the NOE intensities provide evidence of a structural heterogeneity (Fig. S4). Hence, when such data are used in traditional NOE-based structure calculations, it is always possible to arrive at a situation where all structural restraints are fulfilled in one structure at the same time. Ultimately, all time-dependent conformational changes are lost. Using all available experimental data, we demonstrate that a well-converging ensemble of helical structures is obtained, with a surprisingly high degree of order even in the side chains (see Supporting Material, Table S1, and Fig. S5). However, this structural result, which corresponds with the most structured basin (i.e., basin b3) in our PT-MetaD sampling, is in contrast to the experimental evidence from NMR chemical-shift data and CD. Even when only chemical-shift-derived dihedral constraints are used for structure calculation, a well-ordered helix is obtained, because all restraints are simultaneously applied and the dynamic nature of the system is lost. Such an overrepresentation of the helical content in the NOE ensemble supports the idea that, at least for heterogeneous states of proteins and peptides, structural ensembles derived by molecular simulations can better explain the experimental data than the lowest-energy NOE structures (33). Yet, although crosspeak patterns in NOESY spectra are all compatible with the α-helical structure, the NOE intensities provide evidence of structural heterogeneity (see Supporting Material and Fig. S4). Such heterogeneity is in line with our PT-MetaD ensemble (Fig. S5 D), which remarkably is in better agreement with the experimental NOE intensities than the lowest-energy structures calculated with conventional NOE-based approaches (see Supporting Material). Moreover, NOEs calculated by using a 1/r⁶ distance dependence of the PT-MetaD reweighted distances are in remarkable agreement with measured NOEs (Table S2).

Molecular determinants of PrP-H1 conformations

A distinctive feature of the sequence spanning PrP-H1 is the peculiar pattern of negatively (D144, E146, D147, and E152) and positively (R148, R151, and R156) charged residues, which generates a complex salt-bridge network in the native state of the full-length PrP (D144-R148, D147-R151, and E152-R156). This network has been proposed to be a stabilizing factor for the helical conformation (27, 34, 35, 36) and to regulate the conversion to pathogenic Scrapie prion (37). To shed light on the role of salt bridges in the conformational preferences of the PrP-H1 peptide, we reweighted the ensemble by obtaining a surface that reports the number of salt bridges for different conformations of PrP-H1 as sampled in the 2D space formed by the two sampling CVs (Fig. 4 A). Surprisingly, the resulting surface reveals not only that salt bridges are not exclusively formed within the helical basins of the PrP-H1 FES, but also that the highest occurrence of salt bridges is associated with the RC region. A deeper analysis showed that salt-bridge interactions destabilize the α-helical conformations of PrP-H1 because of the large number of possible combinations that are associated with the unfolded state. In particular, the RC state is able to sample nearly 50% of the 144 combinations of pairwise salt-bridges configurations that are statistically associated with the pattern of charged residues contained in the PrP-H1 sequence (12 combinations for the first bridge, six for the second bridge, and two for the third; Fig. 4 C). This is likely due to the lack of restrictions in the backbone conformations (Fig. S6). Conversely, the α-helical conformations are inherently compatible with a restricted number of configurations (Fig. 4, B, D, and E, and Fig. S7). The most restricted configurations are associated with the fully helical conformation (basin b3), which is associated with only four configurations. This reduction of the configurational space of the salt-bridge network is indicative of a reduction of configurational entropy, which is consistent with the reduced stability of basin b3 (Table 1), as well as with the larger susceptibility to the temperature-induced unfolding of this basin compared with the less-helical ones (Fig. S8).

Figure 4.

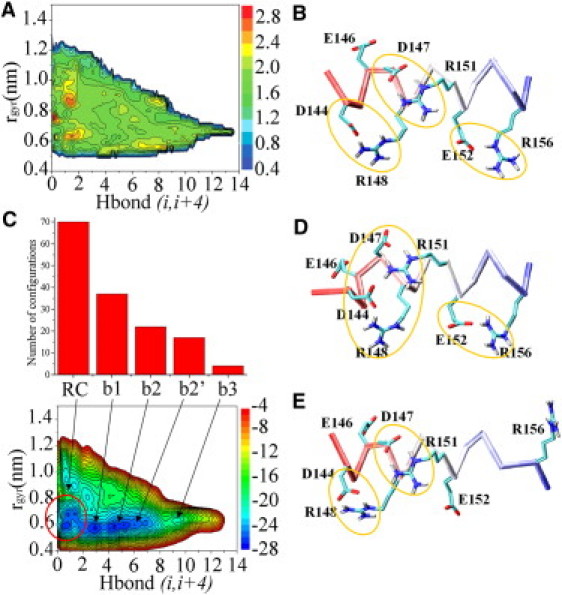
Effect of salt bridges on PrP-H1 conformations. (A) Reweighted surface of the salt bridges. This surface reports the number of salt bridges for different conformations of PrP-H1 as sampled in the 2D space formed by the two sampling CVs. To reweight the salt bridges, we adjusted the definition employed for the number of H-bonds (18) to sum step functions of the distance between charged side chains. (B, D, and E) Examples of possible salt-bridge configurations in the helix conformation. (C) The number of salt-bridge configurations explored in each relevant basin. The occurrences (top) are connected to the basins in the FES (bottom).

Using a similar approach, we addressed the role of the hydrophobic solvent-accessible surface area (SASA; Fig. S9). The reweighted surface of SASA shows that the RC and helical basins present similar SASAs (Fig. S9 B, Table 1), suggesting that, for this peptide, the shielding of hydrophobic surfaces is not a relevant stabilizing factor to discern between RC states and helical conformations. Indeed, the only significant reduction of SASA occurs along the pathway of the collapse from extended conformations, which in our surface corresponds to the transition from a high to a low r_gyr.

Discussion

The characterization of the conformational dynamics adopted by proteins and peptides in solution is a fundamental challenge in biophysics. In this work, we used NMR and metadynamics simulations to characterize the atomic-resolution conformational ensemble of the highly dynamic helix H1 of PrP, a protein that plays a central role in the development of a series of neurodegenerative disorders (e.g., TSE). Many experimental and theoretical studies have suggested that a relevant molecular event at the onset of PrP misfolding involves the detachment of the subdomain composed of strand S1, helix H1, and strand S2 from the subdomain composed of helixes H2 and H3 (Fig. S10) (34, 38, 39, 40, 41, 42, 43). This detachment results in the exposure of helix H1, which likely plays an important role in the misfolding of the entire PrP. For instance, interfering with the pattern of charged residues will affect either the propagation of the prion (37) or the binding to conformational selective antibodies (28, 44, 45). Understanding whether PrP-H1 is crucially involved in the subsequent events that lead to PrP misfolding and fibril formation is key to unveiling the molecular mechanisms underlying TSE.

Despite their central relevance for PrP research, characterization of the structures that PrP-H1 populates in solution at atomic detail remains elusive. One of the difficulties in determining the PrP-H1 structure is the intrinsic conformational heterogeneity adopted by helix H1 when it is not inserted in its native tertiary environment in full-length PrP, which limits the applicability of conventional structural biology approaches. Investigators have studied PrP-H1 at low resolution using experimental methods such as CD and NMR spectroscopy, and found that this isolated sequence exhibits a clear preference for helical conformations. Ziegler and colleagues (27) showed that the PrP-H1 sequence can adopt as much as a 60% helical structure depending on the experimental conditions (e.g., pH, cosolvent, and temperature). Of importance, the conformational properties of PrP-H1 have been shown to be independent of neighboring sequences (27, 46), thereby providing a relevant model for the biological behavior of this sequence in partially (mis)folded states, which have been shown to be important for pathogenic prion conformational changes (43, 47, 48, 49, 50). More specifically, detachment of the S1-H1-S2 subdomain appears to be a key event in these mechanisms.

A comprehensive picture of the conformations explored by PrP-H1 in solution is provided by our PT-MetaD sampling, which explores relevant structural species and describes an ensemble that is dominated by RC conformations in equilibrium with structures of different α-helix content (Fig. 1). The reweighted chemical shifts are in remarkable agreement with the experimental measurements and support the notion that, for heterogeneous states of proteins and peptides, predicted chemical shifts from the structural ensembles can better explain the experimental data than the lowest-energy NOE structures (33). Moreover, populations of secondary structures in the simulations match with the estimate provided by measurements of secondary shifts and CD. By reweighting the PT-MetaD sampling into surfaces that describe in detail the relevant properties of the system, we were able to assess the dependence of NMR observables on the structural parameters and Boltzmann weights of the conformations sampled. In particular, we revealed how chemical shifts vary along the FES phase space and how this modulation can differ for residues along the sequence (Fig. 3). The interconnection among structural states, Boltzmann weights, and ensemble-averaged properties is exemplified by our study of chemical shifts, but is generally applicable to any structural and biological ensemble-averaged property of the system. We could similarly address relevant biological aspects such as the influence of the hydrophobic exposed surface (Fig. S9) or the role of salt bridges (Fig. 4) in PrP-H1 folding and misfolding. In the full-length native structure of PrP, the unique occurrence of negatively and positively charged residues gives rise to a complex salt-bridge network that has been suggested to be a stabilizing factor for the helical conformation (34, 35, 36) and to regulate the conversion to pathogenic Scrapie prion (37). Our investigation, which is based on an exhaustive exploration of the configurations of salt bridges in the FES of PrP-H1, shows that the helical conformation, when the fragment is solvent-exposed and not packed onto the remainder of the protein, is rather destabilized by the salt-bridge network owing to the large number of configurations explored in the unfolded state. This effect is difficult to observe by conventional MD simulations (34, 35), and the results support the use of metadynamics as a powerful tool to examine the conformational properties of proteins and peptides. To assess the efficiency of PT-MetaD in exploring the PrP-H1 FES, we carried out a 100 ns standard MD simulation at 283 K by using the same simulation parameters employed in the PT-MetaD (Fig. S11). This analysis showed that the MD simulation was only able to explore basin b2 of the PT-MetaD FES. In particular, the system was trapped in a conformation with a highly persistent network of side-chain salt bridges. As a result, although standard MD has significant advantages in providing time-resolved information, such as the kinetics of conformational interconversions or rotational autocorrelation functions, it is limited by the difficulty of overcoming free-energy barriers. Giving the results of this analysis, it is likely that this MD simulation would have to be extended by several orders of magnitude to achieve an FES similar to that obtained from 48 ns of PT-MetaD.

The present results have implications for PrP misfolding in view of the β-nucleation model proposed by Morrissey and Shakhnovich (51) in such a way that the energy barrier for preventing PrP misfolding would be mainly associated with preservation of the helix H1 packing in the native-state interface, which is in line with our previous findings that at least four pathological mutations can favor fluctuations that promote PrP-H1 detachment from the native packing interface (34). Our results also indicate that the energy barriers involved in the folding and unfolding processes of PrP-H1 may not be identical, as salt bridges can stabilize the helical or unfolded state in different ways (well-defined and stabilizing interactions in the former and a large number of configurations in the latter). As a consequence, a hysteresis between unfolding and refolding events is created. Once PrP-H1 is unfolded, the large number of configurations of salt bridges, which is maximized in the RC state, enhances the frustration in the folding landscape of PrP-H1, thereby increasing the chances of protein misfolding (52). It is well established that partially unfolded states precede and favor the formation of oligomers along the aggregation pathways. Our data provide evidence that the sequence of PrP-H1 can contribute to the stabilization of such partially unfolded states, which was also shown to be the case for disease-associated mutations (53). Yet, the large number of configurations of the salt bridges network, which is maximized in the RC state, enhances the frustration in the folding landscape of PrP-H1, thereby increasing the chances of protein misfolding (52). It remains to be established whether PrP-H1 is recruited in the core of PrP fibrils (54, 55) or has exclusively kinetic effects in the aggregation process without being converted into β-sheets upon aggregation (56). In this framework, our investigation rules out any propensity toward the β-sheet structure for the monomeric PrP-H1, but dissects the thermodynamic factors that can stabilize, even transiently, local misfolded conformations when the helix is not packed onto the native tertiary interface. This result is remarkably consistent with the evidence that the sequence corresponding to H1 exhibits some residual helicity even in β-PrP (57). In an unfolded state, the sequence of PrP-H1 separates two sequence stretches that become enriched in β-sheet content upon unfolding (48) and contain at least one aggregation initiation site (58). Together, these findings point to a scenario in which PrP-H1, by getting trapped in metastable states (e.g., because of incorrect salt-bridge patterns), may contribute to the exposition of sequences with high aggregation propensities, thereby increasing the probability for formation of intermolecular contacts.

In conclusion, we used NMR and metadynamics simulations to characterize the atomic-resolution conformational ensemble of the highly dynamic PrP-H1. This investigation allowed us to reconstruct the FES of PrP-H1 with high accuracy, as revealed by a chemical-shift analysis, and to overcome the limitations of conventional approaches for studying heterogeneous states of proteins. The reweighting approach allowed us to dissect the contributions of relevant factors to the conformational preferences of PrP-H1. These results underline the importance of accurately determining the conformational FES to account for the ensemble properties of protegins and peptides, which we clearly exemplified by linking the conformational properties of PrP-H1 to possible implications for the misfolding of PrP.

Editor: Alexandre Bonvin.