Abstract
We present a two-component coarse-grained molecular-dynamics model for simulating the erythrocyte membrane. The proposed model possesses the key feature of combing the lipid bilayer and the erythrocyte cytoskeleton, thus showing both the fluidic behavior of the lipid bilayer and the elastic properties of the erythrocyte cytoskeleton. In this model, three types of coarse-grained particles are introduced to represent clusters of lipid molecules, actin junctions, and band-3 complexes, respectively. The proposed model facilitates simulations that span large length scales (approximately micrometers) and timescales (approximately milliseconds). By tuning the interaction potential parameters, we were able to control the diffusivity and bending rigidity of the membrane model. We studied the membrane under shearing and found that at a low shear strain rate, the developed shear stress was due mainly to the spectrin network, whereas the viscosity of the lipid bilayer contributed to the resulting shear stress at higher strain rates. In addition, we investigated the effects of a reduced spectrin network connectivity on the shear modulus of the membrane.
Introduction
Mature human erythrocytes do not have an internal structure; therefore, their mechanical properties originate from the cell membrane, which is the only structural element of the cell (1). The red blood cell (RBC) membrane is composed of a two-dimensional (2D) sixfold spectrin network that is tethered to a lipid bilayer comprised of various types of phospholipids, sphingolipids, cholesterol, and integral membrane proteins (see Fig. 1). The spectrin network consists of spectrin tetramers that are connected via actin filaments and additional proteins that form junctional complexes. Each spectrin tetramer comprises two heterodimers that consist of intertwined and antiparallel α-spectrin and β-spectrin filaments (1). The integral membrane proteins band-3 and glycophorin tether the cytoskeleton network to the phospholipid bilayer via additional peripheral proteins (e.g., Ankyrin and 4.1) (2). The lipid bilayer is essentially a 2D fluid-like structure embedded in a three-dimensional (3D) space. It resists bending but cannot sustain in-plane shear stress because the lipids and most of the proteins can diffuse freely within the membrane to relax the shear stress. The stiffness of RBCs arises primarily from the spectrin network. It is also noted that the material properties of the lipid bilayers play important roles in the function and distribution of the membrane proteins (3).
Figure 1.
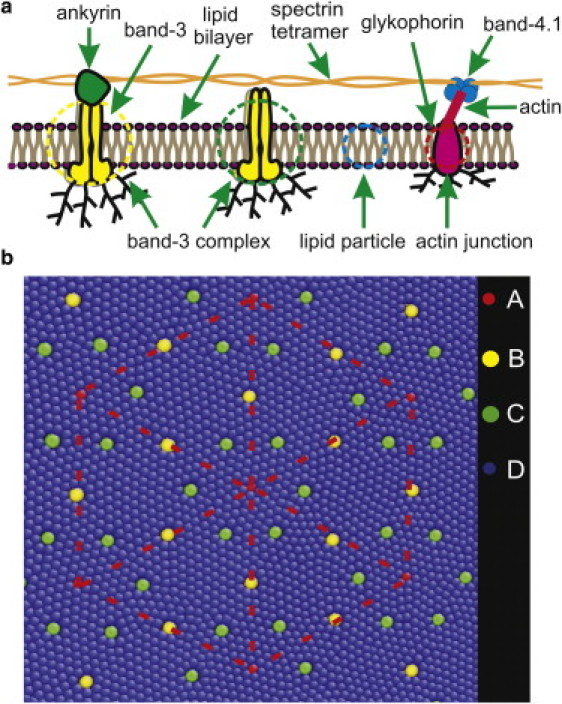
(a) Schematic of the membrane of human RBC. Starting from the left, the first circle corresponds to a band-3 complex connected to the spectrin network, the second circle corresponds to a free band-3 complex, the third circle represents a lipid particle, and the fourth circle signifies an actin junction. (b) Two-component human RBC membrane model. Particles of type A represent actin junctions. Particles of type B represent band 3 complexes connected to the spectrin network. Particles of type C represent free band-3 complexes. Particles of type D represent lipid particles. The dashed line highlights the supporting spectrin network.
Investigators have adopted continuum models based on membrane elasticity (4, 5, 6, 7, 8, 9, 10) to elucidate vesicle shape transitions and estimate thermal fluctuations of fluid membranes at length scales much larger than the bilayer thickness (11, 12). At the opposite end of the length-scale spectrum, researchers have extensively used atomistic simulations to rationalize the molecular mechanisms of various functions of bilayer membranes (13, 14, 15, 16). However, because of their prohibitive computational cost, atomistic models are inadequate for direct comparisons with the length scales and timescales of typical laboratory experiments.
The limitations of atomistic simulations and continuum approaches, along with the practical need to treat the heterogeneous nature of RBC membranes, have motivated the continuing search for coarse-grained molecular-dynamics (CGMD) methods that can bridge the atomistic and continuum models (17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40). A complete picture of CGMD and relevant references can be found in recent reviews (20, 35, 39). CGMD models can be generally categorized into explicit-solvent and implicit-solvent (solvent-free) schemes. Explicit-solvent schemes employ the hydrophobic interactions between membrane and solvent particles (a water molecule or a group of several water molecules) to stabilize the 2D membrane (22, 25, 33). Explicit-solvent models frequently employ dissipative particle dynamics, a very efficient method that uses a soft bead to represent a large volume of the solvent, thus significantly accelerating the computations (41, 42, 43, 44). Investigators extended this technique to lipid bilayers by introducing spring forces between representative particles in the polymer chains (25, 45). In the case of implicit-solvent schemes, the solvent particles are not directly represented in the simulation, and their effect is taken into account by employing effective multibody interaction potentials, based on the local particle density (21, 24, 34), or by implementing different pair-potentials between particles representing the hydrophobic tail and those representing the hydrophilic head of the lipids (26, 30, 31).
To largely extend the accessible length scale and timescale of the membrane model, Drouffe et al. (21) developed an early CGMD lipid membrane model featuring orientation-dependent interactions. In their model, they used an anisotropic attractive interaction between spherical particles, along with a hard-core repulsive interaction and a density-dependent hydrophobic multibody potential, to describe the lipid interactions. Brannigan and Brown (46) developed a solvent-free model in which lipids are represented as rigid, asymmetric spherocylinders that interact through orientation-dependent attractions. Kohyama (40) extended Drouffe et al.'s model by introducing an extra degree of freedom that corresponds to the effective curvature caused by thermal fluctuations. Yuan et al. (47) simulated the biological fluid membranes by introducing a one-particle-thick, solvent-free CG model in which the interparticle interaction is described by a soft-core pairwise potential. The model essentially combines the approaches of Drouffe et al. (21) and Cooke et al. (31). The interaction strength is also dependent on the relative orientations of the particles, but no membrane cytoskeleton is involved. In all of these models, the orientation-dependent interactions are used to describe the hydrophobicity of the tail groups of the lipids, and are essential for the self-assembly of a lipid bilayer in an aqueous environment.
In this work, we extend the CG solvent-free approach followed in the simulation of lipid bilayers (47) to model the entire RBC membrane by introducing a two-component membrane model. Three types of particles are used to represent lipid molecules, actin junctions, and band-3 complexes. The actin junction particles and a number of band-3 particles are connected via the worm-like chain (WLC) potential to form a hexagonal network linked to the lipid bilayer. Additional band-3 particles that do not sense the WLC potential are employed to simulate the band-3 protein complexes that can diffuse freely in the lipid bilayer. An orientation-dependent potential, similar to the potentials introduced by Yuan et al. (47), is employed between all particles to simulate the 2D fluidic nature of the membrane. The article is organized as follows: First, we introduce the CGMD model and show that when the parameters of the potential are tuned, the membrane model exhibits a 2D fluid behavior. We next measure the bending rigidity of the membrane and show that the numerical result is consistent with the experimental results and the continuum model based on bending elasticity (4, 5, 6). We then examine the effects of the potential parameters on the membrane properties and plot the phase diagram of the membrane model. Finally, we apply the two-component model to simulate the shearing of the RBC membrane, and measure the mechanical properties of the membrane with reduced network connectivity.
Simulation Method
Model
The model describes the RBC membrane as a two-component system consisting of the cytoskeleton and the lipid bilayer. Three types of particles are introduced (see Fig. 1 b). The blue-colored particles represent a cluster of lipid molecules with a diameter of 5 nm, a value similar to the thickness of the lipid bilayer. The red particles signify actin junctions that form a canonical hexagonal network representing the spectrin network. An actin junction has a diameter of ∼35 nm and resides in the cytoplasm (48, 49). It is connected to the lipid bilayer via glycophorin, which is comparable in size to the thickness of the lipid bilayer. Thus, the fluidic behavior of the membrane is affected only by the size of the glycophorin, and not by the size of the actin junctions. Therefore, the particles that represent the actin junctions in the model have a diameter of 5 nm, similar to the size of glycophorin. The yellow particles denote band-3 complexes that have a diameter of 7.5 nm (1) and are connected to the spectrin network, whereas the green particles represent the free band-3 complexes that are not connected to the spectrin network. The masses of the particles are given further below.
In the model, each particles carry both translational and rotational degrees of freedom , where and are the position and orientation (director vector) of particle i, respectively. The rotational degrees of freedom obey the normality condition . Thus, each particle effectively carries 5 degrees of freedom. We define as the distance vector between particles i and j. Correspondingly, is the distance, and is a unit vector. The particles interact with one another via a pairwise additive potential
| (1) |
with
| (2) |
where and are the repulsive and attractive components of the pair potential, respectively, and α is a tunable linear amplification factor. The energy well of this potential is essential to regulate the fluid-like behavior of the membrane; therefore, we define a function to enable tuning of the energy well. The effects of function on the potential are discussed further below. The interaction between two particles depends not only on their distance but also on their relative orientation via the function , which varies from −1 to +1 and adjusts the attractive part of the potential. We specify that a = 1 corresponds to the case in which is parallel to and both are normal to vector , and the value a = –1 corresponds to the case in which is antiparallel to and both are perpendicular to vector . The former instance is energetically favored due to the maximum attractive interaction between particles i and j, whereas the latter is energetically disfavored due to the maximum repulsive interaction. In essence, the energy difference between these two cases acts as the thermodynamic driving force responsible for the self-assembly of the lipid bilayer. One simple form of that captures these characteristics is
| (3) |
The equations of motion include the translational and rotational components
| (4) |
| (5) |
where , is a pseudo-mass with units of energy × time2, and the right-hand side of Eq. 5 conforms to the normality constraint .
Pair potential
To stabilize a fluid membrane, the lipid particles should be allowed to move past each other with relatively low resistance while the overall cohesive integrity is preserved. Cooke et al. (31) showed that the classical Lennard-Jones (LJ6-12) potential, , where ε is the unit of energy and d is the unit of length, possesses a very strong repulsive core below the equilibrium distance . This suppresses the position exchange of particles and makes it difficult to form a liquid phase. As the temperature T is raised from absolute zero, the initial crystal phase sublimes to the vapor phase without going through the liquid phase. Compared with traditional particle systems, the vapor phase in the model with orientation disorder is thermodynamically more favorable because of the entropic contributions from its rotational degrees of freedom. To describe a fluid membrane by self-assembled moving particles, we employ the following repulsive and attractive potentials:
| (6) |
The association energy between lipid and lipid particles is ε. We choose the equilibrium distance between lipid particles to be so that the potential described in (6) has the same minimum energy and equilibrium distance as the LJ6-12 potential. Similarly, because the actin particles have the same diameter as the lipid particles, the equilibrium distance between a lipid particle and an actin particle as well as the equilibrium distance between two actin particles are chosen to be . Since the radius of the band-3 particles is 1.5 times larger than the radius of the lipid particles or of the actin particles, the equilibrium distances between a lipid particle and a band-3 particle , and between an actin particle and a band-3 particle are chosen to be . Finally, the equilibrium distance between two band-3 particles is chosen to be . The association energy between lipid and band-3 particles, between lipid and actin particles, and between actin and band-3 particles is chosen to be 1.4ε. Fig. 2, a and b, only show the potential between lipid particles. Another appealing characteristic of the above potential (hereafter denoted by Poly4-8), is that the first, second, and third derivatives of with respect to rij are all continuous at .
Figure 2.
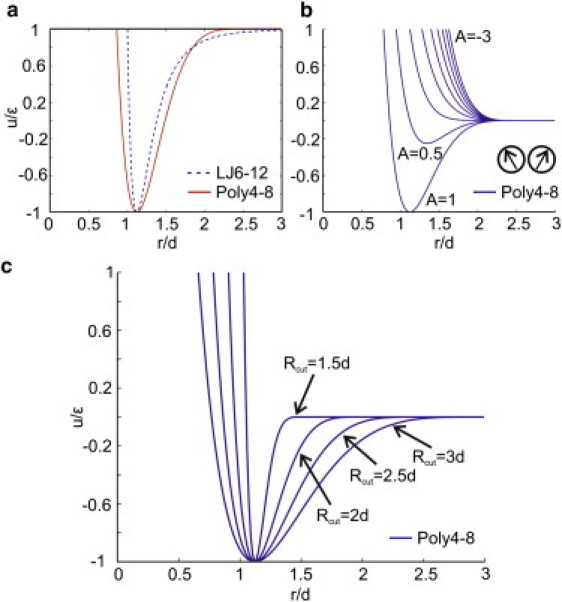
Pairwise interaction potential between lipid particles. (a) Comparison with the Lennard-Jones (LJ6-12) potential. (b) The interaction potential profile as a function of . (c) Increase in the value of the parameter Rcut widens the potential well, giving rise to a softer core of the interparticle interaction . The soft core is essential for stabilization of the membrane at the fluid phase.
Fig. 2a shows that the effective potential in the case of has a wider energy well than the LJ6-12 potential, which gives rise to a larger maneuverability near the equilibrium distance compared with the classical LJ6-12 potential. This characteristic helps particles squeeze past each other and stabilizes the liquid phase of the particle ensemble against the gas phase. The effect of the function on the potential is illustrated in Fig. 2 b. As the function changes from +1 to negative values, the total potential shifts from attractive to repulsive, penalizing the nonparallel arrangement of neighboring particles. This property of the potential ensures the formation of a 2D membrane sheet rather than a dense 3D structure with higher coordination numbers. We emphasize that because the parameter α regulates the energy penalty paid by membrane particles when their relative orientation changes, it plays an important role in adjusting the bending rigidity of the membrane.
One can tune the restoring force near the equilibrium distance between the same or different types of CGMD particles by adjusting the parameter Rcut. Fig. 2 c shows that a decreasing Rcut narrows the potential well between the lipid and lipid particles, which results in a rapid increase of the repulsive force. This increase in repulsive force, in turn, prevents the particles from passing each other and stabilizes them into a solid-like crystal phase. The influence of Rcut on the stabilization of fluid membranes is a general feature of soft-core potentials and is independent of the precise functional form of the potentials (31).
A WLC potential (50, 51) is employed to simulate the spectrin network. The WLC forces between the connected actin and band-3 particles is described by
| (7) |
where , Lmax = 100 nm is maximum or the contour length of the spectrin chain between an actin particle and a band-3 particle. L is the instantaneous chain length or the instantaneous distance between an actin and the corresponding band-3 particles, p = 10 nm is the persistent length of the spectrin filaments (52), kB is the Boltzmann constant, and T is the temperature. We used the WLC model to represent the RBC cytoskeleton without introducing bending rigidity to the spectrin network because the RBC membrane cytoskeleton is a highly flexible structure with bending rigidity κ ∼ 0.024–0.24 kBT (53, 54), which is about two orders of magnitude smaller than the bending rigidity of the lipid bilayer κ ∼ 10–20 kBT (52, 55).
Simulation details
We performed CGMD simulations of a planar membrane to extract the elastic properties of the membrane. Periodic boundary conditions were imposed in the plane of the membrane (x- and y-directions), whereas the z-direction (perpendicular to the membrane surface) was completely free of constraints. The system consists of N = 35,500 particles, including 34,600 lipid particles, 90 actin junction particles, and 810 band-3 complex particles (540 of which are not connected to the spectrin network). The dimension of the membrane is ∼1 μm × 1 μm. We performed a numerical integration of the equations of motion ((4), (5)) using the Beeman algorithm (56, 57). A Nose-Hoover thermostat was employed to control the temperature. The model was implemented in the NAT ensemble (34, 58, 59). Because the model is solvent-free and the membrane is a 2D structure, we controlled the projected area instead of the volume. The projected area was adjusted to result in zero tension for both the lipid bilayer and the spectrin network at the equilibrium state. The timescale that guides the choice of the time step in the CGMD simulations is . The chosen time step is 0.01 ts. In addition, to match the time steps used for translational and rotational degrees of freedom, the pseudomass is chosen to be , where is the mass of the lipid particles. As described further below, we determined an appropriate timescale by comparing the in-plane diffusion coefficient obtained from the simulations with experimental values (60).
We use ε as the energy unit, and d as the unit length to quantify the geometrical and mechanical properties of lipid bilayer and membrane proteins. Given the diameter of the lipid particles , we find . Each CG lipid particle carries a mass of , which we obtained by averaging over those of various lipids that compose an area of ∼20 nm2 of the erythrocytic membrane (1). The band-3 complex consists of band-3 protein and glycophorin A, with molecular masses of 102 kDa and 14 kDa, respectively. It also includes Ankyrin, which connects the band-3 protein with the spectrin cytoskeleton, and protein 4.2, which binds with the band-3 and Ankyrin. Ankyrin and 4.2 proteins have molecular masses of 210 kDa and 72 kDa, respectively (2). Therefore, the total mass of the band-3 complex is ∼398 kDa, corresponding to . As mentioned above, the band-3 complex is approximated as a sphere with diameter of 7.5 nm, equivalent to. An actin junction is composed of 14 kDa glycophorin C, short actin filaments (with a mass of 546 kDa), 80 kDa protein 4.1, 200 kDa adducin, 41 kDa tropomodulin, and 28 kDa tropomyosin (2). Thus, the actin junction is approximated as a sphere with a total mass of 1000 kDa and a diameter of 5 nm, corresponding to and . The maximum or the contour length of the spectrin chain between actin particles and band-3 particles is equivalent to . As shown below, the system is found to be a fluid membrane with bending rigidity well within the experimentally established range at and Rcut = 2.6 d. The amplification factor α in Eq. 2 was chosen to be 1.55.
Results
Self-diffusion
In this section, we show that the proposed model simulates a membrane with the appropriate mechanical and physical properties. Simulations are initiated from a flat triangular crystalline lattice that occupies the entire midplane of the supercell. At zero temperature, the particles form a 2D solid phase with a long-range order. As the temperature increases, the membrane starts to fluctuate and is gradually equilibrated at a fluid phase at the temperature of (see Fig. 3 a). To ensure that the model represents a fluid membrane, it is necessary to examine whether the lipid and band-3 particles can diffuse in a fluidic manner such that the particle's positions are exchangeable. Fig. 3, a and b, shows the positions of the particles of a thermally equilibrated fluid membrane at two separate times. The tiles with different colors are used to differentiate the positions of the particles at the initial moment. After 5×105 time steps, the colored particles are mixed due to diffusion, demonstrating the fluidic nature of the membrane.
Figure 3.
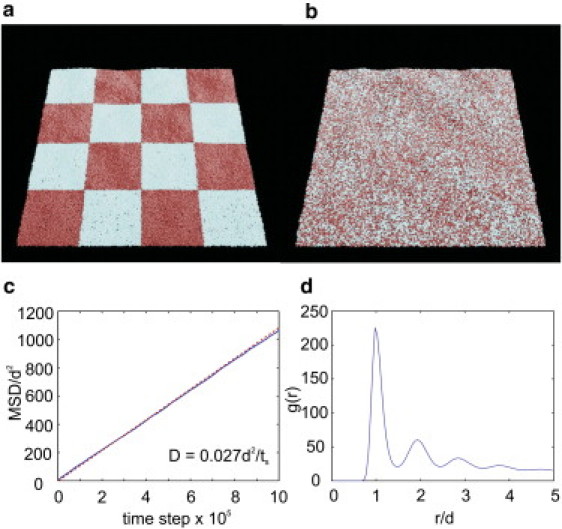
(a) Thermally equilibrated fluid membrane of N = 35,500 particles at a reference time, representing a membrane with dimension of ∼1 μm × 1 μm. Tiles with different colors are used to differentiate the positions of the particles at a reference time. (b) After 5×105 time steps, the particles are seen to be mixed due to diffusion, demonstrating the fluidic behavior of the model membrane. (c) Linear time dependence of the MSD of the two-component membrane model. (d) Radial distribution function in the 2D fluid membrane embedded in 3D.
We further verify the fluidic characteristics of the membrane using two other methods. First, we show in Fig. 3 c that the mean-square displacement (MSD) of lipid particles, defined by , increases linearly with time, indicating that self-diffusion and the changes of the particle connectivity take place easily and that the membrane is essentially a fluid within the simulation time. Using the expression of the diffusion coefficient , we obtain from Fig. 3 c that D = 2.7×10−2 d2/ts, where ts is the timescale. A typical value of the diffusion coefficient for the lipid of the phospholipid bilayer membranes is D ≈ 10−7cm2/s (60). By comparing that with the real value, we can determine the timescale, . Second, we find by examining the radial distribution function at Rcut = 2.6d and (see Fig. 3 d) that the membrane does not possess a crystalline order at a distance larger than the equilibrium distance, further demonstrating the characteristic of the fluid membrane.
Membrane elasticity
Within the framework of continuum mechanics, the free energy of a fluid membrane can be described by the classical Canham-Helfrich theory (4) as
| (8) |
where C1 and C2 are the principal curvatures, C0 is the spontaneous curvature, γ is the surface tension, and κ and are the bending and Gaussian rigidities (61), respectively. The first term on the right-hand side of Eq. 8 is the area-expansion energy, and the second and third terms represent the normal and Gaussian bending energies, respectively. Because the topology of the membrane remains unchanged, the Gaussian bending energy results in a constant contribution, and thus this energy term can be dropped. Surface tension is defined as , where and are the components of the in-plane virial stress (57) in a 3D periodic supercell calculation, and Lz is the height of the supercell, so that γ has the unit of N/m. Because the spectrin network is described by the WLC model, which does not directly introduce resistance to bending, we expect that the Canham-Helfrich theory for lipid bilayers is still valid in the equilibrium. In what follows, we extract the bending rigidity from the power spectrum of the height thermal fluctuations.
Applying the equipartition theorem on the Helfrich free energy in the Monge representation (4, 6, 11, 52), one can express the power spectrum as
| (9) |
where is the discrete Fourier transform of the out-of-plane displacement of the membrane, defined as
| (10) |
where L is the lateral size of the supercell, sets the mesh size equal to size of smallest particles, and q is the norm of the wave vector , i.e., .
To compute the bending rigidity, we first construct an equilibrated membrane at kBT/ε = 0.22 and with zero tension. This effectively excludes the membrane tension effect, and consequently we expect the power spectrum to exhibit only a dependence on the wave vector. Then, we calculate from the raw data of each recorded configuration and average them over all the available configurations to evaluate. Finally, by fitting the numerical data to Eq. 9 for γ = 0 via a minimization procedure based on a nonlinear regression scheme, we obtain the bending rigidity κ = 11.3 kBT of the membrane model (see Fig. 4). The numerical result lies within the experimental range of for a lipid bilayer (52, 55).
Figure 4.
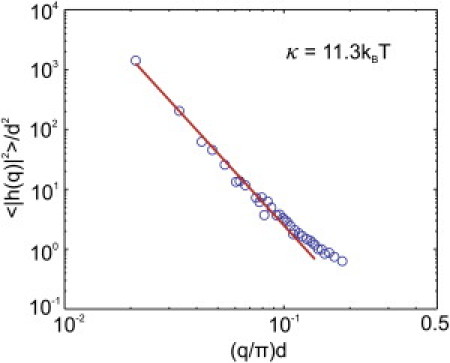
Vertical displacement fluctuation spectrum of the two-component membrane as a function of the wave number q.
Comparison between the two-component membrane model and the corresponding one-component lipid bilayer model
We compare the obtained diffusion coefficient and bending rigidity from the two-component membrane model with the results from the one-component membrane model, which employs only lipid particles, to examine the effects of the cytoskeleton on the membrane. The diffusion coefficient of the one-component lipid bilayer model (see Fig. S1 a in the Supporting Material) is computed as described in the “Self-diffusion” section above, and is found to be D = 4.2×10−2 d2/ts, which is 1.5 times larger than the diffusion coefficient measured in the two-component model. This result shows that the lipid particles diffuse less, primarily because of the interaction with the membrane cytoskeleton and the free band-3 particles. A measurement of the bending rigidity for the one-component lipid bilayer model is obtained as well. The vertical displacement fluctuation spectrum of the lipid bilayer as a function of the wave number is plotted in Fig. S1 b. The result shows that the bending rigidity of the one-component model is approximately the same as that of the two-component model, demonstrating that the cytoskeleton represented by the WLC model does not affect the overall bending rigidity that originates mainly from the lipid bilayer. We note that the model cannot describe the diffusion of band-3 proteins, which are confined by the spectrin network and undergo so-called confined or hop diffusion (62, 63). A subsequent model in which the detailed structure of the spectrin network is considered will address this phenomenon.
Phase diagram and the effects of the interaction potential parameters on membrane properties
We plotted a phase diagram of the membrane model based on the potential parameters Rcut and T. We then investigated the dependence of the diffusion coefficient D on the temperature T and Rcut, as well as the dependence of the bending rigidity on the parameter α, to study the effects of the parameters of the interaction potential on the behavior of the membrane model.
First, we determined the conditions under which the model behaves as a stable fluid membrane. The main parameters that govern the behavior of the model are Rcut and T. We constructed a 2D phase-diagram, as shown in Fig. 5 a, and performed simulations to determine the diffusivity of the membrane model. A similar analysis was conducted by Cooke and Deserno (64). The phase diagram is based on a system consisting of N = 35,500 CG particles. At low temperature and for small Rcut, the model behaves as a gel with very low diffusivity. At large values of Rcut, the model is unstable, independently of the temperature. As the temperature increases, the range of Rcut/d within which the membrane behaves as a stable fluid widens. The gel-fluid boundary is identified by a sudden increase in the diffusion coefficient and the disappearance of the crystalline order at a distance larger than the equilibrium distance. The transition from a fluid to an unstable state (gas phase) is characterized by the observation that the tensionless membrane starts to break apart (64).
Figure 5.
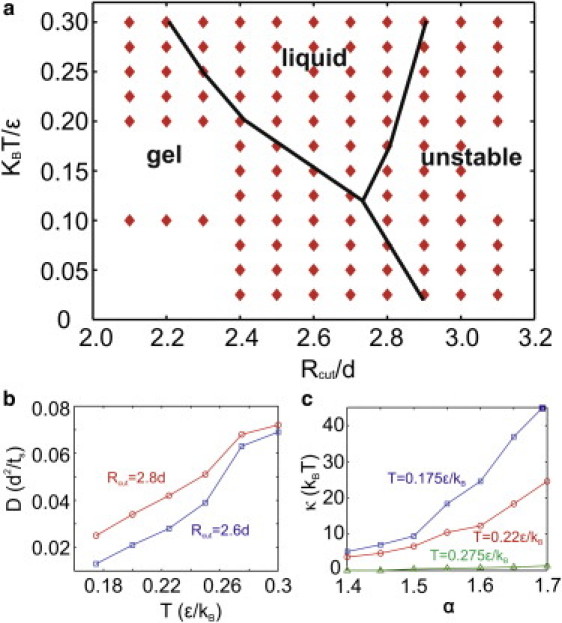
(a) Phase diagram. The hand-drawn lines show the phase boundaries. (b) Dependence of the diffusion coefficient D on the temperature T for Rcut= 2.6d and 2.8d, respectively. (c) Dependence of the bending rigidity κ on the parameter α at temperature T = 0.175, 0.22, and 0.275, respectively.
We then study the dependence of the diffusion coefficient D on the temperature T for Rcut= 2.6d and 2.8d, and α = 1.55. Measurements of D are limited in the fluid phase of the membrane. As shown in Fig. 5 b, D increases monotonically with T for both cases of Rcut= 2.6d and 2.8d, as the higher temperature leads to a larger kinetic energy. On the other hand, an increase in Rcut from 2.6d to 2.8d broadens the interaction potential well between the particles, as shown in Fig. 2 c, resulting in a decrease in the repulsive force. This decrease in repulsive force makes the particles pass each other with lower resistance and thus contributes to an increase in the diffusion coefficient. In addition, we study the dependence of the bending rigidity on the parameter α at three temperatures. Rcut is chosen to be 2.6d. The main role of α in the interaction potential is to regulate the energy well when the two interacting particles are disoriented from their favorable relative orientation (see Fig. 2 b), and thus it is closely related to the bending rigidity of the membrane model. As shown in Fig. 5 c, the bending rigidity κ increases monotonically with α for three different temperatures. We note that κ increases faster when the temperature is lower. As α increases, the function decreases and the total potential shifts from attractive to repulsive, imposing a greater penalty for the nonparallel arrangement of neighboring particles and forcing the membrane to become a flat 2D sheet. Fig. 5 c also shows that the temperature affects the bending rigidity of the membrane. The bending rigidity drops significantly when the temperature increases, because a higher temperature increases the equilibrium distance between the membrane particles.
Application
We applied our two-component membrane model in shearing experiments in which the shear moduli of the membrane were measured. Here, we compare the numerical results with experimentally obtained values. We also examine the effect of the reduction of the spectrin network connectivity on the shear modulus.
As discussed above, phospholipid bilayers behave as 2D fluid-like structures, and thus they can resist bending but cannot sustain static in-plane shear stress because the lipids and proteins can diffuse freely within the membrane. The resistance of the membrane under a low shearing strain rate is due only to the cytoskeleton. At the high shear strain rate, however, the viscosity of the lipid bilayer also contributes to the total resistance to the deformation. The membrane is sheared up to a shear strain of one at a temperature of kBT/ε = 0.22 (see Fig. 6, a and b) at the two strain rates of 0.001d/ts and 0.01d/ts, respectively. The response of the membrane to shearing at the low strain rate of 0.001d/ts is illustrated by the blue line in Fig. 6 c. At this strain rate, the shear viscosity of the lipid bilayer is not detectable and the total resistance is due only to the spectrin network. This becomes apparent from the fact that the red line in Fig. 6 c, which describes the shear-stress/shear-strain response of the corresponding WLC network, follows the pattern of the blue line, which describes the shear-stress/shear-strain response of the entire membrane. It is worth noting that the WLC model captures the experimentally identified stiffening behavior of the RBC membrane (65) and the behavior of a detailed spring-based model of a cytoskeleton network (66). When the strain rate is increased to 0.01d/ts, the viscosity of the lipid bilayer contributes to the total shear resistance (black line in Fig. 6 c). As a result, the initial value of the shear stress is not zero but 8 μN/m, which is equal to the shear stress measured during the shear deformation of a one-component lipid bilayer model (see Fig. S2).
Figure 6.
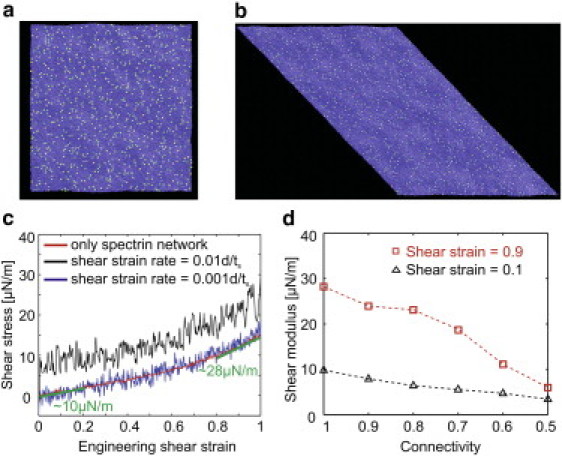
(a) Thermally equilibrated fluid membrane at a temperature of . (b) Sheared membrane at a temperature of and at an engineering shear strain of one. (c) Shear stress-strain response of the membrane at two strain rates. The continuous smooth curve represents the response of the bare spectrin network. The two undulating curves signify the shear stress obtained for strain rates of 0.001d/ts and 0.01d/ts, respectively. (d) Shear moduli of the membrane versus spectrin network connectivity at engineering shear strains of 0.1 and 0.9, respectively.
Up to this point, the connectivity of the spectrin network is maintained at 100%, meaning that each actin junction is connected to its six neighboring junctions through the WLC potential, forming a perfect 2D sixfold structure. However, both experimental evidence (67, 68, 69, 70) and sound theoretical studies (71, 72) show that the connectivity of the spectrin network in the RBC membrane is not 100% and the network is not a perfect 2D sixfold structure. Electron microscopy images showed that although most of the actin junctions are connected to six other actin junctions, a small amount of actin junctions are connected to five or seven actin junctions (67, 68). Subsequent atomic force microscopy results showed a lower connectivity of the cytoskeleton (approximately three or four links per actin junction), leading to square, pentagon-, and hexagon-like structures in the network (69, 73, 74). A CGMD model of the RBC cytoskeleton predicted that the biconcave shape of RBCs can be attained only if the network undergoes constant remodeling to relax the in-plane shear elastic energy to zero during the deformation, meaning that the connectivity of the spectrin network is changeable (72). Recent experimental results showed that remodeling of the spectrin network plays a vital role in determining the cellular deformation and biconcave shape of RBCs (70).
As shown in Fig. 6 c, when the spectrin network connectivity is 100%, the shear modulus of the membrane at small deformations is ∼10 μN/m, whereas it is 28 μN/m at 90% engineering shear strain. The linear elastic shear modulus of the model is larger than the experimentally measured values of 7.3 μN/m (65) and 4–9 μN/m (52), as well as the simulation results of 8.3 μN/m (72). This is probably because the connectivity of the employed spectrin network is 100%, whereas, as noted above, the actual spectrin network is not perfect. Because the membrane's resistance to shearing results mainly from the spectrin network, the shear modulus of the membrane would be expected to decrease as the connectivity of the spectrin network is reduced. To investigate the effect of the spectrin network's connectivity on the mechanical properties of the membrane model, we measured the shear modulus of the membrane when the connectivity of the spectrin network was reduced from 100% to 50%. The resulting shear moduli at small and large deformations are shown in Fig. 6 d, which clearly shows that their values drop dramatically with decreased spectrin network connectivity, especially at large deformations. The shear moduli of the membrane fall within the experimentally measured range of values when the network connectivity is between 60% and 90%. An RBC with a lower spectrin network connectivity is softer and easier to deform when it passes through narrow blood vessels. However, this low connectivity could lead to insufficient surface shear resistance to maintain the cell's biconcave shape and integrity during circulation in the blood. Our simulation results show that when the connectivity drops below 50%, the membrane model does not resist shear deformation, indicating that the RBC will completely lose its ability to recover its biconcave shape after deformation (66).
Conclusion
We have developed a two-component CGMD model for RBC membranes. In this model, the lipid bilayer and the cytoskeleton are considered as an ensemble of discrete particles that interact through a direction-dependent pair potential. Three types of CG particles are introduced, representing a cluster of lipid molecules, actin junctions, and band-3 complexes. The large grain size extends the accessible length scales and timescales of the simulations to approximately micrometers and milliseconds. By tailoring only a few parameters of the intergrain interaction potential, we were able to stabilize the model into a fluid phase manifested by free diffusion of the particles and reproduction of the essential thermodynamic properties of the RBC membrane. An important feature of the proposed model is the combination of the spectrin network with the lipid bilayer, which provides a more compete representation of the RBC membrane compared with a one-component CGMD model and most of the continuum models. This model allows us to study the behavior of the membrane under shearing. The behavior of the model under shearing at different strain rates illustrates that at low strain rates up to 0.001d/ts, the developed shear stress is due mainly to the spectrin network and shows the characteristic nonlinear behavior of entropic networks, whereas the viscosity of the fluid-like lipid bilayer contributes to the resultant shear stress at higher strain rates. The decrease in spectrin network connectivity results in a significant decrease in the shear modulus of the membrane, demonstrating that the cytoskeleton carries most of the load applied on the cell, whereas the lipid bilayer functions only as 2D fluid. The values of the shear moduli measured from the membrane with reduced spectrin network connectivity are in good agreement with previous experimental, theoretical, and numerical results.
Editor: Reinhard Lipowsky.
Footnotes
Two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(11)05363-X.
Supporting Material
References
- 1.Alberts B., Johnson A., et al. Walter P. Garland; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 2.Tse W.T., Lux S.E. Red blood cell membrane disorders. Br. J. Haematol. 1999;104:2–13. doi: 10.1111/j.1365-2141.1999.01130.x. [DOI] [PubMed] [Google Scholar]
- 3.McIntosh T.J., Simon S.A. Roles of bilayer material properties in function and distribution of membrane proteins. Annu. Rev. Biophys. Biomol. Struct. 2006;35:177–198. doi: 10.1146/annurev.biophys.35.040405.102022. [DOI] [PubMed] [Google Scholar]
- 4.Canham P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 5.Evans E.A. Bending resistance and chemically induced moments in membrane bilayers. Biophys. J. 1974;14:923–931. doi: 10.1016/S0006-3495(74)85959-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 7.Feng F., Klug W.S. Finite element modeling of lipid bilayer membranes. J. Comput. Phys. 2006;220:394–408. [Google Scholar]
- 8.Lim H.W.G., Wortis M., Mukhopadhyay R. Stomatocyte-discocyte-echinocyte sequence of the human red blood cell: evidence for the bilayer- couple hypothesis from membrane mechanics. Proc. Natl. Acad. Sci. USA. 2002;99:16766–16769. doi: 10.1073/pnas.202617299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Powers T.R., Huber G., Goldstein R.E. Fluid-membrane tethers: minimal surfaces and elastic boundary layers. Phys. Rev. E. 2002;65:041901. doi: 10.1103/PhysRevE.65.041901. [DOI] [PubMed] [Google Scholar]
- 10.Lipowsky R. In: Encyclopedia of Applied Physics. Trigg G.L., editor. VCH Publishers; Weinheim/New York: 1998. Vesicles and biomembranes; pp. 199–222. [Google Scholar]
- 11.Seifert U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997;46:13–137. [Google Scholar]
- 12.Smondyrev A.M., Berkowitz M.L. Molecular dynamics simulation of fluorination effects on a phospholipid bilayer. J. Chem. Phys. 1999;111:9864–9870. [Google Scholar]
- 13.Feller S.E. Molecular dynamics simulations of lipid bilayers. Curr. Opin. Colloid Interface Sci. 2000;5:217–223. [Google Scholar]
- 14.Saiz L., Bandyopadhyay S., Klein M.L. Towards an understanding of complex biological membranes from atomistic molecular dynamics simulations. Biosci. Rep. 2002;22:151–173. doi: 10.1023/a:1020130420869. [DOI] [PubMed] [Google Scholar]
- 15.Tieleman D.P., Marrink S.J., Berendsen H.J.C. A computer perspective of membranes: molecular dynamics studies of lipid bilayer systems. Biochim. Biophys. Acta. 1997;1331:235–270. doi: 10.1016/s0304-4157(97)00008-7. [DOI] [PubMed] [Google Scholar]
- 16.Tu K.C., Klein M.L., Tobias D.J. Constant-pressure molecular dynamics investigation of cholesterol effects in a dipalmitoylphosphatidylcholine bilayer. Biophys. J. 1998;75:2147–2156. doi: 10.1016/S0006-3495(98)77657-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Noguchi H., Gompper G. Shape transitions of fluid vesicles and red blood cells in capillary flows. Proc. Natl. Acad. Sci. USA. 2005;102:14159–14164. doi: 10.1073/pnas.0504243102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Boey S.K., Boal D.H., Discher D.E. Simulations of the erythrocyte cytoskeleton at large deformation. I. Microscopic models. Biophys. J. 1998;75:1573–1583. doi: 10.1016/S0006-3495(98)74075-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Discher D.E., Boal D.H., Boey S.K. Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophys. J. 1998;75:1584–1597. doi: 10.1016/S0006-3495(98)74076-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Venturoli M., Sperotto M.M., et al. Smit B. Mesoscopic models of biological membranes. Phys. Rev. Lett. 2006;437:1–54. [Google Scholar]
- 21.Drouffe J.M., Maggs A.C., Leibler S. Computer simulations of self-assembled membranes. Science. 1991;254:1353–1356. doi: 10.1126/science.1962193. [DOI] [PubMed] [Google Scholar]
- 22.Goetz R., Gompper G., Lipowsky R. Mobility and elasticity of self-assembled membranes. Phys. Rev. Lett. 1999;82:221–224. [Google Scholar]
- 23.Sunil Kumar P.B., Gompper G., Lipowsky R. Budding dynamics of multicomponent membranes. Phys. Rev. Lett. 2001;86:3911–3914. doi: 10.1103/PhysRevLett.86.3911. [DOI] [PubMed] [Google Scholar]
- 24.Noguchi H., Takasu M. Adhesion of nanoparticles to vesicles: a Brownian dynamics simulation. Biophys. J. 2002;83:299–308. doi: 10.1016/S0006-3495(02)75170-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yamamoto S., Maruyama Y., Hyodo S. Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules. J. Chem. Phys. 2002;116:5842–5849. [Google Scholar]
- 26.Farago O. “Water-free” computer model for fluid bilayer membranes. J. Chem. Phys. 2003;119:596–605. [Google Scholar]
- 27.Hofsäss C., Lindahl E., Edholm O. Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophys. J. 2003;84:2192–2206. doi: 10.1016/S0006-3495(03)75025-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marrink S.J., Mark A.E. Molecular dynamics simulation of the formation, structure, and dynamics of small phospholipid vesicles. J. Am. Chem. Soc. 2003;125:15233–15242. doi: 10.1021/ja0352092. [DOI] [PubMed] [Google Scholar]
- 29.Marrink S.J., Mark A.E. The mechanism of vesicle fusion as revealed by molecular dynamics simulations. J. Am. Chem. Soc. 2003;125:11144–11145. doi: 10.1021/ja036138+. [DOI] [PubMed] [Google Scholar]
- 30.Brannigan G., Philips P.F., Brown F.L.H. Flexible lipid bilayers in implicit solvent. Phys. Rev. E. 2005;72:011915. doi: 10.1103/PhysRevE.72.011915. [DOI] [PubMed] [Google Scholar]
- 31.Cooke I.R., Kremer K., Deserno M. Tunable generic model for fluid bilayer membranes. Phys. Rev. E. 2005;72:011506. doi: 10.1103/PhysRevE.72.011506. [DOI] [PubMed] [Google Scholar]
- 32.Laradji M., Sunil Kumar P.B. Domain growth, budding, and fission in phase-separating self-assembled fluid bilayers. J. Chem. Phys. 2005;123:224902. doi: 10.1063/1.2102894. [DOI] [PubMed] [Google Scholar]
- 33.Markvoort A.J., Pieterse K., et al. Hilbers P.A. The bilayer-vesicle transition is entropy driven. J. Phys. Chem. B. 2005;109:22649–22654. doi: 10.1021/jp053038c. [DOI] [PubMed] [Google Scholar]
- 34.Wang Z.J., Frenkel D. Modeling flexible amphiphilic bilayers: a solvent-free off-lattice Monte Carlo study. J. Chem. Phys. 2005;122:234711. doi: 10.1063/1.1927509. [DOI] [PubMed] [Google Scholar]
- 35.Brannigan G., Lin L.C.L., Brown F.L.H. Implicit solvent simulation models for biomembranes. Eur. Biophys. J. 2006;35:104–124. doi: 10.1007/s00249-005-0013-y. [DOI] [PubMed] [Google Scholar]
- 36.Markvoort A.J., van Santen R.A., Hilbers P.A.J. Vesicle shapes from molecular dynamics simulations. J. Phys. Chem. B. 2006;110:22780–22785. doi: 10.1021/jp064888a. [DOI] [PubMed] [Google Scholar]
- 37.Noguchi H., Gompper G. Meshless membrane model based on the moving least-squares method. Phys. Rev. E. 2006;73:021903. doi: 10.1103/PhysRevE.73.021903. [DOI] [PubMed] [Google Scholar]
- 38.Marrink S.J., Risselada H.J., et al. de Vries A.H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 39.Muller M., Katsov K., Schick M. Biological and synthetic membranes: what can be learned from a coarse-grained description? Phys. Rep. 2006;434:113–176. [Google Scholar]
- 40.Kohyama T. Simulations of flexible membranes using a coarse-grained particle-based model with spontaneous curvature variables. Physica A. 2009;388:3334–3344. [Google Scholar]
- 41.Espanol P., Warren P. Statistical-mechanics of dissipative particle dynamics. Europhys. Lett. 1995;30:191–196. [Google Scholar]
- 42.Hoogerbrugge P.J., Koelman J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992;19:155–160. [Google Scholar]
- 43.Grafmuller A., Shillcock J., Lipowsky R. Dissipative particle dynamics of tension-induced membrane fusion. Mol. Simul. 2009;35:554–560. [Google Scholar]
- 44.Shillcock J.C., Lipowsky R. Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations. J. Chem. Phys. 2002;117:5048–5061. [Google Scholar]
- 45.Groot R.D., Warren P.B. Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997;107:4423–4435. [Google Scholar]
- 46.Brannigan G., Brown F.L.H. Solvent-free simulations of fluid membrane bilayers. J. Chem. Phys. 2004;120:1059–1071. doi: 10.1063/1.1625913. [DOI] [PubMed] [Google Scholar]
- 47.Yuan H., Huang C., et al. Zhang S. One-particle-thick, solvent-free, coarse-grained model for biological and biomimetic fluid membranes. Phys. Rev. E. 2010;82:011905. doi: 10.1103/PhysRevE.82.011905. [DOI] [PubMed] [Google Scholar]
- 48.Byers T.J., Branton D. Visualization of the protein associations in the erythrocyte membrane skeleton. Proc. Natl. Acad. Sci. USA. 1985;82:6153–6157. doi: 10.1073/pnas.82.18.6153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shen B.W., Josephs R., Steck T.L. Ultrastructure of the intact skeleton of the human erythrocyte membrane. J. Cell Biol. 1986;102:997–1006. doi: 10.1083/jcb.102.3.997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bustamante C., Bryant Z., Smith S.B. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 51.Marko J.F., Siggia E.D. Stretching DNA. Micromolecules. 1995;28:8759–8770. [Google Scholar]
- 52.Boal D. Cambridge University Press; Cambridge, UK: 2002. Mechanics of the Cell. [Google Scholar]
- 53.Strey H., Peterson M., Sackmann E. Measurement of erythrocyte membrane elasticity by flicker eigenmode decomposition. Biophys. J. 1995;69:478–488. doi: 10.1016/S0006-3495(95)79921-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gov N., Zilman A.G., Safran S. Cytoskeleton confinement and tension of red blood cell membranes. Phys. Rev. Lett. 2003;90:228101. doi: 10.1103/PhysRevLett.90.228101. [DOI] [PubMed] [Google Scholar]
- 55.Seifert U., Lipowsky R. In: Hoff A.J., editor. Vol. 1. Elsevier, Amsterdam; 1995. Morphology of vesicles; pp. 403–463. (Structure and Dynamics of Membranes: From Cells to Vesicles). [Google Scholar]
- 56.Allen M., Tildesley D. Clarendon Press; New York: 1987. Computer Simulations of Liquids. [Google Scholar]
- 57.Frenkel D., Smit B. Academic Press; San Diego: 2002. Understanding Molecular Simulation: From Algorithms to Applications. [Google Scholar]
- 58.Imparato A., Shillcock J.C., Lipowsky R. Shape fluctuations and elastic properties of two-component bilayer membranes. Europhys. Lett. 2005;69:650–656. [Google Scholar]
- 59.Goetz R., Lipowsky R. Computer simulations of bilayer membranes: self-assembly and interfacial tension. J. Chem. Phys. 1998;108:7397–7410. [Google Scholar]
- 60.Fahey P.F., Webb W.W. Lateral diffusion in phospholipid bilayer membranes and multilamellar liquid crystals. Biochemistry. 1978;17:3046–3053. doi: 10.1021/bi00608a016. [DOI] [PubMed] [Google Scholar]
- 61.Nelson D., Piran T., Weinberg S. World Scientific; Hackensack, NJ: 2004. Statistical Mechanics of Membranes and Surfaces. [Google Scholar]
- 62.Tsuji A., Ohnishi S. Restriction of the lateral motion of band 3 in the erythrocyte membrane by the cytoskeletal network: dependence on spectrin association state. Biochemistry. 1986;25:6133–6139. doi: 10.1021/bi00368a045. [DOI] [PubMed] [Google Scholar]
- 63.Kodippili G.C., Spector J., et al. Low P.S. Imaging of the diffusion of single band 3 molecules on normal and mutant erythrocytes. Blood. 2009;113:6237–6245. doi: 10.1182/blood-2009-02-205450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Cooke I.R., Deserno M. Solvent-free model for self-assembling fluid bilayer membranes: stabilization of the fluid phase based on broad attractive tail potentials. J. Chem. Phys. 2005;123:224710. doi: 10.1063/1.2135785. [DOI] [PubMed] [Google Scholar]
- 65.Mills J.P., Qie L., et al. Suresh S. Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech. Chem. Biosyst. 2004;1:169–180. [PubMed] [Google Scholar]
- 66.Li J., Lykotrafitis G., et al. Suresh S. Cytoskeletal dynamics of human erythrocyte. Proc. Natl. Acad. Sci. USA. 2007;104:4937–4942. doi: 10.1073/pnas.0700257104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Liu S.C., Derick L.H., Palek J. Visualization of the hexagonal lattice in the erythrocyte membrane skeleton. J. Cell Biol. 1987;104:527–536. doi: 10.1083/jcb.104.3.527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Liu S.C., Derick L.H., et al. Palek J. Alteration of the erythrocyte membrane skeletal ultrastructure in hereditary spherocytosis, hereditary elliptocytosis, and pyropoikilocytosis. Blood. 1990;76:198–205. [PubMed] [Google Scholar]
- 69.Liu F.J., Burgess J., et al. Ostafin A. Sample preparation and imaging of erythrocyte cytoskeleton with the atomic force microscopy. Cell Biochem. Biophys. 2003;38:251–270. doi: 10.1385/CBB:38:3:251. [DOI] [PubMed] [Google Scholar]
- 70.Park Y.K., Catherine A.B., et al. Feld M.S. Metabolic remodeling of the human red blood cell membrane. Proc. Natl. Acad. Sci. USA. 2010;107:1289–1294. doi: 10.1073/pnas.0910785107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Dao M., Li J., Suresh S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Eng. C. 2006;26:1232–1244. [Google Scholar]
- 72.Li J., Dao M., et al. Suresh S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophys. J. 2005;88:3707–3719. doi: 10.1529/biophysj.104.047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Swihart A.H., Mikrut J.M., et al. Macdonald R.C. Atomic force microscopy of the erythrocyte membrane skeleton. J. Microsc. 2001;204:212–225. doi: 10.1046/j.1365-2818.2001.00960.x. [DOI] [PubMed] [Google Scholar]
- 74.Takeuchi M., Miyamoto H., et al. Kusumi A. Structure of the erythrocyte membrane skeleton as observed by atomic force microscopy. Biophys. J. 1998;74:2171–2183. doi: 10.1016/S0006-3495(98)77926-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


