α−α Cross-Links Increase Fibrin Fiber Elasticity and Stiffness

Abstract

Fibrin fibers, which are ∼100 nm in diameter, are the major structural component of a blood clot. The mechanical properties of single fibrin fibers determine the behavior of a blood clot and, thus, have a critical influence on heart attacks, strokes, and embolisms. Cross-linking is thought to fortify blood clots; though, the role of α–α cross-links in fibrin fiber assembly and their effect on the mechanical properties of single fibrin fibers are poorly understood. To address this knowledge gap, we used a combined fluorescence and atomic force microscope technique to determine the stiffness (modulus), extensibility, and elasticity of individual, uncross-linked, exclusively α–α cross-linked (γQ398N/Q399N/K406R fibrinogen variant), and completely cross-linked fibrin fibers. Exclusive α–α cross-linking results in 2.5× stiffer and 1.5× more elastic fibers, whereas full cross-linking results in 3.75× stiffer, 1.2× more elastic, but 1.2× less extensible fibers, as compared to uncross-linked fibers. On the basis of these results and data from the literature, we propose a model in which the α-C region plays a significant role in inter- and intralinking of fibrin molecules and protofibrils, endowing fibrin fibers with increased stiffness and elasticity.

Introduction

During hemostasis, thrombin enzymatically removes fibrinopeptides A and B from the soluble and abundant plasma protein fibrinogen, thus converting it to fibrin. Fibrin then spontaneously assembles into two-stranded, half-staggered, ∼10 nm wide protofibrils that further aggregate into 100 nm thick fibrin fibers. A mesh of these fibers forms the mechanical and structural backbone of a hemostatic blood clot. Activated Factor XIII (FXIIIa) further stabilizes fibrin fibers by catalyzing the formation of intermolecular ε-(γ-glutamyl)lysine covalent bonds, often called cross-links, between the α- and γ-peptide chains of the fibrin molecule. γ–γ and α–α cross-links dominate; though, α–γ cross-links can also occur (1). γ–γ cross-links form reciprocally between glutamine 398 or 399 and lysine 406 on adjacent γ-chains. α–α cross-links have numerous donors (Gln-221, -237, -328, -366) in the flexible α-connector (residues 221–391), and acceptors (Lys-418, -448, -508, -539, -556, -580, -601) in the globular α-C domain (residues 392–610). Thus, one α-chain can interact with one or more adjacent fibrin molecules, leading to α-multimers (1). Current understanding of the lateral assembly of protofibrils and the roles of the α-C domain and cross-linking in this process remains incomplete.

Over the last few years it was discovered that fibrin fibers are among the most extensible and elastic protein fibers in nature (2, 3, 4). They can be stretched to about three times their length before rupturing and to nearly twice their length without incurring permanent deformations. Other protein fibers that show similar extensibility and elasticity, such as spider silk, elastin fibers, or fibronectin fibers, typically have an amorphous, rather than an ordered, crystalline, internal fiber structure. Protein fibers that do have a crystalline structure, such as microtubules, collagen fibers, or actin filaments, have very low extensibility (3). Stress fibers, which are heterogeneous bundles of actin filaments, and whose internal structure is not known in detail, show large extensibilities, reaching strains of 2.75 (5). Fibrin fibers are known to assemble in a half-staggered, crystalline-like structure, which appears at odds with their large elasticity and extensibility (2, 4). This apparent contradiction could be resolved by identifying extensible, elastic elements within the fibrin monomer, between the fibrin monomers and/or between the protofibrils.

We have employed a combined atomic force microscopy (AFM)/optical microscopy technique to study the mechanical properties of single fibrin fibers formed from the variant γQ398N/Q399N/K406R. This variant eliminates all γ-chain cross-linking, with minimal change to the structure of the fibrin monomer (6). The single fiber experiments employed here cleanly separate changes in fiber properties from changes in clot morphology, architecture, or branch point properties, thus providing a direct way to study the fundamental effect of changing parameters on fiber properties. The rationale for studying the γQ398N/Q399N/K406R variant in single fiber measurements is that it eliminates all γ-chain cross-linking and thus provides a means to unambiguously study uncross-linked, exclusively α-cross-linked, and fully cross-linked fibers.

Our data show that α–α cross-links endow fibrin fibers with added elasticity, suggesting that the α-C domain plays a key role in fibrin fiber assembly and connecting fibrin monomers and protofibrils with each other. Our data also show that both α–α and γ–γ cross-links increase fiber stiffness. Moreover, our data indicate that γ–γ cross-links reduce extensibility.

Materials and Methods

Recombinant fibrinogen preparation

Recombinant fibrinogen was prepared as previously described (6). Briefly, expression vector pMLP-γ (7), containing the entire γ-chain cDNA, was altered at codon 406 to create the γK406R mutation using the QuickChange site-directed mutagenesis kit (Stratagene, La Jolla, CA). The resulting vector was used as a template for the Q398N and Q399N mutations. Mutations were confirmed by sequencing. Chinese hamster ovary cells, already transfected with the human Aα and Bβ fibrinogen chains, were cotransfected with the mutated γ-chain construct and selection marker to express the γ-variant vector as well as human Aα and Bβ fibrinogen chains. Protein was expressed and purified as described previously (8) and dialyzed against 100 mmol l⁻¹ NaCl, 50 mmol l⁻¹ Tris at pH 7.4, and stored at –80°C.

Fibrin samples for electrophoresis were prepared in parallel with samples prepared for the AFM manipulation studies. Fibrinogen (0.5 mg/ml) and FXIII (Enzyme Research Labs, South Bend, IN; final concentration, 55 Loewy units/ml) were mixed together in fibrin buffer (10 mM Hepes at pH 7.4, 5 mM CaCl₂, and 140 mM NaCl) and separated, half onto the microscope slide for a manipulation sample and half into tubes for electrophoresis testing. Thrombin (0.23 units/ml) was then added and both samples were allowed to clot for 1 h. After an hour, XT reducing agent and XT sampling buffer (Bio-Rad Lab Inc., Hercules, CA) were added to the tubes for electrophoresis and the samples were heated at 100°C for 10 min. The tubes were then stored at −80°C until used for SDS Polyacrylamide gel electrophoresis (SDS-PAGE). SDS-PAGE, 4% stacking, and 7.5% resolving, was used to separate polypeptide chains by molecular mass and Coomassie Blue staining was used to visualize the bands.

Cross-linking of fibrin fibers was tested by SDS-PAGE (Fig. 1). Uncross-linked native and γQ398N/Q399N/K406R fibrin showed three distinct bands; the α- (63 kDa), β- (56 kDa), and γ- (47 kDa) chain. Cross-linked native fibrin showed the β-chain at 56 kDa, the γ-dimer band around 94 kDa, and a higher molecular mass band representing α polymers. The disappearance of the α and γ bands and appearance of higher molecular mass bands indicated the cross-linking of these two polypeptide chains. The γQ398N/Q399N/K406R fibrin only showed α–α cross-linking, both the γ and β band remain at 47 kDa and 56 kDa, respectively; whereas the α band disappeared and a high molecular mass α polymer band appeared.

Figure 1.

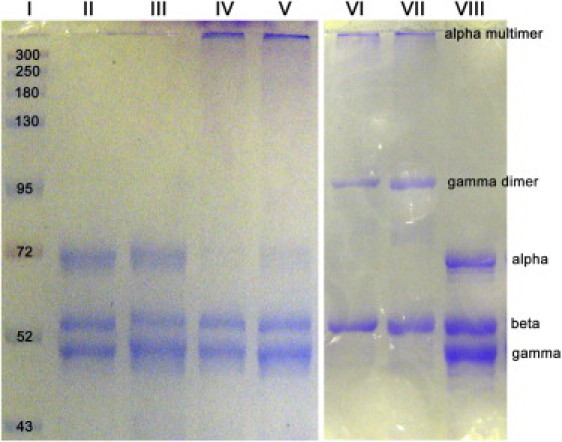
Recombinant fibrinogen preparation and gel electrophoresis. SDS polyacrylamide gel electrophoresis of fibrin. Lane I is the molecular mass standard. Lanes II and III are uncross-linked γQ398N/Q399N/K406R fibrin; the α-, β- and γ-chains are visible. Lanes IV and V are cross-linked γQ398N/Q399N/K406R fibrin. The β- and γ-chains remain while the α-chain disappears due to cross-linking and appears at the top of the gel as a high molecular mass α multimer. Lanes VI and VII are cross-linked native (wild-type) fibrin. Both the α- and γ-chains disappear and a γ-dimer band appears at 94 kDa, as well as the α multimer band at the top of the gel. Lane VIII is uncross-linked native (wild-type) fibrin showing the α, β, and γ bands.

Substrate/sample preparation

The striated surface was prepared as previously reported (2, 9), on a 60 mm × 24 mm, No. 1.5, microscope cover slide (VWR International, West Chester, PA) using a soft lithography and MIMIC (micromolding in capillaries) technique (10). A polydimethylsiloxane (PDMS) stamp was prepared by mixing dimethylsiloxane plus catalyst (Sylgard, Dow Corning, Midland, MI), pouring the mixture over a silicone master (7 μm wide ridges, and 6 μm deep by 13 μm wide trenches) and curing at 70°C for 1 h. The stamp was then removed from the master and stored in 2% SDS.

Tape was placed on a glass slide where the sample was to be prepared. Norland Optical Adhesive-81 (NOA-81, Norland Products, Cranbury, NJ) was placed around the tape and a large rectangle of PDMS was pressed into the glue. The optical glue was cured for 70 s with ultraviolet (UV) light (365 nm) on a UVP 3UV transilluminator (UPV, Upland, CA). The PDMS was removed from the slide leaving a rectangular well formed from the glue. The tape was removed from the center of the well and the striated stamp was placed in a 10 ml drop of Norland Optical Adhesive-81 where the tape was located. Again, the optical glue was cured for 70 s with UV light (365 nm). The stamp was then removed and stored in 2% SDS for subsequent use.

Fibers were formed on top of the striated surface in fibrin buffer (10 mM Hepes at pH 7.4, 5 mM CaCl₂, and 140 mM NaCl) with a final concentration of 0.5 mg/ml Fgn, 0.23 units/ml thrombin, and 55 Loewy units/ml FXIII (cross-linked fibers only). The fibrin was allowed to polymerize for 1 h before being rinsed, labeled with fluorescent beads, and stored in fibrin buffer. Fibrin fibers were fluorescently labeled with 24 nm, yellow-green carboxyl fluorescent beads (Invitrogen, FluoSpheres, Carlsbad, CA) diluted 1/10,000 in calcium free fibrin buffer. To label the fibers, 200 μl of diluted beads were placed on the sample for 10 min, before being rinsed with fibrin buffer.

Optical/lateral force microscopy

The manipulation and data acquisition were performed as previously reported (2, 9). The AFM (Topometrix Explorer, Veeco Instruments, Woodbury, NY) was set on top of a custom-made inverted optical microscope stage (Zeiss Axiovert 200, Göttingen, Germany). The stage allowed independent control of the AFM cantilever, sample, and microscope objective. Using the optical microscope we verified that the fiber chosen for manipulation remained in the focal plane along the length of the fiber to assure that fibers were not sagging between the ridges. The focal plane is ∼925 nm; thus, fibers were sagging less than that distance over a length of 13 μm (distance between ridges). Using the optical microscope we also verified that the fiber chosen for manipulation was oriented perpendicular to the ridges (40× lens, NA 0.75). The AFM cantilever (MikroMasch CSC38, force constant 14 N/m, length 90 μm, width 35 μm, tip height 15 μm; MikroMasch, Wilsonville, OR) was controlled by nanoManipulator software (3rd Tech, Chapel Hill, NC), allowing nanometer-sized steps in all directions. To prepare the cantilever for manipulation, the cantilever tip was first placed significantly above the fiber. The tip was then moved in the x-y plane perpendicular across the center of the fiber. If it did not touch the fiber, the tip was lowered by 500 nm in the z direction and the process repeated. Once the tip made contact, the tip was no longer moved in the z direction. This procedure assured that the fiber was located within 500 nm of the end of the cantilever tip (for a typical tip height of 10 μm).

The nanoManipulator software recorded elapsed time, distance traveled by the AFM tip, and lateral laser shift due to torsion of the cantilever. The force applied to the fiber, F_l, can be calculated by Hooke's law; F_l = K_C·I_l, where K_C is the force constant and I_l is the lateral shift of the laser (left – right photocurrent). Assuming that the photodiode is rotationally symmetric, the force constant can be obtained from K_C = Ewt³ / 6l² (h + t / 2)·S_n, where E, w, t, l, and S_n are the Young's modulus of silicon 1.69 × 10¹¹ N/m², the width, the thickness, the length, and the normal sensor response of the cantilever, and h is the height of the tip. The dimensions of the cantilever were determined by optical microscopy. The previous equations, our lateral force calibration procedure, and the error of our lateral force method are described in detail by Liu et al (11). A typical value for K_C is 7 N/A, for the cantilevers we used.

The radius of the fiber was determined by imaging the fiber on top of the ridge with the AFM. For calculating the stress (see definition below), we then assumed that this diameter remains the same for the length of the fiber across the groove. This assumption is based on scanning electron microscopy images (12) and AFM images (13) of fibrin fibers showing that the diameter is relatively constant for a fiber length of many micrometers with variations of perhaps 10%. The somewhat nonuniform appearance of the fibers in the light microscopy images (Fig. 2, A and B), is most likely due to the sparse fluorescent labeling of fibrin fibers.

Figure 2.

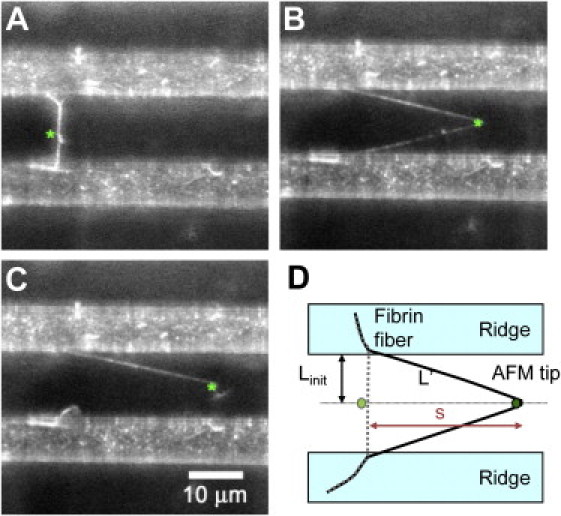
Fibrin fiber mechanical properties. (A–C) Optical images of γQ398N/Q399N/K406R fiber extensibility measurement. The AFM tip is indicated by a green asterisk; the fibrin fiber, attached to 7 μm wide ridges (white bands), extends across a 13 μm wide grove (dark band). (C) Fiber ruptures at a strain of 350%. (D) Top view schematic of the experimental setup. The initial, unstretched fiber, with length L_initial, is shown in gray; the stretched fiber, with length, L', is shown in black, and the AFM tip is shown as a green dot. The AFM tip travels a distance s, using the Pythagorean Theorem, the fiber is stretched to L' = (s² + L_initial²)^1/2. s is obtained from the nanoManipulator AFM data file, L_initial is determined from the optical image.

The optical microscope was used to observe and record movies of the manipulation and to verify the fiber was firmly attached to the ridge. The force curve was also used to verify that the fiber did not slip at the ridge, as sudden drops in force were seen when the fiber slipped or moved along the ridge. Fibers that detached or ruptured at the ridge were excluded (∼15% of all manipulations), because these data reflect the experimental setup, rather than fiber properties. Slipping of the fiber along the cantilever is another possible error in the measurements; however, we did not observe the fiber slipping off the end of the cantilever at strains higher than 10%, suggesting that slipping along the height of the cantilever did not occur during manipulations larger than 10% strain.

The optical image was also used to measure the initial length of the fiber and visually check the strain of the fiber in comparison to the strain calculated from the travel of the cantilever tip.

Definition of terms and geometry of measurement

Stress-strain curves

To analyze our data, we assumed a linear relationship between the stress σ and strain ε; σ = Y · ε (Hooke's law), for small strains ε. We used the engineering stress defined as σ = F/A, where F is the applied force and A is the initial cross-sectional area, and engineering strain, defined as ε = ΔL/L_initial, where ΔL is the change in fiber length and L_initial is the initial length of the fiber. Y is the stretch modulus, or Young's modulus. These definitions are strictly valid only for small strains. Fibrin fibers become stiffer with increasing strain (strain hardening, strain stiffening) (2); and the cross-sectional area most likely becomes smaller with increasing strain. Thus, our approach gives a lower limit for the value of the Young's modulus and the true stress.

However, in addition to reporting the raw force values of stretching fibers, it is also important to report the stress values, so that fibers with different diameters can be compared. We realize that the reported engineering stress is associated with errors at large stains due to the changing cross-sectional area. In fact, there is evidence that the fiber cross-section decreases as the fiber is stretched (14). Nevertheless, in selecting a definition for stress, we still chose engineering stress, because it is the most straightforward definition, and it is the correct definition in the limit of small strains.

Another approach would be to assume that the volume of the fiber remains constant as the fiber is stretched. In this case, the cross-sectional area, A, decreases by a factor of n, and the stress, σ = F/A, increases by a factor of n, as the length increases by a factor of n.

Extensibility is defined as the strain, ε_max at which the fiber ruptures.

Elastic limit is the strain to which a fiber can be stretched, without any discernible permanent deformation upon the release of the stress. Here, a sliding average was used because of the large variations among fibers.

Results and Discussion

The mechanical properties of individual fibrin fibers were determined by pulling on fibers, which were suspended over 13 μm wide groves, with the tip of a nanoManipulator-interfaced AFM (Fig. 2) (2, 9). The nanoManipulator software recorded the distance traveled by the AFM tip, s, and the force applied to the fiber. The optical microscope recorded movies of the manipulation. This setup allows the determination of nanofiber stress-strain curves (Fig. 3 A), from which different mechanical properties can be extracted.

Figure 3.

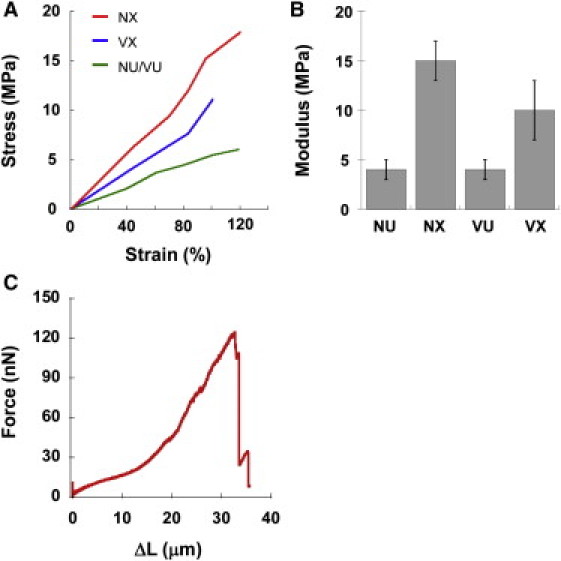
Fibrin fiber modulus. (A) Stress-strain plots. The modulus of individual fibers corresponds to the slope of the stress-strain graphs. (B) Modulus; NU – native, uncross-linked; NX – native, cross-linked; VU – variant, uncross-linked; VX – variant, cross-linked. (C) Representative force-extension curve.

The stiffness (modulus) of a fiber corresponds to the initial slope of these stress-strain curves. Both uncross-linked native (wild-type) and uncross-linked γQ398N/Q399N/K406R fibers had a modulus of 4 ± 3 MPa (average ± standard deviation, n = 27). α–α cross-linked fibers had 2.5× stiffer modulus of 10 ± 12 MPa (n = 17, p = 0.04), and fully cross-linked (native; wild-type) fibers had a 3.75× stiffer modulus of 15 ± 7 MPa (n = 14, p < 0.001), (Fig. 3 B). Whole clot studies of the γQ398N/Q399N/K406R variant showed a 2.5× increase in fiber modulus upon cross-linking, and 3.5× increase for native fibers (6). These whole clot numbers are nearly the same as those for the individual fibers, indicating that the change in modulus of the clots upon cross-linking is mostly due to changes in the individual fibers and not network morphology.

The rupture force is the peak force at which the fiber breaks. The peak force occurred at rupture or immediately before rupture. Fibrin fibers typically show strain hardening (or strain stiffening), meaning that they become stiffer as they are stretched (2) (Fig. 3 C). For uncross-linked fibers the rupture force was 233 ± 184 nN (n = 25 fibers); although it was 368 ± 289 nN (n = 14) and 581 ± 237 nN (n = 12) for cross-linked γQ398N/Q399N/K406R and cross-linked native fibers, respectively.

The extensibility of individual fibers was determined by stretching the fibers until they ruptured (Fig. 2, A–C, rupture in Fig. 2 C), and recording the rupture strain. Data from fibers that detached or ruptured at the ridge were discarded. Uncross-linked and cross-linked γQ398N/Q399N/K406R fibers extended to 243 ± 57% (n = 52), and 236 ± 69% (n = 32, p = 0.623), thus α−α cross-linking had no significant effect on extensibility. In contrast, complete cross-linking significantly reduced extensibility to 177 ± 58% (n = 41, p < 0.001) from 221 ± 44% (uncross-linked native, n = 35), suggesting γ–γ cross-links limit extensibility (Fig. 4 A).

Figure 4.

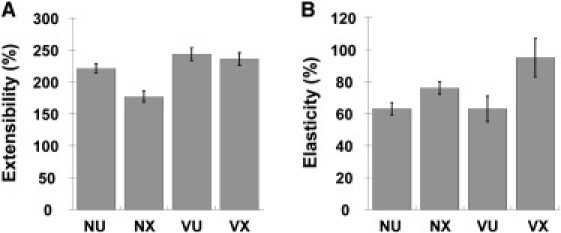
Fibrin fiber extensibility and elasticity. (A) Extensibility; and (B) elasticity of uncross-linked and cross-linked fibers; NU – native, uncross-linked; NX – native, cross-linked; VU – variant, uncross-linked; VX – variant, cross-linked.

The elastic limit was determined through a series of manipulations. Each fiber was stretched forward and then returned back past the starting position until it detached from the tip. We noted that the force required to detach the fiber from the tip (on the way back, past the original starting point) was dependent on the force/distance of the manipulation. For shorter manipulations less force was required to detach the fiber from the tip, whereas manipulations around 100% strain required around 100 nN to detach the fiber from the tip. When the fiber detached from the tip, the fiber was visually inspected to determine whether the fiber had been permanently lengthened, or not. If not, the procedure was repeated to higher strains until the fiber was permanently deformed. The elastic limit was defined as the strain at which half the fibers were permanently deformed. Because not all fibers were stretched to the same strain a sliding average was used to determine the elastic limit. Above the elastic limit >50% of fibers stretched to a given strain deformed and below the elastic limit <50% of manipulated fibers deformed. A sliding average was used because of the variation among fibers, ranging from strains as low as 45% to 120% without deformation. Uncross-linked fibers had an elastic limit of 63 ± 25% (γQ398N/Q399N/K406R, n = 34) and 63 ± 13% (native, n = 48); (Fig. 4 B). Cross-linking increased the elastic limit of native fibers to 76 ± 18% (full cross-linking, n = 49), and that of γQ398N/Q399N/K406R fibers significantly to 95 ± 30% (only α–α cross-linking, n = 48), indicating that α–α cross-links are important to the elastic response of fibrin fibers.

To summarize our main results: As compared to uncross-linked fibers, α–α cross-links result in 2.5× stiffer fibers, unchanged extensibility, and 1.5× higher elasticity; complete cross-linking results in 3.5× stiffer fibers, a 0.8× the extensibility, and 1.2× higher elasticity.

Fundamentally, γQ398N/Q399N/K406R fibrin fibers are interesting to study because they eliminate all γ-chain cross-linking with minimal change to the structure of the fibrin monomer. They, thus, allow the effect of α–α cross-linking on fibrin to be studied independently from γ-cross-linking. The clinical importance of α-chain interactions is apparent in patients with clotting disorders related to the truncations or mutation of the α-C domain of the fibrinogen monomer such as Fibrinogen Dusart, Fibrinogen Perth, and Fibrinogen Marburg (15, 16, 17, 18). The clinical picture in patients with α-chain abnormalities is complex, and varies from episodes of thromboembolism for Fibrinogen Dusart (15), to bleeding for Fibrinogen Perth (16), or both for Fibrinogen Marburg (17), depending on the type of the mutation and its effects on fibrin structure or susceptibility to fibrinolysis. For example, although Fibrinogen Perth (which leads to truncation of the α-chain from residue 517) did not influence susceptibility of the clot to fibrinolysis (16), Fibrinogen Dusart (which is caused by mutation of arginine to cysteine at residue 554 in the α-chain with subsequent binding of albumin via a disulfide bond) increased the resistance of the clot to fibrinolysis (15). Viscoelastic properties have been investigated for Fibrinogen Dusart. A drastic increase in clot stiffness was observed, which the authors attributed to the significant changes in fibrin structure for this variant and in particular to an increase in fiber branching (15).

From a (patho-)physiological point of view, the mechanical properties of fibrin represent one of the most important functional characteristics of the blood clot, together with its resistance to fibrinolysis. The mechanical properties of a blood clot formed during the hemostatic response to an injured blood vessel are critical to withstand the pressures of the flowing blood to prevent bleeding. Stiffness of the fibrin clot likely also plays an important role in thrombosis. It has been reported that fibrin clots from patients with cardiovascular disease are stiffer than those of controls (19, 20, 21), indicating a role for clot stiffness in the propensity to develop cardiovascular disease. Furthermore, it has been suggested that fibrin stiffness may determine the formation of emboli or small fragments of the clot that break off and subsequently occlude a smaller vessel downstream (22). Pulmonary embolism subsequent to deep vein thrombosis is one of the most deadly examples of the latter.

It is interesting to speculate if the somewhat large variability in extensibility and other fiber properties that we see in our data is biologically relevant. (We do not believe all the heterogeneity is due to instrumental variability). As a starting point, we will assume that the large variations are due to some variability or defects in the arrangement of fibrin molecules and protofibrils within a fibrin fiber. These defects may be due to the inevitable errors that occur when assembling thousands of molecules into a single fiber. It has been suggested that these defects are actually the origin of a branch point where protofibrils diverge from their straight, ordered alignment (23). It could be easily imagined that some of these defects may not turn into branch points, but rather result in an aborted branch point. We suggest that the variability in extensibility is due to defects in the regular, internal fiber structure, which should have turned into branch points, but did not. It should also be kept in mind that clots are meant to be temporary structures, as they need to be dissolved to restore blood flow, once wound healing has commenced. In fact, clots carry the seed for their own destruction, as fibrin has binding sites for tissue plasminogen activator and plasminogen, which, in its activated form, digests a clot. Weak spots and fiber defects, as described previously, may be a particularly good starting point for clot dissolution; so these weak spots may serve an important biological function in clot dissolution, while not having a major effect on overall clot stability because there are many fibers in a clot.

There are other natural fibers that have a similarly high elasticity and extensibility as fibrin fibers, such as the catching thread of spider webs, fibronectin fibers connecting cells, or elastin fibers in the extracellular matrix (3). Large extensibilities can endow fibers with high toughness, which is the area under a stress-strain curve, a measure of how much energy a fiber can absorb before breaking. Fibers with elastic, high toughness are found in structures that need to absorb sudden, large forces or bursts of kinetic energy without failing (for instance, the pulling of fibers when a fly is caught in a spider web). Elastic, high toughness might also be required in blood clots. As fibrin fibers form, blood is still flowing, and the elastic, high toughness of the fibers may allow them to absorb these forces and energy without breaking. In addition, activated platelets are incorporated into the clot, and during clot retraction there is pull on the fibrin fibers, increasing tension on the fibers. Our data suggest that on the molecular level the α-C region may be the element that provides fibrin fibers with the elastic extensibility and elastic, high toughness that is needed for the fibers to absorb the sudden force and kinetic energy of flowing blood, and to maintain the connection between platelets.

On the basis of our results and published data, we propose a model for fibrin fiber assembly, elasticity, and extensibility as depicted in Fig. 5. It is widely accepted that the A:a interactions are critical for the directed assembly of fibrin monomers into protofibrils, resulting in regular, half-staggered protofibrils (24, 25). Protofibrils further assemble into ordered, nearly crystalline fibers, though this assembly is poorly understood. The near-crystalline structure of fibrin fibers is difficult to reconcile with the large extensibility and elasticity of fibrin fibers (4), because crystalline protein fibers are typically stiff and show low extensibility and elasticity (3). This apparent contradiction between crystalline structure and high elasticity can be resolved by adding stretchable and elastic elements between and/or within the fibrin and protofibril building blocks. Previously, we and others have proposed a model of extensibility focused on extension of the α-helical coiled coils and potentially the γ-nodule (2, 14, 26, 27). We now extend this model to include the parallel extension of the α-C domain providing additional elasticity to the fiber. This mechanism could replace the unfolding of the γ-nodule. We propose that the α-region, consisting of a ∼60 nm long, flexible, and unstructured α-connector (residues 221–391, containing Gln cross-link donors) and a globular α-C domain (residues 392–610, containing Lys cross-link acceptors), plays a key role in linking fibrin molecules and protofibrils together, thus endowing single fibrin fibers with the elasticity observed in our experiments (Fig. 5). This model is supported by our (and others) experimental observations. Rheology and biophysical experiments indicate that fibrin fibers are relatively open structures consisting of flexibly connected protofibrils (13, 28, 29, 30); this flexible connector is most likely the α-connector. Force spectroscopy experiments also provide direct evidence that the α-C domains can interact with each other (31). Falvo et al. (32) found a positive correlation between increased extensibility and increased length of αC tandem repeats, suggesting the αC connector region adds fiber extensibility. Houser et al. (33) showed that fibrin fiber stress-strain curves agree well with a model in which the α-connectors act like a worm-like chain connecting protofibrils with each other. They propose that the α-C region is the origin of the low modulus, high extensibility and strain stiffening in fibrin fibers.

Figure 5.

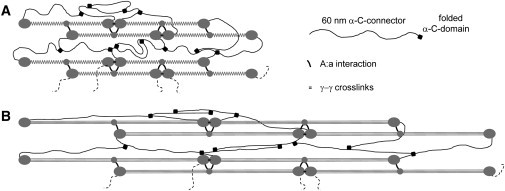
Fibrin fiber model. (A) Cartoon model of unstrained fiber. The main interactions for directed protofibril assembly are the short A:a interactions. The 60 nm long α-C connector can form intermolecular and interprotofibrillar interactions. Addition of FXIII covalently links the α-C domains to the α-C connectors; α multimers can be formed because there are several Glutamine donors on each α-C connector and several Lysine acceptors on each α-C domain. This results in a loose, polymer chain-like structure. Such a structure would result in elastic and extensible fibers. Longitudinal γ–γ cross-links are shown between abutting fibrin monomers, though transverse γ–γ cross-links have also been proposed (40). (B) Cartoon model of strained fiber (ε = 100%). The α-C connectors are stretched, and the α-helical coiled coils are converted to extended β-strands; the α-C connectors provide elasticity to revert back to the unstrained fiber. γ–γ cross-linking stiffens fibers by channeling more of the strain through the coiled coils of the fibrin monomer.

Whole clot experiments with cross-linked and uncross-linked α251 fibrin also indicate that the α-C region plays a key role in the mechanical behavior of uncross-linked and cross-linked fibrin clots. α251 fibrinogen has its α-chain truncated after amino acid 251, thus eliminating most of the α-C domain and all α-cross-links. Uncross-linked clots formed with this variant had thinner fibers, were softer by a factor of three and more susceptible to plastic deformation than their native counterparts (34), suggesting that the noncovalent interactions between α-C domains play a role in fiber assembly and increase fiber rigidity and elasticity. When cross-linked, the α251 clots increase in stiffness by a factor of 1.6-fold in comparison to 2.3-fold of normal fibrin (34), indicating that γ–γ cross-linking accounts for some of the increased stiffness, but not all of it. These data and our data show that both α- and γ-cross-linking together are responsible for the total increase in fiber modulus.

The axis along which stress is propagated may change depending on cross-linking. In uncross-linked fibers the lack of covalent bonds in the α-C domain may cause the intermolecular interactions of the α-C domain to weaken and detach as stress increases leading to a point, the elastic limit, where the α-chain can no longer restore the fiber to its original length. In α–α cross-linked fibers the covalent bonds in the α-C domain may increase the strength of the αC intermolecular interactions and therefore increase the strain at which permanent deformation occurs. However, when both α- and γ-cross-links are present, as in normal cross-linked fibrin fibers, the elastic limit decreases to a lower strain value. We propose that γ-cross-links play a role in lowering the cross-linked elastic limit by changing the pattern of stress propagation through the fibrin monomers, leading to deformation. Located on the γC domain, γ-cross-links may cause forces to propagate along the longitudinal direction of the monomer, channeling stress through the D- and E-domains and the coiled coils. The result of the relocation of stress to these regions may lead to unfolding, causing irreversible deformation.

The decrease in extensibility of normal cross-linked fibrin may be explained in the same manner. Again, the presence of γ–γ cross-links leads to a lower extensibility. This decrease in extensibility may be due to the propagation of force longitudinally along the fibrin monomer. In γQ398N/Q399N/K406R fibrin, containing only α–α cross-links, the extensibility of the fibers are in agreement with uncross-linked fibrin. The role of γ–γ cross-links in the elastic limit and extensibility of the fibrin fiber in the longitudinal direction is interesting in the light of recent reports that demonstrate that fibrin fibers in clots made under flow conditions are orientated in the direction of flow (35, 36, 37). As fibrin fibers are less resistant to flexion than to stretch, the implications of this are that the fibrin clot develops maximal mechanical resistance in relation to the direction of flow. Our data suggest that γ–γ cross-links may play a particular role in this, as they limit extensibility of the fibers along the longitudinal axis.

Experiments and simulation involving the α-C region have been challenging due to its multiple intermolecular interaction sites and its mobility (1, 38); thus, this region has been somewhat ignored. However, recent work indicates that it may play a major role in fibrin fiber assembly and mechanical behavior (31, 32, 33, 34). Further studies on fibrinogen variants, such as α251, at the individual fiber level, whole clot level, and single molecule level will continue to improve our understanding of fibrin cross-linking, fiber formation, and mechanical properties of blood clots. Ultimately, elucidation of blood clot mechanical properties may result in better approaches to dissolve blood clots, as is needed when treating thrombotic events such as heart attacks, strokes, pulmonary embolisms, and deep vein thrombosis. Current treatment options are mostly chemical in nature (e.g., activation of plasmin) to digest clots. An additional mechanical component to blood clot dissolution, perhaps in the form of ultrasound, might dissolve clots faster, as has been demonstrated in pilot studies (39). A better understanding of the mechanical behavior of single fibrin fibers may provide information to improve those mechanical dissolution approaches.

Editor: Daniel Mueller.