Biophysical Neural Spiking, Bursting, and Excitability Dynamics in Reconfigurable Analog VLSI

Abstract

We study a range of neural dynamics under variations in biophysical parameters underlying extended Morris–Lecar and Hodgkin–Huxley models in three gating variables. The extended models are implemented in NeuroDyn, a four neuron, twelve synapse continuous-time analog VLSI programmable neural emulation platform with generalized channel kinetics and biophysical membrane dynamics. The dynamics exhibit a wide range of time scales extending beyond 100 ms neglected in typical silicon models of tonic spiking neurons. Circuit simulations and measurements show transition from tonic spiking to tonic bursting dynamics through variation of a single conductance parameter governing calcium recovery. We similarly demonstrate transition from graded to all-or-none neural excitability in the onset of spiking dynamics through the variation of channel kinetic parameters governing the speed of potassium activation. Other combinations of variations in conductance and channel kinetic parameters give rise to phasic spiking and spike frequency adaptation dynamics. The NeuroDyn chip consumes 1.29 mW and occupies 3 mm × 3 mm in 0.5 μm CMOS, supporting emerging developments in neuromorphic silicon-neuron interfaces.

I. Introduction

Neuromorphic engineering, as an analysis by synthesis approach to computational neuroscience, is increasingly offering physical tools for studying the dynamics of complex neural systems [1]–[4]. While analog neural chips inherently have limited programming capability, recent designs have overcome this limitation by incorporating a large number of parameters in a reconfigurable architecture [5]–[11]. This opens up opportunities in systematic studies of the dependence of the dynamics upon biophysical parameters. Iterative methods, such as gradient descent learning [12] and evolutionary algorithms [13]–[15] can then be applied to estimate the model parameters for biological inference.

Here we present such a study on a silicon biophysical neural model with wide-ranging membrane dynamics and channel kinetics [16] that, within the same architecture as illustrated in Fig. 1, extends the Hodgkin–Huxley (HH) and Morris-Lecar (ML) paradigms from tonic spiking to intrinsically bursting neural dynamics [17] and a variety of other neural dynamics. Neurons exhibit dynamics at a wide range of time scales. However, longer time scales extending beyond 100 ms have been neglected in silicon models. We include mechanisms at such longer time scales that provide network models with new computational abilities, including central pattern generation [18] and memory consolidation in thalamocortical networks [19].

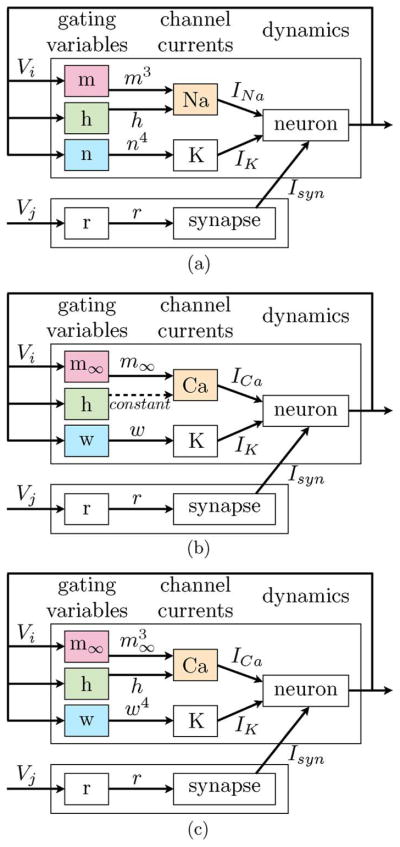
Fig. 1.

The NeuroDyn analog VLSI programmable neural emulation platform [29]–[31] is used to generate both tonic firing and intrinsic bursting dynamics using extensions on Hodgkin–Huxley and Morris-Lecar paradigms. (a) Hodgkin–Huxley. (b) Morris-Lecar. (c) extended Morris-Lecar and Hodgkin–Huxley.

One of the simplest neuron models, a leaky quadratic integrate-and-fire model by Izhikevich [20], uses just two dynamical variables and four parameters to generate 20 distinct types of neuronal dynamics. A further simplified model with linear membrane dynamics has been shown by Mihalas and Niebur [21] to generate an equivalent range of neuronal dynamics. Despite the success of these models to efficiently emulate rich dynamics in analog VLSI [22]–[25], the very compact state representation does not offer a direct biophysical interpretation of their parameters. Our work provides an alternative biophysically-based approach in an extended HH-ML formalism with generalized channel kinetics. We demonstrate a variety of neural dynamics through detailed control of the parameters governing the voltage-dependence profile of the opening and closing channel kinetic rates. Because each parameter is directly related to channel kinetics, the tuning of these parameters may provide insight into neuroscientific or clinical questions related to changes in, for instance, neuromodulators and pharmacological agents acting upon the modeled channels.

A variety of silicon neuron circuits have been proposed to implement models with varying degree of biophysical realism [26]. A parameterized library of biophysically-based analog operators in the HH model framework has been presented in [8]. A floating gate silicon neuron implementation also demonstrates a variety of neural dynamics and bifurcations [27].

Here we use NeuroDyn [28]–[31] as an experimental analog continuous-time platform to study parameterized biophysical neural dynamics over an extended range of time scales within a generalized HH-ML framework [32]. Fidelity between circuit simulation and measurement data, along with a low-power and compact circuit implementation, are key factors in utilizing a continuous-time analog VLSI emulation platform, such as NeuroDyn, as a versatile tool in neuromorphic modeling and silicon-neuron interfaces [33]–[35].

In [28] we demonstrated that the addition of a slow inactivation term to the ML neuron model results in bursting neural dynamics in the NeuroDyn analog VLSI implementation. Calculation of inter-spiking interval (ISI) for both simulated and measured bursting waveforms over the variation of a single conductance parameter g_w governing calcium recovery show agreement in behavior between simulation and circuit measurement data.

Here we present, in addition to tonic spiking and intrinsically bursting dynamics, a wider range of neural dynamics including phasic spiking and spike-frequency adaptation within the same NeuroDyn analog VLSI implementation platform by systematic variation of parameters governing Na⁺ and K⁺ channel kinetics. We also present class 1 and class 2 neural excitability dynamics and show that variation of the dynamical voltage-dependent profile of τ_n governing K⁺ inactivation results in an exchange between the two behaviors. Calculation of ISI for both simulated and measured class 1 and class 2 neural excitability ramp responses show agreement in behavior between simulation and circuit measurement data.

II. NeuroDyn Overview

The NeuroDyn system [28]–[31], illustrated in Fig. 1, consists of 4 neurons with Hodgkin–Huxley type membrane dynamics fully connected through 12 conductance-based synapses. All parameters are individually addressable and individually programmable and are biophysically-based governing the conductances, reversal potentials, and voltage-dependence of the channel kinetics. Each opening and closing channel kinetic rate is approximated with a 7-point spline regression function allowing for detailed control of the channel kinetics. These 14 parameters with two additional terms governing reversal potential and conductance per channel result in a total of 384 parameters each stored on-chip in a 10-bit DAC. Parameter fitting is achieved through rectified linear regression and iterative least squares residue correction. Scalable neural and synaptic arrays can be implemented by abstracting the desired dynamics of the neurons and synapses models and pooling together parameter control from individual to populations of neurons.

The analog VLSI design of the NeuroDyn system, and preliminary experimental results were presented in [29]. First results on coupled neural dynamics with inhibitory synapses were reported in [30]. Details on the circuit implementation and complete experimental characterization of the neural and synaptic circuits, as well as presentation of calibration and parameter fitting procedures to align neural and synaptic characteristics from models or recorded data onto the digitally programmable analog hardware are presented in [31]. In the following sections we focus on the extension of the HH model implemented in NeuroDyn to accommodate generalized dynamics over extended time scales.

III. Methodology

A. Membrane Dynamics

The Hodgkin–Huxley membrane dynamics [36] describe neural dynamics as a sum of conductance-based channel currents. Gating variables m, h, and n describe the voltage-dependent dynamical profiles of each channel and are described by

$$C_{\mathit{mem}}\frac{{dV}_i}{dt}=-I_{{Na}_i}-I_{K_i}-I_{L_i}-I_{{\mathit{syn}}_{ij}}$$ (1)

where i, j = 0 … 3, and

$$\begin{array}{l}{I}_{{Na}_i}=m_i^3{h}_i{g}_{{Na}_i}(V_i-E_{{Na}_i})\\ I_{K_i}=n_i^4{g}_{K_i}(V_i-E_{K_i})\\ I_{L_i}=g_{L_i}(V_i-E_{L_i}).\\ I_{{\mathit{syn}}_{ij}}=r_{ij}{g}_{{\mathit{syn}}_{ij}}(V_i-E_{{\mathit{syn}}_{ij}}).\end{array}$$

In order to emulate bursting neural dynamics, the Hodgkin–Huxley model requires the addition of a slow-modulation due to Ca inactivation dynamics. We accommodate this extra inactivation channel by first considering the two-dimensional “reduced” excitation model as described by Morris-Lecar [37]

$$C_{\mathit{mem}}\frac{{dV}_i}{dt}=-I_{{Ca}_i}-I_{K_i}-I_{L_i}-I_{{\mathit{syn}}_{ij}}$$ (2)

where i, j = 0 … 3, and

$$\begin{array}{l}{I}_{{Ca}_i}=m_{{\infty }_i}{g}_{{Ca}_i}(V_i-E_{{Ca}_i})\\ I_{K_i}=w_i{g}_{K_i}(V_i-E_{K_i})\\ I_{L_i}=g_{L_i}(V_i-E_{L_i})\\ I_{{\mathit{syn}}_{ij}}=r_{ij}{g}_{{\mathit{syn}}_{ij}}(V_i-E_{{\mathit{syn}}_{ij}}).\end{array}$$ (3)

We then reintroduce the variable h_i as a multiplicative term in the calcium conductance in (3), modeling the calcium recovery rather than calcium inactivation, on a slower timescale spanning several action potentials. We also revert to the cubic form of fast Ca (Na) activation in the Hodgkin–Huxley model, of the form (1). We show that we can adapt this model (1) to reproduce rich spiking and bursting dynamics, with only changes in the conductance and channel kinetics, illustrated in Fig. 1 and described below.

B. Channel Kinetics

The neuron channel gating variables are modeled by a rate-based first-order approximation to the kinetics governing the random opening and closing of membrane channels for any of the gating variables x (e.g., m, h, n, w)

$$\frac{{dx}_i}{dt}={\alpha }_{x_i}\left(1-x_i\right)-{\beta }_{x_i}{x}_i$$ (4)

where each channel variable denotes the fractions of corresponding channel gates in the open state, and where the α and β parameters are the corresponding voltage-dependent opening and closing rates. The channel variables can be equivalently expressed as

$${\tau }_{x_i}\frac{{dx}_i}{dt}=x_{{\infty }_i}-x_i$$ (5)

with asymptotes x_∞i = α_xi/(α_xi + β_xi) and time constants τ_xi = 1/(α_xi + β_xi).

We model each of the opening and closing channel kinetics in the NeuroDyn system using the seven-point sigmoidal regression functions implemented as cascaded differential pairs. As described in [31], we use a least squares fit regression technique to determine the appropriate current biases to fit the generalized channel kinetic functions.

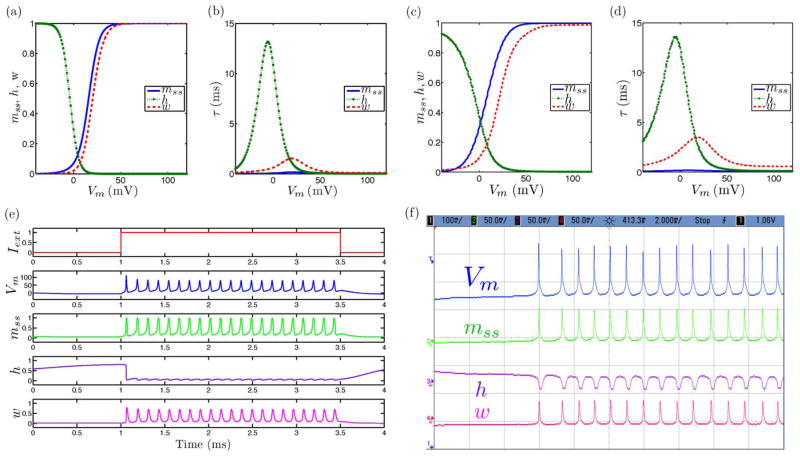
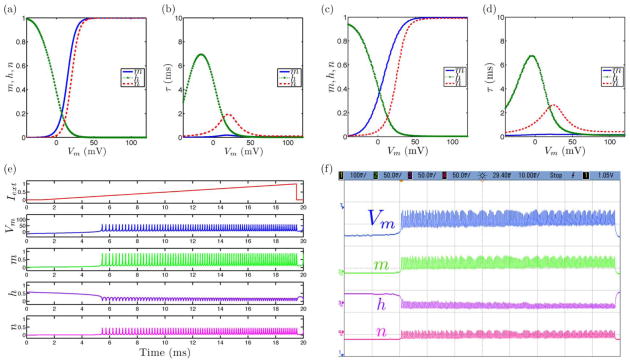
Simulation data was obtained by implementing the models described using MATLAB. The simulation and circuit measurement data illustrating the neural spiking behavior before and after the inclusion of the slow inactivation channel are shown in Fig. 2 and Fig. 3, respectively. Neural spiking behavior before the inclusion of the slow inactivation channel is realized by setting the h gating variable channel kinetics with voltage-independent opening and closing rates. The slow inactivation channel is realized by implementing the the h gating variable channel kinetics as a slow inactivation channel.

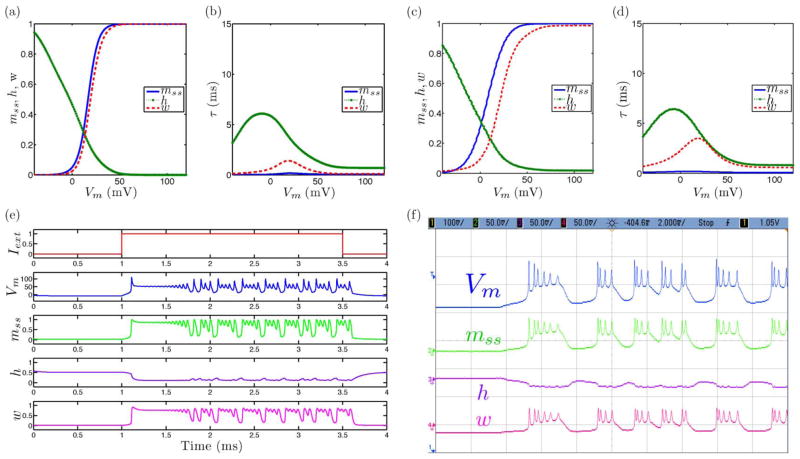
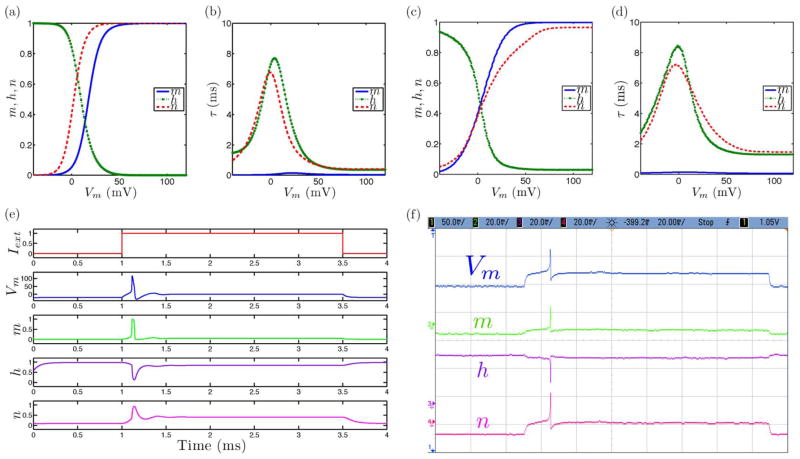
Fig. 2.

Tonic spiking neural dynamics in the ML model with the extension to include slow inactivation dynamics set as a constant parameter showing simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

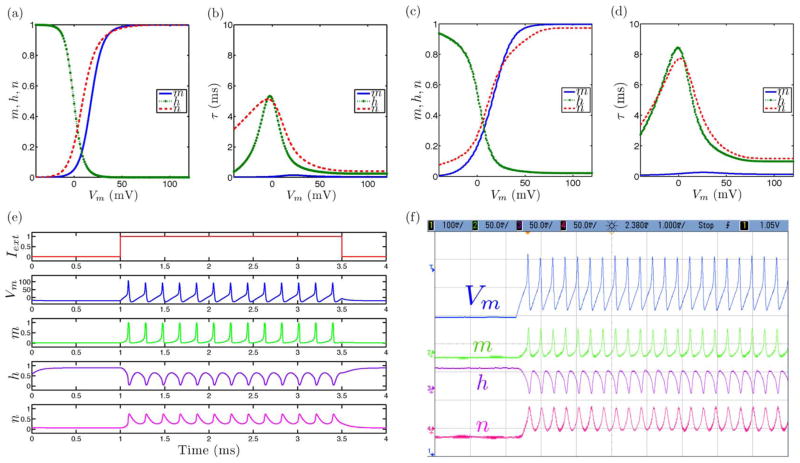
Fig. 3.

Tonic bursting neural dynamics in the ML model with an extension to include slow inactivation dynamics showing simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

IV. Spiking to Bursting Behaviors

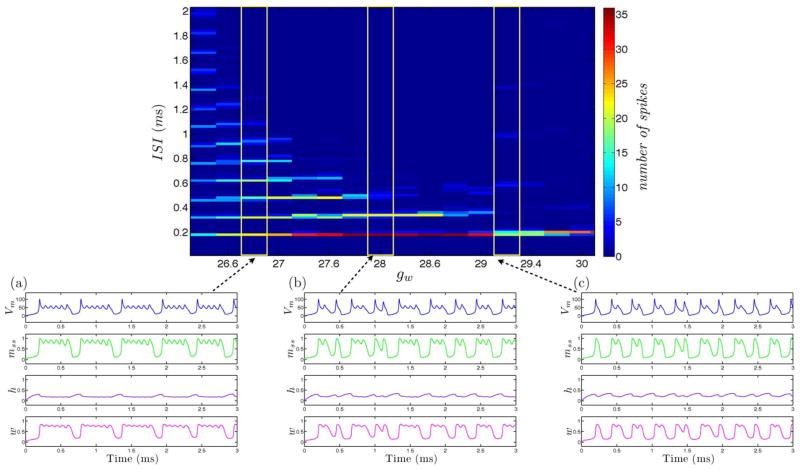
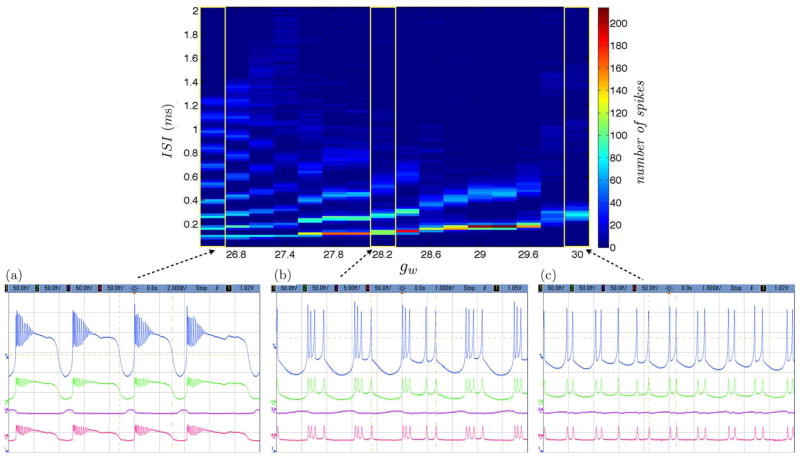
We calculate the ISI histogram for each burst of spikes over the variation of a single parameter g_w governing calcium recovery [17] for both simulation and circuit measurement data as displayed in Fig. 4 and Fig. 5. We observe consistent spiking behavior over a wide regime of neural dynamics. For g_w low conductance values, the neuron spikes and is followed by subthreshold oscillations. As the g_w conductance value is increased, the neuron spikes and the following subthreshold oscillations are more pronounced. And when the g_w conductance value is further increased, the neuron spikes in a bursting manner. When the g_w conductance value is further increased, the number of subsequent bursting spikes is reduced as we observed quadruplets then triplets then doublets and finally single neuron spikes. Mismatch between simulation and measurement results can be attributed to circuit noise which manifests as fluctuations in spike and burst rates as well as the number of spikes per burst.

Fig. 4.

Simulated tonic bursting neuron with variation of a single conductance parameter g_w governing calcium recovery with increasing values from (a) to (c).

Fig. 5.

Measured tonic bursting neuron with variation of a single conductance parameter g_w governing calcium recovery with increasing values from (a) to (c).

V. Additional Spiking Behaviors

A. Phasic Spiking

Phasic spiking dynamics refers to the property of certain neurons to respond with a single action potential corresponding to the onset of an applied excitatory current input pulse. We present simulation and circuit measurement results in Fig. 6. We demonstrate phasic spiking dynamics by increasing values of τ_n with respect to τ_h from the tonic spiking model channel kinetic rate parameters.

Fig. 6.

Phasic spiking neural dynamics with simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

B. Spike Frequency Adaptation

Spike frequency adaptation refers to the property of certain neurons to spike with greater frequency at the onset of an applied pulse of current and decrease in spike frequency through the duration of the pulse. We present simulation and circuit measurement results for spike frequency adaptation dynamics in Fig. 7. We decrease values of τ_h with respect to τ_n in order to more readily observe spike frequency adaptation dynamics.

Fig. 7.

Spike frequency adaptation neural dynamics with simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

C. Neural Excitability

1) Class 1 Neural Excitability

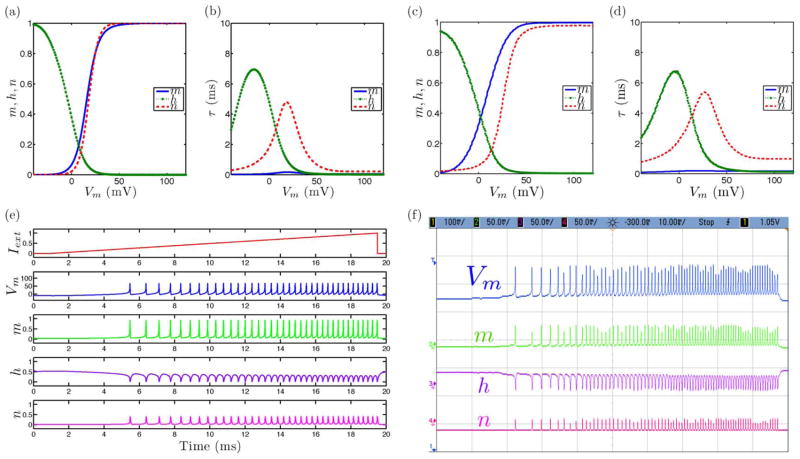
Class 1 neural excitability refers to the property of certain neurons to respond to an applied excitatory current ramp with a train of action potentials. The frequency of the action potentials starts from an arbitrarily low frequency and increases in frequency through the duration of the applied ramp input resulting a large band of frequency response. We present simulation and circuit measurement data for class 1 neural excitability in Fig. 8.

Fig. 8.

Class 1 excitable neural dynamics with simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

2) Class 2 Neural Excitability

In contrast, neurons that exhibit class 2 neural excitability display a narrow band of frequencies in response to an applied excitatory current ramp. Class 2 excitability is further distinguished from class 1 excitability by the high frequency of its initial response to the applied current ramp. We present simulation and circuit measurement data for class 2 neural excitability in Fig. 9. We vary the dynamical profile of gating variable n to decrease the values of τ_n governing K⁺ channel dynamics in order to achieve class 2 neural excitability dynamics. The decrease in τ_n results in a corresponding decrease in refractory period between action potentials.

Fig. 9.

Class 2 excitable neural dynamics with simulated and measured data for (a), (c) steady-state (in)activation dynamics, (b), (d) τ voltage-dependent dynamics, and (e), (f) membrane voltage and gating variable waveforms.

3) Transition from Class 1 to Class 2 Neural Excitability Dynamics

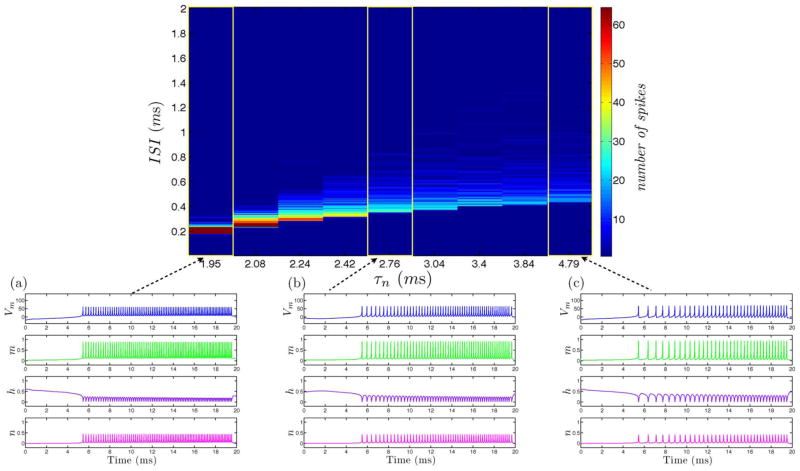
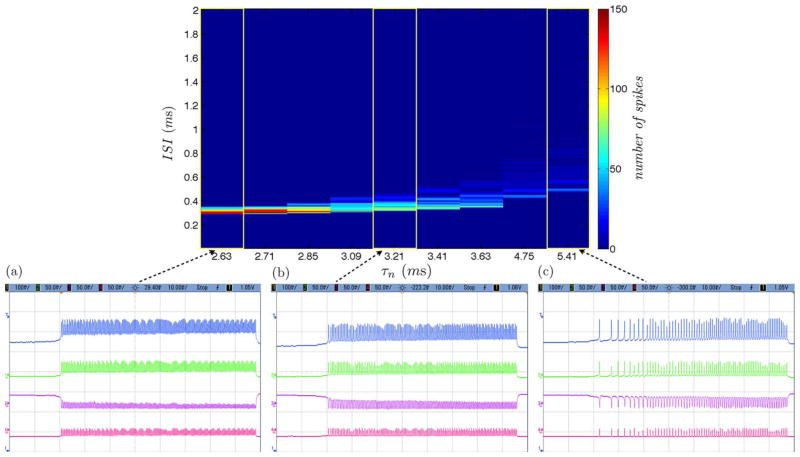
We calculate the ISI histogram for each ramp response over the variation of a set of parameters governing τ_n and corresponding to K⁺ channel dynamics for both simulation and circuit measurement data as displayed in Fig. 10 and Fig. 11. For low values of τ_n, the neuron responds with a narrow band of frequencies at relatively low ISI characteristic of class 2 excitable neural dynamics. As the value for τ_n is increased, the refractory period between action potentials increases and becomes more pronounced at the onset of the current ramp input. This results in a broader band of frequency response over the course of the applied current ramp input. As the value for τ_n is further increased, the band of frequency responses continues to increase as is characteristic of class 1 excitable neural dynamics.

Fig. 10.

ISI Histogram of increasing values τ_n for from (a) to (c) governing K⁺ channel dynamics of simulations between class 1 and class 2 excitable neural dynamics.

Fig. 11.

ISI Histogram of increasing values for τ_n from (a) to (c) governing K⁺ channel dynamics of measurements between class 1 and class 2 excitable neural dynamics.

When current is injected into the HH model, there is a threshold where the firing rate jumps from zero to some finite value. The addition of an “A-current” K⁺ conductance to the model makes the input-output curve contiguous as first shown by Connor and Stevens [38]. In the augmented model, the deinactivation rate of the “A-current” limits the rise time of the membrane potential between action potentials.

VI. Conclusion

Previous studies [39] have shown intrinsically bursting neural dynamics implemented with extensions to the HH model requiring more gating variables. Other models are capable of emulating intrinsic bursting neural dynamics, such as Izhikevich’s simple model [20] which uses just two dynamical variables and Mihalas-Niebur’s neural model [21] which uses three dynamical variables to also govern threshold adaptation. Here we have presented red an extended HH-ML model that reproduces a variety of neural dynamics in three dynamical variables that directly account for the biophysics of membranes and channels over an extended range of time scales in the NeuroDyn neural emulation platform. The neural dynamics has been implemented with individual control over biophysical parameters governing the dynamical profiles of the opening and closing channel rates, reversal potential, and conductance. Intrinsic noise due to analog circuit implementation results in quantitative and qualitative changes in the neuronal dynamics including changes in the onset and regularity of spiking and bursting patterns, although we observed general qualitative correspondence between simulations and circuit experiments. Similarly, noise from thermal, stochastic, and other sources observed in in vivo recordings play an important role in the dynamics of neuronal activity [40], [41]. Thus, the noise inherently present in the analog circuits adds to the biological realism of the implementation avoiding quantization and periodicity artifacts commonly encountered in noise-free digital implementations.

Biographies

Theodore Yu (S’04) received the B.S. and M.S. degrees in electrical engineering from the California Institute of Technology, Pasadena in 2004 and 2005, respectively.

Currently, he is working towards the Ph.D. degree at the University of California, San Diego, in the electrical and computer engineering program. His research interests include neuromorphic analog VLSI models of neural and synaptic circuits, neuron-silicon interfaces, and circuit implementations of learning algorithms.

Terrence J. Sejnowski (SM’91–F’06) is the Francis Crick Professor at The Salk Institute for Biological Studies, where he directs the Computational Neurobiology Laboratory, an Investigator with the Howard Hughes Medical Institute, and a Professor of Biology and Computer Science and Engineering at the University of California, San Diego, where he is Co-Director of the Institute for Neural Computation. The long-range goal of his laboratory is to understand the computational resources of brains and to build linking principles from brain to behavior using computational models. This goal is being pursued with a combination of theoretical and experimental approaches at several levels of investigation ranging from the biophysical level to the systems level. His laboratory has developed new methods for analyzing the sources for electrical and magnetic signals recorded from the scalp and hemodynamic signals from functional brain imaging by blind separation using independent components analysis (ICA). He has authored over 300 scientific papers and 12 books, including The Computational Brain (MIT Press, 1994), with Patricia Churchland.

Dr. Sejnowski received the Wright Prize for Interdisciplinary research in 1996, the Hebb Prize from the International Neural Network Society in 1999, and the IEEE Neural Network Pioneer Award in 2002. He was elected an AAAS Fellow in 2006, to the Institute of Medicine in 2008, the National Academy of Sciences in 2010, and the National Academy of Engineering in 2011.

Gert Cauwenberghs (S’89–M’94–SM’04–F’11) received the M. Eng. degree in applied physics from the University of Brussels, Brussels, Belgium, in 1988, and the M.S. and Ph.D. degrees in electrical engineering from the California Institute of Technology, Pasadena, in 1989 and 1994, respectively.

Currently, he is a Professor of Bioengineering at the University of California, San Diego, where he codirects the Institute for Neural Computation, participates as a member of the Institute of Engineering in Medicine, and serves on the Computational Neuroscience Executive Committee of the Department of Neurosciences graduate program. Previously, he was Professor of Electrical and Computer Engineering at Johns Hopkins University, Baltimore, MD, and Visiting Professor of Brain and Cognitive Science at the Massachusetts Institute of Technology, Cambridge. His research focuses on micropower biomedical instrumentation, neuron-silicon and brain-machine interfaces, neuromorphic engineering, and adaptive intelligent systems.

Dr. Cauwenberghs received the National Science Foundation Career Award in 1997, the ONR Young Investigator Award in 1999, and the Presidential Early Career Award for Scientists and Engineers in 2000. He was Francqui Fellow of the Belgian American Educational Foundation. He was a Distinguished Lecturer of the IEEE Circuits and Systems Society in 20022003. He continues to serve IEEE in a variety of roles, most recently cochairing the IEEE Biomedical Circuits and Systems Conference (BioCAS2011) and the technical program committee of the IEEE Engineering in Medicine and Biology Conference (EMBC2012), both held in San Diego. He is a Senior Editor for the IEEE Sensors Journal and the IEEE Journal on Emerging and Selected Topics in Circuits and Systems, and Editor-in-Chief of the IEEE Transactions on Biomedical Circuits and Systems.