Estimation of 3D shape from image orientations

Abstract

One of the main functions of vision is to estimate the 3D shape of objects in our environment. Many different visual cues, such as stereopsis, motion parallax, and shading, are thought to be involved. One important cue that remains poorly understood comes from surface texture markings. When a textured surface is slanted in 3D relative to the observer, the surface patterns appear compressed in the retinal image, providing potentially important information about 3D shape. What is not known, however, is how the brain actually measures this information from the retinal image. Here, we explain how the key information could be extracted by populations of cells tuned to different orientations and spatial frequencies, like those found in the primary visual cortex. To test this theory, we created stimuli that selectively stimulate such cell populations, by “smearing” (filtering) images of 2D random noise into specific oriented patterns. We find that the resulting patterns appear vividly 3D, and that increasing the strength of the orientation signals progressively increases the sense of 3D shape, even though the filtering we apply is physically inconsistent with what would occur with a real object. This finding suggests we have isolated key mechanisms used by the brain to estimate shape from texture. Crucially, we also find that adapting the visual system's orientation detectors to orthogonal patterns causes unoriented random noise to look like a specific 3D shape. Together these findings demonstrate a crucial role of orientation detectors in the perception of 3D shape.

When we look at a textured object, the projection of the surface markings into the retinal image compresses them in ways that can indicate the object's 3D shape. This compression has two distinct causes. The first cause is distance-dependent: when a surface patch is moved further away from the eye, the texture shrinks isotropically in the image as a function of the distance. The second cause of compression is foreshortening: when a surface is slanted relative to the line of sight, the texture is anisotropically compressed along the direction of the slant, with greater slant leading to greater compression.

It is well known that the visual system can use these texture compression cues to estimate 3D shape (1–9). What is not known, however, is how the visual system measures the compression at each point in the image. A crucial stage in any theory of 3D vision must include an explanation of how the visual system extracts the key information from the image. At present, there is an explanatory gap between the known response properties of cells early in the visual processing hierarchy, which measure local 2D image features (10–16), and cells higher in the processing stream, which respond to various 3D shape properties (17–24). How does the brain put the measurements made in the primary visual cortex (V1) to good use to arrive at an estimate of 3D shape?

Estimating the extent and direction of texture compression is not trivial (6, 7), so it would be useful if the brain could infer surface attitude from some other readily available image measurement. V1 contains cells tuned to specific orientations and spatial frequencies (10–16). We suggest that the visual system could use the output of populations of such cells as a “proxy” for texture compression when estimating shape.

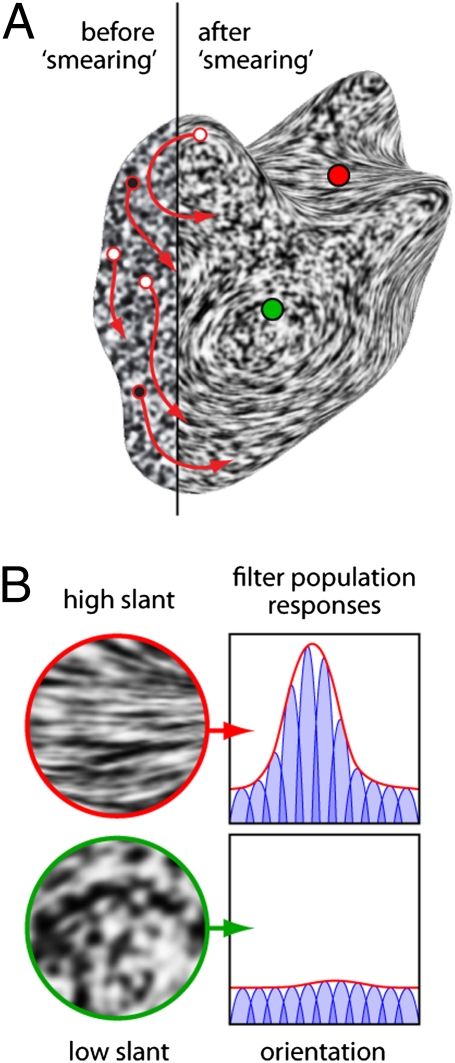
Specifically, the process could work as follows. As mentioned above, when surface texture is projected onto the retina it appears compressed in the image. This compression has powerful effects on local image properties, which we find can be readily measured by populations of filters tuned to different orientations and spatial frequencies. Isotropic compression of the texture (because of surface distance) locally scales the pattern, causing power to shift to higher spatial frequencies. Anisotropic compression (because of surface slant) causes one orientation to dominate the others at the corresponding location in the image. Cells tuned to the dominant orientation respond more strongly, but those tuned to other orientations tend to respond more weakly, leading to a peak in the population response (Fig. 1). This peak response indicates the tilt (25) of the surface (up to an ambiguity of sign); that is, the 3D orientation of the surface relative to the vertical in the image (modulo 180°). Additionally, the size of the peak is related to the surface slant (25) relative to the line of sight. The more slanted the surface, the more anisotropic the texture, and thus the more pronounced the peak in the population response. Thus, taken together, the orientation and height of the peak in the population response could serve as a simple surrogate measure of texture foreshortening, which the visual system could use to estimate surface attitude.

Fig. 1.

Shape from smear. (A) Random noise is filtered in 2D along the red arrows. The result appears vividly 3D, demonstrating a key role of orientation detectors in 3D shape perception. (B) Details from the regions surrounding the red and green dots, with hypothetical cell population responses. Cells (blue curves) are narrowly tuned for orientation; the population response (red curves) is the envelope of cell responses. The red dot lies on a region of high surface slant, creating strongly oriented texture. Cells aligned with the dominant orientation respond more strongly, creating a peaked population response. The green dot lies on a less slanted region with no clear dominant orientation. The population response is flat, indicating a fronto-parallel surface region.

Using wavelet filters as a cartoon model of cell populations we can measure the dominant orientations at each location in the image. When we plot how the dominant orientation varies continuously across the entire image of a surface, we find that the responses are highly organized, forming a smoothly varying “orientation field,” which is systematically related to the 3D shape (Fig. 2). Although additional processing would be required to regularize the orientation field and to derive a complete estimate of the 3D shape from these measurements, the correspondence between the outputs of the filters (which measure local 2D image structure) and the true 3D surface orientations is surprisingly good. We, and others, have argued previously that orientation fields could play an important role in the estimation of shape from shading and specular reflections (26–29). Here, we suggest that similar mechanisms could also play a role in the estimation of shape from texture. Indeed, the idea that continuous variations of orientation can elicit vivid impressions of shape has been known at least since the Op Art paintings of Bridget Riley, and more recently numerous psychophysical and computational studies of perception of contour textures (30–32). Here we suggest a specific mechanism that could relate orientation measurements in the human brain to the perception of shape from orientation patterns.

Fig. 2.

(A) Images generated using the shape-from-smear technique, representing two different 3D shapes. (B) Color coded representations of the orientation fields measured from the images in A using populations of filters tuned to different image orientations. Hue represents dominant local orientation (peak of the population response) at each point in the image. Color saturation indicates the local anisotropy (strength of the peak in the response), with high saturation indicating a strong peak and low saturation (paler colors) indicating a less pronounced peak. (C) Color-coded representation of the 3D surface normals of the two shapes used to generate the images in A. Hue indicates the surface tilt (modulo 180°) to make the color coding comparable to the image orientations depicted in B. Color saturation indicates surface “slant.”

Results

A key test of this hypothesis can be performed by creating 2D patterns with orientation structure that corresponds to a particular 3D shape. If the brain relies on orientation fields to estimate shape, such patterns should look 3D. We generated such patterns from random noise by locally “smearing” (i.e., filtering) the noise in different directions in 2D. Examples are shown in Figs. 1–5. We start with a 3D model of a given shape. From this model, we derive a 2D vector field containing the orientations orthogonal to the projected surface normals of the shape. We then use these vectors to direct line integral convolution (33) (a 2D filtering operation) to coerce the local orientation and spatial frequency statistics of the noise to the desired values. The direction of smear varies across the image so that we can vary the dominant orientation at each location, to simulate different surface tilts. Similarly, the amount of smear varies to control the local anisotropy, so that we can affect the size of the peak in the population response, thereby simulating slant. The result is a 2D pattern consisting of “pure” orientation and spatial frequency signals, in which the response of filter populations is similar to those produced by a given 3D shape. Crucially, however, the process of smearing noise along these directions is not equivalent to physically projecting surface markings into the image. Specifically, when texture patterns are projected into the image, they are compressed in the direction of the slant. In contrast, the smearing process stretches features out in the orthogonal direction, in a way that could never occur by projecting isotropic surface markings into the image. Thus, the patterns stimulate orientation populations without simulating the physics of texture compression. The result is a compelling illusion of 3D shape, suggesting that the brain uses orientation signals as a proxy for image compression when estimating shape from texture. We call this effect “shape from smear.”

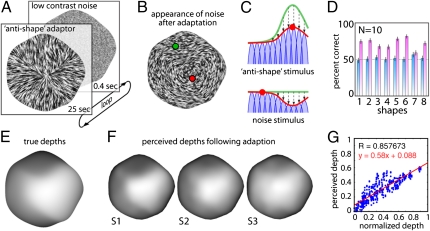
Fig. 5.

Adaptation experiments. (A) Subjects viewed antishape patterns, followed by a brief image of unoriented noise. (B) Simulated appearance of noise after adaptation. (C) Adaptation to the antishape stimulus changes the population response from the green curve (before adaptation) to the red curve (after adaptation). Following adaption, the noise response is peaked at the orientation orthogonal to the antishape adaptor, causing it to appear 3D. (D) Mean percent correct (10 subjects) in the dot depth-discrimination task for each of the eight shapes. Blue bars, without adaptation; pink bars, with adaptation. Performance was higher (P < 0.001) during adaptation for all shapes except shape 7 (P < 0.60). In a second task, subjects adjusted gauge figures to report perceived shape of the noise stimulus in the adapted state. (E) Depth map for the true 3D shape and (F) depth maps reconstructed from responses of three subjects (white is near, dark is far). Subjects never saw images resembling the shape, only noise and adaptation stimuli, which caused the noise to appear 3D. (G) Scatterplot showing perceived depth as a function of predicted depth. Data are pooled across all three subjects and both tested shapes. Only probe locations within the shape are shown.

To test the perception of 3D shape with such stimuli, we presented them to subjects with two dots superimposed at random locations. On each trial, subjects indicated which of the two dots on the surface appeared closer to the observer in depth. For comparison, we also asked subjects to perform the task with two other types of images: (i) full 3D computer renderings, which included shading, highlights, and real texture markings (rendering), and (ii) patterns that were also made by smearing noise, but in which the positions of the vectors in the field were scrambled, thus destroying the global organization (matched noise). Fig. 3 shows that performance with shape-from-smear stimuli was substantially above chance performance, although not as good as with a rendering, which is unsurprising given the additional cues.

Fig. 3.

Example stimuli and results from the dot depth-comparison task. (A) Physically based rendering of an object. (B) Shape-from-smear stimulus derived from the same physical shape. (C) Stimulus with the same distribution of orientations as in B, but with randomly scrambled locations within the image. Nine subjects judged which of two locations, indicated with a red and a green dot, appeared closer in depth. (D) Percent correct for each of the three stimulus types. Error-bars depict SE.

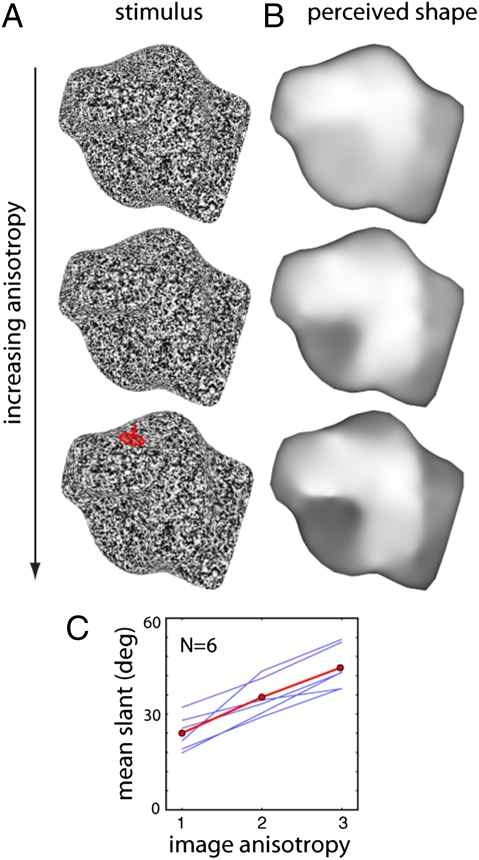
If orientation measurements play a vital role in the perception of 3D shape, then increasing the strength of these signals should progressively increase the strength of the 3D percept. To test this theory, we made stimuli in which we parametrically varied the amount of smear applied to the noise (more smear produces stronger orientation signals). We then asked subjects to adjust the 3D orientation of “gauge figure” probes distributed across the surface, to indicate the perceived local surface orientation (34). Subjects could click a button during the experiment to view a reconstruction of the reported 3D shape to compare with their percept of the shape-from-smear stimuli. The reconstructed shapes (Fig. 4) show that subjects clearly perceived coherent 3D shapes in response to the stimuli. More importantly, the overall depth of the reconstructed shapes progressively increased with the degree of smear, indicating that it is orientation signals that drive the estimation of 3D shape.

Fig. 4.

”Gauge figure” experiment on the effects of texture anisotropy on perceived 3D shape. (A) Stimuli with increasing anisotropy were created by increasing the amount of smearing (filtering) applied to the noise. Subjects adjusted gauge figures (red) to report perceived shape. (B) Perceived depths reconstructed from responses. Dark pixels are distant, bright pixels are near. (C) Mean surface slant of the gauge figures increases as a function of image anisotropy. Blue curves: six individual subjects. Red curve: mean across subjects.

Arguably, the ultimate test for a direct role of orientation detectors in shape estimation would be to modify the orientation detectors in some way, and then measure how this modification affects perceived shape. To do this psychophysically, we used adaptation (Fig. 5). We created stimuli in which the noise was smeared along the directions orthogonal to those corresponding to a given shape. These “antishape” orientation fields themselves yield only a weak and incoherent impression of 3D shape, as there is no globally consistent interpretation of the orientation signals as a surface. However, when subjects view these stimuli for prolonged periods, the brain's orientation detectors adapt to the local orientation signals, changing the way they respond to subsequently presented images. For a short period after viewing the antishape stimulus, the neurons continue to be affected by the adaptation. Thus, when subsequently presented with a brief burst of low contrast unoriented noise, the adaptation makes the noise appear locally oriented. More importantly, we find that the adaptation also causes the noise to appear like a specific 3D shape. This appearance occurs because slow recovery of the neural circuits following adaptation causes the population response to be peaked at the orientation orthogonal to the adaptation: that is, aligned with the true orientation field for the shape of interest (35–37). It is this rebound effect that causes the noise to appear 3D. An example stimulus is shown in Movie S1, described in SI Text.

To measure this effect, we presented subjects with sequences that repeatedly cycled between the adaptor (3 s) and the neutral noise (0.4 s), and asked them to report the shape they perceived during the briefly flashed noise. In one task, we asked subjects to indicate which of two dots appeared closer in depth. As a control, we also asked subjects to perform this task in a nonadapted state, where they perform at chance because the noise appears completely flat. In contrast, following adaptation subjects were substantially better than chance at determining the depths of the predicted 3D shape, indicating that orientation adaption produces a reliable, predictable, illusory surface percept.

In a second task we asked subjects to adjust gauge figures to report the perceived surface attitude at various locations across the illusory surface, so that we could reconstruct the shapes that they perceived in the adapted state. Example results are shown in Fig. 5F. Considering that the retinal stimulation consisted of nothing but antiorientation fields (which on their own do not look 3D) followed by random noise (which also does not look 3D), the correspondence between the perceived shapes and the predicted shapes is quite remarkable.

Discussion

Together, these findings suggest that cells tuned to different orientations and spatial frequencies play a crucial role in the early stages of visual shape estimation by providing an approximate surrogate measure of texture compression. Such measurements are simple, rely on known visual cortical mechanisms, and do not require the visual system to make explicit estimates of the way texture is mapped onto the surface. It therefore seems quite likely that the visual system could use such measurements to estimate shape from texture.

As noted above, many cues are involved in estimating 3D shape. For some cues—most notably binocular stereopsis—the image measurements used by the visual system to estimate depth (i.e., binocular disparities and half-occlusions) are well-established (38–44). However, for other cues—such as texture compression, shading, and perspective—the fundamental image quantities are still unclear. To place our understanding of monocular cues on the same foundations as stereopsis, we must establish the image measurements that form the input to the computations. Our findings suggest that much as disparity estimates can be derived from filter responses, so texture compression can also be derived from populations of cells tuned to different orientations and spatial frequencies.

For a long time, the various monocular cues to 3D shape were thought to be treated differently by the visual system. Intuitively, this theory makes sense because the relationship between 2D image properties and 3D surface properties is different for different cues. However, we and others have previously suggested that measurements similar to the ones proposed here likely play a role in the estimation of shape from shading and specular (mirror-like) reflections (26–29). This theory suggests that at least for the early stages of processing, texture, shading, specular reflections, and possibly some other cues could share more in common than previously thought. The potential importance of this idea is that it means that despite substantial differences in the computations required to estimate different monocular shape cues, the basic image substrate from which the shape estimates are derived (i.e., orientation fields) could be the same.

Nevertheless, it is important to emphasize that we are proposing a theory only of the “front-end” of shape processing, not a complete model of 3D shape reconstruction. Subsequent processing would be required to smooth and remove noise from the orientation fields, resolve the sign ambiguity of the tilt of the surface, and extract higher-level shape quantities from the surface estimate (convexities and concavities, principal axis structure, and so forth). Additionally, to make surface estimates from different cues comparable with one another, and to use the estimates to guide actions, the visual system must transform them into different coordinate frames and translate between depths, surface normals, and surface curvature estimates.

Many important details of the physiology of V1 are missing from the model presented in Figs. 1 and 2. The filter-tuning properties are not modeled on physiological measurements, and we do not model static nonlinearities (12, 13) (other than full-wave rectification), contrast normalization (45–47), nonclassic receptive field properties (48, 49), or any lateral interactions (50) or feedback between neighboring regions. Adding such details improves the quality of the orientation-field measurements by increasing sensitivity to low contrast features, and regularizing the field (51). However, here the experiments focus specifically on the role of orientation measurements per se: that is, whether orientation measurements are the basic substrate in the first place. Further experiments will be required to establish the role of these additional properties of V1 in estimating shape from texture and other monocular cues.

Another significant challenge is to understand how the brain measures and exploits the systematic spatial organization of orientation fields to infer higher-order shape properties. It is interesting to ask what additional shape properties could be inferred from derivatives of orientation (i.e., 2D curvatures), which are known to play a key role in texture segmentation (52). We find that shape-from-smear does not work well when simulating a slanted plane, or when the boundary of the surface is not visible. This finding suggests that 2D curvatures probably also play an important role in 3D shape estimation, and that the object boundary provides key constraints for interpreting the orientation field, possibly by specifying the sign of tilt, which is ambiguous when local orientation measurements are taken in isolation. Boundaries are critically important for other 3D cues (53, 54) and are clearly important here too, although in Fig. S1 we show example patterns with identical boundaries that nonetheless lead to clearly different 3D shape percepts. Additional structure in the texture can also provide additional information about shape. When textures contain regular patterns—especially parallel lines—perspective causes convergence patterns that indicate slant (8, 55). This effect is particularly important for planar surfaces. When reconstructing 3D shape, the visual system somehow spatially pools local orientation information across the image although exactly how remains to be explained.

Methods

Subjects.

Subjects with normal or corrected-to-normal vision were paid 8 Euros/h for participating in the experiments. At the beginning of each session, they were informed that they could terminate the experiment at any time without giving any reason and still receive full compensation.

Stimuli.

Stimuli were 750 × 750 pixel images created from Gaussian white noise using a modified version of line integral convolution (LIC) (33). Before applying LIC, the noise was blurred with a Gaussian filter, the SD of which varied across the image in proportion to the cosine of the slant of the surface. Image contrast was normalized locally after applying LIC, to ensure approximately constant contrast across the image. The resulting oriented pattern was cropped with the silhouette of the 3D shape. For the experiment on the effects of anisotropy (Fig. 4), four gradations of anisotropy were used, ranging from no LIC to a maximum LIC length parameter of 5 pixels. In all experiments, naive subjects viewed the stimuli on a laptop in a darkened room, at a distance of 50–70 cm, responding via keyboard and mouse. Stimuli subtended about 12° visual angle. Before each task, subjects were trained using physics-based renderings of practice objects (different from those used in the main experiments) with texture, shading, and specular cues. These images were rendered using Radiance (56).

Dot Discrimination Tasks.

On each trial, subjects reported whether the red or green dot appeared to lie on a nearer surface point. The tested locations were selected to minimize the correlation between image position and depth, to ensure subjects relied on perceived shape (rather than distance from the contour) to perform the task. Nine subjects took part in the experiment reported in Fig. 3. These subjects were tested on 45 dot pair locations on eight shapes. For the adaptation experiment (Fig. 5), 10 subjects were tested with 20 dot pairs on eight shapes.

Gauge Figure Tasks.

Subjects adjusted the 3D orientation of 75–110 gauge figure (34) probes arranged in a triangulated lattice across the image, to report the perceived surface orientation at each location. For the experiment reported in Fig. 4, having adjusted all probes at least once, subjects clicked a button to view an interactive reconstruction of the reported shape, inferred from the probe settings using the Frankot–Chellapa algorithm (57). Subjects could rotate the reconstruction in 3D to inspect it from multiple directions. Subjects were encouraged to modify their settings and repeat the reconstruction until the reported shape matched their perception of the stimulus as closely as possible. Subjects could add figures to the lattice to report rapid changes in shape accurately. Of the nine subjects that took part in the dot task shown in Fig. 3, six subjects took part in the gauge figure experiment on the effects of anisotropy, reported in Fig. 4. Before the main task subjects received extensive training with physics-based renderings. Subjects were explicitly taught the effects of outlier settings (i.e., when one or a few gauge figures are set incorrectly), which can cause large errors in the reconstructed shapes. Each subject was tested on three levels of anisotropy for a given shape; four different shapes were tested across participants. Of the subjects that took part in this experiment, three participated in the adaptation experiment (Fig. 5). In the adaptation task, no reconstruction was viewed and no additional probe figures could be added. However, after setting all gauge locations in isolation, subjects were presented with all probes simultaneously and could readjust probes to make them consistent with one another. In practice, subjects only made minor adjustments at this stage.

Adaptation Tasks.

In the depth-discrimination task, adaptation lasted for 25 s, followed by a repeating sequence of 0.4 s postadaptor (noise), alternating with 3.0-s top-up adaptation, until response was complete. To prevent retinal after-image effects during the adaptation phase, different noise seeds for the stimulus generation procedure were used to create 10 adaptor images, all sharing the same orientation structure but with randomly different brightness at any given pixel. These adaptors were displayed in a loop, 50 ms per image, so that average brightness over time across the stimulus was roughly uniform. Once subjects had seen the postadaptor, they could respond at any time. Eight different shapes were used, and 20 point-comparisons were made for each shape. Following collection of depth-comparison data for the noise stimuli in the adapted state, data were collected for the inducer stimuli (i.e., the antiorientation field stimuli) in a nonadapted state. Procedures for the gauge-figure experiment were similar, although both initial and top-up adaptation were 4.0 s long. So that subjects could maintain one fixation as long as possible (aiding in maintaining the postadaptation shape percept), figures were grouped into clusters and the center of each cluster was used as a fixation point. Only two shapes were used because of the time-consuming nature of the task, and these were alternated after each cluster of figures to reduce fatigue. Subjects were trained to accustom them to respond to brief bursts of faint oriented patterns. In the first round of practice, the adaptor stimuli consisted of noise and the postadaptors consisted of low-contrast oriented shape-from-smear stimuli derived from training shapes. A second set of training images was similar those to those used in the real experiment, with high-contrast antiorientation field adaptors, and noise for the postadaptors.

Model Filter Populations.

The orientation fields depicted in Fig. 2 were derived using Simoncelli and colleagues’ Steerable Pyramid toolbox (58) for Matlab. The filters consisted of sp1Filters steered through 24 orientations. For each pixel in the image, the dominant orientation was defined as the filter with the maximum response. Anisotropy was defined as the difference between the maximum and minimum responses across filters. The local responses were pooled (blurred) using the “blurDn” function from the toolbox, with the default filter, and “levels” parameter set to 3 (i.e., reducing the resolution by one-eighth). The mapping from anisotropy to color saturation was nonlinear with the following form: S = A^2.5 + 0.15, where S is the saturation and A is the normalized anisotropy from the filter responses.