An enumerative stepwise ansatz enables atomic-accuracy RNA loop modeling

Abstract

Atomic-accuracy structure prediction of macromolecules should be achievable by optimizing a physically realistic energy function but is presently precluded by incomplete sampling of a biopolymer’s many degrees of freedom. We present herein a working hypothesis, called the “stepwise ansatz,” for recursively constructing well-packed atomic-detail models in small steps, enumerating several million conformations for each monomer, and covering all build-up paths. By making use of high-performance computing and the Rosetta framework, we provide first tests of this hypothesis on a benchmark of 15 RNA loop-modeling problems drawn from riboswitches, ribozymes, and the ribosome, including 10 cases that are not solvable by current knowledge-based modeling approaches. For each loop problem, this deterministic stepwise assembly method either reaches atomic accuracy or exposes flaws in Rosetta’s all-atom energy function, indicating the resolution of the conformational sampling bottleneck. As a further rigorous test, we have carried out a blind all-atom prediction for a noncanonical RNA motif, the C7.2 tetraloop/receptor, and validated this model through nucleotide-resolution chemical mapping experiments. Stepwise assembly is an enumerative, ab initio build-up method that systematically outperforms existing Monte Carlo and knowledge-based methods for 3D structure prediction.

Predicting the 3D structures attained by functional macromolecules is a fundamental challenge in computational biophysics and, more generally, in understanding and engineering living systems. There have been numerous recent successes in the high-resolution modeling of small proteins (1–3), protein/RNA complexes (4), and protein/DNA interfaces (5) by optimizing physically realistic energy functions. Nevertheless, rigorous blind trials demonstrate that the predictive power of computational algorithms remains limited, especially if atomic resolution is sought. For essentially all high-resolution modeling problems tackled to date, the shared critical bottleneck of these methods is inefficient sampling of a biopolymer’s vast conformational space (1–7). In addition to hindering accurate modeling, poor sampling precludes rigorous tests of the assumed high-resolution energy functions.

To gain insight into the conformational sampling bottleneck, we have been focusing on some of the smallest well-defined biomolecular folding problems: RNA motifs, as short as four nucleotides (nts) in length (8). In addition to offering “toy puzzles” for computational methods (9), these modular loops, junctions, and tertiary interactions are fundamental building blocks of structured noncoding RNAs; they attain well-defined noncanonical conformations that in turn define the positions of the canonical double helices in three dimensions. A previous study presented a fragment assembly of RNA with full-atom refinement (FARFAR) method (10), tested on a benchmark of 32 RNA motifs. Although FARFAR recovered near-atomic-accuracy models in half the cases, the method was unable to consistently sample models within 1.5 Å rmsd of the crystallographic conformation.

Herein we seek to dissect and resolve this conformational sampling bottleneck by focusing on an apparently simpler problem: the structure prediction of single-stranded irregular RNA loops excised from crystallographic models. Modeling these loops is a lock-and-key problem, where the native loop (the key) is the conformation that best fits the surrounding structure (the lock). As with the analogous protein cases, the RNA loop-modeling problem has important practical significance as a critical component of homology-based structure prediction (11, 12) and in the refinement of models generated by coarse-grained algorithms (13–16). As is illustrated below, even the smallest RNA loops are challenging for computational methods, because they are rich in noncanonical interactions, extrahelical bulges, and unusual torsion combinations.

Our major finding is that a recursive stepwise ansatz enables the systematic sampling of RNA loop conformations at atomic resolution and in polynomial computational time. The ansatz is similar in spirit to ab initio “build-up” strategies previously explored in protein modeling (6, 17, 18, 19) but not yet shown to outcompete Monte Carlo or knowledge-based methods (20). Our focus on small RNA loops allows us to revisit and rigorously test these enumerative strategies. After illustrating the limitations of knowledge-based approaches in loop modeling, we describe the motivations for the stepwise ansatz, its potential advantages and disadvantages, and its implementation as the stepwise assembly (SWA) method in the Rosetta framework. We then demonstrate substantial improvements in sampling power and modeling accuracy of the SWA method over prior approaches. As a further rigorous and practical test, we present a blind prediction of an RNA motif of previously unknown structure, the in vitro evolved C7.2 tetraloop/receptor (21, 22), and its experimental validation by subsequent chemical accessibility measurements. We end the paper with discussions of historical precedents for this ansatz as well as extensions of this strategy to multistranded RNA motifs and protein problems.

Results

A Benchmark for the High-Resolution RNA Loop-Modeling Problem.

The RNA loop-modeling problem offers small but highly challenging cases for atomic-resolution structure prediction. We compiled a benchmark of 15 single-stranded loops that begin and end at different Watson–Crick double helices, drawn from riboswitches, ribozymes, and other structured noncoding RNAs with crystallographic data (resolution better than 2.85 Å; SI Appendix, Table S1). Loop lengths ranged from 4 to 10 nucleotides (longer loops are rare; see SI Appendix, Fig. S1). “Hairpin” loops beginning and ending at the same helix as well as multiple-stranded loops can also be treated but are considered separately (see below).

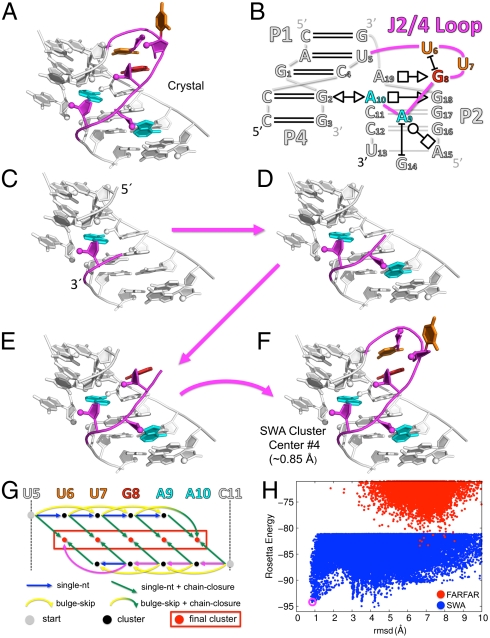
On one hand, these loops assemble into well-defined conformations, forming a significant number of hydrogen bonds—2.6 per nucleotide on average, in the same range as values for an A-form RNA helix (2 to 3). For several cases, independent crystallographic models of the same loop are available and give indistinguishable conformations (SI Appendix, Table S2). On the other hand, the loops are highly noncanonical. More than half of the hydrogen bonds are in base-phosphate or base-sugar interactions rather than in base pairs (23). Further, the loop torsions are irregular. Twenty-seven percent of the nucleotide suites are not part of the 46 most commonly observed RNA rotamers (24); and 8 of the 15 loops contain extrahelical bulges. Several loops display sharp turns, exemplified by the J2/4 loop motif that forms a 140° bend in the three-way junction of a thiamine pyrophosphate (TPP) sensing riboswitch (Figs. 1 A and B). Modeling these intricate loop structures de novo is therefore a well-posed but challenging problem.

Fig. 1.

The stepwise assembly (SWA) structure modeling method. Illustration on the J2/4 loop from the three-way junction of a TPP sensing riboswitch (PDB: 3DV2). (A) Crystallographic conformation of the 5-nt loop (shown in color) with surrounding nucleotides from the crystallographic model shown in white. (B) Schematic of the three-way junction in the annotation of Leontis and Westhof (23); only nucleotides shown in the 3D structure are numbered. (C–F) A build-up path that leads to the experimental conformation; the five nucleotides in the loop are built in a stepwise manner, one at time, starting from the 3′ end. (G) A directed acyclic graph delineates the building steps in the SWA method, recursively covering all possible build-up paths. The building steps taken in C–F are colored in magenta; other building steps are colored according to type. Gray vertices correspond to the starting point with none of the loop nucleotides built. Black vertices correspond to the partially built subregions; models in each subregion were clustered with the 1,000 lowest energy cluster centers carried forward. Red vertices corresponding the ending points with the loop completely built; all models of the full-length loop were clustered together in a final clustering step. (H) Rosetta all-atom energy vs. all-heavy-atom rmsd to the crystallographic conformation for de novo models generated by SWA (blue points) and by the prior method (FARFAR, red points). SWA fourth lowest energy cluster center (purple circle) is within atomic accuracy of the crystallographic model (0.85 Å rmsd).

Limitations of Knowledge-Based Methods.

The difficulty of RNA loop modeling is underscored by the poor accuracy of previous methods for RNA structure prediction. For example, a recently developed homology modeling method, RLooM (11), failed to recover near-native models (under 1.5 Å all-heavy-atom rmsd to the crystallographic loop) in 13 of the 15 benchmark cases, unless directly related loop structures from the same species were permitted (SI Appendix, Supporting Results, and Table S2). As a further test, we updated the high-resolution FARFAR method to carry out loop modeling with chain closure and sampling of extrahelical bulges. FARFAR failed to recover near-native models as one of the five lowest energy cluster centers in more than half of the benchmark cases (11 of 15; ref. 25, Table 1, and SI Appendix, Table S3). Some of the problem cases are quite small; for example, the J2/4 loop of the TPP riboswitch was not solvable by FARFAR but is only five nucleotides in length (Figs. 1 A and B). As in prior work, conformational sampling was the dominant bottleneck. First, for 6 of 11 problem cases, none of the 250,000 models generated gave rmsd accuracy better than 1.5 Å (Table 1). Second, in all cases, this inability to generate near-native structures was traced to the absence of native torsions in the fragment library; the sampling could be rescued by doping native torsions into the fragment library as a “cheat” to aid conformational search (see SI Appendix, Table S4). Third, in 10 of 11 cases, the generated models did not achieve near-native energies; the lowest energy of 250,000 models remained higher than the energy of the optimized experimental loops (Table 1). The inability of FARFAR to solve these small loop-modeling problems suggests that one or more basic assumptions of the fragment assembly approach limit its conformational sampling power.

Table 1.

Accuracy and conformational sampling efficiency of de novo RNA loop modeling

Motif name	Motif properties		Best rmsd* (Å) of five lowest energy clusters†		Lowest rmsd* (Å) achieved		Energy gap to optimized exp. model‡ (RU)
	Length	PDB	FARFAR	SWA	FARFAR	SWA	FARFAR	SWA
5′ J1/2, leadzyme	4	1NUJ	1.96	0.83	1.66	0.51	2.7	−0.8
5′ P1, M-box riboswitch	4	2QBZ	0.72	0.96	0.53	0.61	2.3	−0.5
3′ J5/5a, group I intron	4	2R8S	0.40	0.47	0.30	0.40	0.0	0.0
5′ J5/5a, group I intron	5	2R8S	4.08	1.04	1.05	0.66	0.3	−0.9
Hepatitis C virus IRES IIa	5	2PN4	2.11	5.31	1.04	0.71	−2.6	−5.9
J2/4, TPP riboswitch	5	3D2V	6.66	0.85	1.74	0.73	10.8	−1.0
23S rRNA (44–49)	6	1S72	0.69	0.73	0.47	0.71	2.6	0.0
23S rRNA (531–536)	6	1S72	3.18	2.45	2.44	0.76	6.9	−0.6
J3/1, glycine riboswitch	7	3OWI	1.13	1.35	0.71	0.64	2.5	1.3
J2/3, group II intron	7	3G78	1.59	0.82	1.34	0.77	8.5	−0.2
L1, SAM-II riboswitch	7	2QWY	2.43	1.26	1.43	0.86	3.8	−1.3
L2, viral RNA pseudoknot	7	1L2X	5.44	3.36	1.35	0.91	3.7	−4.1
23S rRNA (2534–2540)	7	1S72	6.39	5.71	3.24	1.39	7.3	−7.3
23S rRNA (1976–1985)	10	1S72	11.19	7.75	5.06	4.58	9.6	−10.8
23S rRNA (2003–2012)	10	1S72	11.36	0.74	5.43	0.64	41.2	3.2
RMSD < 1.50 Å	—	—	4/15	10/15	9/15	14/15	—	—
Energy Gap < 0.0	—	—	—	—	—	—	2/15	13/15

IRES, internal ribosome entry site; SAM, S-adenosylmethionine.

^*All-heavy-atom rmsd to the crystallographic loop. Nucleotides found to be extrahelical bulges (both unpaired and unstacked) in the crystallographic model were excluded from the rmsd calculation. Bold text indicates rmsd within 1.5 Å of the crystallographic model.

^†Generated models were clustered, such that models with pairwise all-heavy-atom rmsd less than 1.5 Å over the entire loop and less than 2.5 Å over each individual loop nucleotide are grouped (see SI Appendix, Supporting Methods). The lowest energy member of each cluster was designated as the cluster center and the five lowest energy cluster centers were considered as the predicted models.

^‡Definition of the optimized experimental model is provided in SI Appendix, Supporting Methods. Bold text indicates that the lowest energy sampled by the de novo run is lower than the energy of the optimized experimental model (i.e., the energy gap is negative). One Rosetta unit (RU) is approximately equal to 1 k_BT (10, 25).

A Stepwise Ansatz.

We reasoned that the conformations of RNA loops might be effectively sampled through direct enumeration at high resolution, rather than by restricting the search space to previously known fragments. We discovered that a recursive step-by-step enumeration (Figs. 1 C–F) permits efficient de novo sampling of these loops, which we illustrate on one of the FARFAR failures above, the J2/4 loop of the TPP riboswitch.

First, we note that exhaustive enumeration of this 5-nt loop at atomic resolution is not feasible with current computational power. Even building one nucleotide of a loop involves sampling several degrees of freedom, including six backbone torsions, four (coupled) sugar-pucker torsions, the glycosidic torsion, and the 2′-OH torsion. While low-resolution (> 3 Å) clustering of exhaustively sampled single-nucleotide conformations results in under 100 “rotamers” (24), clustering with a subangstrom threshold—as is necessary for high-resolution modeling—leads to millions of unique conformations of the nucleotide (SI Appendix, Fig. S2). While computing the Rosetta energy for this number of conformations is achievable in less than 1 hour on a single modern central processing unit (CPU), the available conformations multiply exponentially with the RNA length. Thus, combinatorial enumeration of all available conformations of a 5-nt loop would require approximately 10²³ CPU years, well beyond the computational power achievable in the foreseeable future.

Nevertheless, the feasibility of enumerating the conformations of just one nucleotide suggests an alternative approach to realistic RNA modeling. Enumerative single-nucleotide building permits fine-grained exploration of torsional conformations that form well-packed structures with multiple hydrogen bonds, as is observed in native loops, including rare torsional combinations not covered in the list of consensus rotamers (24). As an illustration, Fig. 1C shows the lowest energy conformation for the first 3′ nucleotide of the J2/4 loop, built by exhaustive sampling followed by local energy minimization. The resulting nucleotide is positioned with atomic accuracy, giving an rmsd of 0.69 Å from the experimental conformation. We discovered that the entire loop could then be recovered through stepwise enumerative building of each additional nucleotide (Figs. 1 C–F), carrying forward an ensemble of the lowest energy well-packed, well-hydrogen-bonded conformations from each previous subregion. In addition to standard single-nucleotide building steps, recovering this loop also required a “bulge-skip” building step (to permit the modeling of extrahelical unpaired/unstacked nucleotides) and a chain-closure building step to complete the RNA loop (e.g., Figs. 1 E–F; see SI Appendix, Supporting Methods for complete descriptions of the three types of building steps).

In a de novo structure prediction scenario, we do not know a priori the appropriate order of building steps that will achieve the experimental conformation, and we cannot guarantee that the lowest energy model for a subregion will carry forward into the lowest energy model for the entire loop. Further, the number of such build-up paths grows exponentially with the number of nucleotides. We solved these path-enumeration issues using a recursive strategy, familiar from dynamic programming approaches utilized in sequence alignment (26) and RNA secondary structure prediction (27). We determined a low-energy ensemble of models for each subregion of the loop as modeled from the 5′ end or from the 3′ end and then joined all combinations of these subregions by chain closure. In particular, we modeled each subregion in one of two ways—either by a standard single-nucleotide building step from a subregion one nucleotide shorter, or by a bulge-skip building step from a subregion two nucleotides shorter. We clustered all models for a subregion and carried forward the 1,000 lowest energy cluster centers (which typically included all models within 6 k_BT of the lowest energy state, mimicking conformations accessed by thermal fluctuations). A directed acyclic graph (28) delineates this deterministic, recursive calculation, as shown in Fig. 1G. In the case of the J2/4 loop example, searching through all possible paths led to a diverse set of well-packed conformations, including low-energy near-native and nonnative models that were missed by FARFAR (Fig. 1H).

This method deterministically enumerates a low-energy subspace of the RNA loop’s available conformations through the stepwise, locally optimal building of individual nucleotides, with the hypothesis that the experimentally observed conformation resides within this subspace. We call this method stepwise assembly (SWA) and its underlying working hypothesis, the stepwise ansatz. This ansatz can only be confirmed through empirical tests on naturally occurring biomolecular structures. We have therefore carried out extensive trials of the stepwise ansatz using RNA loop modeling as a biophysically important but unsolved test problem, described next.

Comprehensive Test of the Stepwise Ansatz.

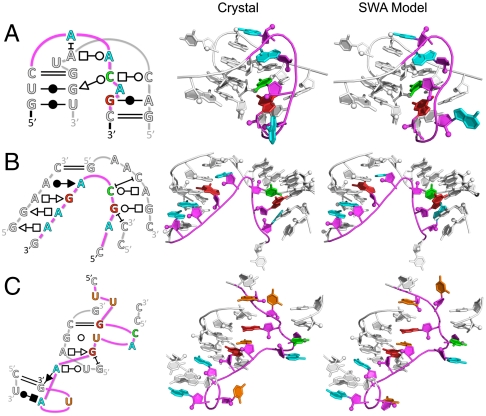
To evaluate the validity of the stepwise ansatz, we applied the SWA method on the entire 15-loop benchmark (SI Appendix, Table S1). In terms of modeling accuracy, SWA substantially outperformed FARFAR, recovering near-native models (< 1.5 Å rmsd) for 10 of 15 test cases, compared to four cases recovered by FARFAR (see Table 1). These included atomic-accuracy models from diverse sources, including a 5-nt loop from the J5/5a hinge in the P4–P6 domain of the group I Tetrahymena ribozyme (rmsd of 1.04 Å; Fig. 2A); a 7-nt loop connecting helices P2 and P3 of the group II intron (rmsd of 0.82 Å; Fig. 2B); and one of the two 10-nt loops in the benchmark, nucleotides 2003–2012 of the large ribosomal subunit from Haloarcula marismortui (rmsd of 0.74 Å; Fig. 2C). In each of these three cases, the high accuracy of the SWA model is reflected not only in low rmsd to the experimental loops but also complete recovery of the base pair and base stack geometries as classified in the Leontis–Westhof scheme (23) (see SI Appendix, Table S5).

Fig. 2.

Comparison of crystallographic and SWA de novo models for three diverse loop motifs. (A) Five-nucleotide loop from the J5/5a hinge in the P4–P6 domain of the group I Tetrahymena ribozyme (PDB: 2R8S). (B) Seven-nucleotide loop connecting helices P2 and P3 of the group II intron (PDB: 3G78). (C) Ten-nucleotide loop from the large ribosomal subunit from H. marismortui (PDB: 1S72, nucleotides 2003–2012). The modeled loop is shown in color whereas surrounding nucleotides are shown in white. Some surrounding nucleotides are not shown to permit unobstructed view of the modeled loop region. The rmsds to the crystallographic conformations (energy cluster rank) of the displayed SWA models are (A) 1.04 Å (fourth), (B) 0.82 Å (first), and (C) 0.74 Å (second). Two-dimensional schematics apply to both the crystallographic and SWA models.

For the remaining five “problem cases,” conformational sampling was no longer the major bottleneck. In all five cases, SWA models achieved lower energies than the optimized experimental models (see Table 1 and SI Appendix, Fig. S3). Further, in four of the five cases, SWA sampled de novo models within 1.5 Å of the experimental conformation, although these models were not selected as one of the five lowest energy cluster centers. In the last case (a second 10-nt ribosomal loop), the optimized experimental model gave significantly worse energy (by 10.8 k_BT) than the SWA models, explaining the absence of near-native models in the low-energy SWA ensemble. These results demonstrated that the stepwise ansatz is valid in all tested cases, and the absence of atomic-accuracy models among the five lowest energy cluster centers for the five problem cases was due to inaccuracies in the Rosetta all-atom energy function. The results were in strong contrast to the FARFAR results above.

Blind Prediction and Experimental Validation.

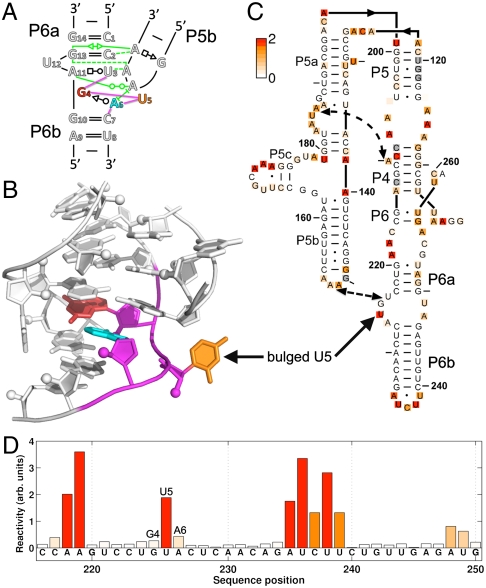
The most stringent tests for structure prediction algorithms are blind trials. The few prior attempts at blind high-resolution RNA structure modeling have not achieved atomic accuracy [see, e.g., refs. (29–31)]. Encouraged by the strong performance of SWA on the benchmark, we predicted the structure of a tetraloop/receptor motif (the C7.2 mutant; Fig. 3A) with no known experimental structure, previously isolated by in vitro selection (21, 22).

Fig. 3.

Blind prediction of the C7.2 tetraloop-docked receptor and validation through single-nucleotide-resolution chemical mapping. (A) Two-dimensional schematic of the C7.2 tetraloop/receptor motif; the 3-nt G4-U5-A6 loop at the core of the receptor (shown in color) is different from receptors with previously solved structures. Tertiary interactions between the GAAA tetraloop and the receptor are colored green. (B) Three-dimensional model of the C7.2 receptor by SWA. Models from other methods are given in SI Appendix, Fig. S5. (C) Chemical reactivities of A and C (based on dimethyl sulfate alkylation) and G and U (based on CMCT carbodiimide modification) shown as white-to-red coloring on a mutant of the P4–P6 domain of the Tetrahymena ribozyme containing the C7.2 receptor; measurements were acquired in 10 mM MgCl₂, 50 mM Hepes, pH 8.0, at 24 °C. (D) Bar graph of reactivities for nucleotides near the C7.2 receptor. Sequence positions are given in conventional P4–P6 numbering with one additional nucleotide inserted between positions 225 and 227 to account for the longer length of C7.2 compared to wild type. See SI Appendix, Figs. S6 and S7 for full datasets, including both wild type and C7.2 mutant data and error analysis.

This sequence served as an appropriate first blind test because it effectively reduces to a small but challenging loop-modeling problem. Much of the sequence aligns with a widely studied tetraloop/receptor motif whose structure has been determined by crystallography in several different RNAs, including the P4–P6 domain of the Tetrahymena ribozyme (32, 33). The main difference is a 3-nt loop (G4-U5-A6) replacing a 2-nt A4-A5 “platform” (SI Appendix, Fig. S4). We modeled this loop by SWA, FARFAR, RLooM, and ModeRNA (12). SWA gave the well-packed C7.2 tetraloop-docked receptor model shown in Fig. 3B as the lowest energy structure. More extensive SWA calculations modeling eight nucleotides (nucleotides 3–7 and 10–12 in Fig. 3A) gave similar structures. In contrast, FARFAR gave models with significantly worse energy (by > 3 k_BT) whereas RLooM and ModeRNA gave models with numerous steric clashes (see SI Appendix, Supporting Results, and Fig. S5).

The SWA model for the C7.2 tetraloop-docked receptor displayed noncanonical features absent in the classic 11-nt receptor (32, 33). The central U5 nucleotide bulged out of the structure. Furthermore, the first and third nucleotides of the loop formed a same-stranded trans Sugar-edge/Watson–Crick G4-A6 base pair (Fig. 3B) that is not isosteric to the cis Sugar-edge/Hoogsteen base pair presented in the A-A platform (34). The Find RNA 3D (FR3D) motif search software (35) found only two other instances of this conformation in the entire database of RNA structures, within a malachite green aptamer and in a UUGUAU RNA sequence bound to the human cleavage factor protein Im (see SI Appendix, Supporting Results). Nevertheless, the neighboring 5′ and 3′ nucleotides in these two precedent structures are positioned differently than in the C7.2 receptor (FR3D geometric discrepancies of 0.72 and 0.89 Å; both higher than the 0.50 Å default cutoff value), explaining the inability of RLooM and ModeRNA to discover these solutions.

The SWA model for the C7.2 tetraloop-docked receptor (Fig. 3B) made predictions that were testable by single-nucleotide-resolution chemical modification experiments. We therefore grafted the C7.2 receptor into the J6a/6b and J6b/6a segments of the P4–P6 RNA (Fig. 3C) and carried out quantitative chemical mappings with dimethyl sulfate (DMS) and 1-cyclohexyl-3-(2-morpholinoethyl)carbodiimide metho-p-toluene sulfonate (CMCT) (36,37). As with the wild-type P4–P6 RNA, the C7.2-grafted mutant showed clear protections of the L5b tetraloop, J6a/6b tetraloop receptor, and the P5a A-rich bulge upon addition of Mg²⁺, verifying the attainment of the RNA’s global tertiary fold (electrophorograms shown in SI Appendix, Fig. S6). Further, as expected, the chemical reactivities of the wild-type RNA and the C7.2 mutant outside the tetraloop/receptor motif were indistinguishable within experimental error (SI Appendix, Fig. S7). Within the C7.2 receptor, nucleotides G4 and A6 were both protected from chemical modification, as predicted in the SWA model (nucleotides 225 and 227 in conventional P4–P6 numbering; Figs. 3 C and D). Most importantly, U5 (nucleotide 226 in conventional numbering) was highly modified by CMCT, with a reactivity value 22 ± 5 times greater than the mean reactivity of Watson–Crick base-paired uridines in the entire P4–P6 RNA. This result provides strong confirmation that U5 is an extrahelical bulge, as predicted. The chemical accessibility data thus validate the de novo SWA model at nucleotide resolution and disfavor first-ranked models from knowledge-based methods (SI Appendix, Fig. S5). Subsequent to obtaining these experimental results, we discovered further evidence in support of the SWA model from sequence variations in the original in vitro selection experiment that isolated the C7.2 receptor (21) (summarized in SI Appendix, Supporting Results).

Discussion

A Stepwise Ansatz Resolves a Conformational Sampling Bottleneck in Structure Prediction.

An inability to guarantee exhaustive conformational sampling has precluded the consistent prediction of biomolecular structure at high resolution (1–6). In Rosetta as well as other frameworks (10–16), potential issues that limit de novo sampling efficiency include these algorithms’ dependence on the database of existing experimental structures; the stochasticity of Monte Carlo fragment assembly; and the loss of information due to the use of coarse-grained phases to smooth and reduce the dimensionality of the search space (7, 9, 38). To address these issues, we developed a working hypothesis, called the stepwise ansatz, and its implementation, the SWA method, that enumeratively searches a physically realistic subspace of a molecule’s all-atom conformations in polynomial computational time [O(N) where N is the number of nucleotides; see SI Appendix, Supporting Methods].

The concept of ab initio step-by-step build-up has been discussed previously, e.g., in enumerative coarse-grained or stochastic all-atom search methods from Dill and coworkers (18, 19), pioneering peptide-modeling work from the 1980s by the Scheraga lab (17), and earlier computational explorations by Levinthal in 1968 (6). However, these prior build-up strategies have not been adopted into the mainstream of structure modeling or shown to outcompete Monte Carlo or knowledge-based methods (19, 20). The prior lack of development appears to stem from the difficulty of searching all possible build-up paths and from the expense of deterministic, enumerative calculations relative to stochastic, knowledge-based methods. For example, modeling a single 5-nt RNA loop herein required 12,000 CPU hours; fortunately, this calculation is now feasible due to the massive parallelization of high-performance computer clusters.

On a challenging benchmark of irregular RNA loop motifs, we have shown that SWA resolves the conformational sampling bottleneck that has hindered knowledge-based methods. In all cases, SWA sampled the experimental loop conformation de novo and/or recovered conformations with energies that surpassed the energy of the optimized experimental loop conformation. Further, in the majority of the cases (10 of 15), the Rosetta all-atom energy function was accurate enough to permit a near-native conformation to be selected as one of the five lowest energy cluster centers. The strongest test of the SWA method is the blind prediction on the C7.2 tetraloop/receptor motif of previously unknown structure. The predicted model includes noncanonical features (including a same-stranded G-A base pair and an extrahelical bulge) and agrees with subsequently measured chemical accessibility data. Further atomic-resolution tests might be achieved if crystals can be obtained for the C7.2 mutant of the P4–P6 RNA.

Stringent Tests of the Rosetta All-atom Energy Function.

Prior studies have reported anecdotal cases of failures of the Rosetta all-atom energy function for macromolecule modeling (9, 39), but the work herein is a unique example of a complete high-resolution de novo modeling benchmark in which every failure case can be traced to inaccuracies in the underlying energy function. While prior work has shown that the Rosetta all-atom energy function provides better energetic discrimination than traditional molecular mechanics force fields (10), this work indicates that approximations in the Rosetta all-atom energy function still remain too inaccurate to permit atomic-resolution RNA modeling on a consistent basis. The energy function does not explicitly model metal ions (e.g., see SI Appendix, Fig. S3), and water is modeled through a crude solvation term (40). Long-range electrostatic effects, higher-order dispersion effects (41), and hydrogen bond cooperativity are presently neglected. Because of its generality and sampling power, the SWA method should permit stringent tests of more recently developed all-atom energy functions, including those that model polarizable moieties (42). For the same reasons, the SWA approach should be powerful for high-resolution structure determination methods that use limited experimental information as pseudoenergy terms to break degeneracies in physics-based energy functions [see, e.g., refs. (43–45)].

A General Enumerative Strategy for Molecular Modeling.

In this work, we have focused mainly on the application of SWA toward single-stranded RNA loop-segments, both to demonstrate the method’s conformational sampling power and to solve a basic practical problem that arises in RNA structure prediction. Nevertheless, the strategy should be generally applicable to a diverse class of molecular modeling problems. For example, noncanonical RNA motifs often involve multiple RNA strands interacting with one another or loops returning to the same helix. Extensions of the SWA method to model these motifs appear accurate and computationally tractable (see SI Appendix, Fig. S8). With further expected improvements in computational power, de novo atomic-accuracy modeling of RNA motifs with lengths up to 15 nucleotides, a size range that includes many RNA aptamers and catalytic sites, should be feasible. Further, the basic concepts underlying SWA are not specific to RNA structure prediction and should be applicable to other frontier problems in high-resolution macromolecular modeling, including efficient prediction of protein loops and small proteins, rigorous tests of protein and protein/RNA energy functions, and enumerative sequence design of functional protein and RNA loops.

Methods

Both the SWA and FARFAR methods were implemented in C++ in the Rosetta codebase. The software is being made available in the next Rosetta release (3.4). Application of RLooM (database version 12-19-08) and ModeRNA (version 1.6.0) follow the instructions given in the released software. DMS and CMCT modification data of the wild-type P4–P6 RNA and the C7.2 P4–P6 mutant were acquired at single-nucleotide resolution, as described previously (46). Complete description of the SWA method; details on updates to the FARFAR method; explicit command-line examples for RNA loop modeling with SWA, FARFAR, RLooM, and ModeRNA; and details of the experimental method are provided in SI Appendix, Supporting Methods.