Electrostatic origin of the mechanochemical rotary mechanism and the catalytic dwell of F1-ATPase

Abstract

Understanding the nature of energy transduction in life processes requires a quantitative description of the energetics of the conversion of ATP to ADP by ATPases. Previous attempts to do so have provided an interesting insight but could not account for the rotary mechanism by a nonphenomenological structure/energy description. In particular it has been very challenging to account for the observations of the 80° and 40° rotational substates, without any prior information about such states in the simulation procedure. Here we use a coarse-grained model of F1-ATPase and generate, without the adjustment of phenomenological parameters, a structure-based free energy landscape that reproduces the energetics of the mechanochemical process. It is found that the landscape along the relevant rotary path is determined by the electrostatic free energy and not by steric effects. Furthermore, the generated surface and the corresponding Langevin dynamics simulations identify a hidden conformational barrier that provides a new fundamental interpretation of the catalytic dwell and illuminate the nature of the energy conversion process.

Understanding the energetics of the biological conversion of ATP to ADP is crucial for elucidating the nature of energy transduction in life processes and also for practical understanding of the action of molecular motors (1, 2). At present it seems that the detailed nature of this biological energy conversion process has remained a major puzzle (1–7). For example, despite the fact that the structures of several ATPases have been elucidated (e.g., refs. 4 and 8) and recent advances in detailed elucidation of some key steps have been made (9–11), it is not completely clear at what stage in the reaction energy is actually released and, in turn, what is the nature of the energy conversion process. Some workers have suggested that the major source of the energy release is the conversion of the free energy of ATP binding into elastic strain, which is subsequently released by a coordinated and tightly coupled conformational mechanism (6). It was also postulated that the energy conversion involves an inertial energy release (12), whereas our works (13, 14) have suggested that the energetics is associated with the electrostatic work, and the origin of the free energy change involves a significant contribution from the charge separation in solution outside the ATPase active sites. Furthermore, biochemical and structural studies have provided a molecular model for the action of ATPases (1–4), and remarkable phenomenological analyses (6, 7) indicated what are the conditions for effective action. However, we still do not have a clear structure function correlation that involves both the chemistry and the conformational coupling. The challenge became even more exciting in view of the remarkable progress in single-molecule studies that directly visualized the γ-subunit rotation in a unidirectional way, while revealing several plausible intermediates that have not been observed in any of the crystal structures (9–11).

Attempts to obtain relevant structure function correlations include quantum mechanical/molecular mechanical studies of the reaction profile of the chemical steps in different subunits (see refs. 13, 15, and 16, and the SI Text) where, with the exception of an empirical valence bond (EVB) study (13), we do not have actual free energy calculations. Studies of the energetics of the reactant and product in different states of the F1-ATPase subunits included microscopic free energy calculations, using molecular mechanical approaches (17), that did not actually simulate the chemical process. At present, the semimacroscopic linear response approximation calculations of the chemical step in different subunit states (13) seems to yield the most reliable results when we also consider a careful analysis of the reference solution reaction (14). Although it is possible to obtain a reasonable insight on the energetics of the chemical steps within each subunits (13, 17), the main challenge is to obtain an insight on the overall energy change in the complete ATPase system, including the barriers for conformational changes, and the overall energetics of the rotary process.

It is important to clarify that the task of quantifying the nature of the conformational changes has not been accomplished yet, despite interesting attempts. Recent molecular dynamics simulation aimed at understanding the effect of the γ-subunit rotation (18, 19) was instructive but could not capture the relevant energy of the actual millisecond process of the complete F1-ATPase motor. Attempts to understand the rotary mechanism, using coarse-grained models (18, 20), forced the rotation rather than reproduce it from structurally based energetics (see Background). Other computational studies are also discussed in the SI Text. Overall it seems to us that studies that do not produce free energy surface of the whole process considering the complete F1-ATPase system, cannot be used to relate the protein structure to the directionality of the ATP hydrolysis/synthesis.

At present it is unlikely that fully microscopic models will capture the overall free energy balance with the current computer resources. The problem is the difficulty of obtaining converging and meaningful free energies for the substantial conformational changes of large and highly charged systems. Alternatively, one can use coarse-grained (CG) models, realizing however, that using CG models without appropriate electrostatic terms (e.g., refs. 18 and 20) is also unlikely to yield the correct free energy trend. Thus we used in this work our CG model that focuses on consistent description of the electrostatic energy of the system (21). We assumed that because this CG model has been very effective in reproducing protein folding energies and other properties (22, 23), it should provide an effective strategy for capturing the energetics underlying the function of molecular motors.

Our CG modeling of F1-ATPase appeared to finally reproduce a very reasonable vectorial free energy surface for the rotary mechanism, without applying unrealistic forces or using phenomenological parameters. The resulting surface accounted for the directionality of the system and allowed us to model its time dependence with first principle considerations. We also generated an electrostatically based barrier that accounted for the observation of the catalytic dwell and the corresponding energy conversion mechanism.

1. Background

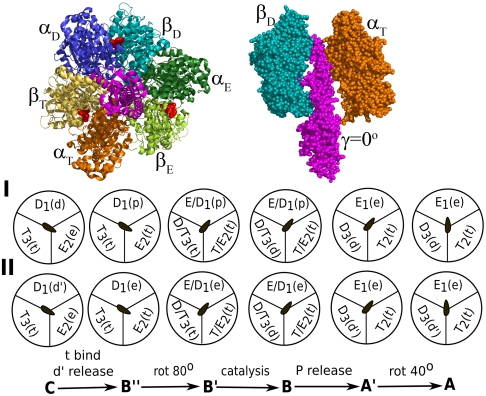
The F1-ATPase is composed of a stator ring and an elongated α-helical rotor, which is part of the complete F0F1 complex. The rotor is known as the γ-subunit and it connects the ring with the membrane bound F0 portion of the enzyme (Fig. 1). The stator ring is composed of three functional dimers, each consisting of a pair of α/β-subunits, where the β-subunits bind the nucleotide involved in the hydrolysis/synthesis process. The dimers can adopt three distinct conformations designated here as open (E), loose (D) or tight (T) forms. During the synthesis cycle, rotation of the rotor utilizes the electrochemical gradient established through the transport of H⁺ ions across the membrane, while the three dimers of the stator ring show conformational alterations between the E, D, or T states, resulting in the production of three ATP molecules in one complete γ rotation. The reversed hydrolysis cycle leads to a spontaneous rotation of the γ in the opposite direction. The conversion of ATP to ADP and inorganic P_i along with the associated conformational changes in the α/β-dimers through one complete 120° rotation of the γ-subunit is described schematically in Fig. 1. Henceforth, ADP + P_i, ATP, ADP, and P_i are designated as d, t, d^′, and p in the subsequent text and figures.

Fig. 1.

Schematic representations of the ATP hydrolysis cycle during the 120° rotation of the γ-subunit. Schemes I and II describe two of the most likely mechanisms. Atomic picture of the system is shown on top. The stage between C to B^′′ may involve three nucleotides supporting trisite mechanism (not shown explicitly) (11).

Fig. 1 describes two alternative mechanistic views, based on the available structural data and kinetic results and to a significant extent on innovative single-molecule experiments that have visualized the rotation of the γ-subunit and have been able to identify key details about the overall cycle (9–11). Of particular relevance is the visualization of the γ-subunit rotation in a unidirectional way as the α/β-dimers perform its ATP synthesis/hydrolysis cycle. The γ rotation was observed to be a stepwise process with three steps of 120°, where each step involved one hydrolysis/synthesis event. The steps are intercepted by a time dwell (known as “catalytic dwell”) that was found to consist of two events at the millisecond range, one of which is the actual chemical step and the other event is most likely the phosphate release step. The figure describes the hydrolysis direction (left to right) that corresponds to the single-molecule studies—i.e., binding of t, release of d^′, 80° rotation, chemistry (t going to d), release of p, and 40° rotation. It must be clarified that some of the steps along the cycle are far from being certain. One of the uncertain facts is the assumption that p leaves E in step B → A^′ in Fig. 1, scheme I [rather than leaving a site with (ADP + Mg) in Fig. 1, scheme II]. Furthermore, the issue of bisite (one or two β-subunits are nucleotide bound at any stage of the cycle) versus trisite (two or three β-subunits are nucleotide bound at any stage of the cycle) is not completely resolved, although recent experiments (11) highlight that the enzyme between states C and B^′′ does involve three nucleotides implying a trisite mechanism (see SI Text).

Our analysis of the energetics of some key steps in the mechanochemical process is summarized in Fig. S1 and Table S1. This analysis involves the computational results of ref. 13 and the experimental studies listed in the table. Overall the energetics in Fig. S1 and Table S1 is still tentative. Computer simulations that may be very useful are still problematic in this respect (see SI Text). A part of the problem is the finding that the release of electrostatic repulsion in the ADP·P_i → ADP + P_i in water (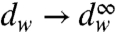) might provide a significant contribution to the solution energy (see refs. 13 and 14 and a more qualitative discussion in ref. 12). Similarly, the separation of the ADP and P_i in the protein and the sequential expulsion of one of these components may be a major energy contribution. In this case, using the bound complex in water as a reference (as was done in, e.g., ref. 17) is problematic. In fact, the results obtained using semimacroscopic calculations (13) might be more reliable at present.

One of the key unresolved questions about the action of F1-ATPase is the nature of the coupling between the subunits. Attempts to delineate the sequence of conformation/binding/chemical events included studies that combined the available experimental information and kinetics as well as simulation studies (18––24). However, none of these could generate a clear structural/energy base for the functional directionality. More specifically, the simulated directionality must result from the free energy landscape and not imposed by targeted molecular dynamics (TMD) (as done in ref. 18) or by using switching functions to move between different structures (as in ref. 20). For example, the assertion in ref. 18 that its CG model reproduced the 85°/35° rotational states simply reflects the fact that this difference in γ rotation already exists in the X-ray of the reference structures. Even the recent use of a simplified model and Langevin dynamics (LD) simulations (20) basically imposed the directionality by jumping between the different states, without having any physically based potential with a downhill directionality (for, e.g., the type generated in our early work; ref. 25). In fact, the use of arbitrarily large external forces in most previous studies has helped to propagate the idea of steric control. Unfortunately, this idea has been postulated without considering electrostatic effects and has not produced a reasonable free energy surface. Additional problems with current studies are discussed in the SI Text. Overall, we are not aware of any structure-based landscape that produced correctly the free energy or functional directionality of F1-ATPase.

2. Results and Discussion

2.1. CG Electrostatic Modeling of the Conformational Landscape.

In this work we have used our CG model (21) to simulate the F1-ATPase consisting of three α/β-dimers and the γ-subunit. As in many CG models, dating back to our original work (22), the protein side chains are represented using single interaction centers, whereas the backbone is represented by all-atom details. The key element of the current model is the representation of the electrostatic effects in a specialized way, considering the self-energy of ionized groups, their charge–charge interactions, and the energetics of different protonation states. All this is done with optimized dielectric constants that were evaluated by reproducing absolute folding energies (23). Our treatment started with the X-ray structure of bovine mitochondrial F1-ATPase (Protein Data Bank ID: 1H8E) (8), and then followed by rotating the γ-subunit in steps of 24° from 0° to 360° (total of 16 frames, starting from the X-ray), while simultaneously changing the coordinates of the α/β-dimers from one conformation to the next, using a linear interpolation scheme between the two known subunit structures. All possible combinations of 16 γ and 16 (α/β)₃ conformations were used to generate the 2D surface, out of which, states D₁E₂T₃/γ = 0°, E₁T₂D₃/γ = 120°, and T₁D₂E₃/γ = 240° correspond to the X-ray conformation. The side-chain/side-chain bad contacts were relaxed through a short relaxation of each frame. As in all of our studies of protein stability, we considered all the CG energy terms in the relaxation run, but then we guarantee the stability of the calculations by considering only the electrostatic energy of the side chains in the evaluation of the final energy.

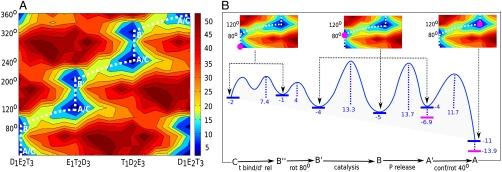
The evaluation of the overall electrostatic free energy surface by using the CG model, without incorporating the effect of the ligands and/or chemistry, are described in Fig. 2A. As seen from the figure, the motion of the system is restricted to a least energy path that produces the functional direction of the F1-ATPase machine. The figure shows that the system undergoes approximately 80° γ rotation from the starting structure (point C) followed by concerted (α/β)₃ dimer conformational changes and γ rotation in the range of 40° (point A). Such an intermediate conformational barrier clearly separating 80°/40° γ rotation has not been reproduced by other studies in an unbiased way.

Fig. 2.

Energetics in kilocalorie per mole of the system; (A) Calculated electrostatic free energy surface in the space defined by the rotation of the γ (vertical coordinate) and the subunit alterations (horizontal coordinate). The states marked along the least energy path (dashed line) correspond to states in Fig. 1. (B) Semiqualitative energetics (in standard state without concentration effect in blue; with the p concentration effect in magenta) along the least energy path based on the considerations in the SI Text.

Our results might seem contradictory to the assumption (10, 26) that most of the available X-ray structure corresponds to the catalytic dwell state. However, 1H8E is different from most of the 2 nucleotide bound structures. It is the only three nucleotide bound mitochondrial F1-ATPase with a different γ orientation than the rest (twisted by 20° ∼ 30°). Moreover, recent considerations (11) suggest that this structure might be somewhere between the 80° rotation instead of being after the rotation, as was thought before. Our results suggest that 1H8E might reflect a state at the beginning of the 80° rotation and hence mimic the ATP dwell state more closely, although further experimental and computational studies will be needed to examine the present prediction.

Next we combined our best estimates (from Fig. S1 and Table S1) of the binding/chemistry effects with the conformational landscape along the least free energy path. Specifically, we produced Fig. 2B after adding the total change in free energy (approximately 10 kcal/mol) and introducing the estimates of the nucleotide binding-release/chemistry/P release steps to the least energy path in accordance with the experimentally observed sequence of their occurrences (see schemes in Fig 1).

A number of interesting observations can be made based on our calculated results. First, the electrostatic surface provides a reasonable estimate of the conformational barrier (ca. 17 kcal) and also reproduces the 80°/40° substates along the γ rotational cycle. Second, the conformational barriers are high enough to suggest that it can dictate the position of the chemical step (see next section). Finally, we notice that the free energy surface for the rotation of the γ-subunit along the ATP hydrolysis direction does not compensate the approximate 10 kcal/mol free energy released in each 120° rotation step, and thus this energy can be used to do mechanical work.

2.2. The Coupling Between Conformational Changes and Chemistry.

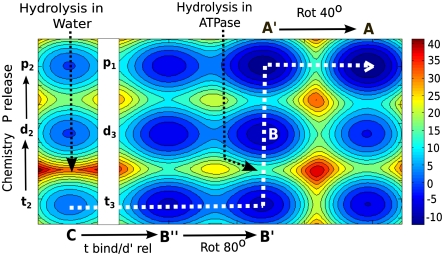
The overall conformational/chemical landscape is described qualitatively in Fig. 3. The figure incorporates key features of the chemical/conformational landscape plus some elements of the binding/release coordinate and yield a fundamental insight. The depicted landscape starts at state C with t in water, where we cannot move from t to the d state as the corresponding chemical barrier separating them is > 30 kcal/mol. When t enters the protein (at state B^′′) the barrier is drastically reduced between 19 kcal/mol (for unisite) and 14 kcal/mol (at the optimal conformational region), but the corresponding rate for the chemical process is slower than the rate for 80° γ rotation. Thus the system moves to state B^′ after 80° rotation. The key region for chemistry occurs at around region B^′, before the region where we found a high barrier that combines the conformational motion of (α/β)₃ along with a γ rotation of an additional approximate 40° (Fig. 2A). As this barrier is higher than the barrier for hydrolysis, the system moves from t₃ to d₃ and probably releases the phosphate and then (or in concert) continues the motion from A^′ to A at the upper part of the map (at this step the conformational barrier decreases partly due to the negative free energy of the transition at this point). The driving force for the directionality in the motion from t₃ to d₃ may involve some extra stability of d₃, although, even with equal energy for the hydrolysis step it is sufficient to have overall downhill gradient in the next few steps (e.g., the p release and conformational relaxation). Nevertheless, we do have the unique computational tools for constructing a more detailed and more accurate landscape (see, e.g., refs. 27, 28) and intend to explore this issue in the near future. However, even the partly empirical treatment of Fig. 3 advances us beyond what is known until now and can provide a consistent understanding of the observed events in the F1-ATPase system.

Fig. 3.

The conformational/catalytic landscape. The figure describes the energetics of the system along the chemical coordinate of one nucleotide (bound to subunit 2 or 3) and the conformational coordinate of the combined system. The functional path is shown in dashed white line (see text for details).

2.3. Modeling the Time Dependence of the System.

Simulating the energy conversion process and assessing the corresponding efficiency requires one to be able to explore the long time behavior of the system, as well as validate different stochastic models (29) used to describe such mechanochemical systems. This challenging task cannot be accomplished at present by microscopic approaches. The use of phenomenological parameters (6) can be very insightful, but it leaves us with major uncertainties. Thus, arguably, the best current option may be to use our renormalization approach (27), which has also been used for related problems (25, 30). This approach allows us to use the CG free energy surface from the previous section in simulating long timescale processes in the range of milliseconds to even longer time scales. Thus it should allow us to explore the origin of the observed time-dependent findings.

In order to model the functional dynamics of F1-ATPase, we generated a reduced effective potential surface that captured the conformational, chemical, and binding contributions to the overall landscape, using an approach similar to that used in our previous studies (25). This was done by mixing a multiminima EVB-type potential energy surfaces (see SI Text for details). The minima and the barriers were adjusted to the best estimates obtained from experimental and theoretical studies (Fig. S1 and Table S1). The behavior along the conformational subspace was adjusted to correspond to the trend in Fig. 2A. The resulting effective landscape in the regions that are most relevant to the least energy path are already described in Fig. 3. The results are given for scheme I in Fig. 1 [p release from E₁(p)], but basically the same trend would be obtained for scheme II [p release from D₃(d)].

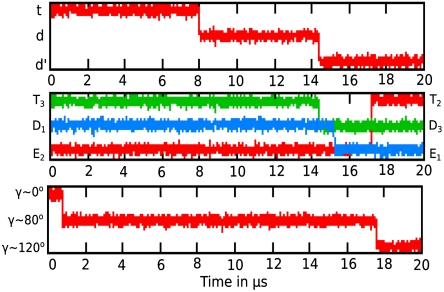
Using the surface in Fig. 3, we run LD simulations, starting from region B^′′ (after the t binding/d^′ release) (see Table S2 for parameters used to run LD). The results reported in Fig. 4 produce a total dwell time (after the 80° rotation and before the 40° rotation) of about 17 µs, where most of the time is spent on crossing two reduced barriers of approximately 10 kcal along with adequate gas-phase shifts mimicking the chemistry and the p release step. Now, as established in our previous studies (25, 30), once the barriers are higher than few kilocalories per mole, the rate constant is exponentially related to the barrier height and the overall trend can be extrapolated from calculations with a relatively smaller barrier instead of running extremely long simulation. The simulation of the type presented in Fig. 4 was performed for conformational barriers of 4, 6, 8, and 10 kcal/mol (scaling the surface by the same factor) and the corresponding time dependency is summarized in Fig. S2. Thus we can use Fig. S2 and extrapolate for the experimentally observed dwell time, which gives an effective chemical barrier of about 15–16 kcal/mol. This is probably an overestimate because the corresponding transition state theory estimate is about 14 kcal/mol. Of course, we can perform more refined calculation of the dwell time by optimizing different parameters (for, e.g., effective mass and friction coefficient) used in the LD for the specific system, but the main point is that the dwell time is in the right range and, more importantly, that we simulated a process where the chemistry occurs before passing the highest conformational barrier. More careful studies are clearly required to clarify this issue. This can be done by considering the effects of changes in concentration on the binding and release steps [by varying the effective gas-phase shift (α_l) in SI Text, Eq. S15]. It will also be interesting to explore the probability of “leakage” where energy released upon formation of d in state B and d^′ in state A^′ is lost without performing the next conformational change and 40° rotation. The leakage is blocked in part because it leads to the D₁(d)E₂(e)T₃(d) state (which is higher in energy) instead of the state A^′.

Fig. 4.

Langevin dynamics simulation of the coupling between the hydrolysis and the rotary step. The figure simulates the timing of the catalytic dwell with reduced barrier (see text) and can be used to convert them to real time following the extrapolation method discussed in the text and analyzed in the SI Text.

2.4. The Role of the Subunit Interaction.

Using the CG model, we also examined the nature of the interaction between the subunits of the F1-ATPase system. We focused on the identification of the domain interactions that determines the nature of the electrostatic free energy surfaces of Fig. 2A. This was done by evaluating the contribution arising from the interactions of the γ-subunit with the (α/β)₃ dimers. Our results imply that the β-subunits are more functionally relevant than the α , when we consider the changes in the electrostatic free energy of α-γ and β-γ interactions (see Fig. S3 and SI Text). This is in accordance with the known fact that the β-subunits have the active ATPase center. We also studied the interaction between each of the neighboring functional dimers (between each pair of α_Eβ_E, α_Dβ_D, and α_Tβ_T) and the contribution due to the dimer–dimer coupling appeared to be small and it does not significantly affect the overall directionality observed in Fig. 2A (see Fig. S4 and SI Text).

In order to understand the role of the γ-subunit in transforming the chemical energy during the F1-ATPase conformational cycle, we mutated ionized residues and studied the effect on the electrostatic surface (see Fig. S5 and SI Text). Overall, the calculations show that mutating almost three-fourths of the γ embedded within the α/β-crown do not affect the least energy path in Fig. 2A, which can qualitatively explain the rotation along the right direction in a recent study of F1-ATPase without the axle part of the γ (31). Most interestingly, our results imply that the lower part of the γ (around the bulge and the β-protrusions) is the important part of the rotor because mutating those residues resulted in a loss of general functionality through reduction of barriers in and around the rotary path accompanied by an increase in the conformational barrier. This effect will presumably lead to more stochastic behavior of the γ rotation with a loss of precisely coupled chemistry and conformational barriers. In considering the significance of the above results, we note that they rationalize in a qualitative way the remarkable finding of the rotation of the axleless F1-ATPase (31). However, more systematic study is required to establish the precise way in which γ and α/β are altering the electrostatic basis of the axleless activity.

2.5. Is Steric Mechanism Driving the System?

As stated in the Introduction, several works proposed a steric mechanism (18, 20) or a somewhat related elastic spring model (19) and asserted that such mechanism emerged from their calculations. However, these works forced the system to move in the desired direction (by applying very large forces) rather than allowing the system to be driven by the chemical potential coupled by the proper external torque. It seems to us that the requirement for a realistic modeling is to have a free energy surface that can reproduce, or at least approximate, the functional energy landscape. Apparently, the previous studies could not capture the energetics of the system, as is indicated by the fact that no energy values in a feasible range were provided. Moreover, these models cannot predict the observed unidirectionality but just imposes it. The use of a microscopic model (19), which only applied torque on the γ-subunits, has provided instructive information on the response of the other subunits to the γ motion, but again this was done with very large force. More importantly, it is not clear how to couple the exact binding/release/chemical coordinates with such treatments.

Despite the difficulties of obtaining meaningful steric energies, we report in the SI Text the results of using our CG model with limited relaxation to assess the trend in the steric energy. The results presented in Fig. S6, obtained after a short relaxation to overcome side-chain/side-chain clashes, show no clear trend and cannot be used to establish a rotary mechanism. On the other hand, the electrostatic free energy surface does show a clear pattern before (figure not shown) and after relaxation (Fig. 2A).

One of the strongest arguments against the steric model is provided by the recent work of Furuike et al. (31), in which it was established that the rotational motion occurs in the right direction even without most of the γ embedded inside the (α/β)-subunits. Although this effect is reproduced by our electrostatic model (The Role of the Subunit Interaction), it is unlikely to be reproduced by a consistent steric model, because most of the γ-subunit packed inside the (α/β)₃ cavity in the native enzyme is now absent.

3. Concluding Remarks

Previous studies attempted to explore the coupling and unidirectionality in biological energy transduction. However, a structure/energy-based model bridging the gap between experiments and theory has not been accomplished. That is, the functional directionality observed in motors must be reproduced by calculated free energy landscape and not imposed by TMD (18) or by switching function (20). Thus, for example, the support for the idea of steric control or elastic spring model (18–20) was obtained by enforcing the directionality rather than producing it. In fact, the steric model is inconsistent with the axleless rotation of F1-ATPase (31) discussed in the previous section. An additional problem is associated with the fact that most of these studies have not considered the key effect of the coupling to the chemical and conformational barrier.

Our work helps to close the gap in quantifying the origin of the directionality by providing a consistent physically based landscape for the entire F1-ATPase system (for a clarification of the landscape concept, see ref. 32). The CG electrostatic landscape plus the chemical contributions reproduced the directionality of the energy conversion process and provided a basis for a detailed analysis of the experimental information from single-molecule spectroscopy. Furthermore, the CG landscape produces a conformational barrier that starts around the 80° region and channels the system toward the hydrolysis direction, thus rationalizing the observations from single-molecule studies of the catalytic dwell following the 80° rotation. Moreover, guiding the chemical step by this specific conformational state may be relevant to the efficiency of the overall mechanochemical process.

The present work left different detailed issues as open questions. This includes the difference between schemes I and II in Fig. 1 and the details of the conformational/chemical landscapes (depicted in Fig. 3). Some of these details will be explored in our future studies (e.g., evaluation of the conformational/chemical landscape by the same approach used in our studies of other systems, for, e.g., refs. 27 and 28). Nevertheless, it is important to reemphasize that the directionality of the system is obtained from the surface of Fig. 3 and reproduces the observed delay time of the catalytic dwell (Fig. 4) in a well-defined deterministic way, rather than imposed by TMD. Note that although some features of the surface in Fig. 3 reflect experimental estimates, the main trend reflects the calculated conformational surface (Fig. 2A) and the previously analyzed ATP energetics. We also note that, although we are dealing with a nonequilibrium conversion of t_w to d_w, the individual steps depicted in Fig. 3 satisfy quasi-equilibrium as discussed in (33).

Recent works invoked the concept of Brownian motors (29, 34) as the underlying theoretical framework for many biological motors. Although this concept has important instructive elements, it seems to highlight the obvious fact of random thermal motions rather than the nature of the free energy landscape and its relationship to the protein structure and function. Once the free energy surface is determined, the motor functionality and the corresponding vectorial process becomes clear because the individual rate constants follows the Boltzmann based transition state theory. Furthermore, attributing functional features to fluctuations between several thermally accessible states (34) (which might look to some as elements of a Brownian ratchet) is not so relevant to the question of how the motor operates. In fact, having the high activation chemical and conformational barriers is not fully compatible with the standard Brownian ratchet model and requires one to use a discrete chemical kinetics description (35). Thus it is not so useful to say that Brownian motions drive the motor (there are always thermal motions in all molecular systems including those that are not functioning as motors). What counts are the rate-limiting high barriers and the overall downhill free energy profile, which is not explained by invoking the obvious stochastic search.

Finally, in a nutshell, the present work presented an actual structure-based landscape and provided powerful insight into the electrostatic origin of the conformational coupling, clarifying the principle used by nature to harness the ATP to ADP dissociation free energy. As shown in Fig. 3, it is very hard to harness the hydrolysis energy in water in biological timescales, because the corresponding barrier is about 30 kcal/mol, and because the chemical energy will not do any useful work if released in water. However, in the ATPase, the barrier is reduced to about 14 kcal/mol, and as shown in Fig. 3, the movement from ATP to ADP and the subsequent release of chemical energy is coupled to the rotational motion and thus is capable of doing reversible work, when coupled to a proper load. This coupling of the chemistry with the conformational barrier releases the same energy that was stored in the water reaction, but now is capable of a remarkable way of utilizing all the chemical free energy toward a vectorial process.

4. Methods

The present work uses a CG model (21) that describes the main chains by an explicit model and represents the side chains by a simplified united atom model. The model has a unique treatment of the electrostatic energy including the self-energy that gives its reliable features. The details of our model are given elsewhere (21, 36) and are also described in the SI Text. It should be clarified that the CG conformational energy includes only the energy of the simplified side chains as is done in our calculations of protein stability (23).

In addition to the CG treatment, we further generated a more simple, reduced-dimension potential energy surface that could be used in Langevin dynamics simulations of long time processes. The energy terms in the reduced dimension surface are similar to those used in our previous studies (25, 30) and are described in detail in the SI Text. The corresponding LD equations are the same as those used in our previous studies (25) and are described in detail in the SI Text.