Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses

Abstract

Use of multivoxel pattern analysis (MVPA) to predict the cognitive state of a subject during task performance has become a popular focus of fMRI studies. The input to these analyses consists of activation patterns corresponding to different tasks or stimulus types. These activation patterns are fairly straightforward to calculate for blocked trials or slow event-related designs, but for rapid event-related designs the evoked BOLD signal for adjacent trials will overlap in time, complicating the identification of signal unique to specific trials. Rapid event-related designs are often preferred because they allow for more stimuli to be presented and subjects tend to be more focused on the task, and thus it would be beneficial to be able to use these types of designs in MVPA analyses. The present work compares 8 different models for estimating trial-by-trial activation patterns for a range of rapid event-related designs varying by interstimulus interval and signal-to-noise ratio. The most effective approach obtains each trial’s estimate through a general linear model including a regressor for that trial as well as another regressor for all other trials. Through the analysis of both simulated and real data we have found that this model shows some improvement over the standard approaches for obtaining activation patterns. The resulting trial-by-trial estimates are more representative of the true activation magnitudes, leading to a boost in classification accuracy in fast event-related designs with higher signal-to-noise. This provides the potential for fMRI studies that allow simultaneous optimization of both univariate and MVPA approaches.

Introduction

The use of multivoxel pattern analysis (MVPA) to predict the cognitive state of a subject during task performance has become a popular focus of fMRI studies (Mur et al., 2009). Generally these analyses attempt to use BOLD fMRI images to classify the task or stimulus conditions encountered while those images were acquired. For example, Haxby et al. (2001) used a classifier to identify which of eight object classes a subject was viewing (e.g., faces, houses) based on similarity of activation patterns to a set of independent scanning runs in which the object class was known. These activation patterns are fairly straightforward to estimate for trials that are blocked or spaced out over time (i.e., slow event-related designs), but for rapid event-related designs the BOLD signal for nearby trials will overlap in time, making the identification of signal unique to specific trials much more difficult. Finding a model that accurately estimates trial-specific signals for faster event-related designs would allow more flexibility in study design for studies targeted at MVPA or representational similarity analysis (Kriegeskorte et al., 2008; Mur et al., 2009).

Obtaining summary images for blocked trials is relatively straightforward. With blocks of task, activation images typically consist of either block averages (Mourao-Miranda et al., 2006; Cox and Savoy, 2003; Kamitani and Tong, 2006) or separate time points within the blocks (Chen et al., 2006; Mourao-Miranda et al., 2006). The approaches for obtaining trial-specific estimates in an event-related design can be described through a general linear model (GLM) where the model estimation is carried out voxelwise and the BOLD time series is the dependent variable. The most straightforward approach (known as beta-series regression: Rissman et al. (2004)) models each trial as a separate regressor as shown by the design matrix X_S in the top left of Figure 1. This approach works well for slow event-related designs, but for rapid event-related designs the estimates can become unstable due to correlation between the trial-specific regressors. For example, if 2 trials are 5s apart the correlation between their regressors would be low (−0.24) whereas if they are 1s apart the correlation is much stronger (0.94). This collinearity results in signal estimates that are highly variable and hence unreliable due to a limited amount of information available that is unique to each specific trial. One solution to this problem is simply to use a slow event-related design (De Martino et al., 2008). Although this does greatly reduce collinearity, slow event-related designs are very inefficient for univariate analysis and also may tax the subject’s attention. The ultimate goal is to decrease the time between trials (ISI), creating a design that is psychologically optimal while retaining the ability to accurately estimate trial-specific activation patterns. This will allow for more exibility in the design of classification studies, decreasing the amount of time the subject will spend in the scanner as well as allowing more stimuli to be presented to the subject. Additionally, it is common to carry out secondary analyses on data for studies that were not originally optimized for a classification analysis, but may have been optimized with other criteria in mind (e.g., detection power). Finding a way to obtain trial-specific activations for faster event-related designs will increase our ability to run secondary MVPA analyses on the data.

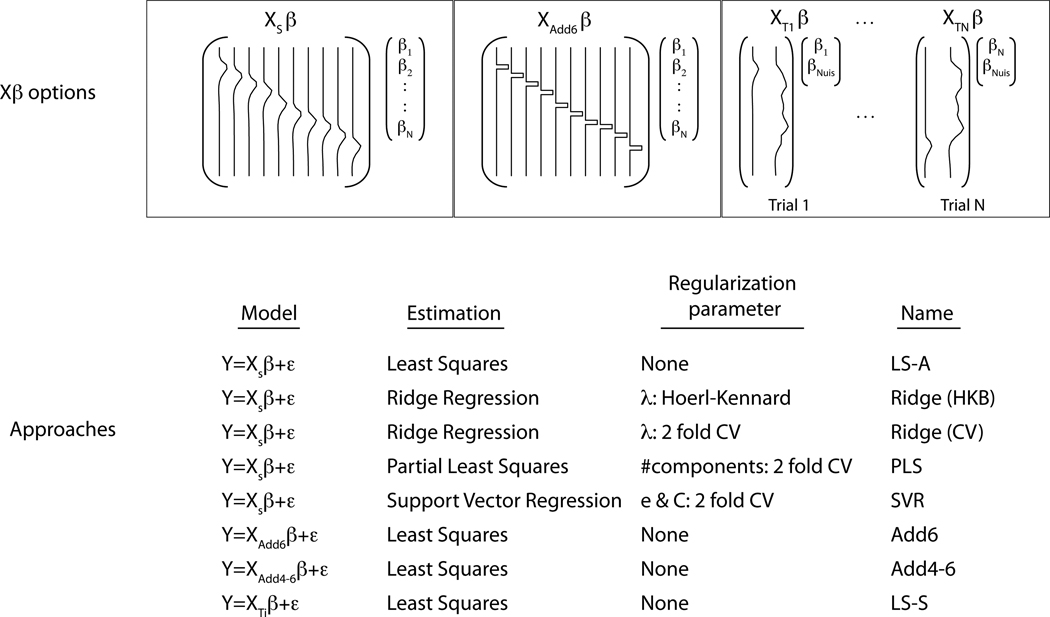
Figure 1.

The model estimation approaches considered for obtaining trial-by-trial parameter estimates. Five of the approaches (least squares, two versions of ridge regression, partial least squares and support vector regression) used the design matrix shown on the top left, X_S. This design matrix contains a single regressor for each trial (in this case 10) in the run, where each regressor is an impulse function convolved with a double gamma HRF. The middle design corresponds to the Add6 model, which models each trial using an unconvolved boxcar function capturing the time point 6 seconds after the time of stimulus presentation. The last design illustrates the LS-S approach, where a trial-specific design matrix is used to obtain the activation estimate for that trial. The design matrices contain two regressors, one for the trial of interest plus a second that models all other trials simultaneously. So, X_T1 is the design to obtain the activation estimate for trial 1 and has a regressor modeling that trial and a second regressor modeling all other trials. The estimate for β₁ from this first design is the activation for trial 1. This process is repeated N times to obtain estimates for all trials. The bottom table lists the regularization parameters used, when needed.

In this study we compare eight models for estimating trial-specific activation and examine the quality of the estimates as well as evaluating their performance in a classification analysis. The models (Figure 1) are briefly described here; further detail can be found in the Methods section. One model does not address collinearity, while 4 of the approaches use regularization and 3 use strategies in regressor construction to reduce collinearity. Least squares estimation using the previously mentioned design matrix X_S, referred to as LS-A (Least Squares - All), is not expected to work well in the presence of collinearity. The four approaches with additional regularization include partial least squares (PLS), support vector regression (SVR) and ridge regression using two strategies for estimating the ridge parameter. These approaches introduce bias in hopes of a beneficial decrease in the variance of the estimates. The other 3 models are estimated using least squares but attempt to reduce collinearity through the structure of the regressors. Two of these models, Add6 and Add4–6, focus on capturing the peak of the response by only modeling the time point(s) at 6s or between 4–6s after stimulus onset respectively. The third, LS-S (Least Squares - Separate), runs a separate GLM for each trial where the trial is modeled as the regressor of interest and all other trials are combined into a single nuisance regressor.

Other studies involving the use of pattern classification for fMRI have focused on different aspects of the classification analysis without much attention spent on how the activation estimates are created for event-related designs. Although some work has focused on how to best summarize activation for blocked designs (Mourao-Miranda et al., 2006), the work presented here is unique to event-related designs. Classification studies have also focused on feature selection, or reducing the set of voxels used in the classification analysis to improve the classification accuracy (Chen et al., 2006; Mourao-Miranda et al., 2006; De Martino et al., 2008) as well as the performance of different classification models (Misaki et al., 2010; Cox and Savoy, 2003; LaConte et al., 2005; Carlson et al., 2003). Lastly, the use of different types of activation estimates - such as using magnitude of the BOLD signal versus a t-statistic as well as different strategies for normalizing the data - have been compared for benefits in classification accuracy (Misaki et al., 2010). The results from the present study can be combined with the insights from these other studies to help create optimal data analysis strategies for MVPA studies.

In what follows, we first outline the eight different estimation strategies as well as the classification approach used to assess their performance. The models are first applied to simulated data in order to characterize the quality of the activation estimates (variability and correlation with true values) and assess their classification performance across different interstimulus interval lengths and noise levels. The best-performing models are then applied to a real data set. We found that the LS-S approach performed as well as or better than all of the other approaches in both simulated and real data analysis.

Methods

Models considered

The estimation approaches considered here for obtaining trial-by-trial estimates of BOLD activation are described in Figure 1. All but one of these approaches attempts to remedy the collinearity problem: the simplest approach does not address collinearity and simply consists of the least squares estimates of the general linear model Y = X_Sβ + ε. The estimate is given by $\widehat{\beta }={(X_S^{\prime }{X}_S)}^{-1}{X}_S^{\prime }Y$, where Y is the vector of the BOLD response time series and X_S is the design matrix of the form depicted in the top left of Figure 1 and β is the vector of trial-by-trial activation estimates. This approach is referred to as LS-A, since least squares is used and all parameters are estimated simultaneously. As mentioned above, this model will most likely suffer from collinearity when stimuli are close in time. Since the collinearity can cause the parameter estimates to be very large in magnitude in either the positive or negative direction, some have tried to remedy this problem by estimating the regression using regularized approaches such as ridge regression (Xue et al., 2010). Three types of regularized regression were considered here: ridge regression, PLS and SVR. Instead of using least squares, ridge regression reduces the variability in the parameter estimates by shrinking the parameter estimates toward 0 through a regularization parameter (commonly called λ) using the estimate $\widehat{\beta }={(X_S^{\prime }{X}_S+\lambda I)}^{-1}{X}_S^{\prime }Y$, where I is a square identity matrix with the same number of columns as X_S (Hoerl and Kennard, 1970). If λ = 0, then no regularization occurs and the estimates are equivalent to least squares, and as λ increases the parameter estimates shrink toward 0, hopefully shrinking the unusually large estimates that resulted from the collinearity. With the proper choice of λ one hopes that a small cost of bias of the parameter estimates will be paired with a large variability reduction and hence more stable parameter estimates.

PLS is based on the singular value decomposition of $X_S^{\prime }Y$ where Y is the vector containing the BOLD response time series. Ultimately the problem of estimating the parameters in a model where the regressors are highly correlated is transformed to a new space that does not suffer from this collinearity. PLS is similar to principal components regression (PCR), which estimates the model using a subset of the principal components of X to carry out the regression. PCR uses the components with maximal variability, omitting components with lower variability. PLS also tries to include components with maximal variability, but additionally strives to find components that are correlated with Y. PLS and PCR are very similar, hence only PLS was considered in this study. Additionally it can be shown that PLS and ridge regression are quite similar, but since PLS works in a discrete fashion (number of components is an integer between 1 and the number columns in X_S) and ridge regression shrinks the parameter estimates in a continuous manner (λ is continuous) both of these methods were included. For a more detailed description of the relationships between ridge regression, PLS and PCR see Hastie et al. (2001).

The last regularized regression approach considered was SVR, which regularizes the parameter estimates β̂ through two parameters. The goal is to find a fitted regression line such that the measured values of the data fall within a distance of ε of the fitted line (|Y − Ŷ| < ε). A second parameter, C, is used to soften the ε margin by allowing some of the values to fall outside of the ε neighborhood of the fitted line; this is often called “slack”. As C decreases more slack is introduced into the model and as ε decreases, the neighborhood around the line becomes smaller. A thorough description of SVR can be found in Scholkopf and Smola (2002).

The other three approaches avoid multicollinearity by using different strategies for building the regressors. The first, referred to as Add6 (middle-top of Figure 1), avoids multicollinearity by simply taking the time point corresponding to 6s after the stimulus presentation, assuming this will capture the peak activation for the stimulus and reduce collinearity almost completely (Polyn et al., 2005). Likewise, a similar model, referred to as Add4–6, models a slightly longer block between 4–6s after the stimulus presentation, which may have a better chance of capturing the peak of the BOLD response. Finally, an approach introduced in Turner (2010), models each trial in a separate linear model where each model has 2 regressors: one for the trial of interest and a second that models all other trials in one other regressor (top-right of Figure 1). Since the trial of interest will not be highly correlated with the nuisance regressor, the collinearity problem is greatly reduced in this model.

Simulation study: data generation

A total of 500 simulations were performed for each of 12 design setups which varied according to level of collinearity and signal-to-noise ratio (SNR). A simulation consisted of a total of 3 runs of data for a single voxel, which allowed for a double cross-validation (see next section and Appendix for a description of double CV). Each run had the same number of stimuli per each of two task types, but the presentation order and timing between stimuli was random within and across runs. The ISI - the time between the end of one trial and the beginning of the next - was randomly chosen from the uniform distribution, U (u_min, u_max), where the interval was either 0–4s, 2–6s, 4–8s or 6–10s within a given run. This allowed us to investigate varying degrees of collinearity, since a shorter ISI would result in a model with higher collinearity. The vector of true trial-by-trial effect sizes, β = [β_trial1,…, β_trialN] was constructed by randomly sampling β_triali according to

$${\beta }_{{\mathit{\text{trial}}}_i}\sim \{\begin{array}{cc}N(5,{0.5}^2)\hfill & \text{if trial type }1\hfill \\ N(3,{0.5}^2)\hfill & \text{if trial type }2,\hfill \end{array}$$ (1)

where the mean values of these distribution were chosen to be within a range exhibited in real data. Using β and the design matrix X_S previously described (top left of Figure 1) the data for each run were simulated as Y = X_Sβ + ε where the error was distributed ε ~ N (0, σ²V) with σ² = 0.8², 1.6², or 3² allowing for different levels of signal-to-noise and V is a correlation matrix following an AR(1) structure where Cor(y_i, y_j) = ρ^|i−j|. The value of ρ was set to 0.12, based on the correlation of the real data described below. Specifically the real data, which are described below, were fitted using the FMRIB Software Library (FSL, www.fmrib.ox.ac.uk/fsl) and the correlation matrix from FSL’s FILM prewhitening algorithm (Woolrich et al., 2001) was fitted with an AR(1) model to estimate the correlation, ρ, which was then averaged over space and subjects to arrive at the final estimate. The parameters that remained fixed across each set of 500 simulations were the mean and variance of the β_triali distribution, the data noise (σ²), the temporal autocorrelation (ρ), and the level of collinearity determined by u_min, and u_max. The design matrix, X_S, and parameter vector β were randomly generated for each run. Twelve sets of simulations were carried out, one for each combination of ISI interval (u_min, u_max) and signal-to-noise level (determined by σ²). When estimating the trial-by-trial estimates, both the BOLD data and design matrix are highpass filtered using a Gaussian weighted running line smoother with σ = 32s.

Simulation study: double cross-validation

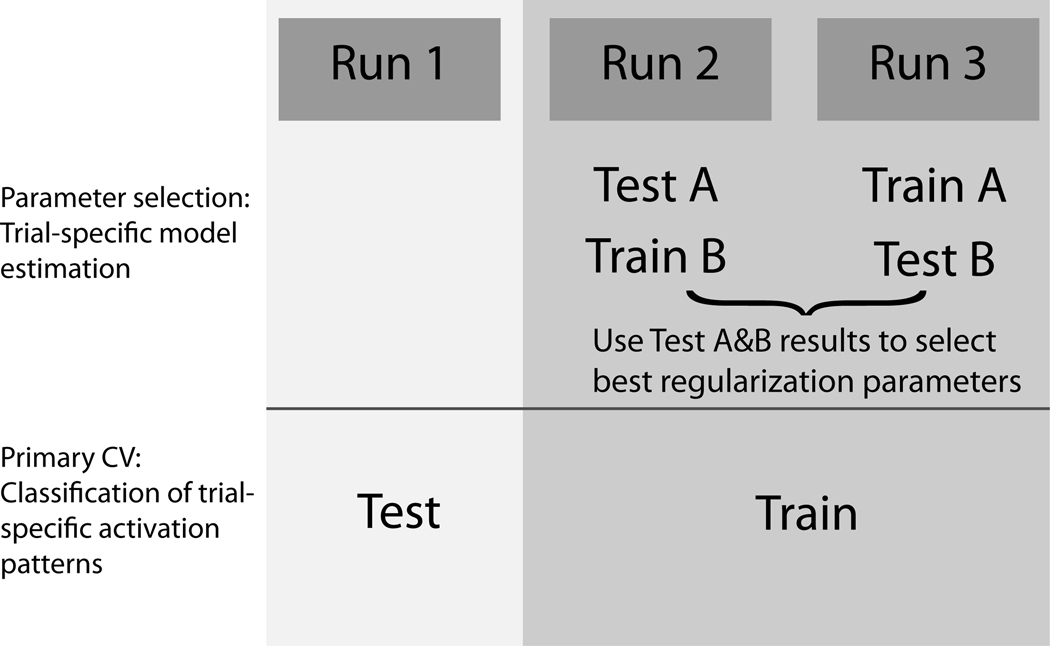
Using 3 runs of data, a double cross-validation approach was used, allowing CV-based accuracy estimates to be calculated (primary CV) as well as CV-based regularization parameter selection for PLS, ridge regression, and SVR (parameter selection CV). Figure 2 outlines the cross-validation procedure.

Figure 2.

Illustration of the double cross-validation that was used in the simulation study. The primary cross-validation was a leave-one-run-out CV across 3 runs, for the purposes of obtaining classification accuracy reflecting the ability of the trial-by-trial parameter estimates to predict task type. One fold of the primary cross-validation is illustrated here. It begins with the parameter selection CV, which is a 2-fold CV used to select the regularization parameters used in ridge regression, PLS and SVR. Once this 2-fold CV is carried out the trial-specific activations can be estimated for all 3 runs. Then the primary CV is carried out, training a classifier to predict trial type using 2 runs of data and then testing this model on the test data.

The parameter selection CV uses only the 2 runs that will later comprise the training data in the classification CV. For the example in Figure 2 this corresponds to the second and third runs. Note that in this case we are estimating regularization parameters that are necessary for obtaining the trial-specific activation estimates. First run 3 is used to estimate the models over a range of regularization parameters and then the performance of the estimates is tested on run 2. Then this is repeated using run 2 to train and run 3 to test. Combining the results from test A and test B, the highest-performing regularization parameters are selected and then used to obtain trial-specific activations for all runs of data.

The primary CV starts with the trial-by-trial parameter estimates for all trials across all 3 runs using one of the modeling strategies in Figure 1. Note that only ridge regression, PLS, and SVR required the previous parameter selection CV. Next a logistic regression model fits the model for predicting trial type from trial-by-trial activation estimates using the training data (Train or runs 2 and 3 in Figure 2). Then the estimated logistic regression model parameters are used to predict the trial type of the test data set (Test or run 1 in Figure 2) and the classification accuracy is the average of the classification accuracy for each trial type. The entire process is then repeated 2 more times using all possible combinations of assigning runs as test and training data, after which the classification accuracies are averaged.

Real data: data description

The data used in this analysis were from an unpublished study of mirror reading (Jimura et al., in preparation). Subjects were scanned for 6 runs lasting 410 secs, during each of which they were presented 32 plain words and 32 mirror-reversed words, varying in length from four to seven letters. Subjects were instructed to read the words presented and decide as quickly as possible whether the stimulus was a living or non-living entity using a keypad button-box. Presentation of stimuli using Matlab was synchronized with the onset of each functional scan to ensure accuracy of event-related acquisition. Word-list order was counterbalanced across subjects, and word length was counterbalanced within each list. The stimulus onsets (interstimulus intervals) were also counterbalanced across subjects and varied randomly for the purposes of the fMRI data acquisition. The ISI has a minimum of 3s and had an inter-quartile range of 3.8–7.8s over runs and subjects. Data were acquired on a Siemens Allegra 3T head-only scanner using a gradient echo EPI pulse sequence (TR=2s, TE=30 ms).

Eighteen healthy subjects were recruited for the study; four subjects were excluded for the following reasons, respectively: excessive head motion in the scanner, non-completion of study (which involved additional training and scanning sessions following the initial session analyzed here), inadequate task performance, and structural abnormalities. This study used 6 runs of data for each subject, with the exception of 4 subjects who only had 5 usable runs of data. Only trials with accurate responses were included; there were an average of 25 accurate responses to mirror-reversed words and 29 accurate responses to plain words per run across all runs.

Prior to applying the trial-specific estimation model, data preprocessing was carried out in FEAT version 5.98, part of FSL. The following preprocessing operations were applied: image time series were aligned using the MCFLIRT tool; the skull was removed from the image using the brain extraction tool (BET); spatial smoothing using a Gaussian kernel of FWHM 5mm; grand-mean intensity normalization of the entire 4D data set by a single multiplicative factor; and highpass temporal filtering (Gaussian-weighted least-squares straight line fitting with σ = 32s). Note that this same highpass filter was applied to the design matrix when estimating the trial-by-trial estimates.

Real data: data analysis

The simulation studies revealed that ridge regression, PLS and SVR performed similarly to either LS-A or Add4–6, and since they require the time-consuming step of running a double CV to select the regularization parameters these 3 approaches were not considered in the real data analysis. The real data analysis focused on the standard approach (LS-A), along with the best (LS-S) and worst (Add6) performers from the simulation study. Additionally the Add4–6 model was studied. The motion parameters and other nuisance variables were included in the model when estimating the activation patterns. A support vector machine approach was used in the classification analysis, implemented using the svm function (www.csie.ntu.edu.tw/~cjlin/libsvm) of the R software package (www.r-project.org/). The data are automatically scaled internally to have zero mean and unit variance and the results are based on the radial basis kernel, which requires two parameters, the cost parameter, C, which is necessary in all SVM models as well as the parameter γ, which is part of the formulation of the radial basis kernel. These parameters were set through a secondary leave-one-run-out CV, similar to that used in the simulation study. On average C was 5.06 and γ was found to be 6.3 × 10⁻⁶ across all methods. We also ran the SVM using a linear kernel, but the accuracy values were lower and more variable than those using the radial basis kernel, so only the results based on the radial basis kernel are reported here. Note that no feature selection was used in our classification analysis results reported here. Although feature selection may improve the classification accuracy we found that it affected all approaches by increasing the classification accuracies in equal amounts. Since we were only interested in comparing differences between classification accuracy we focused on the simpler analysis where the secondary cross validation was only used to select the C and γ parameters.

Results

Simulation study: classification accuracy

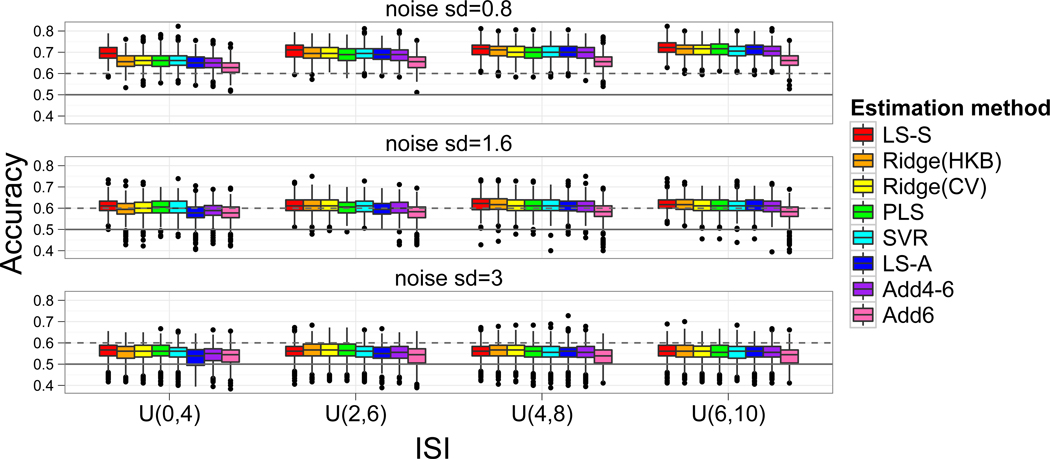
The classification accuracies from the primary CV are shown in Figure 3 and the estimated parameters for the ridge-HKB approach and other approaches that used the secondary CV are in Table 1. The rows of Figure 3 correspond to different noise levels and the columns correspond to differing levels of collinearity according to the length of the ISI (2s, 4s, 6s, and 8s on average). There are eight boxplots for each noise/collinearity setting, corresponding to the eight trial-specific activation estimation techniques described in Figure 1. In general, across the 12 simulation setups, the regularized linear regression approaches (Ridge, PLS and SVR) perform similarly. The modeling approaches that stand out as the best and worst are LS-S and Add6, respectively, where Add6 estimates the trial’s activation using the BOLD magnitude of the TR 6s after the stimulus presentation and LS-S was the iterative modeling approach where each iteration models a single trial as a regressor and all other trials as a second regressor. In general the Add6 model performs very poorly, most likely a combination of failure to capture the peak of the trial’s response and failure to filter out signal due to overlapping trials.

Figure 3.

Accuracy results from simulation studies. Each simulation consisted of 500 iterations and 60 trials split randomly and evenly between two tasks. Each of the 12 sets of boxplots contain the results from the eight different models outlined in Figure 1 and arranged by decreasing levels of collinearity (left to right) and increasing noise (top to bottom). When the noise is lower (top 2 rows) the Add6 model performs the worst across all levels of collinearity. For low noise, high collinearity cases (upper left) the LS-S model outperforms all other models. The solid horizontal line indicates chance (50%), while the dashed line indicates accuracy significantly better than chance according to the binomial distribution.

Table 1.

Regularization parameter estimates found for SVR, ridge regression and PLS. With the exception of Ridge(HKB), all parameters were estimated in the secondary CV and these are the average parameter values over the 500 iterations for each simulation setup.

	U(0,4)	U(2,6)	U(4,8)	U(6,10)
	SVR-ε
noise σ = 0.8	0.466	0.503	0.494	0.483
noise σ = 1.6	0.537	0.562	0.539	0.565
noise σ = 3	0.595	0.631	0.659	0.661
	SVR-C
noise σ = 0.8	2.840	0.496	0.318	0.277
noise σ = 1.6	0.708	0.195	0.159	0.149
noise σ= 3	0.301	0.134	0.120	0.118
	Ridge(λ-HKB)
noise σ = 0.8	10.188	17.734	23.315	28.990
noise σ = 1.6	22.914	49.834	66.571	83.993
noise σ = 3	33.320	79.759	114.133	148.313
	Ridge(λ-CV)
noise σ = 0.8	14.992	1.608	0.310	0.000
noise σ = 1.6	39.201	18.395	6.151	0.698
noise σ = 3	40.000	39.441	32.404	18.840
	PLS-component number
noise σ = 0.8	8.095	12.314	8.709	6.807
noise σ = 1.6	2.051	8.009	8.268	7.635
noise σ= 3	2.000	3.638	4.683	6.013

The LS-S approach tends to outperform all other approaches in low noise, high collinearity settings (upper left panels of Figure 3). As the ISI decreases, LS-S performs more similarly to the other approaches. Likewise, as the noise increases, the performance of all approaches tends toward chance and, with the exception of Add6, the methods tend to perform similarly. Notably, in the first row of the figure (noise sd=0.8) the accuracies for most methods increase considerably when the ISI is increased from 2s on average to 4s on average, with the exception of LS-S, which has similar accuracy levels for both ISIs, indicating a benefit to the use of LS-S with faster ISIs.

The regularization parameter for ridge regression, λ (Table 1), determined by the HKB approach tended to differ from the value found by CV. Although the ridge parameter, λ, should decrease as the ISI increases due to a smaller degree of collinearity, the HKB estimate does not adjust accordingly and actually increases. Although the CV-based λ estimates behave as we would expect, the overall impact on classification accuracy is minimal.

For short ISIs the LS-A approach is expected to perform the worst, since it suffers the most from collinearity and does not employ any regularization strategies. This is generally the case for the shortest ISI tested, which lasted 2s on average (U(0,4)), although in many instances the Add6 model performed worse still.

Simulation study: properties of activation estimates

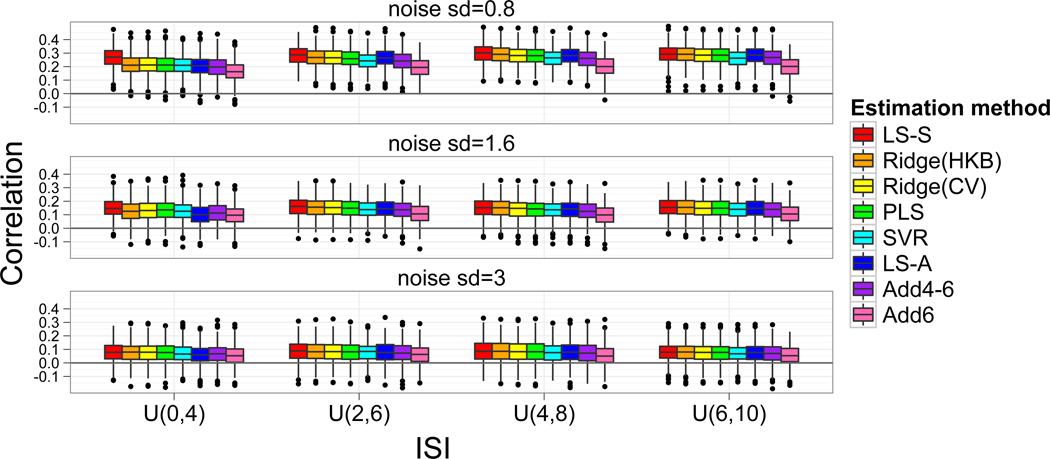
To understand why certain estimates of the trial-by-trial activation performed poorly in the classification analysis we have calculated the correlations of the estimates to the true value of the activation magnitudes in the simulation study (Figure 4). The correlations for β₁ and β₂ were very similar and so they were averaged here. The patterns are very similar to the accuracy patterns in Figure 3, indicating that decreases in accuracy were due to the activation estimates not closely representing the true activation magnitudes. For example, the Add6 approach yielded activation estimates with among the lowest correlations with the true activation magnitude and have the lowest classification accuracy. Although stronger correlations are paired with higher classification accuracies in our simulations, a strong correlation of the true and estimated activation magnitude does not necessarily imply that the resulting classification accuracy would be high, as the true activation magnitudes themselves may not perform well in a classifier depending on how variable they are and how much they differ in magnitude between trial types.

Figure 4.

Correlation of trial-by-trial parameter estimates with true parameter estimate value from simulation studies. The correlations between true and estimated trial activation magnitude were similar for β₁ and β₂ and hence are averaged for each simulation. The organization of the boxplots is similar to Figure 3 with collinearity decreasing from left to right across rows and noise increasing from top to bottom. Methods with weaker correlation between estimated activation and true activation magnitudes tended to have worse classification results.

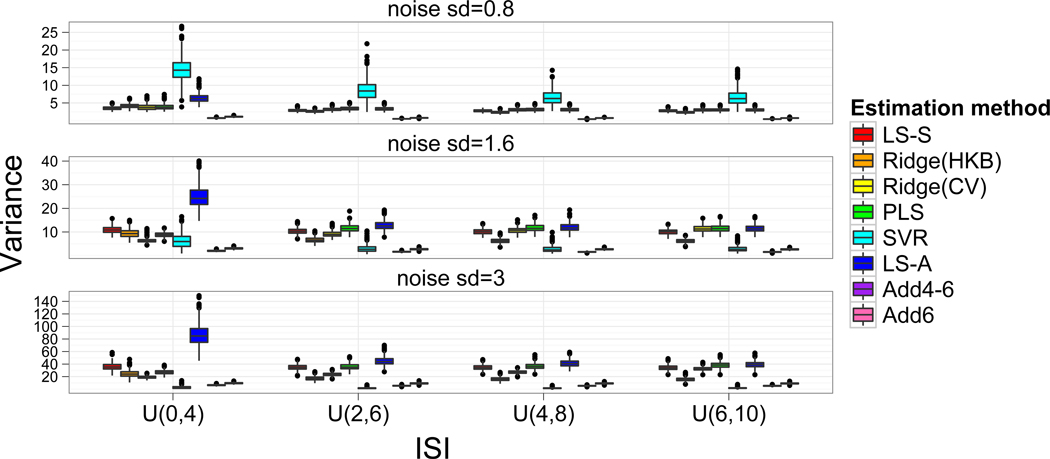
The variances of the trial-by-trial estimates did not vary between β₁ and β₂ and so they were averaged within each simulation. Figure 5 shows these variances for all models. The LS-A model tends to have the highest variance of all the approaches, which is not surprising since the model estimates were unregulated and collinearity will increase the variability of the estimates. This trend decreases with longer ISI due to a diminished multicollinearity. In low noise cases the SVR estimates are most variable, while in the medium and high noise cases the LS-A approach produced estimates with the highest variability, which indicates why both the correlation of the true to estimated activations and classification accuracies are lower for LS-A compared to LS-S. Both Add4 and Add4–6 have very low variability, but this property was not beneficial for the Add6 estimates since the estimates were not representative of the true activation magnitudes.

Figure 5.

Variability of the parameter estimates. For each simulation the variance of the parameter estimates across trials was calculated and variances were similar for β₁ and β₂, so they are averaged for each simulation. As expected the unregulated LS-A model has the highest variance, although in some cases the SVR parameter estimates are much more variable. The variability of LS-S is often similar to the other regulated approaches, but is found to be slightly larger than some of the regulated approaches in higher noise situations.

Real data

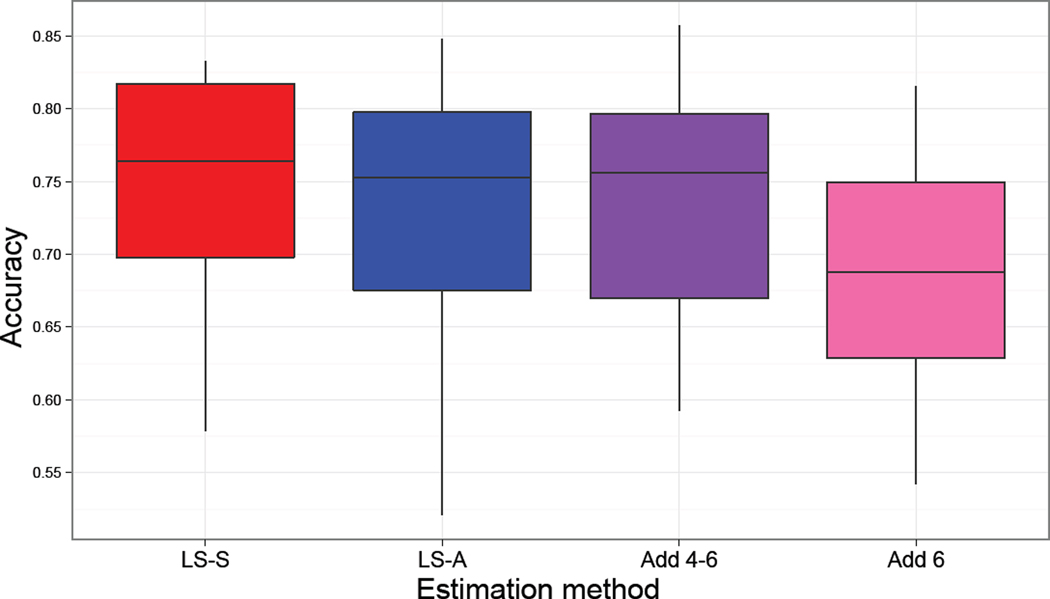
Based on the simulation results, the most interesting models to consider for the real data analysis included LS-S, LS-A, Add4–6 and Add6. Since Ridge, SVR and PLS tended to performed similarly to either LS-A or Add4–6 and require the time-consuming step of running a double CV to select the regularization parameters, they were not considered for the real data analysis. Figure 6 illustrates the balanced accuracies across the 14 subjects from the 6-fold CV (5-fold in four cases) when classifying whether the subject was viewing mirror-reversed or plain words during trials. Note that a secondary leave-one-run-out CV step, similar to that of the simulation study, was used to select the γ and C parameters associated with the radial basis kernel were similar across models with an average cost of C = 5.06 and γ = 6.3 × 10⁻⁶.

Figure 6.

Classification accuracies from the real data analysis. The Add6 accuracy was significantly lower than LS-S (p=0.0002, uncorrected) and Add4–6 (p<0.0001, uncorrected).

Paired t-tests were used to compare classification accuracies between the different modeling approaches. To control for multiple comparisons across the 6 tests a permutation test with 5000 iterations was used to construct the null distribution of the max statistic across the 6 tests, which yielded a corrected p-value threshold of 0.006 to control the type I error at 0.05 for the family of tests. The classification accuracy of Add6 was significantly smaller than LS-S (uncorrected p=0.0002) and Add4–6 (uncorrected p<0.0001) and marginally lower than LS-A (uncorrected p=0.01). The classification accuracy of LS-S was marginally larger than LS-A (uncorrected p=0.01) and no other comparisons were significantly different corrected or uncorrected.

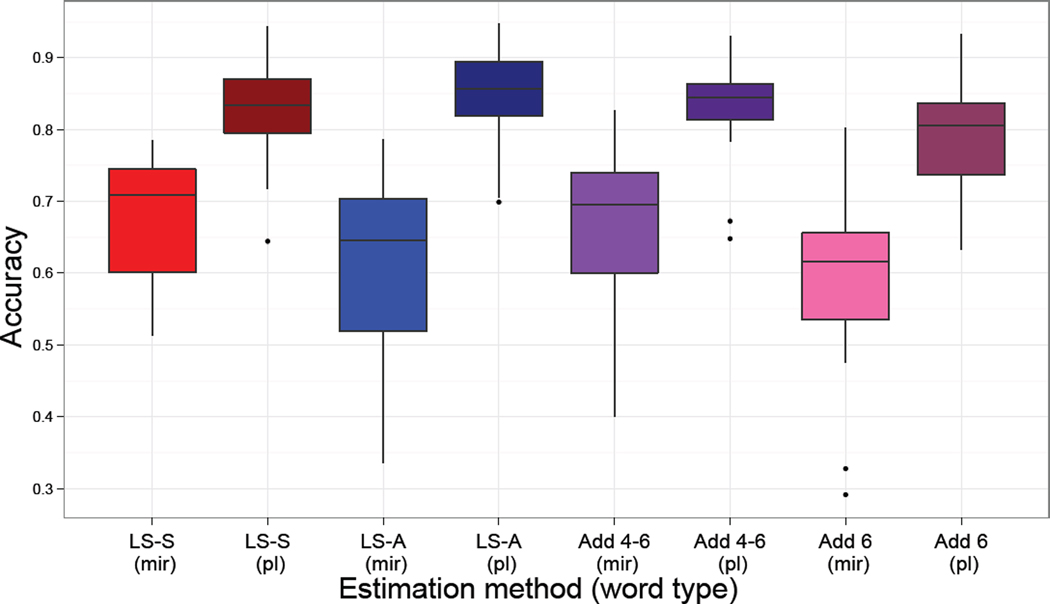
When the accuracies are separated by trial type, into mirrored words and plain words, a trend emerges that the classifier was more accurate classifying plain than mirror-reversed words (Figure 7). This could be due to there being more plain words (29 on average) than mirrored words (25 on average), due to differences in accuracy between conditions, or could be related to the quality of the trial-by-trial estimates. Interestingly LS-A has the highest classification accuracy for plain words (84%), but then the lowest for mirrored words (61.3%). Both LS-S and Add46 classify well in both word types more similarly than the other approaches.

Figure 7.

Classification accuracies from the real data analysis separated by stimulus type. Note that the classification accuracy increase for LS-S and Add4–6 compared to the other methods, as shown in Figure 6, is mostly due to an increase in the classification accuracy of the mirrored words.

Discussion

The goal of our work was to identify the most accurate approach for estimating trial-by-trial signals in rapid event-related designs, for use in subsequent MVPA analysis. The results show that the LS-S model works as well or better among all methods tested here. The simulation analysis showed that the LS-S activation estimates tended to have the highest correlation with the true activation magnitudes, even in cases with a short ISI, which most likely explains the good performance in the classification analysis. The Add6 model performs poorly in all design setups considered in this study. Another finding of our simulation study is that the classification accuracies did not increase much as the ISI increased, which is an important factor considering the quality and cost of data with a longer ISI. The exception was the case of high signal-to-noise ratio, where all but the LS-S approach showed a lower classification accuracy for the shortest ISI. Another benefit of the LS-S approach is that it is very easy to implement since the estimates are obtained using least squares and additional parameters do not need to be estimated, as they do in ridge regression, PLS and SVR.

These results are important because they allow classification studies to be designed with shorter ISIs, which will improve the quality of the data and reduce the cost of the study. For example, in our simulations with 30 trials of each stimulus type, an ISI of 2s compared to 4s on average produces runs of 4 and 8 minutes, respectively. Possibly more useful is that LS-S may provide better results in secondary analyses carried out on event-related fMRI data where the studies were not originally designed for a classification analysis.

Although we have only compared these approaches for the use of activation patterns in classification analyses, it is also likely that these estimates would perform better in other MVPA applications including pattern similarity analysis, such as those reported by Xue et al. (2010). Likewise, in beta series correlation analyses (Rissman et al., 2004) the LS-S estimates would presumably work better due to the improvements in the trial-specific activation estimates.

Interestingly the relationship between the Add4–6 model and other approaches in the real data analysis did not follow exactly the same pattern as we found in the simulation study. Specifically the Add4–6 model performed almost as well as the LS-S model and slightly better than the LS-A model in the real data analysis, whereas in the simulation study LS-A tended to have higher classification than Add4–6. This is most likely due to variability in the true hemodynamic response shape between the simulated and real data.

The current study focused on the use of the support vector classifier, with the radial basis kernel, for the classification of trial type based on activation estimates for the trials. Although we did also consider the support vector classifier with a linear kernel, for all four estimate types considered in the real data analysis (LS-S, LS-A, Add6 and Add4–6) it did not perform as well in terms of the magnitude of the classification accuracies as well as the variance of the classification accuracies across subjects. As explained in Pereira et al. (2009) the Gaussian Naive Bayes classifier typically performs worse than logistic regression or SVM classifiers when feature selection is not used since logistic regression and SVM deal better with noisy data. Therefore, these results may not hold for other classifiers, such as the Gaussian Naive Bayes classifier, but an exhaustive study of this was beyond the scope of this project. Although we found the radial basis kernel worked better in our real data analysis, it is recommend to try both the radial basis kernel and linear kernel for different data sets as the behavior may change.

In the present study, we used raw parameter estimates for subsequent classification analyses. Misaki et al. (2010) found that when using the LS-A approach for obtaining activation patterns, it was beneficial to use the t-statistics for the activation estimate rather than the raw parameter estimates. Since the LS-S approach is also least squares based, it would be easy to obtain t-statistics for use in classification; future studies will need to verify whether or not the t-statistics perform better for LS-S as well. In comparison, ridge regression, PLS and SVR do not have closed form solutions for test statistics corresponding to the parameter estimates and thus it would not be straightforward to apply them in this manner.

Although the classification model for the simulation study (logistic regression) differed from the real data (support vector classification), it is not expected that this had a strong inuence on the results. Since the simulation study was focusing on a single voxel at a time, the logistic regression model was the simplest, most intuitive model to use. For the real data analysis the classification was based on the trial-by-trial estimates across all voxels simultaneously, so support vector classification was required to deal with the wide data problem (more predictive variables than observations). Due to the similarities in the real and simulated data analysis results, it is doubtful that the classification model choice had any impact. The distribution of the ISI for the real data was drawn from a truncated exponential distribution, with a minimum of 3s and an inter-quartile range of 3.8–7.8s. This meant our ISI setting was somewhere between the middle two ISI setups considered in simulations (U(2,6) and U(4,8)). Also, ratio of activation to residual standard deviation in regions that were significantly active to either word type was 4.66/0.75 = 6.21 for the mirrored trials and 2.22/0.75 = 2.96 for the plain words. Recall that in the simulation study the activation for each trial type was 5 and 3, which would mean the simulation with noise sd=0.8 (5/0.8=6.25 and 3/0.8=3.75) is closest to the real data. Given this, our real data parameters are most similar to the parameters corresponding to the results in the second and third columns of the first row of Figure 3; further supporting the analogy between these two types of data, the real data results are similar to the simulated results using this set of parameters, and the accuracies obtained are likewise similar.

Overall we have shown that it is possible to obtain more reliable single-trial parameter estimates from rapid event-related fMRI data using an iterative least squares estimation approach, and that this relatively simple approach outperforms all other methods that were examined. This provides the potential for fMRI studies that allow simultaneous optimization of both univariate and MVPA approaches.

• >In this study we look at trial classification for fast event-related fMRI designs.
• >We examine 8 strategies for obtaining trial-specific activation estimates.
• >We compare approaches in simulated and real data analyses.
• >The newly presented approach produces unbiased, low variance activation estimates.
• >The new approach produces estimates that result in higher classification accuracy.

Appendix A

Double cross-validation

The steps for the double cross-validation for three runs, R1, R2 and R3, are outlined in Figure 2 and are as follows:

1. Separate data into primary test and training sets, referred to as Train and Test. Without loss of generality, start with Train1 set to R2 and R3 and Test1 is set to R1.

2. Parameter selection cross-validation. This is used to select the regularization parameters in the ridge regression, PLS and SVR and so it is a secondary CV.

   1. Separate Train into TestA and TrainA, the first fold of the 2-fold secondary cross-validation. Without loss of generality, assume TestA is R2 and TrainA is R3.

      • Fit the model (ridge regression, SVR or PLS) on the data in TrainA over a range of values for the regularization parameters and obtain β̂_A for each value of the regularization parameter. Note this is a vector of trial-by-trial parameter estimates.

      • Using β̂_A for each regularization parameter value along with the design matrix corresponding to the TestA data, estimate the predicted values of the BOLD time series data for TestA, Ŷ_TestA = X_TestA β̂_A and calculate the root mean square error prediction (RMSEP) for each regularization parameter, defined by

        $$\mathit{\text{RMSEP}}=\sqrt{\frac{1}{T}{\displaystyle \sum }{({\widehat{Y}}_{\mathit{\text{TestA}}}-Y_{\mathit{\text{TestA}}})}^2}.$$ (2)

   2. Switch the secondary test and training sets such that TrainB is R2 and TestB is R3 and repeat the previous step (2a) to obtain a second set of RMSEP values.

3. Average the RMSEP over A and B and use to choose the appropriate regularization parameter and with this parameter fit all three data sets: R1, R2 and R3. Note that the LS-S, LS-A, Add6, and Add46 approaches do not require a secondary CV step as they do not have regularization parameters to set. Similarly, Ridge(HKB) has a closed form estimation for the regularization parameter and does not require the secondary CV.

4. Primary cross-validation. Use the parameter estimates of the primary training data, β̂_R2 and β̂_R3 as well as the corresponding trial type labels to fit a logistic regression model.

   $$\text{log}(\text{odds of trial A})={\beta }_0+X_{{\mathit{\text{logit}}}_{\mathit{\text{Train}}}}\beta$$ (3)

   where X_logitTrain is the design matrix for the logistic regression, which is a column of the trial-by-trial estimates for R2 and R3 stacked, X_logitTrain = [β̂_R2, β̂_R3]′. Then using the trial-by-trial activation estimates of the primary test data, β̂_R1, test how well the parameter from the logistic regression predicts the trial types of Test. Specifically, the odds ratio estimate, Ô = exp^{β̂₁+X_logitTest β̂}, where X_logitTest is the vector of trial-by-trial activation estimates from R1 (β̂_R1), is used to obtain the predicted trial types (A or B), and estimate classification accuracy.

5. Repeat the above steps 1–4 two more times using the other 2 combinations of test/train data: Test1=R2/Train1=R1 and R3 as well as Test1=R3/Train1=R1 and R2.

The RMSEP selection criteria differed across ridge, PLS and SVR. The rules that were used were the following:

• Ridge: Where first derivative (RMSEP(i+1)-RMSEP(i)) is less than 0.001 or if this criteria was not met, the maximum λ was used. Possible values included λ values from 0 to 40 in increments of 0.5.

• PLS: Number of components that minimizes RMSEP. The possible number of components were integer values between 1 and 60, the total number of trials (or regressors) used in the simulations.

• SVR: epsilon and C that minimizes RMESP. Where ε ∈ {0.01, 0.1, 0.2, 0.3, 0.5, 0.8, 1} and C ∈ {0.1, 0.2, 0.5, 0.6, 1, 20}.