Probabilistic techniques for obtaining accurate patient counts in Clinical Data Warehouses

Abstract

Proposal and execution of clinical trials, computation of quality measures and discovery of correlation between medical phenomena are all applications where an accurate count of patients is needed. However, existing sources of this type of patient information, including Clinical Data Warehouses (CDW) may be incomplete or inaccurate. This research explores applying probabilistic techniques, supported by the MayBMS probabilistic database, to obtain accurate patient counts from a clinical data warehouse containing synthetic patient data.

We present a synthetic clinical data warehouse (CDW), and populate it with simulated data using a custom patient data generation engine. We then implement, evaluate and compare different techniques for obtaining patients counts.

We model billing as a test for the presence of a condition. We compute billing’s sensitivity and specificity both by conducting a “Simulated Expert Review” where a representative sample of records are reviewed and labeled by experts, and by obtaining the ground truth for every record.

We compute the posterior probability of a patient having a condition through a “Bayesian Chain”, using Bayes’ Theorem to calculate the probability of a patient having a condition after each visit. The second method is a “one-shot” approach that computes the probability of a patient having a condition based on whether the patient is ever billed for the condition

Our results demonstrate the utility of probabilistic approaches, which improve on the accuracy of raw counts. In particular, the simulated review paired with a single application of Bayes’ Theorem produces the best results, with an average error rate of 2.1% compared to 43.7% for the straightforward billing counts.

Overall, this research demonstrates that Bayesian probabilistic approaches improve patient counts on simulated patient populations. We believe that total patient counts based on billing data are one of the many possible applications of our Bayesian framework. Use of these probabilistic techniques will enable more accurate patient counts and better results for applications requiring this metric.

1. Introduction

Data quality is critical to modern research and clinical practice. Historically, “data quality” could refer simply to physicians having legible handwriting. In this day and age, clinical data is extensively used to compute quality measures, document physician performance, determine payments for meaningful use, discover interesting correlations between medical phenomena, and plan and perform clinical research. If the structured information in Electronic Health Records (EHRs) and Clinical Data Warehouses (CDWs) were 100% complete and accurate, performing these tasks would be straightforward.

Unfortunately, structured information is not complete, nor is it entirely accurate. One commonly used kind of structured information is billing data. Billing data is incomplete because other considerations beyond diagnosis go into invoicing. For example, it is fraudulent to bill patients for conditions they have but a practitioner doesn’t treat. UTHealth’s physicians practice in clinics and hospitals that are geographically close to UT MD Anderson Cancer Center (MDACC). Many UTHealth patients with cancer get their treatment at MDACC, which bills them for this service. These patients’ invoices therefore (legally and appropriately) do not list cancer as a diagnosis at UTHealth, rendering their condition invisible to searches that rely on billing data.

In modern clinical practice in the United States, all patients are routinely classified by ICD-9-CM condition in order to bill insurance companies or Medicare/Medicaid. Billing therefore became a convenient, de facto registry of disease and is now commonly used to find patients with certain conditions. In other words, in practice the question “which of our patients has breast cancer?” is often turned into “Who have we billed for breast cancer?” In essence, we are labeling the patient by assigning billing codes.

Administrative data has become more available due to the rise of the CDW. CDWs collect data from clinical systems such as Electronic Health Records and administrative databases and repurpose it for research, reporting, and study planning [1], [2]. Furthermore, EHRs and CDWs provide the additional benefits of providing large volumes of longitudinal patient information that is relatively easy to access [3].

As mentioned earlier, if the information in EHRs and CDWs is complete and accurate, performing the aforementioned tasks will be straightforward. However, patient labeling in electronic systems can be inaccurate. For example, UTHealth does not bill approximately 50% of patients who have or have had breast cancer for the condition. Further, 80% of patients with endometrial cancer at some point in their lives have not been billed for any related codes at UTHealth [4]. Related research has similar results: only 52% of patients with an ICD-9-CM code for Wegener’s Granulomatosis at St. Alexius Medical Center actually met the diagnostic criteria for the condition [5]. A strategy combining different ICD-9 codes yielded an 88% positive predictive value (PPV) for Lupus Nephritis cases at Brigham & Women’s Hospital in Boston. The authors do not mention how many cases their strategy misses, and their experimental design makes it impossible to compute how many are missed [6]. Many other studies show inaccuracies when counting patients [7–12]. These database counts are also used to draw conclusions; for example, the prevalence of myocardial infarctions for patients on rosiglitazone may be higher than for patients on other hypoglycemic medications [13].

Conversely, Hennessy et al. conducted a validation study to determine the positive predictive value (PPV) of the first listed diagnosis code for sudden cardiac death and ventricular arrhythmias. These researchers conducted record reviews and confirmed that the first diagnosis codes were highly predictive of these conditions [14]. Finally, Schneeweiss points out that data entered into EHRs is subject to physician and organizational bias, where factors contributing to a diagnosis and institutional practices regarding the number of diagnoses reported can impact the data recorded. In particular, Schneeweiss points out that “under-reporting of secondary diagnoses” is a known and common issue [3].

Terris, et al. discuss the sources of bias in data recording, including the impact of physician assessment of impact of findings on a patient’s primary presenting condition as well as the time and resources available to record detailed data. As expected, data most relevant to the primary condition were more likely to be recorded than were data pertinent to secondary conditions [15].

Measuring the quality of data is further complicated by the difficulty of obtaining a “gold standard” for comparison. The common approach is an expensive and time-consuming review by a professional coder. However, even this approach has been shown to be inconsistent, with one study showing a consensus level of 86% with the chief abstractor [16]. One well-controlled study introduced random errors at predefined rates into an existing database (which was considered the gold standard in this case). The significance of the errors on the final results, in particular with regard to low frequency events, was substantial [17].

Measurement error can be divided into two types: noise, and bias. Noise is the result of random fluctuations in the measurement process, recording, or retrieval. Bias is a systematic deviation of measurement from the true state of the world [18], [19]. The inaccuracies in patient counts cited earlier are the result of bias. In UTHealth’s example, they are largely due to the characteristics of its clinical and administrative workflow. In other words, we believe that in UTHealth’s case, they are a kind of bias [4]. This type of bias is also described by Schneeweiss [3]. Our insight is that biases in labeling can be measured and compensated. In this paper, we explore the use of probabilistic techniques to correct for biases in labeled data. We demonstrate our probabilistic approach on billing information, a common source of aggregate data for study planning, reporting, and quality measures.

Organizations such as the Observational Medical Outcomes Partnership (OMOP, http://omop.fnih.org) have focused on using observational data, including claims and EHR data, to detect drug-condition relationships. In addition, OMOP promotes the use of simulated data based on probability distributions of actual patient data. We follow a similar approach in our research. Actual clinical findings can only be inferred when applying these methods to actual clinical data.

As in the OMOP model, we chose to simulate the data warehouse environment with synthesized data, complete with introduced error rates. We implement it on top of a probabilistic model and probabilistic database management system.

2. Background

2.1 Probabilistic databases

Probabilistic databases are database management systems that facilitate handling of uncertainty in data. In particular, these databases are designed to perform probabilistic inference on very large data sets. Typically, these systems implement a “possible worlds” model, where each possibility is represented by a separate attribute, tuple, or set of tuples, each tagged with a probability or confidence level. Consistent with probability theory, the sum of all possible values must equal one. Query support is usually provided in the form of enhancements to the basic query language (usually SQL) for the database [20]. The benefits of probabilistic databases include the ability to provide the user with not only a single query answer, but also a stochastic result or level of confidence based on the underlying data. Another use is for imputing missing data values or extrapolating results stochastically [21]. These databases are applicable to many domains, especially where there is uncertainty regarding the underlying data. For example, a common application of probabilistic databases is in data warehouses built from heterogeneous sources where multiple values exist for a single attribute.

Example systems include Trio (http://infolab.stanford.edu/trio/), from Stanford University [22], the Monte Carlo Database System (MCDB) which stores distribution parameters instead of actual probabilities and provides stochastic prediction capabilities [23] and Cornell University’s MayBMS (http://maybms.sourceforge.net/). Probabilistic databases are an active research area in Computer Science, and new capabilities continue to be developed. For example, Kanahal et al. have added sensitivity analysis functionality to a system in order to help the user identify variables that have high impact on query output [24].

MayBMS extends the PostgreSQL open source database (http://www.postgresql.org) with probabilistic versions of conditional tables as well as commands to create, manipulate, and interrogate them [25]. MayBMS supports a “possible worlds” model, where each record in a conditional table is associated with a probability based on the likelihood of it occurring in one possible world [26].

Overall, probabilistic databases are a relatively immature technology, used predominantly in computer science research. To date, these databases have limited penetration into the field of healthcare. Chung and Hsaio discuss some potential applications of probabilistic databases to the medical field, including data consolidation from disparate sources into a common data warehouse. They present a straightforward model deriving probabilities from the frequency of values found in the source databases [27]. In Edelman et al., researchers used probabilistic linkage to compare and match burn data from five different databases in order to obtain an overall picture of burn injuries in the state of Utah. The researchers used specialized software to match data between sources and return results that had at least 90% confidence in the match [28]. While this particular application did not use a probabilistic database per se, the researchers used similar techniques to those supported by probabilistic databases to reduce over counting of injuries. Probabilistic data and claims databases are increasingly used to determine patient diagnoses.

2.2 Data Model

In order to model uncertainty in a probabilistic database, one must have a probabilistic model and a method for determining probabilities. Since the focus of this research was the probabilistic methods, we developed a lightweight model of patient data and the health care delivery process. In particular, our model represents a common encounter -billing approach and uses probability distributions to generate simulated patient and visit data.

Other patient and patient care models have been developed. OMOP provides an open source model of simulated patient data using first order Markov models to determine patient conditions and medications. Since one of OMOP’s key research goals is to study adverse drug events, more accurate modeling of conditions and associated medications is critical to that application [29].

Other efforts aim to model patient physiology and disease progression in more detail. Such models include Archimedes and Entelos. Archimedes focuses on patient physiology and disease progression [30] and Entelos on disease mechanisms, including patient characteristics [31]. To the best of our knowledge, no existing model describes an outpatient episodic care model such as the one we present here.

2.3 Bayes’ Theorem

Bayes’ Theorem is a central part of probability theory. It was communicated to the Royal Society of London in a letter describing an essay discovered by a Mr. Price among the possessions of Reverend Thomas Bayes after Rev. Bayes’ death [32]. In summary, Bayes’ Theorem describes the relationship between the probability of an event before and after acquiring information, also known as a conditional probability. The probability of an event before gaining information is called the prior probability. The probability of an event after gaining information is the posterior probability. A commonly accepted form of Bayes’ Theorem is presented in Equation 1 [33].

$$P(D|+)=\frac{p(D)\times p(+|D)}{p(D)\times p(+|D)+p(\neg D)\times p(+|\neg D)}$$ (1)

We base our probabilistic model on Bayesian models of clinical test performance. Bayesian models of test performance compute the conditional probability of a disease being present if a test is positive or negative. Tests such as lab tests, imaging studies, clinical diagnosis, and even billing can be evaluated against a gold standard to measure performance. Test performance is measured in sensitivity and specificity. Sensitivity is the probability that a known diseased patient has a positive test. Specificity is the true negative rate. Another commonly used term is the probability that a patient with a positive test will have a disease, the positive predictive value. These probabilities are valid only in populations where the disease prevalence is similar to the one in the gold standard population [34].

Given the prevalence, or prior probability of an event, and the sensitivity and specificity for a test, one can use Bayes’ Theorem to determine the revised, conditional, or posterior probability of an event. A common form of Bayes’ Theorem using these values to determine the probability of the disease (D) given the finding (F) is shown in Equation 2 [34], [33].

$$P(D|F)=\frac{\text{prevalence}\times \text{sensitivity}}{\text{prevalence}\times \text{sensitivity}+(1-\text{prevalence})\times (1-\text{specificity})}$$ (2)

In this project, we use Bayes’ Theorem to calculate the revised probability of the presence of a disease given the prior probability and the new information available, in this case, the presence or absence of billing data for the disease. Bayesian methods are traditionally used to impute missing data [35], and our research follows this approach.

Numerous probabilistic techniques, including Bayes’ Theorem, have been used to model the accrual of patients in clinical trials, with varying degrees of success [36]. In general, Bayes’ Theorem was found to be more reliable as increasing amounts of data were available to compute further posterior probabilities.

3. Methods

To model a typical patient data warehouse, we created a simple model of healthcare delivery.

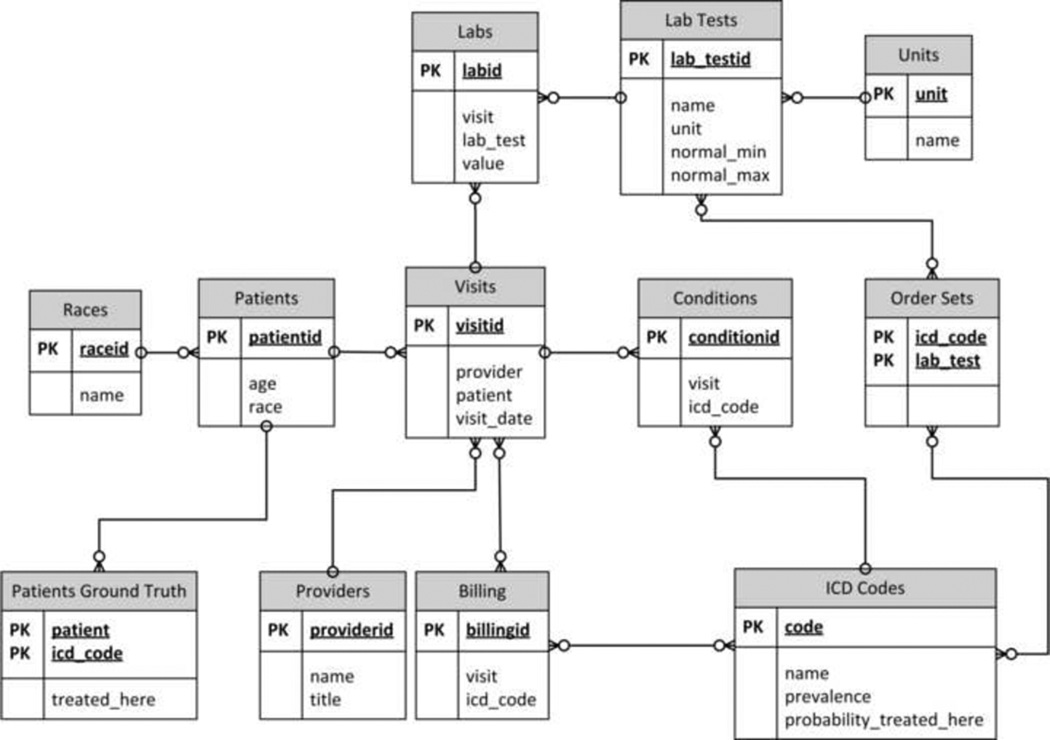
As seen in (FIGURE 1), this model contains patients, who have conditions (represented by ICD Codes) and who visit providers. These patients are sent for lab tests per predefined Order Sets and are billed based on provider diagnosis of conditions, which are designated with ICD codes. Lab tests have predefined ranges that are used to determine whether a test result is normal or abnormal. We also track the Patients’ Ground Truth so we know what condition(s) each patient actually has. The ground truth information is used only for accuracy determination and for simulating expert opinion.

Figure 1.

Entity-Relationship diagram

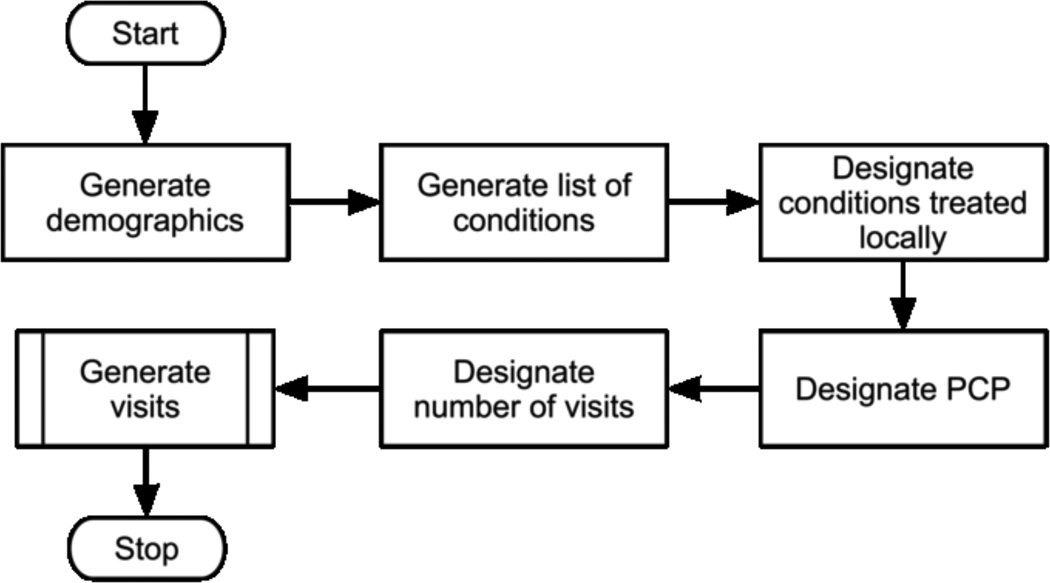
The underlying process for generating the simulated data is described in Figure 2.

Figure 2.

Patient generation workflow (PCP=Primary Care Provider)

3.1 Base Data

Each step illustrated in (FIGURE 2) is necessary to generate the synthetic data required by our analysis. Prior to running the data generation, we populate a number of tables with base data. These tables include: Races, Providers, ICD Codes, Lab Tests and Units. This data can be customized based on the desired characteristics of the synthetic data. For this simulation, we used five races, 10 providers, eight ICD Codes, 10 units, and 32 lab tests.

3.2 Simulated Data Generation

We generate one patient at a time. For each patient we assign an age and race. Next, we assign a number of conditions. This information is stored in the Patients Ground Truth table for evaluation of results. After this step, we assign the patient a primary care provider and determine the number of visits. For each visit, we decide if the PCP is available, and assign a different provider, if not.

Most of the process steps described in (FIGURE 2) are stochastic in nature. For example, initial demographic information including race and age are assigned based on random samples from normal and uniform distributions, respectively. Patient conditions are assigned from the list of predefined conditions in the database by selecting a uniform random number over the range [0, 1). If that number is smaller than the condition’s prevalence then a second random number is generated over the same range. If that second number is less than the “probability_treated_here” value, then we flag the condition as being treated “here”. Our model is simplistic in that each condition is independent of others, that is, having one condition does not make a patient more or less likely to have any other condition.

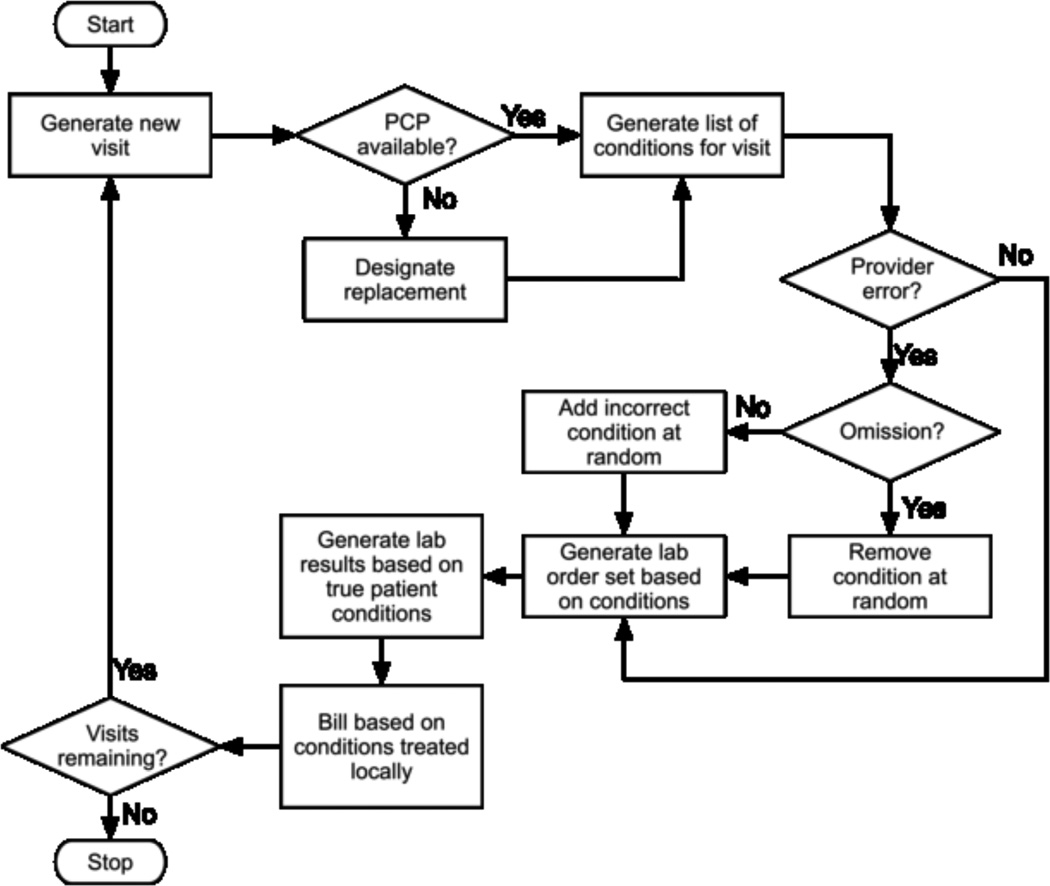
The number of visits is sampled from a Pareto distribution, which is a positively valued, highly left skewed distribution. The data for number of visits in the UTHealth CDW follow this distribution. For each visit, there is a chance that the patient’s PCP is unavailable, in which case an alternate provider is assigned. Since each provider has a likelihood of making a diagnostic error during a visit, changing providers has the potential to impact the diagnostic accuracy of a visit. We then sample a uniform distribution to determine whether or not the provider misses one of the patient’s conditions or if a new condition is added to the problem list for a particular visit.

For each visit, labs are generated based on the predefined Order Sets for each condition the patient has. Extra labs are added at random with a predefined probability and corresponding lab values are assigned.

We generate billing data based on the patient conditions diagnosed and “treated” by the provider. No new errors are introduced into the billing process. Consequently, all billing errors in our model are due to downstream effects of earlier errors, including provider misdiagnosis.

One of the unique characteristics of our model is the use of the “probability treated here” value. As previously mentioned, UTHealth provides clinical services in the greater Houston area. However, UTHealth is located in the same medical center as the University of Texas MD Anderson Cancer Center. Consequently, many of the UTHealth patients with cancer obtain specialty care at MD Anderson. As a result, we have found that billing records of whether or not a patient has cancer do not reflect clinical reality as often as desired [4], since we do not typically treat patients for that condition. As legally required, we do not bill patients for conditions we do not treat. Although this specific situation is somewhat unique to UTHealth, similar distribution skewing conditions happen at other clinical institutions.

We generate additional data in the Generate Visits step(FIGURE 2), at which time additional errors may occur, as shown in Fig. 3. We reviewed the literature and found that error rates vary widely throughout the care process. For example, Nahm describes single entry error rates between 4 and 650 per 10,000 data fields [37]. Diagnostic accuracy also varies. Montnémery reports 76.5% of asthma cases were properly diagnosed during the first visit in Sweden [38] and physician ability to accurately assess the category of rheumatoid arthritis activity varied between 31% and 88% depending on the disease progression class [39]. We conservatively assume that each provider has a different error rate chosen at random between 0 and 2%. This error rate is the probability that the provider commits an error of either omitting an existing condition or diagnosing a nonexistent condition on each visit.

Figure 3.

Visit generation workflow (simplified)

Furthermore, we consider all conditions to be chronic. The presence or absence of a condition is constant throughout the simulation. This assumption is made in order to make the analysis more interesting and relevant by providing an on-going opportunity for diagnosis or misdiagnosis. It is also realistic, as nearly half of all Americans are estimated to have one or more chronic condition by 2004 [40].

3.3 Database Specifics

The patient database generator is written in Python and is parameterized for: number of patients; distribution of visits per patient; and availability of provider. The data generator is available at http://github.com/drh-uth/DataFakehouse.

The database was created in MayBMS version 2.1-beta, which extends the functionality of the PostgreSQL 8.3.3 database. For this research, we created a database of 10,000 patients.

The prevalence of each condition, and the rate at which the institution bills for each condition, are presented in Table 1

Table 1.

Prevalence and probability of treatment for the simulated conditions

Condition	Prevalence	Probability of being treated at the simulated institution
1	30%	90%
2	1%	10%
3	20%	1%
4	60%	70%
5	15%	95%
6	30%	50%
7	10%	30%
8	45%	95%

3.4 Patient Counts

The goal of this research was to evaluate the accuracy of different methods of counting patients in a clinical data warehouse. We analyzed six different approaches to computing these patient counts. These techniques are summarized in Table 2.

Table 2.

Patient count approaches

Approach	Number of Records examined	Source of truth
Actual Count	All	Ground Truth
Count of Billing (C-B)	All	None
Omniscient One Shot (O-OS)	All	Ground Truth
Omniscient Bayesian Chain (O-CH)	All	Ground Truth
Review One Shot (R-OS)	Sample	Simulated Expert Review
Review Bayesian Chain (R-CH)	Sample	Simulated Expert Review

We use two straightforward methods for computing patient counts: Actual Count, which examines the ground truth table and counts the number of patients with the specified condition, and Count of Billing, which returns the number of unique patients with a condition from the billing table.

For the remaining methods, we treat billing like a diagnostic test, having both sensitivity and specificity. We use two methods of computing sensitivity and specificity - the “Omniscient” method, in which we use the ground truth to determine true positive, false positive, true negative and false negative values and the “Simulated Expert Review” approach. The latter approach is more realistic in that it emulates current practices where a representative sample of records are reviewed and labeled by experts. The error rates discovered in the sample are used to extrapolate values for the rest of the data. We use the ground truth to simulate the behavior of the expert chart reviewers.

In addition to these two approaches, we use two methods of computing the posterior probability of a patient having a condition. One technique is a “Bayesian Chain”, where Bayes’ Theorem is used to calculate the posterior probability of each patient having each condition. In this technique we compute a revised probability of the condition after each visit, using the posterior probability of the condition from the previous visit as the prior probability for the subsequent visit. The initial value of the prior probability used in this approach is the overall prevalence of the condition in the general population. Bayes’ Theorem is applied iteratively for each patient after each billing cycle. The calculations for posterior probabilities are shown in Equation 2 and the “Bayesian Chain” equations are stated in Equation 3. In the chaining equations, the initial probability (time = 0) is set to be the condition prevalence. At each iteration, the next, or “chained”, probability (time = t+1) is based on the probability at time t and the sensitivity and specificity of the condition being billed given the presence or absence of the condition.

$$\begin{array}{c}P{(D|\text{Billing})}_0=\text{Prevalence}(D)\hfill \\ P{(D|\text{Billing})}_{t+1}=\frac{P{(D|\text{Billing})}_t\times \text{sensitivity}}{P{(D|\text{Billing})}_t\times \text{sensitivity}+(1-P{(D|\text{Billing})}_t)\times (1-\text{specificity})}\hfill \end{array}$$ (3)

A second “One-shot Bayesian” approach computes the probability of a patient having a condition based on whether or not the patient is ever billed for the condition. To compute this probability, we use a single application of Bayes’ Theorem. This approach is based on Liao’s use of billing codes from electronic medical records to discover patients with rheumatoid arthritis [8].

In order to compute the posterior probability that a patient has a condition using Bayes’ Theorem, sensitivity and specificity values are required. To compute these values we create a table that contains every condition billed, the associated visit, patient and ICD code status (absent or present) and populate it with the data from the model. Four key values are needed to compute these values: billed (absent or present) and patient condition (absent or present). These values correspond to True Positive (TP), False Positive (FP), True Negative (TN) and False Negative (FN), as shown in Table 3.

Table 3.

Contingency table for billing / condition pairs.

Billed for	Condition Present	Condition Absent	Total
Yes	TP	FP	TP+FP
No	FN	TN	FN+TN
Total	TP+FN	FP+TN

TP = True Positive, FP = False Positive, TN = True Negative, FN = False Negative

For the Simulated Review approach we imitate an expert reading through and labeling a small subset of the records in the data warehouse. We select a random sample of 500 records. For each of these records, our simulated experts determine the set of conditions a patient has, regardless of billing. We implement the simulated review by sampling records and looking up the patient’s corresponding entries in the Patients Ground Truth table. True Positive, False Positive, True Negative, and False Negative are computed by comparing the expert opinion to the recorded billing data. In other words, the True Positive rate is the percentage of the 500 sample records that are correctly labeled as the patient having the condition.

For the Omniscient approaches, we do not use a random sample. Instead, we examine every single patient in the entire data warehouse. We thus compare the ground truth to the billed conditions for the entire data warehouse.

The familiar format for a contingency table is shown in Table 3.

Once the contingency tables are populated, sensitivity and specificity for each condition-billing pair are computed, using the formulas in Equations 4 and 5.

$$\text{Sensitivity}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}$$ (4)

$$\text{Specificity}=\frac{\mathit{\text{TN}}}{\mathit{\text{TN}}+\mathit{\text{FP}}}$$ (5)

Finally, we use Bayes’ Theorem (Equation 3) to calculate the posterior probability of each patient having each condition.

For each probabilistic method, we create a probabilistic table to hold possible rows in MayBMS with all possible combinations of conditions for each patient and their probabilities (computed as the product of the probabilities of each condition, given their independence). The table is instantiated using the MayBMS repair key command over the patient field (Figure 4), telling MayBMS that only one patient and combination of conditions really existed. An expected count is obtained using the MayBMS ecount () function. We evaluate the quality of this count by subtracting it from the actual count, as determined by the ground truth, and normalizing it to obtain the error rate for each condition (Equation 6). The error rate is also averaged across all conditions in the database to obtain an average error rate for each technique.

Figure 4.

Example MayBMS code to create a probabilistic table. patients contains all patients in the data warehouse; possible_condition_combinations is a view (not shown) that contains all combinations of all existing conditions a patient might have (i.e. disease 1; disease 2; disease 1 and disease 2, and so on); probability_per_combination is a stored procedure that computes the frequency of each combination in the database (not shown).

The repair key patientid MayBMS statement implies that only one row per patientid exists.

$$\text{Error}=\frac{\mathit{\text{abs}}(\text{predicted count}-\text{actual count})}{\text{actual count}}$$ (6)

We obtain the predicted counts for each method as follows:

Count of Billing

We add all patients who were billed, at least once, for each condition (Figure 5).

Figure 5.

SQL code to count patients billed by condition

Review-One Shot

We perform a simulated review of 500 cases, and compute the sensitivity and specificity of the billing for each condition as described. For each patient, we compute the conditional probability of the patient having the condition given that he or she was billed or not, and obtain the total expected count.

Review-Chaining

We use the same simulated review of 500 cases. For each visit, we compute the probability of the patient having each condition given that he or she was billed (or not) for the condition in that visit. This probability becomes the prior probability for the patient’next visit (Equation 3).

Omniscient methods

We perform the same procedure as above, but review all 10,000 patients in the simulated warehouse.

4. Results

The results are reported as error rates for all eight conditions in the simulation for each counting technique when compared to the ground truth.

5. Discussion

We present two key findings in this paper: a model for generating simulated patient data and a probabilistic method for mining patient data to obtain accurate counts of patients with specified conditions.

5.1 Model

Our data model is simple, but very powerful and appropriate to this application. For example, we assume a normal distribution of ages across patients. We also treat each condition independently. While this approach is not representative of reality in most populations, our focus is on comparison of results from each counting technique. The techniques we present should work equally well using a more complex data generation model.

In the end, we did not use all of the different dimensions of our data model. For example, we did not use race, age or even lab test information in our analysis. Further, the probabilities assigned to many of our model parameters, are not based on hard evidence based research, but were assigned based on clinical experience and rules of thumb. Our goal in this project was not to perfectly model clinical care, but to provide a parameterized model that produces probabilistic data for analysis. Certainly, more parameters could be added and other values adjusted to better model certain populations.

Some key strengths of our model are that it is parameterized and customizable, so the data generated can be easily adjusted to represent a particular patient population. Another benefit is that synthetic data, such as produced by our model, is not subject to privacy rules, allowing researchers to focus on analysis techniques and enabling them to share their data warehouses easily. Simulated data allows rapid prototyping and research turnaround without the added complexities of accessing actual patient data.

A driving force in this research is whether or not a patient is billed for a condition. In reality, patients may have chronic conditions that are not recorded in the patient’s record if the condition is not treated at a facility. A classic example of this is a patient who has cancer (analogous to a chronic condition for this research) and is being seen at a tertiary treatment center for care, but is seeing a primary care physician for diabetes management. In this case, the billing code for diabetes would be entered at the primary care center, but not the cancer condition.

5.2 Model extensions

Our model could be easily extended to meet diverse research needs. One example is that our model allows us to specify a title for each provider. The level of title specified (e.g. RN, MD) could be used to influence the diagnoses reached. For example, some conditions might require diagnosis by a higher-level provider. If that provider is unavailable during a visit, that diagnosis would not be assigned. Visit dates are also assigned in our model. For this exercise, we did not rely on any particular frequency or gap between visits for our analysis. Another logical next step for the model is to allow conditions to develop and to be cured and to eliminate the assumption that conditions are independent.

5.3 Methods

The approach we present in this paper has two interesting dimensions. The first is the decision-theoretical approach to obtaining highly accurate patient counts. We modeled billing as a test for the presence of a condition and computed its sensitivity and specificity. We then applied these measures of the quality of billing as a test to compute the posterior probability of a patient actually having a condition. The second is the application of a probabilistic database engine such as MayBMS to clinical data mining.

An important strength of our approach is that the Bayesian model we present does not require a probabilistic database management system. It is possible to implement a similar technique in any database management system by adding fields to keep track of the probability of conditions. MayBMS simply provides a convenient infrastructure to make such computations easy. MayBMS also has the distinct advantage of being based on a popular database engine, PostgreSQL, which is widely used and well-documented. We used two key extensions: repair key, which weights the available record options based on the provided probabilities, and ecount, which provides the expected count of the values. Once understood, these extensions are simple to apply to the model.

5.4 Results

Patient counts based on billing data are lower than the counts produced by the Bayesian approaches. The average error rate for billing-based counts is 43.7%, while the one-shot techniques have error rates as low as 2.1%. As Table 4 clearly shows, the variability of patient counts between conditions was also large, especially for the less accurate techniques. Conditions that are severely undercounted when using billing data (for example, condition 3) have manageable error rates when using one-shot Bayesian approaches. Conditions that are accurately counted via billing, such as condition 5, may not require the application of Bayesian techniques at all.

Table 4.

Error rates on patient counts by approach

Cond.	C-B	O-CH	O-OS	R-CH	R-OS
1	8.7%	7.2%	3.6%	5.4%	0.4%
2	89.8%	10.6%	4.2%	100.0%	1.8%
3	99.0%	1.9%	0.9%	100.0%	1.7%
4	29.9%	12.6%	0.3%	11.7%	1.4%
5	1.0%	3.4%	0.7%	1.8%	3.6%
6	49.4%	20.2%	1.2%	50.6%	1.3%
7	67.7%	28.4%	6.5%	13.2%	5.3%
8	4.4%	1.6%	2.5%	3.5%	1.3%
Avg. error	43.7%	10.7%	2.5%	35.8%	2.1%
Std. dev.	38.8%	9.5%	2.2%	42.6%	1.6%

In the above table, Count of Billing is the non-probabilistic count of patients who were billed for the condition. O-CH=Omniscient-chaining, O-OS=Omniscient-One shot, R-CH= Review-chaining, and R-OS=Review-One shot.

An interesting finding was the poor performance of the “Bayesian Chain” approach. Bayesian chaining has the theoretical advantage of taking into account additional data over time, which has been shown by Barnard to be a more accurate prediction method when data continues to present [41]. This is a reasonable approach, as most organizations have long term billing data for patients. However, in practice, it is subject to higher error rates. We attribute the higher error rates to the different weights given to a positive bill and a negative bill in the “one-shot” approach. In the “one-shot” approaches we implicitly consider the presence of a single bill for a condition stronger evidence than any number of bills without the condition. This preferential treatment of positive bills is an artifact of the nature of the billing process and regulatory framework in place in the U.S. healthcare system, as patients are far more likely to be NOT billed for a condition they DO have than to be billed for a condition they DO NOT have.

Some limitations of this project are the use of a simulated patient population, arbitrary error rates, the assumption that all conditions are chronic, and our simple probabilistic model that assumes conditions are independent of each other. The chronic condition assumption allows us to evaluate recurring diagnoses over time. While the model reflects some aspects of the clinical reality of the UTHealth population [4], the behavior of the review-based Bayesian approach on a real patient population is still unknown. Error rates affect our results quantitatively, i.e. our numerical results should not be taken as generalizable to any actual patient population, but this does not affect the validity of the technique we demonstrate. In the future, we will expand this research to evaluate Bayesian approaches on more sophisticated population models and, eventually, real clinical data warehouses.

We acknowledge that our assumption of independence between conditions may be controversial. However, we believe that it reflects a user query model that we encounter repeatedly in CDW operation, namely, that researchers preparing a grant application or planning a study desire to obtain a count of patients billed for certain specific ICD-9-CM codes. In this common scenario, the researcher assumes that the billing data accurately represents all patients with that condition. This is the situation we attempt to model; we recognize that a more sophisticated model that leverages known relationships between conditions may be more accurate at finding specific patients correctly. Our model allows us to quickly correct aggregate patient counts without constructing disease-specific dependency models. Other models, such as OMOP’s OSIM2, may be more appropriate for tasks such as discovering drug-condition relationships.

6. Conclusions

Bayesian probabilistic approaches improve patient counts on simulated patient populations. In particular, the approach we present in this paper will improve clinical study feasibility analysis and planning. The one-shot review approach proved to be accurate and will be the simplest and cheapest to implement in actual practice.

The patient database generator proved to be a useful tool for this research. The database structure we designed clearly met the data generation needs for this project. It allowed us to easily produce a non-uniform patient database. The synthetic database has the obvious benefits of not requiring IRB approval or HIPAA compliance. In addition, having the known ground truth for the patient data allows researchers to trivially validate experimental results.

Finally, total patient counts based on billing data are one of the many possible applications of our Bayesian framework. The broader problem of compensating for bias in other kinds of patient labels is susceptible to a similar approach and will be the focus of our future research.