Design considerations for using PET as a response measure in single- and multi-center clinical trials

Abstract

Rationale and Objectives

PET is used to evaluate response to therapy with increasing interest in having PET provide endpoints for clinical trials. Here we demonstrate impacts of PET measurement error and choice of quantification method on clinical trial design.

Materials and Methods

Sample size was calculated for two-arm randomized trials with percent change in ¹⁸F-fluorodeoxyglucose (FDG) PET uptake as an efficacy endpoint. Two methods of uptake quantification were considered: SUVs and kinetic measures from dynamic imaging. Calculations assumed a 20 percentage point difference in treatment groups' average percent change, and yielded 80% power at α=0.05. The range of precision (10% to 40%) in PET uptake measures was based on review of the literature. The range of SUV sensitivities (50% to 100%) relative to kinetic analyses was based on a study of 75 locally advanced breast cancer patients.

Results

Sample sizes increased from 8 to 126 as PET precision worsened from 10% to 40% at full measurement sensitivity to true change. In a subgroup with low initial FDG uptake, a sample size of 126 was required under 20% standard deviation using clinical SUVs. More sophisticated imaging quantification could reduce this sample size to 32.

Conclusions

The dependence of sample size on measurement precision and the sensitivity of imaging measures to true change should be considered in single- and multi-center PET trials to avoid underpowered studies with inconclusive results. Sophisticated PET imaging methods that are more sensitive to changes in uptake may be advantageous in early studies with limited patient numbers.

Introduction

Multi-center trials are the gold standard for establishing new standards for clinical practice in oncology. There is increasing interest in using Positron Emission Tomography (PET) measures to evaluate response to therapy and provide early and robust endpoints for these clinical trials (1, 2). Early response endpoints from functional imaging modalities such as PET versus anatomical radiographic measures (3) could allow trial patients to more quickly crossover to an expanding number of salvage therapies following progression. Standardization to reduce measurement error has been suggested to address some known challenges in application of PET in clinical trials (2, 4–6); however, the combined impact of these standards on clinical trial design has not been evaluated. There has also been relatively little study of the impact of the choice of PET image methodology and analysis on study design, especially sample size or study power estimation.

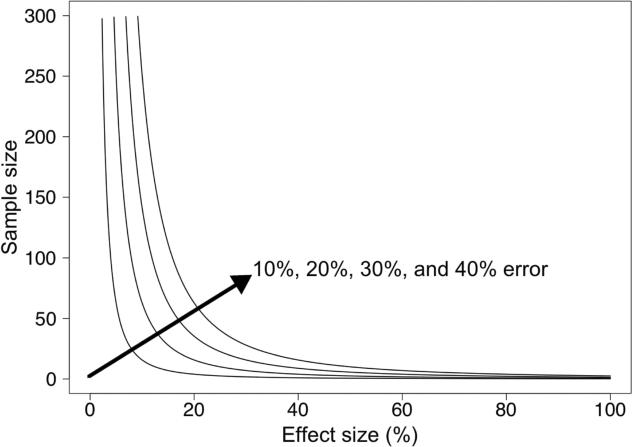
Sample size estimation is an important aspect of study design since it is typically a key driver of trial costs and study duration, especially when patient accrual rates are limited. Sample size requirements are impacted by selected power, significance level, effect size, and measurement error as discussed below. Additional design features such as different classification schemes for response (e.g. EORTC (4) or PERCIST (2)), group randomization, stratification, or expected attrition may also impact sample size, but these aspects were beyond the scope of this study. An example plot of sample size versus effect size in Figure 1 shows the impacts of measurement error and expected effect size on sample size. The required sample size of a study will increase with an increase in measurement error or with a decrease in expected effect size (e.g. selecting a 20% response threshold (7) versus 30% in PERCIST (2), compared to no change on average in a control group) or with a decrease in ability to measure the entire range of change associated with the effect size.

Figure 1.

Impact of measurement error and effect size on required sample sizes from the two-sample t-test (80% power, Type I error rate (α) = 0.05).

Our overall goal in this analysis was to explore the impacts of precision and sensitivity of change in PET measures of uptake on clinical trial design. Here we use reported PET uptake measurement errors from the literature and observed relative sensitivity of static standard uptake value (SUV) versus dynamic flux (Ki) measures observed in breast cancer response to chemotherapy to evaluate the degree to which PET measurement error and sensitivity of analysis method to change may impact clinical trial design. This concept paper is an initial evaluation to illustrate the influence of imaging measure variance and the impact of relative sensitivity of different imaging analysis methods on calculations of trial sample size and power.

Materials and Methods

Trial design and trial parameters

To demonstrate the impact of PET measure sensitivity and variance in clinical trial design, we explore a hypothetical clinical trial comparing two different treatments, in which the average percent change in ¹⁸F-fluorodeoxyglucose (FDG) uptake over the course of therapy is used as a measure of response. The hypothesis is that the average percent change in FDG uptake pre- and post-therapy will differ between the two groups as an indication of relative efficacy. Prior studies have shown that the change in FDG uptake over the course of cancer treatment is an indicator of the quality of response to therapy (8). For example, several studies have shown a significantly larger average decline in breast cancer uptake with therapy for patients who have complete versus partial responses (9, 10). We therefore hypothesized that the change in FDG uptake with therapy could potentially provide an indication of comparative efficacy of two different treatments. The primary PET imaging measure of response in this case is the percentage change in uptake, which is defined as the result of subtracting the first PET measure from second measure, divided by the first measure and multiplied by 100. Differences in therapy-induced declines in FDG uptake can be compared using a two-sample t-test, as has been done in a number of prior studies (10, 11). Based on our experience in studies of locally advanced breast cancer and other malignancies, it is reasonable to assume the percentage change in FDG uptake will be normally distributed as required by the two-sample t-test.

We calculated sample size for a two-arm study to detect a significant difference in the percent change in FDG uptake, assuming a true difference of 20 percentage points in average FDG percent change between the two treatment groups. Our hypothesized effect size of 0.20 is feasible to occur under two types of scenarios: a modestly effective treatment (20% average decline in FDG uptake after a short time period) compared to a treatment with no effect on uptake, or a highly effective treatment with 50% average decline compared to a modestly effective treatment with 30% average decline. The selection of 20% as a meaningful difference between average FDG percent change is based on the Weber et al. minimum for true change in tumor glucose metabolism (7), and the average of the 15% and 25% changes recommended for a partial FDG metabolic response in the 1999 EORTC guidelines (4). The sample size required depends upon significance level, power, effect size, and response variance. The estimated total sample size (n) based on the two-sample t-test is given by:

$$\mathrm{n}=\frac{4\cdot {(Z_{\alpha }+Z_{\beta })}^2\cdot {\sigma }^2}{{\Delta }^2}$$

The traditional sample size formula based on the two-sample t-test has a “2” in the numerator and calculates only the number of patients required in one arm. Our sample size equation has a “4” in the numerator to calculate the total sample size required for both arms of the study. The significance level (α, also called the false positive or Type I error rate) is the acceptable probability of incorrectly rejecting the null hypothesis (declaring a treatment group difference exists when in fact it does not). The power (1-β, or probability of not committing a Type II error) is the probability of finding a treatment group difference under the condition of a specific effect size. The effect size (Δ) is the expected treatment group difference, and the response variance (σ²) is the common variance of the response variable in the two groups. Z_α is the standard normal distribution critical value for a two-sided test of size α, and Z_β is the critical value for power of 1-β. Common parameters for randomized Phase II trials are an α of 0.05 and 80% power, which correspond to Z_α=1.96 and Z_β = 0.84. Under the null hypothesis, the treatments will have equal average change in FDG uptake and Δ = 0. An estimate of variance (σ²) can be determined from review of the literature or may require additional early phase imaging trials.

Measurement error parameters

Similar standard deviation across all imaging sites and for change measures in the two treatment groups (same σ² for both groups) was a simplifying assumption. A minimum measurement error of around 10 percentage points for change between serial scans of patients is expected based on literature under ideal conditions (same scanner for all scans, short time between scans, uniform patient preparation, image generation, and image analysis) (7, 12–15). To measure the PET error due only to instrumentation, researchers have scanned phantoms with known activity concentrations. Error levels are below 10% for phantom studies performed under similar ideal conditions, with PET measure coefficients of variation ranging from 2.5% to 9.8% (depending on image reconstruction parameters) from twenty repeat scans on one scanner of a nonuniform NEMA NU-2 Image Quality phantom with a nine-month half-life (16). However, other recent studies using a common phantom with long-lived isotopes at multiple centers found a coefficient of variation range of 8% to 18% for SUV measurements of hot cylindrical features from all sites when performed by the same reviewer (central analysis), where the coefficient of variation range for the same scans was 30% to 43% when using local site-based SUV measures (17). Long-term variability of PET measures due in part to calibration drift may add an additional 4% measurement error to single- and multi-center site studies where months occur between serial scans (18). Takahashi and colleagues (19) found up to 46% measurement error in SUV across separate scanners. The 95% repeatability coefficients ranged from −34% to 52% when local site-based SUVs were analyzed for SUV measurements from repeat FDG PET scans of 62 patients in a multi-center phase I trial, although the range decreased to −28% to 40% after applying quality assurance to initial results (20). Based on these previous studies we approximate that percent change measures with little measurement error will have a standard deviation of 10 percentage points, and that increased measurement error could result in a standard deviation for percent change of up to 40 percentage points. Figure 1 shows the impact of this measurement error range on sample sizes.

Sensitivity of different methods of PET image analysis to underlying true change

In addition to understanding the error in PET measures, designers of imaging trials need to understand the impact of the choice of analysis method on the sensitivity of the PET estimate to any true changes in the studied biologic function(s). Different quantification methods for image analysis have differing sensitivity to any changes in the underlying biochemistry, physiology, and receptor binding. Our scenarios described below employ the most commonly used PET tracer in clinical practice, ¹⁸F-fluorodeoxyglucose (FDG), which traces the movement of glucose from blood into cells where FDG is trapped following the first step in glycolysis. The most common measure of FDG uptake, the SUV, is based upon a single static measurement. However, simple static uptake measures like the SUV are not able to separate metabolized (phosphorylated) FDG from unmetabolized background FDG, leading to a non-zero uptake measure, even in the absence of active glucose metabolism. In contrast, dynamic PET scans that undergo a full kinetic analysis can compute a metabolic rate of FDG and separate the contribution of metabolized (phosphorylated) FDG from background of non-phosphorylated FDG (21, 22). For lesions with high FDG uptake, the SUV appears to be a reasonable surrogate for PET measures derived from kinetic analysis. However, for lesions with lower initial uptake, SUV has been reported to have reduced sensitivity for detecting true change due to the contribution to SUV from the background of non-phosphorylated FDG in locally advanced breast cancer (23, 24). Reduced FDG SUV sensitivity is also suggested for locally advanced pancreatic cancer by results in Table 1 of Choi et al. where the 57% range of serial percentage change in SUV is much lower than the 204% range of change for flux (Patlak Ki) from kinetic analysis (25). The previous report of similar measurement error for both the percentage change in SUV and Ki (standard deviation equaled 9% and 8%, respectively) (7) indicates the relative difference in measurement sensitivity can be attributed to a difference in which distributions of FDG tracer were quantified and not simply due to a difference in the reproducibility of the quantitation methods. Reduced SUV sensitivity may impact clinical trial design by reducing the observed effect size, requiring a greater sample size to ensure adequate power for detecting true effects.

Table 1.

Selected sample size calculations for randomized trial to detect a true effect of 20% difference in average percent FDG uptake change between two treatments (80% power, Type I error rate (α) = 0.05).

		Sample Size
Trial Scenario	σ *	1st tertile SUVbaseline≤3 50% sens.†	2nd tertile 3≤SUVbaseline≤5.2 70% sens.†	3rd tertile SUVbaseline≤5.2 90% sens.†	kinetic modeling 100% sens.†
Single site	10%	32	17	10	8
Multi-center (good calibration)	20%	126	65	39	32
Multi-center (poor calibration)	40%	503	257	156	126

^*Standard deviation of percent FDG uptake change, with larger values attributable to greater measurement error

^†Sensitivity to a true effect size of 20 percentage point difference FDG uptake change

To estimate sensitivity of percent change in SUV compared to FDG flux (Ki), from kinetic modeling, we analyzed data from 75 patients undergoing FDG PET scanning prior to and midway through neoadjuvant chemotherapy to treat locally advanced breast cancer (26). In this study we report body weight normalized SUVs as unitless values based on the assumption of an average tissue density of 1 g/mL. We fit a linear regression model of the association between percent change as measured by SUV and percent change as measured by flux. Separate slope and intercept terms were fitted for three tertiles based on initial SUV, which correspond to low (SUV ≤ 3), medium (3 ≤ SUV ≤ 5.2), and high (SUV > 5.2). The absolute value of the fitted intercept is the percent decline in SUV that corresponds to a 100% decline in flux: if SUV and flux estimates of percent change are identical other than measurement sensitivity, then the intercept will be −100% and the slope will be 1 (identity). These absolute values of intercepts are the “SUV sensitivity” to true change and can be used to adjust the effect size in sample size calculations. For example, if SUV sensitivity to true change is 80%, and the average percent reductions in flux are 50% and 70% for the two treatment groups, the effect size for flux from kinetic analysis will be (0.70 − 0.50) = 20%, while the effect size for SUV is estimated as (0.80•(0.70 − 0.50)) = 16%. Computations and plotting were conducted using a combination of R version 2.11.1 (R Foundation for Statistical Computing, Vienna, Austria) and Excel (Microsoft). In this investigation of the impact of image analysis method on required sample size, we considered reduced sensitivity to change for static measures (SUV) versus kinetic analysis of dynamic PET scans determined by the reported additional analysis of a recent study (26), which obtained written informed consent from all participants in an Institutional Review Board approved study.

Results

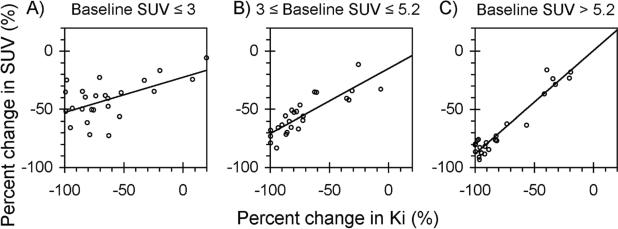
The estimated difference in static FDG SUV versus dynamic flux (Ki) sensitivity to response of locally advanced breast cancer to chemotherapy, based upon the Dunnwald et al. data (26) is shown in Figure 2. The three panels correspond to three tertiles defined by the baseline (pre-chemotherapy) SUV. For the two tertiles with higher initial SUV (Figures 2B and 2C), static and kinetic measurements are well-correlated: as kinetic measures approach 100% decrease in FDG uptake, static measures do as well. For the tertile with lowest initial SUV, the static and dynamic measures are still correlated, but the static measures do not appear as sensitive to change. Fitted linear regression models for the three tertiles estimate the SUV sensitivity to true 100% change in FDG flux (Ki) as 71% to 88% for higher initial SUV, but only 52% for initial SUV of 3 or lower as shown in Figure 2. Based upon this result, sensitivity values of 50%, 70%, and 90% were examined for percentage change measured by SUV for trial design calculations.

Figure 2.

SUV sensitivity to change in FDG uptake measured by FDG flux (Ki) in a cohort of 75 locally advanced breast cancer patients undergoing neoadjuvant chemotherapy, by tertiles of baseline SUV. For a change in Ki of −100%, (A) the predicted percent change in SUV is −52% for the first tertile (baseline SUV ≤ 3), (B) −71% for the second tertile (3 ≤ baseline SUV ≤ 5.2), and (C) −88% for the third tertile (baseline SUV > 5.2).

Figure 3 is a contour plot showing the impact of PET measurement error and SUV sensitivity to true change for planning a two-arm study to detect a 20 percentage point difference in percent change in FDG uptake between two treatments, and Table 1 shows selected values from the contour plot. Both Figure 3 and Table 1 show the impact of measurement error on required sample size increases with decreases in the detectable effect size. The plot and table demonstrate the importance of being able to estimate the sensitivity of an imaging measure to the expected true effect change in a trial's patient cohort in order to avoid calculating too small of a sample size and consequently underpower the study. Table 2 examines the impact of measurement error and sensitivity to true change in terms of power for a given sample size (rather than sample size for a given power, as in Table 1). Required sample sizes to achieve 80% power increased from 8 to 126 as PET precision worsened from 10% to 40% at full sensitivity to true change (right side of Figure 3, where true effect size is 20% and sensitivity is 100%). One of the more challenging scenarios was for a patient population whose tumors had low initial FDG uptake (SUV ≤ 3). For a 20% level of uptake measurement error, a sample size of 126 would be required to detect a true 20 percentage point difference in change in SUV (left side of plot, 50% sensitivity of SUV to change in metabolic rate). Kinetic analysis of dynamic PET images (assuming 100% sensitivity to change in metabolic rate) would require a sample size of only 32 for the same patient population.

Figure 3.

Impact of SUV sensitivity (sens) to measurement error and true effect size of 20% on required sample sizes from two-sample t-tests, with vertical lines corresponding to SUV sensitivity of tertiles for baseline SUV in a cohort of 75 locally advanced breast cancer patients undergoing neoadjuvant chemotherapy (80% power, Type I error rate (α) = 0.05).

Table 2.

Selected power calculations for randomized trial to detect a true effect of 20% difference in average percent FDG uptake change between two treatments (80% power, Type I error rate (α) = 0.05).

		Power
Trial Scenario	N	1st tertile SUVbaseline≤3 50% sens.*	2nd tertile 3≤SUVbaseline≤5.2 70% sens.*	3rd tertile SUVbaseline>5.2 90% sens.*	kinetic modeling 100% sens.*
Single site, σ† =10%	20	61%	88%	98%	99%
	30	78%	97%	99%	99%
Multi-center, σ† =20%	50	42%	70%	89%	94%
	100	71%	94%	99%	99%
Muiti-center, σ† =40%	100	24%	42%	61%	71%
	300	58%	86%	97%	99%

^*Sensitivity to a true effect size of 20 percentage point difference in FDG uptake change

^†Standard deviation of percent FDG uptake change, with larger values attributable to greater measurement error

Discussion

This study used quantitative results from a variety of PET research studies as input parameters to provide an early example of how such analyses can be used to inform potential trial design, especially sample size, for future multi-center clinical trials using PET as a response endpoint. Multi-center clinical trials using serial PET imaging to measure cancer response are feasible, but overall measurement error should be expected to be larger than for single-site studies due to variations in scanners and imaging technique across centers. Using more sensitive dynamic model parameters such as flux (Ki) or metabolic rate of FDG (MRFDG) in place of the more common semi-quantitative values can increase the ability to detect change in uptake and may allow smaller sample sizes, but add to the complexity of imaging and analysis.

Our quantitative finding of reduced SUV sensitivity when baseline SUV is less than 3 (Figure 2A) was also observed in a serial FDG PET study of breast cancer that found response assessment was less accurate when the tumor-to-background ratio was less than 5 (23), which corresponds to a baseline SUV of 2.5 (24) assuming a normal breast tissue SUV of 0.5 (27). This study and others (23) do not support using serial FDG SUV to measure response when average baseline SUV are expected to be less than 3 in breast tissue (Figure 2A). The minimum recommended baseline value for measurement of response by SUV may be higher for other tumor sites such as the liver, which has a higher normal tissue SUV of around 2.5 (27). Efficiency gains for dynamic scans with full kinetic analysis are expected to be greatest for lesions with low initial uptake, since static SUV analysis cannot distinguish between metabolized FDG and unmetabolized background FDG.

Clinical trials are conducted at multiple sites in order to speed accrual, and to ensure generalizability of study results. However, larger sample size does not result in greater power if the amount of variability in the study outcomes is greatly increased. For example in the third column of Table 2, consider the scenario where a study of 30 patients with low initial FDG uptake would have 78% power to show an effect size of 20 percentage points, when the standard deviation of percent change is 10%. A multi-center replication of these results with more than triple the sample size (n = 100) would have only 24% power if measurement bias and error across centers increased the measurement standard deviation to 40%. The appropriate increase in calculated sample size for multi-center trials may be substantially higher if other imaging measures with multi-center or multiple observer reproducibility below 40% are used as endpoints. For example, an interobserver FDG PET/CT reproducibility study found the average between-reader standard deviation for percentage change in tumor SUV was 36%, compared to 157% for unidimensional tumor size by CT, and 547% for two-dimensional CT size (28).

There are several practical limitations to this study, and our analysis was intended only as an initial examination of the impact of imaging methodology and analysis on clinical trial design. We note that the criteria for comparing two treatment regimens may be overly simplistic. A statistically significant difference in percent change will not indicate whether either treatment, or both treatments, has achieved a threshold of response for clinical benefit. Approaches would need to be trial specific and would likely involve more sophisticated simulations of trial outcomes and early phase trial measurement of both static SUV and kinetic imaging parameters from dynamic PET scans. For example, if the baseline tumor to background SUV for a patient cohort is expected to be low, then early phase trial measurement of both static SUV and kinetic imaging parameters from dynamic PET scans may be required to ensure adequate study power. The differences in estimated SUV sensitivities in Figure 2 for patient cohorts with different baseline tumor to background SUV ratios highlight the importance of the participation of imaging scientists in clinical trial design to avoid loss of study power due to inaccurate estimates of the measurable effect size based on the selected imaging endpoint.

The impact of choice of response criteria was not evaluated here since this requires more complex modeling of the distribution of true PET changes and comparative receiver-operating-characteristic analyses of different classification schemes. These conditions may vary by disease and treatment characteristics, and evaluation of response criteria was beyond the scope of this study. In general, selection of a classification scheme with a higher threshold for partial response (e.g. 30% decline for “medically relevant beneficial change” from PERCIST (2) versus 15% or 25% decline for a partial metabolic response from EORTC (4)) corresponds to a larger effect size in Figure 1 when compared to a treatment with no effect, and smaller required sample sizes for treatment group comparisons. However if the threshold for partial response in the selected criteria is too high, then true significant differences between two treatments may be incorrectly labeled as insignificant. Future research should examine the impact of the response criteria on clinical trial design.

Another limitation of the presented research is that the impacts of bias and error for individual SUV values are not addressed directly. These more elaborate scenarios should be evaluated in future simulation studies, augmented by more data on sources of measurement error and bias such as differences in the magnitude of error and biases at community imaging centers versus regional (i.e. expert) imaging sites or national core labs. Understanding the impact of trial design on PET measurement error is critical to ensuring the study is not underpowered due to overly optimistic estimates of error. Similar standard deviation across all imaging sites and for change measures in the two treatment groups (same σ² for both groups) was a simplifying assumption in order to focus on overall measurement error and sensitivity. However, in practice there may be considerable non-stationary differences in error including the measurement site (17, 20), requiring multi-center trial designers to weigh faster patient accrual from more sites versus any increases in sample sizes due to an overall larger error from including sites with more PET measurement error. Also, FDG uptake differences can systematically be affected by partial volume errors due to change in size of viable lesion tissue (29). A study of the impact of non-stationary effects on trial design would be useful, but is beyond the scope of this study and likely requires simulations using stochastic sampling.

Conclusions

If a study using PET quantitations as early endpoints is designed without an understanding of measurement errors and sensitivity of the imaging measure to the expected true change, then the study may be underpowered, which increases the odds of the trial producing incorrect conclusions about the efficacy of novel therapies. If the sensitivity of simplified PET measures such as SUVs to the underlying biology is unknown, then the use of dynamic PET parameters from kinetic analysis is encouraged for early phase studies until any differences in PET measure sensitivity can be assessed. Reducing variances and/or increasing the sensitivity to measure true change can dramatically reduce the required sample size, improving patient safety and reducing study costs and duration.