Abstract
Arterial responses to diverse pathologies and insults likely occur via similar mechanisms. For example, many studies suggest that the natural process of aging and isolated systolic hypertension share many characteristics in arteries, including loss of functional elastin, decreased smooth muscle tone, and altered rates of deposition and/or cross-linking of fibrillar collagen. Our aim is to show computationally how these coupled effects can impact evolving aortic geometry and mechanical behavior. Employing a thick-walled, multi-layered constrained mixture model, we suggest that a coupled loss of elastin and vasoactive function are fundamental mechanisms by which aortic aging occurs. Moreover, it is suggested that collagenous stiffening, although itself generally an undesirable process, can play a key role in attenuating excessive dilatation, perhaps including the enlargement of abdominal aortic aneurysms.
Keywords: aneurysms, vascular growth, remodeling, elastin fatigue, collagen turnover, stress
1 Introduction
Biomechanical properties of arteries play vital roles in vascular physiology and pathophysiology45,50,69,78. These properties result from the complex structure of the arterial wall, which consists mainly of collagen, elastin, proteoglycans, and three cell types. Specifically, the wall contains multiple types of collagen (e.g., I, III, IV, V and VIII), with the fibrillar types I and III dominating overall load bearing capability (~80 to 90%65). When we refer to elastin, we often mean the elastic fibers that tend to be organized as lamellae and consist primarily of elastin (~90%58), but also associated microfibrils such as fibrillins, fibulins, microfibril-associated glycoproteins, and Emilin-161,62,74. Although these microfibrils do not appear to confer much stiffness directly31, they likely organize and help stabilize the elastin. All of these structural constituents are embedded in a ground substance matrix consisting of abundant water and multiple proteoglycans, including versican, biglycan, decorin, and lumican61. The overall stiffness of the arterial wall thus depends on the mass fractions, orientations, and cross-linking of many types of structurally significant constituents as well as their many interactions. Although we eventually seek to understand wall biomechanics in terms of individual constituents, Karnik et al. 59 notes that “The myriad associations and interactions between the many structural proteins, proteoglycans and growth factors of the vascular matrix makes it difficult to distinguish the effects of each element from another.” Hence, it continues to be advantageous to focus on the three primary classes of structural constituents – elastin, fibrillar collagen, and smooth muscle – in conceptual and mathematical models of the arterial wall (cf. Holzapfel and Ogden 45 and Humphrey and Taylor 54).
Unlike other structurally-significant constituents, elastin does not turnover in normal, healthy arteries29,74. That is, it is primarily deposited and arranged within the extracellular matrix during the perinatal period10,11,21, and as a result, it is likely primarily responsible for residual stresses and axial pre-stretches14,42,98,116. These residual stresses appear to endow arteries with nearly constant transmural distributions of circumferential stress under physiological loads18,71,86 and, together with axial prestretches, contribute significantly to arterial homeostasis. Moreover, elastin endows arteries with extensibility, elastic recoil, and resilience. Hence, damage to or degradation of elastin can result in severe vascular consequences, including age-related stiffening, aneurysms, aortic dissections, and so forth3,23,41,83. In contrast, fibrillar collagens appear to turnover continually throughout life, albeit at higher rates during early disease progression or responses to injury and perhaps at lower rates in old age90. Distributed within the media and especially within the adventitia, collagen appears to be largely responsible for the overall strength of the wall, with its high stiffness at modest extensions serving to protect smooth muscle from damage during acute periods of over-loading50. Local imbalances in proteinases and their inhibitors may render collagen susceptible to load-induced failure, which may be the ultimate cause of rupture in aneurysms. Finally, vascular smooth muscle activation controls local caliber and contributes to overall wall stiffness; it also works together with matrix remodeling both in arterial homeostasis and adaptations to altered hemodynamics20,107. Loss of smooth muscle activation can thus play important roles in diverse aspects of arterial physiology and pathophysiology. In this paper, we evaluate computationally the potential roles of loss of elastin, altered collagen cross-linking, and loss of smooth muscle contractility within the context of aging of the human abdominal aorta over long periods.
Structural and functional changes in the aorta due to aging contribute to many cardiovascular diseases, including heart attack, stroke, and end-stage kidney failure. In particular, increased aortic stiffening in aging increases the propagation of the pressure wave, which in turn can increase pulsatility in organs characterized by high flow and low resistance, such as the heart, brain, and kidney, and thereby damage the microcirculation within these organs66. Although general characteristics of aging in large arteries –endothelial dysfunction, increased caliber, and increased stiffness due to both geometric and microstructural changes – are well known41,66,83,92, the underlying mechanisms and time courses have not been well quantified. We suggest that microstructurally-motivated computational models have potential to increase our understanding of these mechanisms, particularly potentially coupled effects. We present here the first such model, one that builds on our recent use of a constrained mixture model to study adaptations of normal arteries to alterations in blood flow, pressure, and stretch106,107. An advantage of the constrained mixture approach is that one can consider separately the individual rates of production and removal of structurally significant constituents as well as their individual deposition stretches and material properties, which is particularly useful in modeling growth and remodeling (G&R).
Whereas our prior constrained mixture models have exploited a membrane assumption, we also extend this approach to model the human abdominal aorta as a multi-layered thick-walled vessel. By focusing on a short segment, we ignore possible taper and regional variations in properties along the length of the model vessel. For mathematical convenience, we consider a uniformly thick, cylindrical geometry, which allows us to capture salient clinical metrics such as evolving geometry, vasoactive capacity, and measures of arterial distensibility. Thick-walled G&R constrained mixture models can also predict other experimentally obtainable measures, such as retraction lengths, opening angles, and evolving passive behaviors (cf. Alford et al. 1 and Kar saj et al. 60). Thus, thick-walled constrained mixture models can furnish a more complete set of predictions to evaluate diverse aspects, modes, and hypothetical consequences of arterial G&R.
2 Theoretical Framework
2.1 Growth and remodeling of an artery
The Cauchy stress tensor t can be written in arterial mechanics, at any G&R time s, as
| (1) |
where p(s) is a Lagrange multiplier due to incompressibility during transient motions, not G&R, I is the identity tensor, F(s) is the deformation gradient tensor that transforms differential position vectors from a “reference” (classically, stress-free) to a “current” configuration at time s, J(s) = det F(s) is a volumetric ratio, C(s) = FT(s) F(s) is the right Cauchy-Green tensor, WR is a strain-energy function, defined per unit reference volume and denoted by the subscript R, and tact(s) is the active stress generated by smooth muscle. The evolving apparent mass density of structurally-significant constituent k can be computed via (cf. Baek et al. 7)
| (2) |
where is the mass density at time 0 and is a variable true mass density production rate, both defined with respect to a reference mixture volume; Qk(s) ∈ [0, 1] is the survival fraction for the cohort deposited prior to time s = 0 that survives to current G&R time s; and qk(s, τ) ∈ [0, 1] is the survival fraction for the cohort deposited at time τ ∈ [0, s] that similarly survives to time s. Specific functional forms for these kinetic relations are discussed below. As equation (2) makes clear, the apparent mass density of any constituent k is, in general, not constant. This formulation is consistent with familiar instances of biological growth, atrophy, and restructuring resulting from diverse processes including development, aging, disease progression, and responses to injury52.
2.2 Homeostatic stretches and constrained motions
Kozel et al. 63 noted that “elastin-producing cells move into and become associated with networks of pre-existing elastic fibers. During this period, the elastic fiber network would assume the motion of the cell, suggesting that components of the fiber were binding to the cell. An interaction with the cell was also evident from the stretching and pulling motions of the fiber seen as the cell moved away.” Furthermore, Czirok et al. 19 suggested that “[o]ne may speculate that the divergent motion of two cells, both attached to the same ECM aggregate, would generate mechanical stress within the cell-ECM composite material. This mechanical stress could be sensed by appropriate receptors, and the resulting biochemical signaling would alter the cells’ direction of motion.” In other words, there is growing evidence that synthetic cells can manipulate newly secreted fibers and incorporate them within extant matrix under a mechanical load.
The concepts of target homeostatic mechanical states for cells and matrix and associated constant stretches imposed during deposition are fundamental to constrained mixture models of G&R52,107. This concept can be described mathematically through the multiplicative motions7
| (3) |
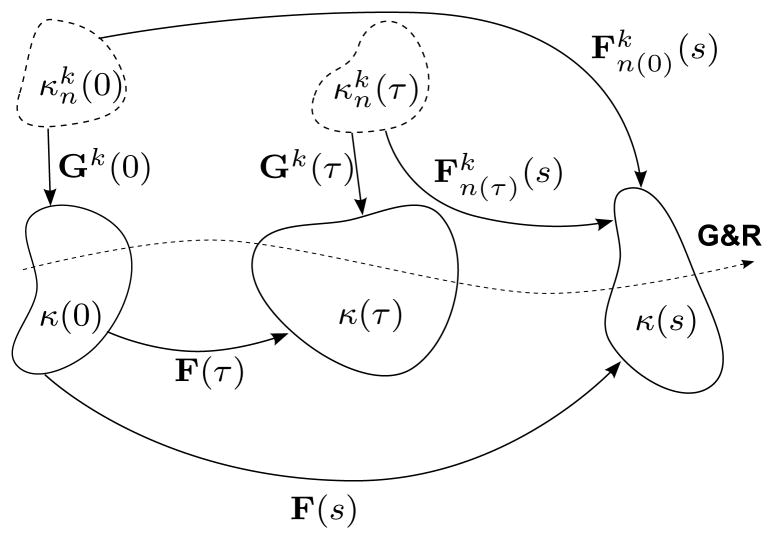
with F(τ) and F(s) representing motions from a common reference configuration of the mixture κ(0) to configurations at deposition time τ and G&R time s, respectively, and Gk(τ) is a positive definite tensor corresponding to a motion of constituent k from its individual natural (stress-free) configuration, as indicated by the subscript notation n(·), to the mixture’s loaded configuration at the time τ of deposition. Figure 1 illustrates these configurations and related motions. Consistent with the idea of constant target states and deposition stretches, Gk(τ) ≡ Gk. Note, too, that, , where xk(s) = x(s) constrains all k structurally significant constituents to deform together with the artery as a whole, while Xk(τ) ≠ X(τ), in general, allows individual natural configurations to evolve separately for each constituent k produced at deposition time τ7,8,107.
Figure 1.
Schema of salient configurations for arterial G&R. New constituents k = c and m having natural (stress-free) configurations (typically unmeasurable and denoted by dashed bodies), are incorporated into evolving in vivo mixture configurations κ(·) (potentially measurable and denoted by solid bodies); deposition tensors Gk(τ) describe motions from individual natural configurations to the in vivo mixture configuration κ(τ) at intermediate time τ ∈ [0, s]. Deformation gradients F(τ) and F(s) describe motions from the reference configuration κ(0) to κ(τ) and κ(s), respectively. Thus, describes motions from to κ(s). Note that the concept of constant target states and deposition stretches requires Gk(τ) ≡ Gk. (not shown) is identically Gk. The special case F(τ) = I, representing tissue maintenance, recovers , as expected. Letting F(τ) = Gk = I, where the reference configuration is identically the natural configuration, recovers the classical result , as desired.
2.3 Stored energy
Anticipating the need to implement fully three-dimensional G&R models, Figueroa et al. 33 defined stored energy per unit mass, rather than per unit volume. They reasoned that such a formulation would be computationally simpler because the stored energy would depend upon the deposition time of each degrading constituent rather than upon the evolving current volume, which would require the coupled solution of evolving mass densities and the current evolving mixture volume (see the Appendix for details). In contrast, we express the evolving strain energy contribution by constituent k per a constant unit reference volume
| (4) |
where is the strain-energy function for each cohort of family k, and . This formulation is a generalization of the rule of mixtures approach whereby , and . Although mass densities ρR(s) ≠ ρR(0), in general, this approach decouples the current (evolving) mixture volume from the solution, allowing us to write J(s) = det F(s) = ρR(s)/ρR(0), or simply the ratio of net mass at time s to that at time 0.
2.4 Kinematics
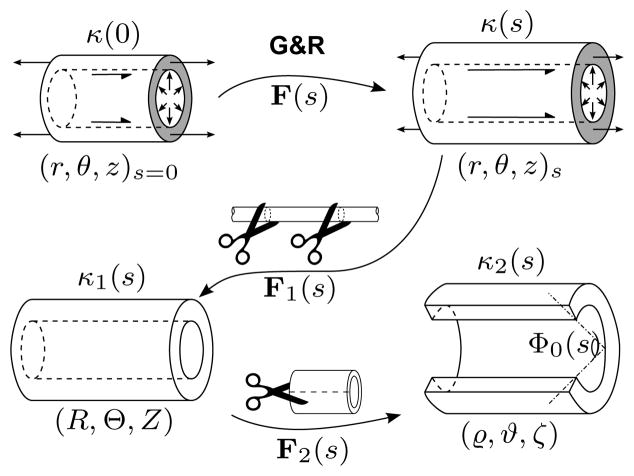
Consider three cylindrical coordinate systems (r, θ, z), (R, Θ, Z), and (ϱ, ϑ, ζ), representing the in vivo loaded, excised unloaded, and radially-cut configurations, respectively (figure 2). The deformation gradient tensor (in matrix notation)
Figure 2.
Schema of in vivo loaded configurations (with arrows denoting distending pressures, applied axial forces, and luminal shear stresses, where applicable) at G&R times 0 and s, denoted by κ(0) and κ(s), respectively and the excised unloaded (κ1(s)) and radially cut (κ2(s)) configurations at time s. Corresponding cylindrical coordinate systems are shown beneath configuration diagrams. F(s) is the same as in figure 1 and thus accounts for the effects of time-dependent G&R. F1(s) describes motions from a current loaded in vivo state to the excised unloaded state, and F2(s) describes motions following the introduction of a radial, stress-relieving cut. Note the relation between Θ0(s) and opening angle Φ0(s) (cf. equation (9)). The shaded annular regions (representing non-free surfaces) remind the reader that κ(0) and κ(s) are axially tethered, unexcised configurations.
| (5) |
describes motions from the original (s = 0) in vivo loaded configuration (i.e., a healthy aorta pressurized and stretched physiologically) to an evolved configuration at time s. Note that λ(s) = l(s)/l(0) is prescribed in the in vivo configuration at all times s, where l(s) and l(0) are current and original axial lengths, respectively. Moreover, ∂r(s)/∂r(0) = J(s) r(0)/[r(s) λ(s)] since the deformation is not isochoric, in general, during G&R. The current radial position r(s) can thus be expressed as a function of an original (before G&R) position within the wall and local volumetric changes, i.e.
| (6) |
where ri(s) and ri(0) are current and original luminal radii, respectively, and J is written explicitly as a function of position as well as time to emphasize that it is, in general, non-homogeneous.
A second deformation gradient tensor
| (7) |
describes motions from the loaded in vivo configuration at time s to the excised unloaded configuration at time s. At a fixed s, the incompressibility constraint requires ∂R(s)/∂r(s) = r(s) Λ(s)/R(s) and , where Ri(s) and L(s) = l(s)/Λ(s) are the evolving unloaded inner radius and length, respectively. Similarly, a third deformation gradient tensor
| (8) |
describes motions from the unloaded configuration at time s to the radially-cut configuration at time s. Similarly, the incompressibility constraint requires ∂ϱ(s)/∂R(s) = π R(s) Γ(s)/[ϱ(s) Θ0(s)] and
, where ϱi(s) and
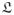 (s) = l(s)/[Γ(s) Λ(s)] are the inner radius and axial length, respectively, in the radially-cut configuration, and Θ0(s) is related to another frequently-used measure of the opened geometry, the opening angle Φ0(s) (see figure 2), via 35
(s) = l(s)/[Γ(s) Λ(s)] are the inner radius and axial length, respectively, in the radially-cut configuration, and Θ0(s) is related to another frequently-used measure of the opened geometry, the opening angle Φ0(s) (see figure 2), via 35
| (9) |
Finally, the deformation gradient corresponding to the motion from the loaded in vivo configuration at time s to the radially-cut configuration at time s is then
| (10) |
and .
2.5 Orientations of fibrillar constituents
We assume that a cohort k of fibrillar collagen is deposited at intermediate time τ in the direction of unit vector mk(τ) with a scalar value of prestretch . Note that mk(τ) need not be constant, in general, although in this implementation it is. The deformation gradient tensor describing motions from individual natural (stress-free) configurations to the configuration at G&R time s for fibrillar constituent k can thus be written (cf. equation (3))
| (11) |
where ⊗ denotes the tensor (dyadic) product. The stretch of an individual fiber at any subsequent G&R time s is
| (12) |
and
| (13) |
is the unit vector in the direction of the fiber due to deformations subsequent to the time of deposition τ. Neither nor mk(τ) is defined with respect to a natural (stress-free) configuration because fibers are only incorporated within physiologically-loaded states. Such individual natural configurations, for which fiber angles are not measurable, exist only conceptually.
2.6 Passive mechanical responses
As in previous implementations8,107, we model the passive mechanical response of (amorphous) elastin using a neo-Hookean strain-energy function29,47
| (14) |
where Fe(s) = F(s) G̃e, and G̃e captures motions during normal development to the reference in vivo state (in maturity33); total stretches experienced by elastin thus do not depend on the time of deposition τ ∈ [0, s]. Tat is, functional elastin is produced and cross-linked during the perinatal period110, and subsequently stretched elastically throughout normal development and maturation14. Elastin is biologically stable in healthy mature arteries, thus there is usually neither production (i.e., me(τ) = 0) nor removal (i.e., Qe(s) = 1). In aging, however, effective elastin is removed via fatigue, as will be discussed below. Nevertheless, growth-induced prestretches can be described by
| (15) |
where .
Finally, we employ exponential strain-energy functions for tension and compression for both fibrillar collagen47
| (16) |
and passive smooth muscle40
| (17) |
where the hat denotes the strain-energy for an individual cohort, deposited at time τ that exists until time s. Recalling equations (11) and (12), and letting νk(τ) = mk(τ)[F−1(τ) Gk]T and ηk(τ) = F−1(τ) Gk mk(τ), we can write
| (18) |
We consider four families of fibrillar collagen: one oriented axially, one circumferentially, and two equivalent helical families at angles of ±π/4 to the axial direction8,107. Mass fractions of these collagenous families differ in the media and adventitia (table 1). Note that proteoglycan-supported collagen, while under compression , has parameter equal to that of smooth muscle 7.
Table 1.
Categories of important parameters and their values for a representative mature abdominal aorta, before any loss of elastin. “Observed” parameters include those reported in literature. “Bounded” parameters are less established, but likely values may either be inferred from experimental observations or estimated such that appropriate selection recovers realistic predictions. The calculated value for satisfies equilibrium at G&R time s = 0.
| Class | Role | Value(s) | Reference(s) | |
|---|---|---|---|---|
| Observed | physical constants | ρ = 1050 kg/m3, μ = 0.037 g/cm s | Humphrey 50 | |
| initial loads | P = 93 mmHg, | Greve et al. 43, Humphrey 50 | ||
| arterial geometry | ah = 6.25 mm, hh = 0.9 mm, rom = ah + 2 hh/3 | Åstrand et al. 4 | ||
| medial constitutive fractions | , φe = 0.55, φm = 0.2 | Feldman and Glagov 32 | ||
|
|
||||
| homeostatic kinetics |
|
Gineyts et al. 38, Langille 67, Stenmark and Mecham97 | ||
| Ke = ln (2)/14600 days−1 | Arribas et al. 3 | |||
|
|
||||
| passive elasticity | ce = 125 kPa | Cardamone et al. 15 | ||
|
|
” | |||
|
|
” | |||
|
|
” | |||
|
|
||||
| vasoactivity | Tmax = 300 kPa, λM = 2, λ0 = 0.4 | ” | ||
|
| ||||
| Bounded | deposition stretches |
|
Dobrin and Canfield 25, Faury 31 | |
| stiffening parameter | βc ∈ [0.1, 0.5] | Pedrigi et al. 84 | ||
| scaling parameter | βm = 0.75 | |||
|
|
||||
| medial collagen fractions |
|
Wicker et al. 114 | ||
| adventitial collagen fractions |
|
” | ||
|
|
||||
| production kinetics |
|
Sluijter et al. 96, Strauss et al. 99,100, Xu et al. 115 | ||
|
|
Valentín and Humphrey 105 | |||
|
|
||||
| shear-constrictor | CB = 0.68, CS = 20 CB | ” | ||
|
| ||||
| Calculated | passive elasticity |
|
||
2.7 Active mechanical response
The stress generated actively by smooth muscle, which depends on both the net ratio of vasoconstrictors to dilators C(s) and muscle fiber stretch, is defined by8,104,105,107
| (19) |
where Tmax(s) is a scaling parameter with units kPa, is the evolving mass fraction of active smooth muscle, λM is the stretch at which the active force generating capability is maximum, λ0 is the stretch at which muscle cannot generate any force, and is the current active muscle fiber stretch8. C(s) affects smooth muscle tone by changing intracellular calcium ion concentrations. Implicit in this formulation is the assumption that muscle can only exert tensile stresses in the circumferential direction, denoted by unit vector eθ.
Endothelial cells are sensitive to flow-induced wall shear stress, releasing vasoconstrictors such as endothelin-1 (ET-1) in response to decreased shear stress72,76 and vasodilators such as nitric oxide (NO) in response to increased wall shear stress37,102. It has proven convenient to define the ratio of constrictors to dilators C(s) as a function of wall shear stress, namely
| (20) |
where CB is a basal ratio that sustains a homeostatic level of vasoactivity, CS is a scaling factor for shear stress induced changes, , and is the homeostatic (target) value of wall shear stress. Assuming fully developed laminar flow of a Newtonian fluid through a tube, τw(s) = 4 μQ(s)/πa3(s), where μ is the viscosity of whole blood (~3.5 centiPoise), and Q(s) is the volumetric flowrate at G&R time s (see table 1).
2.8 Kinetics of turnover
Degradation of structural proteins and apoptosis both appear to be well described by first order type kinetics, with appropriate half-lives17,79. Additionally, there is substantial evidence that the rates of turnover of extracellular matrix and cells are modulated by stretch or stress and thus loading history12,80,100. Hence, we define survival fractions for original constituents (cf. Baek et al. 8 and Valentín et al. 107)
| (21) |
where are rate-type parameters for mass removal with units of days−1. These parameters may evolve as described by , where is an assumed homeostatic constant of decay for both fibrillar collagen and smooth muscle, corresponding to a half-life of 70 days. Thus, we model collagen and smooth muscle degradation as functions of cumulative changes of cohort-specific levels of tension, with
| (22) |
being the normalized difference between fiber tensions at times s and deposition time τ within an individual cohort of constituent k. By calculating a value of for each cohort, this approach is consistent with the hypothesis that fibrillar degradation is selective; individual cohorts experience proportional increases in degradation for corresponding normalized differences in tension from homeostasis. Moreover, this formulation hypothesizes elevated proteolytic production/activation for any departure from normal tensions (both increasing and decreasing), consistent with diverse reported observations36,77,91,94,95. In the special case Δζ̂k(s) = 0 ∀ s, we recover a simple exponential decay with , consistent with first order kinetics, as desired. Extending equation (21) to account for the degradation of constituents deposited, at intermediate times τ, let
| (23) |
with the only difference being the lower limit of integration.
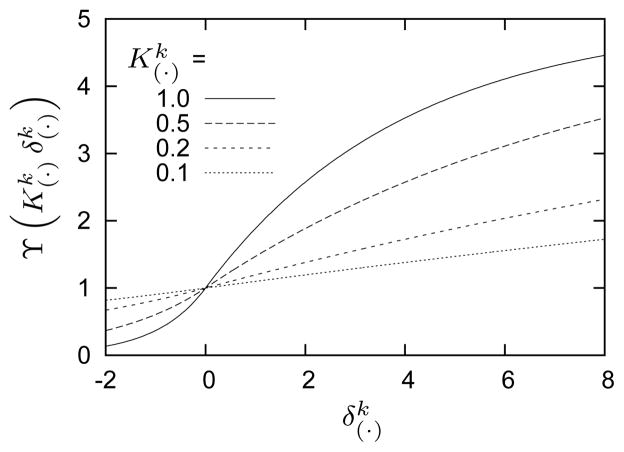
For illustrative purposes, consider positive piecewise stress-mediated functions for rates of mass density production
| (24) |
where
| (25) |
are basal rates of mass density production, are maximal limiting values for mass density productions, and are rate parameters that govern constituent level stress- and wall shear stress-driven mass production, respectively, and and . Figure 3 illustrates the above relationships, with associated kinetic parameters listed in table 1. The quantity Δσk(s) = σk(s)/σk(0) − 1 is a scalar measure of the change in stress borne by each constituent where
Figure 3.
Functional relationship between normalized mass production rate and a change in mechanical stimulus for indicated values of and where (cf., equation (25)). The sigmoidal behavior approximates observed saturation limits for mass production rates as functions of shear-induced changes in NO or ET-128,72,73. Also note the nearly linear behavior near , retaining features of previously implemented models105.
| (26) |
and txk(s) is the current extra stress borne by fibrillar constituent k.
The ratio of the shear stress scaling factor to the basal constrictor concentration CS/CB serves as a biochemical input to mass density production because most vasoactive constrictors (for example, ANG-II, ET-1) are also mitogens and promoters of collagen synthesis16,89 whereas vasodilators such as NO inhibit cellular proliferation, migration, and matrix turnover37,88. Consequently, we require production to be proportional to the normalized change in constrictor concentration, where ΔC(s) = C(s)/CB − 1 = −(CS/CB ) Δ τw(s). Unlike Δσk(s), which affects corresponding individual fiber family production rates separately, Δτw(s) influences the production of all constituents simultaneously; this biochemical signal does not directly depend on fiber family orientation, age, or loading history. Additional specialization, to include specific consequences of gene expression and molecular-level phenomenon, will need to be addressed once knowledge of cell/matrix biology, chemical signaling, genetics, etc. are expanded and improved.
2.9 Solution Procedure
Recalling equation (1), let tx(s) denote the extra part of the stress, that is, that part depending on deformation, where
| (27) |
After imposing a perturbation (for example, some degree of elastin damage or change in hemodynamic loading), we determine the inner radius that satisfies equilibrium locally in any relevant configuration (cf. figure 2). For an axisymmetric cylindrical geometry, radial equilibrium is50
| (28) |
where tθθ(r(s)) and trr(r(s)) are, respectively, circumferential and radial components of the Cauchy stress tensor, written explicitly as functions of time-varying radial position r(s). Integrating over the mural thickness yields, at each time s in our quasi-static problem, a global form describing radial equilibrium is
| (29) |
where ri(s) and ra(s) are current luminal and adventitial radii, respectively; the Lagrange multiplier vanishes within the integral, leaving only extra stresses. Boundary conditions trr(ri(s)) = −Pi(s) and trr(ra(s)) = −Pa(s) require
| (30) |
where P(s) = Pi(s) − Pa(s) is the current transmural pressure. Effects of perivascular tethering can be modeled by prescribing a reaction at the adventitial surface via Pa(s), as described by Humphrey and Na 51, but there is a need for more data on perivascular effects on the aorta. Hence, we neglect perivascular tethering (Pa(s) = 0).
We calculate, via the secant method, the time-varying inner radius that satisfies radial equilibrium (equation (30)). Spatial integration is performed using a Gauss-Legendre quadrature, and temporal integrations of strain-energy functions and kinetics are performed using a trapezoidal rule quadrature. Evolving geometry drives removal and production of mass via equations (21) to (25), and G&R proceeds iteratively via finite differences in time.
Although not required for solving the evolving inner radius ri(s), since the in vivo axial length l(s) is defined at all G&R times s, the applied axial force f(s) of a pressurized, open ended cylinder is
| (31) |
where tzz is the axial component of Cauchy stress. The Lagrange multiplier p (r(s)) can be solved using
| (32) |
In addition to tracking the evolving in vivo state, this model facilitates the tracking of geometry and mechanical responses of the evolving excised unloaded configurations. The unloaded (though still intact) configuration has boundary conditions of tRR(Ri(s)) = tRR(Ra(s)) = 0 and zero net axial force. In contrast to the case of the in vivo configuration, in which l(s) is prescribed for all times s, the unloaded length L(s) is unknown. Static equilibrium is described by the system of equations
| (33a) |
| (33b) |
There is also assumed to be no active contribution in this configuration (tact(s) = 0). Equations (33a) and (33b) are solved via a generalized pseudo-Newton method. One can replace equation (33b) with , but (33b) obviates the need to compute the Lagrange multiplier.
Taber and Humphrey 101 noted that the configuration of an excised artery with a radial stress-relieving cut can be determined by solving for that geometry which, in addition to satisfying radial equilibrium, yields conditions of zero bending moment and net axial force. These conditions are described by the system of equations
| (34a) |
| (34b) |
| (34c) |
Boundary conditions tϱϱ(ϱi(s)) = tϱϱ(ϱa(s)) = 0 facilitate calculation of the Lagrange multiplier via (cf. equation (32))
| (35) |
and the system of equations (34a) to (34c) is again solved via a generalized pseudo-Newton method. As in the case of the unloaded configuration, smooth muscle does not generate an active contribution.
3 Illustrative Hypotheses and Numerical Experiments
In the spirit of a prior G&R study104, we investigate multiple mechanisms by which G&R may proceed and compare predicted results from numerical experiments. Specifically, we posit that aging results, in part, from a progressive loss of functional elastin, compromised smooth muscle contractility, and altered collagen.
3.1 Degradation of elastin
Elastin is a highly elastic and normally biologically stable arterial protein. This is due, in part, to myriad cross-links, including desmosine and isodesmosine74, that are promoted primarily by lysyl oxidase but also transglutaminases. Nevertheless, elastin is susceptible to both proteolytic degradation by matrix metalloproteinases in diseases (especially MMP-2, -9, -12, -13) and fatigue-type degeneration in aging3,62,70,85, which appear to be accelerated in hypertension (due to increased pulse pressure) and Marfan syndrome (due to deficiency in fibrillin-1, which stabilizes elastin). Indeed, losses of functional elastin likely cause or are caused by many arterial diseases and injuries3,41,83. We prescribe a first order kinetics relation for the time-dependent survival fraction of elastin in the human abdominal aorta,
| (36) |
where Ke = ln(2)/14600 day−1 (a half-life of 40 years, consistent with Arribas et al. 3).
3.2 Progressive vasoactive dysfunction
In addition to endowing arteries with important passive mechanical properties, elastin is also a potent biological regulator of smooth muscle cell activity. For example, intact “elastin induces actin stress fiber organization [and a quiescent contractile phenotype], inhibits proliferation, regulates migration and signals via a non-integrin, heterodimeric G-protein-coupled pathway”59. Scaling Tmax(s) (equation (19)) proportionally to Qe(s) (equation (36)) allows us to simulate the potentially deleterious consequences of elastin degradation on vasoactivity. In particular, we prescribe
| (37) |
where βm is a scaling parameter that controls the degree of proportionality between elastin content and vasoactivity. Equation (37) effectively simulates progressively compromised vasoactive function with decreasing content of elastin.
3.3 Progressive stiffening of collagen
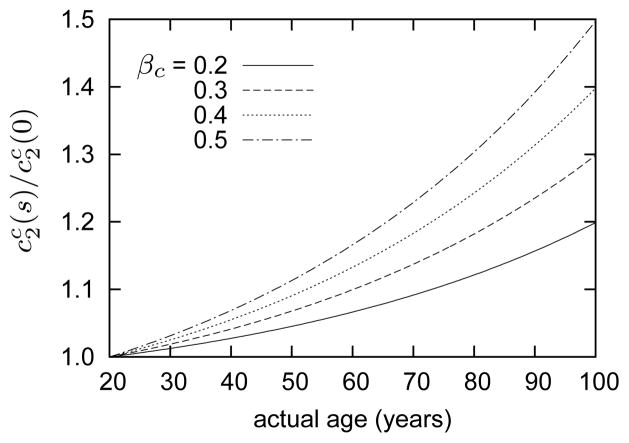
Arteries stiffen with age and hypertension, due in part to a thickening of the wall and an increase in the ratio of collagen to elastin. In addition, however, such stiffening can result from advanced glycation end-products (AGEs), which increase cross-links in collagen. Indeed, increased collagen cross-linking and overall stiffening of the arterial wall is an important contributing factor to age-related cardiovascular disease2,9,41. Pedrigi et al. 84 reported significant stiffening of a highly collagenous tissue (porcine lens capsule) after culture in a hyperglycemic (e.g., diabetic) environment for 14 weeks, which can be modeled well by increasing the dimensional parameter for collagen. To investigate possible effects of pathological stiffening of collagen fibers in aging, we considered cases in which the mechanical parameter gradually increased by prescribing
| (38) |
where βc describes the degree of stiffening (e.g., for βc = 0.2, see figure 4). Although glycation likely involves other important mechanisms (e.g., increased resistance to enzymatic degradation), we restrict our attention to a simple increase in mechanical stiffness.
Figure 4.
Time courses of normalized collagen parameter for indicated values of βc (cf., equation (38)). Stiffening commences at G&R time s = 0 (20 years of age). Note that βc does not define a constant degree of collagenous stiffening; rather, it defines the degree of stiffening at G&R time s = 80 years (e.g., 20% stiffening at age 100, but only ~6% stiffening at age 60 for βc = 0.2).
4 Results
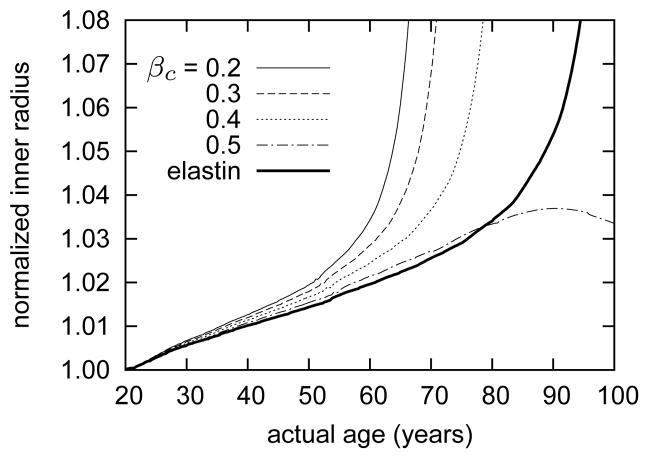
The model predicts a gradual increase in inner radius ri(s) as elastin degrades, per equation (36), and smooth muscle loses contractility, per equation (37). Figure 5 shows effects on luminal enlargement due to varying the collagenous stiffening parameter βc. Note that computational G&R time 0 corresponds to a healthy, mature human abdominal aorta prior to the onset of “aging”, that is, at age 20. Figure 5 shows that, for the case of βc = 0.2, unbounded enlargement begins roughly at G&R time s = 40 years, which corresponds to an individual aged 60 years. The predicted gradual increases in inner radius and wall thickness are qualitatively consistent with observations for aging abdominal aorta in humans4,108.
Figure 5.
Time courses of evolving loaded inner radii ri(s), normalized with respect to the inner radius at actual age of 20 years (i.e., G&R time s = 0), for indicated values of βc. The bold solid curve shows the predicted evolving inner radius for the case of elastin loss with no collagenous stiffening or vasoactive dysfunction (βc = 0 and Tmax(s) = Tmax(0)). Recall that the loss of elastin commences (G&R time s = 0) at 20 years of age. Due to the coupled effects of elastin loss and vasoactive dysfunction, the simulated arteries gradually lose the ability to reset the inner radius at a fixed value. Increasing collagenous stiffening delays unbounded growth, and the case of βc = 0.5 shows an eventual reversing trend. The model suggests that collagenous stiffening could attenuate aneurysmal enlargement in the absence of other complications, as, for example, disturbed hemodynamics or thrombus formation. Elastin loss, by itself (bold solid curve), can induce unbounded luminal expansion; this trend commences far later than cases for which vasoactive capacity is also progressively compromised.
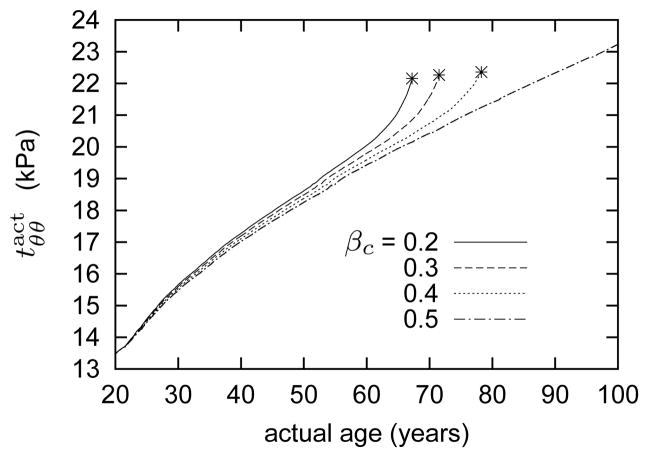
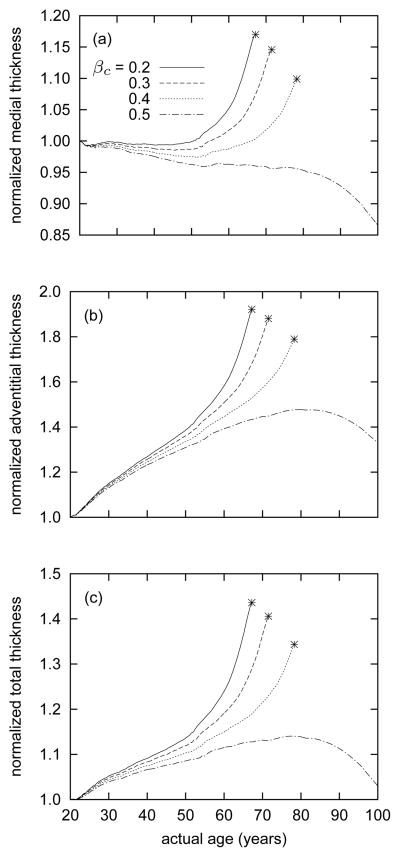
As the elastin degrades, the wall loses an important aspect of its “memory.” That is, although smooth muscle may, via endothelial – medial coupling, still respond to changes in wall shear stress as inner radius changes, the only structure within the artery that retains a mechanically passive “memory” of the normal geometry degrades inexorably. Indeed, even in the case of elastin loss in the absence of collagenous stiffening and vasoactive dysfunction (βc = 0 and Tmax(s) = Tmax(0)), the model predicts eventual unbounded luminal expansion – albeit nearly 20 years later than in the case of βc = 0.4. This prediction highlights the important role of arterial elastin in preserving luminal radius. In response to the initially modest increase in inner radius, the model predicts increased active muscle stress contributions (figure 6), which assists in maintaining inner radius within 4% of its target value for the first 40 years of G&R. In vivo, such increases would be expected both because of the decrease in wall shear stress, which would lead to endothelial cells down regulating NO and upregulating ET-1, and an increase in muscle fiber length that would enable more force generation. As time progresses and more elastin is degraded, however, vasoactive function decreases (via equation (37)) and the artery enters a phase of unbounded G&R. Beyond a certain point, continually deposited collagen and active muscle are unable to arrest or reverse radial expansion. Rather, despite increasing accumulations of medial and adventitial collagen (figure 7), as mass turnover increases as the inner radius increases, the artery “grows around” a larger inner radius.
Figure 6.
Time courses of evolving active stress generated by smooth muscle. Stars denote limiting points beyond which results become singular, corresponding to unbounded luminal expansion. As elastin degrades and the artery’s inner radius increases (see figure 5), which decreases wall shear stress, smooth muscle seeks to generate compensatory increases in intramural stresses that aid in restoring both wall shear stress and overall wall stress toward normal values (equations (19) and (20)). As the inner radius increases without bound and the muscle fiber stretch approaches λM (see equation (19)), smooth muscle loses its ability to generate active stress and the vessel loses its ability to maintain or restore its preferred caliber unless increased collagen, or muscle mass, can compensate (cf. figure 5).
Figure 7.
Time courses of evolving medial (panel a), adventitial (panel b), and total (panel c) thicknesses for indicated values of βc. Stars denote limiting points beyond which results become singular, corresponding to unbounded luminal expansion. In all cases, medial thickness decreases slightly up to an actual age of 50 years (i.e., G&R time s = 30 years), due to loss of elastin. In contrast, adventitial thickness increases steadily throughout G&R, except the case of βc = 0.5 beyond 80 years of age. Except for the case of βc = 0.5, the media begins to thicken after 50 years of age.
As the collagen stiffening parameter βc increased, however, the model predicted a delay in the unbounded growth; indeed, when βc = 0.5, the unbounded growth was not only prevented, it was reversed in part. This process of collagenous stiffening is essentially competing with luminal expansion (cf. Baek et al. 6); if collagen becomes sufficiently stiff before the artery reaches a point at which growth becomes unbounded, then the artery can eventually reverse the usual dilating trend. These predictions suggest that stiffening of collagen confers a protective effect and prevents the artery from entering into a phase of unbounded G&R. Anecdotally, this prediction is consistent with the clinical observation that diabetes can protect abdominal aortic aneurysms from rupture, presumably because of the increased glycation cross-links30,75.
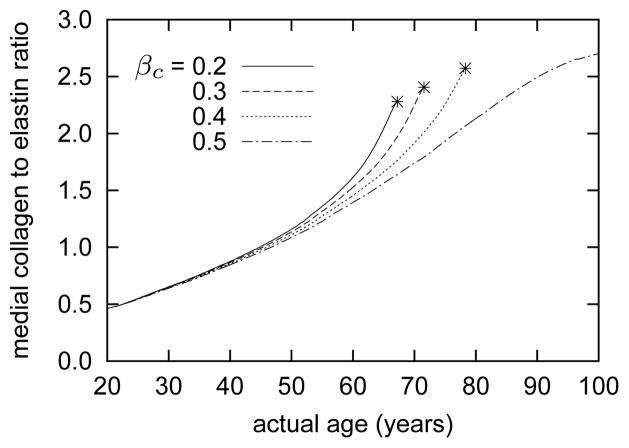
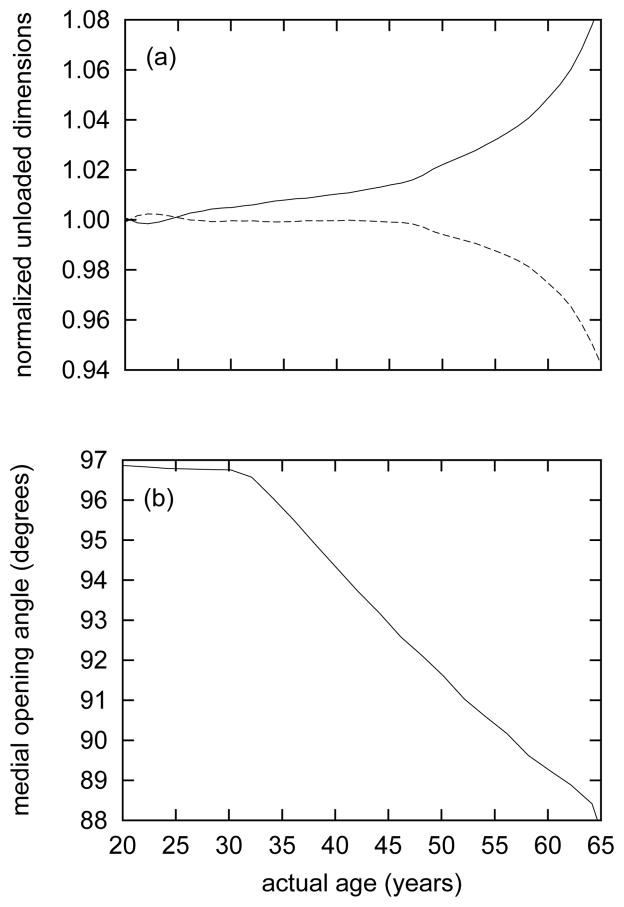
As a result of the predicted gradual increase in the medial collagen to elastin ratio shown in figure 8, the unloaded dimensions increase. That is, unloaded inner radius Ri(s) and axial length L(s) become greater as the artery ages. Figure 9 (panel a) shows these trends in terms of the normalized unloaded inner radius Ri(s)/Ri(0) and “retraction” stretch Λ(s)/Λ(0). As highly-prestretched elastin is replaced with stiffer collagen and smooth muscle, the passive retraction and radial recoil decreases. Observations from both animal models and older individuals support both of these findings22,34,56,57,113.
Figure 8.
Time courses of evolving collagen to elastin ratios within the media, for indicated values of βc. Stars denote limiting points beyond which results become singular (unbounded luminal expansion). Gradual loss of elastin and compensatory accumulation of collagen lead to dramatic increases in this ratio.
Figure 9.
Time courses of evolving normalized inner radius Ri(s)/Ri(0) (solid curve) and “retraction” stretch Λ(s)/Λ(0) (dashed curve) in the excised, unloaded configuration κ1(s) (panel a) and the evolving medial opening angle Φ0(s) for configuration κ2(s) (panel b). All results for βc = 0.2. Note the nearly constant medial opening angles up to actual age of 30 years (G&R time s = 10), corresponding to the modest changes in medial thickness (cf., figure 7, panel a). As the media thickens, Φ0 decreases steadily.
Because elastin degradation was uniform within the media, the model did not predict strong gradients in elastin as observed in aged arteries32. Due in part to the absence of such a gradient, the predicted evolving medial opening angle Φ0(s) is opposite that observed by Saini et al. 93 and Badreck-Amoudi et al. 5 despite being comparable to reported values for the media. As shown by Cardamone et al. 15, a gradient of elastin mass fractions (more elastin present near the adventitial portion of the media, for example) would likely influence the transmural stress distributions to the degree that the evolving opening angle would increase with age. It is interesting that Fonck et al. 34 and Greenwald et al. 42 reported that treatment with elastase, which results in uniform elastin degradation (i.e., not resulting in the gradients in elastin content described by Feldman and Glagov 32), decreased the residual stress related opening angle, contrary to trends observed in aged arteries.
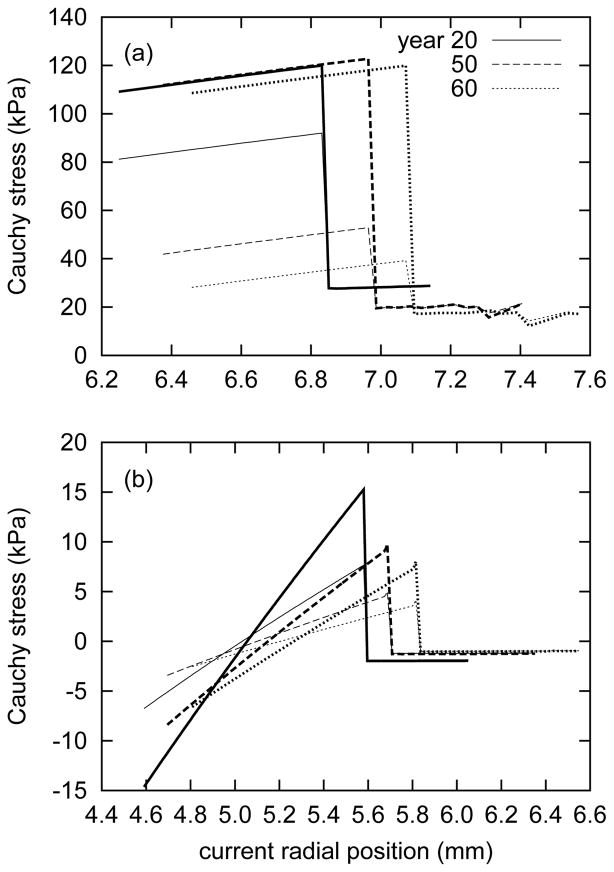
Figure 10 shows the predicted transmural Cauchy stress distributions over time for the intact vessel. In the normal, healthy aorta, the model predicts circumferential Cauchy stresses of approximately 120 kPa within the loaded media, and a nearly equibiaxial state of stress in the adventitia (figure 10, panel a). Interestingly, axial stresses within the media are predicted to decrease substantially with aging, while the circumferential stresses remain relatively unchanged. This trend is due primarily to the presence of smooth muscle generating circumferential stresses and the ability of the media to replace circumferentially- and helically-aligned collagen in response to elastin degradation. Elastin, which is normally under an equibiaxial state of stress, bears lower stresses over time, and because the axial load it normally bears is not taken by axially-aligned collagen, the Cauchy stress (a cumulative measure of internal stresses) in the axial direction gradually decreases. Also, since the in vivo axial length is constrained, static equilibrium depends more upon the circumferential stresses. The artery is predicted to remodel in a manner such that circumferential Cauchy stress distribution in the media is preserved, at the expense of lower axial stresses and thus a nearly equibiaxial stress field.
Figure 10.
Evolving transmural circumferential (bold curves) and axial (light) Cauchy stresses for the loaded in vivo configuration (panel a) and the excised, intact configuration (i.e., residual stresses; panel b) at indicated actual ages. All results for βc = 0.2. The sharp discontinuity marks the interface between the medial and adventitial layers. As a result of the lack of axially-oriented fibers of collagen in the media, the in vivo circumferential Cauchy stresses are higher than the axial stresses. The adventitia, lacking both elastin and active smooth muscle, bears substantially lower equibiaxial stresses. As the artery ages, in vivo axial Cauchy stresses decrease, particularly within the media. Also, stress gradients within the media diminish in the unloaded configuration.
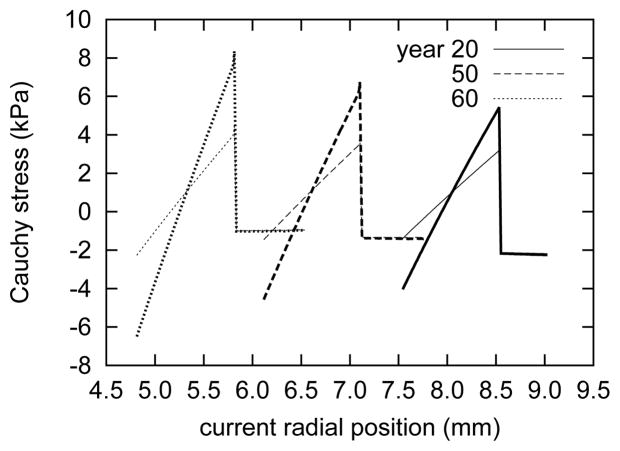
Figure 10 (panel b) illustrates predicted (residual) stress gradients within the media in the unloaded, intact state. As expected for a uniform loss of elastin within the media, the stress gradients diminish with age. The adventitia is predicted to bear a modest, essentially uniform, compressive stress (cf. Holzapfel and Ogden 46). Similar gradients are present in the radially-cut media (figure 11). This result emphasizes that even for zero tractions, one cannot necessarily presume that a soft tissue is under a state of zero stress. In fact, even within a radially-cut (opened) artery, strong gradients remain within the media.
Figure 11.
Evolving transmural circumferential (bold curves) and axial (light) Cauchy stresses for the opened configuration κ2(s) of the entire artery at indicated actual ages. All results for βc = 0.2. The progressively smaller inner radii ρi(s) accompany a dramatic decrease in opening angle Φ0(s) (see figure 2). As in the case of the in vivo and excised configurations, the circumferential Cauchy stress gradients are stronger than those in the axial direction.
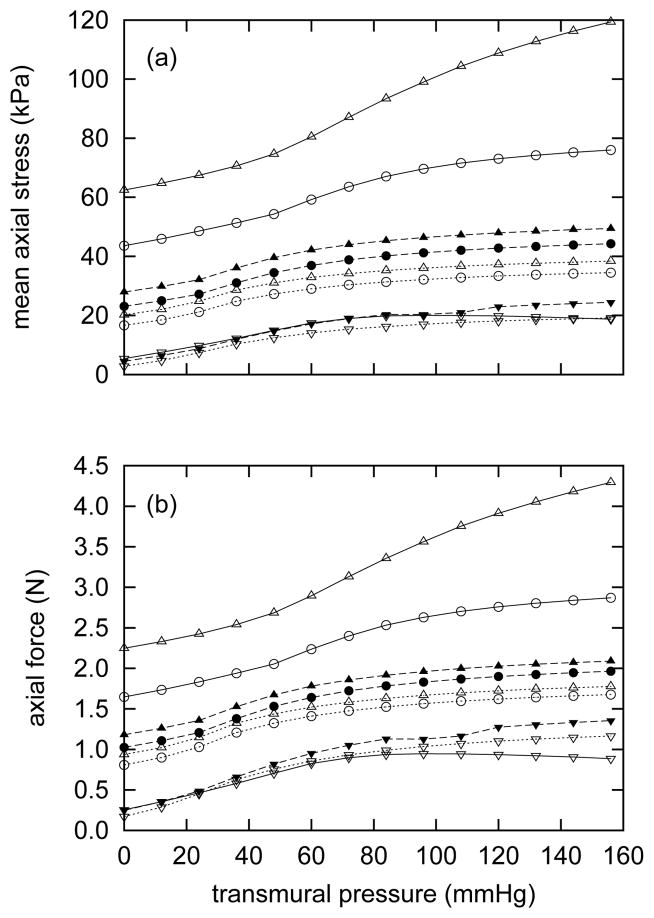
Figure 12 shows evolving mean axial stress- and force-pressure behaviors at three different axial stretches. The predicted behavior at time s = 0 is qualitatively similar to that observed in abdominal aorta in rats112. As time advances and the artery loses elastin but thickens, mean axial stresses decrease at all stretches (figure 12, panel a). One can further appreciate the loss of highly-prestretched elastin by noting that axial forces at all stretches (figure 12, panel b) also decrease over time, despite the substantial thickening. Axial force is closely related to collagen to elastin ratio55, whereas the mean axial stress also depends on total wall thickness. These results are intuitively consistent with a thickening artery with a decreasing retraction stretch.
Figure 12.
Evolving passive axial stress (panel a) and axial force (panel b) as functions of transmural pressure. Curves represent responses at axial stretches of λ = 1.05 (triangles), λ = 1.0 (circles) and λ = 0.8 (inverted triangles) at actual ages of 20 years (open symbols with solid lines) 50 years (filled symbols with dashed lines), and 60 years (open symbols with dotted lines). All results for βc = 0.2. Note the generally decreasing trends for both mean axial stress and retraction force, consistent with the increased arterial thicknesses (figure 7) and unloaded lengths (figure 9, panel a).
Overall, these computational results graphically illustrate the importance of functional elastin to passive behavior. The necessarily increased collagen to elastin ratio, resulting from progressive elastin degradation and collagen production, has a strong influence on the passive pressure-radius behavior (figure 13). The predicted response of the healthy artery shows a sigmoidal shape characteristic of elastic arteries112. As the artery ages, this sigmoidal trend becomes less pronounced, and eventually approaches a response more like that of a collagenous tissue. Although the artery becomes more distensible at lower pressure, stiffer collagen and smooth muscle contribute disproportionally more to the overall mechanical response at higher pressures. This prediction is consistent with work by Dobrin et al. 26 and Fonck et al. 34 that show that degradation of elastin causes arteries to distend more in response to pressurization, particularly at lower pressures (for example, 165% distension relative to control at 25 mmHg and 131% at 100 mmHg26). Over time, the passive response at higher pressures is predicted to stiffen continually as collagen and muscle accumulate. Collagen and muscle, with their relatively low respective deposition stretches of 1.08 and 1.2, cannot serve as appropriate substitutes for elastin, herein assumed to have a prestretch G̃e = 1.3, in normalcy.
Figure 13.
Evolving passive pressure-radius behavior at indicated actual ages at the in vivo length l(0). Inner radius ri(s, P) is normalized with respect to the current unpressurized inner radius ri(s, P = 0 mmHg). Results for βc = 0.2. Note the strongly sigmoidal behavior at time s = 0, characteristic of large elastic arteries. As elastin degrades and stiffening collagen accumulates, the sigmoidal behavior diminishes and the curves shift to the left at physiologic pressures.
5 Discussion
The present model predicts that gradual removal of elastin and reduction in vasoactivity initiates a complex G&R sequence, resulting in differential growth within the arterial wall. Radial expansion occurs due to the loss of highly prestretched elastin, coupled with a diminished ability to actively maintain inner radius. The behaviors predicted by simulating coupled elastin loss and vasoactive dysfunction (for example, substantial increased circumferential passive stiffening) are qualitatively similar to observed behaviors. The large increase in thickness, which requires sustained elevated production rates, and the dramatically altered passive behaviors are likely energetically unfavorable and thus represent suboptimal adaptations. As with many biological systems, arteries are remarkably fault-tolerant; multiple redundant mechanisms allow compensatory responses to instantaneous changes in metabolic demands as well as irreversible injuries or damage to elastin. Interestingly, the predicted trends suggest that stiffening of collagen is one such local compensatory mechanism. Depending on the degree of stiffening, this phenomenon could limit dilatation and perhaps prevent the development of an aneurysm by steering the trajectory of G&R away from a “run-away” unbounded luminal expansion. That is, the model predicts what is essentially a long-term competition between radial expansion and collagenous stiffening. As in many compensatory adaptations, however, the complexities of the arterial system reveal that there could also be detrimental consequences of an otherwise favorable occurrence. Stiffening of the abdominal aorta affects the hemodynamics, including an increase in the local pulse wave velocity that could affect cardiac function as well as adaptations in other regions of the vasculature41,66,83. There is, therefore, a pressing need to integrate G&R codes within models of the hemodynamics to understand more fully not only the effects of cell and matrix turnover on wall mechanics but also overall system dynamics54. Indeed, Greenwald 41 puts it this way: “As the conduit arteries age, changes in their composition and structure lead inexorably to an increase in the stiffness of their walls, resulting … in raised systolic and pulse pressure and greater mechanical load on the left ventricle, the systemic circulation as a whole and a consequent increase in the risk of stroke, myocardial infarction, renal failure and other sequelae of essential hypertension.”
Conspicuous arterial changes due to aging include an increased wall stiffness (due in part to an increased collagen-to-elastin ratio) that increases systolic and pulse pressure (due in part to an increased pulse wave velocity and corresponding pressure augmentation due to earlier wave reflections) as well as an increased caliber despite neointimal thickening, a lengthening of loosely tethered arteries such as the abdominal aorta, and decreased contractility and/or so-called endothelial dysfunction41,58,83. Notwithstanding the utility of the collagen-to-elastin ratio in many correlative studies, in aging the diminished, remaining elastin often shows signs of disorganization, fragmentation, or calcification whereas the collagen tends to have increased cross-linking (i.e., glycation-based cross-links in addition to normal enzymatic-based cross-links9,84); together, these effects on hemodynamics and wall mechanobiology exacerbate those due to the increased collagen-to-elastin ratio. Amongst the many biochemomechanical changes in aging arteries, it appears that there is a decrease in flow-induced NO production and corresponding increase in ET-1, ACE, ANG-II, and AT1 receptors111, which together promote increased MMP-2 production and smooth muscle proliferation, migration (into the intima), and synthesis of collagen via increased TGF-β28,88.
Whereas our study was motivated primarily by effects of aging on the abdominal aorta, which among other things increases risk for the development of atherosclerosis or aneurysms, our results are also likely relevant to arterial adaptations/maladaptations in both hypertension and Marfan syndrome. It has been suggested that essential hypertension can lead to “elastic fibre fatigue and accelerated degradation, leading to loss of arterial wall resilience”3. Indeed, this hypothesis finds support via in vitro mechanical studies by Lillie and Gosline 70 that show that long-term cyclic loading can cause elastic fibers to fail at extensions well less than normal; they propose that this fatigue-type damage may initiate due to a failure of or separation from microfibrils, not elastin per se. It is possible that elastin fragmentation occurs as a result of fatigue41,70.
Marfan patients have dramatically reduced levels of the elastin-associated microfibril fibrillin-187 and frequently present with fragmented elastic laminae. Mouse models of Marfan syndrome suggest that a “breach of the internal or external elastic laminae in fibrillin-1-deficient mice allows infiltration of inflammatory cells into the media, resulting in intense elastolysis that contributes to the structural collapse of the aortic wall”23. Finally, Marfan syndrome patients tend to suffer from dissections of the ascending aorta. One key question is, Why this particular site? It is interesting that the collagen-to-elastin ratio is remarkably low in the ascending aorta (0.49 based on values of 19.6% collagen and 41.1% elastin in the canine24, which are consistent with values from Leung et al. 68 of 0.23 based on 11% collagen and 48% collagen in the rabbit). Note, too, that the ascending aorta is unique in that it experiences considerable axial and torsional deformations during the cardiac cycle.
6 Conclusions
Gleason et al. 40 and Gleason and Humphrey 39 showed computationally that allowing elastin to turnover may enable optimal arterial adaptations to increased blood flow and blood pressure, as in normal development, but disallowing elastin to turnover may lead to “sub-optimal” adaptations. Despite the ability of vascular cells to produce new elastin in the mature arterial wall in response to disease or injury, potential reparative processes are generally not effective3,64, perhaps due to the inability to recapitulate all of the necessary temporal and spatial processes that occur in development58,109. Indeed, elastin fragments can stimulate smooth muscle proliferation, migration, and synthesis of collagen, perhaps by interacting with elastin-laminin receptors, opening calcium channels, and activating tyrosine kinase signaling pathways3.
The present work highlights the importance of the complementary effects of elastin content and vasoactivity in normal (healthy) vascular function. As previous computational studies suggest104,107, these complementary roles endow arteries with a number of unique properties that optimize structure and function. In particular, elastin production and cross-linking during development provide a highly elastic material that “remembers,” by way of its biological stability, a preferred state. Active smooth muscle plays a similar role in controlling a preferred inner radius. The passive mechanical behaviors of collagen and smooth muscle also seem to be tuned to optimize an artery’s behavior for a particular role. This remarkable system gives rise to a high degree of optimization via some constant cellular behaviors; synthetic and force generating cells follow the same general guidelines throughout the vascular tree, but diverse conditions during development result in correspondingly diverse vascular function.
Degradation of elastin results in an immediate increase in vascular caliber and decrease in passive wall stiffness34, but it also likely stimulates a marked increased production of collagen and thus additional stiffening. Passive stiffening is a characteristic of aging arteries13,44,83, and degradation and loss of elastin have been proposed as defining characteristics of aged arteries41,82. Hypertension results in increased medial collagen and arterial stiffness48,49, and is also associated with changed unloaded geometry56,103. Unloaded axial lengths increase as collagen to elastin ratios increase27,34. This also occurs as arteries age81. The manifold deleterious consequences of increased arterial stiffness are varied and described elsewhere41.
Development of the arterial system, like other organ systems, occurs via complementary effects of unique genetic instructions and an associated series of temporally synchronized biochemomechanical cues throughout relevant intervals, which endow arteries with their functionally distinctive properties within the vascular tree110. This progression gradually transforms the arterial system from its initial embryonic state to a highly optimized system, in what we call maturity. We posit that aging can be considered similarly; its progression is, in part, genetically preprogrammed but occurs after maturity. As in the cases of perinatal development, the process of arterial aging depends upon genetic predispositions and epigenetic factors, including lifestyle habits, health history, and any pharmacological and/or surgical interventions. Clearly, an understanding of arterial aging rests upon insights into the internal state of the mature artery, which in turn arises from early developmental processes. Although phenotypic expression of genetic information and modes of G&R likely differ in early development and aging, fundamental mechanisms (i.e., vasoactivity, constituent turnover, and deposition prestretches) are presumably operative in both situations.
Continual improvements in understanding of arterial development, physiology, and pathologies notwithstanding, our ability to identify and characterize detailed interactions remains limited. Scientific investigators have historically advanced the state of knowledge by identifying or theorizing important mechanisms and proposing general principles by which these mechanisms operate, despite the obstacle that details concerning how these functions manifest physically often remain unclear. Similarly, the study of arterial biomechanics has progressed via iteratively refined conceptual models, based on intuition, observation, and well-understood principles of physiology and continuum mechanics104,105. It is our hope that although comprehensive knowledge of biochemomechanical cell/matrix interactions remains elusive due to conceptual or methodological limitations, theories and models, such as those described in this work, will continue to serve as guides by motivating future work.
Acknowledgments
This work was supported, in part, by NIH grant HL-086418 via the program, Collaborations with National Centers for Biomedical Computing (SimBios at Stanford University) and NIH grant HL-105297.
Appendix
We may define mass densities ρk(s) and mass density production rates mk(τ) with respect to the current mixture volume, as did Humphrey and Rajagopal52,53, yielding
| (A.1) |
where ρ(s) = Σkρk(s). This formulation exploits a constant total mass density (ρ(s) ≡ ρ(0) ∀s), thereby preserving the normal, intuitive physical interpretation for mass density. The primary disadvantage of this formulation is that mass densities are defined with respect to the current volume, thereby coupling the evolving volume to the solution.
We relate the rates of mass density production (also defined per current unit volume) to volumetric changes by writing
| (A.2) |
where m̃ = m − r is the net rate of change of local mass density (mass per current volume per time), m is the true rate of mass density production, r is the local rate of mass removal, ρ is the mass density, and
| (A.3) |
Note that equals the total mass within the evolving volume. Appropriate substitutions yield
| (A.4) |
or
| (A.5) |
Because ρ(0) = ρ(s) ∀ s and J = det F,
| (A.6) |
Finally, integrating and recalling that J(0) = 1, we obtain
| (A.7) |
This last equation reminds the reader that the spatial approach results in a coupled solution for volume and mass density.
As described in §2.3, one can formulate the problem without requiring constant apparent mass density. By defining mass density and strain energy in terms of the original reference volume, we can exploit a more convenient approach in which strain energy does not depend on a current reference volume, while still preserving Σφk = 1, as desired.
References
- 1.Alford PW, Humphrey JD, Taber LA. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech Model Mechanobiol. 2008;7(4):245–262. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Aronson D. Cross-linking of glycated collagen in the pathogenesis of arterial and myocardial stiffening of aging and diabetes. J Hypertens. 2003;21(1):3–12. doi: 10.1097/00004872-200301000-00002. [DOI] [PubMed] [Google Scholar]
- 3.Arribas SM, Hinek A, Gonzalez MC. Elastic fibres and vascular structure in hypertension. Pharmacol Ther. 2006;111(3):771–791. doi: 10.1016/j.pharmthera.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 4.Åstrand H, Rydén-Ahlgren Å, Sandgren T, Länne T. Age-related increase in wall stress of the human abdominal aorta: An in vivo study. J Vasc Surg. 2005;42(5):926–931. doi: 10.1016/j.jvs.2005.07.010. [DOI] [PubMed] [Google Scholar]
- 5.Badreck-Amoudi A, Patel CK, Kane TP, Greenwald SE. The effect of age on residual strain in the rat aorta. J Biomech Eng. 1996;118(4):440–444. doi: 10.1115/1.2796029. [DOI] [PubMed] [Google Scholar]
- 6.Baek S, Rajagopal KR, Humphrey JD. Competition between radial expansion and thickening in the enlargement of an intracranial saccular aneurysm. J Elasticity. 2005;80(19):13–31. [Google Scholar]
- 7.Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128(1):142–9. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- 8.Baek S, Valentín A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: II. constitutive relations and model simulations. Ann Biomed Eng. 2007;35(9):1498–1509. doi: 10.1007/s10439-007-9322-x. [DOI] [PubMed] [Google Scholar]
- 9.Bailey AJ, Paul RG, Knott L. Mechanisms of maturation and ageing of collagen. Mech Ageing Dev. 1998;106(1–2):1–56. doi: 10.1016/s0047-6374(98)00119-5. [DOI] [PubMed] [Google Scholar]
- 10.Bendeck MP, Langille BL. Rapid accumulation of elastin and collagen in the aortas of sheep in the immediate perinatal period. Circ Res. 1991;69(4):1165–9. doi: 10.1161/01.res.69.4.1165. [DOI] [PubMed] [Google Scholar]
- 11.Bendeck MP, Keeley FW, Langille BL. Perinatal accumulation of arterial wall constituents: relation to hemodynamic changes at birth. Am J Physiol. 1994;267(6 Pt 2):H2268–79. doi: 10.1152/ajpheart.1994.267.6.H2268. [DOI] [PubMed] [Google Scholar]
- 12.Bendeck MP, Irvin C, Reidy M, Smith L, Mulholland D, Horton M, Giachelli CM. Smooth muscle cell matrix metalloproteinase production is stimulated via αvβ3 integrin. Arterioscler Thromb Vasc Biol. 2000;20(6):1467–72. doi: 10.1161/01.atv.20.6.1467. [DOI] [PubMed] [Google Scholar]
- 13.Briones AM, Gonzalez JM, Somoza B, Giraldo J, Daly CJ, Vila E, Gonzalez MC, McGrath JC, Arribas SM. Role of elastin in spontaneously hypertensive rat small mesenteric artery remodelling. J Physiol. 2003;552(Pt 1):185–195. doi: 10.1113/jphysiol.2003.046904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cardamone L, Valentín A, Eberth J, Humphrey J. Origin of axial prestretch and residual stress in arteries. Biomech Model Mechanobiol. 2009;8(6):431–446. doi: 10.1007/s10237-008-0146-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cardamone L, Valentín A, Eberth JF, Humphrey JD. Modelling carotid artery adaptations to dynamic alterations in pressure and flow over the cardiac cycle. Math Med Biol. 2010 doi: 10.1093/imammb/dqq001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen JK, Haimes HB, Weinberg CB. Role of growth factors in the contraction and maintenance of collagen lattices made with arterial smooth muscle cells. J Cell Physiol. 1991;146(1):110–116. doi: 10.1002/jcp.1041460115. [DOI] [PubMed] [Google Scholar]
- 17.Cho A, Courtman DW, Langille BL. Apoptosis (programmed cell death) in arteries of the neonatal lamb. Circ Res. 1995;76(2):168–75. doi: 10.1161/01.res.76.2.168. [DOI] [PubMed] [Google Scholar]
- 18.Chuong CJ, Fung YC. On residual stresses in arteries. J Biomech Eng. 1986;108(2):189–92. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- 19.Czirok A, Zamir EA, Filla MB, Little CD, Rongish BJ, Schatten GP. Extracellular Matrix Macroassembly Dynamics in Early Vertebrate Embryos. Vol. 73. Academic Press; 2006. pp. 237–258. [DOI] [PubMed] [Google Scholar]
- 20.Dajnowiec D, Langille BL. Arterial adaptations to chronic changes in haemodynamic function: coupling vasomotor tone to structural remodelling. Clin Sci (Lond) 2007;113(1):15–23. doi: 10.1042/CS20060337. [DOI] [PubMed] [Google Scholar]
- 21.Davidson JM, Hill KE, Alford JL. Developmental changes in collagen and elastin biosynthesis in the porcine aorta. Dev Biol. 1986;118(1):103–111. doi: 10.1016/0012-1606(86)90077-1. [DOI] [PubMed] [Google Scholar]
- 22.Del Corso L, Moruzzo D, Conte B, Agelli M, Romanelli AM, Pastine F, Protti M, Pentimone F, Baggiani G. Tortuosity, kinking, and coiling of the carotid artery: expression of atherosclerosis or aging? Angiology. 1998;49(5):361–371. doi: 10.1177/000331979804900505. [DOI] [PubMed] [Google Scholar]
- 23.Dietz HC, Mecham RP. Mouse models of genetic diseases resulting from mutations in elastic fiber proteins. Matrix Biol. 2000;19(6):481–488. doi: 10.1016/s0945-053x(00)00101-3. [DOI] [PubMed] [Google Scholar]
- 24.Dobrin P. chapter Physiology and pathophysiology of blood vessels. Futura; New York: 1997. The Basic Science of Vascular Disease; pp. 69–105. [Google Scholar]
- 25.Dobrin PB, Canfield TR. Elastase, collagenase, and the biaxial elastic properties of dog carotid artery. Am J Physiol Heart Circ Physiol. 1984;247(1):H124–131. doi: 10.1152/ajpheart.1984.247.1.H124. [DOI] [PubMed] [Google Scholar]
- 26.Dobrin PB, Baker WH, Gley WC. Elastolytic and collagenolytic studies of arteries. implications for the mechanical properties of aneurysms. Arch Surg. 1984;119(4):405–409. doi: 10.1001/archsurg.1984.01390160041009. [DOI] [PubMed] [Google Scholar]
- 27.Dobrin PB, Schwarcz TH, Mrkvicka R. Longitudinal retractive force in pressurized dog and human arteries. J Surg Res. 1990;48(2):116–20. doi: 10.1016/0022-4804(90)90202-d. [DOI] [PubMed] [Google Scholar]
- 28.Dooley A, Gao B, Shi-Wen X, Abraham DJ, Black CM, Jacobs M, Bruckdorfer KR. Effect of nitric oxide and peroxynitrite on type I collagen synthesis in normal and scleroderma dermal fibroblasts. Free Radic Biol Med. 2007;43(2):253–264. doi: 10.1016/j.freeradbiomed.2007.04.017. [DOI] [PubMed] [Google Scholar]
- 29.Dorrington K, McCrum N. Elastin as a rubber. Biopolymers. 1977;16(6):1201–1222. doi: 10.1002/bip.1977.360160604. [DOI] [PubMed] [Google Scholar]
- 30.Dua MM, Miyama N, Azuma J, Schultz GM, Sho M, Morser J, Dalman RL. Hyperglycemia modulates plasminogen activator inhibitor-1 expression and aortic diameter in experimental aortic aneurysm disease. Surgery. 2010;148(2):429–435. doi: 10.1016/j.surg.2010.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Faury G. Function-structure relationship of elastic arteries in evolution: from microfibrils to elastin and elastic fibres. Pathologie Biologie. 2001;49(4):310–325. doi: 10.1016/s0369-8114(01)00147-x. [DOI] [PubMed] [Google Scholar]
- 32.Feldman SA, Glagov S. Transmedial collagen and elastin gradients in human aortas: Reversal with age. Atherosclerosis. 1971;13(3):385–394. doi: 10.1016/0021-9150(71)90081-5. [DOI] [PubMed] [Google Scholar]
- 33.Figueroa CA, Baek S, Taylor CA, Humphrey JD. A computational framework for fluid-solid-growth modeling in cardiovascular simulations. Comput Meth Appl Mech Eng. 2009;198(45–46):3583–3602. doi: 10.1016/j.cma.2008.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fonck E, Prod’hom G, Roy S, Augsburger L, Rüfenacht DA, Stergiopulos N. Effect of elastin degradation on carotid wall mechanics as assessed by a constituent-based biomechanical model. Am J Physiol Heart Circ Physiol. 2007;292(6):H2754–63. doi: 10.1152/ajpheart.01108.2006. [DOI] [PubMed] [Google Scholar]
- 35.Fung YC. Biomechanics: Motion, Flow, Stress, and Growth. Springer; 1990. [Google Scholar]
- 36.Galis ZS, Khatri JJ. Matrix metalloproteinases in vascular remodeling and atherogenesis: The good, the bad, and the ugly. Circ Res. 2002;90(3):251–262. [PubMed] [Google Scholar]
- 37.Garanich JS, Pahakis M, Tarbell JM. Shear stress inhibits smooth muscle cell migration via nitric oxide-mediated downregulation of matrix metalloproteinase-2 activity. AJP - Heart and Circulatory Physiology. 2005;288(5):H2244–2252. doi: 10.1152/ajpheart.00428.2003. [DOI] [PubMed] [Google Scholar]
- 38.Gineyts E, Cloos PA, Borel O, Grimaud L, Delmas PD, Garnero P. Racemization and isomerization of type I collagen c-telopeptides in human bone and soft tissues: assessment of tissue turnover. Biochem J. 2000;345(Pt 3):481–485. [PMC free article] [PubMed] [Google Scholar]
- 39.Gleason RL, Humphrey JD. A mixture model of arterial growth and remodeling in hypertension: altered muscle tone and tissue turnover. J Vasc Res. 2004;41(4):352–63. doi: 10.1159/000080699. [DOI] [PubMed] [Google Scholar]
- 40.Gleason RL, Taber LA, Humphrey JD. A 2-d model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J Biomech Eng. 2004;126(3):371–81. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- 41.Greenwald SE. Ageing of the conduit arteries. J Pathol. 2007;211(2):157–172. doi: 10.1002/path.2101. [DOI] [PubMed] [Google Scholar]
- 42.Greenwald SE, Moore JE, Rachev A, Kane TPC, Meister JJ. Experimental investigation of the distribution of residual strains in the artery wall. J Biomech Eng. 1997;119(4):438–444. doi: 10.1115/1.2798291. [DOI] [PubMed] [Google Scholar]
- 43.Greve JM, Les AS, Tang BT, Draney Blomme MT, Wilson NM, Dalman RL, Pelc NJ, Taylor CA. Allometric scaling of wall shear stress from mice to humans: quantification using cine phase-contrast mri and computational fluid dynamics. Am J Physiol Heart Circ Physiol. 2006;291(4):H1700–1708. doi: 10.1152/ajpheart.00274.2006. [DOI] [PubMed] [Google Scholar]
- 44.Hayashi K, Handa H, Nagasawa S, Okumura A, Moritake K. Stiffness and elastic behavior of human intracranial and extracranial arteries. J Biomech. 1980;13(2):175–184. doi: 10.1016/0021-9290(80)90191-8. [DOI] [PubMed] [Google Scholar]
- 45.Holzapfel GA, Ogden RW. Biomechanics of Soft Tissue in Cardiovascular Systems. Springer-Verlag; Vienna, New York: 2003. [Google Scholar]
- 46.Holzapfel GA, Ogden RW. Modelling the layer-specific 3d residual stresses in arteries, with an application to the human aorta. J R Soc Interface. 2010;7:787–799. doi: 10.1098/rsif.2009.0357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elasticity. 2000;61(1–3):1–48. [Google Scholar]
- 48.Hu JJ, Baek S, Humphrey JD. Stress-strain behavior of the passive basilar artery in normotension and hypertension. J Biomech. 2007;40(11):2559–2563. doi: 10.1016/j.jbiomech.2006.11.007. [DOI] [PubMed] [Google Scholar]
- 49.Hu JJ, Fossum TW, Miller MW, Xu H, Liu JC, Humphrey JD. Biomechanics of the porcine basilar artery in hypertension. Ann Biomed Eng. 2007;35(1):19–29. doi: 10.1007/s10439-006-9186-5. [DOI] [PubMed] [Google Scholar]
- 50.Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York: 2002. [Google Scholar]
- 51.Humphrey JD, Na S. Elastodynamics and arterial wall stress. Ann Biomed Eng. 2002;30(4):509–523. doi: 10.1114/1.1467676. [DOI] [PubMed] [Google Scholar]
- 52.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Models Methods Appl Sci. 2002;12(3):407–30. [Google Scholar]
- 53.Humphrey JD, Rajagopal KR. A constrained mixture model for arterial adaptations to a sustained step change in blood flow. Biomech Model Mechanobiol. 2003;2(2):109–26. doi: 10.1007/s10237-003-0033-4. [DOI] [PubMed] [Google Scholar]
- 54.Humphrey JD, Taylor CA. Intracranial and abdominal aortic aneurysms: Similarities, differences, and need for a new class of computational models. Annu Rev Biomed Eng. 2008;10(1):221–46. doi: 10.1146/annurev.bioeng.10.061807.160439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Humphrey JD, Eberth JF, Dye WW, Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. Journal of biomechanics. 2009;42(1):1–8. doi: 10.1016/j.jbiomech.2008.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jackson ZS, Gotlieb AI, Langille BL. Wall tissue remodeling regulates longitudinal tension in arteries. Circ Res. 2002;90(8):918–25. doi: 10.1161/01.res.0000016481.87703.cc. [DOI] [PubMed] [Google Scholar]
- 57.Jackson ZS, Dajnowiec D, Gotlieb AI, Langille BL. Partial off-loading of longitudinal tension induces arterial tortuosity. Arterioscler Thromb Vasc Biol. 2005;25(5):957–962. doi: 10.1161/01.ATV.0000161277.46464.11. [DOI] [PubMed] [Google Scholar]
- 58.Jacob MP. Extracellular matrix remodeling and matrix metalloproteinases in the vascular wall during aging and in pathological conditions. Biomed Pharmacother. 2003;57(5–6):195–202. doi: 10.1016/s0753-3322(03)00065-9. [DOI] [PubMed] [Google Scholar]
- 59.Karnik SK, Brooke BS, Bayes-Genis A, Sorensen L, Wythe JD, Schwartz RS, Keating MT, Li DY. A critical role for elastin signaling in vascular morphogenesis and disease. Development. 2003;130(2):411–23. doi: 10.1242/dev.00223. [DOI] [PubMed] [Google Scholar]
- 60.Kar saj I, Sorić J, Humphrey J. A 3-D framework for arterial growth and remodeling in response to altered hemodynamics. Int J Engr Sci. 2010 doi: 10.1016/j.ijengsci.2010.06.033. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kelleher CM, McLean SE, Mecham RP. Vascular extracellular matrix and aortic development. Curr Top Dev Biol. 2004;62:153–88. doi: 10.1016/S0070-2153(04)62006-0. [DOI] [PubMed] [Google Scholar]
- 62.Kielty CM, Wess TJ, Haston L, Ashworth JL, Sherratt MJ, Shuttleworth CA. Fibrillin-rich microfibrils: elastic biopolymers of the extracellular matrix. J Muscle Res Cell Motil. 2002;23(5–6):581–96. [PubMed] [Google Scholar]
- 63.Kozel BA, Rongish BJ, Czirok A, Zach J, Little CD, Davis EC, Knutsen RH, Wagenseil JE, Levy MA, Mecham RP. Elastic fiber formation: a dynamic view of extracellular matrix assembly using timer reporters. J Cell Physiol. 2006;207(1):87–96. doi: 10.1002/jcp.20546. [DOI] [PubMed] [Google Scholar]
- 64.Krettek A, Sukhova GK, Libby P. Elastogenesis in human arterial disease: A role for macrophages in disordered elastin synthesis. Arterioscler Thromb Vasc Biol. 2003;23(4):582–587. doi: 10.1161/01.ATV.0000064372.78561.A5. [DOI] [PubMed] [Google Scholar]
- 65.Kucharz E. The Collagens, Biochemistry and Pathophysiology. Springer-Verlag; Berlin: 1992. [Google Scholar]
- 66.Lakatta EG, Wang M, Najjar SS. Arterial aging and subclinical arterial disease are fundamentally intertwined at macroscopic and molecular levels. Med Clin North Am. 2009;93(3):583–604. doi: 10.1016/j.mcna.2009.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Langille BL. Remodeling of developing and mature arteries: endothelium, smooth muscle, and matrix. J Cardiovasc Pharmacol. 1993;21:S11–7. doi: 10.1097/00005344-199321001-00003. [DOI] [PubMed] [Google Scholar]
- 68.Leung DY, Glagov S, Mathews MB. Elastin and collagen accumulation in rabbit ascending aorta and pulmonary trunk during postnatal growth. correlation of cellular synthetic response with medial tension. Circ Res. 1977;41(3):316–23. doi: 10.1161/01.res.41.3.316. [DOI] [PubMed] [Google Scholar]
- 69.Levy BI, Tedgui A. Biology of the Arterial Wall. Kluwer Academic; Dordrecht: 1999. [Google Scholar]
- 70.Lillie MA, Gosline JM. Limits to the durability of arterial elastic tissue. Biomaterials. 2007;28(11):2021–2031. doi: 10.1016/j.biomaterials.2007.01.016. [DOI] [PubMed] [Google Scholar]
- 71.Liu SQ, Fung YC. Zero-stress states of arteries. J Biomech Eng. 1988;110(1):82–4. doi: 10.1115/1.3108410. [DOI] [PubMed] [Google Scholar]
- 72.Malek A, Izumo S. Physiological fluid shear stress causes downregulation of endothelin-1 mRNA in bovine aortic endothelium. Am J Physiol. 1992;263(2 Pt 1):C389–96. doi: 10.1152/ajpcell.1992.263.2.C389. [DOI] [PubMed] [Google Scholar]
- 73.Malek AM, Izumo S. Control of endothelial cell gene expression by flow. J Biomech. 1995;28(12):1515–1528. doi: 10.1016/0021-9290(95)00099-2. [DOI] [PubMed] [Google Scholar]
- 74.Mithieux SM, Weiss AS. Elastin. Adv Protein Chem. 2005;70:437–61. doi: 10.1016/S0065-3233(05)70013-9. [DOI] [PubMed] [Google Scholar]
- 75.Miyama N, Dua MM, Yeung JJ, Schultz GM, Asagami T, Sho E, Sho M, Dalman RL. Hyperglycemia limits experimental aortic aneurysm progression. J Vasc Surg. 2010;52(4):975–983. doi: 10.1016/j.jvs.2010.05.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mondy JS, Lindner V, Miyashiro JK, Berk BC, Dean RH, Geary RL. Platelet-derived growth factor ligand and receptor expression in response to altered blood flow in vivo. Circ Res. 1997;81(3):320–327. doi: 10.1161/01.res.81.3.320. [DOI] [PubMed] [Google Scholar]
- 77.Nichol J, Khan A, Birbach M, Gaynor J, Gooch K. Hemodynamics and axial strain additively increase matrix remodeling and mmp-9, but not mmp-2, expression in arteries engineered by directed remodeling. Tissue Eng Part A. 2008 doi: 10.1089/ten.tea.2008.0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Nichols W, O’Rourke M. McDonald’s Blood Flow in Arteries. 3. Edward Arnold; London: 1990. [Google Scholar]
- 79.Niedermüller H, Skalicky M, Hofecker G, Kment A. Investigations on the kinetics of collagen-metabolism in young and old rats. Exp Gerontol. 1977;12(5–6):159–68. doi: 10.1016/0531-5565(77)90001-8. [DOI] [PubMed] [Google Scholar]
- 80.O’Callaghan CJ, Williams B. Mechanical strain-induced extracellular matrix production by human vascular smooth muscle cells: role of TGF-β1. Hypertension. 2000;36(3):319–24. doi: 10.1161/01.hyp.36.3.319. [DOI] [PubMed] [Google Scholar]
- 81.Okamoto RJ, Xu H, Kouchoukos NT, Moon MR, Sundt TM., III The influence of mechanical properties on wall stress and distensibility of the dilated ascending aorta. J Thorac Cardiovasc Surg. 2003;126(3):842–50. doi: 10.1016/s0022-5223(03)00728-1. [DOI] [PubMed] [Google Scholar]
- 82.O’Rourke MF. Arterial aging: pathophysiological principles. Vasc Med. 2007;12(4):329–341. doi: 10.1177/1358863X07083392. [DOI] [PubMed] [Google Scholar]
- 83.O’Rourke MF, Hashimoto J. Mechanical factors in arterial aging: A clinical perspective. J Am Coll Cardiol. 2007;50(1):1–13. doi: 10.1016/j.jacc.2006.12.050. [DOI] [PubMed] [Google Scholar]
- 84.Pedrigi RM, Staff E, David G, Glenn S, Humphrey JD. Altered multiaxial mechanical properties of the porcine anterior lens capsule cultured in high glucose. J Biomech Eng. 2007;129(1):121–125. doi: 10.1115/1.2401192. [DOI] [PubMed] [Google Scholar]
- 85.Rabinovitch M. Pulmonary hypertension: pathophysiology as a basis for clinical decision making. J Heart Lung Transplant. 1999;18(11):1041–1053. doi: 10.1016/s1053-2498(99)00015-7. [DOI] [PubMed] [Google Scholar]
- 86.Rachev A, Greenwald SE. Residual strains in conduit arteries. J Biomech. 2003;36(5):661–670. doi: 10.1016/s0021-9290(02)00444-x. [DOI] [PubMed] [Google Scholar]
- 87.Ramirez F, Pereira L. Mutations of extracellular matrix components in vascular disease. Ann Thorac Surg. 1999;67(6):1857–8. doi: 10.1016/s0003-4975(99)00437-3. discussion 1868–70. [DOI] [PubMed] [Google Scholar]
- 88.Rizvi MAD, Myers PR. Nitric oxide modulates basal and endothelin-induced coronary artery vascular smooth muscle cell proliferation and collagen levels. J Mol Cell Cardiol. 1997;29(7):1779–1789. doi: 10.1006/jmcc.1996.0480. [DOI] [PubMed] [Google Scholar]
- 89.Rizvi MAD, Katwa L, Spadone DP, Myers PR. The effects of endothelin-1 on collagen type I and type III synthesis in cultured porcine coronary artery vascular smooth muscle cells. J Mol Cell Cardiol. 1996;28(2):243–252. doi: 10.1006/jmcc.1996.0023. [DOI] [PubMed] [Google Scholar]
- 90.Rodriguez-Feo JA, Sluijter JPG, de Kleijn DPV, Pasterkamp G. Modulation of collagen turnover in cardiovascular disease. Curr Pharm Des. 2005;11(19):2501–2514. doi: 10.2174/1381612054367544. [DOI] [PubMed] [Google Scholar]
- 91.Ruberti JW, Hallab NJ. Strain-controlled enzymatic cleavage of collagen in loaded matrix. Biochem Biophys Res Commun. 2005;336(2):483–489. doi: 10.1016/j.bbrc.2005.08.128. [DOI] [PubMed] [Google Scholar]
- 92.Safar ME. Arterial aging–hemodynamic changes and therapeutic options. Nat Rev Cardiol. 2010;7(8):442–449. doi: 10.1038/nrcardio.2010.96. [DOI] [PubMed] [Google Scholar]
- 93.Saini A, Berry C, Greenwald S. Effect of age and sex on residual stress in the aorta. J Vasc Res. 1995;32(6):398–405. doi: 10.1159/000159115. [DOI] [PubMed] [Google Scholar]
- 94.Seliktar D, Nerem R, Galis Z. The role of matrix metalloproteinase-2 in the remodeling of cell-seeded vascular constructs subjected to cyclic strain. Ann Biomed Eng. 2001;29(11):923–934. doi: 10.1114/1.1415522. [DOI] [PubMed] [Google Scholar]
- 95.Seliktar D, Nerem RM, Galis ZS. Mechanical strain-stimulated remodeling of tissue-engineered blood vessel constructs. Tissue Eng. 2003;9(4):657–666. doi: 10.1089/107632703768247359. [DOI] [PubMed] [Google Scholar]
- 96.Sluijter JPG, Smeets MB, Velema E, Pasterkamp G, de Kleijn DPV. Increase in collagen turnover but not in collagen fiber content is associated with flow-induced arterial remodeling. J Vasc Res. 2004;41(6):546–55. doi: 10.1159/000081972. [DOI] [PubMed] [Google Scholar]
- 97.Stenmark KR, Mecham RP. Cellular and molecular mechanisms of pulmonary vascular remodeling. Annu Rev Physiol. 1997;59:89–144. doi: 10.1146/annurev.physiol.59.1.89. [DOI] [PubMed] [Google Scholar]
- 98.Stergiopulos N, Vulliemoz S, Rachev A, Meister JJ, Greenwald SE. Assessing the homogeneity of the elastic properties and composition of the pig aortic media. J Vasc Res. 2001;38(3):237–246. doi: 10.1159/000051052. [DOI] [PubMed] [Google Scholar]
- 99.Strauss BH, Chisholm RJ, Keeley FW, Gotlieb AI, Logan RA, Armstrong PW. Extracellular matrix remodeling after balloon angioplasty injury in a rabbit model of restenosis. Circ Res. 1994;75(4):650–8. doi: 10.1161/01.res.75.4.650. Print. [DOI] [PubMed] [Google Scholar]
- 100.Strauss BH, Robinson R, Batchelor WB, Chisholm RJ, Ravi G, Natarajan MK, Logan RA, Mehta SR, Levy DE, Ezrin AM, Keeley FW. In vivo collagen turnover following experimental balloon angioplasty injury and the role of matrix metalloproteinases. Circ Res. 1996;79(3):541–550. doi: 10.1161/01.res.79.3.541. [DOI] [PubMed] [Google Scholar]
- 101.Taber LA, Humphrey JD. Stress-modulated growth, residual stress, and vascular heterogeneity. J Biomech Eng. 2001;123(6):528–35. doi: 10.1115/1.1412451. [DOI] [PubMed] [Google Scholar]
- 102.Uematsu M, Ohara Y, Navas JP, Nishida K, Murphy TJ, Alexander RW, Nerem RM, Harrison DG. Regulation of endothelial cell nitric oxide synthase mRNA expression by shear stress. Am J Physiol. 1995;269(6 Pt 1):C1371–8. doi: 10.1152/ajpcell.1995.269.6.C1371. [DOI] [PubMed] [Google Scholar]
- 103.Vaishnav RN, Vossoughi J, Patel DJ, Cothran LN, Coleman BR, Ison-Franklin EL. Effect of hypertension on elasticity and geometry of aortic tissue from dogs. J Biomech Eng. 1990;112(1):70–74. doi: 10.1115/1.2891128. [DOI] [PubMed] [Google Scholar]
- 104.Valentín A, Humphrey JD. Evaluation of fundamental hypotheses underlying constrained mixture models of arterial growth and remodelling. Phil Trans R Soc Lond A. 2009;367(1902):3585–3606. doi: 10.1098/rsta.2009.0113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Valentín A, Humphrey JD. Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J Biomech Eng. 2009;131(10):101006. doi: 10.1115/1.3192144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Valentín A, Humphrey JD. Modeling effects of axial extension on arterial growth and remodeling. Med Biol Eng Comput. 2009;47(9):979–987. doi: 10.1007/s11517-009-0513-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Valentín A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J R Soc Interface. 2009;6(32):293–306. doi: 10.1098/rsif.2008.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Virmani R, Avolio AP, Mergner WJ, Robinowitz M, Herderick EE, Cornhill JF, Guo SY, Liu TH, Ou DY, O’Rourke M. Effect of aging on aortic morphology in populations with high and low prevalence of hypertension and atherosclerosis. Comparison between occidental and Chinese communities. Am J Pathol. 1991;139(5):1119–1129. [PMC free article] [PubMed] [Google Scholar]
- 109.Wagenseil JE, Mecham RP. New insights into elastic fiber assembly. Birth Defects Res C Embryo Today. 2007;81(4):229–240. doi: 10.1002/bdrc.20111. [DOI] [PubMed] [Google Scholar]
- 110.Wagenseil JE, Ciliberto CH, Knutsen RH, Levy MA, Kovacs A, Mecham RP. The importance of elastin to aortic development in mice. Am J Physiol Heart Circ Physiol. 2010 doi: 10.1152/ajpheart.00194.2010. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Wang M, Zhang J, Spinetti G, Jiang LQ, Monticone R, Zhao D, Cheng L, Krawczyk M, Talan M, Pintus G, Lakatta EG. Angiotensin II activates matrix metalloproteinase type II and mimics age-associated carotid arterial remodeling in young rats. Am J Pathol. 2005;167(5):1429–1442. doi: 10.1016/S0002-9440(10)61229-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Weizsäcker HW, Kampp TD. Passive elastic properties of the rat aorta. Biomed Tech (Berl) 1990;35(10):224–234. doi: 10.1515/bmte.1990.35.10.224. [DOI] [PubMed] [Google Scholar]
- 113.Wenn CM, Newman DL. Arterial tortuosity. Australas Phys Eng Sci Med. 1990;13(2):67–70. [PubMed] [Google Scholar]
- 114.Wicker BK, Hutchens HP, Wu Q, Yeh AT, Humphrey JD. Normal basilar artery structure and biaxial mechanical behaviour. Comput Meth Biomech Biomed Eng. 2008;11(5):539–551. doi: 10.1080/10255840801949793. [DOI] [PubMed] [Google Scholar]
- 115.Xu C, Zarins CK, Bassiouny HS, Briggs WH, Reardon C, Glagov S. Differential transmural distribution of gene expression for collagen types I and III proximal to aortic coarctation in the rabbit. J Vasc Res. 2000;37(3):170–82. doi: 10.1159/000025728. [DOI] [PubMed] [Google Scholar]
- 116.Zeller PJ, Skalak TC. Contribution of individual structural components in determining the zero-stress state in small arteries. J Vasc Res. 1998;35(1):8–17. doi: 10.1159/000025560. [DOI] [PubMed] [Google Scholar]