High-Resolution Solid Modeling of Biological Samples Imaged with 3D Fluorescence Microscopy

Abstract

Optical-sectioning, digital fluorescence microscopy provides images representing temporally- and spatially-resolved molecular-scale details of the substructures of living cells. To render such images into solid models for further computational analyses, we have developed an integrated system of image acquisition, processing, and rendering, which includes a new empirical technique to correct for axial distortions inherent in fluorescence microscopy due to refractive index mismatches between microscope objective immersion medium, coverslip glass, and water. This system takes advantage of the capabilities of ultra-high numerical aperture objectives (e.g. total internal reflection fluorescence microscopy) and enables faithful three-dimensional rendering of living cells into solid models amenable to further computational analysis. An example of solid modeling of bovine aortic endothelial cells and their nuclei is presented. Since many cellular level events are temporally and spatially confined, such integrated image acquisition, processing, rendering, and computational analysis, will enable, in silico, the generation of new computational models for cell mechanics and signaling.

INTRODUCTION

Three-dimensional imaging from optical sectioning microscopy is a well-accepted and routine method for elucidating time- and position-dependent molecular processes in single cells (Helmke et al., 2001; Poenie et al., 2004; Roux et al., 2004; Sleeman, 2004). Of particular interest is the improvement of image contrast and resolution through computational and physical methods of removing out-of-focus light from optical sections. For example, deconvolution methods computationally remove from the image the point-spread function of an optical system, which has been convolved with the light-emitting object. Confocal and multiphoton microscopy remove out-of-focus light through physical means: either by a pinhole placed in a conjugate image plane of a scanned laser (confocal) or by selective excitation of fluorophores at the focal point (2-photon). Although each of these methods has advantages and disadvantages related to the speed of acquisition, computational overhead, and cost, they all yield high-resolution, three-dimensional representations of molecular details of the substructures of living cells.

From such high-resolution studies, it is apparent that at all spatial and temporal scales, biological systems are complex and interconnected (Murakoshi et al., 2004; Tzima et al., 2002; Wang et al., 2005). Thus, mathematical modeling of cell mechanics, molecular messengers, their spatial localization, and temporal regulation can be a useful tool to summarize experimental data and predict, computationally, the response of a cell to external stimuli. Recent advances in optical fluorescence microscopy and computer power, and the commercial availability of advanced computational software, provide unique opportunities for routine cell-specific, subcellular level computational biology.

In this study, we developed an integrated platform of image acquisition, image processing, and solid-model rendering to enable finite element analysis (FEA) of the structure, mechanics, and function of living cells. With the exception of custom image processing algorithms for the correction of axial distortion and algorithms to convert 3D image data sets into solid models, this platform consisted entirely of commercially available hardware and software, thus providing researchers accessibility to versatile tools for 3D cellular computational modeling.

MATERIALS AND METHODS

Widefield Microscopy

The optical setup is based on an Olympus IX71 fluorescence microscope fitted with a xenon arc lamp (Olympus, Japan) for fluorescence excitation. The samples were mounted to the microscope on a piezoelectric z-stage (Mad City Labs, Madison, WI), to adjust focal depth (resolution ~1 nm), and a stepper-motor-driven stage for x,y-translational positioning (resolution ~20 nm) (MadCity Labs, Madison, WI). Widefield fluorescent images were acquired using a PlanApo 60x/1.45 NA TIRFM oil-immersion objective (Olympus, Japan) and a Sensicam QE CCD camera (Cooke, Romulus, MI). To minimize photobleaching, a TTL-modulated shutter (Uniblitz, Rochester, NY) was used to illuminate the sample only during image exposure. Z-stage movement, shutters, and camera triggers were coordinated through the use of a custom LabVIEW program and an A/D board (National Instruments, Austin, TX). The amount of z-stage movement was set to a constant 0.2 µm per image representing a slight over-sampling as determined by the Rayleigh depth of field (Autoquant Imaging, 2004).

The total sampling distance in the z-direction was approximately twice the full apparent depth of the object. Exposure time was adjusted to provide a peak grayscale value at ~80% of the maximum bin value for the camera (Autoquant Imaging, 2004).

Samples

Microphseres

FocalCheck™ polystyrene fluorescent beads (diameter 15 or 6 µm, index of refraction 1.5) (Molecular Probes, Carlsbad, CA) were dried onto no. 1 coverslips and immersed in oil with an index of refraction of 1.33 to simulate the aqueous biological environment. Beads immersed in water were also imaged as a comparison.

Confluent Endothelial Cells

Bovine aortic endothelial cells (BAECs) (passages 3–10) were grown to confluence in Dulbecco’s modified eagle medium supplemented with 10% fetal calf serum, 2 mM l-glutamine, 100 U/mL penicillin and streptomycin (BioSource, Camarillo, CA) in a culture well on a no. 1 coverslip (Labtek, Campbell, CA). The cytoplasm was stained with Calcein AM, and the nucleus was counterstained with Hoechst 33258 (Molecular Probes). Imaging was performed with cells in phosphate-buffered saline (PBS) and 1% albumin at room temperature (Biosource).

Empirical Axial Distortion Correction

The axial spacing of 2D images in a 3D image stack must be adjusted to account for axial distortions accompanying imaging through media with different indices of refraction (see Discussion for origins of axial distortion). To correct 3D data sets of cells with unknown axial dimensions, we developed an empirical, nonlinear axial distortion correction function (ADCF) based on 3D image stacks of fluorescent microspheres of known dimensions. FocalCheck™ fluorescent microspheres (Molecular Probes) (ex. = 488 nm, em. = 530 nm) were mounted in 1.33 index of refraction oil (Cargille Laboratories, Cedar Grove, NJ) and sealed between a no. 1 coverslip and a glass microslide. (Use of oil with an index of refraction that was equivalent to water preserved adhesion to the glass and axial distortion observed in aqueous solutions). A stack of 2D 16 bit images of a single well-isolated bead was acquired at 0.2 µm increments of the z-stage. These image sets were deconvolved in AutoDeblur (AutoQuant, Albany, NY) using 10 iterations of 3D blind deconvolution.

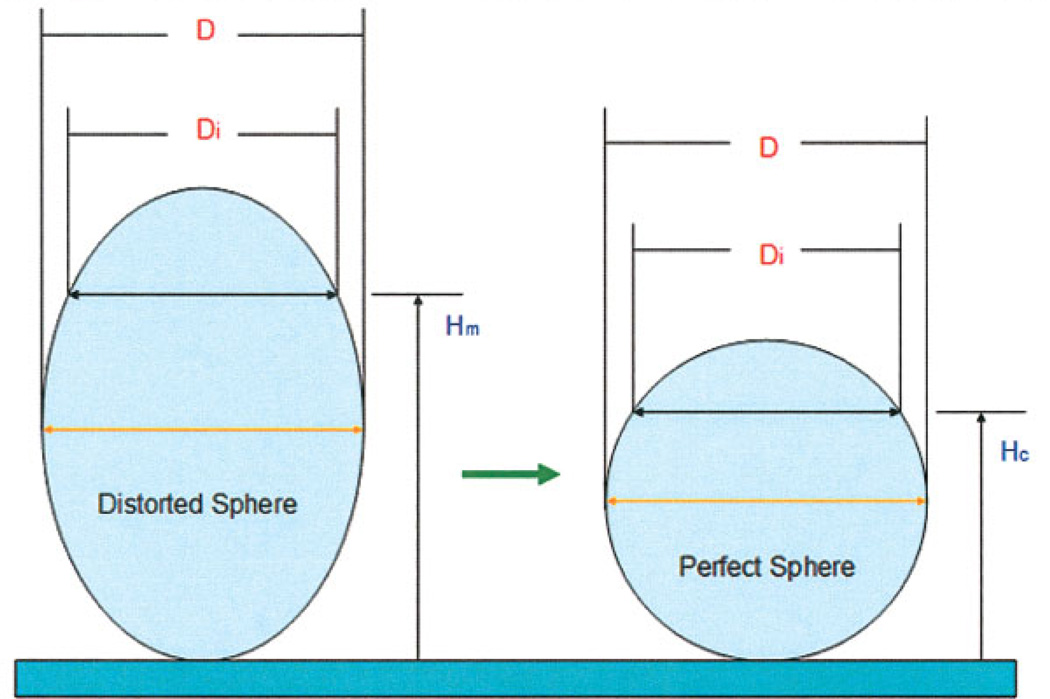
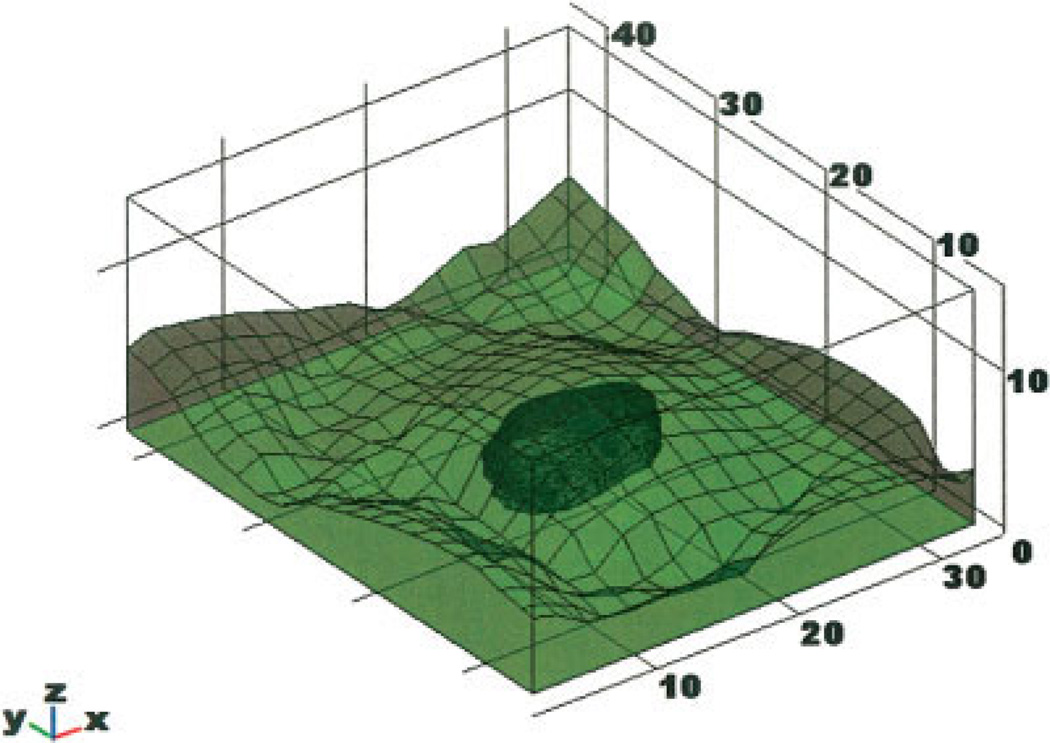
The resultant stack was analyzed using a custom MATLAB-based program (MathWorks, Natick, MA) to calculate the ADCF. First, a 3D matrix of pixel intensities was generated from the image stack. Noise was removed using a median filter (window of 3 pixels), followed by a Gaussian filter (window of 5 pixels and a depth of 5). An appropriate threshold was selected manually (based on visual inspection of the image) and used to create a binary matrix. The projected radius of the bead was then calculated in each of the vertical sections of the matrix. As illustrated in Figure 1, the known radius of the bead (measured at the widest point) was used to generate an ideal sphere. The z-position of each image slice was reassigned to the z-position at which the image diameter matched the ideal sphere. This procedure is illustrated graphically in Figure 1.

Fig. 1.

Graphical representation of the ADCF algorithm: The maximum diameter of the distorted sphere (D) is measured to determine the ideal sphere shape. The projected diameter of each slice (D_i) is determined and assigned a new position (H_c) based on projected diameter a perfect sphere should have. The corrected position (H_c) is then related to the distorted position (H_m) for curve fitting purposes. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

In this algorithm, H_m and H_c take the form of arrays. The values of H_m are evenly spaced and are determined directly from the movement of the z-stage during imaging. It is not required that H_c values be spaced evenly; the nonuniform spacing accounts for the nonlinear distortion introduced by the optics. H_c was plotted against H_m and the resulting data were fit with a polynomial of high order using least-squares regression as performed by the MATLAB function polyfit (Fig. 4). The exponents and coefficients were automatically exported to a separate data file and used to adjust z-spacing for image stacks for objects of unknown axial dimensions. The resultant polynomial curve fit serves as an ADCF that accounts for the nonlinear image separation and axial elongation caused by the imaging system.

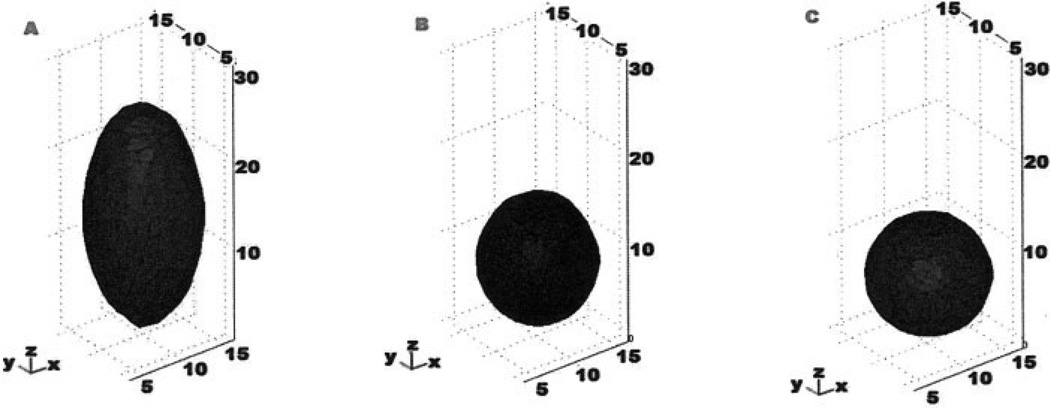
Fig. 4.

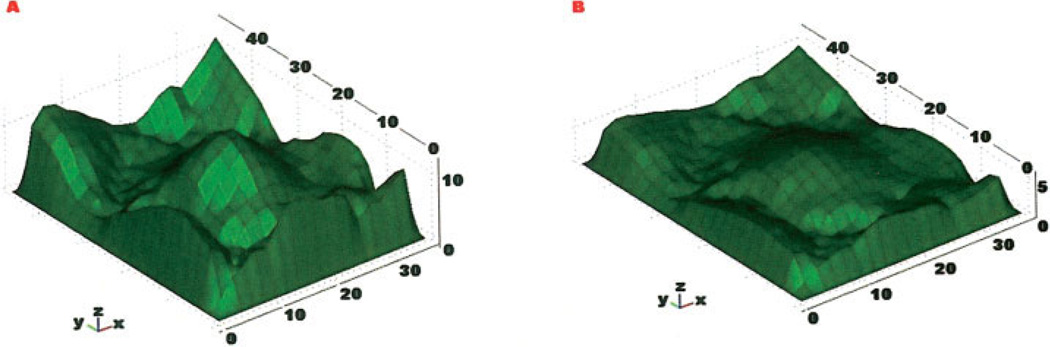
Three-dimensional visualization of 15 µm FocalCheck™ microsphere. A: Uncorrected bead which has a height of ~24 µm. B: Bead shape corrected by a linear factor. C: Bead corrected with the ADCF. Axes in microns.

Solid Modeling

After filtering (described earlier) and scaling with the ADCF, objects were converted to solid models. Depending on the complexity of the cellular object to be modeled, the solid geometry was created in MATLAB using a Qhull-based algorithm (for complex or convoluted geometries with interior features), or a custom “blanket rendering” algorithm for large scale surface topographies.

Qhull-Based Solid Model Generation

In this approach, a three-dimensional surface was created from the binary matrix by calling the isosurface function in MATLAB. This isosurface was then converted to a patch surface that could optionally be displayed for 3D visualization purposes. The number of faces in the patch object was reduced by a linear factor to ensure that geometric complexity did not preclude further computational analysis. This patch was then converted to a cell array of 3D triangular faces by connecting the vertices in the patch. The triangular faces were then progressively joined to generate substructures of the main object. Substructures were also progressively joined to piece together the main object. Once all faces had been joined to the main object, they were coerced to a solid. The solid was then ready for FEMLAB importation directly as a geometry object. For large structures, this approach is computationally expensive, and generated solids that were difficult to mesh due to the memory constraints of the 32 bit operating system. Therefore, an alternative “blanket rendering” approach was developed for larger structures such as portions of a confluent endothelial cell monolayer.

Blanket Rendering Solid Model Generation

In this algorithm, the widest slice in the binary array was determined automatically; for a bead, the widest slice is the bead center, for calcein-stained adherent cells, the widest slice is the cell base. A surface was then created by mapping the height of the highest point above and below the widest slice. In practice, this procedure can be thought of as dropping a blanket over the 3D surface. An arbitrary 3D function was fit to these surfaces of the form z = f(x,y). This function was interpolated on a grid of points in the xy-plane, forming a smooth surface that could be exported to FEMLAB. The top and bottom surfaces were joined in FEMLAB to create a solid model ready for further computational analysis.

RESULTS

Deconvolution of Fluorescent Microspheres

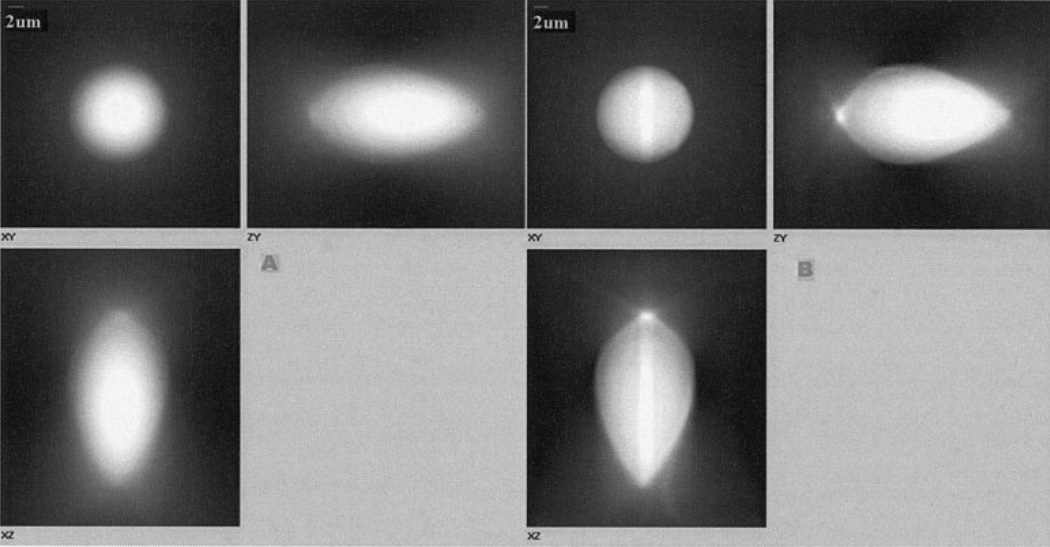
Deconvolution of images was used to more accurately determine object edges and geometries. The effects of deconvolution on 15 µm fluorescent microspheres are shown in Figure 2. The deconvolved bead image of Figure 2B, in comparison the corresponding raw image in Figure 2A, suggests that, while deconvolution removes much of the out-of-focus light and helps delineate bead edges, it fails to completely compensate for distortion along the z-axis.

Fig. 2.

FocalCheck™ 15 µm microsphere imaged under widefield fluorescence. A: Raw image set viewed as a 3 view max projection. B: Image set after 10 iterations of the blind deconvolution algorithm.

Axial Distortion Correction Function

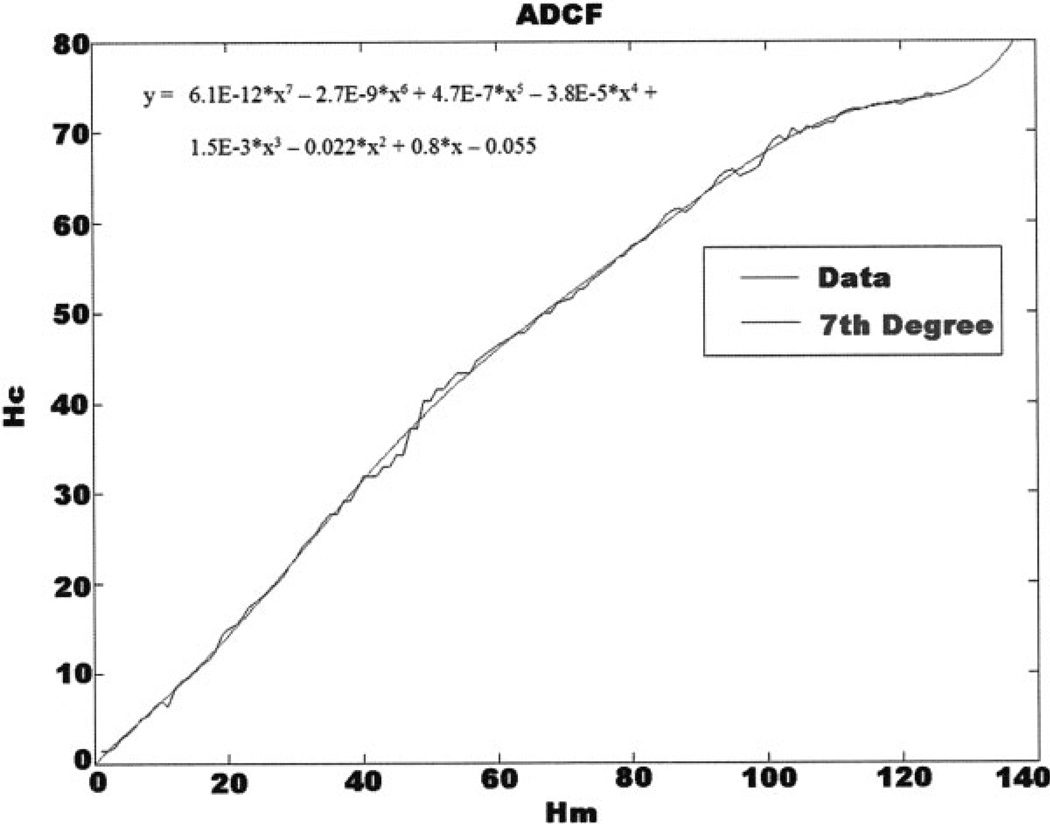
The ADCF was computed as described in Methods. Plots of image slice z-positions (H_m) for an ideal sphere were plotted against slice positions (H_c) for the actual sphere (Fig. 3). A slope of 1 for the H_c(H_m) curve corresponds to a perfect sphere. From Figure 3, it is evident that this function characterizes an elongated sphere and that this elongation is not constant for different z-positions (nonconstant slope). The curvefit was used to generate corrected z-positions of slices from samples of unknown shape.

Fig. 3.

Plot of corrected slice position (H_c) versus actual slice z-position (H_m). ADCF was generated by fitting a 7th order Polynomial to the H_c(H_m) data. Slices are spaced at 0.2 µm.

To test the ability of the ADCF to correct for axial distortions, image stacks of beads were corrected by a linear correction factor and the nonlinear ADCF (Fig. 4A) and converted to solid models using the Qhull-based approach. Solid models generated from an uncorrected image stack, one generated using a linear correction factor, and a model generated using the ADCF are shown in Figures 4A–4C, respectively. A linear correction factor resulted in a nonspherical shape, while the ADCF resulted in a near perfect spherical solid model.

ADCF Applied to Biological Samples

To demonstrate the utility of the ADCF to correct for axial distortions in biological samples of unknown axial geometry, the correction algorithm and solid modeling technique was applied to image stacks of BAECs. In this case we imaged an ROI around one cell in a confluent monolayer. Solid modeling in this case was accomplished by the “blanket rendering” approach. In Figure 5A, the results of generating a model with no ADCF and using the ADCF are shown. For the uncorrected case, the height of the cell was determined to be ~12 µM, while for the corrected case (Fig. 5B), the height of the cell was ~5 µM, which is consistent with atomic force microscopy (AFM) measurements of similar cells (Barbee et al., 1995).

Fig. 5.

Blanket-rendered cell solid models. A: Uncorrected BAEC monolayer portion. B: ADCF-corrected BAEC monolayer portion.

The ADCF was then also applied to the nucleus of the cell creating a multicomponent solid model. The ADCF-corrected solid model combined with the nucleus is shown in Figure 6.

Fig. 6.

ADCF-corrected solid model including nucleus.

DISCUSSION

In this paper, we present a method that can be used to rapidly create usable solid models of biological samples from fluorescence images, and a simple algorithm to account for optical distortions that arise from index of refraction mismatch that is independent of the optical setup used. The method allows for easy importation to and integration with a commercially available FEA package. The method also allows for counterstaining of internal cell structures, and integration of these structures into a multicomponent cell solid model. We believe these methods provide needed tools toward the development of cell-specific computational modeling.

Deconvolution, filtering, and smoothing were necessary preprocessing steps to prepare images for solid model generation. It is possible that these image processing steps generated unintended geometric artifacts and distortions in the solid model representation of the object beyond axial distortion. Although it is not possible to rule these types of artifacts out entirely, we have shown this procedure produces realistic topographies of adherent confluent endothelial cells when compared to AFM-generated cell topographies by others (Barbee et al., 1995). Because of the high signal-to-noise ratios in fluorescence imaging, and the ability of deconvolution to remove out-of-focus light and improve edge detection, it is more likely that these preprocessing steps remove existing imaging artifacts rather than introduce new ones. However, these preprocessing steps were not effective in correcting for axial distortions, necessitating the determination of the ADCF.

Axial distortions originate from objective defects, missing image information, and errors in the optical system. First, although spherical aberration is a feature of some microscope objectives, most modern objectives are corrected for spherical aberration for a designated coverslip thickness, immersion media, wavelength, and sample index of refraction. Some objectives employ a correction collar to adjust the degree of correction depending on the setup. However, sample indices of refraction are often not constant everywhere, especially in biology. In addition, coverslips can vary in thickness from one to another or across a single coverslip. These effects can combine to introduce unexpected spherical aberration into a three-dimensional data set even when using high-quality microscope objectives.

Second, in wide-field fluorescence imaging, there exists information in the object that is missing in the image data set. This missing information is manifested as a “cone of missing frequencies” in the Fourier transform of the image set. The missing cone is a region of the spatial frequency in which the optical transform function (OTF) is exactly zero due to the microscope’s inability to resolve spatial frequencies along the optical axis (McNally et al., 1994). Subsequently, information in this region is not passed to the image, or to an experimentally obtained point spread function (PSF), resulting in nonlinear elongation of the image along the z-axis. There are three reasons why deconvolution cannot compensate for the distortion caused by the cone of missing frequencies. First, the distortion is often nonlinear, which violates a deconvolution criterion of linearity. Second, experimentally-obtained or theoretical PSFs are inherently finite. Therefore, they do not possess the property that leads to the missing cone, namely that the integrated intensity in each plane should be the same (McNally et al., 1994). Third, numerically-obtained PSFs are subject to round-off error resulting in the OTF having small values where it would otherwise be zero in the missing cone (McNally et al., 1994).

A third source of axial distortion arises when using high numerical aperture (oil immersion) objectives to image biological samples in aqueous media in which the sudden change of index of refraction causes bending of the illumination light path as governed by Snell’s Law. This distortion is manifested as a simple elongation resulting from the unequal movement of focal plane and objective (Diaspro et al., 2002).

These three forms of distortion are superimposed on one another and produce a nonlinear elongation of the object represented in the 3D data set (see Fig. 2) (Diaspro et al., 2002). Because each of these aberrations shares a common source, it is difficult and often impossible to accurately represent the axial dimensions in the 3D solid model through computational or optical methods alone. These various distortions have been characterized mathematically using ray tracing (Booth and Wilson, 2001). However, ray tracing is insufficient to characterize the total distortion because, first, rays (particularly off-center rays from High NA objectives) do not remain paraxial when penetrating the aqueous environment beyond a few microns (Neuman et al., 2005), and, second, ray tracing does not account for the “cone of missing frequencies” apparent in Fourier transforms of 3D image sets collected with widefield optical microscopy (McNally et al., 1994).

Thus, in this study, we developed a nonlinear empirical function to correct for all known and unknown sources of axial distortion of 3D image data sets by generating the ADCF via processing of images of a fluorescent microsphere whose dimensions and shape were known precisely. It is possible that we could have chosen other optical setups (matched indices of refraction) or other imaging modalities (e.g. confocal) to obtain less distorted images directly. Although the use of an oil immersion (n = 1.515) objective with an NA = 1.45 to image cells in aqueous media (n = 1.33) exacerbates axial distortions, it improves light collection efficiency and lateral resolution. More importantly, this objective enables the use of objective-based total internal reflection fluorescence microscopy (Axelrod, 2001), allowing determination of basal surface topographies. Thus, locations of focal adhesions can be obtained and used in computational models to characterize mechanical coupling of the cell to the substrate (not shown). This correction algorithm represents a novel method to improve image formation with high NA objectives while maintaining accurate axial dimensions.

Kuypers et al. have developed a novel technique to determine the thickness of fluorescent thin layers using confocal microscopy that accounts for refractive index mismatch between the immersion medium and the sample (Kuypers et al., 2005). In their method, the lower and upper edges of a completely fluorescent sample are detected through novel analysis of the slope of the fluorescence intensity along the optical axis with corrections for refractive index mismatch. Although an excellent approach for measuring the thickness of very thin fluorescent samples, this technique was not appropriate for the correction of adherent cells obtained with widefield fluorescence in our study, does not yield a continuously varying axial correction function, and does not appear to be sensitive enough to detect distortions originating <10 µm from the coverglass.

Volume rendering of cells and tissues can create impressive three-dimensional images by reconstructing stacks of confocal or widefield fluorescence images into spatially-oriented grid points either on a convex hull or in point-cloud data. Such methods have provided improved volume estimation and 3D visualization (Kubinova et al., 1999). However, even after deconvolution of confocal data sets, when the index of refraction between immersion medium and sample were not matched, accurate volumes were not obtained (Difato, 2004). Also, the computational usefulness of grid data beyond visualization and volume estimation is somewhat limited. Solid models are generally needed for complex computation (beyond volume estimation, etc.) on the 3D space generated by the data set.

There have been significant advances in generating solid models from data originating from magnetic resonance imaging and computer-aided tomography produce striking 3D solid models with little distortion (Mehta, 1997). These imaging modalities have the ability to image at many angles (up to 3608), with direct compensation for 3D distortion. However, on the cellular level, the acquisition of accurate three-dimensional data is not so straight forward due to the difficulty in imaging from multiple directions and the inherent inadequacies of microscopes to correctly acquire axial data. Cellular FEA has been reported for simulated cells and membranes (Yamaguchi et al., 2000), idealized cells (Mack et al., 2004), and living cells (Charras and Horton, 2002). Although simulation of cell structures can provide insight into the general behavior of systems, these methods lack the ability to directly correlate computational data with experimental values obtained on the same cells. AFM is currently used for high-resolution surface imaging of cells and can be integrated with other imaging modalities (Mathur et al., 2000). It has also been used for simultaneous mechanical characterization of cells to create models for FEA of cell deformations with applied external forces (Charras and Horton, 2002; Ohashi, 2002). While the concurrent collection of detailed surface topography and mechanical properties are an advantage of AFM, the collection of images is slow, the true height of the cell is difficult to obtain, and cells must be fixed to image their internal structures (Chen et al., 2005). Furthermore, the need of AFM for a stylus protruding from above the sample precludes the use of closed flow chambers, simultaneous use of some other imaging modalities (e.g. transmitted light microscopy), and the depiction of convoluted structures and the basal regions of cells. Electron microscopy (EM) has also been used to create solid models from thin serial sections (Silber et al., 2004). However EM also requires fixed samples that preclude its use in correlating computational analysis and experimentation on the same cells.

To prepare corrected image stacks for FEA, a MATLAB program was constructed to generate solid models. This program rapidly creates solid models from a sequence of fluorescence images in a form that can be readily imported into a FEA software package. We have chosen the program FEMLAB (COMSOL, Sweden) for FEA. The reasons for this choice include FEMLAB’s integration with MATLAB and the parametric CAD program SolidWorks, its ability to employ coupled multiphysics solutions in a single problem, and the multitude of solution types that it offers in a single software package. Furthermore, FEMLAB provides the means to input user-generated partial differential equations and to couple them with finite element methods allowing for sophisticated modeling of the interplay between complex cellular geometry, mechanics, and biochemical signaling. Finally, the versatility of FEMLAB and the ability to generate predictive models, in-house, allows for direct correlation of model and experiment. Other excellent software programs have been developed for 3D computational modeling on single cells including virtual cell (reviewed in Slepchenko et al., 2003) and MCell (Coggan et al., 2005). Virtual cell software provides solutions of partial differential equations in user-generated 3D geometries while MCell is a Monte Carlo-based solver. However, currently, neither is capable of coupling cell mechanics to biochemical reactions, an area of intense study among cell biologists and bioengineers (reviewed in Davies, 1995; Huang et al., 2004). In fact, there exists no commercially-available software dedicated to computational cell mechanics. Thus, we believe that the current study provides a bridge between cell biology and solid modeling of cell mechanics and dynamic cellular processes. As the understanding of biological phenomena increase in complexity and scope, a flexible and versatile modeling program like FEMLAB can provide the means to represent data from disparate sources and to provide new solutions to many problems in biology.

In conclusion, we report a new integrative method of rapid optical-sectioning, deconvolution microscopy, that takes advantage of ultra-high numerical aperture objectives while correcting for their inherent axial distortions, thus providing input for high-resolution solid models of cells and subcellular organelles which are amenable to FEA. This method employs rapid 3D widefield deconvolution fluorescence imaging to obtain optical sections of the sample. An empirical correction function (ADCF) compensates for the inherent distortions along the z-axis and produces improved object representation, including internal cellular structures (e.g. nucleus). With the rapid improvements in optics, computer hardware, and modeling software, the methods presented bridge the gap between living cells and cell-specific computational modeling and provide accessibility of such detailed cellular investigations to scientists and students.