Recognition confidence under violated and confirmed memory expectations

Abstract

Our memory experiences typically covary with those of the others’ around us, and on average, an item is more likely to be familiar than not, if a companion recommends it as such. Although it would be ideal if observers could use the external recommendations of others as statistical priors during recognition decisions, it is currently unclear how or if they do so. Furthermore, understanding the sensitivity of recognition judgments to such external cues is critical for understanding memory conformity and eyewitness suggestibility phenomena. To address this we examined recognition accuracy and confidence following cues from an external source (e.g., “Likely old”) that forecast the likely status of upcoming memory probes. Three regularities emerged. First, hit and correction rejection rates expectedly fell when subjects were invalidly versus validly cued. Second, hit confidence was generally higher than correct rejection confidence, regardless of cue validity. Finally, and most noteworthy, cue validity interacted with judgment confidence such that validity heavily influenced the confidence of correct rejections, but had no discernable influence on the confidence of hits. Bootstrap informed Monte Carlo simulation supported a dual process recognition model under which familiarity and recollection processes counteract to heavily dampen the influence of external cues on average reported confidence. A third experiment tested this model using source memory. As predicted, because source memory is heavily governed by contextual recollection, cue validity again did not affect confidence, although as with recognition, it clearly altered accuracy.

Great pains are usually taken in the laboratory to prevent observers from using contextual cues to strategically improve their memory performance or bolster their confidence. For example, during recognition tests the base rates of old and new items are usually equated and the two item classes are randomly intermixed within the test list. These and other procedures stem from a belief that subjects are prone to capitalizing on environmental cues that suggest the likely status of memoranda by biasing their reports accordingly. An unfortunate consequence of these approaches, however, is that we know little about how observers actually respond during conditions in which environmental cues are potentially useful for memory judgment. For example, consider the case in which one encounters a face evoking a particular level of familiarity at a high school reunion. Whether or not one should acknowledge this person as known, and the confidence in this decision, should depend not only upon the level of assessed familiarity, but also on the context in which that familiarity occurs. For example, if one’s spouse or friend indicates that the encountered person is a classmate (versus perhaps the spouse of a classmate), then one’s recognition decision should be biased towards this. More formally, this anecdote illustrates that Bayesian reasoning also applies to memory judgments when environmental cues from reliable sources are available. Put simply, the nature and the confidence of one’s recognition reports should reflect not only internal evidence, but it should also incorporate the useful information provided by contextual cues, in this case the recommendation of a confidant.

Little is known about how observers integrate external recommendations into their recognition judgments, although one research area that has examined a somewhat similar question has focused on a construct known as “social conformity”. Following the pioneering research of Asch (1955), in which naïve observers conformed to confederates’ clearly incorrect perceptual assessments of a line display, more recent studies have examined these social conformity effects for a variety of judgments (e.g., Baron, Vandello, & Brunsman, 1996), and an increasing number of studies have investigated these effects on explicit recognition judgments (Axmacher, Gossen, Elger, & Fell, 2010; Reysen, 2005; Wright, Gabbert, Memon, & London, 2008; Gabbert, Memon, & Wright, 2007; Allan & Gabbert, 2008; Meade & Roediger, 2002; Walther et al., 2002; Wright, Self, & Justice, 2000; Schneider & Watkins, 1996). Typically, the recognition studies engaged one or more confederates whose recognition responses in the critical trials precede those of the actual participant and were purposefully incorrect. As in the perceptual decision literature, the findings reveal that in general observers will shift their recognition memory decisions towards the confederates’ responses, even when they are incorrect.

Although social conformity research clearly demonstrates observers are influenced by the reports of others, the research applying social conformity to recognition memory has several shortcomings. First, observers do not know the reliability of the other respondents in these designs and therefore the degree to which they should be ideally influenced by these reports is largely undefined. Second, these designs do not often collect confidence reports and so the sensitivity of observer confidence in light of environmental cues is unclear. This is an important shortcoming since the confidence expressed in a memory decision heavily influences its perceived veracity in social and legal contexts (Brewer & Burke, 2002). Finally, and most important, these social conformity experiments are specifically set up to induce incorrect responses, not to evaluate the degree to which observers successfully incorporate environmental cues into memory judgments. While these investigations clearly demonstrate that external consensus among confederates can induce an incorrect recognition response, they do not further our understanding of how observers ideally use the recommendations of a non-deceptive source of external recommendations to improve recognition outcomes.

The current research question is also relevant to the eyewitness testimony literature given the multiple demonstrations that eyewitnesses can be highly sensitive to suggestive misinformation, and that this can lead to false memory identifications and distorted reports (Gabbert, Memon, & Allan, 2003). However, eyewitness research often examines an unusual situation in that the focus is not on the ability of the observer to maximize correct responding, but instead on his or her ability to prevent environmental sources from “contaminating” judgments. From this perspective, even an observer with poor internal evidence is not supposed to capitalize on external cues suggestive of a suspect’s status, but instead to report that he or she has no basis for deciding despite these external indicators. Critically, understanding the ability of observers to resist such external influences would be informed by understanding whether and how they typically capitalize on such information when they are instead trying to maximize success, as opposed to limiting external influence. Finally, in terms of basic research questions, the current findings potentially inform an ongoing debate regarding the dimensionality of the evidence that observers evaluate when making recognition judgments and the manner in which observers map this evidence onto reported confidence during simple recognition judgments. We consider these models more extensively after presenting the empirical data. Before moving onto the methods, we generally describe the manipulation used across all three experiments.

To examine the ability of observers to incorporate environmental cues into verbal recognition judgments, we developed an Explicit Mnemonic Cueing procedure that is a coarse analogue of the Posner Cueing paradigm often used in spatial visual attention research (Posner, Snyder, & Davidson, 1980). During the procedure, each memory probe is preceded by a cue (“Likely Old” or “Unlikely Old”) that forecasts its status. Observers are informed of the cue’s approximate long term validity and the key question is how the cue influences their recognition accuracy and confidence. Intuitively, if one correctly believes the external cues are reliable, then the expectation is that both accuracy and confidence should decline on the minority of trials in which the cue is invalid compared to valid, because under invalid cueing situations, observers will find themselves disagreeing with an external source of information that is known to be generally accurate. As we demonstrate below, this intuitive prediction is only partially correct.

Experiment 1A and 1B

Except where noted, the methods for experiments 1A and 1B were the same

Methods

Participants

Experiments 1A and 1B each included 32 Washington University undergraduate students (18–23 years old, 22 and 18 females respectively) who participated in return for course credit. One participant was excluded from Experiment 1B due to chance performance leaving 63 for analysis. Informed consent was obtained in accordance with the Institutional Review Board of the university.

Materials

A total of 480 words were randomly drawn for each subject from a pool of 1,216 words total. From this, four lists of 120 items (60 old and 60 new items for each cycle) were used in four study/test cycles. The items in the pool had on average 7.09 letters, and 2.34 syllables, with a Kucera-Francis corpus frequency of 8.85.

Procedures

The participants were tested using standard PCs with a maximum of four participants per session seated at separate computer consoles. They were informed that they would initially perform a syllable counting task with the goal of incidentally encode a series of words, and that these words would be subsequently utilized as probes for a memory test. Thus, during encoding, participants indicated whether each serially presented word had more than one syllable; with the task cue “More than 1 syllable? Yes or No” appearing underneath each word. Participants were given 2 and 1.5 sec. to respond in Experiments 1A and 1B respectively. If they failed to respond within this time period the response was scored as incorrect and the next trial appeared. Immediately following study, the 60 studied items were randomly intermixed with 60 new items and presented serially for a recognition judgment using a six-point confidence rating scale (very confident old, somewhat confident old, guessing old, guessing new, somewhat confident new, and very confident new). Participants were instructed to use the keys 1 to 6 on the computer keyboard to rate their confidence. The key assignment was counterbalanced between subjects, i.e., for about one half of the participants the key 1 stood for very confident old and the 6 to very confident new, whereas for the other half the opposite assignment was used. Recognition responses were self-paced. In both Experiments there were three tests that used predictive cues and one baseline recognition test without the cues. The only difference between the experiments, aside from the encoding duration noted above, was when the baseline recognition test was administered. In Experiment 1A the baseline recognition test occurred first, followed by three cued-recognition tests, whereas in Experiment 1B it occurred last, following the three cued-recognition tests [Footnote 1]. During the cued recognition test trials, each test probe was preceded by a cue that probabilistically forecasted the memory status of the upcoming probe (“Likely Old” or “Unlikely Old”). For clarity, in the remainder of the manuscript we refer to these as the “Likely Old” and “Likely New” cues respectively [Footnote 2]. The cue appeared one second before its associated test probe and their presentation order was random. Seventy five percent of the cues were valid, while 25% were invalid. Participants were in fact told that 80% of the cues were valid in order to emphasize perceived cue utility.

Results and Discussion

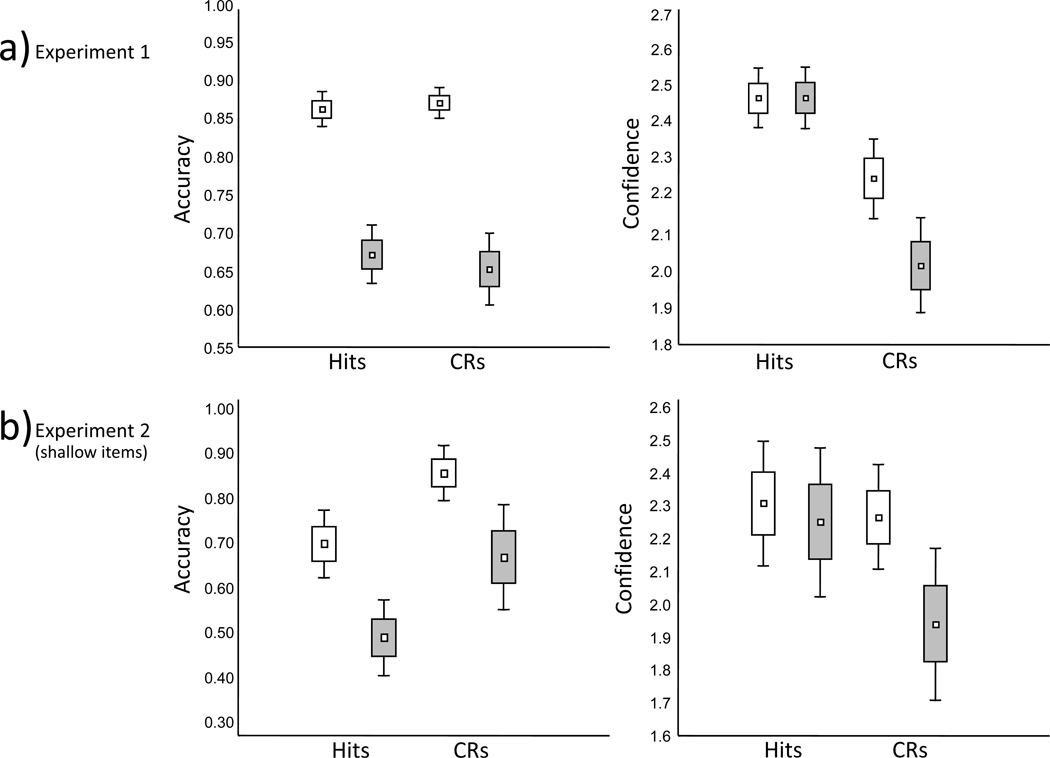
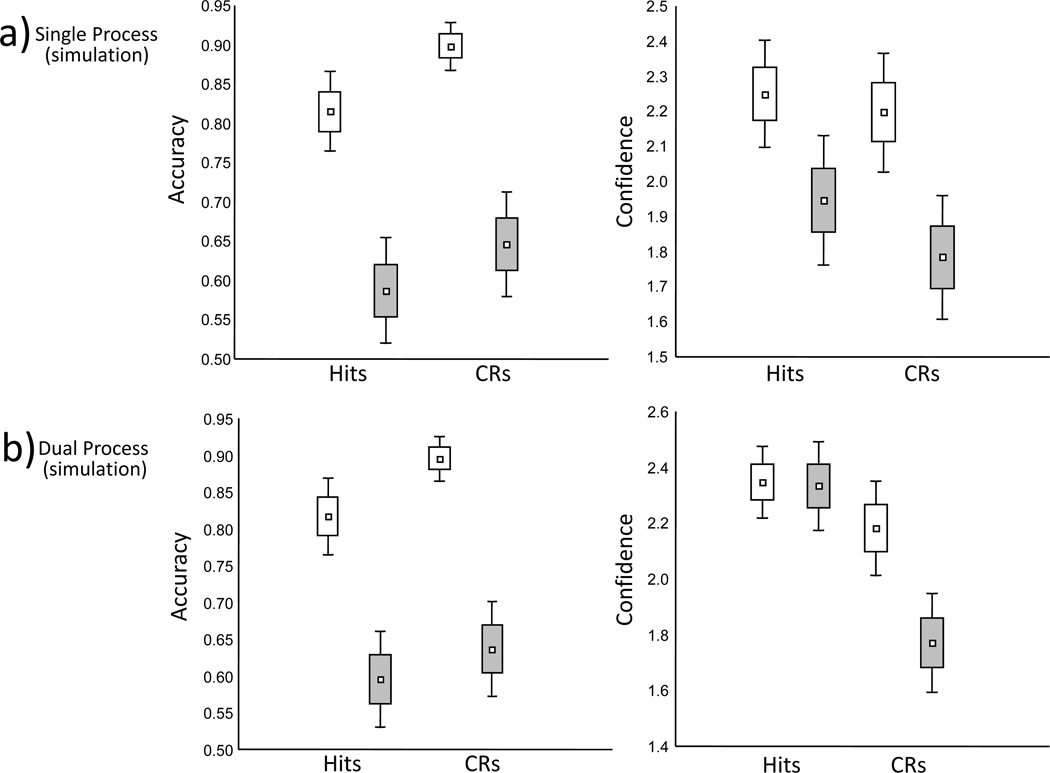
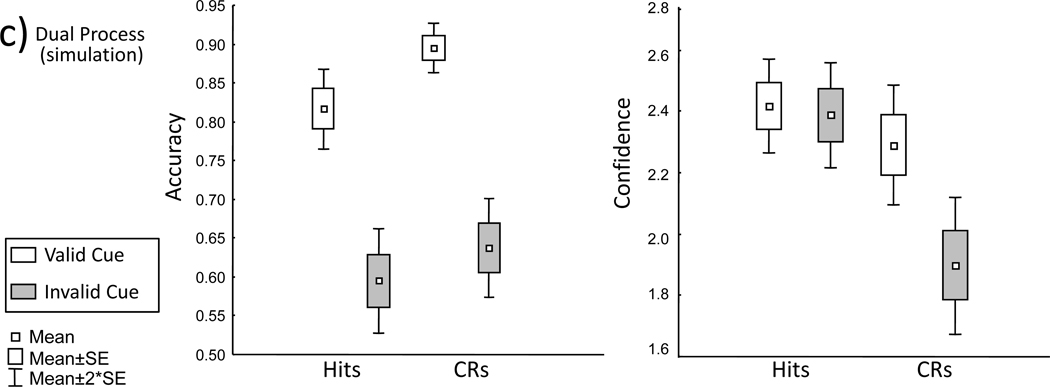
Recognition proportions and confidence were analyzed separately. The data for correct reports are shown in Figure 1a and the full data shown in Tables 1, 2, and 3. Only cued-recognition tests were examined since the response to these conditions is of primary interest and because there were large differences in when the standard, uncued recognition task was administered to the two groups (viz., 1^st test in Experiment 1A, 4^th test in Experiment 1B). The recognition proportions and confidence for the uncued data, however, are reported in Tables 1 and 2.

Figure 1.

Percent correct and mean confidence ratings from Experiments 1, 2 (shallow targets only), and 3. CRs = Correct rejections; C/A = Concrete/Abstract task; P/U = Pleasant/Unpleasant task.

Table 1.

Proportions of correct responses according to cue-probe validity for Experiments 1, 2, and 3.

		Non-cued		Valid cueing		Invalid cueing
		M	SD	M	SD	M	SD
Experiment 1	Hit	.79	.13	.86	.09	.67	.15
	CR	.83	.09	.87	.08	.65	.19
Experiment 2	Hit Deep	.90	.10	.91	.06	.83	.11
	Hit Shallow	.60	.12	.72	.13	.51	.16
	CR	.80	.16	.83	.14	.64	.22
Experiment 3	C/A hit	.79	.16	.85	.13	.65	.16
	P/U hit	.79	.16	.85	.11	.69	.18

Note. M = Mean; SD = Standard deviation; CR = Correct Rejections; C/A hit = Correct responses to Concrete/Abstract source task; P/U hit = Correct responses to Pleasant/Unpleasant source task.

Table 2.

Mean confidence according to cue-probe validity for experiments 1, 2, and 3.

		Non-cued		Valid cueing		Invalid cueing
		M	SD	M	SD	M	SD
Experiment 1	Hit	2.55	.32	2.47	.33	2.47	.34
	CR	2.23	.47	2.24	.45	2.00	.53
	Miss	1.94	.55	1.78	.53	1.96	.47
	FA	1.95	.57	1.83	.51	1.80	.50
Experiment 2	Hit Deep	2.74	.18	2.71	.19	2.67	.21
	Hit Shallow	2.33	.36	2.26	.36	2.24	.48
	CR	2.12	.38	2.15	.35	1.88	.43
	Miss Deep	1.80	.60	1.69	.51	1.84	.56
	Miss Shallow	1.82	.41	1.68	.42	1.90	.42
	FA	1.85	.59	1.78	.55	1.77	.61
Experiment 3	C/A hit	2.16	.40	2.16	.44	2.10	.41
	C/A miss	1.76	.43	1.79	.37	1.81	.43
	P/U hit	2.44	.40	2.43	.37	2.42	.36
	P/U miss	1.83	.55	1.64	.33	1.73	.45

Note. M = Mean; SD = Standard deviation; CR = Correct Rejections; C/A hit = Correct responses to Concrete/Abstract source task; C/A miss = Incorrect responses to Concrete/Abstract source task; P/U hit = Correct responses to Pleasant/Unpleasant source task; P/U miss = Incorrect responses to Pleasant/Unpleasant source task.

Table 3.

Response proportions for each confidence level and total frequencies according to cue-probe validity for experiments 1 and 2.

		Valid Cueing				Invalid Cueing
		High	Med.	Low	F	High	Med.	Low	F
Exp 1.	Hit	.53 (.19)	.20 (.12)	.13 (.12)	7324	.42 (.19)	.16 (.11)	.09 (.08)	1902
	CR	.38 (.26)	.32 (.19)	.17 (.17)	7393	.23 (.23)	.23 (.17)	.19 (.16)	1849
	Miss	.04 (.07)	.05 (.04)	.05 (.05)	1176	.09 (.12)	.13 (.10)	.10 (.12)	932
	FA	.04 (.04)	.04 (.04)	.05 (.04)	1105	.07 (.08)	.10 (.09)	.17 (.17)	985
Exp 2.	Hit Deep	.72 (.14)	.13 (.08)	.06 (.05)	2042	.63 (.16)	.13 (.10)	.07 (.06)	620
	Hit Shallow	.37 (.17)	.16 (.08)	.18 (.12)	1612	.27 (.17)	.12 (.07)	.12 (.09)	385
	CR	.30 (.19)	.36 (.15)	.17 (.11)	1870	.17 (.17)	.26 (.17)	.21 (.14)	480
	Miss Deep	.02 (.03)	.03 (.03)	.04 (.03)	202	.04 (.05)	.07 (.08)	.05 (.05)	129
	Miss Shallow	.05 (.10)	.10 (.06)	.12 (.08)	635	.11 (.13)	.21 (.10)	.16 (.13)	364
	FA	.06 (.10)	.05 (.06)	.06 (.05)	374	.11 (.15)	.07 (.06)	.18 (.17)	270

Note. CR = Correct rejection; FA = False alarm; Med. = Medium confidence; F = Total frequencies for each response outcome.

Response Proportions

There was no main effect of experiment group or interaction with this factor and so the data are collapsed across Experiment 1A and 1B in the following analysis. Cueing effects on recognition rates were examined via ANOVA with factors of response type (proportions of hits vs. CRs) and cue validity (valid vs. invalid). The analysis revealed a main effect of cue validity [F(1,62) = 86.10, MSe = .030, p < .001, η² = .579], no effect of response type [F(1,62) = .09, MSe = .02, p > .75, η² = .001], and no interaction between these factors [F(1,62) = 2.65, MSe = .004, p > .10, η² = .004] (see Table 1). Overall, the analysis suggests that participants were influenced by the cues and that they were less likely to respond correctly when invalidly versus validly cued. The lack of an interaction between cue validity and response type indicates both hits and correct rejections were similarly impaired by invalid versus valid cueing as illustrated in Figure 1a.

The results clearly indicate that subjects can change the basis of recognition reports on a trial-by-trial basis. This is noteworthy given that the current design does not use any form of corrective feedback, whereas prior demonstrations of within list criterion shifts have often relied on feedback manipulations (Han & Dobbins 2008, 2009; Rhodes & Jacoby 2007; Verde & Rotello, 2007 Exp. 5).

Response Confidence

Even though the mean confidence for all responses outcomes are reported on Table 2, we focus on confidence for correct responses here and in the remainder of the report because of the small trial counts for errors. The confidence ratings were re-scaled such that 3 indicated the highest confidence (i.e., very confident old or very confident new) and 1 the lowest (i.e., guessing old or guessing new). As with the analysis of proportions, the data were collapsed across the two experiment groups because this factor was not significant and did not interact with the others in the study. An ANOVA with factors of response type (hits versus CRs) and cue validity (valid versus invalid) yielded a main effect of cue validity [F(1,62) = 26.48, MSe = .035, p < .001, η² = .08], a main effect of response type [F(1,62) = 82.02, MSe = .093, p < .001, η² = .5] and importantly, an interaction between the two [F(1,62) = 47.34, MSe = .020, p < .001, η² = .087] (Figure 1a, Table 1). The main effect of response type reflected generally greater confidence in hits than correct rejections. The main effect of cue validity was conditioned by the interaction. As confirmed by post-hoc comparisons, confidence in hits was unaffected by the validity of the cues [t(62) = .002, p > .997, d < .01] . In contrast, the validity of the cues affected confidence during correct rejections [t(62) = 7.65, p < .001, d = .49] with confidence declining during invalid compared to valid cueing.

Overall these data demonstrate that the validity of cueing has dissociable effects on response rates and response confidence. Whereas the analysis of response proportions revealed solely a main effect of cue validity, the analysis of confidence revealed a main effect of response type, and most importantly, an interaction between response type and cue validity. Invalid cueing did not significantly reduce confidence for hits, but it did reduce confidence for correct rejections. Thus, even though hits and correct rejection rates both declined during invalid cueing, only the confidence for correct rejections tracked this behavioral decline. Intuitively, this outcome is quite surprising because the response proportion data clearly indicate that observers believed the cues to be generally valid. Given this, it might be expected that subjects would reduce their confidence when providing a judgment that conflicts with the external cues, and indeed this occurred for correct rejections. For hits however, confidence remains high and similar regardless of the external cues’ validity.

Experiment 2

The hit and correct rejection rates during Experiment 1 were comparable and fairly high. Thus, simple ceiling effects on performance cannot explain the insensitivity of confidence to cue validity during hits compared to the clear influence of this manipulation on confidence during correct rejections. Nonetheless, in Experiment 2 we sought to manipulate the level of recognition in order to verify whether confidence in hits remained unaffected by cue validity across two vastly different levels of old item detection.

Except where noted, the methods were identical to those used in Experiment 1.

Method

Participants

Twenty-five Washington University undergraduate students (18–23 years old, 17 females) participated in return for credit, and in accordance with Institutional Review Board guidelines. All participants were included in the analysis.

Materials

A total of 450 words were drawn randomly for each subject from a pool of 1,216 words total. From the list, three lists of 150 items (100 old and 50 new items for each cycle) were used in three study/test cycles.

Procedures

Two orienting tasks were administered during encoding. For half the materials subjects performed a shallow “Alphabetical order?” orienting task, whereas for the remaining half they semantically rated the words using a deep “Concrete or abstract?” orienting task. In the alphabetical order task, participants were instructed to indicate whether or not the first and last letters of each word were in alphabetical order. The levels of processing manipulation was randomly intermixed during encoding and indicated via a prompt positioned on the top of the screen (“Alphabetical order?” versus “Concrete or abstract?”). This prompt appeared 500 ms prior to the word onset and remained until the response was made. Responses were self-paced and a blank screen was displayed for 500 ms between trials. Each subsequently administered recognition test contained 100 studied items (50 deeply and 50 shallowly encoded) intermixed with 50 new items. For each test, 120 of the items were cued (40 deep, 40 shallow, 40 new) with the remaining items uncued. This resulted in a total of 360 cued trials across the 3 study/test cycles. Cue validity was 75% with subjects informed that 80% of the cues would be valid. Thus, for each item type (deep, shallow, new) within each of the 3 tests, 30 were validly cued, 10 invalidly cued, and 10 were not cued.

Results and Discussion

Response Proportions

Because levels of processing cannot be manipulated for new items we analyzed hits and correct rejections separately (Table 1 and Figure 1b). As with Experiment 1, cue validity affected correct rejections [t(24) = 4.85, p < .001, d = 1.06] with invalid cues reducing performance compared to valid cues. For hits, an ANOVA with factors of levels of processing (deep vs. shallow) and cue validity (valid vs. invalid) revealed a main effect of levels of processing [F(1,24) = 125.80, MSe = .013, p < .001, η² = .638], a main effect of cue validity [F(1,24) = 33.97, MSe = .015, p < .001, η² = .199] and an interaction between the two [F(1,24) = 11.45, MSe = .009, p < .003, η² = .039]. The interaction reflected the fact that the relative decline for invalid versus valid cueing was more prominent for shallow than deep items. This latter result may reflect a genuine resistance of deeply encoded traces to invalid cueing or instead may result from near ceiling levels of performance for these materials. Nonetheless, post hoc comparisons clearly demonstrated prominent declines in performance for both deep [t(24) = 3.76, p < .001, d = .90] and shallow [t(24) = 5.50, p < .001, d = 1.37] hit rates for invalid versus valid cueing.

Confidence Analysis

Because the levels of processing manipulation cannot be balanced across old and new items, correct rejections and hits were again considered separately (Table 2 and Figure 1b). Cue validity modulated confidence in correct rejections [t(24) = 4.54, p < .001, d = .67] with less confidence for invalidly than validly cued trials. For hit confidence, an ANOVA with factors of levels of processing (deep vs. shallow) and cue validity (valid vs. invalid) revealed a main effect of levels of processing [F(1,24) = 57.85, MSe = .085, p < .001, η² = .704] with no main effect of cue validity [F(1,24) = 1.10, MSe = .025, p > .30, η² = .005] and no evidence for an interaction between the two (F < 1). The null effect of cue validity was further confirmed in separate t tests contrasting valid and invalid cue trials for shallow hit confidence [t(24) = .50, p > .61, d = .19] and deep hit confidence [t(24) = 1.39, p > .17, d = .06].

Overall the current data reinforce the key findings of Experiment 1, namely, the dissociable effects of cue validity on response rates versus response confidence. Invalid versus valid cueing reduced correct response rates for deep items, shallow items and new items; thus it is clear that observers believed the cues to be generally valid. However, this manipulation did not similarly affect confidence. Only confidence in correct rejections fell in response to the invalid cueing. In contrast, confidence in hits was unaffected by the cueing manipulation. The levels of processing manipulation confirmed that the resistance of hit confidence to the cueing manipulation is not an artifact of a particular level of old item detection, as the null pattern occurred for both deep and shallow items that yielded clearly different detection rates. As shown in Figure 1b, the level of performance for shallow targets was generally below that of correct rejections, yet only the latter demonstrated confidence changes as a function of cue validity. Thus, the null effect of cueing on confidence is selective to studied materials, regardless of whether they are correctly identified at a higher or lower average rate than new materials. In short, there is something unique about the mnemonic evidence provided by these materials, compared to new materials, which precludes cue induced declines in confidence.

Finally, it is clearly not the case that confidence for old reports is universally insensitive to differences in performance. Subjects were considerably more confident when correctly endorsing deep as opposed to shallow items, as demonstrated by the prominent main effect of levels of processing on confidence (Table 1). Thus, what is required is a model that for hits demonstrates an unaltered confidence in response to changes in criterion (i.e., cue induced changes in performance) but a clear change in response confidence as evidence levels change. Additionally, the model should anticipate that on average, hit confidence will be greater than correct rejection confidence, as demonstrated by the main effects present in Figure 1a and 1b.

Single and dual process approaches to recognition judgment

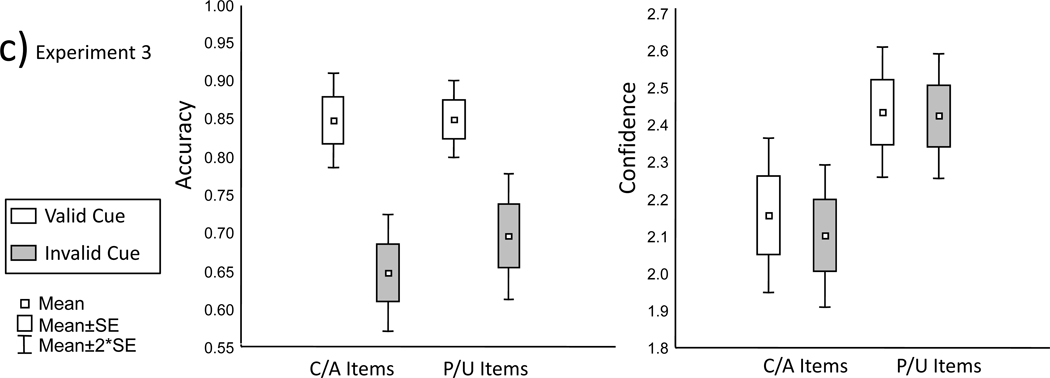
How surprising is the current confidence/accuracy dissociation demonstrated in Experiments 1 and 2? It is quite odd to find a situation in which subjects believe an external source of information is generally valid and yet they do not downgrade their confidence when disagreeing with that source (in the case of hits). Again, as noted above, we know participants believed the external source to be valid because the hit rates are responding markedly to the validity of the cues. However, a more formal consideration of the unexpectedness of this phenomenon requires specifying decision models of recognition judgment. Two high-level models that enjoy widespread support are the unequal variance signal detection model and the dual process signal detection model, hereafter usually referred to as the single and dual process models for brevity. These models are extensions of the basic equal variance signal detection model illustrated in the left panel of Figure 2. Under this basic model, recognition judgments are based on a single dimension of continuous evidence termed familiarity or strength, which is normally distributed for both studied and new materials. Although studied materials are generally more familiar than those newly encountered within the experiment, the overlap of the distributions forces the observer to categorically parse the continuous evidence dimension into judgment regions using hypothetical decision standards called criteria. If asked to simply judge materials as old or new, a single criterion is placed along the dimension. If instead the observer is asked to also rate the confidence of classifications, it is assumed that additional criteria are maintained such that increasingly extreme evidence values (with respect to the old/new criterion) garner greater confidence. If the evidence for each class of items is normally distributed, then the function relating cumulative confidence to cumulative accuracy, termed the receiver operating characteristic (ROC), will yield a characteristic shape (Macmillan & Creelman, 2004).

Figure 2.

Schematics of equal variance signal detection model, and the unequal variance and dual process extensions of this model. Ro (“high”) indicates that recollection leads to high confidence old reports when it occurs. When it does not, (1-Ro), then confidence for old materials is assigned using the equal variance signal detection process.

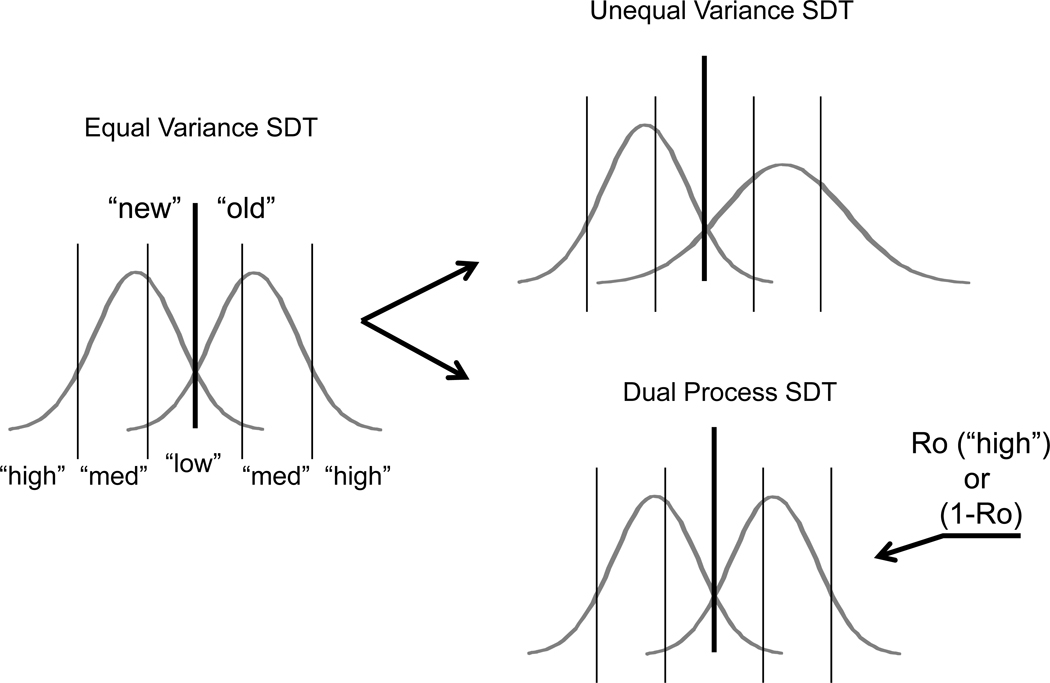
The shape of the empirical recognition memory ROC does not have the symmetry that the equal variance signal detection model demands. This can be seen in the aggregate ROC for the two cueing conditions (“Likely Old” and “Likely New”) shown for the Experiment 1 data in Figure 3. In line with the usual finding, the empirical ROCs from the two cue conditions of Experiment 1 are “pushed up” along the left portion and asymmetric about the negative diagonal of the plot. To accommodate the asymmetry of the recognition ROC the single and dual process models extend the basic model in two different ways. The single process model assumes that the variance of the old item distribution is greater than the new. This assumption captures the idea that the encoding process itself somehow imparts additional variability to the strength of subsequently tested items. For example, some items may receive additional consideration during study because the observer finds them personally relevant or particularly interesting, whereas others may be more minimally processed or considered. Critically, the model remains one dimensional; decisions are made solely with respect to a single continuous, scalar evidence variable. From the vantage of the observer, he or she is working with magnitudes along a single dimension and nothing else. This does not mean that various separable influences cannot influence these final magnitudes. However, at the time of decision the observer has no way of discerning or isolating these different underlying influences because they have been fused into a single, subjective scalar evidence value. Here, perceived heaviness serves as a useful analogy in that it is known to be influenced both by the actual weight of objects and learned object characteristics that drive expectations (e.g., Brayanov & Smith, 2010). Critically however, observers cannot consciously parse these two contributions and indeed under most circumstances are presumably unaware that these two separate factors are influencing their subjective ratings of heaviness.

Figure 3.

Aggregate receiver operating characteristics (ROCs) for the total data from Experiment 1, under the two possible cue conditions.

In contrast, the dual process model assumes that the greater variability in old item confidence reports arises because for old materials observers can explicitly discern two separable types of information during testing, namely item familiarity or fluency, which reflects an equal variance signal detection process and contextual recollection which operates in a threshold manner. The latter reflects explicit retrieval of prior thoughts, actions, or other contextual elements associatively linked to the probe during the prior encounter (viz. remembrances). In the Yonelinas (1994) model recollection is treated as a threshold phenomenon, meaning that it can completely fail, such that for some subset of old items (1-Ro) the observer cannot explicitly remember anything specific about the prior encounter. Critically, if recollection of study context information occurs during simple item recognition paradigms, it is assumed to lead to the most confident endorsements. That is, if observers explicitly remember something about the prior occurrence of the item, they are assumed to confidently endorse it as recognized because the remembered contextual content is extremely diagnostic in this particular task. In contrast to recollection, the dual process model treats familiarity as an equal variance signal detection process. Thus, the model is not one dimensional because old item responses are governed by two independent evidence variables (familiarity and recollection) to which two separate response strategies can be applied. In contrast, new item responses are governed by only one evidence variable (familiarity).

Given these models descriptions, it is possible to generate formal predictions of the current cueing effects under well specified constraints of how each subject places the confidence criteria. Critically, these predictions can be made wholly independently of the current empirical findings and thus they constitute a formal test of how well each model generalizes to these new cueing findings under various explicit assumptions about criterion behavior.

Bootstrap informed Monte Carlo predictions

Here we develop a Monte Carlo simulation that begins with normative parameters from each model to see if either model naturally predicts the current empirical confidence/accuracy dissociation pattern. The current method combines resampling techniques (Efron & Tibshirani, 1993) with Monte Carlo simulation in order to generate a distribution of predicted model outcomes and then to ask if the empirical data are likely given these generated outcomes. Critically, the predictions made by the simulated decision models are developed wholly independently of the empirical findings reported above, and there is minimal input from the experimenter regarding the values of the parameters used in the simulation. There are two key components to the procedure, namely a) defining the parameter space to be used in the Monte Carlo simulation and b) implementing the Monte Carlo simulation of the old/new criterion shifts in response to the cues.

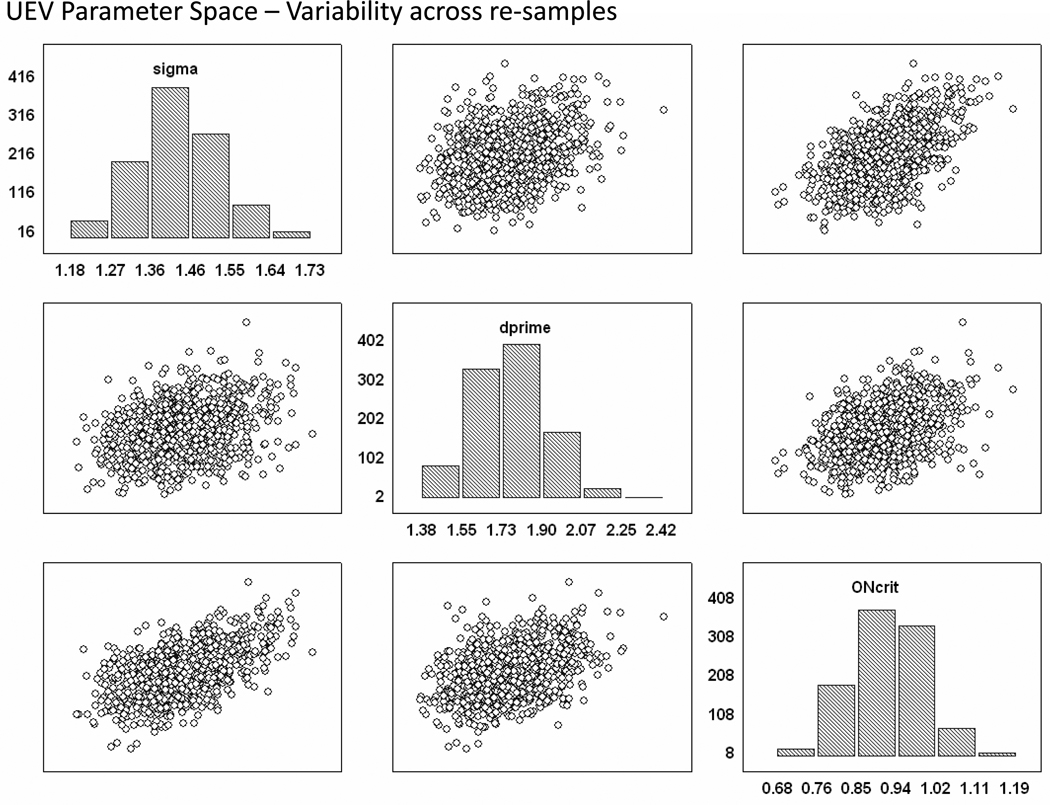
Defining the Parameter Spaces for the Two Models

To define an unbiased parameter space for each decision model we relied upon the “plug in principle” (Efron & Tibshirani 1993) in which one repeatedly re-samples, with replacement, from a set of observations (in this case sets of fitted model parameters) in order to define a pseudo-population. The variability across these re-samples in this pseudo-population represents an estimate of that which would be expected if the experiment were actually conducted repeatedly on randomly sampled participants from the population. We began with the fitted data of 26 subjects from an independent recognition memory experiment in which observers encoded 180 items using a syllable counting task and then were immediately given a single item old/new recognition task consisting of 360 items following study. Following each recognition judgment, a 3-point confidence rating was provided indicating high (3), medium (2), or low (1) confidence. Responding was self-paced. The average parameters for the fits of the individuals are shown in Table 4. These parameters were obtained by fitting each participant’s ROC using non-linear least squares fitting and the Excel Solver algorithm (for example, Yonelinas, Dobbins, Szymanski, Dhaliwal, & King 1996; Heit & Hayes 2011). For the single process model this approach iteratively adjusts two evidence parameters (d’ and old item variability (σ)), along with an old/new classification criterion, and two upper and two lower confidence criteria (7 parameters in total) in order to minimize the squared difference between the model’s predictions and the observed ROC points (5 ROC points constructed from 10 observed data values). For the dual process model the algorithm adjusts a recollection probability (Ro) for old items, a familiarity parameter (d’), an old/new familiarity classification criterion and two pairs of low and high familiarity confidence criteria (7 parameters in total). The average fitted evidence parameters for the two models listed in Table 4 are typical of what has been previously reported (Yonelinas & Parks, 2007; Bird, Davies, Ward, & Burgess, 2011). Both models account for more than 99.7% of the variance in the individual ROCs, based on the correlation between observed and predicted data points. Also, the unequal variance model demonstrates a slight numerical advantage in terms of sum of squared errors of prediction, although it was not reliable across individuals via non-parametric sign test [15 of 26 cases, p = .56].

Table 4.

Mean Parameters of dual process and unequal variance SDT model fits to the control data feeding bootstrap Monte Carlo simulation.

	d’	σ	Ro	O/N crit	SSE
DP model	1.11(.57)	1	.29(.20)	.88(.37)	.003(.003)
UEV model	1.77(.81)	1.43(.51)	n/a	.92(.40)	.002(.002)

Note. σ = old distribution variability; Ro = recollection; O/N crit = old and new criteria; SSE = sum of squared deviations. Standard deviations in parentheses.

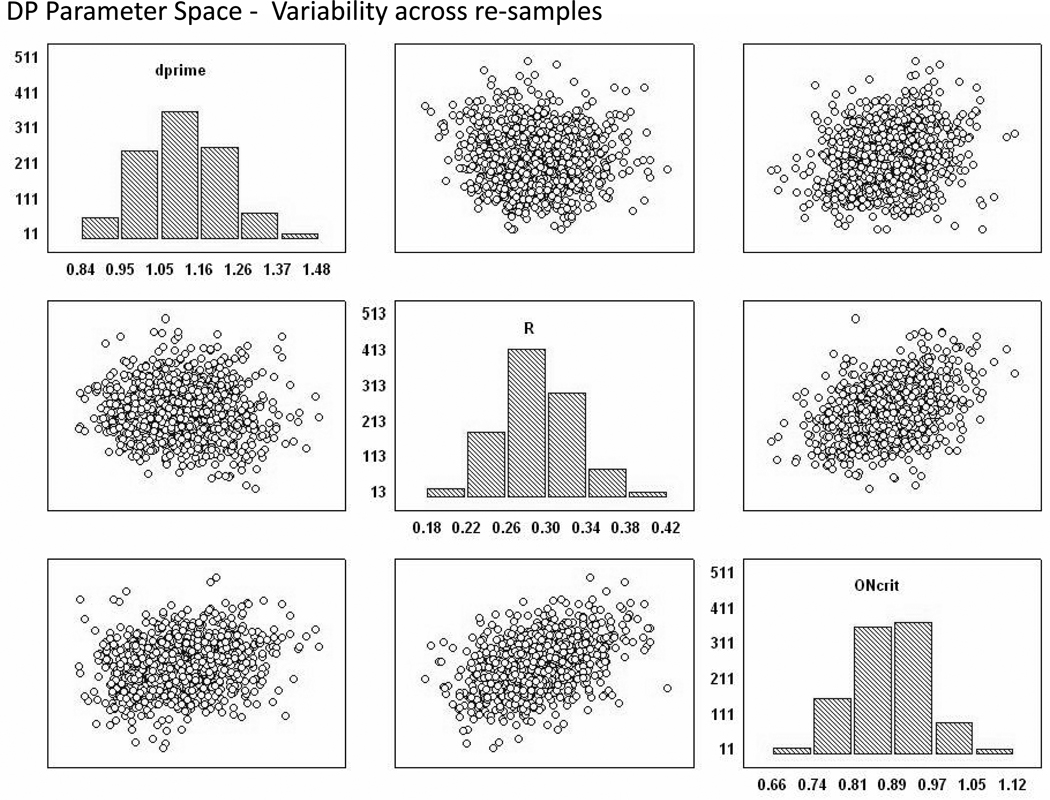
For each model there were three key parameters that were re-sampled from the set of fitted parameters in order to define the parameter space used in the Monte Carlo simulation, namely, the two evidence parameters (d’ & σ for single process, or d’ & Ro for dual process) and the old/new decision criterion location. The two evidence parameters define the entire possible ROC surface of each subject (i.e., all possible hit and correct rejection rate pairings that could result from a cue induced criterion shift under that model), while the old/new criterion defines the predicted starting point along that surface in the absence of any environmental cues. In short, these three parameters define the expected starting point of an observer when there are no environmental cues present to bias his or her reports, and they define the range of possible performance outcomes that can result when shifting the old/new criterion away from the neutral point in response to the external cues. To define the full parameter space we drew 1000 re-samples (with replacement) from these two sets of fitted parameters using the rboot function provided by the Stixbox toolbox implemented in Matlab [http://www.maths.lth.se/matstat/stixbox/]. The three parameters were drawn in a case wise fashion when re-sampling from the sets, which preserves the interrelationships among the three. Figures 4 and 5 show the variability in the sample averaged parameters across the 1000 re-samples. Each point in the figure represents the average value of a particular parameter in a given sample of 26. The minor diagonal of the plot illustrates the variability of each parameter across the 1000 re-samples whereas the off-diagonal scatter plots show the covariance of the parameters across the re-samples. For example, looking at the upper right scatter plot of Figure 4, one can see that there is a positive relationship between the average old/new criterion location and the average old item standard deviation parameters across the 1000 samples of size 26. Again, this sample-to-sample variability in the average parameters represents what would be expected if the models were correct and one repeated this type of recognition experiment 1000 times in the undergraduate population using a sample size of 26. Thus, this procedure defines the unbiased parameter spaces (at the level of samples) for the two models. Because the initial set of parameters used for re-sampling were the best fitting parameters of each model, the models are on equal footing when attempting to predict the current empirical pattern.

Figure 4.

Parameter space for the unequal variance signal detection model achieved through bootstrapping procedures. The three parameters, sigma, d’, and the old/new criterion define the starting point of each case submitted to the Monte Carlo simulation procedure.

Figure 5.

Parameter space for the dual process signal detection model achieved through bootstrapping procedures. The three parameters, d’, R, and the old/new criterion for familiarity define the starting point of each case submitted to the Monte Carlo simulation procedure.

Critically, the bootstrap procedure eliminates the need for the experimenter to make questionable, subjective decisions when defining the spaces. For example, one might wonder what the appropriate range of old item standard deviation parameter values should be under the single process model. The need to make an arbitrary choice is removed by the re-sampling procedure, which uses prior independent data to generate this expected range [see upper left histogram of Figure 4]. Additionally, the procedure also establishes the covariance among model parameters because of the case wise sampling. For example, Figure 4 makes it clear that there is an expected positive relationship between the old item standard deviation parameter (sigma) and the positioning of the old/new criterion (ONcrit) across the samples under the single process model (Figure 4 upper right panel scatter plot). This makes sense if subjects are striving to maximize performance since the intersection of the old and new item distributions will move rightwards as the old item standard deviation increases. Again, the benefit of the bootstrap procedure is that the experimenter does not need to arbitrarily decide the magnitude of this parameter covariance, which instead, is a function of the covariance in the original independent sample of parameters.

Having established the parameter spaces for the two models, we next simulate the predictions the models make about observer confidence in response to shifts of the old/new criterion away from the neutral criterion location specified in the parameter space. These shifts represented the Monte Carlo modeled responses of the hypothetical subjects in response to the external cues.

Monte Carlo Simulation Predictions

To generate the Monte Carlo predictions we implemented old/new criterion shifts for each case, within each re-sample, representing a simulated response to the “Likely Old” and “Likely New” cues. That is, the subject is assumed to shift the old/new criterion to the right for “Likely New” cues and to the left for “Likely Old” cues. For generality, different ranges of old/new criterion shifts were considered and are presented in Table 5. Critically, we know that some form of old/new criterion shift must be occurring in response to the external cues because the empirical hit and correct rejection rates are heavily influenced by cue validity (Table 1; Figure 1ab). Following the simulated criterion shift, we then placed two confidence criteria (high and medium confidence) to the right and left of the new old/new position using two minimal constraints on their locations. Namely, the high confidence criterion was constrained to fall outside of the medium confidence criterion which simply reflects the assumption that observers do not rate evidence closer to the old/new criterion more confidently than evidence farther from it. This assumption is inherent in the use of confidence as an ordinal indication of criterion location. The second constraint was that the maximum distance the high confidence criterion could fall from the shifted old/new criterion location was 2.5 standard units. This constraint is necessary to prevent criteria so extreme as to preclude any high and medium confidence reports, and corresponds to the practice of encouraging participants to spread responses across all available confidence options (and removing those who fail to provide reports in all or most confidence categories). These were the only two constraints placed on how the confidence criteria could behave for each case, thus the outcomes of the simulation constitute predictions that arise when very minimal assumptions are made about how real observers place their confidence criteria. These assumptions closely embody the manner in which researchers post-hoc fit data using these models because practitioners let fitting algorithms adjust the criteria as necessary in order to improve subject level fits, and hence allow highly idiosyncratic criterion positioning for each criterion within a participant (subject to the minimal constraints noted above) and highly idiosyncratic criterion behavior across each fitted participant. Given this, the simulation outcomes represent natural predictions of the models as they are currently implemented, and any clear prediction failures would constitute a surprising outcome requiring ad hoc explanation. Another way of stating this is that the simulation outcomes represent the predicted outcomes under the models when minimal assumptions are made about how observers choose to place the confidence criteria. If a model fails to anticipate the current empirical findings, then it means that either additional assumptions regarding confidence criterion behavior are required, or that the model is fundamentally untenable.

Table 5.

Bootstrap Monte Carlo Simulation outcomes.

		Range of shift values
		0–.5	0–.75	0–1.00
DP Model	Main Effect	0.993	0.995	0.996
	Interaction	0.423	0.676	0.853
UEV Model	Main Effect	0.317	0.305	0.294
	Interaction	0.113	0.151	0.202

Note: 1000 replications with n = 26. Proportions indicate successful predictions of empirical statistical findings.

Unequal Variance Model Predictions

To illustrate the unequal variance SDT Monte Carlo predictions we begin with a single re-sampled group. Each case within this group has three sampled key performance parameters [d’, old item variability (σ), starting old/new criterion (c_o/n) position] that characterize typical performance of subjects in the absence of external cueing. For each case, a random shift of the old/new criterion was implemented by drawing a random offset from a uniform distribution (ranges shown in Table 5). One offset was added to the sampled old/new criterion start position reflecting a rightward shift in response to a “Likely new” cue whereas a separate random offset was subtracted from the old/new criterion reflecting a leftward movement in response to a “Likely old” cue away from the neutral point. Following this, two confidence criteria above and below each shifted old/new criterion were sampled from a uniform distribution imposing the two minimal constraints noted earlier. That is, no criterion could fall greater than 2.5 units away from the shifted old/new position, and the high confidence criteria had to be more extreme than the medium confidence criteria. The obtained response proportions resulting from these sampled criteria for this case were then used to calculate the mean confidence of hits and correct rejections under the two cue conditions. For example, if a case generated .29, .15, and .15 for the high, medium, and low confidence hit proportions under the “Likely new” cue (a rightward shift), then the mean conditional hit confidence was [.29*3 +.15*2+.15*1]/[.29 + .15 + .15]. This would be the predicted mean confidence for invalidly cued hit outcomes because the observer moved the criterion to the right, but the evidence nonetheless fell above the shifted location resulting in hits.

When all 26 cases in the re-sample were finished, we then ran the same statistical tests on mean confidence that were performed on the actual empirical data to see if the simulation produced similar effects. First, the average confidence of hits was compared to the average confidence of correct rejections based on the empirical finding that the former should be reliably greater (one-sided t-test, critical t = 1.71 for 26 cases). Second, the interaction between cue validity and confidence was tested. Under this analysis, a leftward criterion shift forms an invalid condition for correct rejections (i.e., the cue indicated “old” but the item was new) and a rightward shift would reflect a valid cue condition for correct rejections. The reverse is true for hits. Thus, the contrast calculated the effect of cue validity on correct rejection confidence (valid less invalid) and then subtracted the analogous contrast for hit confidence. If this value is reliably greater than 0 across the cases in the re-sample then the validity effect is larger for correct rejections. Finally, we also examined mean hit and correct rejection confidence separately for the re-sample, determining whether either hit or correct rejection confidence differed across valid versus invalid cueing conditions. The simulation then recorded the outcomes of the tests and the procedure was replicated for the remaining 999 re-samples. Three different ranges of old/new criterion shifts were considered to verify the findings were consistent across a broad range of possible cue induced shifts of the old/new criterion (Table 4). To examine the degree of successful generalization of the model, all one has to do is tally the number of times the statistical tests matched the current empirical statistical outcomes.

As Table 5 and Figure 6a show, the empirical data are unlikely under the unequal variance SDT model simulation. For the largest range of old/new criterion shifts considered [0–1.00] only 29% of the statistical tests demonstrated a reliably higher hit versus correct rejection confidence. Figure 6a demonstrates that across the re-samples, the mean confidence for hits was larger than correct rejections, but only slightly so. This results from the contribution of the increased old item variance which “pushes” the mass of the distribution away from the old/new criterion and hence increases hit confidence compared to correct rejections. However, the sampled old item standard deviation parameter, which was re-sampled from actual fits of the model to independent empirical data, is insufficient to drive this effect far enough to yield a reliable confidence advantage for hits compared to correct rejections. In the case of the interaction between cue validity and the confidence of different response types, the model fared worse, predicting this outcome only 20% of the time. It is clear from Figure 6a that the criterion shifts affected both the confidence in hits and the confidence in correct rejections. That is, in 96% of the re-samples correct rejection confidence was significantly reduced by invalid versus valid cueing and in 89% of the re-samples hit confidence was likewise significantly reduced by invalid versus valid cueing. The robustness of both confidence declines precludes the signal detection model from frequently demonstrating the interaction actually present in the empirical data and thus the model is clearly not tenable under the current assumptions of confidence criterion placement. As we show following the dual process simulation, the single process model requires a very specific pattern of constraint to be placed on the movement of the individual confidence criteria in response to the cues in order to yield the correct outcomes.

Figure 6.

Outcomes of the bootstrap fed Monte Carlo simulation procedures. Panels a) and b) illustrate single and dual process predictions when confidence criteria are minimally constrained across each case within the sample. Panel c) illustrates the dual process predictions when an interval scaling constraint is imposed on the model.

Dual Process SDT Model Predictions

The dual process simulation proceeded virtually identically to that of the single process approach. Again, bootstrapped re-samples of parameters (n=26) were drawn in a case wise fashion from the empirical fits to the independent data set (d’, Ro, and c_o/n). Following this the same procedure was used to generate the confidence predictions under right and leftward shifts of the old/new criterion for each case, within each re-sample. The key difference was that during hits, recollection was assumed to yield uniformly confident endorsements (3) whereas in its absence, confidence was instead determined from the equal variance signal detection proportions resulting from the confidence criterion placements. Psychologically, this reflects the assumption that observers are not affected by the external cues on trials in which recollection of prior contextual information occurs; recollection rates are unaffected and confidence remains uniformly high. The simulations generated distributions of outcomes consistent with the current findings (Figure 6b). For the 0 to 1.00 shift simulation, the dual process model correctly predicted the main effect of hit greater than correct rejection confidence in 99% of the re-samples. It predicted the interaction between cueing condition and confidence on different response types in 85% of the re-samples. Furthermore, the model closely captures the form of this interaction. In accordance with the data, it rarely generated an effect of cue validity on hit confidence (4.5%), but frequently generated an effect of cue validity on correct rejection confidence (96%). Indeed, in every column of Table 5 the dual process model was significantly more likely to anticipate the key main effect and interaction present in the empirical findings than the single process model and so the model is quite viable even when minimal assumptions are made about confidence criterion placement both within and across observers.

Overall the simulation results demonstrate that the dual process model accurately predicts the current confidence findings using minimal, but uniform assumptions about the way each confidence criterion is placed. Conversely, the single process model did not generalize, which means that either the model is fundamentally incorrect (i.e., recognition evidence is not unidimensional), or the different confidence criteria are not governed by the same placement rules or constraints. The bootstrap Monte Carlo simulation is highly useful in this regard because the simulation data can be mined to find the special constraints that may be necessary in order to make the unequal variance model feasible. That is, one can isolate the small minority of re-samples that actually yielded the correct predictions and examine how the criteria behaved in these particular re-samples. Figure 7 illustrates the confidence criterion behavior for the re-samples in which the model correctly generated a null effect of cueing on hit confidence (i.e., the difference was not statistically significant), but a significant effect of cueing on correct rejection confidence. There were 107 out of the 1000 re-samples that satisfied these conditions. The plot shows the difference between each criterion under the “Likely New” and “Likely Old” cue conditions (i.e., the rightward minus the leftward position of each criterion) and hence illustrates how each criterion moved in response to the cues. The plot demonstrates that in order to make the correct null prediction regarding hit confidence, both of the hit confidence criteria must move considerably less (and to the same degree) compared to the old/new criterion and the correct rejection confidence criteria. Thus, if the upper confidence criteria react in this particular “sluggish” manner to the changing old/new criterion position (and hence the external cues), then the single process model is capable of generating the correct dissociation. It is important to note that this finding represents an unexpected outcome that requires an ad hoc explanation. That is, the behavior would not have been predicted given the way the single process model is typically post hoc fit to data because practitioners have not previously constrained the upper confidence criteria to behave fundamentally differently from the old/new criterion or the lower confidence criteria in response to environmental cues.

Figure 7.

Criterion movement behavior required for success confidence predictions for the single process versus dual process models. Values represent the difference in position of the criterion under the simulated “Likely New” less “Likely Old” cueing conditions.

Returning to the dual process model, Figure 7 demonstrates that average criterion movement at the group level is quite similar although the movement is slightly numerically less for the upper than the lower confidence criteria. This movement similarity reflects the fact that upper and lower confidence criteria were governed by the sampling process (viz., draws from a uniform distribution) and held to the same minimal constraints. Thus, the movement behavior when averaged across participants is quite similar. However, the criteria were not forced to move similarly at the level of each individual subject/case, nor forced to move similarly above and below the old/new criterion for each subject, and thus the similar movement observed in Figure 7 is the result of averaging across the cases within each re-sample. Notably, the dual process model would be much simpler if this uniform behavior was enforced at the level of each subject, that is, if one assumed that individual observers did not maintain large numbers of separate, manipulable decision standards in working memory during recognition memory testing (c.f., Benjamin, Diaz & Wee, 2009). Currently, both the single and dual process models assume that observers actively maintain 10 separately manipulable decision criteria (8-confidence and 2-old/new) during testing, which greatly exceeds estimated working memory capacity estimates across various domains (e.g., Conway et al. 2005; Fukuda, Awh & Vogel 2010). Indeed, this number seems particularly implausible given the fact that observers are also concurrently engaged in demanding episodic retrieval attempts. Thus, not only must 10 standards be maintained, they must be maintained in the context of a dual task conditions which usually demonstrate further declines in working memory capacity (Unsworth & Engle, 2007). Finally, although we have focused only on the two cue conditions in the simulations for simplicity, it must be noted that in Experiments 2 and 3 (reported below), that neutral/uncued trials were also intermixed in the design. Under the typical unconstrained approach to modeling the criteria, this additional condition would drive the number of simultaneously held decision standards up to 15 and we are simply not aware of any working memory model that remotely suggests that observers can maintain 15 separately manipulable decision standards in mind under dual task conditions.

One potential alternative to assuming the maintenance of scores of separate decision standards arises from recent research suggesting that perhaps the internal evidence space may be parsed in an equal interval fashion (Mickes, Wixted, & Wais, 2007). Assuming an equal interval internal scale greatly simplifies the decision models because it completely eliminates the assumption that observers actually maintain large numbers of separately manipulable criteria in working memory during the course of the experiment. Instead, only the old/new criterion locations and a scaling value are needed. For example, if a given individual uses an interval of X units to parse evidence, then an item receives low confidence if it is less than X units from the old/new criterion, medium confidence if it is between 1X and 2X units away, and high confidence if it is greater than 2X units away. This parsing applies no matter where the old/new criterion is shifted and therefore, instead of maintaining 10 criterion values under the two cue conditions, it is assumed that observers only maintain two old/new criteria and a scaling or resolution value. This is a reduction of 7 free parameters and is considerably more plausible from a limited capacity working memory perspective.

To simulate this simpler model we reran the dual process simulation, but instead of sampling 8 confidence criteria (four for a leftward shift and four for a rightward shift) we simply sampled 1 random scaling interval for each subject from a uniform range of 0 to 1.5 units along with the two shifted old/new criterion locations in response to the cues. Again, the sampled interval represents the scaling value that the subject uses to parse his or her internal evidence continuum. The predictions of this greatly simplified model are quite similar to those of the original dual process model (Figure 6c) and in fact it is perhaps even more in line with the empirical findings. The simulation accurately predicted the main and interaction confidence effects in all of the re-samples. Additionally, it only yielded an effect of cue validity on hit confidence in 15.8% of the re-samples, but yielded a corresponding effect of cue validity on correct rejection confidence in all of the re-samples. Thus, if one assumes interval scaling of the evidence on the part of the subjects, an extremely simple dual process model again easily predicts the current empirical pattern. There is no need to simulate the single process model under the interval scaling constraint, because the prior simulation demonstrates that unequal movement across the decision criteria is a requisite for the model to produce the correct pattern of data (Figure 7 left panel). Given this, it would clearly fail if the spacing between criteria was constrained to be equal.

In summary, the modeling demonstrates that the dual process model predicts the current findings when minimal assumptions are made about confidence criterion placement at the level of each individual, and also when a highly simplifying interval scaling assumption is made that abandons the notion that different confidence criteria are separately maintained in working memory. The primary factor that causes both the generally higher hit confidence and the dissociation of hit and correct rejection confidence is the presence of recollection for old materials, which serves to both elevate and stabilize confidence independently of the influence of the external cues on the old/new criterion position used for familiarity. In contrast, the single process model fails under both of these situations and hence the model is not viable if one assumes that the confidence criteria are uniformly governed and/or minimally constrained. However, the model is capable of producing the effects if the old/upper confidence criteria lag considerably behind the old/new criterion and new/lower confidence criteria when shifting in response to the environmental cues (Figure 7). The figure also suggests that both upper confidence criteria must lag to the same degree.

One final aspect of the dual process model simulation that may seem surprising is its ability not only to predict the presence of an interaction in mean confidence, but its ability to closely predict the exact form of that interaction. In the behavioral data there is no appreciable difference in confidence for hits under invalid versus valid cues. Analogously, the simulation generated this null finding in 95.5% of the re-samples in the unconstrained version and 84.2% of the interval scaling constrained re-samples. This might seem unexpected since one might intuitively think that the shifting old/new familiarity criterion would have at least some noticeable effect on the net confidence of hits, even though hit confidence is heavily determined by the recollection process on some portion of the trials. However, the remarkable stability of the hit confidence is governed by two phenomena, the first of which can be easily appreciated simply by considering the dual process equation for hits, namely, Ro + (1-Ro)F_c. The subscript “c” indicates that the familiarity hit rate is governed by the placement of the old/new familiarity criterion. Now consider what happens when the familiarity criterion moves rightward in response to a “Likely New” cue. Clearly the overall hit rate will decline and also, on average, the confidence in hits based solely on familiarity will fall. The latter results because as the familiarity criterion moves rightward, less of the old item distribution is available to fall above the sampled high confidence criterion position. However, although the criterion shift leads to a decline in the expected confidence of familiarity based judgments, it also has the effect of reducing the relative preponderance of familiarity based judgments within the overall hit rate. This in turn means that recollection will play a proportionally greater role in determining the average measured confidence. Thus, a rightward shift of the familiarity criterion yields two opposing effects; it serves to reduce the confidence of familiarity based responses, while serving to elevate the proportion of total hit responses governed by recollection, which instead tends to drive averaged confidence upwards. The same logic applies for leftward shifts of the criterion: these will elevate familiarity confidence, but they will also water down the contribution of recollection to the total hit rate, tending to reduce averaged confidence. Thus, the mechanics of the dual process decision model actively dampen the effects of familiarity criterion movement on averaged expressed confidence across hit trials.

The second factor contributing to the remarkably stable hit confidence under the dual process model is the highly conservative starting criterion position in Table 4. For the average familiarity d’ estimate of 1.11 the unbiased old/new criterion position would be approximately .55 (viz., d’/2), however, the fitted location in the sample used for the bootstrapping was a much more conservative .88. Under the dual process approach this is consistent with the idea that in the presence of moderate levels of recollection observers are fairly conservative in their use of familiarity in isolation for recognition endorsements. Thus, it could well be that this conservative starting point, along with the muting or damping effects of recollection noted above, are fairly important for accurately producing the null hit confidence phenomenon. The bootstrap Monte Carlo method is again very useful in this regard because one can test this hypothesis by simply altering the parameter space accordingly. That is, one can replace the conservative old/new criterion values in the parameter space with those that would instead be neutral given each observer’s familiarity d’, namely, criteria halfway between the means of the new and old item distributions for the cases. If this manipulation increases the tendency to see reliable cueing effects on hit confidence, then the conservative placement of the old/new criterion in the actual parameter space is indeed a contributing factor to making the correct confidence predictions. This is in fact what occurred. We reran the simulation on the initial (i.e., no interval scaling constraint) 0–1.0 shift simulation and simply replaced the old/new criteria in the parameter space with the optimal criterion for each case’s d’ value (viz., d’/2). This shifts each case’s starting position leftward centering it between the new and old familiarity evidence distributions. The simulation demonstrated that this clearly disrupted the model’s accuracy. Whereas the original model yielded a null cue validity effect on hit confidence in 95.5% of the re-samples, this altered version yielded the null effect in only 64.8% of the re-samples, a difference clearly significant given 1000 observations.

Finally, through simulation we can also confirm that the recollection parameter and the starting criterion position are jointly contributing the null confidence effect for hits. To do this we re-ran the model again using a neutral criterion starting position; but in addition, we halved the recollection values in the parameter space. This further reduced the prediction accuracy of the model. Now the correct null prediction for hit confidence declined from 64.8% to 36.7% of the re-samples, again, clearly significant given 1000 observations. These findings demonstrate that the success of the dual process model predictions depends on both a conservative starting point for the old/new familiarity criterion and on appreciable levels of recollection. They also underscore the utility of the bootstrapped Monte Carlo approach since the joint effects of these two model parameters are somewhat difficult to intuit a priori. Finally, these results strongly validate the bootstrap approach to initially defining the parameter space. When this space was defined in accordance with prior findings in basic recognition data, using unbiased re-sampling procedures, it yielded predictions that closely correspond to the observed cueing data. However, altering this objectively defined space disrupts these predictions.

Discussion of Simulations

The simulations demonstrate several important findings. First, they demonstrate that the dual process model generates the correct pattern of confidence and accuracy data when observers are assumed to use a uniform rule when placing confidence criteria (Figure 6b) or a common interval in parsing the evidence continuum (Figure 6c). Under the model, the confidence/accuracy dissociation is largely driven by the offsetting influences of criterion shifts and recollection for old materials. These shifts alter the confidence in familiarity based judgments, but they also alter the relative preponderance of familiarity and recollective based reports in the total hit rate. These two outcomes tend to cancel one another, yielding a generally high and stable level of confidence despite the validity of external cues. It is also noteworthy that the model can generate the correct predictions when the notion of separately maintained and manipulable confidence criteria is abandoned. Under the interval scaling simulation subjects do not actively maintain scores of decision standards but instead they differ in the scaling interval or resolution at which they parse their own internal familiarity evidence. As noted above this greatly reduces the number of decision parameters assumed in the model, fits more naturally with the known limitations of working memory, and despite its simplicity, yields accurate predictions (Figure 6c).

Turning to the single process model, explaining the current empirical data requires a decision process that results in different degrees of movement for different confidence criteria (Figure 7 left panel). We are not aware of any signal detection model that anticipates the relative criterion movement patterns illustrated in Figure 7. However, a recent report has demonstrated an interesting pattern of confidence findings when comparing response scales varying in granularity. Mickes et al. (2007) provided subjects increasingly fine grained confidence report scales in an attempt to use the variance of their confidence reports as a direct proxy for the variance in underlying evidence assumed under the unequal variance signal detection model. When the variance of the confidence reports was directly calculated and compared to estimates obtained by fitting procedures similar to those above, a close correspondence was found leading the authors to suggest that the confidence ratings were varying directly with the underlying internal memory evidence values, and that the data supported the unequal variance model of item recognition. However, there was a second aspect of the data that Mickes et al. (2007) et al. noted was curious and which prompted further investigation in Mickes, Hwe, Wais, and Wixted (2011). Irrespective of the number of potential confidence options provided to participants, they appeared to reserve some relatively fixed proportion of highly accurate old responses for the highest numerical confidence value made available. For example, if given 10 possible numerical options for rating increasing confidence in old reports subjects appeared to reserve the “10” option for a proportion of highly accurate old judgments. However, when a new group was given say 30 possible options for reporting old recognition confidence, and also heavily instructed to use all of the scale, they nonetheless exhibited similar behavior; that is, they simply allocated a similar proportion of highly accurate old responses to the now highest “30” option. This led Mickes et al. (2011) to conclude that observers cannot scale strong memories, that is, they are unable to make fine confidence distinctions for some range of evidence at the upper end of the decision axis. One potential dual process explanation for this finding is that it reflects the different way that observers tend to assign recollective and familiarity based decisions to the confidence scales. If, during simple recognition, observers continued to treat recollection as largely infallible, then regardless of the granularity of the response scale they would simply assign the highest possible endorsement value to trials in which vivid recollection occurs. This would result in an apparent unwillingness to scale the upper range of the evidence from a single process standpoint.

Instead, Mickes et al. (2011) favored a learning account of the phenomenon. Under this approach, it is assumed that observers cannot scale these strong memories because prior to the experiment, they have never learned to do so. Focusing particularly on error driven learning they suggested that a failure to make erroneous judgments in this range of the evidence scale precludes the possibility of learning to scale these memory decisions when asked to do so in the laboratory. However, several questions remain about the proposed, unstudied learning process before it can be applied to predictions in other contexts. For example, it would seem that extremely high confidence correct rejections should also be influenced by a lack of error driven feedback prior to testing, yet the account currently only focuses on the highest confidence old reports. Additionally, how this account relates to the remaining criteria governing confidence is unclear, which also presumably differ in their relative tendencies to yield errors outside the laboratory. These questions aside, the learning account of Mickes et al. (2011) does not appear to be directly applicable here because of the vastly larger responses scales (e.g., 20 gradations of confidence) used in their report. Under their interpretation, our highest level “old” reports (“3”) are presumably far from this error free portion of the evidence scale, and so the behavior exhibited here is presumably not germane.

As a final test of the dual process model, we sought to extend its predictions to a domain typically thought to heavily depend upon recollection, namely source memory (Johnson, Hashtroudi, & Lindsay, 1993).

Experiment 3

The extension of the dual process predictions to the cueing effects in source memory paradigms is straightforward. Under the model, successful endorsement of studied materials in part relies upon context recollection, and such recollection dampens the influence of external cue validity on average confidence. However, to the extent that source attributions also depend on some continuous form of fluency or familiarity, the model anticipates a shift in the correct response rates in line with cue validity. In short, the model predicts that correct source responding will demonstrate the same pattern as recognition hits in Experiments 1 and 2, namely, a confidence accuracy dissociation such that cue validity clearly modulates accuracy (because it modulates the criterion for fluency or familiarity), but has little if any effect on the expressed confidence of correct judgments. It is important to note that this prediction does not make the assumption that source memory need to be governed solely by a threshold recollection process, and does not require that one assume source memory yields linear ROCs in probability space. This is necessarily true because the dual process model did not require these assumptions to render the correct predictions in the simulations of recognition behavior which also does not entail these assumptions. Instead, the prediction merely requires that recollection of source information modulate the confidence in response to the external cues in the same manner during correct source judgments, as it did for correct “old” judgments during recognition.

In contrast, the predictions of the single process model are unclear. As noted above, the simulation demonstrates that this model can only mirror the empirical recognition data if one makes very specific assumptions about the placement of confidence criteria, assuming that the “old” confidence criteria respond less vigorously, and to the same extent, compared to the remaining criteria. However, there is no current signal detection framework that anticipates this particular criterion behavior in the Explicit Mnemonic Cueing recognition task, and we suspect that even if one could be fashioned it may well not provide any basis for making predictions about source memory. Given this, we do not offer any predictions from the single process model perspective.

Method

Participants

Eighteen Washington University undergraduate students participated in return for course credit. Informed consent was obtained for all participants, as required by the university’s institutional review board.

Materials

A total of 500 words were drawn for each subject from a pool of 1,216 words total. Two hundred fifty were concrete and 250 abstract. Concrete and abstract words were selected based on their concreteness rating. Concrete words had a concreteness rating between 500 and 700 (mean: 572.95). Abstract words had a concreteness rating between 200 and 400 (mean: 318.38).

Procedures

The experiment consisted of two self-paced study/test cycles. Two hundred fifty items were presented during each study cycle; half of these items were judged for concreteness and the other half were judged for pleasantness. During study, items were presented individually on screen. For each item, participants saw a cue under the word asking participants either, “Is the word abstract?” or “Is the word pleasant?” Participants indicated their judgments using the “1” and “2” keys on the number pad of the keyboard. During test, studied items were presented individually on screen and participants were asked to judge whether the item was previously judged for concreteness or pleasantness by pressing either the “1” or “2” key on the number pad. Following the source judgment, participants rated their confidence in the source judgment (“low,” “medium,” or “high” confidence) using the “1,” “2,” and “3” keys, respectively. Participants moved onto the next item once the confidence judgment was made.

Source cues were present on 80% of the trials (200 cued trials, 50 baseline trials). Participants were correctly instructed that cues would be correct 75% of the time (150 valid trials, 50 invalid trials). On cued trials, participants saw one of two cues: “likely abstract task” or “likely pleasant task.” The cue appeared 500 ms before the word appeared and remained on screen during both the source and confidence judgments. On baseline trials, participants simply saw three question marks appear on screen in place of the cue (“? ? ?”) 500 ms before the word appeared on screen. As with cued trials, the baseline cue remained on screen during both the source and confidence judgments.

Results and Discussion

As with the recognition data, we examined accuracy and confidence separately, focusing on correct responding (Figure 1c). Full accuracy and confidence data are provided in Tables 1 and 2. For accuracy, a Response Type (pleasantness task hit vs. concreteness task hit) by Cue Validity (valid vs. invalid cue) repeated measures ANOVA demonstrated a main effect of Cue Validity [F(1,17) = 39.03, MSe = .014, p < .001, η² = .679]. As with recognition, performance clearly fell with invalid compared to valid predictive cues. There was also a Response Type by Cue Validity interaction [F(1,17) = 5.75, MSe = .002, p < .05, η² = .016] which occurred because the invalid cue-induced decline in performance tended to be greater for items from the concreteness task source than from the pleasantness task source. Whereas the hit rate for the two sources was similar under valid cues (t < 1), under invalid cueing the hit rate for pleasantness source task items (.69) was numerically higher than that for concreteness source task items (.65), although this only trended towards significance [t(17) = 1.91, p = .072, d = .28]. Thus, there was slight evidence suggesting that source memory for the pleasantness rating task materials may have been more resistant to invalid cueing than that for the concrete task, which we reconsider in the discussion. Regardless, source performance for both tasks robustly declined under invalid versus valid cueing [concreteness task items: t(17) = 7.11, p < .001, d = 1.36; pleasantness task items: t(17) = 4.87, p < .001, d = 1.05].

Turning to mean confidence, a Response Type (pleasantness task hit vs. concreteness task hit) by Cue Validity (valid vs. invalid cue) repeated measures ANOVA demonstrated only a main effect of Response Type [F(1,17) = 30.23, MSe = .053, p < .001, η² = .633]. Critically, however, Cue Validity had no main effect on confidence [F(1,17) = 1.92, MSe = .010, p > .18, η² = .01] nor did it interact with confidence across the two types of source hits [F(1,17) = 2.41, MSe = .004, p > .13, η² = .005] (Figure 1c).

The findings support the dual process model predictions. Although the validity of the cues markedly modulated source accuracy, lowering hits for both tasks when invalid, confidence did not respond in tandem. Instead, as with hit confidence during recognition, confidence was largely unaffected by the validity of the cues (Figure 1c).

Additionally, although unpredicted, there was a clear difference in mean confidence for the correct identification of pleasantness versus concreteness task items (Figure 1c). The general confidence advantage for pleasantness task items may be linked to the accuracy findings above that moderately suggested these items were more resistant to invalid cueing than the concreteness task items. This is in turn consistent with prior work showing that pleasantness task encoding tends to lead to superior free recall compared to other routinely used “deep” processing tasks (e.g., Nairne, Pandeirada, & Thompson, 2008), and specifically, that pleasantness task encoding leads to superior recall compared with concreteness task encoding (Roediger & Gallo, 2001). These differences during free recall may be linked with differences in the rates or vividness of context recollection for these materials that jointly renders these items somewhat more resistant to invalid cueing and leads to generally higher confidence endorsements compared to the concreteness task. Regardless of the exact mechanism responsible for the generally higher confidence across these two classes of source items, the finding illustrates that confidence is not generally insensitive during this task which serves to highlight that in contrast, it was insensitive to cue validity. Conceptually, these findings correspond well with the findings of Experiment 2 that demonstrated that average hit confidence was highly sensitive to levels of processing, but highly insensitive to cue validity.

General Discussion

The current findings demonstrate a new regularity of memory judgment. When observers actively use cues from a generally reliable external source to inform judgments, they are unsurprisingly less accurate on the minority of trials in which those cues are invalid, compared to the majority of trials in which those cues are valid. This decline in success rates occurs regardless of whether the correct conclusion is that the item was encountered in the specified experiment context (recognition or source memory hits), or instead was novel to the experiment context (recognition correct rejections). Critically, the average confidence in these reports only tracks relative success rates when participants correctly conclude the items are novel to the current experiment context. Confidence for correct study endorsements does not demonstrate this same pattern. When observers correctly report the items as previously encountered during either recognition or source memory attributions, their average confidence in these reports is unaltered by the validity of the external cues. This is surprising because it represents a case in which the external cue is strongly influencing report accuracy, but not affecting report confidence. Thus, even though observers clearly believe the cues to be valid (hence the prominent accuracy influences), they only downgrade their confidence when disagreeing and correctly concluding that the item is new, not when disagreeing and concluding that the item is old.

The confidence/accuracy dissociation in hits cannot be simply explained away as a ceiling effect on confidence reports or as a general insensitivity in hit confidence as Experiment 2 demonstrates. During this experiment hit confidence was markedly affected by a levels of processing manipulation and, furthermore, the confidence accuracy dissociation occurred for shallowly encoded materials whose average confidence was clearly far from ceiling and well above floor (Figure 1b). These empirical findings demonstrate that novel and studied items evoke information at test that differs fundamentally in its mapping onto confidence, and in the sensitivity of this mapping to external cueing influences.

Monte Carlo simulation demonstrated that a dual process model easily generated the current confidence/accuracy dissociation using minimal assumptions regarding confidence criterion placement at the level of each subject. This model and its conceptualization in the prior literature anticipates well the findings because it assumes that observers treat contextual recollection as highly diagnostic during these types of tasks, and hence the mapping of recollection to high confidence is predicted to be relatively immune to the influence of external cues. Instead, these cues are assumed to influence the criterion used for familiarity or fluency based attributions. Because both the confidence and accuracy of reports to novel items are directly influenced by this criterion, they move in tandem across valid and invalid cues. In contrast, as discussed in the simulation section, the mechanics of the dual process equation for hits generates largely opposing influences on net hit confidence as the criterion for familiarity or fluency shifts in response to the external cues. Although a lax criterion increases the confidence of familiarity based hits, it also reduces the relative preponderance of recollection based trials in the overall hit rate, producing opposing tendencies on net confidence. The reverse is true for an increasingly stringent familiarity criterion, which will serve to lessen the confidence of familiarity based responses, but also to lessen the relative role familiarity plays in the overall hit rate (hence increasing the relative contribution of recollection). In short, this simple dual process model predicts that confidence in hits should be highly stable in the face of influences that shift the familiarity criterion. Perhaps as important, manipulations that instead change the relative levels of evidence across studied item classes should induce clear changes in hit confidence despite its relative insensitivity to criterion changes. This is precisely the pattern observed in Experiment 2. Thus, at the broadest level, the dual process model accurately predicts that hit confidence will be largely insensitive to changes in the criterion used for familiarity judgments within a particular class of studied item (provided moderate levels of recollection are evoked), while simultaneously being quite sensitive to changes in the levels of processing across studied classes of items.

Utility of the Bootstrapped Monte Carlo Simulation Method

Much of the debate surrounding the number and nature of retrieval processes contributing to recognition judgment has centered the results of post hoc fitting of models to confidence-based ROCs (Ratcliff & Starns, 2009; Yonelinas, 2001). This is not unreasonable since a useful decision model of recognition should clearly be capable of accommodating this functional relationship between confidence and accuracy. However, sole reliance on this approach has known drawbacks because the post hoc fit of a model depends only partly on its theoretical validity (Pitt et al. 2003). With all other things being equal, it is informative when a model badly misfits the data compared to a competitor, however, when models generally fit well, then fitting is a poor basis for judgment. Against this backdrop, the current findings demonstrate the utility of the simulation approach, and in particular the bootstrapped informed simulation method presented here, which instead emphasizes model generalizability and forces the experimenter to explicitly outline and defend the constraints and rules governing the behavior of parameters that are not a priori constrained by the bootstrap re-sampling procedure. In the current investigation, the behavior of the evidence parameters and initial starting position of the recognition criterion are objectively governed solely by re-sampling, and explicit constraints governing the placement of the confidence criteria following criterion shifts were examined.

Perhaps one reason simulation is not used more widely is the concern that the outcome of presented simulations is often heavily steered by the experimenter’s choice of parameters and their covariation. The bootstrapping method of defining the parameter space largely sidesteps this issue because the range and variability of the majority of parameters arises from their empirical variability in an independent sample. Indeed, there were only two parameter constraints initially made in the current simulations. First, we chose the range within which the old/new criterion shifted in response to the external cues for both models. However, as Table 5 demonstrates, the dual process model success extended across a wide range, alleviating this concern. Second, we limited how extreme the high confidence criteria could be with respect to the old/new criterion location. This was necessary to avoid criteria as extreme as to preclude high or medium confidence responses and is well justified by the tendency of theorists to encourage respondents to use the entire confidence scale when reporting, and to discard subjects who do not do so. Despite these minimal restrictions, the dual process model successfully generated the confidence/accuracy dissociations seen in the current data.

A second aspect of the simulation method that proved useful, was that it enabled us to discover the special constraints on confidence criterion placement that were necessary for the single process model to mirror the empirical findings using data mining techniques. This approach led to the discovery that the model required “sluggish” and similar movement of the upper confidence criteria in relation to the remaining criteria in order to yield the correct pattern. Although we know of no strong theoretical reason to anticipate this required behavior, it is important to illustrate that it is central for the model’s success in this experimental situation. In this light, the simulation does not disprove the single process model; it merely illustrates the criterion behavior that is necessary to make it “work” in this context, and demonstrates that relative to the dual process model, a much more specific set of criterion constraints is necessary for the model to be viable. Finding a theoretical framework that explains why the criterion should move in this particular manner and which makes testable predictions in other domains such as source memory, poses a challenge for the single process approach that may or may not be met with future models.

The simulation technique was also useful for greatly simplifying the dual process model. Because the model successfully characterized the confidence/accuracy dissociation when all confidence criteria moved similarly at the group level (i.e., averaged across cases) it stood to reason it would repeat this successful prediction if instead an interval scaling assumption at the level of each subject was enforced. Thus, instead of assuming observers maintain tens of explicit decision criteria in working memory, one instead assumes that they parse their internal familiarity evidence scale in a regular manner. This greatly reduces the number of decision parameters in the model, from 10 to 3, yet it still anticipated the confidence/accuracy dissociation. In contrast, the simulation demonstrated that the interval scaling assumption was untenable under the single process model because the model clearly requires differential movement of the confidence criteria in order to yield the correct patterns. Although not essential for the successful predictions of the dual process model, we find the interval scaling assumption attractive primarily because there is little in the prior working memory literature to suggest that observers can maintain 10 or 15 separate decision standards in working memory while conducting a demanding secondary memory retrieval task.

One final benefit of the simulation approach used here was that we were able to identify a second factor other than the recollection process itself which contributed to the stability of hit confidence in the face of changing cue validity under the dual process model. Because the parameter space was defined objectively through bootstrapping, we were able to tinker with that space in different ways in an attempt to break the successful predictions of the model. This approach suggested that a conservative old/new criterion for the use of familiarity also contributed to the model’s ability to correctly predict the empirical data, because when the space was altered to introduce a more neutral criterion, the model’s success markedly declined. Of course, had we subjectively imposed a conservative familiarity criterion during simulation, then we would have been open to the criticism that we were defining the parameters opportunistically in order to achieve the correct outcomes. As noted above and in the simulation section, the bootstrapping procedure sidesteps this issue, because it determines the behavior of the vast majority of parameters without experimenter intervention. The fact that this procedure objectively yielded a complex parameter space (Figure 4 and 5) that produced the correct predictions highlights its importance. Thus, as a general research strategy, the bootstrap informed Monte Carlo approach allows one to objectively define the behavior of a vast majority of model parameters and then to test well defined constraints on the remaining parameters through Monte Carlo simulation. If the constraints yield correct patterns in light of empirical data, and if they are supported by prior theory, then one finds support for the proposed model.

Significance of findings for Eyewitness and Conformity Research

Although a better understanding of the relationship between confidence and accuracy is likely central for understanding eyewitness and conformity research, a simple take home message from these findings is initially difficult to articulate. On the one hand, the data clearly confirm what has long been recognized in the eyewitness and social conformity literatures, namely, that external information can profoundly influence observer accuracy (Figure 1). However, the confidence of reports also matters quite a bit in eyewitness contexts, and here one can regard the data as either encouraging or disheartening. On the encouraging side, the stable confidence of hits across cue validity suggests that there is a highly reliable type of retrieval evidence, namely context recollection, which in these paradigms is insensitive to external influences (see also Meissner, Tredoux, Parker, & MacLin, 2005). On the other hand, if one were hoping that relative confidence would always reflect relative performance levels, then the data for hits are disheartening because very large cue induced changes in hit rates have little impact on the average expressed confidence of reporting.

The contradictory nature of these two viewpoints, however, is more apparent than real because the current findings result from amalgamating the data across multiple trials. At the level of each individual trial, which is how the simulations were fashioned, the dual process interpretation and its relevance to the eyewitness literature is much clearer. If an observer reports an item as evoking contextual recollections, then he or she is expected to respond highly confidently regardless of whether external cues suggest the item is old (valid cue) or new (invalid cue). In contrast, if he or she reports the item as familiar, but cannot report recollective details, then the current data suggest that his or her report and its confidence are much more likely to have been swayed by external cue influences. This concern also generally applies if the observer reports the item as new. Of course, this explanation presupposes the existence of recollection and its relative uniqueness to studied versus novel materials. While the highly successful predictions of the dual process model of the current data support this presupposition, they do not speak to how one would reliably assess whether recollection had or had not occurred at the trial level. Furthermore, the stability of recollection confidence in light of external cue influences presumably depends upon task domain. In the current experiments, context recollection is assumed highly diagnostic because it should rarely if ever occur for new items during simple item recognition with these materials. Its diagnostic value is quite high in source memory as well because each item was processed only using one or the other relatively distinct processing task (viz., the sources are mutually exclusive and distinctive). Given this, recollection of task specific context is presumably held in high regard by the subjects and correspondingly, likely does not often occur for the inappropriate material.

Finally, it is important to emphasize that the subjects are fully aware that the current cues are probabilistic and hence the cues will be incorrect on some small minority of trials. Under these conditions, recollection of contextual details in conjunction with an invalid cue has a ready explanation provided it occurs infrequently. If instead observers were inaccurately led to believe that the external cues were never incorrect, then it may be the case that they would view the conflict between recollective retrieval and an invalid recommendation as a reason to downgrade their confidence. In short, provided the cues are known to be probabilistic there is no need to question the veracity of one’s recollections when they conflict with the cue on some small minority of trials. However, this does not mean that cueing manipulations cannot be devised that instead actively lead one to question the veracity or utility of one’s own recollections. Of course, actual eyewitness situations may or may not depart considerably from these clear cut laboratory distinctions.

Conclusions

The current findings demonstrate that the use of explicit mnemonic cues can dissociate the accuracy and average confidence of reports, yielding different patterns across studied and novel materials. While the findings generally support a dual process interpretation, they also point to the general utility of the manipulation regardless of one’s preferred decision model. The fact that report confidence and accuracy do not always respond in tandem to external cue influences represents an important, new contribution to our understanding of the relationship between the confidence and accuracy of memory judgments. We hope that others will find this procedure useful and future research targeting other tasks or special populations may benefit from this approach.