Fitting Multilevel Models with Ordinal Outcomes: Performance of Alternative Specifications and Methods of Estimation

Abstract

Previous research has compared methods of estimation for multilevel models fit to binary data but there are reasons to believe that the results will not always generalize to the ordinal case. This paper thus evaluates (a) whether and when fitting multilevel linear models to ordinal outcome data is justified and (b) which estimator to employ when instead fitting multilevel cumulative logit models to ordinal data, Maximum Likelihood (ML) or Penalized Quasi-Likelihood (PQL). ML and PQL are compared across variations in sample size, magnitude of variance components, number of outcome categories, and distribution shape. Fitting a multilevel linear model to ordinal outcomes is shown to be inferior in virtually all circumstances. PQL performance improves markedly with the number of ordinal categories, regardless of distribution shape. In contrast to binary data, PQL often performs as well as ML when used with ordinal data. Further, the performance of PQL is typically superior to ML when the data includes a small to moderate number of clusters (i.e., ≤ 50 clusters).

Psychologists, as well as researchers in allied fields of health, education, and social science, are often in the position of collecting and analyzing nested (i.e., clustered) data. Two frequently encountered types of nested data are hierarchically clustered observations, such as individuals nested within groups, and longitudinal data, or repeated measures over time. Both data structures share a common feature: dependence of observations within units (i.e., observations within clusters or repeated measures within persons). Because classical statistical models like analysis of variance and linear regression assume independence, alternative statistical models are required to analyze nested data appropriately.

In psychology, a common way to address dependence in nested data is to use a multilevel model (sometimes referred to as a unit-specific model, or conditional model). A model is specified to include cluster-level random effects to account for similarities within clusters and the observations are assumed to be independent conditional on the random effects. A random intercept captures level differences in the dependent variable across clusters (due to unobserved cluster-level covariates), whereas a random slope implies that the effect of a predictor varies over clusters (interacts with unobserved cluster-level covariates). Alternative ways to model dependence in nested data exist, including population-average (or marginal) models which are typically estimated by Generalized Estimating Equations (GEE; Liang & Zeger, 1986). These models produce estimates of model coefficients for predictors that are averaged over clusters, while allowing residuals to correlate within clusters. Population-average models are robust to misspecification of the correlation structure of the residuals, whereas unit-specific models can be sensitive to misspecification of the random effects. However, unit-specific models are appealing to many psychologists (and others), because they allow for inference about processes that operate at the level of the group (in hierarchical data) or individual (in longitudinal data). Indeed, in a search of the PsycARTICLES database, we found that unit-specific models were used more than fifteen times more often than population-average models in psychology applications published over the last five years.ⁱ To maximize relevance for psychologists, we thus focus on the unit-specific multilevel model in this paper. Excellent introductions to multilevel modeling include Raudenbush and Bryk (2002), Goldstein (2003), Snijders and Bosker (1999) and Hox (2010).

Though the use of multilevel models to accommodate nesting has increased steadily in psychology over the past several decades, many psychologists appear to have restricted their attention to multilevel linear models. These models assume that observations within clusters are continuous and normally distributed, conditional on observed covariates. But very often psychologists measure outcomes on an ordinal scale, involving multiple discrete categories with potentially uneven spacing between categories. For instance, participants might be asked whether they “strongly disagree,” “disagree,” “neither disagree nor agree,” “agree,” or “strongly agree” with a particular statement. Although there is growing recognition that the application of linear models with such outcomes is inappropriate, it is still common to see ordinal outcomes treated as continuous so that linear models can be applied (Agresti, Booth, Hobert & Caffo, 2000; Liu & Agresti, 2005).

Researchers may be reluctant to fit an ordinal rather than linear multilevel model for several reasons. First, researchers are generally more familiar with linear models and may be less certain how to specify and interpret the results of models for ordinal outcomes. Second, to our knowledge, no research has expressly examined the consequences of fitting a linear multilevel model to ordinal outcomes. Third, it may not always be apparent what estimation options exist for fitting multilevel models with ordinal outcomes, nor what the implications of choosing one option versus another might be. Indeed, there is a general lack of information on the best method of estimation for the ordinal case. Unlike the case of normal outcomes, the likelihood for ordinal outcomes involves an integral that cannot be resolved analytically, and several alternative estimation methods have been proposed to overcome this difficulty. The strengths and weaknesses of these methods under real-world data conditions are not well understood.

The goals of this paper are thus twofold. First, we seek to establish whether and when fitting a linear multilevel model to ordinal data may constitute an acceptable data analysis strategy. Second, we seek to evaluate the relative performance of two estimators for fitting multilevel models to discrete outcomes, namely Penalized Quasi-Likelihood (PQL) and Maximum Likelihood (ML) using adaptive quadrature. These two methods of estimation were chosen for comparison because of their prevalence within applications and their availability within commonly used software (PQL is a default estimator in many software programs, such as HLM6, the GLIMMIX procedure in SAS, and is currently the only estimator available in SPSS, and ML with adaptive quadrature is available in the GLIMMIX and NLMIXED SAS procedures as well as Mplus, GLLAMM, and Supermix).

We begin by presenting the two alternative model specifications, the multilevel linear model for continuous outcomes versus a multilevel model expressly formulated for ordinal outcomes. We then discuss the topic of estimation and provide a brief review of previous literature on fitting multilevel models to binary and ordinal data, focusing on gaps involving estimation in the ordinal case. Based on the literature, we develop a series of hypotheses which we test in a simulation study that compares two model specifications, linear versus ordinal, under conditions that might commonly occur in psychological research. Futher, we compare the estimates of ordinal multilevel models fit via PQL versus ML with adaptive quadrature. The findings from our simulation translate directly into recommendations for current practice.

Alternative Model Specifications

Multilevel Linear Model

We first review the specification of the multilevel linear model. For exposition, let us suppose we are interested in modeling the effects of one individual-level (level-1) predictor X_ij and one cluster-level (level-2) predictor W_j, as well as a cross-level interaction, designated X_ijW_j. To account for the dependence of observations within clusters, we will include a random intercept term, designated u_0j, and a random slope for the effect of X_ij, designated u_1j, to allow for the possibility that this predictor varies across clusters. This model is represented as:

$$\begin{array}{ll}\text{Level}1:\hfill & Y_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}\hfill \\ \text{Level}2:\hfill & {\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{W}_j+u_{0j}\hfill \\ \hfill & {\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{W}_j+u_{1j}\hfill \\ \text{Combined}:\hfill & Y_{\mathit{\text{ij}}}={\gamma }_{00}+{\gamma }_{01}{W}_j+{\gamma }_{10}{X}_{\mathit{\text{ij}}}+{\gamma }_{11}{W}_j{X}_{\mathit{\text{ij}}}+u_{0j}+u_{1j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}\hfill \end{array}$$ (1)

All notation follows that of Raudenbush and Bryk (2002), with coefficients at level 1 indicated by β, fixed effects indicated by γ, residuals at level 1 indicated by r, and random effects at level 2 indicated by u. Both the random effects and the residuals are assumed to be normally distributed, or

$$\left[\begin{array}{c}{u}_{0j}\\ u_{1j}\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{c}{\tau }_{00}\\ {\tau }_{10}& {\tau }_{11}\end{array}\right]\right)$$ (2)

and

$$r_{\mathit{\text{ij}}}\sim N(0,{\sigma }^2)$$ (3)

An important characteristic of Equation (1) is that it is additive in the random effects and residuals. In concert with the assumptions of normality in Equations (2) and (3), this additive form implies that the conditional distribution of Y_ij is continuous and normal.

The use of linear models such as Equation (1) with ordinal outcomes can be questioned on several grounds (Long, 1997, p. 38-40). First, the linear model can generate impossible predicted values, below the lowest category number or above the highest category number. Second, the variability of the residuals becomes compressed as the predicted values move toward the upper or lower limits of the observed values, resulting in heteroscedasticity. Heteroscedasticity and non-normality of the residuals cast doubt on the validity of significance tests. Third, we often view an ordinal scale as providing a coarse representation for what is really a continuous underlying variable. If we believe that this unobserved continuous variable is linearly related to our predictors, then our predictors will be nonlinearly related to the observed ordinal variable. The linear model then provides a first approximation of uncertain quality to this nonlinear function. The substitution of a linear model for one that is actually nonlinear is especially problematic for nested data when lower-level predictors vary both within and between clusters (have intraclass correlations exceeding zero). In this situation, estimates for random slope variances and cross-level interactions can be inflated or spurious (Bauer & Cai, 2009).

Multilevel Models for Ordinal Outcomes

In general, there are two ways to motivate models for ordinal outcomes. One motivation that is popular in psychology and the social sciences, alluded to above, is to conceive of the ordinal outcome as a coarsely categorized measured version of an underlying continuous latent variable. For instance, although attitudes may be measured via ordered categories “strongly disagree” to “strongly agree,” we can imagine that a continuous latent variable underlies these responses. If the continuous variable had been measured directly, then the multilevel linear model in Equation (1) would be appropriate. Thus, for the continuous underlying variable, denoted $Y_{\mathit{\text{ij}}}^{\ast }$, we can stipulate the model

$$\begin{array}{ll}\text{Level}1:\hfill & Y_{\mathit{\text{ij}}}^{\ast }={\beta }_{0j}+{\beta }_{1j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}\hfill \\ \text{Level}2:\hfill & {\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{W}_j+u_{0j}\hfill \\ \hfill & {\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{W}_j+u_{1j}\hfill \\ \text{Combined}:\hfill & Y_{\mathit{\text{ij}}}^{\ast }={\gamma }_{00}+{\gamma }_{01}{W}_j+{\gamma }_{10}{X}_{\mathit{\text{ij}}}+{\gamma }_{11}{W}_j{X}_{\mathit{\text{ij}}}+u_{0j}+u_{1j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}\hfill \end{array}$$ (4)

To link the underlying $Y_{\mathit{\text{ij}}}^{\ast }$ with the observed ordinal response Y_ij we must also posit a threshold model. For Y_ij scored in categories c=1, 2…, C, we can write the threshold model as:

$$\begin{array}{l}{Y}_{\mathit{\text{ij}}}=1\text{if}{Y}_{\mathit{\text{ij}}}^{\ast }<{\nu }^{(1)}\hfill \\ Y_{\mathit{\text{ij}}}=2\text{if}{\nu }^{(1)}\le Y_{\mathit{\text{ij}}}^{\ast }<{\nu }^{(2)}\hfill \\ ⋮\hfill \\ Y_{\mathit{\text{ij}}}=C\text{if}{Y}_{\mathit{\text{ij}}}^{\ast }\ge {\nu }^{(C-1)}\hfill \end{array}$$ (5)

where ν^(c) is a threshold parameter and the thresholds are strictly increasing (i.e., ν⁽¹⁾ < ν⁽²⁾… < ν^(C–1)). In words, Equation (5) indicates that when the underlying variable $Y_{\mathit{\text{ij}}}^{\ast }$ increases past a given threshold we see a discrete jump in the observed ordinal response Y_ij (e.g., when $Y_{\mathit{\text{ij}}}^{\ast }$ crosses the threshold ν⁽¹⁾, Y_ij changes from a 1 to a 2).

Finally, to translate Equations (4) and (5) into a probability model for Y_ij we must specify the distributions of the random effects and residuals. The random effects at Level 2 are conventionally assumed to be normal, just as in Equation (2). Different assumptions can be made for the Level 1 residuals. Assuming r_ij ∼ N (0,1) leads to the multilevel probit model, whereas assuming r_ij ∼ logistic(0,π²/3) leads to the multilevel cumulative logit model. In both cases, the variance is fixed (at 1 for the probit specification and at π²/3 for the logit specification) since the scale of the underlying latent variable is unobserved. Of the two specifications, we focus on the multilevel cumulative logit model because it is computationally simpler and because the estimates for the fixed effects have appealing interpretations (i.e., the exponentiated coefficients are interpretable as odds ratios).

Alternatively, the very same models can be motivated from the framework of the generalized linear model (McCullagh & Nelder,1989), a conceptualization favored within biostatistics. Within this framework, we start by specifying the conditional distribution of our outcome. In this case, the conditional distribution of the ordinal outcome Y_ij is multinomial with parameters describing the probabilities of the categorical responses. By modeling these probabilities directly, we bypass the need to invoke a continuous latent variable underlying the ordinal responses.

To further explicate this approach we can define cumulative coding variables to capture the ordered-categorical nature of the observed responses. C – 1 coding variables are defined such that $Y_{\mathit{\text{ij}}}^{(c)}=1\text{if}{Y}_{\mathit{\text{ij}}}\le c$ (the cumulative coding variable for category C is omitted as it would always be scored 1). The expected value of each cumulative coding variable is then the cumulative probability that a response will be scored in category c or below, denoted as ${\phi }_{\mathit{\text{ij}}}^{(c)}=P(Y_{\mathit{\text{ij}}}\le c)=P(Y_{\mathit{\text{ij}}}^{(c)}=1)$.

The cumulative probabilities are predicted via the linear predictor, denoted η_ij, which is specified as a weighted linear combination of observed covariates/predictors and random effects. For our example model, the linear predictor would be specified through the equations

$$\begin{array}{ll}\text{Level}1:\hfill & {\eta }_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{X}_{\mathit{\text{ij}}}\hfill \\ \text{Level}2:\hfill & {\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{W}_j+u_{0j}\hfill \\ \hfill & {\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{W}_j+u_{1j}\hfill \\ \text{Combined}:\hfill & {\eta }_{\mathit{\text{ij}}}={\gamma }_{00}+{\gamma }_{01}{W}_j+{\gamma }_{10}{X}_{\mathit{\text{ij}}}+{\gamma }_{11}{W}_j{X}_{\mathit{\text{ij}}}+u_{0j}+u_{1j}{X}_{\mathit{\text{ij}}}\hfill \end{array}$$ (6)

where the random effects are assumed to be normally distributed as in Equation (2).

The model for the observed responses is then given as

$$Y_{\mathit{\text{ij}}}^{(c)}=g^{-1}\left[{\nu }^{(c)}-{\eta }_{\mathit{\text{ij}}}\right]+r_{\mathit{\text{ij}}}$$ (7)

where ν^(c) is again a threshold parameter that allows for increasing probabilities when accumulating across categories and g⁻¹(.) is the inverse link function, a function that maps the continuous range of [ν^(c) − η_ij] into the bounded zero-to-one range of predicted values (model-implied cumulative probabilities) for the cumulative coding variable (Hedeker & Gibbons, 2006; Long, 1997). Any function with asymptotes of zero and one could be considered as a candidate for g⁻¹(.) but common choices are the Cumulative Density Function (CDF) for the normal distribution, which produces the multilevel probit model, and the inverse logistic function,

$$g^{-1}[{\nu }^{(c)}-{\eta }_{\mathit{\text{ij}}}]={\phi }_{\mathit{\text{ij}}}^{(c)}=\frac{exp({\nu }^{(c)}-{\eta }_{\mathit{\text{ij}}})}{1+exp({\nu }^{(c)}-{\eta }_{\mathit{\text{ij}}})}$$ (8)

which produces the multilevel cumulative logit model.

Both motivations lead to equivalent models, with the selection of the link function in Equation (7) playing the same role as the choice of residual distribution in Equation (4). The two approaches thus differ only at the conceptual level. Regardless of which conception is preferred, however, a few additional features of the model should be noted. First, the full set of thresholds and overall model intercept are not jointly identified. One can set the first threshold to zero and estimate the intercept, or set the intercept to zero and estimate all thresholds. The former choice seems to be most common, and we will use that specification in our simulations. Additionally, an assumption of the model, which can be checked empirically, is that the coefficients in the linear predictor are invariant across categories (an assumption referred to as proportional odds for the multilevel cumulative logit model). This assumption can be relaxed, for instance by specifying a partial proportional odds model. For additional details on this assumption and the partial proportional odds model, see Hedeker and Gibbons (2006).

Alternative Estimation Methods

To provide a context for comparison of estimation methods, first consider a general expression for the likelihood function for cluster j:

$$L_j(\mathbf{\theta }|Y_j)=\int f({\mathbf{\text{Y}}}_j|{\mathbf{\text{u}}}_j,\mathbf{\theta })h({\mathbf{\text{u}}}_j|\mathbf{\theta })d{\mathbf{\text{u}}}_j$$ (9)

where θ is the vector of parameters to be estimated (fixed effects and variance components), Y_j is the vector of all observations on Y_ij within cluster j, and u_jis the vector of random effects. The density function for the conditional distribution of Y_j is denoted f (·) and the density function for the random effects is denoted h(·), both of which implicitly depend on the parameters of the model. Integrating the likelihood over the distribution of the random effects returns the marginal likelihood for Y_j, that is, the likelihood of Y_j averaging over all possible values of the random effects. This averaging is necessary because the random effects are unobserved. The overall sample likelihood is the product of the cluster-wise likelihoods, and we seek to maximize this likelihood to obtain the parameter estimates that are most consistent with our data (i.e., parameter estimates that maximize the likelihood of observing the data we in fact observed).

In the linear multilevel model, both f (·) and h(·) are assumed to be normal and in this case the integral within the likelihood resolves analytically; the marginal likelihood for Y_j is the multivariate normal density function (Demidenko, 2004, pp. 48-61). No such simplification arises when f(·) is multinomial and h(·) is normal, as is the case for ordinal multilevel models. Obtaining the marginal probability of Y_j would, in theory, require integrating over the distribution of the random effects at each iteration of the likelihood-maximization procedure, but this task is analytically intractable. One approach to circumvent this problem is to implement a quasi-likelihood estimator (linearizing the integrand at each iteration) and another is to evaluate the integral via a numerical approximation.

The idea behind quasi-likelihood estimators (PQL and MQL) is to take the nonlinear model from Equation (7) and apply a linear approximation at each iteration. This linear model is then fit via normal-theory ML using observation weights to counteract heteroscedasticity and non-normality of the residuals. This is an iterative process with the linear approximation improving at each step. More specifically, the linear approximation typically employed is a first-order Taylor series expansion of the nonlinear function g⁻¹(ν^(c) – η_ij) . Algebraic manipulation of the linearized model is then used to create a “working variate” Z_ij which is an additive combination of the linear predictor ν^(c) – η_ij and a residual e_ij (see online appendix for more details). The working variate is constructed somewhat differently in MQL and PQL; it is constructed exclusively using fixed effects in the former but using both fixed effects and empirical Bayes estimates of the random effects in the latter (see Goldstein, 2003, pp. 112-114; Raudenbush & Bryk, 2002, pp. 456-459). The residual is the original level-1 residual term scaled by a weight e_ij = r_ij/ w_ij derived from the linearization procedure to render the residual distribution approximately normal, i.e., e_ij ∼ N(0,1/w_ij). The resultant model for the “working variate”, Z_ij = (ν^(c) − η_ij)+e_ij, approximately satisfies assumptions of the multilevel linear model, and can be used to construct an approximate (or quasi-) likelihood.

An alternative way to address the analytical intractability of the integral in Equation (9) is to leave the integrand intact but approximate the integral numerically. Included within this approach is ML using Gauss-Hermite quadrature, adaptive quadrature, Laplace algorithms, and simulation methods. Likewise, Bayesian estimation using Markov Chain Monte Carlo with non-informative (or diffuse) priors can be viewed as an approximation to ML that implements simulation methods to avoid integration. Here we focus specifically on ML with adaptive quadrature. With this method, the integral is approximated via a weighted sum of discrete points. The locations of these points of support (quadrature points) and their respective weights are iteratively updated (or adapted) for each cluster j, which has the effect of re-centering and re-scaling the points in a unit-specific manner (Rabe-Hesketh, Skrondal & Pickles, 2002). At each iteration the adapted quadrature points are solved for as functions of the mean or mode and standard deviation of the posterior distribution for cluster j. Integral approximation improves as the number of points of support per dimension of integration increase, at the expense of computational time. Computational time also increases exponentially with the dimensions of integration, which in Equation (9) corresponds to the number of random effects. The nature of the discrete distribution employed differs across approaches (e.g. rectangular vs. trapezoidal vs. Guass-Hermite) where, for example, rectangular adaptive quadrature considers a discrete distribution of adjoining rectangles.

Prior Research

Fitting a Multilevel Linear Model by Normal-Theory ML

The practice of fitting linear models to ordinal outcomes using normal-theory methods of estimation remains common (Agresti, Booth, Hobert & Caffo, 2000; Liu & Agresti, 2005). To date, however, no research has been conducted to evaluate the performance of multilevel linear models with ordinal outcomes from which to argue against this practice. A large number of studies have, however, evaluated the use of linear regression or normal-theory Structural Equation Modeling (SEM) with ordinal data (see Winship & Mare, 1984, and Bollen, 1989, pp. 415-448 for review). These studies are relevant here because the multilevel linear model can be considered a generalization of linear regression and a submodel of SEM (Bauer, 2003; Curran, 2003; Mehta & Neale, 2005). Overall, this research indicates that, for ordinal outcomes, the effect estimates obtained from linear models are often attenuated, but that there are circumstances under which the bias is small enough to be tolerable. These circumstances are when there are many categories (better resembling an interval-scaled outcome) and the category distributions are not excessively non-normal. Extrapolating from this literature, we expect multilevel linear models to perform most poorly with binary outcomes or ordinal outcomes with few categories and best with ordinal outcomes with many categories (approaching a continuum) and roughly normal distributions (Goldstein, 2003, p. 104).

Fitting a Multilevel Cumulative Logit model by Quasi-Likelihood

Simulation research with PQL and MQL to date has focused almost exclusively on binary rather than ordinal outcomes. This research has consistently shown that PQL performs better than MQL (Breslow & Clayton, 1993, Breslow & Lin, 1995; Goldstein & Rasbash, 1996; Rodriguez & Goldman, 1995, 2001). In either case, however, the quality of the estimates depends on the adequacy of the Taylor series approximation and the extent to which the distribution of the working variate residuals is approximately normal (McCulloch, 1997). When these approximations are poor, the estimates are attenuated, particularly for variance components. In general, PQL performs best when there are many observations per cluster (Bellamy et al., 2005; Ten Have & Localio, 1999; Skrondal & Rabe-Hesketh, 2004, pp. 194-197), for it is then that the provisional estimates of the random effects become most precise, yielding a better working variate. The performance of PQL deteriorates when the working variate residuals are markedly non-normal, as is usually the case when the outcome is binary (Breslow & Clayton, 1993; Skrondal & Rabe-Hesketh, 2004, pp. 194-197). The degree of bias increases with the magnitude of the random effect variances (Breslow & Lin, 1995; McCulloch, 1997; Rodriguez & Goldman, 2001).ⁱⁱ

Though it is well-known that PQL can often produce badly biased estimates when applied to binary data (Breslow & Lin, 1995; Rodriguez & Goldman, 1995; 2001; Raudenbush, Yang & Yosef, 2000), it is presently unknown whether this bias will extend to multilevel models for ordinal outcomes. The assumption seems to be that the poor performance of PQL will indeed generalize (Agresti, et al., 2000; Liu & Agresti, 2005), leading some to make blanket recommendations that quasi-likelihood estimators should not be used in practice (McCulloch, Searle, & Neuhaus, 2008, p. 198). This conclusion may, however, be premature. For instance, Saei and MacGilchrist (1998) detected only slight bias for a PQL-like estimator when the outcome variable had four categories and was observed for three individuals in each of 30 clusters. Beyond the specific instance considered by Saei and McGilchrist (1998), we believe that the bias incurred by using PQL will diminish progressively with the number of categories of the ordinal outcome (due to the increase in information with more ordered categories). To our knowledge, this hypothesis has not previously appeared in the literature on PQL, nor has the quality of PQL estimates been compared over increasing numbers of categories.

Fitting the Multilevel Cumulative Logit Model by ML with Adaptive Quadrature

ML estimation for the multilevel cumulative logit model is theoretically preferable to quasi-likelihood estimation because it produces asymptotically unbiased estimates. Moreover, a number of simulation studies have shown that ML using quadrature (or other integral approximation approaches) outperforms quasi-likelihood estimators such as PQL when used to estimate multilevel logistic models with binary outcomes (Rodriguez & Goldman, 1995; Raudenbush, Yang & Yosef, 2000). As one would expect given its desirable asymptotic properties, ML with numerical integration performs best when there is a large number of clusters.

There are, however, still compelling reasons to compare the ML and PQL estimators for the cumulative logit model. First, although ML is an asymptotically unbiased estimator, it suffers from small sample bias (Demidenko, 2004, p. 58; Raudenbush & Bryk, 2002, p. 53). When the number of clusters is small, ML produces negatively biased variance estimates for the random effects. Additionally, this small-sample bias increases with the number of fixed effects. For ordinal outcomes, the fixed effects include C – 1 threshold parameters, so a higher number of categories may actually increase the bias of ML estimates. Second, Bellamy (2005) showed analytically and empirically that when there is a small number of large clusters, as often occurs in group-randomized trials, the efficiency of PQL estimates can equal or exceed the efficiency of ML estimates. Third, as discussed above, PQL may compare more favorably to ML when the data are ordinal rather than binary, as the availability of more categories may offset PQL's particularly strong need for large clusters.

Research Hypotheses

From the literature reviewed above, we now summarize the research hypotheses that motivated our simulation study.

1. A linear modeling approach may perform adequately when the number of categories for the outcome is large (e.g., 5+) and when the distribution of category responses is roughly normal in shape, but will prove inadequate if either of these conditions is lacking.

2. ML via adaptive quadrature will be unbiased and most efficient when there is a large number of clusters, but these properties may not hold when there are fewer clusters. In particular, variance estimates may be negatively biased when the number of clusters is small and the number of fixed effects (including thresholds, increasing with number of categories) is large.

3. PQL estimates will be attenuated, especially when the variances of the random effects are large and when the cluster sizes are small. More bias will be observed for variance components than fixed effects.

4. PQL will perform considerably better for ordinal outcomes as the number of categories increases. With sufficiently many categories, PQL may have negligible bias and comparable or better efficiency than ML even when cluster sizes are small.

Of these hypotheses, no prior research has been conducted directly on Hypothesis 1, which is based on research conducted with related models (linear regression and SEM). Hypotheses 2 and 3 follow directly from research on binary outcomes. We believe Hypothesis 4 to be novel, notwithstanding the limited study of Saei and MacGilchrist (1998), and it is this hypothesis that is most important to our investigation.

Simulation Study

Design and Methods

To test our hypotheses, we simulated ordinal data with 2, 3, 5 or 7 categories, and we varied the number of clusters (J=25, 50, 100 or 200), the cluster sizes (n_j = 5, 10, or 20), the magnitude of the random effects, and the distribution of category responses. Our population-generating model was a multilevel cumulative logit model, with parameter values chosen to match those of Raudenbush, Yang, and Yosef (2000) and Yosef (2001), which were based on values derived by Rodriguez and Goldman (1995) from a multilevel analysis of health care in Guatemala. Whereas Rodriguez and Goldman (1995) considered three-level data with random intercepts, Raudenbush, Yang and Yosef (2000) modified the generating model to be two levels and included a random slope for the level-1 covariate. We in turn modified Raudenbush, Yang and Yosef's (2000) generating model to also include a cross-level interaction. The structure of the population generating model was of the form specified in Equations (4) and (5) or, equivalently, Equations (6) and (7).

The fixed effects in the population model were γ₀₀ = 0, γ₀₁ = 1, γ₁₀ = 1, γ₁₁ = 1. Following Raudenbush, Yang and Yosef (2000) and Yosef (2001), the two predictors were generated to be independent and normally distributed as X_ij ∼ N(.1,1) and W_j ∼ N(−.7,1).ⁱⁱⁱ In one condition, the variances of the random effects were τ₀₀ = 1.63, τ₁₀ = .20, τ₁₁ = .25, as in Raudenbush, Yang and Yosef (2000). We also included smaller and larger random effects by specifying τ₀₀ = .5, τ₁₀ = .03, τ₁₁ = .08 and τ₀₀ =8.15, τ₁₀ = .50, τ₁₁ = 1.25, respectively. Using the method described by Snijders and Bosker (1999, p. 224) these values imply residual pseudo-Intraclass Correlations (ICCs) of . 13, .33, and .72, holding X_j at the mean. For hierarchically clustered data, an ICC of .33 is fairly large, whereas an ICC of .13 is more typical. For long-term longitudinal data (e.g., annual or biennial), an ICC of .33 might be considered moderate, whereas the larger ICC of .72 would be observed more often for closely spaced repeated measures (e.g., experience sampling data). Since typical effect sizes vary across data structures, we shall simply refer to these conditions in relative terms as “small”, “medium” and “large.”

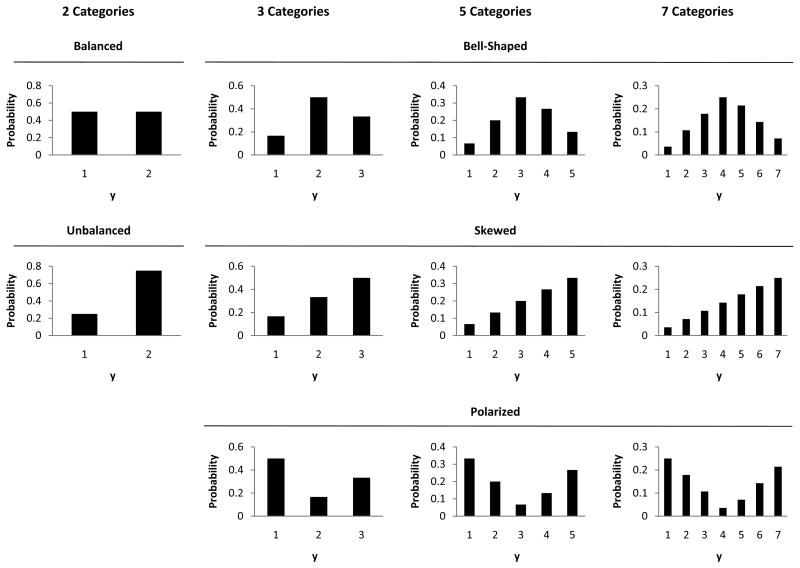
The thresholds of the model were varied in number and placement to determine the number of categories and shape of the category distribution for the outcome. For the binary data, thresholds were selected to yield both balanced (P(Y = 1) = .50) and unbalanced (P(Y = 1) = .75) marginal distributions. Note that for binary data, manipulating the shape of the distribution necessarily also entails manipulating category sparseness. In contrast, for ordinal data, we considered three different marginal distribution shapes, bell-shaped, skewed, and polarized, while holding sparseness constant by simply shifting which categories had high versus low probabilities. For the bell-shaped distributions the middle categories had the highest probabilities, whereas for the skewed distributions the probabilities increased from low to high categories, and for the polarized distribution the highest probabilities were placed on the end-points. The resulting distributions are shown in Figure 1.^iv As stated in Hypothesis 1, the bell-shaped distribution, approximating a normal distribution, was expected to be favorable for the linear model, although in practice skewed distributions are common when examining risk behaviors and polarized distributions are common with attitude data (e.g., attitudes towards abortion). The PQL and ML estimators of the multilevel cumulative logit model were not expected to be particularly sensitive to this manipulation.

Figure 1.

Marginal category distributions used in the simulation study (averaged over predictors and random effects). Notes. Within 3-, 5-, and 7-category outcome conditions, marginal frequencies are held constant but permuted across categories to manipulate the distribution shape (bell-shaped, skewed, or polarized) without changing sparseness. Within 2-category outcome conditions, it is impossible to hold marginal frequencies constant while manipulating shape (balanced or unbalanced).

SAS version 9.1 was used for data generation, some analyses, and the compilation of results. The IML procedure was used to generate 500 sets of sample data (replications) for each of the 264 cells of the study. The linear multilevel model was fit to the data with the MIXED procedure using the normal-theory REML estimator (maximum 500 iterations). The multilevel cumulative logit models were fit either by PQL using the GLIMMIX procedure (with Residual Subject-specific Pseudo-Likelihood, RSPL, maximum 200 iterations), or by ML with numerical integration using adaptive Gauss-Hermite quadrature with 15 quadrature points in Mplus version 5 (with Expectation-Maximization algorithm, maximum 200 iterations).^v,vi The NLMIXED and GLIMMIX procedures also provide ML estimation by adaptive quadrature, but computational times were shorter with Mplus. The MIXED (REML) and GLIMMIX (PQL) procedures implement boundary constraints on variance estimates to prevent them from going below zero (no such constraint is necessary when using ML with quadrature).

Complicating comparisons of the three model fitting approaches, results obtained from the linear and cumulative logit models are not on the same scale. To resolve this problem, linear model estimates were transformed to match the scale of the logistic model estimates. Fixed effects and standard errors were multiplied by the factor $s=\sqrt{{\pi }^2/3{\widehat{\sigma }}^2}$ (where σ̂² is the estimated Level 1 residual variance from the linear model, and π²/3 is the variance of the logistic distribution) and variances and covariance parameter estimates were multiplied by s². A similar rescaling strategy has been recommended by Chinn (2000) to facilitate meta-analysis when some studies use logistic versus linear regression (see also Bauer, 2009).

Performance Measures

We examined both the bias and efficiency of the estimates. Bias indicates whether a parameter tends to be over- or underestimated, and is computed as the difference between the mean of the estimates (across samples) and the true value, or

$$B=E({\widehat{\theta }}_r)-\theta$$ (10)

where θ is the parameter of interest, θ̂_r is the estimate of θ for replication r, and E(θ̂_r) is the mean estimate across replications. A good estimator should have bias values near zero, indicating that the sample estimates average out to equal the population value. Bias of 5-10% is often considered tolerable (e.g., Kaplan, 1989). Likewise, to evaluate efficiency, one can examine the variance of the estimates,

$$V=E\left[{\left({\widehat{\theta }}_r-E\left({\widehat{\theta }}_r\right)\right)}^2\right]$$ (11)

A good estimator will have less variance than other estimators, indicating more precision and, typically, higher power for inferential tests.

Bias and variance should be considered simultaneously when judging an estimator. For instance, an unbiased estimator with high variance is not very useful, since the estimate obtained in any single sample is likely to be quite far from the population value. Another estimator may be more biased, but have low variance, so that any given estimate is usually not too far from the population value. An index which combines both bias and variance is the Mean Squared Error (MSE), which is computed as the average squared difference between the estimate and the true parameter value across samples

$$\mathit{\text{MSE}}=E\left[{\left({\widehat{\theta }}_r-\theta \right)}^2\right]$$ (12)

It can be shown that MSE = B²+ν, thus MSE takes into account both bias and efficiency (Kendall and Stuart, 1969, Section 17.30). A low MSE is desirable, as it indicates that any given sample estimate is likely to be close to the population value.

Results

We first consider the estimates of the fixed effects, then the dispersion estimates for the random effects. To streamline presentation, some results are provided in an online appendix. In particular, bias in threshold estimates is presented in the online appendix as thresholds are rarely of substantive interest (and are not estimated with the linear model specification). The pattern of bias in threshold estimates obtained from PQL and ML was (predictably) the mirror image of the pattern described below for the other fixed effects.^vii

Fixed Effect Estimates

Our first concern was with identifying factors relating to bias in the estimators. Accordingly, a preliminary ANOVA model was fit for each fixed effect, treating model fitting approach as a within-subjects factor and all other factors as between-subjects, and using Helmert contrasts to (1) compare the linear model estimates to the estimates obtained from the logistic (cumulative logit) model fit, and (2) differentiate between the two logistic model estimators, PQL and ML. The three fixed effect estimates of primary interest were the main effect of the lower-level predictor X_ij, the main effect of the upper-level predictor W_j, and the cross-level interaction of X_ijW_j. Binary conditions were excluded from the ANOVAs (since the binary distribution shapes differed from the ordinal distribution shapes), but summary plots and tables nevertheless include these conditions. Given space constraints, we provide only brief summaries of the ANOVAs, focusing on the contrasts between estimators. Effect sizes were computed using the generalized eta-squared $({\eta }_G^2)$ statistic (Olejnik and Algina, 2003; Bakeman, 2005). ${\eta }_G^2$ values computed for mixed designs are comparable to partial η² values for fully between-subject designs. Our interpretation focuses on contrast effects with ${\eta }_G^2$ values of .01 or higher, shown in Table 1.

Table 1.

Top ${\eta }_G^2$ effect sizes for contrasts of fixed effect estimates across model specifications/estimators

	Fixed Effect Estimates
Design Factor	Xij (γ̂10)	Wj (γ̂01)	XijWj (γ̂11)
Contrast 1: Linear versus Logistic Model
Main Effect	0.37	0.11	0.44
× Number of Categories	0.02	0.01	0.03
× Distribution Shape	0.02	< 0.01	0.03
Contrast 2: PQL versus MLLogistic Model
Main Effect	0.06	0.03	0.07
× Size of Random Effects	0.02	0.01	0.02
× Number of Categories	0.01	< 0.01	0.01
× Cluster Size	0.01	< 0.01	0.01

Note. “×” indicates an interaction of the designated between-subjects factor of the simulation design with the within-subjects contrast for method of estimation.

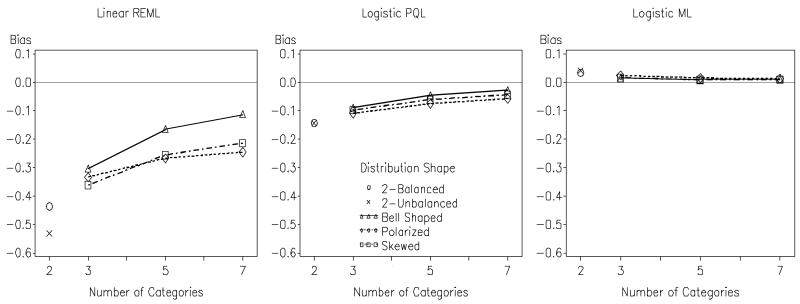
The largest effect sizes were obtained for the main effect of the first Helmert contrast, comparing the estimates obtained from the linear versus cumulative logit model specifications. As hypothesized, two interaction effects involving the first contrast were identified for all three fixed effects: the number of categories and the distribution shape. Table 1 shows that effect sizes were larger for the effects of X and XW than W, but the pattern of differences in the estimates was similar (see online appendix). As depicted in Figure 2, averaging over the three fixed effects, the bias of the linear REML estimator was quite severe with binary data, especially when the distribution was unbalanced. The degree of bias for this estimator diminished as the number of categories increased, and was least pronounced with the bell-shaped distribution. The bias of the linear REML estimator approached tolerable levels (<10%) only with seven categories and a bell-shaped distribution. In comparison, both estimators of the multilevel cumulative logit model produced less biased estimates that demonstrated little sensitivity to the shape of the distribution.

Figure 2.

Average bias for the three fixed effect estimates (excluding thresholds) across estimator, number of outcome categories, and distribution shape. Notes. The normal-theory REML (Restricted Maximum Likelihood) estimator was used when fitting the linear multilevel model. The estimators of PQL (Penalized Quasi-Likelihood) or ML (with adaptive quadrature) were used when fitting the multilevel cumulative logit (logistic) model. Points for two-category conditions are not connected to points for 3-7 category conditions because their distribution shapes do not correspond. Results show that bias is large and sensitive to distribution shape when using the linear model but not when using the cumulative logit model (either estimator). Results are collapsed over the number of clusters, cluster size, and the magnitude of the random effects.

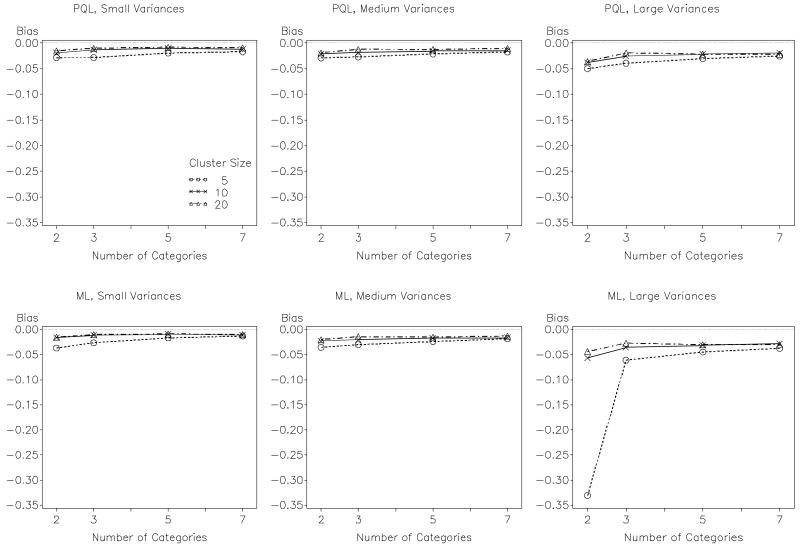
The second Helmert contrast, comparing the PQL and ML estimates of the multilevel cumulative logit model resulted in the second largest effect sizes. As hypothesized, the top three factors influencing differences in PQL versus ML estimates of all three fixed effects were the magnitude of the variance components, number of categories, and cluster size. Figure 3 presents the average bias of the three fixed effects as a function of these three factors (results were similar across fixed effects; see online appendix). In general, PQL produced negatively biased estimates whereas ML produced positively biased estimates. As expected, PQL performed particularly poorly with binary outcomes, especially when the variances of the random effects were large and the cluster sizes were small. With five to seven categories, however, PQL performed reasonably well even when the random effect variances were moderate. With very large random effects, PQL only performed well when cluster sizes were also large. In absolute terms, the bias for ML was consistently lower than PQL. Somewhat unexpectedly, ML estimates were more biased with binary outcomes than with ordinal outcomes.

Figure 3.

Average bias for the three fixed effect estimates (excluding thresholds) across logistic estimators, number of outcome categories and cluster size. Notes. Logistic estimators were either PQL (Penalized Quasi-Likelihood) or ML (Maximum Likelihood) with adaptive quadrature. Results show that PQL produces somewhat negatively biased fixed effect estimates, particularly when random effects have large variances, whereas the estimates obtained from logistic ML show small, positive bias. In both cases, bias decreases with the number of categories of the outcome. Results are collapsed over number of clusters and distribution shape and do not include linear multilevel model conditions.

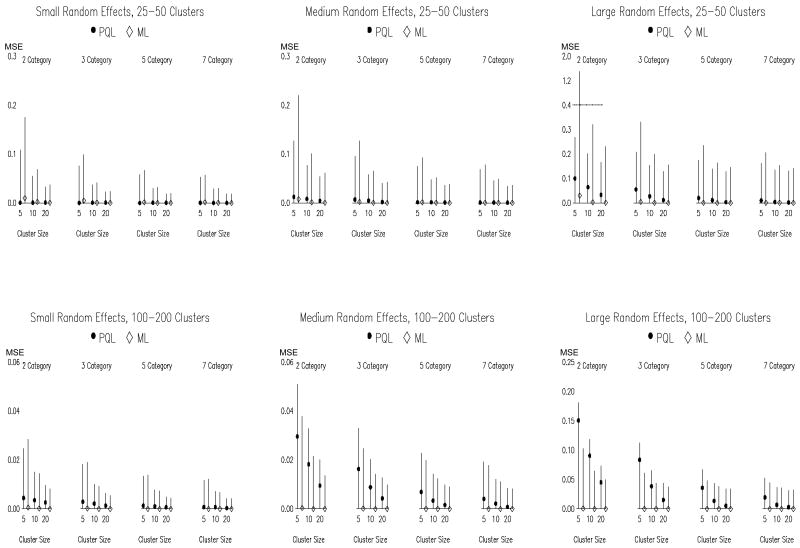
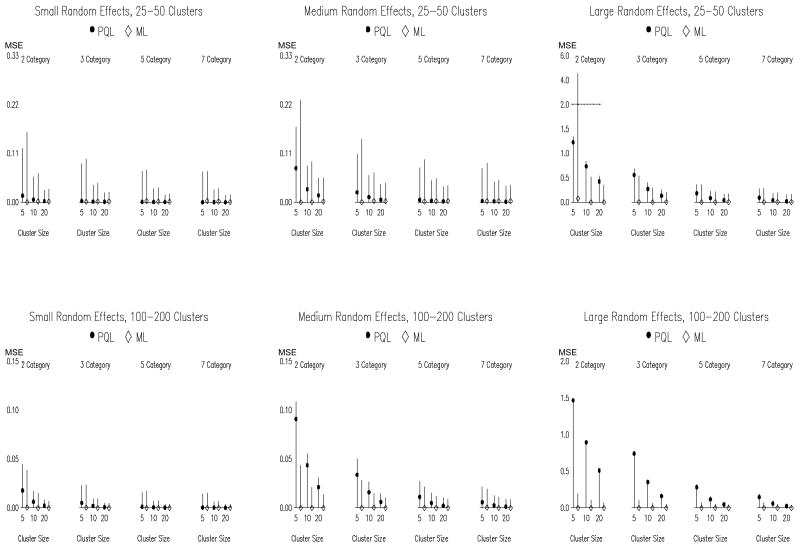
To gain a fuller understanding of the differences between the PQL and ML estimators of the multilevel cumulative logit model, we plotted the MSE, sampling variance and bias of the estimates in Figure 4 as a function of all design factors except distribution shape. In the figure, the overall height of each vertical line indicates the MSE. The MSE is partitioned between squared bias and sampling variance by the symbol marker (dot or diamond). The distance between zero and the marker is the squared bias, whereas the distance between the marker and the top of the line is the sampling variance. Note that the scale differs between panels to account for the naturally large effect of number of clusters on the sampling variance, and the increase in sampling variance associated with larger random effects. There is also a break in the scale for the upper right panel due to exceptionally high sampling variance observed for ML with binary outcomes and few, small clusters.

Figure 4.

Mean-Squared Error (MSE) for the fixed effects (excluding thresholds) across number of outcome categories, number of clusters, and cluster size. Notes. MSE is indicated by the height of the vertical lines, and it is broken into components representing squared bias (portion of the line below the symbol) and sampling variance (portion of the line above the symbol). The scale differs across panels and is discontinuous in the upper right panel. MSE is averaged across the three fixed effects.Results are plotted for multilevel cumulative logit models; PQL denotes Penalized Quasi-Likelihood and ML denotes Maximum Likelihood with adaptive quadrature. This plot does include linear multilevel model conditions.

Figure 4 clarifies that, in most conditions, the primary contributor to the MSE was the sampling variance, which tended to be lower for PQL than ML. An advantage was observed for ML only when there were many clusters and the random effects were medium or large, especially when there were also few categories and low cluster sizes. In all other conditions, PQL displayed comparable or lower MSE, despite generally higher bias, due to lower sampling variance. Both bias and sampling variance decreased with more categories, considerably lowering MSE.

Finally, we also considered the quality of inferences afforded by PQL versus ML for the fixed effects. Bias in the standard error estimates was computed for each condition as the difference between the average estimated standard error for an effect and that effect's empirical standard deviation across replications. Figure 5 presents the average SE for the fixed effects in the same format as Figure 3 (results were again similar across fixed effects; see online appendix). SE bias was generally minimal for both estimators except for ML with binary outcomes and small cluster size. Given the low level of SE bias, the quality of inferences is determined almost exclusively by point estimate bias. Indeed, confidence interval coverage rates (tabled in the online appendix) show that ML generally maintains the nominal coverage rate whereas PQL has lower than nominal coverage rates under conditions when PQL produces biased fixed effects.

Figure 5.

Average bias for the standard errors (SE) of the three fixed effect estimates (excluding thresholds) across number of outcome categories and cluster size. Notes. Results are plotted for multilevel cumulative logit models; PQL denotes Penalized Quasi-Likelihood and ML denotes Maximum Likelihood with adaptive quadrature. This plot does include linear multilevel model conditions.

Estimates of Dispersion for the Random Effects

An initial examination of the variance estimates for the random effects revealed very skewed distributions, sometimes with extreme values. We thus chose to evaluate estimator performance with respect to the standard deviations of the random effects (i.e., $\sqrt{{\tau }_{00}}$ and $\sqrt{{\tau }_{11}}$), rather than their variances. Stratifying by the magnitude of the random effects, preliminary ANOVA models were fit to determine the primary sources of differences in $\sqrt{{\widehat{\tau }}_{00}}$ and $\sqrt{{\widehat{\tau }}_{11}}$ between the three estimators. The same two Helmert contrasts were used as described in the previous section. Effect sizes are reported in Table 2.

Table 2.

Top ${\eta }_G^2$ effect sizes for contrasts of random effect dispersion estimates across model specifications/estimators.

Design Factor	Variance Components
	Small		Medium		Large
	τ̂00	τ̂11	τ̂00	τ̂11	τ̂00	τ̂11
Contrast 1: Linear versus Logistic Model
Main Effect	< 0.01	< 0.01	0.05	0.02	0.21	0.11
× Number of Categories	0.01	< 0.01	0.02	< 0.01	0.04	0.01
× Cluster Size	< 0.01	0.01	< 0.01	< 0.01	0.01	0.01
Contrast 2: PQL versus ML Logistic Model
Main Effect	< 0.01	< 0.01	0.02	0.01	0.27	0.15
× Number of Categories	< 0.01	< 0.01	0.01	0.01	0.07	0.05
× Cluster Size	< 0.01	< 0.01	0.01	0.01	0.05	0.05
× Number of Clusters	0.01	< 0.01	0.01	< 0.01	0.01	0.01

Note. “×” indicates an interaction of the designated between-subjects factor of the simulation design with the within-subjects contrast for method of estimation.

In all the ANOVA results for the dispersion estimates, larger random effect sizes resulted in more pronounced estimator differences and more pronounced factor effects on estimator differences. The largest effect sizes were again associated with overall differences in estimates produced by the linear model versus cumulative logit models. For $\sqrt{{\widehat{\tau }}_{00}}$, interactions with the first contrast were detected for the number of categories of the outcome and, to a much smaller degree, cluster size. For $\sqrt{{\widehat{\tau }}_{11}}$, no interactions with the first contrast consistently approached ${\eta }_G^2$ values of .01.

Results for the second contrast indicated that PQL and ML estimates of dispersion also diverged with the magnitude of the random effects. The number of categories had an increasing effect on estimator differences with the magnitude of the random effects, as did cluster size. The number of clusters also had a small effect on estimator differences.

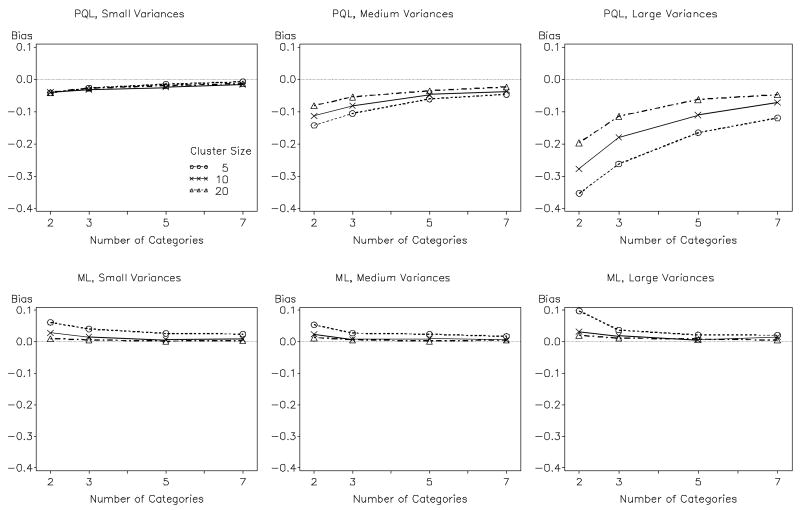
To clarify these results, Tables 3-6 display the mean and standard deviation of the dispersion estimates $\sqrt{{\widehat{\tau }}_{00}}$ and $\sqrt{{\widehat{\tau }}_{11}}$ respectively, as a function of characteristics of the outcome variable and estimator. For both the random intercept (Table 3) and slope (Table 4), the estimates obtained from the linear model show the most bias, but they improve markedly as the number of categories increases. Like the linear model estimator, PQL performance improves markedly as the number of categories increases, whereas the estimates obtained from ML are generally less biased (but more variable) when there are fewer categories. Indeed, the ML estimates actually become negatively biased as the number of categories increases, a trend that is consistent with the known negative bias of ML dispersion estimates as a function of the number of fixed effects (with more categories requiring the addition of more thresholds).

Table 3.

Mean and Standard Deviation of Random Intercept Dispersion Estimate, $\sqrt{{\widehat{\tau }}_{00}}$, as a Function of the Number of Categories, Collapsing Over Number of Clusters, Cluster Size and Category Distribution

Categories	Small random effect variance (τ00=0.50)			Medium random effect variance (τ00=1.63)			Large random effect variance (τ00 =8.15)
	Population $\sqrt{{\tau }_{00}}$ = 0.71			Population $\sqrt{{\tau }_{00}}$ = 1.28			Population $\sqrt{{\tau }_{00}}$ = 2.85
	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML
2	0.57 (.16)	0.63 (.19)	0.69 (.23)	0.94 (.16)	1.07 (.20)	1.26 (.28)	1.75 (.26)	1.95 (.32)	2.91 (.97)
3	0.63 (.16)	0.66 (.17)	0.68 (.19)	1.07 (.17)	1.16 (.19)	1.25 (.22)	2.10 (.27)	2.27 (.33)	2.84 (.46)
5	0.67 (.16)	0.69 (.15)	0.68 (.16)	1.17 (.17)	1.21 (.18)	1.25 (.19)	2.42 (.27)	2.52 (.32)	2.81 (.39)
7	0.69 (.15)	0.69 (.15)	0.68 (.15)	1.21 (.18)	1.23 (.17)	1.24 (.19)	2.54 (.31)	2.62 (.32)	2.81 (.36)

Notes. Standard deviation of estimates presented in parentheses. REML=Restricted Maximum Likelihood; ML= Maximum Likelihood; PQL= Penalized Quasi-Likelihood.

Table 6.

Mean and Standard Deviation of the Random Slope Dispersion Estimate $\sqrt{{\widehat{\tau }}_{11}}$ as a Function of the Number of Clusters and Cluster Size, Collapsing Over Number of Categories and Category Distribution.

Clusters/Cluster Size	Small random effect variance (τ11=0.08)			Medium random effect variance (τ11=0.25)			Large random effect variance (τ11=1.25)
	Population $\sqrt{{\tau }_{11}}$ = 0.28			Population $\sqrt{{\tau }_{11}}$ = 0.50			Population $\sqrt{{\tau }_{11}}$ = 1.12
	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML
25 Clusters
5 Members	0.26 (.28)	0.34 (.33)	0.37 (.31)	0.37 (.32)	0.44 (.35)	0.51 (.37)	0.82 (.39)	0.80 (.42)	1.12 (.94)
10 Members	0.24 (.20)	0.26 (.23)	0.28 (.20)	0.39 (.22)	0.42 (.25)	0.44 (.24)	0.84 (.24)	0.92 (.30)	1.05 (.36)
20 Members	0.25 (.15)	0.25 (.17)	0.24 (.14)	0.42 (.14)	0.45 (.18)	0.45 (.18)	0.85 (.19)	1.00 (.23)	1.06 (.26)
50 Clusters
5 Members	0.22 (.22)	0.26 (.25)	0.32 (.23)	0.36 (.25)	0.38 (.27)	0.48 (.28)	0.83 (.28)	0.74 (.34)	1.09 (.41)
10 Members	0.24 (.16)	0.24 (.18)	0.27 (.16)	0.40 (.16)	0.41 (.19)	0.45 (.19)	0.86 (.18)	0.91 (.22)	1.10 (.24)
20 Members	0.26 (.11)	0.24 (.13)	0.25 (.12)	0.43 (.10)	0.45 (.12)	0.47 (.13)	0.86 (.15)	1.00 (.16)	1.09 (.17)
100 Clusters
5 Members	0.21 (.18)	0.23 (.20)	0.29 (.19)	0.36 (.20)	0.35 (.22)	0.47 (.23)	0.83 (.21)	0.73 (.29)	1.10 (.28)
10 Members	0.24 (.13)	0.23 (.15)	0.26 (.14)	0.42 (.11)	0.42 (.14)	0.48 (.14)	0.85 (.15)	0.90 (.18)	1.10 (.17)
20 Members	0.27 (.08)	0.25 (.10)	0.26 (.09)	0.43 (.07)	0.46 (.08)	0.49 (.09)	0.86 (.13)	1.00 (.13)	1.11 (.12)
200 Clusters
5 Members	0.21 (.15)	0.21 (.17)	0.28 (.16)	0.37 (.15)	0.35 (.19)	0.47 (.17)	0.84 (.15)	0.73 (.26)	1.11 (.19)
10 Members	0.25 (.10)	0.23 (.12)	0.26 (.11)	0.42 (.08)	0.42 (.11)	0.49 (.10)	0.86 (.13)	0.90 (.15)	1.11 (.12)
20 Members	0.28 (.06)	0.26 (.07)	0.27 (.07)	0.44 (.06)	0.46 (.06)	0.49 (.06)	0.86 (.12)	0.99 (.11)	1.11 (.09)

Notes. See Table 3 notes.

Table 4.

Mean and Standard Deviation of the Random Slope Dispersion Estimate $\sqrt{{\widehat{\tau }}_{11}}$ as a Function of the Number of Categories, Collapsing Over Number of Clusters, Cluster Size and Category Distribution

Categories	Small random effect variance (τ11=0.08)			Medium random effect variance (τ11=0.25)			Large random effect variance (τ11=1.25)
	Population $\sqrt{{\tau }_{11}}$ = 0.28			Population $\sqrt{{\tau }_{11}}$ = 0.50			Population $\sqrt{{\tau }_{11}}$ = 1.12
	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML
2	0.23 (.16)	0.21 (.20)	0.31 (.23)	0.35 (.17)	0.32 (.22)	0.49 (.27)	0.68 (.19)	0.64 (.30)	1.14 (.63)
3	0.23 (.16)	0.24 (.19)	0.28 (.18)	0.38 (.17)	0.39 (.19)	0.47 (.20)	0.79 (.18)	0.83 (.25)	1.09 (.30)
5	0.25 (.16)	0.26 (.18)	0.27 (.16)	0.42 (.17)	0.45 (.18)	0.47 (.17)	0.91 (.18)	.97 (.20)	1.08 (.24)
7	0.25 (.16)	0.27 (.18)	0.27 (.15)	0.44 (.17)	0.48 (.17)	0.47 (.17)	0.95 (.18)	1.02 (.19)	1.08 (.21)

Notes. See Table 3 notes.

Similarly, Tables 5 and 6 present the mean and standard deviation of the dispersion estimates $\sqrt{{\widehat{\tau }}_{00}}$ and $\sqrt{{\widehat{\tau }}_{11}}$, respectively, as a function of sample size. Both the linear model and PQL showed decreased levels of negative bias as the cluster sizes increased. For the linear model, the effect of cluster size was most evident with the random slope. For the random intercept, ML typically produced negatively biased dispersion estimates, attenuating as the number of clusters increased. In contrast, the bias of the PQL estimates increased slightly with the number of clusters. For the random slope, ML performed well when the population random effect was medium or large, but showed some positive bias when the population random effect was small, particularly at the smallest sample sizes. As anticipated, PQL was again negatively biased, and generally benefited from larger cluster sizes. PQL estimates generally exhibited less sampling variability than ML estimates, with ML estimates being particularly unstable for the combination of large random effects, few clusters, and small cluster sizes.

Table 5.

Mean and Standard Deviation of the Random Intercept Dispersion Estimate $\sqrt{{\widehat{\tau }}_{00}}$ as a Function of the Number of Clusters and Cluster Size, Collapsing Over Number of Categories and Category Distribution.

Clusters/Cluster Size	Small random effect variance (τ00=0.50)			Medium random effect variance (τ00 =1.63)			Large random effect variance (τ00=8.15)
	Population $\sqrt{{\tau }_{00}}$ = 0.71			Population $\sqrt{{\tau }_{00}}$ = 1.28			Population $\sqrt{{\tau }_{00}}$ = 2.85
	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML	Linear – REML	Logistic – PQL	Logistic – ML
25 Clusters
5 Members	0.63 (.33)	0.68 (.33)	0.66 (.35)	1.11 (.34)	1.17 (.34)	1.22 (.42)	2.28 (.57)	2.30 (.54)	2.92 (1.41)
10 Members	0.64 (.21)	0.68 (.22)	0.65 (.23)	1.11 (.25)	1.20 (.26)	1.21 (.28)	2.26 (.50)	2.45 (.49)	2.80 (.62)
20 Members	0.64 (.15)	0.68 (.16)	0.66 (.16)	1.11 (.22)	1.22 (.22)	1.21 (.23)	2.24 (.47)	2.56 (.45)	2.76 (.53)
50 Clusters
5 Members	0.64 (.23)	0.65 (.23)	0.67 (.25)	1.12 (.24)	1.14 (.24)	1.26 (.28)	2.26 (.44)	2.21 (.42)	2.87 (.57)
10 Members	0.65 (.14)	0.67 (.15)	0.68 (.16)	1.11 (.19)	1.18 (.18)	1.25 (.20)	2.45 (.40)	2.40 (.38)	2.83 (.42)
20 Members	0.65 (.11)	0.68 (.11)	0.68 (.11)	1.11 (.17)	1.21 (.15)	1.25 (.16)	2.23 (.39)	2.53 (.34)	2.81 (.36)
100 Clusters
5 Members	0.65 (.15)	0.65 (.16)	0.69 (.17)	1.11 (.18)	1.12 (.17)	1.26 (.19)	2.24 (.38)	2.16 (.37)	2.85 (.37)
10 Members	0.65 (.10)	0.67 (.10)	0.69 (.11)	1.11 (.15)	1.17 (.13)	1.26 (.14)	2.23 (.36)	2.37 (.33)	2.83 (.29)
20 Members	0.65 (.08)	0.68 (.08)	0.70 (.08)	1.11 (.14)	1.21 (.11)	1.26 (.12)	2.23 (.34)	2.52 (.28)	2.83 (.25)
200 Clusters
5 Members	0.65 (.11)	0.65 (.11)	0.70 (.12)	1.11 (.14)	1.12 (.13)	1.27 (.13)	2.23 (.34)	2.14 (.34)	2.84 (.26)
10 Members	0.65 (.08)	0.67 (.07)	0.70 (.08)	1.11 (.13)	1.17 (.10)	1.27 (.10)	2.24 (.33)	2.35 (.30)	2.85 (.20)
20 Members	0.65 (.07)	0.68 (.05)	0.70 (.05)	1.11 (.12)	1.21 (.08)	1.27 (.08)	2.23 (.32)	2.51 (.25)	2.84 (.18)

Notes. See Table 3 notes.

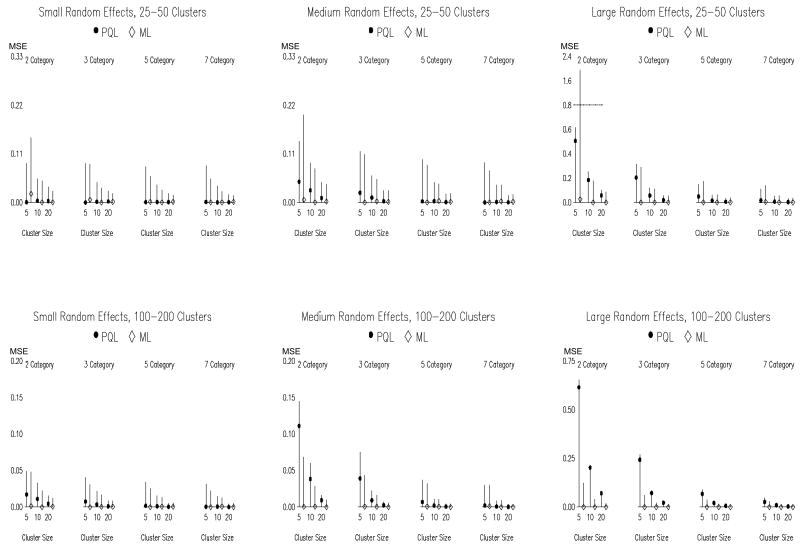
To contextualize these differences between the PQL and ML estimators, Figures 6 and 7 present (squared) bias, variance, and MSE for the $\sqrt{{\widehat{\tau }}_{00}}$ and $\sqrt{{\widehat{\tau }}_{11}}$ estimates in the same format as Figure 4. The results generally parallel the results presented previously for the fixed effects. Although the PQL random effect dispersion estimates are more biased, their sampling variance is also often smaller. PQL thus produces lower MSE values than ML in many conditions. A consistent and appreciable MSE advantage for ML is observed only when there are many clusters (e.g., 100 or 200) and medium to large random effects. Further, this advantage diminishes as the cluster size and/or number of categories increases.

Figure 6.

Mean-Squared Error (MSE) for the standard deviation of the random intercept, across number of outcome categories, number of clusters, and cluster size. Notes. The scale differs across panels and is discontinuous in the upper right panel. See Figure 4 notes for definition of quantities in this plot.

Figure 7.

Mean-Squared Error (MSE) for the standard deviation of the random slope, across number of outcome categories, number of clusters, and cluster size. Notes. The scale differs across panels and is discontinuous in the upper right panel. See Figure 4 notes for definition of quantities in this plot.

Discussion

Summary

An initial question we sought to address was, “When can the results of a multilevel linear model fit to an ordinal outcome be trusted?” Our results suggest the answer, “Rarely.” Only when the marginal distribution of the category responses was roughly normal and the number of categories was seven did the negative bias of the linear model decrease to the acceptable level of approximately 10% for the fixed effects. The dispersion estimates of the random effects were similarly negatively biased. In almost all cells of the design, the linear model estimates were inferior to the cumulative logit model estimates (from either PQL or ML). In contrast, neither PQL nor ML estimators of the multilevel cumulative logit model demonstrated much sensitivity to the category distribution. In sum, these results argue against the practice of fitting multilevel linear models to ordinal outcomes.^viii

The second major aim of this study was to evaluate the relative performance of two estimators of the multilevel cumulative logit model, PQL versus ML with adaptive quadrature. In general, our results suggest that PQL has been somewhat unfairly maligned. While we did indeed find that PQL estimates of fixed effects, and especially dispersion parameters, were negatively biased in many conditions, PQL nevertheless often outperformed ML in terms of MSE. In other words, the degree of excess bias associated with using PQL was often within tolerable levels and compensated for by lower sampling variability (similar to what Bellamy et al., 2005, found for binary outcomes). As shown in other studies, PQL performed best when the random effects were small and the cluster sizes were large. In addition, a new result of our study is that the performance of PQL greatly improves with the number of categories for the outcome. The ML estimator also behaved as expected. Consistent with asymptotic theory, ML was least biased and most efficient for data with 100 or 200 clusters. With 25 or 50 clusters, however, ML estimates were more variable and often had higher MSE than PQL estimates.

A final finding worth noting is that all of the estimators generally perform better for ordinal than binary data. Furthermore, there is a sharp reduction in MSE associated with increasing the number of categories available for analysis, particularly in moving from two levels to three or more. These results indicate that ordinal scales are generally preferable to binary and underscore previous pleas for researchers to abandon the practice of dichotomizing ordinal scales (Sankey and Weissfeld, 1998; Strömberg, 1996).

Limitations and Directions for Future Research

As with all simulation studies, the conclusions we draw from our results must be limited by the range of conditions we evaluated. We discuss these limitations here as potentially fruitful directions for future research. First, we studied only one model for ordinal outcomes, the cumulative logit model. We did not evaluate model performance with alternative link functions, such as the probit. Also, as mentioned previously, the cumulative logit model imposes an assumption of invariant slopes across categories (i.e., proportional odds), which is not always tenable in practice. A generalized logit or partial proportional odds model might then be preferable. For the interested reader, Hedeker and Gibbons (2006, p. 191-194, 202-211) provide a useful discussion of the proportional odds assumption, how to check this assumption empirically, and models that relax this assumption.

Second, we manipulated the shape of the ordinal outcome distributions while holding category sparseness constant. Although we regard it as a strength of our design that shape and sparseness were not confounded for ordinal outcomes, these two factors are inextricably confounded for binary outcomes. Our binary outcome results should be interpreted in light of this fact. Additionally, because we did not manipulate the sparseness of the ordinal outcomes, our results do not speak to the possible effects of sparseness on model estimates.

Third, our study was limited to multilevel models with random effects. A worthy topic of future research to compare the results of models fit by PQL or ML to the results obtained using GEE. Although unit-specific and population-average model estimates differ in scale and interpretation, marginalized estimates obtained from PQL or ML are comparable to the estimates obtained from GEE (Liang & Zeger, 1986).

Fourth, there are different approaches to implementing ML with numerical integration beyond adaptive quadrature (e.g. Laplace algorithms), different versions of adaptive quadrature (e.g. quadrature points iteratively updated based on mode versus mean of posterior), and different modifications of PQL in use (e.g. PQL2; Goldstein & Rabash, 1996). The generalization of these results across these other estimation algorithms cannot be fully guaranteed.

Recommendations

Notwithstanding the limitations noted above, we believe that our results can be used to better inform the analysis of ordinal outcomes in nested data. As noted, our results clearly indicate that use of a linear model with ordinal outcomes should be avoided. In selecting the multilevel cumulative logit model as more appropriate for ordinal outcomes, the central question is then which estimator is to be preferred, PQL or ML with adaptive quadrature?

The answer to this question depends not only on the bias and sampling variability of the estimates, but also on other factors. For instance, one issue that must be considered when choosing between PQL and ML is whether one wishes to evaluate the relative fit of competing models. Because PQL uses a quasi-likelihood, rather than a true likelihood, it does not produce a deviance statistic that can be used for model selection (e.g., by likelihood ratio test or penalized information criteria). This is a significant limitation of PQL that is not shared by ML. If comparing between competing models is a key goal of the analysis then ML may be preferred to PQL on these grounds alone. Another factor that might influence estimator selection is computational efficiency. PQL is much faster, particularly when the number of random effects (dimensions of integration) is large. Finally, a third factor related to estimator selection is model complexity. Some models may only be feasible with one estimator or the other. For instance, PQL readily admits the incorporation of serial correlation structures for the level-1 residuals.

Beyond these factors, our simulation results suggest that the preferred choice between PQL and ML depends on the characteristics of the data. If data are obtained on 100 or more clusters, cluster sizes are small, dispersion across clusters is anticipated to be moderate to large, and the outcome variable has only two or three categories, then ML is the best choice. Under virtually all other conditions, however, PQL is a viable, often superior alternative. In particular, if data are available on 50 clusters or less, PQL will generally have lower MSE -- even with just two- or three-category outcomes. The bias of the PQL estimates is also tolerable when either cluster sizes are large or outcomes have five or more categories.

Table 7 translates our results for PQL and ML into a table of working recommendations for fitting multilevel cumulative logit models (primarily based on MSE but also considering bias). These are gross recommendations and we encourage researchers to consider the more detailed results of our simulation before making a final selection. Situations under which ML with adaptive quadrature or PQL perform similarly (and thus either could be chosen) are denoted with the table entry “PQL, ML-AQ.” Situations under which PQL is preferable are denoted “PQL” and situations where ML-AQ is clearly preferable are denoted “ML-AQ.” Note that the cell of Table 7 corresponding to few clusters, small cluster size, binary outcomes, and large random effects is empty because the performance of both estimators was unacceptable (PQL showed excessive bias, whereas ML showed excessive sampling variability). For this situation, researchers will need to look outside of the two estimators studied here (e.g., MCMC might perform better through the implementation of mildly informative priors that prevent estimates from becoming excessively large).

Table 7.

Working recommendations for estimator choice when fitting multilevel cumulative logit models in practice

		Small VC (e.g. ICC=.13)		Large VC (e.g. ICC=.71)
		DV has many categories (5+)	DV has few categories (2)	DV has many categories (5+)	DV has few categories (2)
Many clusters (e.g. 100-200)	Large clusters (e.g. 20)	PQL, ML-AQ	PQL, ML-AQ	PQL, ML-AQ	ML-AQ
	Small clusters (e.g. 5)	PQL, ML-AQ	PQL, ML-AQ	ML-AQ	ML-AQ
Few clusters (e.g. 25-50)	Large clusters (e.g. 20)	PQL, ML-AQ	PQL, ML-AQ	PQL, ML-AQ	PQL, ML-AQ
	Small clusters (e.g. 5)	PQL, ML-AQ	PQL	PQL, ML-AQ

Notes. PQL=Penalized Quasi-Likelihood; ML-AQ= Maximum Likelihood with Adaptive Quadrature. Situations under which ML with adaptive quadrature or PQL perform similarly are denoted “PQL, MLAQ.” The selection of an estimator in these conditions should depend on the investigator's focus (fixed effects versus variance components) or other factors (such as computational speed or the desire to perform nested model comparisons). Situations under which PQL performs consistently better are denoted “PQL” and situations under which ML-AQ performs consistently better are denoted “ML-AQ.” Even in these conditions, however, the magnitude of performance differences is not always large. Consult Figures 2-7 and Tables 3-6 for more detailed information on estimator differences.

To see how Table 7 might be used in practice, we will consider two common situations. First, many samples of hierarchical data consist of a relatively small number of groups but a fairly large number of individuals in each group. For instance, a study might sample thirty students from each of thirty schools. In this instance, the variance components are likely to be on the smaller side, and PQL can be expected to perform as well or better than ML regardless of the number of categories of the outcome. Second, many experience sampling studies include a modest number of participants, say 25-50, but many repeated measures per person. Experience suggests that variance components are often sizeable in such studies. If our outcome is binary, we might choose ML due to the higher bias of PQL (despite similar MSE). Alternatively, if our outcome is a 5-level ordinal variable then PQL becomes a more attractive option: the bias of PQL will then be within tolerable levels and PQL will have lower MSE than ML. One additional factor that might tip the balance in favor of PQL is that PQL easily incorporates serial correlation structures for the residuals at level 1, and serial correlation is often present with experience sampling data.

In conclusion, although further research on the estimation of multilevel models with ordinal data is warranted, it is our hope that the results of the present study can help analysts to make better-informed choices when fitting multilevel models to ordinal outcomes.