Assembly of vorticity-aligned hard-sphere colloidal strings in a simple shear flow

Abstract

Colloidal suspensions self-assemble into equilibrium structures ranging from face- and body-centered cubic crystals to binary ionic crystals, and even kagome lattices. When driven out of equilibrium by hydrodynamic interactions, even more diverse structures can be accessed. However, mechanisms underlying out-of-equilibrium assembly are much less understood, though such processes are clearly relevant in many natural and industrial systems. Even in the simple case of hard-sphere colloidal particles under shear, there are conflicting predictions about whether particles link up into string-like structures along the shear flow direction. Here, using confocal microscopy, we measure the shear-induced suspension structure. Surprisingly, rather than flow-aligned strings, we observe log-rolling strings of particles normal to the plane of shear. By employing Stokesian dynamics simulations, we address the mechanism leading to this out-of-equilibrium structure and show that it emerges from a delicate balance between hydrodynamic and interparticle interactions. These results demonstrate a method for assembling large-scale particle structures using shear flows.

The study of ordered structures and symmetries of equilibrium phases in condensed matter is central to our understanding of its various material properties (1). Once driven out of equilibrium, a material can exhibit richer phases with many unexpected structures (2–6). However, the dynamics of these nonequilibrium phases are much less understood relative to their equilibrium counterparts (7–9). Sheared hard-sphere colloidal suspensions provide a simple system for probing many out-of-equilibrium structures. For example, sliding layers in sheared colloidal crystals (10, 11), shear-induced crystallization of colloidal fluids (5), and formation of shear transformation zones—localized regimes of shear-induced structural rearrangement—in colloidal glasses (12) have been observed in such systems.

The simplest and lowest ordered structure predicted to arise from sheared hard-sphere colloidal suspensions is a one-dimensional (1D) string structure, where particles link into strings under shear. This structure has received much attention since it was first found in a numerical simulation (13). Despite intensive study (13–23), however, there is still heated debate over whether such a structure exists in experiments (10, 23, 24) or is an artifact of certain numerical algorithms (20–23). In part, this controversy persists due to the lack of experimental techniques that provide direct visualization of the suspension structure. Since the string structure is predicted to exist in less concentrated suspensions below the crystallization threshold, previous scattering experiments, which average over large sample volumes, have not provided detailed information to unambiguously confirm or disprove the existence of this less regular structure (10, 24). Here, by employing fast confocal microscopy, we show that sheared hard-sphere colloidal suspensions form strings aligned normal to the plane of shear. In combination with Stokesian dynamics simulations (25), we elucidate the mechanical mechanism leading to the observed structures.

Results and Discussion

Experimental Observations of Vorticity-Aligned Strings.

Our colloidal suspension consists of d = 0.96 μm silica particles suspended in an index-matched glycerol/water mixture (see Materials and Methods). We apply a plane sinusoidal shear to the suspensions with a fixed shear strain amplitude γ = 3.51 ± 0.16 and controllable shear angular frequency ω. The structure of particles in the flow (x)—vorticity (z) plane is imaged at different locations along the shear gradient direction (y). With the hard-sphere particles under shear, the relevant dimensionless parameters are the volume fraction of the suspension, ϕ, and the Péclet number 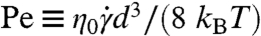, which is the ratio of the diffusion and advection time scales. η₀ is the viscosity of the solvent and 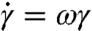is the amplitude of shear rate.

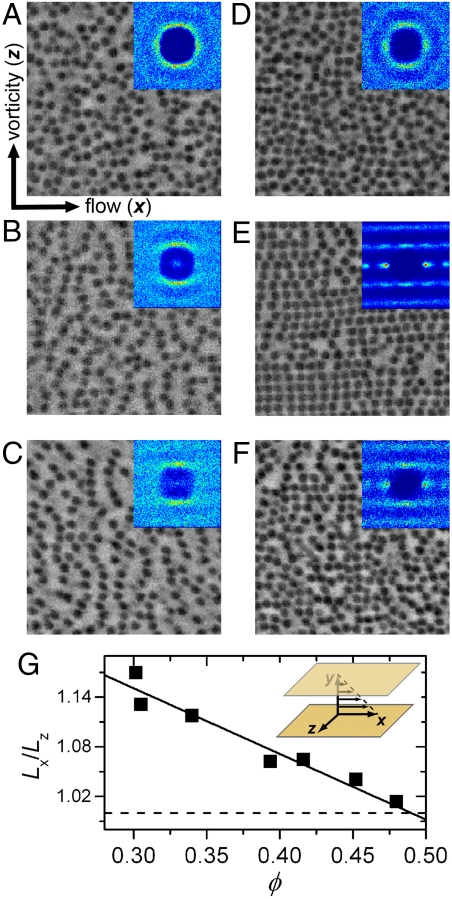
We explore particle configurations at different Pe in a sample with ϕ = 0.34, well below the crystallization threshold for hard-sphere colloidal suspensions. The sample is confined between the two shear plates at a separation h = 7.0d. At this gap size, the particles form weak layers parallel to the flat shear plates (x-z layers) in equilibrium. These layers enhance strongly with increasing shear (6). We image the particle structure in these x-z layers. Without shear or at low Pe, the particle distribution is nearly isotropic (Fig. 1A). The corresponding pair correlation function, g(x,z), shows a uniform ring for the first shell of neighboring particles (Fig. 1A, Inset). However, at intermediate Pe, the suspension develops a string structure, where chains of particles align predominately along the vorticity direction (Fig. 1B). The lifetime of these strings is longer than a full period of the shear cycle and is much longer than our imaging speed (Movie S1). This trend is also shown in the change of g(x,z): the ring at low Pe breaks into two crescents along the z direction indicating the 1D symmetry of the string structure (Fig. 1B, Inset). As Pe is increased further, the vorticity-aligned string structure becomes more pronounced (Fig. 1C). Although the existence of a string structure is consistent with some simulations (13–19), the orientation of the strings is unexpected: it is normal to the numerically predicted flow direction. To make sure that the vorticity-aligned string structure is not an artifact of our confocal imaging techniques, we perform two numerical and experimental control tests. First, we deshear the raw images by shifting each scan line backwards affinely using the average shear velocity, which cancels any possible shear-induced particle distortions. Second, we switch the shear direction by 90° such that the vorticity direction is normal to the confocal scanning direction. In both controls, we find the same vorticity-aligned string structure at large Pe (Fig. S3).

Fig. 1.

String structure in sheared colloidal suspensions. (A)–(C) The real-space structures of particles in an x-z layer are shown for a suspension of ϕ = 0.34 under confinement h = 7.0d at Pe = 0.72 (A), Pe = 72 (B), and Pe = 337 (C). The corresponding pair correlation function g(x,z) is shown in the inset of each plot. g(x,z) is defined as the probability of finding a particle at position (x, z) with respect to the center of each particle. Each g(x,z) measurement averages over about 5,000 particles. The intensity scale in each inset was adjusted for clarity. (D)–(F) show the structure and g(x,z) for the ϕ = 0.46 sample under otherwise the same experimental conditions as (A)–(C). (G) shows the ratio of the distances between neighboring particles along the x and z directions, L_x/L_z, versus ϕ at Pe = 70. L_x/L_z = 1 is indicated by the dashed line. The solid line is a linear fit of the data. The inset of (G) shows a definition of our coordinate system. All these measurements are for the 2nd particle layer in the x-z plane counted from the top stationary plate.

When samples with higher ϕ are sheared, we find that the vorticity-aligned strings in the x-z layers are pushed closer along the x direction. Finally, at ϕ = 0.46 near the crystallization threshold, we observe that strings locally collapse into crystalline islands with fourfold symmetry (Fig. 1 D, E). These square crystalline islands melt gradually at an even higher Pe above 40 (Fig. 1F). To quantify the smooth transition between the string structure and the shear-induced crystalline phase at intermediate Pe, we measure the average distance between neighboring particles along the x and z direction, L_x, L_z, over a range of ϕ (Fig. 1G). L_x/L_z starts at 1.15 for the string structure at low ϕ and approaches 1.0 for the square crystalline phase at high ϕ. L_x/L_z extrapolates to 1.0 at ϕ = 0.50 ± 0.03, corresponding to the fluid-crystal transition for hard-sphere suspensions in 3D.

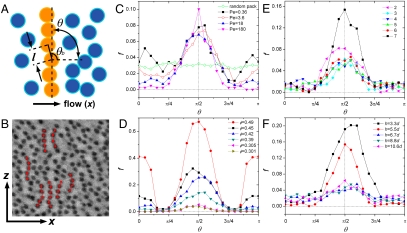
While L_x/L_z and g(x,z) provide detailed information about the distribution of neighboring particle pairs, quantifying larger scale structures requires further analysis. To determine how the resulting string structure depends on the experimental parameters, we perform a cluster analysis. First we identify all the strings within the x-z layers that are aligned along an angle θ with respect to the flow direction x (Fig. 2 A, B). Then we count the fraction of particles in the strings, f(θ). Consistent with the direct observations shown in Fig. 1 A–C, we find that with increasing Pe, the flat distribution for f(θ) develops a strong peak at θ = π/2 (Fig. 2C), which indicates the formation of vorticity-aligned strings. In accord with the trends shown in Fig. 1G, with increasing ϕ strings get sufficiently close that our algorithm identifies a significant number of particle strings along the flow direction (Fig. 2D). Furthermore, inside each sample, particles in the x-z layers nearer to the boundary plates—where layering order is strongest (6, 26)—show an enhanced string structure as indicated by the higher peak at π/2 (Fig. 2E). Consistent with this layering order dependence, we find that decreasing h, which enhances the confinement of samples and hence induces stronger layering order (26), also results in enhanced strings at π/2 (Fig. 2F).

Fig. 2.

Characterization of the string structure. (A), To identify strings aligned along θ direction with respect to x in x-z plane, we perform an angle-dependent cluster analysis: Two particles with their center-to-center distance l < 1.24d and the bond orientation θ_b in a small range Δθ = π/9 around θ, |θ_b-θ| ≤ Δθ, are included within clusters, and only large clusters with cluster size N≥4 are counted as strings. This analysis, while imitating how we identify strings with the naked eye, characterizes the string structure of particles on a large scale beyond their first neighbors. As a comparison, g(x,z) provides more accurate information on the correlation between neighboring particles (Fig. 1 A–F inset). (B) shows an example of identified strings aligned along θ = π/2. We measure the fraction of particles in the strings along θ over the total number of particles, f(θ), for different controlled parameters. (C) shows f(θ) versus Pe for the 2nd particle layer in a sample of ϕ = 0.34 and h = 6.7d. The number of layers is always counted from the top plate. (D) shows f(θ) of the 2nd particle layer for samples of different ϕ with h = 6.8d and Pe = 71. (E) shows f(θ) in different x-z layers along y with ϕ = 0.34, h = 7.4d (8 layers in total) and Pe = 54. We exclude the boundary layers, which show strong crystalline structure even without shear at low ϕ. (F) shows f(θ) of the 2nd particle layer for different confinement, h, with ϕ = 0.34 and Pe = 54.

Measurement of Anisotropic Particle Diffusion.

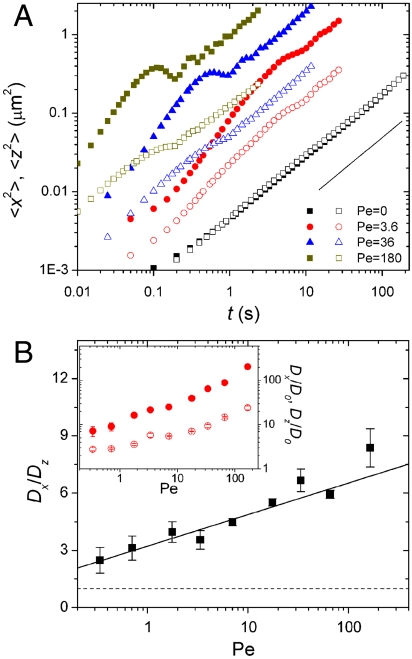
To gain further insight into the symmetry-breaking mechanisms that lead to string formation, we experimentally investigate the microscopic dynamics of individual particles. Specifically, we measure the effective particle diffusion in the x-z plane in the reference frame of the oscillating shear (Fig. 3A). By comparing the effective diffusion constant in the x and z directions, D_x/D_z, we find a broken symmetry in the particle dynamics: with increasing Pe the enhancement of particle diffusion along x is much stronger than enhancement along z (Fig. 3B). Since the experiments are conducted at constant γ, the increase of D_x/D_z cannot be due to Taylor dispersion (27). Owing to the anisotropic particle diffusion, particle density along z has to increase relative to that along x in order to maintain a uniform osmotic pressure within the layer. Consequently, close-packed strings along the vorticity direction gradually emerge with increasing Pe.

Fig. 3.

Effective particle diffusion in the x-z plane. (A) shows the mean squared displacement of particles along the x direction, 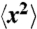, (solid symbols) and along the z direction, 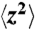, (empty symbols) in the reference frame of the oscillatory shear. To obtain particle motions in the shear frame, the global shear motion, measured with particle image velocimetry, is subtracted from the motion of individual particles. A residual oscillatory shear motion can still be identified at a short time scale. The solid line has an exponent of 0.81. Particles show subdiffusive behavior even in equilibrium, which may result from the formation of rough particle layers due to confinement. Particle motions are measured in the 2nd layer of the suspension with ϕ = 0.34 and h = 7.3d. The subdiffusion constant D_x and D_z are obtained by fitting the slope of 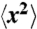and 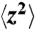versus time t in the log-log scale at later time with power 0.81. (B) shows D_x/D_z and the inset of (B) shows D_x/D₀ and D_z/D₀ versus Pe, respectively, where D₀ is the diffusion constant of particles without shear.

Using Stokesian Dynamics Simulations to Determine the Mechanism for String Formation.

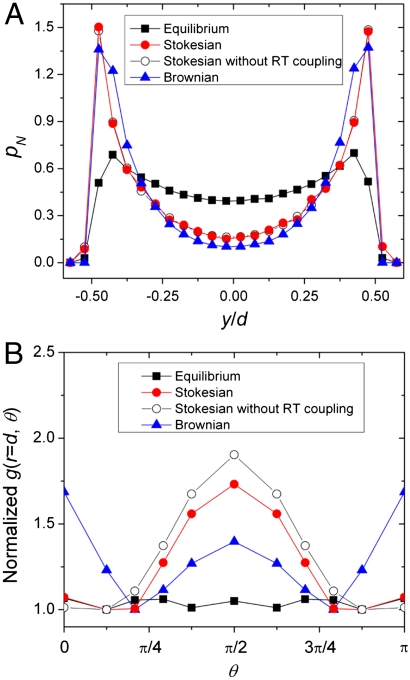
To parse the contributions from different physical factors to the observed structure and dynamics, we employ Stokesian dynamics simulations (25). In our simulations, spheres immersed in a 3D fluid are confined by an external potential (See Materials and Methods). For computational efficiency, we study a small system with only two layers of particles (Fig. 4A) confined by an external potential. We quantify particle structure in the x-z layers with g(r = d,θ), which corresponds to the first peak of g(x,z) in the polar coordinate (Fig. 4B). In the absence of shear, the suspension equilibrates and g(r = d,θ) is flat. Under steady shear, our simulation shows a clear signature of vorticity-aligned string structure as indicated by the large peak in g(r = d,θ) near θ = π/2 (Fig. 4B). Thus, our simulation on a small system is already able to capture the basic string formation observed in the experiments.

Fig. 4.

String formation in Stokesian dynamics simulations. (A) shows the probability distribution of particles along y under different simulation conditions. (B) shows the first peak of g(x,z), g(r = d,θ), versus θ. g(r = d,θ) is normalized by its minimal value near π/8. Black squares show the equilibrium structure with Pe = 0. Red disks show the results from Stokesian dynamics simulations with Pe = 50. Blue triangles show results from Brownian dynamics simulations with Pe = 50 after the hydrodynamic couplings between particles have been turned off. Empty circles show results from Stokesian dynamics simulations when the hydrodynamic couplings between the particle rotations and translational motions are turned off. The volume fraction of the sample is chosen such that g(x,z) show comparable values in Stokesian dynamics simulations and in experiments with ϕ = 0.34 samples.

Two more sets of simulations are performed to test the importance of the hydrodynamic interactions. We first turn off the hydrodynamic interactions between particles. In this limit, the simulations become similar to previous Brownian dynamics simulations of sheared particles (14–17, 19). We find that instead of vorticity-aligned strings, particles form strings aligned along the flow direction, as indicated by the stronger peaks of g(r = d,θ) near θ = 0 and θ = π in Fig. 4B. This finding highlights the fact that hydrodynamic couplings between particles are essential for formation of vorticity-aligned strings. In another simulation, we turn off the coupling between the rotational motions of particles about their centers and their translational motions. Such a situation would be realized by nonrotating spheres immersed in a liquid with slip boundary conditions. We find that the results are qualitatively similar to the results with full hydrodynamic couplings (Fig. 4B). This finding indicates that the direct coupling between rotational and translational degrees of freedom of particles is not essential for formation of the vorticity-aligned string structure.

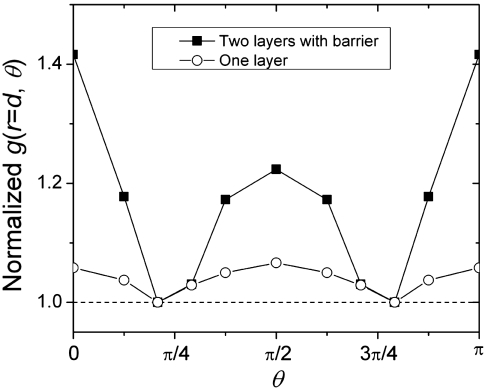
Furthermore, we explore the role of particle layers in the formation of vorticity-aligned strings in our simulations. We first work in the highly confined limit with only one particle layer: spheres are so confined by the external potential that no displacement in the y direction is allowed (see Materials and Methods). The results show that vorticity-aligned strings do not emerge under shear (Fig. 5). Consistent with this result, when we insert a strong potential barrier between the two particle layers in our small system presented above (see Materials and Methods), we find that instead of vorticity-aligned strings, particles with full hydrodynamic coupling preferentially form strings aligned along the flow direction (Fig. 5). Both of these results indicate that particle migration in y across different layers is crucial for the formation of vorticity-aligned strings.

Fig. 5.

Effects of layers on the string structure. The first peak of g(x,z),g(r = d,θ) is shown for Stokesian dynamics simulations at Pe = 50 with particles confined in one layer (circles), and for Stokesian dynamics simulations at Pe = 50 with extra an flat potential barrier inserted in the middle of the suspension at y = 0 (squares).

Mechanism for String Formation.

Based on our numerical results, we propose a detailed physical picture of how the vorticity-aligned strings form. As the basic element, the relative motion of a particle pair can be divided into motion along the line connecting their centers (radial motion) and the rotation around the center of mass of the pair (rotational motion). With increasing shear, both motions are unaltered in the vorticity direction (z), but are faster in the x and y directions by a factor of Pe in the dilute limit. When the pair gets closer, however, the hydrodynamic coupling (lubrication) between the two particles strongly represses their radial motion. Hence, for close pairs at large Pe, the rotational motion in the x-y plane becomes the dominant mode. Specifically, the relative motion of a particle pair, which is arranged along z, is unaltered with increasing Pe. But a particle pair arranged along the flow direction rotates out of the x-z plane increasingly faster with increasing shear. This out-of-plane rotation induces strong particle migrations along y and leads to random collisions between particles of different linear shear velocities—an effect that is even stronger in the situation where the particles are already organized into layers. These collisions strongly enhance particle diffusion in the x-z plane (28–30). Due to the linear velocity profile, momentum transfer between two colliding particles should on average be largest along the flow direction. Hence, this mechanism enhances diffusion to a greater degree along the flow direction than along the vorticity direction as observed in the experiments, which eventually leads to the formation of vorticity-aligned strings with increasing Pe as required by the balance of the osmotic pressure.

Conclusions

In general, our results in conjunction with previous studies (13–19, 22) help clarify the conditions necessary for obtaining string structures with different orientations in hard-sphere colloidal suspensions. We conclude that: (i) in Brownian dynamics simulations without hydrodynamic couplings between particles, strings form along the flow direction (13–17); (ii) with confinement that allows no motion in y, the vorticity-aligned string structure does not exist; (iii) with both hydrodynamic coupling and freedom for particles to migrate in y, a string structure with log-rolling strings along the vorticity direction prevails. Determining how these results are altered by additional interactions between the particles remains an active area of research (31–34). It is also of great interest to determine how particle layering order plays a role in the string formation.

Our studies demonstrate that when driven out-of-equilibrium, a simple system with isotropic components can show anisotropic particle dynamics and display intriguing 1D order. In many ways, our system is analogous to equilibrium systems comprised of asymmetric particles that also exhibit anisotropic diffusion. For example, discotic liquid crystals can form columnar structures with 1D order (1). Furthermore, we illustrate that by employing the anisotropic shear-induced particle diffusion (28–30), one can regulate the effective direction-dependent particle interactions, and therefore, accelerate rates at which particles form contacts—a method potentially useful for rapid bioanalysis if biofunctionalized particles are used (35–37).

Materials and Methods

Colloidal Suspensions and Experimental Methods.

The average diameter of our silica particles is d = 0.96 μm with polydispersity of 5%. The solvent we use is a mixture of glycerin (80 weight%) and water, which matches the refractive index of the particles and has viscosity η₀ = 0.06 Pa·s. By adding a small amount of fluorescein dye into the mixture, we can image the three-dimensional (3D) structure of suspensions with confocal microscopy. Our particles are weakly charged in the suspensions and, in the range of volume fractions we study (0.30 < ϕ ≤ 0.49), they exhibit near hard-sphere behavior with thermal and hydrodynamic interactions. Suspensions are loaded into a plane shear cell with an accurately controlled spacing, h, between the top and bottom shear plates. We can vary h from 1 μm up to 100 μm. Hence, we are able to study the effect of confinement on the structure of sheared suspensions in our experiment. While the top plate is held fixed, a sinusoidal motion is applied to the bottom plate by a piezoelectric actuator. The imaging plane of our confocal microscope (61.4 μm × 61.4 μm) is parallel to the flow velocity (x)—vorticity (z) plane. To obtain the full 3D structure, the location of the imaging plane is varied along the shear gradient (y) direction. A further detailed description of our experimental apparatus can be found in ref. 6, and a detailed description of our confocal imaging techniques can be found in the SI Text.

Numerical Methods.

We use Stokesian dynamics to simulate the sheared colloidal suspensions (22, 25, 29). In this approach, the configuration space trajectories are composed of successive displacements of the colloidal particles each taken over a short time step Δt. The influence of hydrodynamic interactions is incorporated through the resistance tensor, which only depends on the configuration of all the colloidal particles. At the beginning of each time step, the resistance tensor is evaluated and then used to determine the displacements of all the colloidal particles. We initially generate N = 110 spheres of unit diameter d, the center of mass of which falls in the range 0 < x < 15, 0 < z < 15, and -a < y < a, where a = 0 for the single layer simulations and a = 0.475 for the double layer simulations (Fig. 4A). To control the center of mass of particles in y, we apply an external potential that is 0 for |y| ≤ a and U_y = (f/2)·(|y| - a)² for |y| > a with f = ∞, a = 0 for the single layer simulations, and f = 10,000 k_BT, a = 0.475 for the double layer simulations. Periodic boundary conditions in the x and z directions are used. For one set of simulations, an additional potential barrier U_y0 is added to repress the inter layer exchanges (see text), where U_y0 is 0 for |y| > 0.3 and 40 k_BT·[1 + cos(πy/0.3)] for |y| ≤ 0.3. The interparticle potential was chosen to be isotropic and can be represented by the continuous but nearly hard sphere potential function over the separation r as U(r)/k_BT = C(r - 0.5)^-α with C = 8 × 10^-9 and α = 32. The unit time of the simulation is defined in terms of the characteristic time of the system: the diffusive time scale d²/D when Pe < 1 and the inverse shear rate 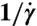when Pe > 1. D is the short time diffusion constant of particles. In each simulation 40,000 time steps of Δt = 5 × 10^-4 are taken initially to allow the system to settle into steady state, after which 400,000 time steps were taken for computing average properties.