Genetic code translation displays a linear trade-off between efficiency and accuracy of tRNA selection

Abstract

Rapid and accurate translation of the genetic code into protein is fundamental to life. Yet due to lack of a suitable assay, little is known about the accuracy-determining parameters and their correlation with translational speed. Here, we develop such an assay, based on Mg²⁺ concentration changes, to determine maximal accuracy limits for a complete set of single-mismatch codon–anticodon interactions. We found a simple, linear trade-off between efficiency of cognate codon reading and accuracy of tRNA selection. The maximal accuracy was highest for the second codon position and lowest for the third. The results rationalize the existence of proofreading in code reading and have implications for the understanding of tRNA modifications, as well as of translation error-modulating ribosomal mutations and antibiotics. Finally, the results bridge the gap between in vivo and in vitro translation and allow us to calibrate our test tube conditions to represent the environment inside the living cell.

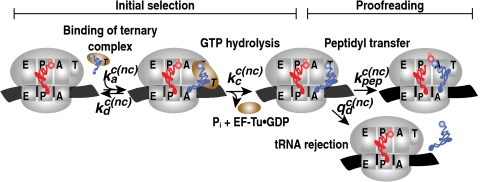
Translation of the ancient and universal genetic code into protein on ribosomes requires precise mRNA decoding by aminoacyl-tRNAs (aa-tRNAs) and rapid formation of nascent peptide chains (1, 2). Codon reading by aa-tRNAs ultimately relies on the specificity of cognate in relation to noncognate codon–anticodon interactions, but two ribosome-dependent specificity enhancements greatly improve mRNA decoding (3). Firstly, bases A1492 and A1493 in the 16S rRNA of the 30S subunit have stereospecific, A-minor interactions with the first two codon–anticodon base pairs but not with the third (4–6), suggesting higher frequency of misreading of the third codon base than of the first two bases (3), in line with the wobble hypothesis (7). Secondly, the ribosome enhances the accuracy of codon reading by a two-step mechanism in which initial codon selection by a tRNA is followed by a proofreading step (8–11). That is, the ternary complex consisting of aa-tRNA, elongation factor Tu (EF-Tu), and GTP is, when cognate, activated for GTP hydrolysis on EF-Tu with high probability, whereas a noncognate ternary complex is likely to dissociate from the ribosome before GTP hydrolysis. After GTP hydrolysis on EF-Tu, a cognate aa-tRNA is selected for peptidyl transfer with high probability, whereas a noncognate aa-tRNA is likely to dissociate from the ribosome in a proofreading step before peptidyl transfer (8, 9) (Fig. 1).

Fig. 1.

Schematic representation of tRNA selection on the ribosome. The end point of initial selection of tRNA in ternary complex is hydrolysis of the EF-Tu-bound GTP. After hydrolysis of GTP, tRNA can be discarded in the proofreading step.

In spite of the central role that is played by ribosome aided reading of the genetic code in all areas of biology, very little is known about the basal parameters that provide the boundary conditions for rapid and accurate mRNA translation into protein. Most important among these parameters is the maximal possible discrimination between a cognate and a noncognate codon–anticodon interaction: the “d value.” It defines the upper limit of the current single step accuracy, A, by which any aa-tRNA can separate its cognate from a specific noncognate codon. When the current accuracy approaches the d value, the cognate codon reading efficiency must decrease toward zero (1, 2). There exists, in other words, a general efficiency-accuracy trade-off in mRNA translation, and it has therefore been suggested that the bacterial ribosome has evolved to an overall accuracy of codon reading that maximizes the growth rate rather than the current accuracy (1, 2). In line with this hypothesis, mutants with hyper-accurate as well as error-prone ribosomes grow more slowly than wild type (12). Therefore, characterization of the d values of the genetic code is essential for the understanding of code evolution, the impact of the stereospecificity provided by rRNA, why proofreading of tRNAs has evolved, the roles of tRNA modifications in codon reading, as well as the mechanisms of error-affecting antibiotic drugs and ribosomal mutations. Such a characterization can only be performed with in vitro techniques, and its full scientific impact will require calibration of the biochemistry of code translation to in vivo conditions. Here, we demonstrate in a special case how all d values of codon reading can be precisely estimated, and we also make a first attempt to calibrate our in vitro protein synthesis system by comparing our results to known misreading frequencies in the living cell.

Results

The Efficiency-Accuracy Trade-Off in Codon Reading by tRNAs.

The efficiency-accuracy trade-off for initial selection of aa-tRNA in ternary complex may in a common special case be written as (13) (SI Text)

[1]

Here, the Michaelis–Menten parameter (k_cat/K_m)^c defines the efficiency by which a ternary complex cognate to the A-site codon enters and successfully passes the initial selection step of the ribosome by hydrolysis of GTP on EF-Tu in the ternary complex (1, 2, 14); is the rate constant for cognate ternary complex binding to the A site; d is the maximal accuracy by which the ternary complex can select its cognate (c) rather than a particular noncognate (nc) codon, and the current accuracy, A, is given by (k_cat/K_m)^c/(k_cat/K_m)^nc. The d value accounts for the difference in binding free energy between a ternary complex in cognate and noncognate codon contact as well as for the faster GTPase activation in cognate than in noncognate ternary complexes (3, 15) (SI Text).

Modulation of Efficiency and Accuracy in Codon Reading by [Mg²⁺] Variation.

We have found that the current accuracy, A, in Eq. 1 can be varied, while the association rate constant and the maximal accuracy d remain unchanged. This observation means that plots of (k_cat/K_m)^c versus A are straight lines (Eq. 1). These intercept the x axis at zero efficiency when A = d, and can thus be used for systematic and direct characterization of all d values of the genetic code. The accuracy variation was implemented by adding extra Mg²⁺ ions in the 0–10 mM range to the standard Mg²⁺ concentration of 5 mM in our polymix-buffer-based system for protein synthesis in the test tube with Escherichia coli components of high purity (16). We performed experiments at 37 °C, where E. coli bacteria grow optimally (17), and most accuracy-relevant in vivo data are available (18). 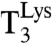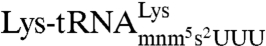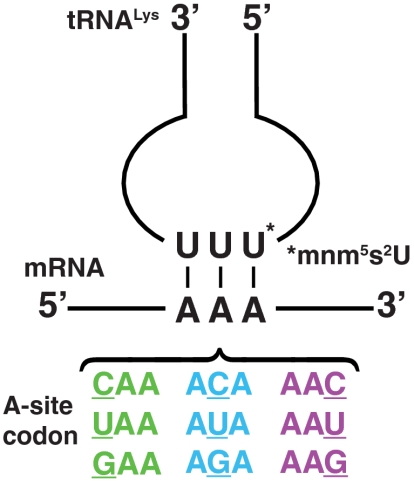The Mg²⁺ concentration dependent (k_cat/K_m)^c and (k_cat/K_m)^nc parameters for [³H]GTP hydrolysis were measured when ternary complex (), consisting of , EF-Tu, and [³H]GTP, interacted with 70S initiation complexes programmed with cognate or noncognate codons for 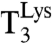. The 70S complexes contained f[³H]Met-tRNA^fMet in the P site (Fig. 1) and the cognate Lys codons AAA or AAG, or any noncognate codon differing from AAA by one base change, in the A site (Fig. 2).

Fig. 2.

The efficiency-accuracy trade-off in initial selection was evaluated for reading all possible single-mismatch codons, compared to the fully matched AAA codon.

When 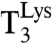interacted with AAA- or AAG-programmed ribosomes in excess after rapid mixing in a quench-flow instrument, [³H]GDP was rapidly formed as illustrated for AAA reading with addition of zero (Fig. 3A, Inset) and 6 mM (Fig. 3B, Inset) extra Mg²⁺ concentration. The experiments were evaluated as first-order reactions in which [³H]GTP in 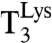was converted to [³H]GDP on EF-Tu. The rate constant was given by [R_a] × (k_cat/K_m)^c, where [R_a] was the concentration of active ribosomes. The activity was operationally defined as the ability of AAA-programmed ribosomes to rapidly form the dipeptide fMet-Lys.

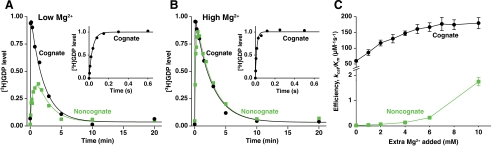
Fig. 3.

Efficiency of GTP hydrolysis increases with increasing Mg²⁺ concentration. (A and B) Time evolution of the [³H]GDP level after mixing of with ribosomes programmed with noncognate GAA (green squares) or cognate AAA (black circles) codon with no (A) or 6 mM (B) extra Mg²⁺ addition (see also Fig. S1 for a complete set of mismatch experiments at 2 mM extra Mg²⁺). The initial [³H]GDP increase is determined by the rate of hydrolysis of [³H]GTP in ternary complex. The decrease is due to spontaneous exchange of [³H]GDP for unlabeled GTP on EF-Tu after GTP hydrolysis, and rapid regeneration of [³H]GTP. The slow initial increase of [³H]GDP in noncognate cases (green squares), is faster in high (B) than in low (A) Mg²⁺ concentration, and much slower than in the cognate cases (black line). The noncognate and cognate curves in A and B were obtained in parallel experiments and jointly fitted for precise estimates of the noncognate k_cat/K_m values for GTP hydrolysis. (Insets) [³H]GDP level for the cognate reaction as measured in quench-flow to obtain the cognate k_cat/K_m values for GTP hydrolysis. (C) Efficiency of GTP hydrolysis, k_cat/K_m, for noncognate reading of GAA codon (green squares) and cognate reading of AAA codon (black circles) at varying Mg²⁺ concentration. Data represent weighted averages from at least two experiments ± propagated standard deviation.

Similar experiments were performed by hand in a longer timescale for ribosomes programmed with AAA and, in parallel, a noncognate codon. For AAA-programmed ribosomes, [³H]GDP decreased exponentially (after an unresolved initial phase) with a rate determined by slow exchange of [³H]GDP to unlabeled GTP on EF-Tu in the absence of EF-Ts, followed by rapid conversion of free [³H]GDP to [³H]GTP by pyruvate kinase (see Materials and Methods). This behavior is illustrated for addition of zero (Fig. 3A, black) and 6 mM (Fig. 3B, black) extra Mg²⁺ concentration. For ribosomes programmed with a noncognate codon, the initial phase of [³H]GDP increase was slowest with no extra addition of Mg²⁺ and became successively faster as the added Mg²⁺ concentration increased, as illustrated in the GAA codon case (Fig. 3 A and B, green). The method is further illustrated by a series of experiments with addition of 2 mM extra Mg²⁺ concentration for ribosomes programmed with all noncognate codons differing from AAA by a single base change (Fig. S1). All experiments were modeled by a scheme in which (i) [³H]GDP appeared with a first order rate constant given by [R_a] × (k_cat/K_m)^c in the cognate and [R_a] × (k_cat/K_m)^nc in the noncognate cases, (ii) [³H]GDP disappeared with a first order rate constant determined by the spontaneous dissociation of [³H]GDP from free EF-Tu·[³H]GDP, (iii) [³H]GTP was slowly exchanged for unlabeled GTP in unreacted ternary complex (see SI Text). By joint evaluations of the experiments performed in parallel for the cognate and noncognate reactions, precise and unambiguous estimates of all (k_cat/K_m)^nc values were obtained (Table 1).

Table 1.

Mg²⁺-dependent variations in efficiency of GTP hydrolysis (k_cat/K_m) for 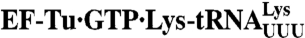reading its cognate codon (AAA) and all single-mismatch codons

		Extra Mg2+ added, mM
Codon *		0	1	2	3	4	5	6	7	8	10
AAA	kcat/Km	60 ± 4	86 ± 9	117 ± 9	130 ± 13	147 ± 7	161 ± 14	167 ± 14	177 ± 21	175 ± 16	180 ± 18
AAG	μM-1 s-1†	—	—	31 ± 2	—	57 ± 5	—	—	—	111 ± 8	—
UAA		18 ± 1	—	67 ± 3	—	158 ± 6	—	—	—	—	—
AUA		—	—	31 ± 1	—	71 ± 2	—	150 ± 5	—	—	—
AAU		58 ± 3	—	222 ± 12	—	490 ± 120	—	—	—	—	—
CAA	kcat/Km	—	—	19.0 ± 0.7	—	59 ± 2	—	146 ± 6	—	—	—
ACA	mM-1 s-1†	—	—	11.6 ± 0.7	—	36 ± 2	—	112 ± 5	—	—	—
AAC		25 ± 2	—	86 ± 5	—	194 ± 11	—	—	—	—	—
GAA		19 ± 1	36 ± 2	66 ± 4	—	139 ± 10	—	327 ± 16	—	—	1,750 ± 160
AGA		—	—	35 ± 2	—	93 ± 4	—	323 ± 46	—	—	—

^*Variation from the cognate codon (AAA) is underlined.

^†Data represent the weighted average from two or more experiments ± the propagated standard deviation.

Whereas the (k_cat/K_m)^nc parameter for the GAA-programmed ribosomes increased almost 100-fold from 19 at low to 1,750 mM^-1 s^-1 at high Mg²⁺ concentration with no sign of rate saturation, (k_cat/K_m)^c for the AAA-programmed ribosomes increased only threefold from 60 μM^-1 s^-1 to an apparent plateau at about 180 μM^-1 s^-1 (Fig. 3C and Table 1).

Estimation of d Values from Linear Efficiency-Accuracy Trade-Off Relations.

The dataset in Table 1 was used to estimate the current accuracy ratio A = (k_cat/K_m)^c/(k_cat/K_m)^nc at different Mg²⁺ concentrations, where the efficiency (k_cat/K_m)^c corresponded to cognate reading of AAA by 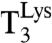and (k_cat/K_m)^nc to noncognate 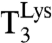reading of all codons differing from AAA by one base change. We plotted (k_cat/K_m)^c for the reading of AAA by 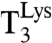versus the accuracy A and found straight efficiency-accuracy trade-off lines with well-defined d values from the x-axis intercepts in all cases (Fig. 4A). Such straight lines are predicted from Eq. 1 on the condition that, when A is varied, 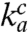and d remain unaltered. If, in contrast, either the 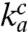value or the d value had varied significantly with the Mg²⁺ concentration, the efficiency-accuracy plots in Fig. 4A would have been distinctly nonlinear. The discovery that the linearity condition is fulfilled makes separate measurement of the 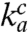value redundant. This feature is crucial for the method we have developed as well as for calibration of accuracy data obtained in vitro to those in vivo (see Discussion). For technical convenience (see SI Text), we also plotted the inverse of (k_cat/K_m)^c versus the inverse of (k_cat/K_m)^nc (Fig. 4B). Here, the slopes of the resulting straight lines estimated the d values, as summarized in Table 2 and Fig. 4C.

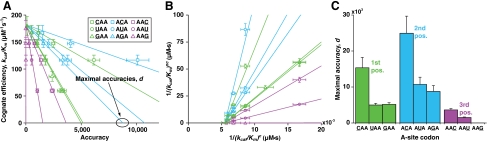
Fig. 4.

The rate-accuracy trade-off in initial selection. (A) Rate-accuracy trade-off lines in plots of the cognate k_cat/K_m (AAA codon) versus the accuracy (calculated as the ratio of cognate k_cat/K_m over noncognate k_cat/K_m; Table 1) on all single-mismatch codons. The maximal accuracy, d, is in each misreading case determined by the intercept of the line with the x axis. Data represent weighted averages from at least two experiments ± propagated standard deviation in both dimensions. (B) The inverted noncognate k_cat/K_m versus the inverted cognate k_cat/K_m at different Mg²⁺ concentrations (calculated from data in Table 1). The slopes of the straight lines give the maximal accuracy, d, for all nine single-mismatch codons (Table 2). Symbols as in A. Data represent weighted averages from at least two experiments ± propagated standard deviation in both dimensions. (C) d values as estimated from data and linear fits shown in B.

Table 2.

The d values for misreading of single-mismatch codons by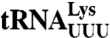

A-site codon *	Maximal accuracy, d†
CAA	15,400 ± 2,900
UAA	4,990 ± 460
GAA	5,170 ± 460
ACA	24,900 ± 4,800
AUA	10,700 ± 2,000
AGA	8,800 ± 1,600
AAC	3,640 ± 340
AAU	1,530 ± 140
AAG	9.0 ± 1.5

^*Deviation from the fully matched AAA codon is underlined.

^†Relative to the matched AAA codon.

With AAA as the cognate codon, the maximal accuracy, d, ranged from about 1,500 (misreading of AAU) to about 25,000 (misreading of ACA). The d value separating reading of the cognate AAA from the likewise cognate AAG codon, was about 10 (Fig. 4C and Table 2).

The d values of the present dataset displayed two major trends. Firstly, the d value corresponding to the same mismatch was highest in the second, intermediate in the first, and smallest in the third codon position. Secondly, the d value corresponding to misreading at the same codon position was in general highest for the U∶C, intermediate for the U∶U, and smallest for the U∶G mismatch (Fig. 4C).

The efficiency of cognate codon reading must go to zero when the current accuracy, A, is tuned toward the maximal accuracy, d (Eq. 1). Therefore, the initial in vivo selectivity must be considerably smaller than the d values of Table 2. If, to exemplify, it is assumed that there is a kinetic loss in cognate codon reading efficiency of 10% in the living cell, the current initial selection, A, of each noncognate codon would be about 10 times smaller than the corresponding d value. Accordingly, initial selection would range from 150 (misreading of AAU) to 2,500 (misreading of ACA), suggesting that the need for further accuracy increase in codon reading without severe loss of kinetic efficiency has been the ultimate cause for the evolution of a proofreading step.

Accuracy Enhancement by Proofreading.

We also designed experiments to estimate the overall accuracy of peptide bond formation, which includes the accuracy enhancement provided by proofreading of tRNA following initial selection of ternary complex (8, 9). For this aim, we estimated the k_cat/K_m values for fMet-Lys formation when 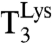reacted with noncognate GAA-programmed ribosomes at varying Mg²⁺ concentration (Fig. 5). With no extra Mg²⁺ ions, the overall accuracy was 150,000 (lowest closed triangle in Fig. 5C), partitioned in an initial selection factor of 3,000 (lowest open triangle in Fig. 5C), and a proofreading factor of 50 (i.e., 150,000/3,000). At the Mg²⁺ concentration corresponding to 10% cognate efficiency loss (second highest triangles in Fig. 5C), the overall accuracy was 5,000, partitioned in initial selection and proofreading factors of 500 and 10, respectively. In vivo data, based on luminescence from a Lys529 (AAA) to Glu529 (GAA) luciferase mutant, show that the overall (normalized) accuracy by which Lys-tRNA^Lys discriminates against the GAA codon is larger than 1,300 (18) (SI Text). This finding suggests that the living cell is tuned to an accuracy level at which the efficiency loss in cognate codon reading is larger than 2%, implying current accuracy levels, A, larger than 2% of their corresponding d values (see Discussion).

Fig. 5.

The rate-accuracy trade-off in overall selection. (A) Rate of noncognate f[³H]Met-Lys dipeptide formation for GAA reading at increasing concentration of 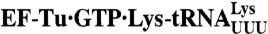ternary complex (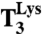). The curves represent fitting of the data to a single exponential equation (see SI Text). (B) Mg²⁺ concentration dependence on noncognate dipeptide formation rates at titration of 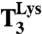. The curves represent fitting of the data to the Michaelis–Menten equation (see SI Text). Data represent weighted averages from at least two experiments, such as shown in A, ± propagated standard deviation. (C) Rate-accuracy trade-off plots in log–log scale for initial selection (Δ) and overall accuracy (▴) for Lys-tRNA^Lys selection of the AAA in relation to the GAA codon. The initial selection (Δ) is the same as plotted in linear scale in Fig. 4 A and B. Data represent weighted averages from at least two experiments ± propagated standard deviation in both dimensions.

Determination of d values also for the proofreading step, which may or may not be the same as the d values for initial selection, requires a precise estimate of the excess hydrolysis of GTP associated with cognate peptide bond formation. Due to insignificant variation of this excess parameter with the Mg²⁺ ion concentration, so that the efficiency decrease due to reduced Mg²⁺ concentration was mainly attributed to the initial selection step, reliable d-value estimates for the ribosomal proofreading function were out of reach in the present approach.

Discussion

The present in vitro work has revealed a surprisingly simple, linear relation between codon reading efficiency and accuracy of codon translation by a Lys-tRNA^Lys-containing ternary complex (Fig. 4A). Our approach, based on variation of the concentration of free Mg²⁺ ions in a polymix buffer system containing polyamines and other ionic components of the living cell (16), can be extended to cognate and noncognate codon reading also by other ternary complexes. The linearity of these trade-off lines (Fig. 4A) shows that variation of the Mg²⁺ concentration in the polymix buffer background affects neither the rate constant of cognate ternary complex association with the ribosome nor the d values that separate the cognate from the noncognate reactions. This previously unknown feature of code translation suggests that the Mg²⁺ dependent efficiency-accuracy trade-off observed here provides the authentic d values of initial tRNA selection without kinetic interference from accuracy-unrelated steps in the reaction pathway leading from free ternary complex to GTP-hydrolysis. It also suggests that, if the accuracy of the living cell is regulated for maximal fitness in a growth rate dependent manner, a likely candidate is growth-dependent control of the cellular pumps that set the cytoplasmic concentration of free Mg²⁺ ions. Such a scenario was hypothesized a long time ago (1), but then without the strong experimental support provided by the present observations. Recent findings from living yeast cells have demonstrated that translational accuracy correlates negatively with the intracellular Mg²⁺ concentration, thereby highlighting the exciting possibility of growth-dependent intracellular control of ribosomal accuracy (19).

The two clear patterns of misreading frequencies shown in Fig. 4C have implications for how the genetic code is designed. Even though a complete model of misreading in vivo would need the characterization of all tRNA readings of all possible codons, some tentative generalizations can be made. Firstly, in a given codon position, a U-C mismatch is less likely to occur than a U-U or U-G mismatch (Fig. 4C and Table 2). Secondly, the second codon position seems to be most tightly controlled, with larger d values than the two other codon positions for the same type of mismatches. This finding is in line with the observation that the second codon position plays the largest role in determining the chemical properties of incorporated amino acids (20). Thirdly, third position mismatch readings are most frequent because of comparatively small d values, which is in accord with an early proposal by Crick, formulated to underpin the wobble hypothesis (7). A structural basis for this remarkable feature of the code has been suggested from NMR data (4, 5) and X-ray crystallography structures of the ribosome (3, 6). The proposal here is that bases A1492 and A1493 in the 16S rRNA of the 30S subunit have stereospecific interactions with the first two codon–anticodon base pairs but not with the third base pair: This ribosome-dependent stereospecificity increases the d values above what can be achieved from differences in binding constants for matching and nonmatching Watson–Crick base pairing (3).

The trade-off line for the overall accuracy of codon reading (Fig. 5C) now makes it possible to calibrate accuracy data obtained in the test tube with the translational accuracy in the living cell. The in vivo accuracy of protein synthesis has received considerable attention in the past, and an average missense error frequency of 4 × 10^-4 has been suggested by Parker (21). In a more recent approach, Kramer and Farabaugh studied the bioluminescence from luciferase mutants (18). Their assay was based on induction of bioluminescence by mistranslation by 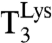of mutated variants of codon 529 in the open reading frame of a luciferase mRNA. Taken at face value, their obtained error frequencies had a median value of 3 × 10^-4 (18), similar to Parker’s averaged estimate. Although these error frequency estimates are likely to be too large because of significant background luminosity, they provide an upper limit to the in vivo error frequencies associated with misincorporation of lysine (18).

Another estimate of the translational accuracy in vivo can be based on the concentration of free Mg²⁺ ions in the living E. coli cell. In the present study, the concentration of free Mg²⁺ was varied between 1.3 and 7.5 mM, assuming one-to-one binding of Mg²⁺ to the strongly chelating NTPs at 2 mM total concentration, and a K_d of approximately 6 mM for the weakly Mg²⁺ chelating phosphoenolpyruvate (PEP) (22). Because the concentration of free Mg²⁺ in the E. coli cell is likely to be between 1 and 2 mM (23), the trade-off lines in Fig. 4A suggest that intracellular ribosomes operate at a current initial selection accuracy, A, above 40% of the corresponding d value and, accordingly, at an efficiency below 60% of its maximal value, as defined by the rate constant for association of cognate ternary complex to the ribosomal A site. Because of the linearity of the efficiency-accuracy trade-off lines, this statement is expected to be universally true for cognate and noncognate reading of all types of codons by all types of ternary complexes.

Another set of d values, related to the initial accuracy by which a Phe-tRNA^Phe-containing ternary complex favored its cognate UUC codon over a set of noncognate codons, can be deduced from the elemental rate constants of ribosome-dependent GTPase activation on EF-Tu, as presented in refs. 15 and 24. These experiments, for technical reasons performed at 20 °C, suggest remarkably high d values and low current accuracy levels. These results could mean that both d values and accuracy tuning vary with temperature, a scenario now testable by the more direct approach of the present work.

The present experimental strategy will now make it possible to answer some outstanding questions regarding the accuracy of codon reading in the living cell: Is quantitative discrimination against the same types of mismatches universal or idiosyncratic to individual tRNAs? Is the efficiency of cognate codon reading tuned to uniformity by structural design and tRNA modifications? Are accuracy-affecting antibiotic drugs and ribosomal mutations altering the d values of codon reading (different x-axis intercepts in Fig. 4A) or just the current accuracy, A, at unaltered d values (different positions at trade-off lines with unchanged x-axis intercepts in Fig. 4A). Finally, we propose that quantitative estimates of the d values of the genetic code in conjunction with the remarkably simple efficiency-accuracy trade-off revealed by the present experiments will clarify how the accuracy in living cells has been evolutionarily tuned for maximal fitness of growing bacteria (1).

Materials and Methods

Reagents and Buffer Conditions.

Ribosomes (E. coli strain MRE 600), synthetic mRNAs, initiation factors, elongation factors, and f[³H]Met-tRNA^fMet were prepared according to ref. 25 and references therein. Transfer RNA^Lys and tRNA^Glu were from Chemical Block, bulk tRNA was prepared as described (26), radioactive compounds were from GE Healthcare, and all other chemicals were from Merck or Sigma-Aldrich. All experiments were carried out in polymix buffer [95 mM KCl, 5 mM NH₄Cl, 0.5 mM CaCl₂, 8 mM putrescine, 1 mM spermidine, 5 mM potassium phosphate, 1 mM dithioerythritol, and 5 mM Mg(OAc)₂] (16) with Mg(OAc)₂ additions between 0 and 10 mM. For energy supply and regeneration, 10 mM PEP, 50 μg/mL pyruvate kinase (PK), and 2 μg/mL myokinase (MK) were used together with 2 mM ATP+GTP (ribosome mixture, 1∶1 ATP/GTP; ternary complex mixture, only ATP for GTP-hydrolysis experiments, 1∶1 ATP/GTP for noncognate dipeptide experiments).

GTP Hydrolysis in Cognate Ternary Complex Reactions.

To estimate cognate k_cat/K_m values, 70S initiation complexes with f[³H]Met-tRNA^fMet in the P site, and the A site programmed with Lys codon AAA or AAG, were formed by incubation (10 min at 37 °C) of 70S ribosomes (1.2 μM), f[³H]Met-tRNA^fMet (2 μM), mRNA (2 μM), initiation factor 1 (IF1) (1.2 μM), IF3 (1.2 μM), and IF2 (0.6 μM), ATP (1 mM), GTP (1 mM) in polymix buffer with energy supply, energy regeneration components, and varying additions of Mg(OAc)₂. [³H]GTP-labeled ternary complexes were formed by initial incubation in polymix (15 min at 37 °C) of EF-Tu•GDP (0.4 μM), [³H]GDP (0.4 μM), ATP (2 mM), PEP (10 mM), and varying additions of Mg(OAc)₂ in the absence of PK and MK. This preincubation was followed by a second incubation in polymix (15 min at 37 °C) after addition of PK, MK, tRNA^Lys (4 μM), Lys (400 μM), and Lysyl-tRNA synthetase (LysRS) (1.5 units per μL). Equal volumes of 70S initiation complex and ternary complex mixtures were rapidly mixed in a temperature controlled quench-flow instrument (RQF-3; KinTek Corp.) as described (25). After quenching with formic acid (FA), the samples were centrifuged 15 min at 20,800  × g, [³H]GTP and [³H]GDP in the supernatant were separated on a MonoQ ion-exchange column (GE Healthcare) and analyzed by on-line scintillation counting (βRAM3; INUS, Inc.) (27). To estimate the concentration of active 70S initiation complex, 15 μL ribosome mixture was incubated 1 min at 37 °C with 15 μL ternary complex mixture after addition of 220 pmol EF-Ts in 1 μL. After quenching with 15 μL FA (50%), the amount of f[³H]Met-Lys dipeptide formed, taken to be equal to the amount of active 70S initiation complex (50–80% of the total 70S concentration, depending on Mg²⁺ concentration), was estimated by RP-HPLC analysis as described (28).

GTP Hydrolysis in Noncognate Ternary Complex Reactions.

For each noncognate reaction, two types of 70S initiation complexes were prepared in parallel. One was A-site programmed with AAA (cognate to tRNA^Lys), the other was A-site programmed with CAA (Gln), UAA (STOP), GAA (Glu), ACA (Thr), AUA (Ile), AGA (Arg), AAC (Asn), or AAU (Asn) (each one noncognate to tRNA^Lys with a single mismatch, Fig. 2). A mixture of 70S ribosomes (2 μM), f[³H]Met-tRNA^fMet (3 μM), IF1 (2 μM), IF3 (2 μM), IF2 (1 μM), ATP (1 mM), GTP (1 mM), energy supply, and energy regeneration components was prepared. To one-half was added the cognate, and to the other half, a noncognate mRNA (3 μM) for 10-min incubations at 37 °C. EF-Tu·[³H]GTP·Lys-tRNA^Lys ternary complexes were prepared essentially as described above, but now with 0.6 μM EF-Tu and 0.6 μM [³H]GDP. The GTP-hydrolysis reactions were started by mixing equal volumes of ternary complex and either one of the two ribosome mixtures. The reactions were quenched after different incubation times by the addition of FA (17% final concentration) and the [³H]GDP and [³H]GTP levels were analyzed as described above. The amount of active 70S initiation complex programmed with a to tRNA^Lys noncognate codon in the A site was obtained by estimation of the amount of peptide bond formed on the 70S complex during incubation (10 s at 37 °C) together with the corresponding cognate ternary complex present in excess over the 70S initiation complex. For 70S initiation complexes programmed with UAA (stop codon), their specific activity was estimated as the amount of released f[³H]Met from the P-site bound f[³H]Met-tRNA^fMet during incubation (1 min at 37 °C) with a class-1 release factor present in large excess (5 μM) over the 70S initiation complex. In 3 of the 27 noncognate reaction conditions, the comparatively rapid GTP-hydrolysis reactions, analyzed with quench-flow technique, made the cognate control reactions redundant (see SI Text). To validate the basal condition of proportionality between reaction rates and k_cat/K_m values, the rate of GTP hydrolysis for the highest k_cat/K_m value (codon GAA at 10 mM extra Mg²⁺) was estimated at two ribosome concentrations differing by a factor of two. This twofold concentration change led to reaction rate estimates of 0.90 ± 0.12 s^-1 for the higher and 0.46 ± 0.06 s^-1 for the lower concentration and thus to the same k_cat/K_m estimate, thereby confirming k_cat/K_m-limited kinetics.

Dipeptide Formation in a Noncognate Reaction.

To estimate the Mg²⁺ concentration-dependent variation of k_cat/K_m for noncognate fMet-Lys formation, GAA-programmed ribosomes were prepared by incubation (10 min at 37 °C) of 70S ribosomes (0.15–0.25 μM), f[³H]Met-tRNA^fMet (0.275 μM), mRNA (0.5 μM), IF1 (0.25 μM), IF3 (0.25 μM), and IF2 (0.125 μM), ATP (1 mM), GTP (1 mM) in polymix buffer with energy supply, energy regeneration components, and varying additions of Mg(OAc)₂. EF-Tu·GTP·Lys-tRNA^Lys ternary complexes were prepared at varying concentrations of Mg(OAc)₂ by incubating (15 min at 37 °C) tRNA^Lys (0.4–10 μM), EF-Tu (4 μM in excess over each tRNA^Lys concentration), Lys (400 μM), LysRS (1.5 units per μL), and EF-Ts (3 μM) in the presence of ATP, GTP (1 mM each), and energy regeneration system. The rate of noncognate dipeptide formation was evaluated at different Mg²⁺ concentrations by incubating ternary complex (0.2–5 μM final) in excess over active ribosomes (0.06–0.1 μM final) for different times. The reactions were quenched and the extent of dipeptide formation was evaluated as described above. The reactions were monitored until dipeptides had been formed on a major fraction of active ribosomes (Fig. 5A). The active concentration of ribosomes was also confirmed by incubating the ribosome mixture with cognate Glu-tRNA^Glu containing ternary complexes in excess for 10 s. The concentration of Lys-tRNA^Lys ternary complex was assayed by incubating the factor mixture with AAA-programmed ribosomes for 10 s for subsequent analysis of the extent of dipeptide formation.