Nature of curvature coupling of amphiphysin with membranes depends on its bound density

Abstract

Cells are populated by a vast array of membrane-binding proteins that execute critical functions. Functions, like signaling and intracellular transport, require the abilities to bind to highly curved membranes and to trigger membrane deformation. Among these proteins is amphiphysin 1, implicated in clathrin-mediated endocytosis. It contains a Bin-Amphiphysin-Rvs membrane-binding domain with an N-terminal amphipathic helix that senses and generates membrane curvature. However, an understanding of the parameters distinguishing these two functions is missing. By pulling a highly curved nanotube of controlled radius from a giant vesicle in a solution containing amphiphysin, we observed that the action of the protein depends directly on its density on the membrane. At low densities of protein on the nearly flat vesicle, the distribution of proteins and the mechanical effects induced are described by a model based on spontaneous curvature induction. The tube radius and force are modified by protein binding but still depend on membrane tension. In the dilute limit, when practically no proteins were present on the vesicle, no mechanical effects were detected, but strong protein enrichment proportional to curvature was seen on the tube. At high densities, the radius is independent of tension and vesicle protein density, resulting from the formation of a scaffold around the tube. As a consequence, the scaling of the force with tension is modified. For the entire density range, protein was enriched on the tube as compared to the vesicle. Our approach shows that the strength of curvature sensing and mechanical effects on the tube depends on the protein density.

In cells, the formation of closed membrane carriers needed for membrane trafficking requires a panoply of proteins that transiently interact with the lipid membrane to control the shape, size, and composition of the nascent bud. Recently, membrane shaping and remodeling by proteins has attracted attention (1), motivated by the role membrane curvature plays in intracellular trafficking. Indeed, to generate membrane intermediates that transport cargo between organelles, many proteins have acquired through evolution the ability to sense and/or to generate membrane curvature (1).

Among these proteins are those in the BAR (Bin-Amphiphysin-Rvs) family, implicated in endocytosis and in membrane-triggered actin polymerization (2). They contain a membrane-binding module, known as the BAR domain, consisting of a crescent-shaped dimer (3), and in the most common case of the N-BAR, is combined with N-terminal amphipathic helices (1). The first studies on N-BAR domain proteins showed that they strongly deformed membranes, usually forming tubular structures (4). Since then, several biochemical studies have explored the sensing and membrane-deforming functions of N-BAR proteins by measuring curvature-dependent binding (5) and by studying the effect of mutation or deletion of the N-terminal helices on tubulation (4). Meanwhile, inspired by earlier theoretical work on the effect of bound proteins and inclusions on lipid membranes (6–10), simulation work has focused on membrane curvature generated by oligomerized N-BAR proteins (11, 12), and modeling based on elastic theory has looked at the membrane curvature induced by helix insertion (13).

Despite these contributions, there is still not a comprehensive picture of the physical parameters that govern the functioning of the BAR domain. Importantly, theoretical work to date focused only on the interaction between protein and isolated curved membrane patches, without considering the connection of the curved patch to a membrane reservoir as encountered in vivo. In this study, we quantitatively evaluated the mechanical action of amphiphysin 1 when binding to the membrane as a function of parameters such as membrane tension, curvature, and bound protein density.

We chose amphiphysin 1 as a paradigm for the study of N-BAR domains, which is enriched in the necks of clathrin-coated pits prior to endocytic bud fission (14, 15). It is thought that amphiphysin 1 assists in recruiting dynamin to the neck in dynamin-dependent endocytosis (4). We have used an in vitro system in which the tension, curvature, and protein density can be varied, encompassing the entire range of physiological conditions for these parameters. This system consists of membrane nanotubes pulled by optical tweezers from giant unilamellar vesicles (GUVs) aspirated into a micropipette; the initial tube diameter (10–100 nm) is directly controlled by the tension of the GUV (16, 17). Once formed, the GUV and nanotube are exposed to a solution of full length, Alexa 488 labeled human amphiphysin 1 (referred to as amph1*). By measuring the protein densities on the GUV and tube, the pulling force, and the tube radius in the presence of bound protein, we identified how the interplay between protein and curved membrane depends on the bound protein density on the GUV. The first result is that the amphiphysin 1 density on the tube is always enriched compared to that on the GUV, for all protein densities on the GUV. The mechanical effects on the tube of amphiphysin 1 binding strongly depend, however, on the GUV density: At low densities (less than 1,000 μm^-2 on the GUV), amphiphysin amplifies curvature, but also is strongly enriched on curved membranes. Based on a theoretical model, we show that simultaneous curvature sensing and inducing at low densities results from the spontaneous curvature of the membrane generated by protein. In the extreme case of vanishing densities on the GUV, no tube deformation was detected, despite a clear enrichment of protein on the tube proportional to its curvature, in agreement with theory. At high densities (greater than 1,000 μm^-2 on the GUV), amphiphysin has a strong mechanical effect, as the tube radius no longer depends on tension, which is consistent with the formation of a protein scaffold forming around the tube. These results agree with simple modeling based on membrane bending energy, protein–membrane and protein–protein interactions. Our work provides an understanding of how the action of amphiphysin 1 depends on its bound density.

Results

Amphiphysin 1 requires the presence of negatively charged lipids to bind to the membrane due to the positive residues on the side of the BAR domain in contact with the membrane (3). We found that the simplest lipid mixture yielding GUVs on which amph1* binding was observed, and being easy to produce using an adapted electroformation procedure (SI Text), was an equimolar lipid mixture of dioleylphosphatidylcholine (DOPC): dioleoylphosphatidylethanolamine (DOPE): dioleylphosphatidylserine (DOPS) (1∶1∶1), supplemented with 0.5% (mol/mol) of a red lipid dye [Bodipy TR-ceramide (Cer*)]. All the experiments discussed below were carried out using GUVs with this composition.

Two Regimes of Amphiphysin-Membrane Interaction.

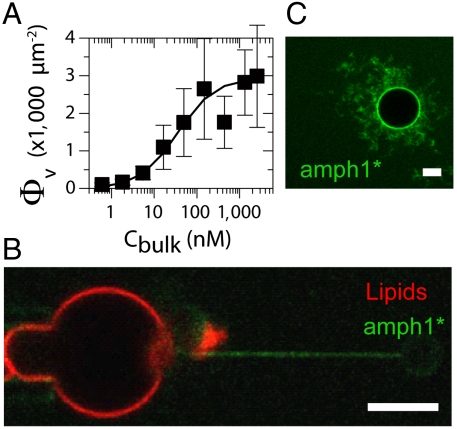
To characterize the amphiphysin interaction with the membrane, we first evaluated amphiphysin 1 binding on our GUVs as a function of bulk concentration. Evolution of bound amph1* on the GUVs was measured using confocal microscopy. To quantify the absolute protein density on the membranes, the fluorescence signal was calibrated using a method adapted from ref. 18; see SI Text and Fig. S1. We have measured the amph1* fluorescence signal on GUVs incubated in buffers containing increasing concentrations of amph1*. The density of bound proteins on the GUV, Φ_v, was found to increase nonlinearly with concentration of amph1* in bulk, C_bulk. Results are shown in Fig. 1A, in which we fit the data to a Langmuir isotherm, Φ_v = Φ_max/(1 + K_d/C_bulk), where K_d is the dissociation constant (19). The fit gives K_d ≈ 35 nM, a small value that reflects fast protein adsorption but slow desorption (see SI Text and Fig. S2). Φ_v reaches a saturation density of about 3,000 μm^-2 for C_bulk in the micromolar range. This value can be compared with the area per N-BAR domain on a flat membrane, equal to 50 nm² (3), corresponding to a close-packing (CP) density Φ_CP = 20,000 μm^-2. The plateau density of 3,000 μm^-2 we measured in these conditions thus corresponds to 15% of Φ_CP. Based on the isotherm, we divided our study of amphiphysin-membrane interaction into two regimes: (i) For Φ_v ≲ 1,000 μm^-2 (C_bulk < K_d), no apparent membrane deformations were detected on the GUV, referred to as the low-density regime. In the dilute limit of this regime, where no bound protein can be detected on the GUV, we observed that, once a tube was pulled, the protein was found to be clearly enriched on tubes (Fig. 1B), suggesting curvature-sensing behavior. More generally in this regime, in addition to protein enrichment on the tube, we will investigate whether preexisting tube curvature is amplified by bound protein. (ii) For Φ_v ≳ 1,000 μm^-2 (C_bulk > K_d), unaspirated GUVs with bound protein frequently exhibit extensive tubular deformations, indicating a strong mechanical effect (see Fig. 1C), referred to as the high-density regime.

Fig. 1.

Two regimes for amphiphysin 1 binding to a GUV membrane DOPC∶DOPE∶DOPS (1∶1∶1). (A) Adsorption isotherm of amphiphysin 1 on GUV. The amphiphysin density, Φ_ν, deduced from the fluorescence signal, as a function of the protein bulk density C_bulk. Data are fitted with Φ_v = Φ_max/(1 + K_d/C_bulk) with Φ_max = 3,000 μm^-2 and K_d = 35 nm (error bars correspond to standard deviation. N = 6 vesicles for each point). (B) For C_bulk < K_d, the amphiphysin signal (green) is undetectable on the GUV, the fluorescent lipid signal is in red, and amphiphysin is visible on the tube. (C) At high C_bulk (here equal to 1 μM) amphiphysin binds to the GUV and forms tubes rich in amphiphysin (green fluorescence). (Scale bar: 5 μm.)

Based on these observations, we quantitatively study how the curvature-sensing and amplifying capabilities of amphiphysin 1 depend on the GUV density. We first consider low protein densities.

Low-Density Regime.

We consider here Φ_v ≲ 1,000 μm^-2. The nanotube curvature was controlled using a technique developed recently in our laboratory that enables measuring the tube pulling force at a given tension, σ, fixed by micropipette aspiration (20, 21), and the tube composition using confocal microscopy (16, 17). For a single-component membrane in the absence of protein, the tube radius R_t is given by 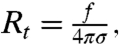where 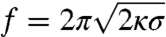is the pulling force on the tube and κ is the bending rigidity (22). R_t ranges from 7–10 nm up to a few 100 nm. A GUV was aspirated at low tension (ca. 10^-5 N/m) and a tube was pulled with an optically trapped bead bound to the GUV. The tension was then increased step by step. The force f was found to vary linearly with 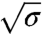(open symbols in Fig. 2A), consistent with ref. 22. From the slope, we deduced κ = 12 ± 2 k_BT, where k_B is Boltzmann’s constant and T the temperature. Once at high tension (ca. 10^-4 N/m), the injection pipette containing the amph1* solution was brought close to the GUV; the injection flow was low enough not to perturb the force measurement (see SI Text and Fig. S3). The aspiration pressure was kept constant until the amph1* fluorescence signal on the membrane equilibrated (typically 5–10 min). The tension was then decreased stepwise under continuous protein injection, with a waiting period of 1–2 min to reach mechanical equilibrium. The fluorescence intensities and force were then recorded.

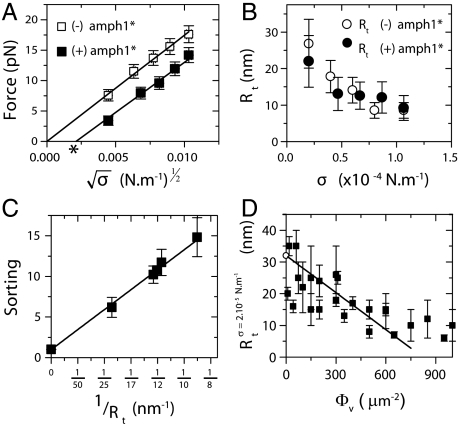
Fig. 2.

Low-density regime. (A) Force curve shift due to amphiphysin binding in the low-density regime. Here, Φ_v = 280 ± 100 μm^-2. The force is lower with protein (▪) than without (□). Data are fitted to 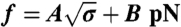, where A = 55 ± 2 pN^1/2·nm^1/2 and B = 0 without protein and A = 52 ± 2 × pN^1/2·nm^1/2 and B = -3.5 ± 2 pN with protein. (B) The radius, R_t, versus tension, σ, with protein (○) or without (●). Radius is deduced from fluorescence. (C) Linear variation of the sorting ratio as a function of 1/R_t. Data correspond to five independent experiments. A fit using Eq. 3 gives 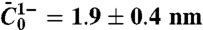. (D) Variation of R_t, at fixed tension σ = 2 × 10^-5 N/m, versus Φ. The data are fitted to R_t = 32 - (38 ± 5) × 10^-3Φ_v nm (line), as deduced from Eq. 2. Round symbol corresponds to expected radius for a 10 k_BT membrane (32 nm).

Changes in the forces are a first way to probe mechanical action of the protein on the membrane. From Fig. 2A, we see that the force drops in the presence of protein, but still varies linearly with 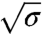, as it does in the absence of protein; in addition, the slope decreases and there is a nonzero intercept, σ^∗. As a second way to probe the effect of protein on membrane mechanics, we measured the tube radius in the presence of bound amph1*. Our setup provides two methods to determine the radius. First, one can calculate it from the force and tension measurement (see above). This relation, however, should be used with caution because it might be modified in the presence of protein; see below. The second method is a direct, model-independent determination based on the lipid fluorescence of the tube, which is proportional to the radius, R_t. By normalizing the lipid fluorescence of the tube by the fluorescence of the GUV, and considering that the dye is homogeneously distributed in the membrane, we can estimate directly the tube radius (see SI Text). We first verified that, with no protein, both measurement techniques give, within experimental error, the same value of the radius at several different tensions (Fig. S4). In Fig. 2B, we show that, after protein injection, the radius is lowered, but still decreases with increasing tension. Thus, we find that the reductions of the force and the radius in the presence of amph1* are clear indications of the membrane-deforming abilities of this protein.

Next, to quantify the curvature-sensing ability of amph1*, we measured the protein sorting ratio, 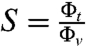, where Φ_t is the protein density on the tube (see Materials and Methods). Based on Fig. 1B, we expect a dependence of S on curvature (1/R_t). In Fig. 2C, we observe a strong protein enrichment on the tube, which increases with curvature.

The affinity of amphiphysin 1 for curved membranes results from the lowering of the membrane bending energy upon binding to the outer leaflet, which can be described in terms of membrane spontaneous curvature (7, 10, 13). At low protein densities, we assume that proteins bind to the membrane independently of each other, giving rise to a spontaneous curvature proportional to the protein area fraction 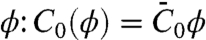(6, 13), where 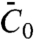is the effective spontaneous curvature of the protein at the molecular level. 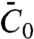does not correspond directly to the shape of the N-BAR domain; it is determined by the interplay of α-helix insertion and binding of the concave face of the dimer to charged lipids (23) underneath. Note that the protein area density, Φ, is related to ϕ by Φ = ρϕ, where ρ is the inverse of the area per protein. The free energy of the tube, consisting of bending and protein entropy of mixing terms, is approximated for small differences Δϕ = ϕ_t - ϕ_v between the protein area fractions on the tube and GUV (see SI Text and Fig. S5 for more details) as

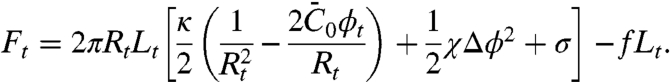[1]

In Eq. 1, L_t is the tube length and 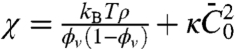, given approximately in the low-density regime by 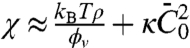. We note that the entropic stiffness 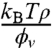is complemented by a term coming from the spontaneous curvature. The tube radius and force are obtained by minimization of F_t with respect to R_t and L_t, yielding

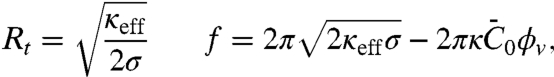[2]

where 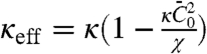Finally, minimization with respect to ϕ_t gives the relative enrichment of protein in the tube over the vesicle; the sorting 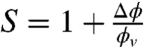is thus given by

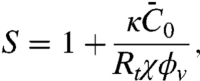[3]

which increases linearly with 1/R_t.

Based on our model, we now discuss quantitatively the mechanical effects of amph1* binding on tubes. First, the spontaneous curvature has an effect on the force at low densities. Theory predicts a linear relation between the force and 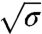, in agreement with our experiments (see Fig. 2A). From a fit of Fig. 2A to Eq. 2, we extract σ^∗ and κ_eff. Indeed, from Eq. 2, we expect that for small ϕ_v the force vanishes at 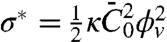. In Fig. S6A, we plot σ^∗ versus 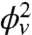; a linear fit yields 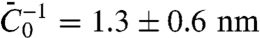. For small values of ϕ_v, we expect that the effective bending rigidity varies as 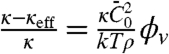. In Fig. S6B, we plot 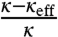versus ϕ_v, yielding 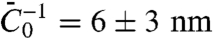. Second, we see from Fig. 2D how the tube radius is modified by protein binding. Fig. 2D shows that, at fixed tension, the radius decreases with Φ_v. Based on our model, the spontaneous curvature causes a lowering of the radius. Consistently, for small values of ϕ_v Eq. 2 gives 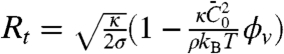. We use this expression to fit the radius data in Fig. 2D for Φ_v < 600 μm^-2, giving .

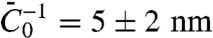We next compared our theoretical prediction of the protein sorting with the experimental data, for Φ_v = 280 ± 100 μm^-2. We have fitted Eq. 3 to Fig. 2C, which provides another value of the spontaneous curvature, 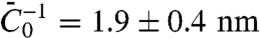, for which we have used ρ ≈ 1/50 nm^-2 and have neglected the entropic part of χ. Thus, at low protein densities, we see that protein enrichment on the tube and mechanical effects are simultaneously observed. By comparing our theory with experiments, we are able to extract an estimate of the mechanical parameter 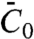that characterizes the deformations caused by amphiphysin 1.

To further understand the low-density regime, we investigated the dilute limit, corresponding to densities on the GUV indistinguishable from the background level (we used the amplitude of the background noise intensity for an overestimate of Φ_v, ref. 24, ≲100 μm^-2). In this case, Fig. 1B shows that amph1* is enriched on the tube, but is undetectable on the GUV. We observed furthermore that upon protein injection and adsorption there was no detectable change in the dependence of f on 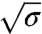(see Fig. 3A, filled symbols). Because our force resolution is limited to 1 pN, any changes in the force due to protein binding must be less than this value. This result on the force is consistent with the dilute limit of Eq. 2, in which the protein effect on the force vanishes. We also see from our fluorescence data (Fig. 3B) that, within experimental error, protein binding in the dilute limit has no detectable influence on the radius. In addition, there is no measurable difference between the radius calculated from the force (R_t^force) and from direct fluorescence measurements (R_t^fluo) (Fig. 3B). Thus, we find that, in this limit, the binding of amph1* has no detectable effect on membrane tube mechanics, as predicted by a limiting case of our model.

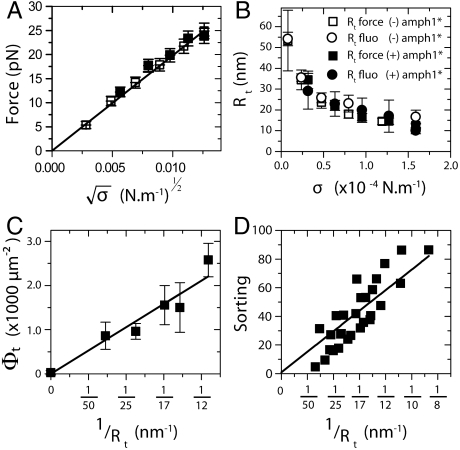
Fig. 3.

The dilute limit. The results presented in this figure correspond to a single GUV with Φ_v < 50 μm^-2. (A) No difference between the tube force as a function of 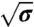with protein (□) or without (▪). The linear fit to the force, 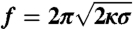, gives κ = 12 ± 2 k_BT. (B) The radius, R_t, versus tension, σ, with protein (empty symbols) or without (full symbols). Radius is deduced either from fluorescence (round symbols) or from force (square symbols) measurements. (C) Amphiphysin density on the tube, Φ_t, versus tube curvature, 1/R_t. R_t was found from force measurements. A linear fit yields Φ_t = A/R_t μm^-2, where A = 29 ± 2 μm^-1. (D) Linear variation of the sorting ratio as a function of 1/R_t. Data correspond to five independent experiments. A fit using Eq. 4 gives .

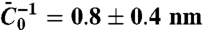In contrast, the dilute limit of our model predicts a finite relative enrichment of protein on the tube versus that on the GUV. In this limit, S (see Eq. 3) is given by

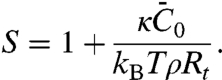[4]

An important consequence of Eq. 4 is that protein sorting is independent of ϕ_v, in contrast with the mechanical effects of protein binding, which vanish as ϕ_v tends to zero.

In Fig. 3C, we find a linear dependence of Φ_t on tube curvature, and importantly in Fig. 3D a strong sorting signal that is linear with curvature. We have fitted the theoretical sorting expression, Eq. 4, to data compiled from five different vesicles (Fig. 3D). To estimate the parameter 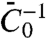from Fig. 3D, we used κ = 12 k_BT, which gives 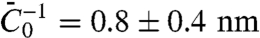. We remark that this value is of the same order of magnitude as that obtained theoretically for α-helix insertions in bilayers (13).

We thus conclude that, in the dilute limit, bound amph1* density is sensitive to curvature, yet has no detectable mechanical effect on the tube; it behaves mainly as a curvature sensor.

High-Density Regime.

We consider next Φ_v ≳ 1,000 μm^-2. In this regime, we observe significant labeling of amph1* on both the tube and the GUV (Fig. S7A). Similar to the low-density regime, after protein injection there is a downward shift in the force compared with that in the absence of protein; see Fig. 4A, where Φ_v = 1,100 ± 200 μm^-2. However, in striking contrast with the force at low densities, the force scales linearly with σ, instead of with 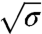(Fig. 4A and Fig. S8). The tension at which the force vanishes, σ^∗, reaches values up to four times higher than in the low-density regime, (see Fig. S9 in which Φ_v ≈ 2,000 μm^-2 and 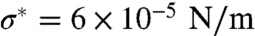). When the tension is decreased below σ^∗ and the optical trap is turned off, the tube does not retract (Fig. S7B).

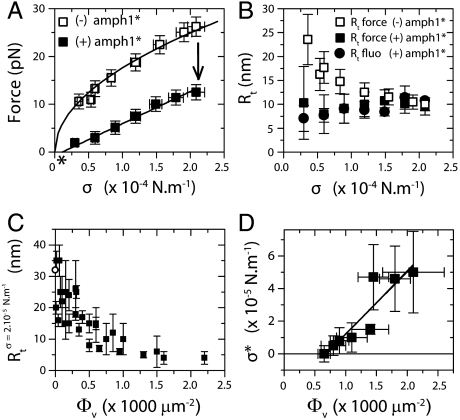
Fig. 4.

High-density regime. The experiments presented in A and B correspond to a single GUV with Φ_v = 1,100 ± 100 μm^-2. (A) The force is lower with protein (▪) than without (□). Force data without protein are fitted to 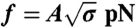, where A = 56 ± 1 pN^1/2 nm^1/2, and without to f = B(σ - σ^∗), where B = 67 ± 4 nm and σ^∗ = (1.0 ± 0.9) × 10^-5 N/m (the asterisk denotes σ^∗). (B) R_t versus σ with no protein (empty symbols) and with protein (full symbols). The radius is found from fluorescence (round symbols) or from force (square symbols) measurements. With no protein, the radius was determined from the force according to R_t = f/4πσ; in its presence, the radius was found using R_t = f/2πσ. (C) R_t as a function of Φ_v, as measured by fluorescence. (D) Tension at zero force, σ^∗, versus Φ_v. Data were fitted to Eq. 6, neglecting the logarithmic term, σ^∗ = AΦ_v + B, where A = (4 ± 1) × 10^-8 Nm^-1 μm^-2 and B = (-2.7 ± 1.4) × 10^-5 Nm^-1.

Given that the force on the tube is strongly affected by amph1* in the high-density regime, we expected that the tube radius should also change markedly. We measured the radius in the high-density regime using the lipid fluorescence method described above. After injection, as the tension was then lowered, the radius remained constant, at roughly 7–10 nm (full circles in Fig. 4B), in contrast with the increase in radius with decreasing tension for bare tubes (empty symbols in Fig. 4B). Our fluorescence measurements on seven different tubes in this regime, corresponding to different values of Φ_v, show that, on average, the radius is equal to 7 ± 2 nm; see Fig. 4C.

In this regime, the density of amph1* bound to the tube, Φ_t, is also quasi-constant: It rapidly saturates with tension (Fig. S9C) and reaches values higher than the saturation density on the GUV, Φ_max, of the order of 4,000–6,000 μm^-2. These density values are summarized in the SI Text (Table S1), together with the densities on the GUVs, showing an enrichment of amph1* on the tube relative to the GUV, but weaker than for the narrowest tubes in the dilute limit; see Fig. 3C.

The scaling of the force with tension and our radius measurements in the high-density regime cannot be explained with the model used in the low-density one, in which protein–protein interactions were neglected; this suggests that they play an important role in this regime, as in ref. 17. The importance of protein–protein interactions is supported by several lines of evidence. First, electron microscopy has revealed that N-BAR domains form striations on tubules, suggestive of higher-order oligomerization (4). Polymerization mediated by interactions between N-terminal helices has been observed in F-BAR domains, a related family of protein module (25). It is thus expected that these N-terminal helix-mediated interactions are important in proteins containing the N-BAR domain, as predicted by simulations (12). In our experiments, the independence of tube radius on tension (Fig. 4B) suggests that proteins reorganize into a scaffold-like structure whose radius is imposed on the tube. To verify this hypothesis, we performed fluorescence recovery after photobleaching (FRAP) experiments on tubes coated with amph1* in the high-density regime. Results are shown in Fig. S10. On the tube, no recovery is seen 5 min after bleaching, confirming interactions between amphiphysin dimers. On the contrary, a rapid recovery is seen when FRAP was performed on the same GUV, indicative of different organization of proteins on the GUV than on the tube, associated with the difference in area density. Based on this evidence, we have developed a theoretical model of tube mechanics at high densities in which the radius is fixed by protein–protein interactions, an approach which has been successfully applied to dynamin polymerization around membrane tubes (17).

Here, we assume that the bulk concentration is high enough that all negatively charged lipids on the GUV and tube are protein bound; thus, as the tension is varied during the experiment, there may be exchange of proteins between the tube and the GUV, but no exchange with the bulk solution. We also assume that proteins in the tube are in a condensed phase with a well-defined bound area fraction, ϕ_t. In this regime, the tube free energy is

[5]

where R_a is the constant tube radius, fixed by the protein scaffold; W is the enthalpy density that includes membrane bending and protein–protein interactions; and f_m is the protein mixing entropy density; see SI Text. The force can be found by minimization of the free energy with respect to tube length; the system consisting of the pipette-aspirated tongue, the vesicle, and the tube is subjected to the constraints of total membrane area and total number of bound proteins (see SI Text). When the length of the tube is altered, it is assumed that the concentration on the tube remains unchanged. We may show then that (see SI Text) the force may be expressed as

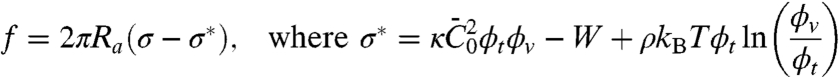[6]

defines the tension below which the tube is stable under no force. In this expression, the first term comes from the gain in elastic energy in transferring proteins from an energetically unfavorable situation on the vesicle to the tube; the second comes from the gain in enthalpy; and the last term comes from the entropy penalty in further enriching protein on the tube. From this analysis, for tensions significantly greater than σ^∗, it follows that the radius is 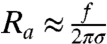. In Fig. 4B, we show the radius as a function of tension as measured by fluorescence and as calculated from the pulling force, and both are in good agreement. Importantly, we are able to measure the protein’s ability to stabilize membrane tubes as a function of protein density on the GUV, as given by σ^∗; see Fig. 4D. Neglecting the small logarithmic term in Eq. 6, a linear fit to Fig. 4D yields 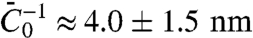, where the value of Φ_t used is the average over all vesicles, equal to 5,000 μm^-2 (See Table S1). We thus see that, although the tube radius is fixed by the protein scaffolding, the pulling force is influenced by the quantity of protein on the vesicle.

Discussion

Prior studies of amphiphysin 1 binding to membranes assessed the deforming ability of the protein by comparing wild-type and mutated forms (3–5), often with curvature sensing and curvature inducing separately occurring (26). We have shown in this study that amphiphysin 1 can act as a curvature sensor and a curvature inducer simultaneously, for a wide range of densities. Moreover, by varying the protein density, and without performing any mutation, the relative strength of curvature sensing and amplifying can be tuned: At very low densities, this protein mainly senses curvature, whereas at high densities, it strongly deforms membranes by forming a scaffold-like structure around tubes. We note that similar scaffolding behavior on tubes has been measured for dynamin (17).

In the high-density regime, we have measured the tube radius, R_a, using fluorescence and force measurements to be 7 ± 2 nm. Within experimental precision, this measurement compares well with the internal radii of amphiphysin-covered membrane tubules studied in vitro by electron microscopy (4). Though our measurement of R_a is close to the radius of curvature of the N-BAR dimer, in general the radius depends strongly on the type of organization that occurs on the membrane; simulations find radii varying between 13 and 80 nm, depending on the packing arrangement (12).

With our experimental approach, we have been able to evaluate, from five independent measurements, the effective spontaneous curvature, 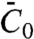, of amphiphysin 1. We emphasize here that 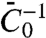is not the same as the tube radius R_a measured in the high-density regime, nor is it the spontaneous curvature measured in ref. 27. This parameter determines the relative enrichment of protein on the tube in the dilute limit. Furthermore, it is the mechanical parameter of the protein that controls the curvature amplification by the protein in the low-density regime, in which interactions between proteins can be ignored. In this regime, the deformation of the tube by proteins can be described completely by 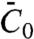, without recourse to a detailed knowledge of the structure of the protein. We found that, even in the high-density regime, the pulling force depends on 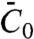, because the tube is connected to a large vesicle on which the interaction between protein and membrane is governed by 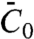. We found that the five values of 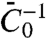, obtained using force and fluorescence measurements, spanned over three decades in GUV density, were all of the same order of magnitude (on the order of 3 nm).

The exact role of the N-BAR domain has been intensively discussed in the past due to its particular structure. The crescent shape was thought to either mold the membrane or bind to highly curved membranes, in both cases the membrane curvature matching the shape of the protein. Our study gives a different view of the membrane–N-BAR domain interaction: That amphiphysin 1 binds to a wide range of membrane curvatures and that the degree of membrane deformation depends on the protein density argues against the protein solely deforming the membrane through a sculpting action. Instead, at low densities, the mechanical action of the protein on the membrane depends on 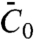and on the GUV density Φ_v. Beyond a certain protein density, the tube radius no longer depends on the GUV density, and interestingly, the corresponding density on the tube is well below the close-packing value, suggesting that lateral interactions between the protein terminal helices play an important role in creating the scaffold-like structure on the tube. The existence of such lateral interactions between the N-terminal amphipathic helices of N-BAR domain proteins has been demonstrated recently using Förster resonance energy transfer in ref. 28.

Our in vitro study can help shed light on in vivo results. When moderately overexpressed, most BAR proteins do not bind strongly to the plasma membrane and have a diffuse cytosolic staining (3, 29, 30). However, if the protein density on the membrane is increased under strong overexpression, numerous tubules are observed (3), pointing to a membrane-shaping function. A specific case of membrane shaping is that of muscular amphiphysin 2 (M-Amph2), a splice variant of amphiphysin 1 with an additional membrane-binding domain, which has been reported to play a critical role in the formation of tubular invaginations (T-tubules) in striated muscle cells (29, 31). Interestingly, when wild-type fluorescent M-Amph2 is expressed in nonmuscle cells, strong labeling on the plasma membrane and tubule formation are observed; however, deletion of a specific domain binding to PIP₂ (exon10), a lipid concentrated in the plasma membrane, suppresses plasma membrane labeling and tubulation (29). This suggests that this domain induces stronger membrane-protein interactions, thus a higher protein density on the plasma membrane and tubulation. These in vivo experiments compare well with our in vitro results and illustrate that the cell control of bulk protein concentration and binding affinity determines whether BAR proteins act mainly as a curvature-sensing or membrane-shaping agent. In the case of amphiphysin 1, it has been shown that this protein binds to the highly curved necks of clathrin-coated pits just prior to vesicle scission, with no detectable binding on the surrounding flat membrane prior to the event (32). Our results favor the hypothesis that, in endogenous conditions, amphiphysin 1 acts predominantly as a curvature sensor and not as a scaffolding agent.

Materials and Methods

Giant Unilamellar Vesicles.

All the data presented in this study have been obtained with GUVs having the same lipid composition: DOPC∶DOPE∶DOPS (1∶1∶1) + 0.03% di-stearoyl phosphatidyl ethanolamine-PEG(2000)-Biotin (Avanti Polar Lipids, Inc.) and 0.5% BODIPY TR ceramide (Cer* Invitrogen). To obtain yields with this composition containing a high amount of negatively charged lipids, we adapted the electroformation protocol described in ref. 33. Ten microliters of lipid mix at 0.5 mg/mL was dried on conductive indium-tin oxide coated glass (Präzisions Glas and Optik, GmbH) for a few minutes at 60 °C then under high vacuum for at least 1 h. The lipid film was then rehydrated in a sucrose solution (osmolarity 100–300 mOsm) and GUVs were allowed to grow for 30 min under a sine voltage (850 mV, 10 Hz).

Force and Tension Measurements.

Our experimental setup has been described elsewhere (16). The force f exerted by the tube was found from the displacement of the bead x - x₀ from its equilibrium position x₀ in the optical trap using the linear relationship f = k(x - x₀), where k is the trap stiffness. The bead position was measured off line by video tracking (21) and k was determined by the viscous drag method (34). The membrane tension σ was determined using 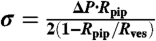, where R_pip is the pipette radius, R_ves the vesicle radius, and ΔP is the difference of hydrostatic pressure caused by the vertical displacement of the water reservoir connected to the pipette (20).

Protein Density on the Tube.

To measure the protein densities on the membrane, we used a fluorescence calibration method adapted from ref. 18. The amphiphysin density on the GUV,Φ_v, is given by 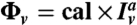, where 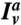is the fluorescence signal on the GUV coming from labeled amphiphysin, and cal is an experimentally measured conversion constant. The protein density on the tube Φ_t is given by 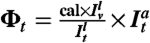, where 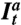, , 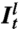and 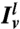are the fluorescence intensities per pixel of amph1* on the tube, of the lipid Cer* on the tube, and of Cer* on the GUV. The lipid intensities are used here to eliminate geometric factors (see SI Text and Fig. S1).