Accurate van der Waals coefficients from density functional theory

Abstract

The van der Waals interaction is a weak, long-range correlation, arising from quantum electronic charge fluctuations. This interaction affects many properties of materials. A simple and yet accurate estimate of this effect will facilitate computer simulation of complex molecular materials and drug design. Here we develop a fast approach for accurate evaluation of dynamic multipole polarizabilities and van der Waals (vdW) coefficients of all orders from the electron density and static multipole polarizabilities of each atom or other spherical object, without empirical fitting. Our dynamic polarizabilities (dipole, quadrupole, octupole, etc.) are exact in the zero- and high-frequency limits, and exact at all frequencies for a metallic sphere of uniform density. Our theory predicts dynamic multipole polarizabilities in excellent agreement with more expensive many-body methods, and yields therefrom vdW coefficients C₆, C₈, C₁₀ for atom pairs with a mean absolute relative error of only 3%.

The van der Waals interaction (1) is a long-range attraction between chemical species, arising from instantaneous charge fluctuations on each. This interaction is present even when there is no chemical bond, and even when each species has no permanent multipole moment. Its significance first came to light when van der Waals (vdW) (2) formulated the equation of state for real gases and liquids in 1873 by taking this correlation effect into consideration. The vdW interaction is much weaker in strength than a normal chemical bond, but it has important effects on the properties of materials (3). For example, it is responsible for many phenomena such as sublimation of iodine, naphthalene, dry ice, and other organic molecules, high interlayer mobility of graphite, foldings of long biomolecular chains such as DNA, RNA, proteins, polymers, etc. The vdW interaction has been extensively studied (4, 5) on account of its ubiquity and importance for soft matter relevant to human activity. Many theoretical methods, including CI (6, 7) (configuration interaction), MBPT (8) (many-body perturbation theory), coupled cluster (9) methods, or their combinations such as CI+MBPT (10, 11), have been developed to estimate this effect. These methods are highly accurate (within about 1%) but computationally expensive. A cheap but usefully accurate method is density functional theory (12) (DFT). While this theory has achieved a high level of sophistication and has become the mainstream electronic structure theory, it often fails in practice to describe vdW systems, because the long-range part of the vdW interaction is absent in commonly used DFT approximations [e.g., (13–15)].

In the large separation limit of two spherically symmetric interacting densities A and B, second-order perturbation theory yields the (nonretarded) potential energy E_vdW, which can be expressed as a power series (16),

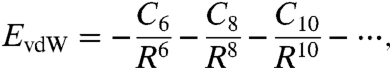[1]

where R is the separation between centers, C₆ describes the instantaneous dipole-dipole interaction, C₈ the dipole-quadrupole interaction, and C₁₀ the quadrupole-quadrupole and the dipole-octupole interactions. [Note that, if higher-order perturbation theory is employed, odd-order terms C_2k+1R^-(2k+1) appear (17) in the power series of Eq. 1 for k≥5.] This series is obviously divergent as the internuclear distance of two atoms tends to zero, where the true vdW (or dispersion) energy remains finite. To fix this problem, each term of the series, C_2kR^-2k, may be multiplied by a damping function f(R), which suppresses the singularity at R = 0. Several such damping functions have been proposed [e.g., (18–20)]. The intermolecular or atom-pair potential energy is obtained as the sum of two contributions: the large part obtained from ordinary DFT methods and the small part which accounts for the vdW interaction. Therefore, in the simulation of intermolecular potentials, the main task is to find a simple and yet accurate way to evaluate these vdW coefficients C_2k. Many efforts [e.g., (21–24)] have been devoted to the study of the leading coefficient C₆, while higher-order coefficients C₈ and C₁₀ are less investigated. There are two good reasons for this fact. First, unlike C₆, these higher-order coefficients essentially cannot be measured directly by experiments (25) and calculation of them is much more difficult (*). Second, it was believed that the higher-order contribution is small in comparison to the leading term [only 20% of the leading term (26)]. So, the vdW potential energy is often truncated to the leading term, -C₆R^-6. However, a detailed study (23) of vdW effects on the lattice constant and cohesive energies of alkali metals shows that the higher-order contributions can be as large as 50% of the leading term, consistent with an analysis of ref. 27. This study suggests that higher-order contributions cannot be neglected in the evaluation of the vdW effect. A simple and yet accurate evaluation of these higher-order coefficients is of strong interest in many branches of science such as chemistry, physics, materials science, molecular biology, drug design, etc. Several models (28, 29) were proposed to estimate these higher-order coefficients. However, none of these models is satisfactory. For example, an empirical model (29) with the static multipole polarizability as input has achieved good accuracy for higher-order vdW coefficients, but at the cost of introducing additional empirical parameters beyond those used for C₆. A disadvantage of empirical models is that the physics behind the models is neither transparent nor transferable from one case to another, due to empirical fitting. A nonempirical model was proposed (28), without any empirical parameter beyond the static dipole polarizability. Although an excellent accuracy was achieved with the model for C₆, the errors for C₈ and C₁₀ significantly increased (to 20%) from that for C₆ (3%).

Nonempirical Model for the Dynamic Multipole Polarizability

We have developed a method for systematic calculations of higher-order vdW coefficients C₈, and C₁₀, on the basis of a simple generalization of an approach (23) for C₆. The only needed input is the electron density and the static multipole polarizabilities of an atom, without empirical fitting. The contribution from second-order perturbation theory to the vdW coefficient C_2k [the whole contribution (17) for C₆, C₈, and C₁₀]for two spherically-symmetric densities can be expressed (30) exactly as an integral over u of the product of the dynamic multipole polarizabilities α_l(iu) for l ≤ k - 2, for each density; i.e.,

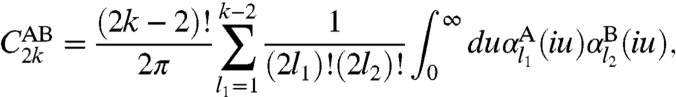[2]

where l₂ = k - l₁ - 1, 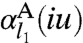is the 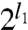-pole dynamical polarizability of system A, and 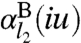is the 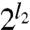-pole dynamical polarizability of system B: l = 1 (dipole), 2 (quadrupole), 3 (octupole), etc. Here iu is an imaginary argument that replaces the real frequency ω. For C₆ , only the dipole polarizabilities are needed, while C₈ requires also the quadrupole polarizabilities, etc. For simple frequency dependences, the integral over frequency can be evaluated analytically.

All the properties of a many-electron system are functionals of the ground-state density n(r) (12), although some like the dynamic multipole polarizabilities α_l(iu) cannot be found from the density functional for the ground-state total energy. Here we will model the nonlocal density functionals for the dynamic multipole polarizabilities in a way that is exact in the zero- and high-frequency limits. The model interpolates between those limits in a way that is exact for a paradigm density from textbooks on classical electromagnetism: the metal sphere of uniform density. Because the u-dependence of α_l(iu) is simple, our formula transfers with little error from the paradigm density to the density of a real atom.

Let us consider a metallic sphere of uniform density, with radius R (small enough to neglect retardation), in empty space. The dynamic multipole polarizability of the sphere is given by (31)

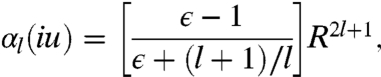[3]

where ϵ is the dielectric function of the sphere. By setting 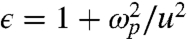, we find

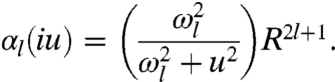[4]

Here ω_l is the multipole resonance frequency of the sphere given by 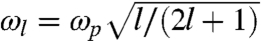, with 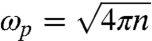being the plasmon frequency of the extended uniform electron gas and n being the electronic density of the sphere under consideration. A familiar limit of Eq. 4 is the static dipole polarizability R³.

Next we make a nonempirical model for α_l(iu) in terms of the electron density, by imposing exact constraints on a simple expression. First, we demand recovery of the correct zero-frequency limit α_l(0). Second, we demand recovery of the correct high-frequency (u → ∞) limit (29, 32),

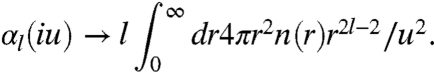[5]

Third, we make our expression exact (31, 33, 34) for a classical metallic sphere of uniform density inside and zero density outside a radius R [see Eq. 4]. Taking all three conditions into consideration, our model dynamic multipole polarizability of any spherical density is expressed as

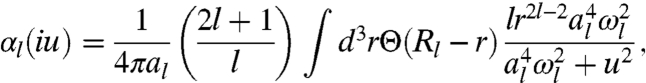[6]

where Θ(x) is a step function: Θ(x) = 1 for x > 0, and Θ(x) = 0 for x ≤ 0. The metallic sphere has a natural sharp cutoff of all integrals over r , which we extend even to the diffuse density of an atom (^†). Unbiased sharp cutoffs are also used in the construction of nonempirical density functionals for the exchange-correlation energy (35–37) and a model dynamic dipole polarizability (38). The parameter a_l and the cutoff radius R_l are determined by the two imposed constraints. According to the static limit condition, we have

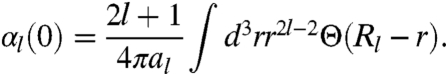[7]

Without the cutoff, the right-hand side of Eq. 7 would diverge. For spherically-symmetric systems, the radial cutoff is

[8]

Imposing the high-frequency limit of [5] leads to

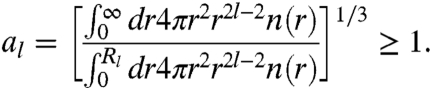[9]

For a metallic sphere of uniform density with radius R, we find a_l = 1 and R_l = R. Then Eq. 6 correctly reduces to Eq. 4. Because Eqs. 8 and [9] and are coupled together, they must be solved self-consistently. The results are displayed in Table 1. From Table 1 we see that there is a relationship among the parameters a_l: a₁ < a₂ < a₃. This ordering arises because, if we keep the same cutoff radius for different order l, the denominator will get smaller relative to the numerator as l increases, due to the cutoff. One desired feature of the present model is that, for l = 1, our expressions Eqs. 6, [7], and [9] reduce to those of our earlier model (23).

Table 1.

Static multipolar polarizabilities α_l(0) and cutoff radii R_l (both in atomic units), and parameters a_l of atoms

Atom	α1(0)	α2(0)	α3(0)	R1	R2	R3	a1	a2	a3
H	4.50(a)	15.0(a)	131.25(a)	1.726	1.856	2.194	1.143	1.469	1.863
He	1.38(b)	2.331(d)	9.932(d)	1.155	1.268	1.508	1.116	1.405	1.784
Ne	2.67(b)	7.33(e)	42.1(e)	1.409	1.545	1.794	1.047	1.200	1.422
Ar	11.1(b)	51.84(f)	534.85(f)	2.249	2.277	2.564	1.025	1.180	1.364
Kr	16.8(b)	98.43(f)	1269.6(f)	2.571	2.574	2.892	1.012	1.149	1.332
Xe	27.4(b)	223.3(e)	3640.6(e)	3.023	3.020	3.348	1.008	1.124	1.296
Li	164.1(c)	1424(g)	39688(g)	5.507	4.526	4.888	1.018	1.333	1.680
Na	162.6(c)	1878(g)	55518(g)	5.470	4.719	5.128	1.006	1.246	1.679
K	290.2(c)	5000(g)	176940(g)	6.629	5.682	6.033	1.004	1.184	1.645
Be	37.8(b)	299.9(d)	4765(d)	3.401	3.298	3.590	1.041	1.301	1.613
Mg	71.7(b)	845.4(d)	16772(d)	4.171	4.007	4.276	1.012	1.222	1.559
Ca	158.6(b)	3083(e)	65170(e)	5.425	5.143	5.190	1.007	1.168	1.557 *

For the H atom, the Bohr radius is 1.00, a conventional vdW radius is α₁(0)^1/3 = 1.65, and the classical turning radius is 2.00

^*(a) From ref. 43. (b) From ref. 44. (c) From ref. 45. (d) From ref. 46. (e) From ref. 8. (f) From ref. 47. (g) From ref. 48.

The central idea described in the previous paragraph is parallel to the one that has been used before to construct nonemprical density functionals for the exchange-correlation energy (14, 15, 39): Make the functional exact for a paradigm density, and satisfy other exact constraints for a broader class of densities of interest. We believe that our use of a paradigm density (the metallic sphere or “local density approximation” in the vdW DFT) is what leads to accurate higher-order vdW coefficients without empiricism.

Application to Atom-Atom-Pair Interaction

Dynamic Multipole Polarizability.

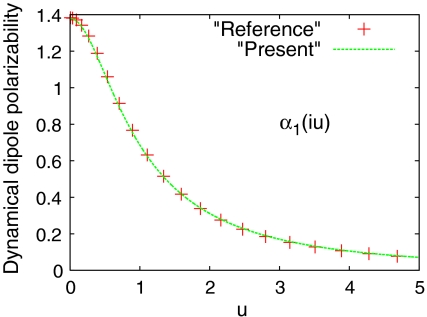
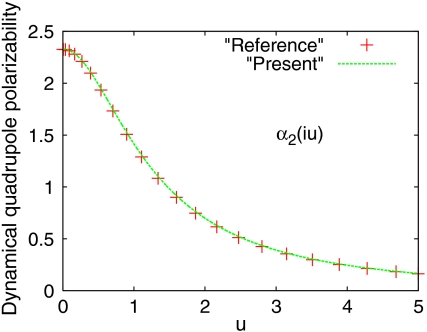
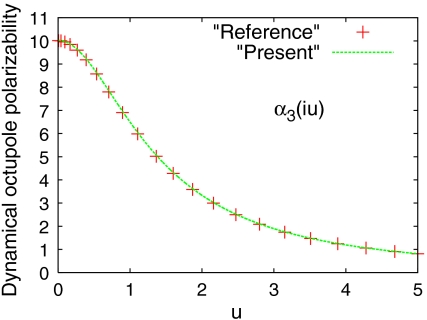
We apply the present model to calculate the dynamic multipole polarizabilities of the He atom and compare them to the corresponding reference values (16, 40) from high-level many-body calculations, as shown in Figs. 1–3. We observe from Figs. 1–3 that our model dynamic multipole polarizabilities are in excellent agreement with the reference values within the whole range of frequencies. We also apply the present theory to the H atom for which the exact dynamic multipole polarizabilities are available (41), and find that the deviation of the model dynamic polarizabilities from the exact ones is also indistinguishable (see Figs. S1, S2, S3).

Fig. 1.

Dynamical dipole polarizability α₁(iu) (in atomic units where e² = ℏ = m = 1) of the He atom: reference value (42) (red) and present model (green). ω = iu is the imaginary frequency.

Fig. 2.

The same as Fig. 1, but for quadrupole polarizability. Reference value is taken from ref. 16.

Fig. 3.

The same as Fig. 2, but for octupole polarizability.

vdW Coefficients.

Finally, we evaluate C₈ and C₁₀ of 78 diverse atom-atom-pair interactions by substituting the model dynamic multipole polarizabilities Eqs. 6, [8], and [9], into the exact expression [2]. (The explicit expressions for C₆, C₈, and C₁₀, and detailed numerical results, are given in the SI Text). The atoms selected in this study include rare-gas atoms (He, Ne, Ar, Kr, Xe), hydrogen and alkali-metal atoms (H, Li, Na, K), and alkaline-earth atoms (Be, Mg, Ca). For convenience, the static multipole polarizabilities as input data are tabulated in Table 1. The results are summarized in Table 2. The mean absolute relative error (MARE) is calculated as mean absolute relative deviation of the present theory from the reference values obtained from high-level many-body methods updated from those of ref. 23. Detailed information has been tabulated and displayed in SI Text, Table S1, Table S2, Table S3. From Table 2 we can see that the MARE remains almost the same for C₆, C₈, and C₁₀. In order to better understand the present theory, a comparison of the cutoff radii on the dipole, quadrupole, and octupole polarizabilities has been made. The results are displayed in Table 1. From Table 1 we observe that the cutoff radii are also close to each other for all three, and to a conventional vdW radii α₁(0)^1/3, as expected, because all cutoff radii equal the sphere radius R for a metallic sphere. Nearly the same MARE and cutoff radius strongly suggest that the main physics behind the model dynamic dipole polarizability correctly transfers to the model dynamic multipole polarizabilities. The theory described here is not limited to the dynamic multipole polarizabilities and the higher-order vdW coefficients studied here. In principle, the formulas of this paper generate dynamic multipole polarizabilities and vdW coefficients (arising from second-order perturbation theory) to any multipolar order with the same quality, due to the correct transfer of the physics from one order to another, and thus provide a nearly correct account of the vdW interaction. For a recent application of C₆, C₈, and C₁₀, see ref. 47. The present theory may be generalized to other systems with the static multipole polarizability tensors (42, 48) as input.

Table 2.

Mean absolute relative error of C₆, C₈, and C₁₀ based on 78 atom-atom-pair interactions calculated with the present theory

vdW coefficients	C6	C8	C10
Mean absolute relative error (%)	3.2	3.0	3.1

Conclusions and Outlook

We have formulated a unified theory for the dynamic multipole polarizabilities and vdW coefficients, and have achieved the same accuracy as for the leading-order coefficient C₆. Consistent accuracy is significantly important, because it guarantees that our model should also be able to describe other many-body vdW interactions (such as Axilrod-Teller-Muto three-body terms) as well. While the present theory considers only systems of spherical density, it can serve as a good starting point for extension to nonspherical densities, due to its excellent accuracy. One such extension would use the static multipole polarizability tensors (42) for the real nonspherical density as input to a generalization of our expressions that is exact for a finite metal of uniform density and similar nonspherical shape. Another such extension would write the real nonspherical density as a sum of effective atom densities (21, 22). For these effective atoms, only the densities and not the orbitals are directly available. Our expressions have the advantage that they require only the densities and not the orbitals. The second extension could in principle describe the vdW interaction between two separated molecules, or between two distant pieces of the same molecule (e.g., a polymer). Because the only needed input for the present theory is the electronic density and the static polarizabilities, which are accessible from the ground-state DFT (49, 50), we have in principle a true DFT approach for the dynamic multipole polarizabilities and vdW coefficients, and therefore may save a significant amount of computer time, compared to other methods including time-dependent DFT (51). Even without extension, the theory proposed here may be applicable to fullerenes (52) and other nearly spherical nanoparticles (53).