Abstract
This study investigates the longitudinal heritability in Thought Problems (TP) as measured with ten items from the Adult Self Report (ASR). There were ~9,000 twins, ~2,000 siblings and ~3,000 additional family members who participated in the study and who are registered at the Netherlands Twin Register. First an exploratory factor analysis was conducted to examine the underlying factor structure of the TP-scale. Then the TP-scale was tested for measurement invariance (MI) across age and sex. Next, genetic and environmental influences were modeled on the longitudinal development of TP across three age groups (12–18, 19–27 and 28–59 year olds) based on the twin and sibling relationships in the data. An exploratory factor analysis yielded a one-factor solution, and MI analyses indicated that the same TP-construct is assessed across age and sex. Two additive genetic components influenced TP across age: the first influencing TP throughout all age groups, while the second arises during young adulthood and stays significant throughout adulthood. The additive genetic components explained 37% of the variation across all age groups. The remaining variance (63%) was explained by unique environmental influences. The longitudinal phenotypic correlation between these age groups was entirely explained by the additive genetic components. We conclude that the TP-scale measures a single underlying construct across sex and different ages. These symptoms are significantly influenced by additive genetic factors from adolescence to late adulthood.
Electronic supplementary material
The online version of this article (doi:10.1007/s10519-011-9478-x) contains supplementary material, which is available to authorized users.
Keywords: Thought problems, Measurement invariance, Longitudinal study, Extended twin design, Heritability
Introduction
The Thought Problems (TP) scale is one of the empirically defined syndrome scales from the Achenbach System of Empirically Based Assessment (ASEBA), a widely used series of instruments for the assessment of mental health (Achenbach and Rescorla 2003) across different ages and raters. The TP-scale measures symptoms common in several mental disorders: hallucinations, OCD-symptoms, strange thoughts and behaviors, self-harm and suicide attempts. TP has been associated with psychiatric disorders such as OCD (Geller et al. 2004; Ivarsson et al. 2007), pediatric bipolar disorder (Diler et al. 2009), mania (Diler et al. 2008), 22q11 deletion syndrome (Sobina et al. 2009) and several psychotic features (Kasius et al. 1997). When considered together with the Rule Breaking syndrome scale from the ASEBA, TP is predictive for schizophrenia (Morgan and Cauce 1999). Together with the Somatic Complaints scale, the TP-scale can be predictive for mania or hypomania (Morgan and Cauce 1999).
The TP-scale has received less attention than the other subscales of the ASEBA. It is mainly comprised of low-prevalence items and is the subscale with the lowest internal consistency (Cronbach’s alpha = .51; Achenbach and Rescorla 2003). TP also has a relatively low long-term stability (.36 for a mean interval of ~3.5 years; Achenbach and Rescorla 2003). These features make the TP scale difficult to analyze, unless large sample sizes are available.
The heritability of TP has been estimated in children (4–16 years old) and ranged from .32 to .75, while shared environmental influences ranged from 0 (not detectable) to .21. Dominant (non-additive) genetic influences have not been reported for this age group (Edelbrock et al. 1995; Schmitz et al. 1995; Polderman et al. 2006; Abdellaoui et al. 2008; Lin et al. 2006; Kuo et al. 2004). These estimates were based on parental or teacher ratings of children’s behavior. The study with the largest sample size (~9,000 7-year old twin pairs) estimated the heritability at 61% and 65% for ratings from the twins’ mothers and fathers, respectively (Abdellaoui et al. 2008). This study also concluded that the rater agreement on TP between the parents was 67%, while the remaining 33% consisted of a unique view on the phenotype and/or measurement error.
The current study analyzes TP-data from self-reports in 12–59 years old subjects. It could be argued that, given the content of some of the items of the TP-scale, self-ratings might assess the phenotype differently. Since TP-scores seem to change more with age than scores of the other ASEBA problem scales, the influence of genes and environment may also differ from estimates obtained in children.
This study is conducted in a large sample of adolescent and adult twins and their family members, who between 1991 and 2010 took part in longitudinal survey studies. We first investigate whether the TP-scale assesses a single or multiple constructs through an exploratory factor analysis. Based on the outcome of this analysis, we test whether the TP-scale measures the same construct(s) across different ages and sex in measurement invariance (MI) analyses (Horn and McArdle 1992; Meredith 1993; Vandenberg 2000; Vandenberg and Lance 2000). This is important, because in order to consider genotype by sex and genotype by age interaction, it needs to be established that different patterns in familial resemblance in these groups are not caused by differences in measurement (Lubke et al. 2004). If the TP-scale is indeed measurement invariant, genetic and environmental influences on the longitudinal development of TP can be examined with data from monozygotic (MZ) and dizygotic (DZ) twins and their siblings.
Methods
Participants
Data came from the longitudinal survey study of the Netherlands Twin Registry (NTR), in which Dutch twins and their family members are assessed every 2–4 years since 1991 (Boomsma et al. 2002a). Details about sample selection and response rates are described in Boomsma et al. (2002a, 2006). We analyzed data from twins, siblings, offspring, parents and spouses collected in 1991, 1995, 1997 and 2009/2010. Data from twins were available at all time points, while for the other family members data were available for the surveys collected in 1997 and 2009/2010.
For the EFA and MI analyses, the sample was divided into three age groups (12–18, 19–27 and 28–59 year olds) and two sex groups, which resulted in six groups (3 age groups × 2 sex groups). For each subject one random measurement was chosen from the longitudinal dataset. Additional MI analyses (within age groups) were carried out analyzing data from twins. Here, one random measurement was chosen per age group (which could lead to twins being included in multiple age groups).
For the longitudinal genetic modeling, data from twin pairs and two additional siblings (brother and sister) were analyzed. The ages of subjects within each survey varied greatly, therefore the data were reorganized so that the longitudinal design was based on age intervals instead of survey intervals (Mehta and West 2000). The sample was divided into three age groups (12–18, 19–27 and 28–59 year olds). Multiple measurements for each subject were included, but only one measurement per age group (chosen at random).
For the EFA and MI analysis 15,320 subjects were included (twins and family members). Data from 9,067 twins were analyzed for the additional MI analysis (MI within age groups; 4,080 measurements in the first, 5,814 in the second, and 3,307 in the third age group). For the longitudinal genetic analyses, data from 11,107 subjects were included (8,446 subjects with one, 2,126 with two and 535 with three measurements). A breakdown by age group, sex and zygosity of all samples is given in Supplementary Tables 1 to 3.
DNA or blood group polymorphisms were used to determine zygosity for 38% of the same-sex twin pairs. For the other 62% zygosity was determined from surveys completed by parents and twins. The surveys asked questions regarding the resemblance of the twins and whether they were mistaken for each other as children by family members and strangers. When there was inconsistency across time or persons, the majority of the judgments determined the outcome. If there were inconsistencies between survey questions and DNA, the DNA zygosity was used. Correspondence between zygosity determined by survey questions and DNA was 98% if there were no (longitudinal or rater) inconsistencies in the parental and twin questionnaire reports, otherwise it was 97% (Willemsen et al. 2005).
Measures
Behavioral and emotional problems were assessed with the Adult Self Report (ASR; Achenbach and Rescorla 2003), which is part of the Achenbach System of Empirically Based Assessment (ASEBA). The ASR consists of 126 items. The TP-scale consists of 10 items (shown in Table 1). The items have three response categories: (0) not true; (1) somewhat or sometimes true; (2) very true or often true.
Table 1.
Frequencies of the item responses in samples from the EFA and MI analyses and the factor loadings as estimated in the EFA
| Frequencies of item responses (EFA + MI between age groups, i.e., all available subjects) | Frequencies of item responses (MI within age groups, i.e., twins only) | Factor loadings (EFA) | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 0 | 1 | 2 | ||
| 9: I can’t get my mind off certain thoughts | .59 | .33 | .08 | .59 | .32 | .09 | .52 |
| 18: I deliberately try to hurt or kill myself | .99 | .01 | .003 | .98 | .01 | .004 | .62 |
| 36: I accidentally get hurt a lot | .87 | .12 | .02 | .84 | .14 | .02 | .39 |
| 40: I hear sounds or voices that other people think aren’t there | .98 | .02 | .004 | .97 | .02 | .005 | .70 |
| 46: Parts of my body twitch/make nervous movements | .91 | .07 | .02 | .90 | .08 | .02 | .51 |
| 63: I would rather be with older people than people my own age | .66 | .29 | .05 | .62 | .32 | .06 | .38 |
| 66: I repeat certain acts over and over | .94 | .05 | .01 | .94 | .05 | .01 | .56 |
| 70: I see things that other people think aren’t there | .98 | .02 | .01 | .97 | .02 | .01 | .71 |
| 84: I do things that other people think are strange | .88 | .11 | .02 | .87 | .11 | .02 | .73 |
| 85: I have thoughts that other people would think are strange | .88 | .10 | .02 | .87 | .11 | .02 | .84 |
For the factor analyses (EFA and MI) item scores were analyzed. The Cronbach’s alpha was .57 in the complete sample of 15,320 individuals, which is slightly higher than .51 as reported in the ASEBA manual (Achenbach and Rescorla 2003). Missing items were handled with the weighted least square estimation (WLSMV) with missing data in Mplus (for the EFA and MI analyses), and the raw data maximum likelihood approach in Mx (for the additional MI analyses), allowing the use of all available data (Muthén and Muthén 2007; Neale et al. 2006b).
For the genetic modeling the log-transformed sum scores were analyzed only in subjects who had at most two missing items. If one or two items were missing, these were given the average value of the available items for an individual. Of the 14,303 measurements, there were 505 with 1 item missing (166 from age group 1, 179 from age group 2, and 160 from age group 3) and 146 with 2 items missing (22 from age group 1, 49 from age group 2, and 75 from age group 3). Including the individuals with (a) missing item(s) did not lead to a decreased variance.
Exploratory factor analysis (EFA)
The software package Mplus Version 5.21 (Muthén and Muthén 2007) was used to explore the factor structure of the TP-items in an exploratory factor analysis (EFA) for ordinal data with the WLSMV estimator. An underlying normal distribution was assumed for each item, where the three response categories are divided by two thresholds estimated from the data. Dependency among observations of family members was corrected for with the ‘complex’ option, which has shown to be effective in the context of family data (Rebollo et al. 2006). Mplus gives several descriptive model fit statistics to help determine how many common factors to include in the model to adequately account for the correlation among the item scores. In this study, model fit was evaluated with the root mean square error of approximation (RMSEA), because it performs well in factor models with categorical data and is robust to large sample sizes and model complexity (Yu 2002; Schermelleh-Engel and Moosbrugger 2003). An RMSEA value smaller than .05 is considered a good fit, between .05 and .08 an adequate fit, between .08 and .10 a mediocre fit, and values >.10 are not considered acceptable (Yu 2002; Schermelleh-Engel and Moosbrugger 2003). The decision for the factor model was based on parsimony, the eigenvalues and whether the fit was acceptable (good or adequate, i.e., the cutoff value of the RMSEA was .08).
Measurement invariance
An essential step in examining age and sex differences is testing for measurement invariance (MI) (Horn and McArdle 1992; Meredith 1993). MI was tested for the six age × sex groups with a multi-group confirmatory factor analysis (MGCFA) for ordinal data, assuming an underlying continuously distributed liability, which is subject to a series of thresholds that categorize the phenotype. For each item, two thresholds are estimated because there are 3 response categories (visualized in Supplementary Figure 1), meaning that the factor model is only indirectly connected to the measured variables. Flora and Curran (2004) showed that especially with large sample sizes, confirmatory factor analyses perform well with ordinal data.
Four models reflecting four levels of MI are tested that form a nested hierarchy and are represented by increasing levels of cross-group equality constraints. The first level of measurement invariance is configural invariance, which implies that the same factor structure holds for all six groups, but parameter estimates may vary across groups. Configural invariance is tested by fitting the hypothesized factor model in each of the age × sex groups separately and in a multigroup analysis of the total sample. If the model fits well, the next level of MI, metric invariance, is tested. Metric invariance means that the latent factor scores predict the item responses equally well across groups, i.e., that the common factors have the same meaning across groups. This is tested by constraining the factor loadings to be equal across the six groups. The third level of MI is strong factorial invariance, which implies that comparisons of group means are meaningful, i.e., that differences in latent response means reflect differences in factor means. Strong factorial invariance holds if factor loadings and thresholds can both be constrained to be equal across groups. The fourth and most stringent step is testing for strict factorial invariance. This is tested by constraining factor loadings, thresholds and the residual variances of the latent responses to be equal across groups. If strict factorial invariance holds, comparisons of latent response means and observed variances across groups are meaningful (i.e., they reflect true differences in the latent factor mean and variance, hence the factor represents the same construct across groups). Supplementary Figure 1 shows a visual representation of the constraints for each level of MI. See Flora and Curran (2004) and Millsap and Yun-Tein (2004) for a more detailed description on ordered-categorical measures in this context. Mplus Version 5.21 (Muthén and Muthén 2007) was used to test for MI, using the THETA parameterization. As for the EFA, the WLSMV estimator was used, the ‘complex’ option was used to correct for dependency among observations of family members and the RMSEA was used as a model fit index.
By testing for MI between the three age groups, it is assumed that MI also holds within the age groups. This assumption is tested by investigating MI as a continuous function of age in Mx (Neale et al. 2006a, b; Kubarych et al. 2010). With this approach, due to practical limitations, we chose to test MI in twins and with respect to factor loadings and thresholds only, similar to the metric invariance and strong factorial invariance tests respectively in the between group MI tests. For a more detailed description of these tests, see the “Appendix” and Supplementary Figure 2.
Genetic modeling
The contribution of genetic and environmental influences on TP can be inferred from the resemblance between MZ twins, DZ twins and siblings. This design is based on the assumption that DZ twins and siblings share on average ~50% of their segregating genes and MZ twins share ~100% of their genome. Therefore, genetic effects are assumed to be present if MZ twin correlations are larger than DZ twin correlations. For a more detailed description of how additive genetic (A), non-additive or dominant genetic (D), shared environmental (C) and unique environmental influences (E, also includes measurement error) are inferred from twin and sibling correlations, see for example Boomsma et al. (2002b) or Plomin et al. (2008).
The genetic analyses were done in Mx (Neale et al. 2006b). All models were fitted to the raw data with maximum likelihood estimation procedures. First, correlations, means and variances of TP sum scores were computed for sibs and twins of all zygosity groups (MZM, DZM, MZF, DZF, DOS) in a fully saturated model. The difference between DZ and sibling correlations was tested by constraining them to be equal and comparing the fit to the fit of the fully saturated model. Sex differences between twin/sibling correlations were tested in the same way. Homogeneity of means was tested by constraining the means to be equal across zygosity (twins and siblings), sex and age groups. To test whether the large range of ages within the age groups needs to be corrected for, it was tested whether including age as a covariate (linear and quadratic) on the means in the saturated model led to a better fit. For the linear age covariate age was standardized (to z-scores) and for the quadratic age covariate age was standardized and then squared, to reduce the correlation between the two covariates. Based on the twin correlations, it was determined whether to estimate the A, C and E or the A, D and E parameters, since a model that includes A, C, D and E would not be identified. If MZ twin correlations are more than twice the DZ correlation, an ADE model would be more sensible, otherwise the ACE model is fitted (Boomsma et al. 2002b; Plomin et al. 2008).
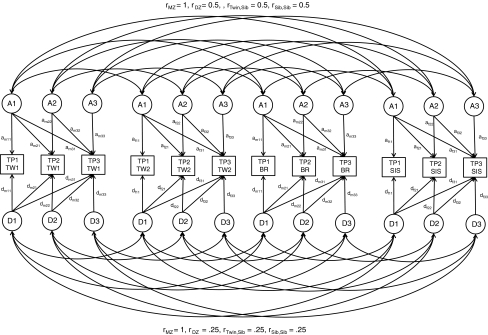
Next, a Cholesky decomposition (Neale and Cardon 1992), with constraints/covariates based on their significance in the saturated model, was fitted to the TP-data. This model is described in the path diagram in Fig. 1 for an opposite-sex twin pair with a male and a female sibling. The addition of siblings to this classical twin design has been shown to increase the power to detect dominant genetic and shared environmental influences (Posthuma and Boomsma 2000). The measured phenotypes are represented in rectangles, and the unmeasured latent sources of variance are in circles. The genetic (A and D) and environmental (C and E) sources of variance are each represented by three factors: the first influencing the variances and covariances of TP for all three age groups, the second explaining the variances and covariances of only the second and third age group, and the third explaining the variances and covariances of the third age-group only. This model allows for the investigation of longitudinal changes in the genetic/environmental factors (in the form of new genetic factors arising, like A2 or A3 in Fig. 1, for additive genetic influences) and longitudinal stability of the genetic/enviromental influences (in the form of longitudinal correlations, derived from a21, a31 and a32 in Fig. 1, for additive genetic influences).
Fig. 1.
Path diagram for longitudinal ADE model on thought problems (TP) for three age groups. The figure shows data from an opposite sex twin pair (TW1 = male, TW2 = female) and their two siblings (BR, brother, SIS, sister). The rectangles represent the log-transformed TP sum-scores (TP1 = TP measured at ages 12–18, TP2 = 19–27, TP3 = 28–59). The circles the latent unmeasured factors (A, additive genetic effects; D, dominant genetic effects; E, non-shared environmental effects, and is omitted in the figure for simplicity, but is modeled in a similar way). In parameter subscripts, m stands for male and f stands for female
Significance of the estimated parameters and differences between groups (sex, age groups, zygosities) in the saturated and Cholesky models were obtained by comparing the full models with the constrained models. In Mx, the fit of different models can be compared by means of likelihood ratio tests (Neale and Maes 1999). The χ 2 value is obtained by subtracting the −2 log likelihood (−2LL) of the more restricted model from the −2LL of the less restricted model. The Δdf is the difference between the degrees of freedom of the two models. According to the standard approach, if the χ 2 test results in a non-significant p value (p ≥ .05), the constrained model is preferred. The χ 2 value however is inflated when using large sample sizes and complex models, causing small discrepancies in large samples to seem significant. Given the large sample sizes and the complexity of the Cholesky model with three age groups and two siblings, we chose an alternative fit index: the Bayesian Information Criterion (BIC; Schwartz 1978), which performs well with large sample sizes and complex models (Markon and Krueger 2004). Models with a lower BIC value were chosen as a better fit over the model with a higher BIC.
Results
EFA and MI
The endorsement frequencies of the items for subjects in the EFA and MI analyses are shown in Table 1. The endorsement of the positive answer categories was almost identical in these datasets and was relatively low. The frequencies of the positive answer categories were highest for items 9 (category 1: .33, category 2: .08) and 63 (category 1: .29, category 2: .05), and lowest for the item on suicide attempts (item 18: category 1: .01 for the total sample, category 2: .003) and the hallucination symptoms (items 40: category 1: .02, category 2: .004; item 70: category 1: .02, category 2: .01).
The EFA yielded a one-factor solution as a good fit for the ten items with an RMSEA of .038. The eigenvalues also strongly support the one-factor solution (eigenvalues 1–10: 4.20, .93, .90, .85, .79, .67, .61, .52, .28, .27).
Table 1 shows the factor loadings from the EFA. Item 85 (I have thoughts that other people would think are strange, factor loading = .84) has the highest factor loading. Items 36 and 63 have the lowest factor loadings (.39 and .38 respectively). Removing these two items lead to a worse fit (RMSEA = .048) and a lower first eigenvalue (eigenvalues 1–10: 3.85, .90, .86, .68, .61, .55, .28, .27). Therefore all items were retained, also allowing for comparisons with previous studies using this scale.
The fit of the configural invariance models was good in all groups (RMSEA < .05), except in the adult males, where it could be considered adequate (RMSEA = .065). In the multigroup analysis, the configural invariance model also had a good fit (RMSEA = .044), indicating that the one-factor model holds in all age × sex groups. Of the remaining MI tests, the metric invariance model showed a good fit (RMSEA = .047), while the strong factorial and strict factorial invariance had an adequate fit (RMSEA = .053 and .060 respectively; see Table 2). Testing for MI within the age groups yielded similar results. MI with respect to both factor loadings and thresholds across age held within in all three age groups. For more details on the MI tests within age groups, see the “Appendix”, Supplementary Figure 2 and Supplementary Table 4.
Table 2.
Model fitting results for measurement invariance tested across sex and age
| N | Free parameters | RMSEA | |
|---|---|---|---|
| Exploratory factor analysis: one-factor solution | 15,320 | 10 | .038 |
| Configural invariance: Males—12–18 years old | 1,255 | 30 | .041 |
| Configural invariance: Females—12–18 years old | 1,488 | 30 | .032 |
| Configural invariance: Males—19–27 years old | 2,129 | 30 | .044 |
| Configural invariance: Females—19–27 years old | 3,284 | 30 | .035 |
| Configural invariance: Males—28–59 years old | 2,497 | 30 | .065 |
| Configural invariance: Females—28–59 years old | 4,667 | 30 | .037 |
| Configural invariance: Total sample | 15,320 | 180 | .044 |
| Metric invariance | 15,320 | 180 | .047 |
| Strong factorial invariance | 15,320 | 90 | .053 |
| Strict factorial invariance | 15,320 | 40 | .060 |
Longitudinal genetic analysis
There were no significant mean or variance differences for the TP-score between the different zygosities, sibs or sex based on the BIC values (values not shown). The mean TP-scores were equal for adolescents and young adults (non-transformed mean TP-score = 1.34), but dropped significantly in later adulthood (non-transformed mean TP-score = .91). The variance did not differ significantly between the age groups. BIC values also indicated that the age covariate effects were not significant in the saturated model, and were therefore not included in the ACE/ADE Cholesky model (see Table 4).
Table 4.
Summary of the model fitting results of the longitudinal genetic analyses
| −2 LL | #par | df | χ2 | ∆df | P | BIC | |
|---|---|---|---|---|---|---|---|
| Saturated model | |||||||
| 1. Fully saturated | 1961.155 | 120 | 13,834 | −58715.507 | |||
| 2. rDZ = rSib (versus 1) | 1980.646 | 100 | 13,854 | 19.491 | 20 | .490 | −58792.065 |
| 3. No sex differences for twin/sibling correlations (versus 1) | 2005.494 | 81 | 13,873 | 44.339 | 39 | .257 | −58861.629 |
| 4. Covariate standardized age dropped (versus 1) | 2004.964 | 114 | 13,840 | 43.809 | 6 | <.001 | −58719.494 |
| 5. Covariate squared standardized age dropped (versus 1) | 1983.825 | 114 | 13,840 | 22.670 | 6 | .001 | −58730.063 |
| ADE model (models include restrictions from models 2–5) | |||||||
| 1. ADE-model | 2211.950 | 29 | 13,929 | −59000.051 | |||
| 2. AE-model (versus 6) | 2222.021 | 23 | 13,935 | 10.071 | 6 | .122 | −59020.906 |
| 3. AE-model—A3 dropped (versus 7) | 2228.579 | 22 | 13,936 | 6.558 | 1 | .010 | −59021.943 |
| 4. AE-model—A3 and a22 dropped (versus 8) | 2239.785 | 21 | 13,937 | 11.206 | 1 | .001 | −59020.655 |
| 5. AE-model—A3 and a32 dropped (versus 8) | 2237.624 | 21 | 13,937 | 9.045 | 1 | .003 | −59021.735 |
| 6. AE-model—A3, e21, e31 and e32 dropped (versus 8) | 2251.165 | 19 | 13,939 | 22.586 | 3 | <.001 | −59023.595 |
| 7. AE-model—A3, e21, e31 and e32 dropped + proportion variance explained by A equal for all age groups (versus 11) | 2263.957 | 15 | 13,943 | 12.792 | 4 | .012 | −59034.460 |
The within-person longitudinal correlations were .37 between adolescence and young adulthood, .37 between adolescence and adulthood, and .26 between young adulthood and adulthood. Table 3 shows the cross-twin-within-time and the cross-twin–cross-time correlations. The DZ correlations did not differ significantly from the sibling-correlations as indicated by BIC values (see Table 4). The MZ-correlations are consistently higher than the DZ correlations in all three age groups, indicating genetic influences on the TP-scores. The twin correlations within age also suggest dominant genetic influences in young adults and adults, indicated by MZ correlations larger than twice the DZ correlations. The cross-twin-cross-time correlations show that past TP-scores of one twin are more predictive of future TP-scores for the co-twin in MZ pairs than in DZ/sibling pairs. This suggests that the longitudinal stability of TP-scores may be explained by genetic factors.
Table 3.
Cross-twin–within-time and cross-twin–cross-time correlations as estimated in the saturated model (with and without sex differences)
| Cross-twin–within-time | Cross-twin–cross-time | |||||
|---|---|---|---|---|---|---|
| 12–18 | 19–27 | 28–59 | 12–18 to 19–27 | 12–18 to 28–59 | 19–27 to 28–59 | |
| MZM | .29 | .35 | .24 | .20 | .28 | .29 |
| DZM | .17 | .11 | .16 | .11 | .12 | .04 |
| MZF | .39 | .43 | .31 | .28 | .14 | .26 |
| DZF | .30 | .21 | .07 | .23 | .07 | .12 |
| DOS (mf/fm) | .24 | .15 | .08 | .10/.17 | .12/.01 | .08/.17 |
| MZ | .34 | .40 | .30 | .24 | .17 | .27 |
| DZ | .27 | .19 | .10 | .19 | .10 | .10 |
MZM, male monozygotic twin pairs; DZM, male dizygotic twin/sibling pairs: MZF, female monozygotic twin pairs; DZF, female dizygotic twin/sibling pairs; DOS, opposite sex dizygotic twin/sibling pairs; MZ, all monozygotic twin pairs; DZ, all dizygotic twin/sibling pairs; mf, male–female correlation; fm, female–male correlation
The significance of each A and D parameter was tested, as well as longitudinal correlations of unique environmental effects (=e21, e31 and e32 only). The first and second additive genetic factor in the longitudinal model significantly influenced TP in the three age groups (see Table 4). The genetic correlation between TP in adolescence and young adulthood was .92, between young adulthood and adulthood .87, and .62 between adolescence and young adulthood. The longitudinal correlations among the unique environmental influences were not significant. The proportions of variance explained by genetic and unique environmental influences did not differ between the three age groups. The variance explained by additive genetic influences was 37% in all age groups, and the remaining 63% was explained by unique environmental influences or measurement error. The unstandardized genetic components also barely change over time. The unstandardized genetic components for A are: .029 for young adolescents, .027 for young adults and .025 for adults. The unstandardized genetic covariance components are: .026 between adolescents and young adults, .023 between young adults and adults, and .016 between adolescents and adults. The unstandardized components for E are: .049 for young adolescents, .047 for young adults and .042 for adults.
Discussion
This study investigated the strength and the structure of the relations between the TP-items with an exploratory factor analysis (EFA), whether the TP-scale is measurement invariant across age and sex, and examined the longitudinal genetic and environmental influences on the TP-scale using the genetic relatedness of the twin subjects and their siblings.
The EFA yielded a one-factor structure. Further examination of the one-factor structure in a multigroup confirmatory factor analysis led to the conclusion that the TP-scale is measurement invariant between adolescent, young adult and adult males and females. Testing for MI within age groups confirmed MI with respect to both factor loadings and thresholds. This means that between and within the age groups, differences between observed thresholds and observed variances across age and sex appear to be due to common factor variation and real differences in the TP-construct/factor mean.
The longitudinal genetic analyses detected additive genetic influences on TP. TP was influenced by the same additive genetic component from adolescence to adulthood, but an additional genetic component arises during young adulthood, and keeps influencing the trait throughout adulthood. The additive genetic factor explained 37% of the variance across all age groups. The genetic correlation between adolescents and young adults was very high (.92). The genetic correlation between young adults and adults was .87, and .62 between adolescents and young adults. This indicates that the largest part of the young adult variation was explained by the same genetic component as in adolescents, and that the genetic component that arose during young adulthood explained the largest part of the adult variation. Dominant genetic and shared environmental influences were not detectable. The remaining variance was explained by unique environmental influences and may also partly reflect measurement error. There were no significant longitudinal correlations between the unique environmental factors, i.e., unique environmental factors in one age group did not influence TP in another age group. The mean scores were about equal in the first two age groups, and decreased significantly in the adult group.
The results of the EFA, MI and the longitudinal heritability analyses imply that (1) there is a single construct underlying the ten TP-items, (2) longitudinal changes in the TP-scores can be explained as true changes in the underlying TP-construct, and (3) there are two genetic components that accompany the longitudinal development of TP: the first influencing TP throughout all age groups, while the second arises during young adulthood and stays influent throughout adulthood. The longitudinal stability is reported to be lower for this scale than for other ASR scales. The ASR-manual reports a longitudinal stability of .36 for a mean interval of ~3.5 years (Achenbach and Rescorla 2003). The longitudinal correlations are in the same range in this study (.37 between adolescence and young adulthood, .37 between adolescence and adulthood, and .26 between young adulthood and adulthood). The results of this study imply that the longitudinal correlation is not due to environmental factors, but can be explained entirely by genetic factors.
The one-factor structure for the ten TP-items and the fact that the total TP-scores share additive genetic influences across age suggest that the Thought Problems scale may be measuring an underlying liability for multiple symptoms. When taking a closer look at the items, they seem to point towards schizo-obsessive symptoms. There is growing evidence that comorbidity of schizophrenic and obsessive–compulsive symptoms may possibly result from a pathophysiological linkage between the two disorders. Schizophrenia and OCD occur together more often than expected, based on their separate lifetime prevalence rates, and seem to share common functional circuits and dysfunctions of neurotransmitter systems (Tibbo and Warneke 1999; Stein 2004). See Tibbo and Warneke (1999), Stein (2004), Reznik et al. (2001), Bottas et al. (2005), and Poyurovski et al. (2006) for reviews and discussions about the schizo-obsessive disorder as a new diagnostic entity.
The TP-scale includes items that cover classical OCD-symptoms and are also included in the Obsessive Compulsive Scale of the Achenbach questionnaire (items 9, 66, 84 and 85; Hudziak et al. 2006). TP also includes items that cover symptoms that could be interpreted as OCD-symptoms as well as psychotic symptoms (items 84, 85, 40, 70). Besides being a classical schizophrenic symptom, hallucinations—covered by items 40 (=auditory hallucinations) and 70 (=visual hallucinations)—are not uncommon in OCD-patients (Hermesh et al. 2004; Fontenelle et al. 2008). Studies have linked intrusive cognitions—such as hallucinations and obsessions—with inhibitory dysregulation in the brain, which both schizophrenic and OCD patients suffer from (Badcock et al. 2005, 2007; Walters et al. 2003). Studies of schizophrenic patients, with and without OCD, showed that subjects with OCD showed more suicide attempts (item 18) and motor symptoms (item 46) than patients without OCD (Tibbo et al. 2000; Krüger et al. 2000; Sevincok et al. 2007; Patel et al. 2010). Effective treatment strategies also differed between the two groups for the motor symptoms. Items 36 and 63 have considerable lower factor loadings (see Table 1) and are more difficult to relate to schizo-obsessive disorders. Item 36 could perhaps be linked to the motor symptoms. Item 63 however not only has the lowest factor loading of all ten items in the EFA (see Table 1), but is also hardest to fit theoretically into the construct the TP-scale seems to measure. The significant genetic influences on the variation of this scale support previous findings about the heritability of TP and are in line with the findings that relatives of OCD-schizophrenia patients had significantly higher risks for OCD-schizophrenia than relatives of schizophrenia patients without OCD (Poyurovski et al. 2005).
There are certain limitations in this study that should be considered when interpreting these results. Because of the highly varying ages in each of the four surveys used in this study (1991, 1995, 1997 and 2009/2010), relatively large age intervals had to be defined for the age subgroups in the genetic modeling analyses, resulting in a somewhat low temporal resolution of the longitudinal results. Also, since we only included one measurement per age group and data from siblings were collected only in 1997 and 2009/2010, the majority of the subjects only had one measurement in the longitudinal analyses. Another limitation is the overall low score of the TP-scale in this sample, which makes it more difficult to draw conclusions at a clinical level.
It appears that the ten TP-items measure a single TP-construct, that measurement invariance holds for the TP-scale and that there are significant additive genetic influences on its variation in different age groups that correlate high over time. When considering the symptoms the TP-items cover, the most plausible known corresponding clinical entity is the schizo-obsessive disorder. Further investigation is needed on the relationship between the TP-scale and schizo-obsessive disorder. Future studies also have to determine the effectiveness of this scale in clinical settings. Since the TP scale measures the same construct influenced by the same genes in younger and older subjects and in males and females, pooling their data together in linkage-analyses and (genome-wide) association studies may increase power in candidate gene studies.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
This study was supported by the Spinozapremie (NWO/SPI 56-464-14192); Neuroscience Campus, Amsterdam (NCA); Center for Medical Systems Biology (CMSB, NWO Genomics); ZonMW Addiction (grant 31160008); The European Research Council (ERC-230374). Statistical analyses were carried out on the Genetic Cluster Computer (http://www.geneticcluster.org) which is financially supported by the Netherlands Scientific Organization (NWO 480-05-003) along with a supplement from the Dutch Brain Foundation and the VU University Amsterdam. We wish to thank all participants in the longitudinal survey studies.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Appendix: Measurement invariance within age groups
Methods
By testing for MI between the three wide age groups, it is assumed that MI also holds within the age groups. This assumption is tested in three (adolescents [12–18], young adults [19–27] and adults [28–59]) single group item-factor analyses (Neale et al. 2006a; Kubarych et al. 2010). For a detailed description of how this model is applied to ordinal data, see Kubarych et al (2008) and Wirth and Edwards (2007). The path model with one TP factor underlying the 10 items is shown in Supplementary Figure 2. Boxes represent the ten observed TP-items; solid line circles represent factors; broken line circles represent special nodes used to estimate the covariate moderation effects; diamonds represent the covariate effects (age, transformed to a z-score); triangles represent unit constants for estimating means and threshold covariate effects; single-headed arrows represent linear regression effects; and double headed arrows represent variances and covariances. The covariate effects on the factor mean and variance are represented by B and D respectively through the special nodes DF. The factor loadings are denoted L #, and the covariate effects on the factor loadings are represented by J # through the special nodes DL. The moderation effects of the item thresholds (m #) are estimated by parameters K #. For each item, two thresholds are estimated because there are 3 response categories. Separate MZ and DZ twin correlations are only allowed between the TP factors (TP TW1 and TP TW2) and between the item residuals (R1 # and R2 #).
Given this model, MI can be evaluated at two levels. (1) If the factor loadings change as a function of age, this may bias the factor mean and variance. This can be tested by comparing the fit of a model with moderated factor variance (D free) with the fit of a model where the moderation on the factor loadings is allowed (J # free). If the latter fits better, the TP scale may not be measurement invariant. (2) If the item thresholds change as a function of age due to causes other than the factor, the factor mean may be biased. Analogous to the first test, this can be tested by comparing the fit of a model where only the factor mean is allowed to vary as a function of age (by freeing B) with the fit of a model where the item threshold locations are allowed to vary across age (by freeing all K #). If the model with moderated item thresholds fits better than the model with the moderated factor mean, the TP scale would not be considered measurement invariant. Hence, we distinguish between the genuine effects, reflected by changes in variance and factor mean, and changes in the functioning of the measurement instrument, which may be reflected by changes in the factor loadings and items thresholds.
Models were tested in Mx (Neale et al. 2006b), which compares the fit of different models by likelihood ratio tests (Neale and Maes 1999). The χ 2 value is obtained by subtracting the −2 log likelihood (−2LL) of the more restricted model from the −2LL of the less restricted model. The Δdf is the difference between the degrees of freedom of the two models. According to the standard approach, if the χ 2 test results in a non-significant P value (P ≥ .05), the constrained model is preferred. The χ 2 value however is inflated when using large sample sizes, causing small discrepancies in large samples to seem significant. Given the large sample sizes and the complexity of model, we chose an alternative fit index: the Bayesian Information Criterion (BIC; Schwartz 1978), which has been shown to perform well with large sample sizes and complex models (Markon and Krueger 2004). Models with a lower BIC value were chosen as a better fit over the model with a higher BIC.
Results
The results of the MI tests are shown in Supplementary Table 4. In all three age groups, first a full MI baseline model (model 1) was fitted, where the covariate effects were constrained to zero. Freeing the covariate effects of age on the latent factor variance in model 2 did not result in a better fit than model 1 in any of the age groups, indicating that the variance does not change over time within the age groups. Freeing the covariate effects of age on the factor loadings in model 3 did not result in a better fit than model 2 in any of the age groups, indicating that the TP-scale is measurement invariant on this level. In model 4 the covariate effect on the factor mean of age was freely estimated. Based on the BIC, comparisons with model 1 suggested a better fit for freely estimated age parameters in adolescents only, indicating factor mean changes across age in that age group. Model 5 (with freely estimated age effects on item thresholds) did not show a better fit than model 4 in any of the three age groups, indicating that allowing the thresholds to vary across age does not results in a better fit than allowing only the factor mean to vary across age. This suggests that differences in thresholds across age are due to differences in the factor mean in all three age groups, i.e., the TP-scale is measurement invariant on this level as well.
Footnotes
Edited by Gitte Lubke.
References
- Abdellaoui A, Bartels M, Hudziak JJ, Rizzu P, van Beijsterveldt CEM, Boomsma DI. Genetic influences on thought problems in 7-year-olds: A twin-study of genetic, environmental and rater effects. Twin Res Human Genet. 2008;11(6):571–578. doi: 10.1375/twin.11.6.571. [DOI] [PubMed] [Google Scholar]
- Achenbach TM, Rescorla LA. Manual for ASEBA adult forms & profiles. Burlington: University of Vermont, Research Center for Children, Youth, & Families; 2003. [Google Scholar]
- Badcock JC, Waters FAV, Maybery MT, Michie PT. Auditory hallucinations: Failure to inhibit irrelevant memories. Cogn Neuropsychiatry. 2005;10(2):125–136. doi: 10.1080/13546800344000363. [DOI] [PubMed] [Google Scholar]
- Badcock JC, Waters FAV, Maybery M. On keeping (intrusive) thoughts to one’s self: Testing a cognitive model for auditory hallucinations. Cogn Neuropsychiatry. 2007;12:78–89. doi: 10.1080/13546800600753120. [DOI] [PubMed] [Google Scholar]
- Boomsma DI, Busjahn A, Peltonen L. Classical twin studies and beyond. Nat Rev Genet. 2002;3:872–882. doi: 10.1038/nrg932. [DOI] [PubMed] [Google Scholar]
- Boomsma DI, Vink JM, van Beijsterveldt CEM, de Geus EJC, Beem AL, Mulder EJCM, Derks EM, Riese M, Willemsen GHM, Bartels M, van den Berg M, Kupper HM, Polderman JC, Posthuma D, Rietveld MJH, Stubbe JH, Knol LI, Stroet TH, van Baal GCM. Netherlands twin register: a focus on longitudinal research. Twin Res. 2002;5:401–406. doi: 10.1375/136905202320906174. [DOI] [PubMed] [Google Scholar]
- Boomsma DI, de Geus EJC, Vink JM, Stubbe JH, Distel MA, Hottenga JJ, Posthuma D, van Beijsterveldt CEM, Hudziak JJ, Bartels M, Willemsen G. Netherlands twin register: from twins to twin families. Twin Res Human Genet. 2006;9(6):849–857. doi: 10.1375/twin.9.6.849. [DOI] [PubMed] [Google Scholar]
- Bottas A, Cooke RG, Richter MA. Comorbidity and pathophysiology of obsessive-compulsive disorder in schizophrenia: is there evidence for a schizo-obsessive subtype of schizophrenia? J Psychiatry Neurosci. 2005;30(3):187–193. [PMC free article] [PubMed] [Google Scholar]
- Diler RS, Uguz S, Seydaoglu G, Avci A. Mania profile in a community sample of prepubertal children in Turkey. Bipolar Disord. 2008;10:546–553. doi: 10.1111/j.1399-5618.2008.00580.x. [DOI] [PubMed] [Google Scholar]
- Diler RS, Birmaher B, Axelson D, Goldstein B, Gill MK, Strober M, Kolko DJ, Goldstein TR, Hunt J, Yang M, Ryan ND, Iyengar S, Dahl RE, Dorn LD, Keller MD. The Child Behavior Checklist (CBCL) and the CBCL-bipolar phenotype are not useful in diagnosing pediatric bipolar disorder. J Child Adolesc Psychopharmacol. 2009;19(1):23–30. doi: 10.1089/cap.2008.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelbrock C, Rende R, Plomin R, Thompson L. A twin study of competence and problem behavior in childhood and early adolescence. J Child Psychol Psychiatry. 1995;36:775–785. doi: 10.1111/j.1469-7610.1995.tb01328.x. [DOI] [PubMed] [Google Scholar]
- Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychol Methods. 2004;9:466–491. doi: 10.1037/1082-989X.9.4.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontenelle LF, Lopes AP, Borges MC, Pacheco PG, Nascimento AL, Versiani M. Auditory, visual, tactile, olfactory, and bodily hallucinations in patients with obsessive-compulsive disorder. CNS Spectr. 2008;13(2):125–130. doi: 10.1017/s1092852900016278. [DOI] [PubMed] [Google Scholar]
- Geller DA, Biederman J, Faraone S, Spencer T, Doyle R, Mullin B, et al. Re-examining comorbidity of obsessive-compulsive and attention deficit hyperactivity disorder using an empirically derived taxonomy. Eur Child Adolesc Psychiatry. 2004;13:83–91. doi: 10.1007/s00787-004-0379-x. [DOI] [PubMed] [Google Scholar]
- Hermesh H, Konas S, Shiloh R, Dar R, Marom S, Weizman A, Gross-Isseroff R. Musical hallucinations: prevalence in psychotic and nonpsychotic outpatients. J Clin Psychiatry. 2004;65:191–197. doi: 10.4088/JCP.v65n0208. [DOI] [PubMed] [Google Scholar]
- Horn J, McArdle JJ. A practical and theoretical guide to measurement invariance in aging research. Exp Aging Res. 1992;18:117–144. doi: 10.1080/03610739208253916. [DOI] [PubMed] [Google Scholar]
- Hudziak JJ, Althoff RR, Stanger C, van Beijsterveldt CEM, Nelson EC, Hanna GL, Boomsma DI, Todd RD. The obsessive-compulsive scale of the child behavior checklist predicts obsessive-compulsive disorder: a receiver operating characteristic curve analysis. J Child Psychol Psychiatry. 2006;47:160–166. doi: 10.1111/j.1469-7610.2005.01465.x. [DOI] [PubMed] [Google Scholar]
- Ivarsson T, Melin K, Wallin L. Categorical and dimensional aspects of co-morbidity in obsessive-compulsive disorder (OCD) Eur Child Adolesc Psychiatry. 2007;17:20–31. doi: 10.1007/s00787-007-0626-z. [DOI] [PubMed] [Google Scholar]
- Kasius MC, Ferdinand RF, van den Berg H, Verhulst F. Associations between different diagnostic approaches for child and adolescent psychopathology. J Child Psychol Psychiatry. 1997;38:625–632. doi: 10.1111/j.1469-7610.1997.tb01689.x. [DOI] [PubMed] [Google Scholar]
- Krüger S, Bräuning P, Höffler J, Shugar G, Börner I, Langkrär J. Prevalence of obsessive-compulsive disorder in schizophrenia and significance of motor symptoms. J Neuropsychiatry Clin Neurosci. 2000;12:16–24. doi: 10.1176/jnp.12.1.16. [DOI] [PubMed] [Google Scholar]
- Kubarych TS, Aggen SH, Hettema JM, Kendler KS, Neale MC. Assessment of generalized anxiety disorder symptoms in women in the National Comorbidity survey and Virginia Twin study of psychiatric and substance use disorders: a comparative study. Psychol Assess. 2008;20:206–216. doi: 10.1037/a0012764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubarych TS, Aggen SA, Kendler KS, Torgersen S, Reichborn-Kjennerud T, Neale MC. Measurement non-invariance of DSM-IV narcissistic personality disorder criteria across age and sex in a population based sample of Norwegian twins. Int J Methods Psychiatr Res. 2010;19(3):156–166. doi: 10.1002/mpr.318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo P, Lin C, Yang H, Soong W, Chen W. A twin study of competence and behavioral/emotional problems among adolescents in Taiwan. Behav Genet. 2004;34:63–74. doi: 10.1023/B:BEGE.0000009477.70657.9d. [DOI] [PubMed] [Google Scholar]
- Lin CCH, Kuo P, Su C, Chen WJ. The Taipei Adolescent Twin/Sibling Family Study I: behavioral problems, personality features, and neuropsychological performance. Twin Res Human Genet. 2006;9(6):890–894. doi: 10.1375/twin.9.6.890. [DOI] [PubMed] [Google Scholar]
- Lubke GH, Dolan CV, Neale MC. Implications of absence of measurement invariance for detecting sex limitation and genotype by environment interaction. Twin Res Human Genet. 2004;7(3):292–298. doi: 10.1375/twin.7.3.292. [DOI] [PubMed] [Google Scholar]
- Markon KE, Krueger RF. An empirical comparison of information-theoretic selection criteria for multivariate behavior genetic models. Behav Genet. 2004;34:593–610. doi: 10.1007/s10519-004-5587-0. [DOI] [PubMed] [Google Scholar]
- Mehta PD, West SG. Putting the individual back into individual growth curves. Psychol Methods. 2000;5(1):23–43. doi: 10.1037/1082-989X.5.1.23. [DOI] [PubMed] [Google Scholar]
- Meredith W. Measurement invariance, factor analysis, and factorial invariance. Psychometrika. 1993;58:525–543. doi: 10.1007/BF02294825. [DOI] [Google Scholar]
- Millsap RE, Yun-Tein J (2004) Assessing factorial invariance in ordered-categorical measures. Multivar Behav Res 39(3):479–515
- Morgan CJ, Cauce AM. Predicting DSM-III-R disorders from the youth self-report: analysis of data from a field study. J Am Acad Child Adolesc Psychiatry. 1999;38:1237–1245. doi: 10.1097/00004583-199910000-00012. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 5. Los Angeles: Muthén & Muthén; 2007. [Google Scholar]
- Neale M, Cardon L (1992) Methodology for genetic studies of twins and families. North Atlantic Treaty Organization, Scientific Affairs Division. Kluwer Academic, Dordrecht
- Neale MC, Maes HH. Methodology for genetic studies of twins and families. Dordrecht: Kluwer; 1999. [Google Scholar]
- Neale MC, Aggen SH, Maes HH, Kubarych TS, Schmitt JE. Methodological issues in the assessment of substance use phenotypes. Addict Behav. 2006;31:1010–1034. doi: 10.1016/j.addbeh.2006.03.047. [DOI] [PubMed] [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: statistical modeling. 6. Richmond: Department of Psychiatry, Medical College of Virginia; 2006. [Google Scholar]
- Patel DD, Laws KR, Padhi A, Farrow JM, Mukhopadhaya K, Krishnaiah R, Fineberg NA. The neuropsychology of the schizo-obsessive subtype of schizophrenia: a new analysis. Psychol Med. 2010;40:921–933. doi: 10.1017/S0033291709991255. [DOI] [PubMed] [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioral genetics. New York: Worth Publishers and W.H. Freeman Company; 2008. [Google Scholar]
- Polderman T, Posthuma D, De Sonneville L, Verhulst F, Boomsma DI. Genetic analyses of teacher ratings of problem behavior in 5-year-old twins. Twin Res Human Genet. 2006;9:122–130. doi: 10.1375/twin.9.1.122. [DOI] [PubMed] [Google Scholar]
- Posthuma D, Boomsma DI. A note on the statistical power in extended twin designs. Behav Genet. 2000;30(2):147–158. doi: 10.1023/A:1001959306025. [DOI] [PubMed] [Google Scholar]
- Poyurovski M, Kriss V, Weisman G, Faragian S, Schneidman M, Fuchs C, Weizman A, Weizman R. Familial aggregation of schizophrenia-spectrum disorders and obsessive-compulsive associated disorders in schizophrenia probands with and without OCD. J Clin Psychiatry. 2005;64:1300–1307. doi: 10.4088/JCP.v64n1104. [DOI] [PubMed] [Google Scholar]
- Poyurovski M, Weizman A, Weizman R. Obsessive-compulsive disorder and comorbidity; chapter 4: schizo-obsessive disorder. Hauppauge: Nova Science Publishers; 2006. pp. 35–46. [Google Scholar]
- Rebollo I, De Moor MHM, Dolan CV, Boomsma DI. Phenotypic factor analysis of family data: correction of the bias due to dependency. Twin Res Human Genet. 2006;9:367–376. doi: 10.1375/twin.9.3.367. [DOI] [PubMed] [Google Scholar]
- Reznik I, Mester R, Kotler M, Weizman A. Obsessive-compulsive schizophrenia: a new diagnostic entity? J Neuropsychiatry Clin Neurosci. 2001;13(1):115–116. doi: 10.1176/appi.neuropsych.13.1.115. [DOI] [PubMed] [Google Scholar]
- Schermelleh-Engel K, Moosbrugger H. Evaluating the fit of structural equation models: tests of significance and descriptive goodness-of-fit measures. Methods Psychol Res Online. 2003;8:23–74. [Google Scholar]
- Schmitz S, Fulker DW, Mrazek DA. Problem behavior in early and middle childhood: an initial behavior genetic analysis. J Child Psychol Psychiatry. 1995;36:1443–1458. doi: 10.1111/j.1469-7610.1995.tb01674.x. [DOI] [PubMed] [Google Scholar]
- Schwartz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. doi: 10.1214/aos/1176344136. [DOI] [Google Scholar]
- Sevincok L, Akoglu A, Kokcu F. Suicidality in schizophrenic patients with and without obsessive-compulsive disorder. Schizophr Res. 2007;90:198–202. doi: 10.1016/j.schres.2006.09.023. [DOI] [PubMed] [Google Scholar]
- Sobina C, Kiley-Brabecka K, Monka SH, Khurib J, Karayiorgoua M. Sex differences in the behavior of children with the 22q11 deletion Syndrome. Psychiatry Res. 2009;166(1):24–34. doi: 10.1016/j.psychres.2008.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein DJ. Neurobiology of the obsessive-compulsive spectrum disorders. Biol Psychiatry. 2004;47(4):296–304. doi: 10.1016/S0006-3223(99)00271-1. [DOI] [PubMed] [Google Scholar]
- Tibbo P, Warneke L. Obsessive-compulsive disorder in schizophrenia: epidemiologic and biologic overlap. J Psychiatry Neurosci. 1999;24(1):15–24. [PMC free article] [PubMed] [Google Scholar]
- Tibbo P, Kroetsch M, Chue P, Warneke L. Obsessive-compulsive disorder in schizophrenia. J Psychiatr Res. 2000;34:139–146. doi: 10.1016/S0022-3956(99)00048-5. [DOI] [PubMed] [Google Scholar]
- Vandenberg RJ. Toward a further understanding of and improvement in measurement invariance methods and procedures. Organ Res Methods. 2000;5(2):139–158. doi: 10.1177/1094428102005002001. [DOI] [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organ Res Methods. 2000;3:4–7. doi: 10.1177/109442810031002. [DOI] [Google Scholar]
- Walters FAV, Badcock JC, Maybery MT, Michie PT. Inhibition in schizophrenia: association with auditory hallucinations. Schizophr Res. 2003;62:275–280. doi: 10.1016/S0920-9964(02)00358-4. [DOI] [PubMed] [Google Scholar]
- Willemsen G, Posthuma D, Boomsma DI. Environmental factors determine where the Dutch live: results from the Netherlands twin register. Twin Res Human Genet. 2005;8(4):312–317. doi: 10.1375/twin.8.4.312. [DOI] [PubMed] [Google Scholar]
- Wirth RJ, Edwards MC. Item factor analysis: current approaches and future directions. Psychol Methods. 2007;12:58–79. doi: 10.1037/1082-989X.12.1.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu CY (2002). Evaluating cutoff criteria of model fit indices for latent variable models with binary and continuous outcomes. Dissertation from University of California, Los Angeles. http://www.statmodel.com/papers.shtml
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.