A Note on False Positives and Power in G × E Modelling of Twin Data

Abstract

The variance components models for gene–environment interaction proposed by Purcell in 2002 are widely used. In both the bivariate and the univariate parameterization of these models, the variance decomposition of trait T is a function of moderator M. We show that if M and T are correlated, and moderator M is correlated between twins as well, the univariate parameterization produces a considerable increase in false positive moderation effects. A simple extension of this univariate moderation model prevents this elevation of the false positive rate provided the covariance between M and T is itself not also subject to moderation. If the covariance between M and T varies as a function of M, then moderation effects observed in the univariate setting should be interpreted with care as these can have their origin in either moderation of the covariance between M and T or in moderation of the unique paths of T. We conclude that researchers should use the full bivariate moderation model to study the presence of moderation on the covariance between M and T. If such moderation can be ruled out, subsequent use of the extended univariate moderation model, as proposed in this paper, is recommended as this model is more powerful than the full bivariate moderation model.

Introduction

In the classical twin model, phenotypic variance is decomposed into genetic and environmental variance components, which are usually assumed to be homoskedastic, i.e., constant across relevant environmental or genetic conditions. Heteroskedasticity will arise if the genetic and/or environmental variance components vary in size as a function of a given variable, or moderator. Such a moderator can be truly environmental in nature (e.g., exposure to radiation from a nuclear plant, the level of iodine in soil or drinking water1), or be a trait that itself is subject to genetic influences (e.g., eating or exercise habits, educational attainment level, personality traits). If moderators have a limited number of levels, their effects can be modelled in a multi-group design. However, a multi-group approach does not naturally account for group order, and quickly becomes impractical if the moderator is characterized by many levels (i.e., continuous in the extreme case). As few as, say, 3 or 4 levels may already require a challenging number of groups, especially if the moderator differs within twin pairs (i.e., is not ‘shared’), and the sample includes additional family members (e.g., parents, siblings, partners). In such circumstances, behavioural geneticists often turn to the moderation models proposed by Purcell (2002). The popularity of these model is evident given its frequent use in twin studies on moderation in the context of, for instance, cognitive ability (Bartels et al. 2009; Grant et al. 2010; Harden et al. 2007; Johnson et al. 2009a; Turkheimer et al. 2003; van der Sluis et al. 2008), personality (Bartels and Boomsma 2009; Brendgen et al. 2009; Distel et al. 2010; Hicks et al. 2009a, b; Johnson et al. 2009b; Tuvblad et al. 2006; Zhang et al. 2009), health (Johnson and Krueger 2005; Johnson et al. 2010; McCaffery et al. 2008, 2009), and brain morphology (Lenroot et al. 2009; Wallace et al. 2006).

In both the univariate and the bivariate moderation models proposed by Purcell (2002), the moderation effects are modelled directly on the path loadings of the genetic (A), shared environmental (C) and nonshared environmental (E) variance components.2 In this moderation model, the variances of A, C, and E are fixed to 1 (standard identifying scaling), but the path coefficients are modelled as (a + β _a M _i), (c + β _c M _i), and (e + β _e M _i), respectively. In these expressions for the moderated loadings, a, c and e are intercepts, i.e., the parts of the variance components that are independent of moderator M, M _i is the value of the moderator for a specific twin i, and β _a, β _c, and β _e, are the regression weights of the moderator for the genetic and the environmental variance components, respectively.3 In the standard homoskedastic ACE-model, the β coefficients are assumed to be zero. In the moderation model proposed by Purcell, the total variance of trait T is thus calculated as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{Var}}\left( {{\text{T}}|{\text{M}}_{\text{i}} } \right) = \left( {a + \beta_{a} M_{i} } \right)^{ 2} + \left( {c + \beta_{c} M_{i} } \right)^{ 2} + \left( {e + \beta_{e} M_{i} } \right)^{ 2} $$\end{document} 1

for i = 1, 2, and the expected covariances within MZ and DZ twin pairs are:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} {\text{Cov}}_{\text{MZ}} ({\text{T}}_{ 1} ,{\text{T}}_{ 2} |{\text{M}}_{ 1} ,{\text{M}}_{ 2} ) & = (a + \beta_{a} M_{1} )(a + \beta_{a} M_{2} ) + (c + \beta_{c} M_{1} )(c + \beta_{c} M_{2} ) \\ {\text{Cov}}_{\text{DZ}} ({\text{T}}_{ 1} ,{\text{T}}_{ 2} |{\text{ M}}_{ 1} ,{\text{M}}_{ 2} ) & = . 5(a + \beta_{a} M_{1} )(a + \beta_{a} M_{2} ) + (c + \beta_{c} M_{1} )(c + \beta_{c} M_{2} ). \\ \end{aligned} $$\end{document} 2

Besides moderating the variance decomposition of trait T, the moderator itself may be correlated with the trait T via A, C, and/or E. The full bivariate moderation model (depicted in Fig. 1a), in which the variances of both trait T and moderator M, as well as their covariance, are decomposed into the three sources of variation (A, C, and E), allows one to test both the presence of moderation on the variance components unique to trait T, and the presence of moderation effects on the variance components common to trait T and moderator M, i.e., on the cross paths. Investigation of moderation of the covariance between the M and T, such as modeled via the 3 cross paths, is of interest if one wishes to understand the nature of, or the process underlying, the relation between M and T. With 17 parameters (15 describing the variance part of the model: 3 parameters unique to the moderator, 6 to describe the covariance between T and M, and 6 to describe the variance decomposition unique to T; and 2 parameters describing the means part of the model: the estimated means of M and T, respectively), this bivariate moderation model describes the relations between T and M in great detail. In practice, describing (decomposing) a small covariance between M and T with as much as 6 parameters, can be computationally challenging, and solutions can be quite sensitive to starting values. Also, Rathouz et al. (2008) have shown that this model sometimes produces spurious moderation effects. More practically, programs like Mx (Neale et al. 2006) do not allow the simultaneous modeling of categorical and continuous variables, which complicates this bivariate parameterization of T and M if the two variables do not have the same measurement level.4 Finally, when the moderator of interest is a family-level variable, i.e., a variable that is by definition equal for twin 1 and twin 2, such as socioeconomic status in childhood (SES) or parental educational attainment level, then a bivariate parameterization is infeasible as the moderator does not show any variation within families.

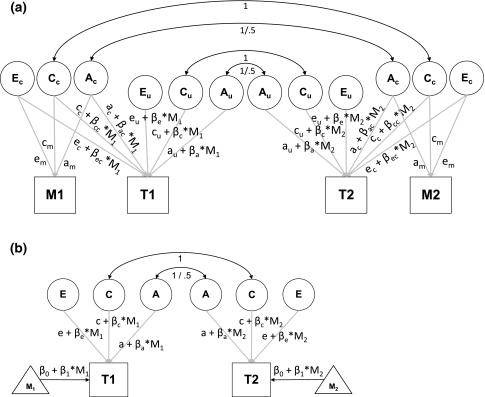
Fig. 1.

a Full bivariate moderation model for a twin pair as proposed by Purcell (2002). Ac, Cc, and Ec are the variance components common to the moderator M and the trait T; Au, Cu, and Eu are the variance components unique to T. All latent variables have unit variance. Path loadings for M are denoted by a_m, c_m, and e_m. The loadings of the cross-paths connecting M to T consist of parts that are unrelated to moderator M, i.e., a_c, c_c, and e_c, and parts that depend on M via weights β _ac, β _cc, and β _ec. Similarly, the loadings of the paths unique to T consist of parts that are unrelated to M, i.e., a_u, c_u, and e_u, and parts that depend on M via weights β _a, β _c, and β _e. b Univariate moderation model for a twin pair as proposed by Purcell (2002). All latent variables have unit variance. Path loadings for T consist of parts that are unrelated to moderator M, i.e., a, c, and e, and parts that depend on M via weights β _a, β _c, and β _e. M is also included in the means model of T, where β ₀ denotes the intercept and β ₁ the regression weight of T on M

For these reasons, researchers have resorted to what we call Purcell’s (2002) univariate moderation model (e.g., Bartels et al. 2009; Bartels and Boomsma 2009; Dick et al. 2009; Distel et al. 2010; Grant et al. 2010; Harden et al. 2007; McCaffery et al. 2008, 2009; Taylor et al. 2010; Timberlake et al. 2006; Turkheimer et al. 2003; Wallace et al. 2006). In this model, the moderator M is included in the means model of T as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} T_{1}\,=\,\beta_{0} + \beta_{1} *M_{1} , \\ T_{2} = & \beta_{0} + \beta_{1} *M_{2} , \\ \end{aligned} $$\end{document} 3

where T ₁ and T ₂ are the trait values of twins 1 and 2, M ₁ and M ₂ are their individual moderator values, β ₀ is the intercept, and β ₁ is the regression weight for moderator M. The parameters β ₀ and β ₁ are assumed to be equal across twins within a pair, and across zygosity (Fig. 1b). With 8 parameters (6 to describe the variance part of the model: 3 related, and 3 unrelated to the moderator; and 2 parameters to describe the means model: the regression weight β ₁ and the intercept β ₀), this parameterization is more parsimonious than the bivariate moderation model, and often less susceptible to computational problems. In addition, low correlations between M and T, or different measurement levels of M and T, do not cause problems in this univariate moderation model.

It is important to realize that the bivariate moderation model considers the joint distribution of M and T, while the univariate moderation model considers moderation of the variance decomposition of T conditional on M. With M included in the means model of T, the univariate moderation model does not allow further investigation of the nature of the covariance between M and T but specifically focuses on the question whether the decomposition of the variance unique to T depends on M. Entering M in the means model of T to allow for a main effect is believed to effectively remove from the covariance model any (genetic) effects that are shared between trait and moderator (Purcell 2002, p. 563). In essence, the variance common to M and T is partialled out, and the moderator effects of M are modeled on the residual variance of T, T′, i.e., the variance of T that was not shared with M. As a result, the effects that M has on the variance decomposition of the residual T′ are believed to be independent of (i.e., not due to) any (unmodeled) (genetic) correlation between M and T (Purcell 2002, p. 563).

However, although M₁ is indeed unrelated to the for-M₁-corrected residual \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document}, this residual \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} is not necessarily uncorrelated to the moderator M₂ of the co-twin. In this paper, we first show that non-zero semi-partial correlations between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ can result in a considerable increase in false positive moderation effects on variance components A and C, especially if the correlation between T and M runs fully (or predominantly) via E (rather than via A and/or C). We subsequently study whether a simple extension of the univariate moderation model prevents this increase of false positive rate. In the first part of this paper, we focus on illustrations and simulations in which the correlation between trait T and moderator M runs either exclusively via A, or via C or via E. Although these settings may be considered quite special, they conveniently simplify the explanation of the problem of non-zero semi-partial correlations in the univariate moderation model proposed by Purcell, and clarify how this model would need to be extended. In the subsequent investigation of the usefulness of this extended version of the univariate model, the simulations are extended to more realistic conditions.

Semi-partial correlations

Consider a moderator M and a trait T, both with variance 1 and mean 0, and measured in a sample of MZ and DZ twins. Suppose that in both M and T, variance components A, C, and E account for 40%, 30%, and 30% of the variance, respectively, and that these percentages are stable across the entire population (i.e., there is no moderation). This implies that rMZ_t1,t2 = rMZ_m1,m2 = .7 and rDZ_t1,t2 = rDZ_m1,m2 = .5. Now suppose that the cross-trait correlation between T and M equals .24 (i.e., r_m1,t1 = r_m2,t2 = .24) and that the T–M correlation is either exclusively due to A (loading cross-path equals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.15} $$\end{document}), or to C (loading cross-path equals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.2} $$\end{document}), or to E (loading cross-path equals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.2} $$\end{document}; see Fig. 2a–c).

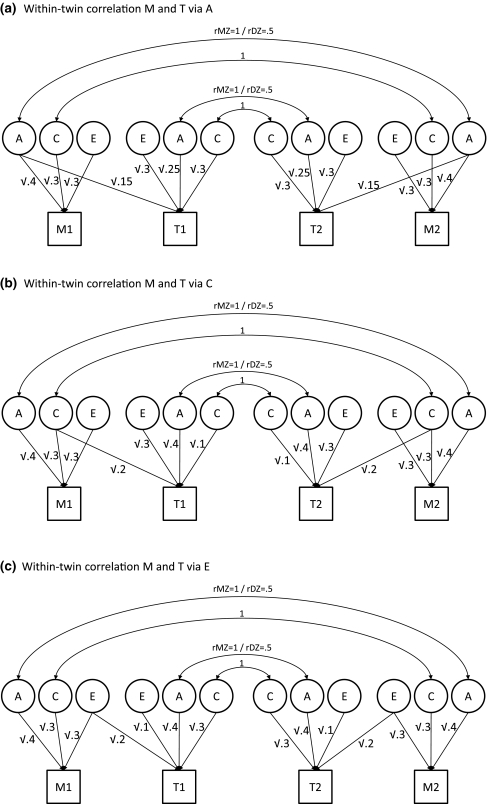
Fig. 2.

a–c Bivariate models in which the correlation of ~.24 between moderator M and trait T either exclusively runs via A (a), exclusively via C (b), or exclusively via E (c). The variance of both trait T and moderator M are for 40% due to A, for 30% to C, and for 30% due to E. All latent variables have unit variance

If the relation between T and M runs exclusively via E, then in both MZ and DZ twins, the cross-trait cross-twin correlation between M₂ (the moderator of twin 2) and T₁ (the trait of twin 1) is 0, just as the correlation between M₁ and T₂ is 0, i.e., r_m2,t1 = r_m1,t2 = 0. If the correlation between T and M runs via C, then the correlation between M₂ and T₁, and between M₁ and T₂, is in both MZ and DZ twins calculated as \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3*.2} = .24 $$\end{document}. Finally, if the correlation between T and M runs via A, then this correlation is \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4*.15} = .24 $$\end{document} in MZ twins and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} *.5*\sqrt {.15} = .12 $$\end{document} in DZ twins.

Now suppose that we want to investigate whether M moderates the variance decomposition of T, and rather than modeling this in a bivariate model (Fig. 1a), we choose to include M in the means model of T (Fig. 1b), such that we can study the moderation effects of M on the variance decomposition of the residual variance T′. We thus regress T₁ on M₁ and T₂ on M₂, and obtain residuals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{2}^{\prime } $$\end{document}. We know that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₁ (and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{2}^{\prime } $$\end{document} and M₂) will be uncorrelated, but what is the correlation between the residual \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ (or between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{2}^{\prime } $$\end{document} and M₁)? The semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ (which equals the semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{2}^{\prime } $$\end{document} and M₁), denoted as r_m2(t1·m1), is calculated as5:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ r_{m2(t1 \cdot m1)} = \frac{{r_{t1,m2} - r_{t1,m1} r_{m1,m2} }}{{\sqrt {1 - r_{t1,m1}^{2} } }}. $$\end{document} 4

Table 1 shows the correlations between T₁ and M₂, and the semi-partial correlations between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ for MZ and DZ twins in the three different scenarios (i.e., within-twin correlation between T and M runs either exclusively via A, exclusively via C, or exclusively via E).

Table 1.

Correlations and semi-partial correlations between M₂ and T₁ if the within-twin correlation between T and M runs via A, via C, or via E

	rm2,t1	rm2(t1·m1)
T and M correlated via A
MZ	.24	.074
DZ	.12	0
T and M correlated via C
MZ	.24	.074
DZ	.24	.124
T and M correlated via E
MZ	0	−.173
DZ	0	−.124

Note: r_m2,t1 denotes the correlation between moderator of twin 2 (M₂), and the trait of twin 1 (T₁). r_m2(t1·m1) denotes the semi-partial correlation between the moderator of twin 2 (M₂) and the trait of twin 1 (T₁) corrected for the moderator of twin 1 (M₁). In these calculations, the variances of both T and M were 40%, 30%, and 30% due to A, C, and E, respectively

Clearly, as a result of partialling out M₁ from T₁, the semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ is lower than the correlation between T₁ and M₂. However, the semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ is often not equal to zero: especially if the correlation between T₁ and M₂ was zero to begin with (i.e., if T and M are correlated via E), the semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ is quite large and negative. Estimated across an entire study sample (while weighing for the MZ/DZ ratio), these non-zero semi-partial correlations can be quite considerable (e.g., in the case that T and M are correlated via E), and are likely to cause problems in the univariate moderation model. After all, these non-zero semi-partial correlations, whether positive or negative, will somehow need to be accommodated in the model. Considering the univariate moderation model as depicted in Fig. 1b, a non-zero semi-partial correlation between \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document} and M₂ is most likely to be accommodated via the effects that M has on the variance components A and C, i.e., via β _a and β _c, as these are the only links between M₂ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{1}^{\prime } $$\end{document}, and M₁ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{2}^{\prime } $$\end{document}, respectively. In Simulation study 1, we investigated first whether these non-zero semi-partial correlations do indeed cause problems in the univariate moderation model. We expect problems to be greatest if the semi-partial correlation deviates more from zero (i.e., in the case that T and M are correlated via E). Second, we investigated whether these problems indeed manifest themselves mostly through β _a and β _c.

Simulation study 1

To investigate the effect of partialling out M on T within each individual twin on the significance of parameters β _a, β _c, and β _e, we simulated data according to the models shown in Figs. 2a–c, i.e., with correlations between T and M running either exclusively via A, exclusively via C, or exclusively via E. In these simulated data, T and M were both standard normally distributed. Also, T and M were correlated, but moderation effects of M on the cross paths and on the variance components of the residual of T were absent. For each scenario, we simulated 2000 datasets each comprising Nmz = Ndz = 500 pairs. We then fitted to these datasets the standard univariate moderation model with moderator M modeled on the means (Fig. 1b), and then constrained either β _a, β _c, or β _e to zero to test for the significance of each parameter individually, i.e., a 1-df test. The difference between the −2 log-likelihood of the full model (the specific moderation parameter estimated freely) and the −2 log-likelihood of the restricted model (the specific moderation parameter fixed to 0), denoted as χ²_diff, is χ²-distributed. Since moderation parameters β _a, β _c, and β _e were zero in these simulated data, we expect the distribution of the χ²_diff as calculated across all 2000 data sets to follow a central χ²(1) distribution. Given an nominal α of .05, we expected 5% of χ²_diff test to be significant, i.e., larger than the critical value of 3.84.

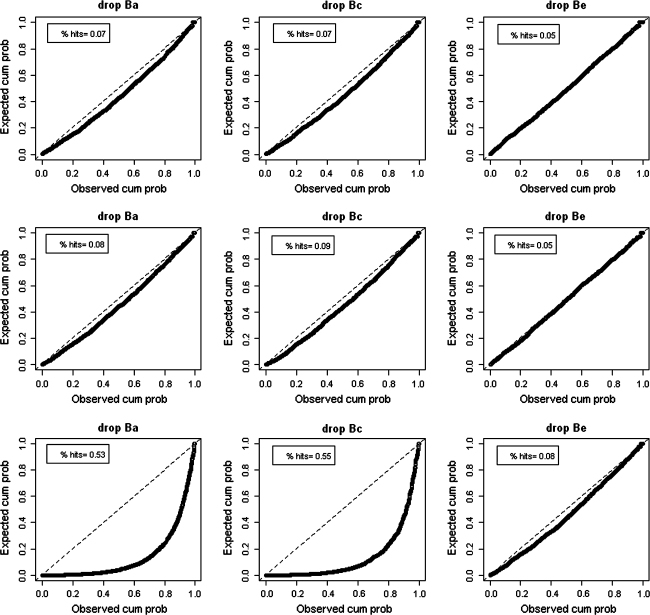
Figure 3 shows PP-plots for the simulations in which T and M are correlated via A (upper part), via C (middle part) or via E (lower part). In these plots, the p-values observed in the simulations are plotted against the nominal p-values. The observed p-value for each χ²_diff-value observed in the 2000 simulations, is calculated as the proportion of the remaining 1999 χ²_diff-values that is equal to or larger than this specific χ²_diff-value. The nominal p-value for each χ²_diff-value observed in the 2000 simulations, is obtained by reference to the χ²(1)-distribution. Deviations from the 45° line show whether the use of the regular χ²(1) test would result in conservative (above the line) or liberal (below the line) decision. The figures also show the percentage of hits calculated across the 2000 simulations. Given α = .05, the percentage of hits is expected to be close to 5%. Note that the standard error of the ML estimator of the p-value in the simulations is calculated as sqrt(p * (1 − p)/N), where p denotes the percentage of significant tests observed in the simulations (nominal p-value) given a chosen α, and N the total number of simulations. The 95% confidence interval for a correct nominal p-value of .05 (given α = .05) and N = 2000 thus corresponds to CI-95 = (p − 1.96 * SE, p + 1.96 * SE), and thus equals .04–.06. This implies that, given α = .05, any observed nominal p-value outside the .04–.06 range should be considered incorrect: p-values <.04 suggest that the model is too conservative, while p-values >.06 suggest that the model is too liberal.

Fig. 3.

PP-plots for the univariate moderation model in Simulation study 1, in which T and M are correlated exclusively via A (upper part), exclusively via C (middle part), or exclusively via E (lower part). Deviations from the 45° line show whether the use of the regular χ²(1) test would result in conservative (above the line) or liberal (below the line) decision. % hits denotes the percentage of likelihood-ratio tests smaller than the critical value 3.84 (i.e., significant given α = .05). A hit rate of .05 is expected given α = .05, and given that moderation effects were absent in the data. Hit rates outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high)

The results of Simulation study 1 as depicted in Fig. 3 are summarized in Table 2, which also includes results for some additional simulations settings. In testing β _a under these three scenarios, the number of false positives (i.e., χ²_diff tests >3.84) was inflated if the correlation between T and M ran via A or C: 6.85 and 7.60%, rather than 5%, respectively. If the correlation between T and M ran via E, however, the false positive rate was even more seriously inflated: 53.23%. This inflation is clearly visible in Fig. 3 (PP-plot lower left corner). Similar results were obtained for the tests of β _c: if the correlation between T and M ran via A or C, the false positive rate was 6.85 and 8.75%, respectively, while the false positive rate was 55.33% if the correlation between T and M ran via E. In testing for the significance of β _e, the false positive rate was only significantly elevated if the correlation between T and M ran via E (7.50%), but not if the correlation ran via A or C (4.57 and 5.26%, respectively). The additional simulations summarized in Table 2 show that the false positive rate of the univariate moderation model is a) correct if M₁ and M₂ are unrelated, i.e., when the variance in M is completely due to nonshared environmental influences E, b) slightly too low if M₁ and M₂ are correlated 1, i.e., when the variance in M is completely due to shared environmental influences C, and c) correct if the covariance between M and T runs in equal proportions via A, C and E. This latter result shows that the extent to which the false positive rate of the univariate moderation model is elevated depends on the specific mix of, or ratio in which, A, C and E contribute to the covariance between M and T since the positive and negative semi-partial correlations as described in Table 1 can more or less cancel each other out.

Table 2.

Results Simulation study 1: false positive rates under Purcell’s univariate moderation model

		Drop β a	Drop β c	Drop β e
Settings Simulation study 1
r(T,M) = .24 via A only	% hits	.07	.07	.05
r(T,M) = .24 via C only	% hits	.08	.09	.05
r(T,M) = .24 via E only	% hits	.53	.55	.08
Additional simulations
r(T,M) = .24 via A, C and E in equal proportionsa	% hits	.04	.05	.07
r(T,M) = .62 via A, C and E in equal proportionsb	% hits	.05	.05	.06
r(M1,M2) = 0c	% hits	.05	.05	.04
r(M1,M2) = 1d	% hits	.03	.03	.05

Note: The first three simulation settings are described under Simulation study 1. β _a, β _c, and β _e denote the moderation parameters on the variance components unique to T (see Fig. 1). For all settings, 2000 datasets were simulated and analyzed. % hits denotes the percentage of likelihood-ratio tests smaller than the critical value 3.84 (i.e., significant given α = .05). A hit rate of .05 is expected given α = .05, and given that moderation effects were absent in the data. Hit rates outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high)

^aLoadings of the cross paths for A, C and E all equaled \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.02} $$\end{document}

^bLoadings of the cross paths for A, C and E all equaled \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.13} $$\end{document}

^cM₁ and M₂ are uncorrelated between twins, i.e., fully E

^dM₁ and M₂ are correlated 1 between twins, i.e., fully C

Summarizing, Simulation study 1 shows that under the univariate moderation model, in which T₁ is corrected for M₁ only, and T₂ is corrected for M₂ only, the false positive rate can be (much) higher than the nominal α-level, especially if the correlation between T and M runs predominantly via E.

Solution: extension of the univariate moderation model?

In this section we aim to investigate whether we can solve the problems that can result from non-zero semi-partial correlations by extending the univariate moderation model. An obvious solution is to extend the means model such that the trait value of twin 1 is not only corrected for the moderator value of twin 1, but also for any residual association to the moderator value of the co-twin, as this would result in a residual \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ T_{1}^{\prime \prime } $$\end{document} (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ T_{2}^{\prime \prime } $$\end{document}) that is uncorrelated to both M₁ and M₂. Taking into account the way regression coefficients in a multiple regression model with two predictors are calculated, it is easy to show that the parameters in the means models should generally also differ across zygosity.

Consider the regression of T₁ on both M₁ and M₂:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{T}}_{ 1} = \beta_{0} + \beta_{ 1} *{\text{M}}_{ 1} + \beta_{2} * {\text{M}}_{ 2} $$\end{document} 5

where β ₀ denotes the intercept, and β ₁ and β ₂ denote the regression weight of M₁ and M₂, respectively. Regression weight β ₁ is a measure of the relationship between T₁ and M₁ while controlling for M₂, and is in the completely standardized case calculated as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta_{1} = \frac{{r_{t1,m1} - r_{t1,m2} r_{m1,m2} }}{{1 - r_{m1,m2}^{2} }}. $$\end{document} 6

Similarly, regression weight β ₂ is a measure of the relationship between T₁ and M₂ while controlling for M₁, and is calculated as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta_{2} = \frac{{r_{t1,m2} - r_{t1,m1} r_{m1,m2} }}{{1 - r_{m1,m2}^{2} }}. $$\end{document} 7

Note that β ₂ = zero, if M₁ and M₂ are uncorrelated, because then r_m1,m2 = r_t1,m2 = 0, in which case this extension equals the general univariate model. Note also the similarity between Eqs. 6 and 7 and Eq. 4: the calculation of the regression weights in multiple regression with two predictors resembles the calculation of semi-partial correlations, except for the square root in the denominator. From Eqs. 6 and 7, it can be seen that β ₁ and β ₂ will only be equal across zygosity groups if both r_t2,m1 (= r_t1,m2) and r_m1,m2 are equal across zygosity, i.e., if neither M and the relation between M and T are affected by genetic factors. In all other situations, β ₁ and β ₂, and as a result β ₀, should be estimated separately in MZ and DZ twins, allowing their values to differ across zygosity. Allowing all three betas in the means model to differ across zygosity will result in a general extended univariate moderation model, the specification of which is independent of the nature of the correlations between M and T and M₁ and M₂. This extension implies that β ₀, β ₁ and β ₂ need to be different across MZ and DZ groups, so that the means models for MZ and DZ twins 1 and 2 become:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} {\text{MZ:}}\quad {\text{T}}_{ 1} & = \beta_{{0,{\text{mz}}}} + \beta_{{1,{\text{mz}}}} *{\text{M}}_{ 1} + \beta_{{1,{\text{mz}}}} *{\text{M}}_{ 2} , \\ {\text{T}}_{ 2} & = \beta_{{0,{\text{mz}}}} + \beta_{{1,{\text{mz}}}} *{\text{M}}_{ 2} + \beta_{{2,{\text{mz}}}} *{\text{M}}_{ 1} , \\ \end{aligned} $$\end{document} 8

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} {\text{DZ:}}\quad {\text{T}}_{ 1} & = \beta_{{0,{\text{dz}}}} + \beta_{{ 1 , {\text{dz}}}} *{\text{M}}_{ 1} + \beta_{{2,{\text{dz}}}} *{\text{M}}_{ 2} , \\ {\text{T}}_{ 2} & = \beta_{{0,{\text{dz}}}} + \beta_{{1,{\text{dz}}}} *{\text{M}}_{ 2} + \beta_{{2,{\text{dz}}}} *{\text{M}}_{ 1} . \\ \end{aligned} $$\end{document} 9

With 12 parameters (6 to describe the variance part of the model: 3 related, and 3 unrelated to the moderator; and 6 parameters to describe the means models: 3 for MZ twins, and 3 for DZ twins), this extended univariate moderation model is still more parsimonious than the bivariate moderation model (17 parameters of which 15 concern the variance decomposition). We conducted Simulation study 2 to investigate whether the false positive rate of this extended univariate moderation model is correct, and comparable to the false positive rate of the full bivariate moderation model.

Simulation study 2

To investigate whether the extended univariate moderation model results in the correct false positive rate of 5%, we re-analyzed the data-sets created under Simulation study 1 using the extended univariate moderator model. Again we tested the significance of moderator parameters β _a, β _c and β _e. As these parameters were simulated to be zero, we expected the χ²_diff to be χ(1) distributed across the 2000 datasets, independent of whether T and M were correlated via A, via C, or via E. In addition, these same data sets were analyzed using the full bivariate moderation model (as depicted in Fig. 1a) in which all 17 parameters were estimated freely (Note that we did not use the full bivariate moderation model to analyze the data with r_M1,M2 = 1 or r_M1,M2 = 0 because in practice one would never choose a bivariate parameterization under these circumstances).

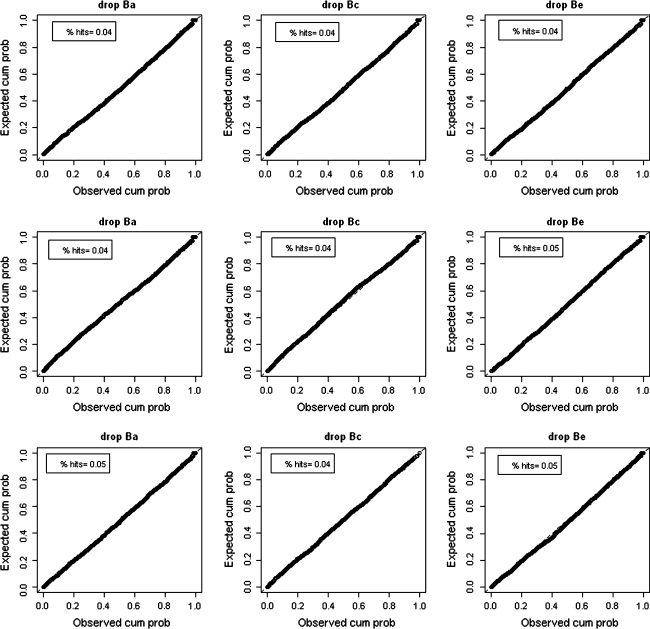
The results for both the extended univariate moderation model and the full bivariate moderation model are described in Table 3, and depicted as PP-plots in Fig. 4 for the extended univariate moderation model. The false positive rate of the extended univariate moderator model is in most cases not significantly different from 5%, and where it is (when variance in M is completely due to C, and thus r_M1,M2 = 1), it is too low, i.e. the test is too conservative. In contrast, the false positive rate of the full bivariate model is always too low, and significantly lower than the false positive rate of the extended univariate model, when testing β _a or β _c, irrespective of the nature of the correlation between M and T. Apparently, slight misfit in the full bivariate moderation model resulting from dropping one parameter can quite easily be accommodated by adjustment of the remaining parameters, resulting in a too low false positive rate. In addition, it is important to realize that the variance components unique to trait T under the bivariate model (A_u, C_u and E_u in Fig. 1a) are not the same as the variance components of the residual T″ in the extended univariate parameterization. In Appendix 1, we show how the residual T″ is calculated when M and T are correlated via A, or C, or E. The fact that the variance decomposition of T″ is not the same under the bivariate and the univariate moderation model implies that either model can constitute a more or less erroneous approximation, depending on the real data generating process, which is generally unknown.

Table 3.

Results Simulation study 2: false positive rates under the extended univariate moderation model and the full bivariate moderation model when the covariance between T and M is not moderated

	Drop β a		Drop β c		Drop β e
	% hits	nsim	% hits	nsim	% hits	nsim
rM,T .24 via A
Ext univariate	.04	2000	.04	2000	.04	1998
Full bivariate	.01	2000	.01	2000	.04	2000
	p < .001		p < .001		p = .88
rM,T .24 via C
Ext univariate	.04	2000	.04	2000	.05	2000
Full bivariate	.01	1999	.01	1998	.04	2000
	p < .001		p < .001		p = .08
rM,T .24 via E
Ext univariate	.05	1998	.04	1999	.05	1999
Full bivariate	.01	1996	.01	1996	.05	2000
	p < .001		p < .001		p = .65
rM,T = .24 via A, C and E in equal proportions
Ext univariate	.04	2000	.05	2000	.05	2000
Full bivariate	.02	2000	.01	2000	.05	2000
	p < .005		p < .001		p = .43
rM,T = .62 via A, C and E in equal proportions
Ext univariate	.05	1998	.05	2000	.05	2000
Full bivariate	.02	2000	.02	2000	.05	2000
	p < .001		p < .001		p = .94
rM1,M2 = 0 (fully E), rM,T = .24
Ext univariate	.05	1999	.05	2000	.04	1999
rM1,M2 = 1 (fully C), rM,T = .24
Ext univariate	.03	2000	.03	2000	.05	1999

Note: β _a, β _c, and β _e denote the moderation parameters on the variance components unique to T (see Fig. 1). nsim denotes the number of data sets (out of 2000) for which the extended univariate moderation model and the full bivariate moderation model converged without problems. % hits denotes the percentage (of the nsim converged models) that the likelihood-ratio test was smaller than the critical value 3.84 (i.e., significant given α = .05). % hits outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high). The p-values concern p-values of the binomial test for comparing two proportions, used to test whether the number of hits under the extended univariate moderation model is significantly different from the number of hits under the full bivariate moderation model. Note that the full bivariate moderation model was not used to analyze data generated according to the final two settings (r_M1,M2 = 0 and r_M1,M2 = 1) because one would never use a bivariate model for data with such a variance–covariance structure

Fig. 4.

PP-plots for the extended univariate moderation model in Simulation study 2, in which T and M are correlated exclusively via A (upper part), exclusively via C (middle part), or exclusively via E (lower part). Deviations from the 45° line show whether the use of the regular χ²(1) test would result in conservative (above the line) or liberal (below the line) decision. % hits denotes the percentage of likelihood-ratio tests smaller than the critical value 3.84 (i.e., significant given α = .05). A hit rate of .05 is expected given α = .05, and given that moderation effects were absent in the data. Hit rates outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high)

Summarizing the results of Simulation study 2, we conclude that the extension of the univariate moderation model avoids the inflated false positive scores that were observed for the standard univariate moderation model, while the full bivariate moderation model actually proved too conservative. However, Simulation studies 1 and 2 concerned scenarios in which the covariance between M and T was itself not subject to moderation, i.e., β _ac, β _cc, and β _ec on the cross paths between M and T in Fig. 1a were fixed to 0. That is, the covariance between M and T did not dependent on the level of M. In practice, however, it is possible that the covariance between M and T fluctuates as a function of M. Simulation study 3 was conducted to investigate the false positive rate of the extended univariate and the full bivariate moderation models in the context of data in which the covariance between M and T is moderated. These simulations are of specific interest since moderator-dependent variation in the strength of the covariance between M and T is not well accommodated by the estimated regression parameters β _0,MZ, β _1,MZ, β _2,MZ, β _0,DZ, β _1,DZ, and β _2,DZ in Eqs. 8 and 9, and problems are therefore to be expected for the extended univariate moderation model.

Simulation study 3

We again simulated data for standard normally distributed moderator M and trait T in 500 MZ and 500 DZ twin pairs. Suppose again that A, C, and E account for 40%, 30%, and 30%, respectively, of the variance in M. The parts of the cross paths between M and T that do not depend on M (a _c, c _c, and e _c in Fig. 1a) are all set to .05, and A, C, and E unique to T (a _u, c _u, and e _u in Fig. 1a) are set to .35, .25 and .25, respectively. That is, if moderation is fully absent, the correlation between M and T equals .39, while genetic and (common) environmental effects explain 40%, 30% and 30% of the variance in T, respectively. We now introduce moderation on the cross paths by setting either β _ac, β _cc, or β _ec to .10. Moderation on the unique parts of T is, however, absent (i.e., β _a, β _c, and β _e in Fig. 1a are set to 0). For each of these settings we simulated 2000 data sets. Note that we deliberately choose the moderation parameters on the cross paths to be quite substantial: if the false positive rate of the extended univariate model is affected by moderation of the cross paths, then we are sure to pick it up. If the false positive rate of the extended univariate model is not affected by moderation of the cross paths, then the size of this moderation should not matter.

We then fitted to these datasets a) the full bivariate moderation model including all 17 parameters, and b) the extended univariate moderation model in which both moderators M₁ and M₂ are modeled on the means with means parameters differing across zygosity (Eqs. 8 and 9). Within these models we constrained either β _a, β _c, or β _e to zero to test for the significance of each parameter individually, i.e., a 1-df test. Since moderation parameters β _a, β _c, and β _e were simulated as 0 in these data, we expect the distribution of the χ²_diff as calculated across all 2000 data sets to follow a central χ²(1) distribution. Given an nominal α of .05, we expected 5% of χ²_diff test to be significant, i.e., larger than the critical value of 3.84.

The results of these simulations are summarized in Table 4. When moderation on the cross paths is absent (Baseline: β _ac = β _cc = β _ec = 0), the false positive rate of the extended univariate model is correct, while the false positive rate of the full bivariate model is deflated for β _au and β _cu. The false positive rate of the full bivariate model, however, remains largely unchanged when moderation on the cross paths is introduced. In contrast, the false positive rate of the extended univariate model becomes considerably inflated, especially for β _a and β _c. Clearly, when the covariance between M and T is not stable across levels of M, the sample-wise regression coefficients β _0,MZ, β _1,MZ, β _2,MZ, β _0,DZ, β _1,DZ, and β _2,DZ in Eqs. 8 and 9 do not sufficiently accommodate the varying association between M and T. As a result, the remaining moderation, which is actually located on the cross paths, is now picked up in the extended univariate moderation model as if it were located on the unique paths of T. Additional simulations (not shown), in which either β _ac , β _cc or β _ec equaled .10 while the other two cross path moderation parameters equaled .05, showed even higher hit rates for the extended univariate model (up to 65%), while the hit rate of the full bivariate moderation model remained .05 or lower.

Table 4.

Results Simulation study 3: false positive rates under the extended univariate moderation model and the full bivariate moderation model when the covariance between T and M is moderated

	Drop β a		Drop β c		Drop β e
	% hits	nsim	% hits	nsim	% hits	nsim
Baseline: β ac = β cc = β ec = 0
Ext univariate	.05	1999	.05	2000	.05	1999
Full bivariate	.02	2000	.01	2000	.05	2000
	p < .001		p < .001		p = .42
β ac = .10; β cc = β ec = 0
Ext univariate	.18	1998	.18	1999	.08	1996
Full bivariate	.03	2000	.02	2000	.06	2000
	p < .001		p < .001		p < .01
β cc = .10; β ac = β ec = 0
Ext univariate	.13	2000	.13	1999	.07	1999
Full bivariate	.02	2000	.02	2000	.05	2000
	p < .001		p < .001		p < .01
β ec = .10; β ac = β cc = 0
Ext univariate	.23	2000	.23	1998	.08	1997
Full bivariate	.02	2000	.01	2000	.04	2000
	p < .001		p < .001		p < .001

Note: β _a, β _c , and β _e denote the moderation parameters on the variance components unique to T; β _ac, β _cc, and β _ec denote the moderation parameters on the cross paths between M and T (see Fig. 1). nsim denotes the number of data sets (out of 2000) for which the extended univariate moderation model and the full bivariate moderation model converged without problems. % hits denotes the percentage (of the nsim converged models) that the likelihood-ratio test was smaller than the critical value 3.84 (i.e., significant given α = .05). % hits outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high). The p-values concern p-values of the binomial test for comparing two proportions, used to test whether the number of hits under the extended univariate moderation model is significantly different from the number of hits under the full bivariate moderation model

In summary, the results of Simulation study 3 show that the extended univariate moderation model can be used as a moderation detection method, but is not very suited to establish the exact location of the moderation as it cannot distinguish moderation on cross paths from moderation on the unique paths of T.

False negatives

We have shown that the false positive rate (i.e., type I error rate) is correct under the extended univariate moderation model, but only if the covariance between M and T is free of moderation by M. We now address the false negative rate, i.e., the type II error, of the extended univariate moderation model compared to the full bivariate model. In a fourth and fifth simulation study, we investigate whether the false negative rate of the extended univariate moderation model is comparable to the false negative rate of the bivariate moderation model when the covariance between M and T is not subject to moderation (Simulation study 4) or when this covariance is subject to moderation as well (Simulation study 5).

Simulation study 4

Data were simulated as described in Simulation study 1, with moderation on the cross paths being absent. We now, however, introduced moderation on the paths unique to T, with moderation parameters being either β _a = .08, or β _c = .10, or β _e = .035 (As shown in Table 5, the power to detect moderation on E variance is much greater than the power to detect moderation of A or C variance, which is why β _e was chosen much smaller than both β _a and β _c). Note that the effect size of the chosen moderation parameters depends on the nature of the correlation between T and M. For example, β _a was set at .08. If the correlation ran via C or E, then the genetic variance of trait T was calculated as (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document} + .08 * M)². If the correlation between T and M ran via A, however, then the genetic variance of T was calculated as .15 + (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.25} $$\end{document} + .08 * M)², where .15 is associated with the cross-path relating T and M.

Table 5.

Results Simulation study 4: false negative rates under the extended univariate moderation model and the full bivariate moderation model when the covariance between T and M is not moderated

	Drop β a		Drop β c		Drop β e
	% hits	nsim	% hits	nsim	% hits	nsim
T and M correlated via A
Ext univariate	.20	1999	.31	1998	.48	2000
Full bivariate	.07	1998	.21	2000	.50	2000
	p < .001		p < .001		p = .47
T and M correlated via C
Ext univariate	.27	1999	.16	1999	.47	2000
Full bivariate	.25	2000	.03	1998	.48	2000
	p = .18		p < .001		p = .95
T and M correlated via E
Ext univariate	.48	1999	.47	1999	.91	1997
Full bivariate	.25	1998	.28	1989	.91	2000
	p < .001		p < .001		p = .83

Note: β _a, β _c and β _e denote the moderation parameters on the variance components unique to T (see Fig. 1). nsim denotes the number of data sets (out of 2000) for which the extended univariate moderation model and the full bivariate moderation model converged without problems. % hits denotes the percentage (of the nsim converged models) that the likelihood-ratio test was smaller than the critical value 3.84 (i.e., significant given α = .05). % hits outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high). The p-values concern p-values of the binomial test for comparing two proportions, used to test whether the number of hits under the extended univariate moderation model is significantly different from the number of hits under the full bivariate moderation model

For each of these 9 settings (r_t,m runs via A, C or E, and moderation is present on either A, C, or E) we simulated 2000 datasets and analyzed these using either the full bivariate moderation model (estimating moderation parameters on the cross paths as well as on the paths unique to T) or the extended univariate moderation model (estimating moderation on the variance components of the residual T″). We then tested whether the moderation parameter of interest (either β _a, or β _c, or β _e) was significant given α = .05.

The results of these simulations are presented in Table 5. In 5 out of 9 scenarios, the power of the extended univariate moderation model was significantly higher than the power of the full bivariate moderation model. Note that we can indeed speak of higher power because we know from the results of Simulation study 2 that the false positive rate of neither models is inflated. The lower power of the full bivariate moderation model is probably due to the variance being decomposed into as many as 15 parameters, compared to the 6 of the extended univariate moderation model: misfit resulting from fixing one of the moderation parameters to zero can more easily be absorbed by the remaining 14 parameters.

Simulation study 5

Data were simulated as described in Simulation study 3 with covariance between M and T running via A, C and E, and moderation on the cross paths was introduced by setting either β _ac, β _cc, or β _ec to .10 (see Table 6 for description of the scenarios). Moderation on the unique parts of T was now simulated to be present as well, with moderation parameters being either β _a = .08, or β _c = .10, or β _e = .035 (as in Simulation study 4). For each scenario, we simulated 2000 datasets and analyzed these using both the full bivariate moderation model (estimating moderation parameters on the cross paths as well as on the paths unique to T) and the extended univariate moderation model (estimating moderation on the variance components of the residual T″). We then tested whether the moderation parameter of interest (either β _a, or β _c, or β _e) was significant given α = .05.

Table 6.

Results Simulation study 5: false negative rates under the extended univariate moderation model and the full bivariate moderation model when the covariance between T and M is moderated

	Drop β a		Drop β c		Drop β e
	% hits	nsim	% hits	nsim	% hits	nsim
Baseline: β ac = β cc = β ec = 0
Ext univariate	.29	2000	.34	1996	.56	1999
Full bivariate	.25	2000	.26	1999	.57	2000
	p < .01		p < .001		p = .72
β ac = .10; β cc = β ec = 0
Ext univariate	.35	1989	.17	1997	.07	1998
Full bivariate	.23	2000	.03	2000	.05	2000
	p < .01		p < .001		p = .01
β cc = .10; β ac = β ec = 0
Ext univariate	.14	1996	.45	1995	.07	1998
Full bivariate	.04	2000	.25	2000	.05	2000
	p < .01		p < .001		p = .03
β ec = .10; β ac = β cc = 0
Ext univariate	.22	1996	.22	1998	.50	1995
Full bivariate	.02	2000	.01	2000	.57	2000
	p < .01		p < .001		p < .001

Note: β _a, β _c , and β _e denote the moderation parameters on the variance components unique to T; β _ac, β _cc, and β _ec denote the moderation parameters on the cross paths between M and T (see Fig. 1). nsim denotes the number of data sets (out of 2000) for which the extended univariate moderation model and the full bivariate moderation model converged without problems. % hits denotes the percentage (of the nsim converged models) that the likelihood-ratio test was smaller than the critical value 3.84 (i.e., significant given α = .05). % hits outside the .04–.06 range should be considered incorrect (i.e., significantly too low or too high). The p-values concern p-values of the binomial test for comparing two proportions, used to test whether the number of hits under the extended univariate moderation model is significantly different from the number of hits under the full bivariate moderation model

The results of these simulations are presented in Table 6. In all scenarios, the extended univariate moderation model picks up moderation more often than the full bivariate moderation model. However, these results can, except for the Baseline model, not be interpreted as the extended univariate moderation model having more power than the full bivariate moderation model. Given the results of Simulation study 3, which showed that the extended moderation model picks up the moderation on the cross paths as if it is moderation on the unique paths, we conclude that the power of the extended univariate moderation model is too high, or at least that the location of the moderation that is detected, is uncertain. That is, β _a, β _c, and β _e are biased in the extended univariate moderation model because the moderation on the cross paths (β _ac, β _cc, and β _ec) is not adequately accommodated by the regression coefficients in the means part of the model.

Discussion

In this paper, we showed that the univariate moderation model proposed by Purcell (2002) produces (highly) inflated false positive rates if the moderator M is correlated between twins, and M and T are correlated as well. We investigated an extension of this model as a solution to this problem, and conclude that the extended univariate moderation model works well, but only if moderation on the covariance between M and T is absent. Moderation of the covariance between M and T is, however, not accommodated adequately in the extended univariate moderation model, and as a result, moderation of the covariance is picked up as moderation on the variance components unique to T. In the absence of moderation of the covariance between M and T, the extended univariate moderation model is actually more powerful than the full bivariate moderation model, but in the presence of moderation of the covariance between M and T, the extended univariate moderation model detects moderation of the variance components unique to T, as such misspecifying the actual location of the moderation.

Fortunately, most published papers in which the univariate moderation model was used concern moderation effects of family-level moderators such as SES, parental educational attainment level, or the age of the twins, i.e., variables that are by definition equal in both twins. As we have shown, non-zero semi-partial correlations are not a problem in that case and the false positive rate is rather too low than too high (i.e., the model is slightly conservative). In a few published papers, however, moderators were studied that did show variation between twins (e.g., McCaffery et al. 2008, 2009; Timberlake et al. 2006: moderators under study were educational attainment level of the twins, exercise level of the twins, and the twins’ self-reported religiosity, respectively). Whether the moderation effects reported in these papers are genuine or spurious (i.e., the result of non-zero semi-partial cross-trait cross-twin correlations) depends, as we have shown, on the nature of the correlation between T and M, on the nature of the correlation between M₁ and M₂, and on the absence or presence of moderation of the covariance between M and T. Re-analysis of these data using the full bivariate moderation model, or the extended univariate moderation model if the presence of moderation of the covariance has been excluded, is advised. Overall, we conclude that researchers should use the full bivariate moderation model to study the presence of moderation on the covariance between M and T. If such moderation can be ruled out, subsequent use of the extended univariate moderation model is recommended as this model is more powerful than the full bivariate moderation model.

Appendix 1

In this appendix we derive the residual covariance matrix of T″ in MZ and DZ twins after partialling out the effects of M₁ and M₂.

SolveT″

Let us suppose that T and M are correlated exclusively via C. The expected variance–covariance matrix of M₁, M₂, T₁ and T₂ in the MZ twins is:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{tot,MZ} = \left[ {\begin{array}{*{20}c} {\Upsigma_{M} } & {\Upsigma_{MT} } \\ {\Upsigma_{TM} } & {\Upsigma_{T} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{1}^{2} + c_{1}^{2} + e_{1}^{2} } & {a_{1}^{2} + c_{1}^{2} } & {c_{12} c_{1} } & {c_{12} c_{1} } \\ {a_{1}^{2} + c_{1}^{2} } & {a_{1}^{2} + c_{1}^{2} + e_{1}^{2} } & {c_{12} c_{1} } & {c_{12} c_{1} } \\ {c_{12} c_{1} } & {c_{12} c_{1} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } \\ {c_{12} c_{1} } & {c_{12} c_{1} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } \\ \end{array} } \right] $$\end{document}

and, in the DZ twins:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{tot,DZ} = \left[ {\begin{array}{*{20}c} {\Upsigma_{M} } & {\Upsigma_{MT} } \\ {\Upsigma_{TM} } & {\Upsigma_{T} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{1}^{2} + c_{1}^{2} + e_{1}^{2} } & {.5a_{1}^{2} + c_{1}^{2} } & {c_{12} c_{1} } & {c_{12} c_{1} } \\ {.5a_{1}^{2} + c_{1}^{2} } & {a_{1}^{2} + c_{1}^{2} + e_{1}^{2} } & {c_{12} c_{1} } & {c_{12} c_{1} } \\ {c_{12} c_{1} } & {c_{12} c_{1} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } & {.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } \\ {c_{12} c_{1} } & {c_{12} c_{1} } & {.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } \\ \end{array} } \right] $$\end{document}

Note that all elements in Σ_TM = Σ_MT are equal (c₁₂c₁): i.e., when the correlation between M and T runs via C, then r_t1,m1 = r_t1,m2 = r_t2,m1 = r_t2,m2. We use \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{\text{T}}^{*} $$\end{document} to denote the covariance matrix of T after correction for M₁ and M₂. Without loss of generalization, we assume that T and M are both standardized:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} Var(M) & = a_{1}^{2} + c_{1}^{2} + e_{1}^{2} = 1 \\ Var(T) & = a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} = 1 \\ \end{aligned} $$\end{document}

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{\text{T}}^{*} $$\end{document} then equals:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{T}^{*} = \Upsigma_{T} - \Upsigma_{TM} \Upsigma_{M}^{ - 1} \Upsigma_{TM}^{t} = \Upsigma_{T} - \Upsigma_{\Updelta } , $$\end{document}

where superscript t denotes transposition and −1 denotes the inversion.

It can be shown that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{\Updelta ,MZ} = \left[ {\begin{array}{*{20}c} {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{\Updelta ,DZ} = \left[ {\begin{array}{*{20}c} {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right]. $$\end{document}

Note that all elements in Σ_Δ,MZ are equal because all elements in Σ_TM = Σ_MT are equal (c₁₂c₁). Likewise, all elements in and Σ_Δ,DZ are equal, yet different from the elements in Σ_Δ,MZ when the variable for which the trait is corrected is itself influenced by genetic factors (in the denominator a²₁ for MZ twins versus .5a²₁ for DZ twins). We can now calculate \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{\text{T}}^{*} $$\end{document} for both MZ and DZ twins:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} \Upsigma_{T,MZ}^{*} & = \left[ {\begin{array}{*{20}c} {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } \\ {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {1 - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {(a_{2}^{2} + c_{2}^{2} + c_{12}^{2} ) - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ {(a_{2}^{2} + c_{2}^{2} + c_{12}^{2} ) - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {1 - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right] \\ \end{aligned} $$\end{document}

and

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} \Upsigma_{T,DZ}^{*} & = \left[ {\begin{array}{*{20}c} {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } & {.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } \\ {.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} } & {a_{2}^{2} + c_{2}^{2} + c_{12}^{2} + e_{2}^{2} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {1 - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {(.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} ) - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ {(.5a_{2}^{2} + c_{2}^{2} + c_{12}^{2} ) - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} & {1 - \frac{{2c_{12}^{2} c_{1}^{2} }}{{1 + .5a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right] \\ \end{aligned} $$\end{document}

Because Σ_Δ differs across zygosity, the diagonal elements of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{\text{T}}^{*} $$\end{document} also differ across zygosity, i.e., MZ and DZ twins have different residual variances. The extent of the difference depends on the extent to which the moderator is affected by genetic factors (i.e., the residual variances of MZ and DZ twins will be more different if the genetic influences on M are larger, i.e., if a²₁ is larger), and the nature of the correlation between T and M, i.e., the elements in Σ_TM.

If T and M are correlated via C, all elements in Σ_TM are identical (i.e., c₁₂c₁). If T and M are exclusively correlated via E, then Σ_TM is again identical for MZ and DZ twins, and equals:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{TM} = \left[ {\begin{array}{*{20}c} {e_{12} e_{1} } & 0 \\ 0 & {e_{12} e_{1} } \\ \end{array} } \right]. $$\end{document}

It can be shown that:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{gathered} \Upsigma_{\Updelta ,MZ} = \left[ {\begin{array}{*{20}c} {\frac{{e_{21}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & { - e_{21}^{2} } \\ { - e_{21}^{2} } & {\frac{{e_{21}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{\Updelta ,DZ} = \left[ {\begin{array}{*{20}c} {\frac{{e_{21}^{2} e_{1}^{2} }}{{1 - \left( {\tfrac{1}{2}a_{1}^{2} + c_{1}^{2} } \right)^{2} }}} & {\frac{{ - e_{21}^{2} e_{1}^{2} }}{{\tfrac{1}{2}a_{1}^{2} + e_{1}^{2} }}} \\ {\frac{{ - e_{21}^{2} e_{1}^{2} }}{{\tfrac{1}{2}a_{1}^{2} + e_{1}^{2} }}} & {\frac{{e_{21}^{2} e_{1}^{2} }}{{1 - \left( {\tfrac{1}{2}a_{1}^{2} + c_{1}^{2} } \right)^{2} }}} \\ \end{array} } \right],\;{\text{and}}\;{\text{that}} \hfill \\ \Upsigma_{T,MZ}^{*} = \left[ {\begin{array}{*{20}c} {1 - \frac{{e_{21}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {a_{2}^{2} + c_{2}^{2} + e_{21}^{2} } \\ {a_{2}^{2} + c_{2}^{2} + e_{21}^{2} } & {1 - \frac{{e_{21}^{2} }}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{T,DZ}^{*} = \left[ {\begin{array}{*{20}c} {1 - \frac{{e_{21}^{2} e_{1}^{2} }}{{1 - \left( {\tfrac{1}{2}a_{1}^{2} + c_{1}^{2} } \right)^{2} }}} & {\tfrac{1}{2}a_{2}^{2} + c_{2}^{2} + \frac{{e_{21}^{2} e_{1}^{2} }}{{\tfrac{1}{2}a_{1}^{2} + e_{1}^{2} }}} \\ {\tfrac{1}{2}a_{2}^{2} + c_{2}^{2} + \frac{{e_{21}^{2} e_{1}^{2} }}{{\tfrac{1}{2}a_{1}^{2} + e_{1}^{2} }}} & {1 - \frac{{e_{21}^{2} e_{1}^{2} }}{{1 - \left( {\tfrac{1}{2}a_{1}^{2} + c_{1}^{2} } \right)^{2} }}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$\end{document}

If T and M are exclusively correlated via A, then Σ_TM is not equal across zygosity:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{TM,MZ} = \left[ {\begin{array}{*{20}c} {a_{12} a_{1} } & {a_{12} a_{1} } \\ {a_{12} a_{1} } & {a_{12} a_{1} } \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{TM,DZ} = \left[ {\begin{array}{*{20}c} {a_{12} a_{1} } & {.5*a_{12} a_{1} } \\ {.5*a_{12} a_{1} } & {a_{12} a_{1} } \\ \end{array} } \right] $$\end{document}

and it can be shown that:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} \Upsigma_{\Updelta ,MZ} & = \left[ {\begin{array}{*{20}c} {\frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ {\frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {\frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right],\;{\text{and}} \\ \Upsigma_{\Updelta ,DZ} & = \left[ {\begin{array}{*{20}c} {\frac{{a_{21}^{2} a_{1}^{2} \left(1\tfrac{1}{4} - a_{1}^{2} - c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} & {\frac{{a_{21}^{2} a_{1}^{2} \left(1 - \tfrac{5}{8}a_{1}^{2} + \tfrac{10}{8}c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} \\ {\frac{{a_{21}^{2} a_{1}^{2} \left(1 - \tfrac{5}{8}a_{1}^{2} + \tfrac{10}{8}c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} & {\frac{{a_{21}^{2} a_{1}^{2} \left(1\tfrac{1}{4} - a_{1}^{2} - c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} \\ \end{array} } \right], \\ \end{aligned} $$\end{document}

and that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{gathered} \Upsigma_{T,MZ}^{*} = \left[ {\begin{array}{*{20}c} {1 - \frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {a_{2}^{2} + c_{2}^{2} - \frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ {a_{2}^{2} + c_{2}^{2} - \frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} & {1 - \frac{{2(a_{21}^{2} a_{1}^{2} )}}{{1 + a_{1}^{2} + c_{1}^{2} }}} \\ \end{array} } \right],\;{\text{and}} \hfill \\ \Upsigma_{T,DZ}^{*} = \left[ {\begin{array}{*{20}c} {1 - \frac{{a_{21}^{2} a_{1}^{2} \left(1\tfrac{1}{4} - a_{1}^{2} - c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} & {\tfrac{1}{2}a_{2}^{2} + c_{2}^{2} - \frac{{a_{21}^{2} a_{1}^{2} \left(1 - \tfrac{5}{8}a_{1}^{2} + \tfrac{10}{8}c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} \\ {\tfrac{1}{2}a_{2}^{2} + c_{2}^{2} - \frac{{a_{21}^{2} a_{1}^{2} \left(1 - \tfrac{5}{8}a_{1}^{2} + \tfrac{10}{8}c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} & {1 - \frac{{a_{21}^{2} a_{1}^{2} \left(1\tfrac{1}{4} - a_{1}^{2} - c_{1}^{2} \right)}}{{\tfrac{3}{4}a_{1}^{4} + c_{1}^{2} e_{1}^{2} + 1}}} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$\end{document}

Implication for the variance decomposition of the residual of T

Now that we know how the residual variances are calculated under the extended univariate moderation model when correlations between M and T run exclusively via A, C or E, we can fill in the values used in Simulation studies 1 and 2 to study the differences in variance decomposition between the full bivariate model and the extended univariate model (moderation is assumed absent).

In all these simulations we assumed

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{for}}\;{\text{MZ}}\;{\text{twins}}\quad \Upsigma_{M,MZ} = \Upsigma_{T,MZ} = \left[ {\begin{array}{*{20}c} 1 & {.7} \\ {.7} & 1 \\ \end{array} } \right] $$\end{document}

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{and}}\;{\text{for}}\;{\text{DZ}}\;{\text{twins}}\quad \Upsigma_{M,DZ} = \Upsigma_{T,DZ} = \left[ {\begin{array}{*{20}c} 1 & {.5} \\ {.5} & 1 \\ \end{array} } \right]. $$\end{document}

Simulation settings when T and M are correlated via C

(Notation/parameter names as used in Fig. 1a, settings as depicted in Fig. 2b):

MODERATOR

a_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document}; c_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}; e_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}, such that A_m = .4, C_m = .3, and E_m = .3

CROSS PATHS

a_c = 0; c_c = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.2} $$\end{document}; e_c = 0

TRAIT

a_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document}; c_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.1} $$\end{document}; e_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document} such that A_u = .4, C_u = .1 and E_u = .3

For both MZ and DZ twins, Σ_TM equals:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{TM} = \left[ {\begin{array}{*{20}c} {\sqrt {.3} \sqrt {.2} } & {\sqrt {.3} \sqrt {.2} } \\ {\sqrt {.3} \sqrt {.2} } & {\sqrt {.3} \sqrt {.2} } \\ \end{array} } \right]. $$\end{document}

The residual variance–covariance matrices equal

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{T,MZ}^{*} = \left[ {\begin{array}{*{20}c} {.9294118} & {.6294118} \\ {.6294118} & {.9294118} \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{T,DZ}^{*} = \left[ {\begin{array}{*{20}c} {.92} & {.42} \\ {.42} & {.92} \\ \end{array} } \right]. $$\end{document}

These residual matrices can be read into a program like Mx (Neale et al. 2006) and would subsequently under the extended univariate model yield unstandardized estimates of A_u, C_u and E_u of .4028, .2218, and .2993, respectively. The corresponding values of A_u, C_u and E_u in the bivariate model are .4, .1, and .3.

Simulation settings when T and M are correlated via E

MODERATOR

a_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document}; c_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}; e_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}, such that A_m = .4, C_m = .3, and E_m = .3

CROSS PATHS

a_c = 0; c_c = 0; e_c = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.2} $$\end{document}

TRAIT

a_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document}; c_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}; e_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.1} $$\end{document} such that A_u = .4, C_u = .3 and E_u = .1

So for both MZ and DZ twins, Σ_TM equals:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{TM} = \left[ {\begin{array}{*{20}c} {\sqrt {.3} \sqrt {.2} } & 0 \\ 0 & {\sqrt {.3} \sqrt {.2} } \\ \end{array} } \right]. $$\end{document}

such that the residual variance–covariance matrices equal

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{T,MZ}^{*} = \left[ {\begin{array}{*{20}c} {.882352} & {.782353} \\ {.782352} & {.882352} \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{T,DZ}^{*} = \left[ {\begin{array}{*{20}c} {.92} & {.54} \\ {.54} & {.92} \\ \end{array} } \right]. $$\end{document}

When these residual matrices are read into Mx, we get under the extended univariate model unstandardized estimates of A_u, C_u and E_u of values .5555, .2482, and .1001, respectively. The corresponding values of A_u, C_u and E_u in the bivariate model are .4, .3, and .1.

Simulation settings when T and M are correlated via A

MODERATOR

a_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.4} $$\end{document}; c_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}; e_m = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}, such that A_m = .4, C_m = .3, and E_m = .3

CROSS PATHS

a_c = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.15} $$\end{document}; c_c = 0; e_c = 0

TRAIT

a_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.25} $$\end{document}; c_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document}; e_u = \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sqrt {.3} $$\end{document} such that A_u = .25, C_u = .3 and E_u = .3

for MZ and DZ twins, Σ_TM equal:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{TM,MZ} = \left[ {\begin{array}{*{20}c} {\sqrt {.4} \sqrt {.15} } & {\sqrt {.4} \sqrt {.15} } \\ {\sqrt {.4} \sqrt {.15} } & {\sqrt {.4} \sqrt {.15} } \\ \end{array} } \right],\;{\text{and}}\;\Upsigma_{TM,DZ} = \left[ {\begin{array}{*{20}c} {\sqrt {.4} \sqrt {.15} } & {.5*\sqrt {.4} \sqrt {.15} } \\ {.5*\sqrt {.4} \sqrt {.15} } & {\sqrt {.4} \sqrt {.15} } \\ \end{array} } \right]. $$\end{document}

The residual variance–covariance matrices equal

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upsigma_{T,MZ}^{*} = \left[ {\begin{array}{*{20}c} {.9294118} & {.6294118} \\ {.6294118} & {.9294118} \\ \end{array} } \right],\,{\text{and}}\,\Upsigma_{T,DZ}^{*} = \left[ {\begin{array}{*{20}c} {.94} & {.47} \\ {.47} & {.94} \\ \end{array} } \right]. $$\end{document}

When these residual matrices are read into Mx, we would get under the extended univariate model unstandardized estimates of A_u, C_u and E_u of values .3372, .2975, and .3004, respectively. The corresponding values of A_u, C_u and E_u in the bivariate model are .25, .3, and .3.