Boosted classification trees result in minor to modest improvement in the accuracy in classifying cardiovascular outcomes compared to conventional classification trees

Abstract

Purpose: Classification trees are increasingly being used to classifying patients according to the presence or absence of a disease or health outcome. A limitation of classification trees is their limited predictive accuracy. In the data-mining and machine learning literature, boosting has been developed to improve classification. Boosting with classification trees iteratively grows classification trees in a sequence of reweighted datasets. In a given iteration, subjects that were misclassified in the previous iteration are weighted more highly than subjects that were correctly classified. Classifications from each of the classification trees in the sequence are combined through a weighted majority vote to produce a final classification. The authors' objective was to examine whether boosting improved the accuracy of classification trees for predicting outcomes in cardiovascular patients. Methods: We examined the utility of boosting classification trees for classifying 30-day mortality outcomes in patients hospitalized with either acute myocardial infarction or congestive heart failure. Results: Improvements in the misclassification rate using boosted classification trees were at best minor compared to when conventional classification trees were used. Minor to modest improvements to sensitivity were observed, with only a negligible reduction in specificity. For predicting cardiovascular mortality, boosted classification trees had high specificity, but low sensitivity. Conclusions: Gains in predictive accuracy for predicting cardiovascular outcomes were less impressive than gains in performance observed in the data mining literature.

Introduction

There is an increasing interest in using classification methods in clinical research. Classification methods allow one to assign subjects to one of a mutually exclusive set of outcomes or states. Accurate classification of disease or health states (disease present/absent) allows subsequent investigations, treatments and interventions to be delivered in an efficient and targeted manner. Similarly, accurate classification of health outcomes (e.g. death/survival, disease recurrence/disease remission; hospital readmission/non-readmission) allows appropriate medical care to be delivered.

Classification trees employ binary recursive partitioning methods to partition the sample into distinct subsets [1-4]. Within each subset, subjects are classified according to the outcome that occurred for the majority of subjects in that subset. At the first step, all possible dichotomizations of all continuous variables (above vs. below a given threshold) and of all categorical variables are considered. Using each possible dichotomization, all possible ways of partitioning the sample into two distinct subsets are considered. The binary partition that results in the greatest reduction in misclassification is selected. Each of the two resultant subsets is then partitioned recursively, until predefined stopping rules are achieved. Advocates for classification trees have suggested that these methods allow for the construction of easily interpretable decision rules that can be easily applied in clinical practice. Furthermore, classification and regression tree methods are adept at identifying important interactions in the data [5-7] and in identifying clinical subgroups of subjects at very high or very low risk of adverse outcomes [8]. Advantages of tree-based methods are that they do not require that one parametrically specify the nature of the relationship between the predictor variables and the outcome. Additionally, assumptions of linearity that are frequently made in conventional regression models are not required for tree-based methods. While their use in clinical research is increasing, concerns have been raised about the accuracy of tree-based methods of classification and regression [4].

In the data mining and machine learning literature, alternatives to and extensions of classical classification methods have been developed in recent years. One of the most promising extensions of classical classification methods is boosting. Boosting is a method for combining ‘the outputs from several ‘weak’ classifiers to produce a powerful “committee”’ [4]. A ‘weak’ classifier has been described as one whose error rate is only slightly better than random guessing [4]. Breiman has suggested that boosting applied with classification trees as the weak classifiers is the “best off-the-shelf” classifier in the world [4]. Boosting appears to be relatively unknown in the medical literature. Furthermore, given its potential under-use, the ability of boosting to accurately predict outcomes in cardiovascular patients is unknown.

The current study had three objectives. First, to introduce readers in the medical community to boosting classification trees for use in classification problems. Second, to examine the accuracy of boosted classification trees for predicting mortality in cardiovascular patients. Third, to compare the predictive accuracy of boosted classification trees with that of conventional classification trees in this clinical context.

Boosted classification trees

In this paper, we will focus on the AdaBoost.M1 algorithm proposed by Freund and Schapire [9]. Boosting sequentially applies a weak classifier to series of reweighted versions of the data, thereby producing a sequence of weak classifiers. At each step of the sequence, subjects that were incorrectly classified by the previous classifier are weighted more heavily than subjects that were correctly classified. The predictions from this sequence of weak classifiers are then combined through a weighted majority vote to produce the final prediction. The reader is referred elsewhere for a more detailed discussion of the theoretical foundation of boosting and its relationship with established methods in statistics [10-11].

Assume that the response variable can take two discrete values: ϒ∈{-1,1}. Let X denote a vector of predictor variables. Finally, let G(X) denote a classifier that produces a prediction taking one of the two values {-1,1}. When used with boosting, the classifier G(X) is referred to as the base classifier. Hastie, Tibshirani and Friedman provide the following heuristic explanation of how the AdaBoost.M1 algorithm works [4] as shown in Box 1.

Box 1

1. Define weights for each subject in the sample. Initialize these weights to be equal to w_i=1/n, i=1, …,N, where N is the number of subjects in the sample.

2. For m = 1 to M, where M is the number of times that the procedure is repeated (the number of iterations):

a. Fit a classifier G_m(x) to the derivation data using weights w_i.

b. Compute the error rate:

$${\text{err}}_{\text{m}}=\frac{\sum _{i=1}^N{w}_{i}I(y_i\ne G_m(x_i))}{\sum _{i=1}^N{w}_i}$$

c. Compute α_m=log((1-err_m)/err_m). This is the logit of the correct classification rate.

d. Set $w_{\text{i}}\leftarrow w_{\text{i}}\text{exp}[{\alpha }_{m}I(y_i^1{G}_m(x_i))],i=1,...,N$

3. Output:

$$G(x)=\text{sign}\left[\sum _{m=1}^M{\alpha }_{\text{m}}{G}_m(x)\right]$$

Thus, in the first step of the process, all subjects are assigned equal weights (weights = 1/ N). The classifier is fitted to the data, and a classification is obtained for each subject. The first misclassification rate, err1, is the proportion of subjects that are incorrectly classified, while α₁ is the logit of the correct classification rate. Finally, the sample weights are updated. Weights remain unchanged for those subjects that were correctly classified, whereas subjects that were incorrectly classified are weighted more heavily in the modified sample. This process is then repeated a fixed number of times (M times). Then the final classification is a weighted majority vote of the M classifiers; classifiers with higher correct classification rates are weighted more heavily in the weighted majority vote.

The AdaBoost.M1 algorithm for boosting can be applied with any classifier. However, it is most frequently used with classification trees as the base classifier [4]. Even using a ‘stump’ (‘stump’ is a classification tree with exactly one binary split and exactly two terminal nodes or leaves) as the weak classifier has been shown to produce substantial improvement in prediction error compared to a large classification tree [4].

Conventional classification trees are simple to interpret and to represent graphically. The contribution of each candidate predictor variable to the classification algorithm is easy to assess and evaluate. However, for boosted classification trees, which are obtained by a weighted majority vote by a sequence of classification, it is more difficult to assess the relative contribution of candidate predictor variables. For a conventional decision tree T, Breiman et al. have suggested a numeric score to reflect the importance of candidate predictor variable X_i [1]:

$$I_l^2(\text{T})=\sum _{t=1}^{J-1}{\widehat{i}}_t^{2}I(v(t)=l)$$

The above sum is over the J-1 internal nodes of the tree. At node t, variable X_V(t) is used to generate the binary split. Splitting on this variable results in an improvement of ${\widehat{i}}_t^2$ in the squared error risk for subjects in node t. In a conventional tree, the importance of a candidate predictor variable is the sum of the squared improvement in squared error risk over all nodes for which that predictor variable was chosen as the variable for the binary split. The above definition of variable importance for conventional trees can be modified for use with boosted classification trees:

$$I_l^2=\frac{1}{M}\sum _{m=1}^M{I}_l^2(T_m)$$

Thus, the importance of a candidate predictor variable is the average of that candidate predictor variable's importance across the M classification trees grown in the iteratively weighted datasets [4]. Candidate variables with importance scores of zero were not used for producing binary splits in any of the individual classification trees in the iterative boosting process.

Methods

Data sources

Two different datasets were used for assessing the accuracy of boosted classification trees for predicting cardiovascular outcomes. The first consisted of patients hospitalized with acute myocardial infarction (AMI), while the second consisted of patients hospitalized with congestive heart failure (CHF). Both datasets consist of patients hospitalized at 103 acute care hospitals in Ontario, Canada between April 1, 1999 and March 31, 2001. Data on patient history, cardiac risk factors, comorbid conditions and vascular history, vital signs, and laboratory tests were obtained by retrospective chart review by trained cardiovascular research nurses. These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, an ongoing initiative intended to improve the quality of care for patients with cardiovascular disease in Ontario [12]. Patient records were linked to the Registered Persons Database using encrypted health card numbers, which allowed us to determine the vital status of each patient at 30-days following admission.

For the AMI sample, detailed clinical data were available on a sample of 11,506. Subjects with missing data on key continuous baseline covariates were excluded, resulting in a final sample of 9,484 patients. We conducted a complete case analysis since the objective of the current study was to evaluate the performance of boosting classification trees for classifying cardiovascular outcomes. Patient characteristics are reported separately in Table 1 for those who died within 30 days of hospital admission and for those who survived to 30 days following hospital admission. Overall, 1,065 (11.2%) patients died within 30-days of admission.

Table 1.

Demographic and clinical characteristics of the 9,484 acute myocardial infarction (AMI) patients in the study sample

Variable	30-day death: No N = 8,419	30-day death: Yes N = 1,065	P-value
Demographic characteristics
Age	68(56-77)	80 (73-86)	<.001
Female	2,888 (34.3%)	523(49.1%)	<.001
Vital signs on admission
Systolic blood pressure on admission	148 (129-170)	129 (106-150)	<.001
Diastolic blood pressure on admission	83(71-96)	72 (60-88)	<.001
Heart rate	80 (67-96)	90 (72-111)	<.001
Respiratory	20 (18-22)	22 (20-28)	<.001
Presenting signs and symptoms
Acute congestive heart failure/pulmonary edema	394(4.7%)	143 (13.4%)	<.001
Cardiogenic shock	51 (0.6%)	99 (9.3%)	<.001
Classic cardiac risk factors
Diabetes	2,138 (25.4%)	353(33.1%)	<.001
History of hypertension	3,851 (45.7%)	514 (48.3%)	0.120
Current smoker	2,853 (33.9%)	208 (19.5%)	<.001
History of hyperlipidemia	2,713(32.2%)	192 (18.0%)	<.001
Family history of coronary artery disease	2,728 (32.4%)	138 (13.0%)	<.001
Comorbid conditions
Cerebrovascular accident or transient ischemic attack	781 (9.3%)	196 (18.4%)	<.001
Angina	2,756 (32.7%)	375 (35.2%)	0.105
Cancer	238 (2.8%)	53 (5.0%)	<.001
Dementia	239 (2.8%)	133 (12.5%)	<.001
Peptic ulcer disease	466 (5.5%)	58 (5.4%)	0.905
Previous AMI	1,893 (22.5%)	296(27.8%)	<.001
Asthma	456 (5.4%)	63 (5.9%)	0.500
Depression	576 (6.8%)	110 (10.3%)	<.001
Peripheral arterial disease	603 (7.2%)	126 (11.8%)	<.001
Previous PCI	288 (3.4%)	19 (1.8%)	0.004
Congestive heart failure (chronic)	334 (4.0%)	138 (13.0%)	<.001
Hyperthyroidism	99 (1.2%)	22(2.1%)	0.015
Previous CABG surgery	563 (6.7%)	72 (6.8%)	0.928
Aortic stenosis	119 (1.4%)	41 (3.8%)	<.001
Laboratory values
Hemoglobin	141 (129-151)	128 (114-142)	<.001
White blood count	9 (8-12)	12 (9-15)	<.001
Sodium	139 (137-141)	139 (136-141)	<.001
Potassium	4 (4-4)	4 (4-5)	<.001
Glucose	8 (6-11)	10 (7-14)	<.001
Urea	6 (5-8)	9 (7-15)	<.001

For continuous variables, the sample median (25^th percentile - 75^th percentile) is reported. For dichotomous variables, N (%) is reported.

For the CHF sample, detailed clinical data were available on a sample of 9,945 patients hospitalized with a diagnosis of CHF. Subjects with missing data on key continuous baseline covariates were excluded from the study, resulting in a final sample of 8,240 CHF patients. Patient characteristics are reported separately in Table 2 for those who died within 30 days of hospital admission and for those who survived to 30 days following hospital admission. Overall, 887 (10.8%) patients died within 30-days of admission.

Table 2.

Demographic and clinical characteristics of the 8,240 congestive heart failure (CHF) patients in the study sample

Variable	30-day death: No N = 7,353	30-day death: Yes N = 887	P-value
Demographic characteristics
Age, years	77 (69-83)	82 (74-88)	<.001
Female	3,692 (50.2%)	465 (52.4%)	0.213
Vital signs on admission
Systolic blood pressure, mmHg	148 (128-172)	130 (112-152)	<.001
Heart rate, beats per minute	92 (76-110)	94 (78-110)	0.208
Respiratory rate, breaths per minute	24 (20-30)	25 (20-32)	<.001
Presenting signs and physical exam
Neck vein distension	4,062 (55.2%)	455 (51.3%)	0.026
S3	728 (9.9%)	57 (6.4%)	<.001
S4	284 (3.9%)	18 (2.0%)	0.006
Rales > 50% of lung field	752 (10.2%)	151(17.0%)	<.001
Findings on chest X-Ray
Pulmonary edema	3,766 (51.2%)	452 (51.0%)	0.884
Cardiomegaly	2,652 (36.1%)	292 (32.9%)	0.065
Past medical history
Diabetes	2,594 (35.3%)	280 (31.6%)	0.028
CVA/TIA	1,161 (15.8%)	213 (24.0%)	<.001
Previous MI	2,714 (36.9%)	307 (34.6%)	0.18
Atrial fibrillation	2,139(29.1%)	264 (29.8%)	0.677
Peripheral vascular disease	950 (12.9%)	132 (14.9%)	0.102
Chronic obstructive pulmonary disease	1,211 (16.5%)	194 (21.9%)	<.001
Dementia	458 (6.2%)	184 (20.7%)	<.001
Cirrhosis	52(0.7%)	11 (1.2%)	0.085
Cancer	814 (11.1%)	136 (15.3%)	<.001
Electrocardiogram – First available within 48 hours
Left bundle branch block	1,082 (14.7%)	150 (16.9%)	0.083
Laboratory tests
Hemoglobin, g/L	125 (111-138)	120 (105-136)	<.001
White blood count, 10E9/L	9 (7-11)	10 (8-13)	<.001
Sodium, mmol/L	139 (136-141)	138 (135-141)	<.001
Potassium, mmol/L	4 (4-5)	4 (4-5)	<.001
Glucose, mmol/L	8 (6-11)	8 (6-11)	0.02
Blood urea nitrogen, mmol/L	8 (6-12)	12 (8-17)	<.001
Creatinine, μmol/L	104 (82-141)	126 (93-182)	<.001

For continuous variables, the sample median (25^th percentile - 75^th percentile) is reported. For dichotomous variables, N (%) is reported.

In each sample, the Kruskal-Wallis test and the Chi-squared test were used to compare continuous and categorical characteristics, respectively, between patients who died within 30 days of admission and those who survived to 30 days following admission. In each sample, there were statistically significant differences in several baseline characteristics between those who died within 30 days of admission and those who survived to 30 days following admission.

Boosted classification trees for predicting 30-day AMI and CHF mortality

Each of the AMI and CHF samples was randomly divided into a derivation (or training) sample and a validation (or test) sample (the terms ‘derivation’ and ‘validation’ samples are predominantly used in the medical literature, while the terms ‘training’ and ‘test’ samples are used predominantly in the data mining and machine learning literature - we have chosen to use terminology from the medical literature in this article). Each derivation sample contained two thirds of the original sample, while each validation sample contained the remaining one third of the original sample.

Boosting using classification trees as the base classifier (G(X)) was used for classifying outcomes within 30 days of admission for patients hospitalized with either a diagnosis of AMI or CHF. This was done separately for each of the two diagnoses. Four different sets of classifiers were considered. First, we used ‘stumps’, or classification trees with only a depth of one (the root node is considered to have depth zero), and with two terminal nodes or leaves (a tree with depth k will have 2^k terminal nodes). We also used classification trees of depth 2, 3, and 4. For each boosted classification tree, 100 iterations were used (M = 100 in the Ada.Boost.M1 algorithm described in Section 2). The variables described in Tables 1 and 2 were considered as candidate predictor variables for classifying AMI and CHF mortality, respectively.

Classifications were obtained for each subject in each of the validation samples using the boosted classifiers grown in the respective derivation sample. The accuracy of the boosted classification trees was assessed in several ways. First, the overall misclassification rate was determined in the validation sample. Second, the sensitivity, specificity, positive predictive value, and negative predictive value were determined. Sensitivity is the proportion of subjects who died that were correctly classified as dying within 30 days of hospitalization. Specificity is the proportion of subjects who did not die within 30-days of admission that were correctly classified as not dying within 30 days of admission. The positive predictive value is the proportion of subjects who were classified as dying within 30 days of admission who did in fact die within 30 days of admission. Finally, the negative predictive value is the proportion of subjects who were classified as not dying within 30 days of admission who in fact did not die within 30 days of admission.

The Ada.Boost algorithm was implemented using the ada function from the identically named package available for use with the R statistical programming language [13-14].

Comparison with classification trees for predicting 30-day AMI and CHF mortality

We compared the predictive accuracy of classifications obtained using boosted classification trees with those obtained using conventional classification trees. To do so, we derived classification trees in our derivation samples for predicting 30-day mortality. For the AMI sample, an initial classification tree was grown using all 33 candidate predictor variables listed in Table 1. Once the initial classification tree had been grown, the tree was pruned. Ten-fold cross validation was used on the derivation dataset to determine the optimal number of leaves on the tree [3]. The desired tree size was chosen to minimize the misclassification rate when 10-fold cross validation was used on the derivation dataset. If two different tree sizes resulted in the same minimum misclassification rate, then the smaller of the two tree sizes was chosen. The initial classification tree was pruned so as to produce a final tree of the desired size. A similar process was used for growing classification trees to predict 30-day CHF mortality. The classification trees were grown in the derivation samples and classifications were obtained for each subject in the validation sample. The accuracy of the classifications was determined using identical methods to those described in the previous section. The classification trees were grown using the tree function from the identically named package available for use with the R statistical programming language.

Assessing variability of classification accuracy

We conducted a series of analyses to compare the variability in the performance of boosted classification trees with that of conventional classification trees. The AMI sample was randomly divided into derivation and validation samples, consisting of two thirds and one third of the original AMI sample. Boosted classification trees were fit to the derivation sample, as described above. Similarly, a conventional classification was grown in the derivation sample. The predictive accuracy of each method was then assessed in the validation sample. This process was then repeated 1,000 times. Measures of predictive accuracy were averaged over the 1,000 random splits of the original AMI data. This process was then repeated using the CHF sample.

Results

AMI sample

The accuracy of the boosted classification tree generated in the derivation sample when applied to the validation sample is reported in Table 3. We considered four base classifiers: classification trees of depths 1 through 4. As the depth of the base classifier increased from 1 to 4, the misclassification rate increased from 10.6% to 11.9%. As the depth of the base classifier increased, sensitivity increased from 0.25 to 0.31. For all four base classifiers, specificity was high, ranging from 0.96 to 0.98. The choice of the depth of the classification tree used as the base classifier reflected the classic tradeoff between sensitivity and specificity: as the depth of the base classifier increased, sensitivity increased while specificity decreased. The negative predictive value was 0.91 for all four base classifiers. The 30-day mortality rate for patients classified as dying within 30-days of admission is equal to the positive predictive value. Thus, the observed 30-day mortality rate in patients classified as dying within 30-days of admission ranged from 0.50 to 0.64. The 30-day mortality rate for patients classified as not dying within 30-days of admission is equal to one minus the negative predictive value. Thus, the observed probability of death within 30 days of admission for patients classified as not dying within 30-days of admission was equal to 0.09.

Table 3.

Accuracy of boosted classification trees for predicting 30-day mortality in AMI and CHF patients in the validation samples

Depth of base classifier	Misclassification rate	Sensitivity	Specificity	Positive predictive value	Negative predictive value
30-day AMI mortality
1	10.6%	0.25	0.98	0.64	0.91
2	10.8%	0.26	0.98	0.61	0.91
3	11.5%	0.27	0.97	0.53	0.91
4	11.9%	0.31	0.96	0.50	0.91
30-day CHF mortality
1	10.6%	0.07	0.99	0.55	0.90
2	10.8%	0.12	0.98	0.48	0.90
3	11.2%	0.13	0.98	0.42	0.90
4	12.4%	0.13	0.97	0.31	0.90

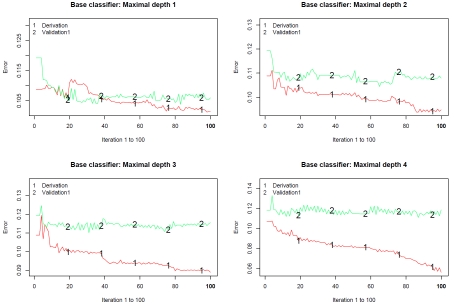
Figure 1 describes the misclassification rate in both the derivation and validation samples at each of the 100 steps of the classification algorithm. Figure 1 consists of four panels, one for each of the base classifiers employed (tree depths ranging from 1 to 4, respectively). Several results are worth noting. First, the misclassification rate in the derivation sample tended to decrease as the iteration number increased. However, the misclassification rate in the validation sample attained a plateau after approximately 10-20 iterations. Second, the misclassification rate in the derivation sample tended to decrease as the depth of the base classifier increased. Third, the discordance between the misclassification rate in the derivation sample and that in the validation sample increased as the depth of the base classifier increased.

Figure 1.

Classification error for predicting AMI mortality in derivation and validation samples.

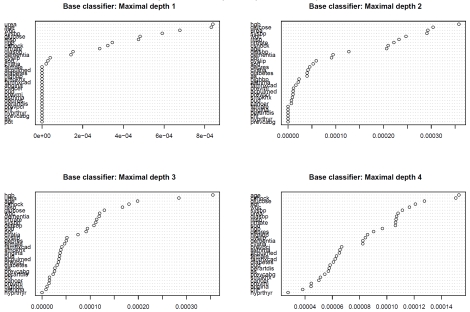
Variable importance plots for each of the four boosted classification trees are described in Figure 2. The top left panel describes the variable importance plots when ‘stumps’ were used as the base classifier (classification trees of depth 1 and with two terminal nodes or leaves). Nineteen of the covariates (gender, acute pulmonary edema on admission, diabetes, hypertension, current smoker, family history of coronary artery disease, angina, cancer, peptic ulcer disease, previous AMI, asthma, peripheral arterial disease, previous PCI, chronic CHF, hyperthyroidism, previous CABG surgery, aortic stenosis, and potassium) had variable importance scores of zero, indicating that they were uninformative in predicting 30-day mortality. Age and urea were the most important variables for predicting 30-day AMI mortality, followed by systolic blood pressure and glucose. When the base classifier was modified to allow for greater depth, some of the variables that initially had no role in classification changed to having a modest importance in classification. Glucose was one of the six most important predictors in each of the four boosted classification trees. Urea, age, white blood count, systolic blood pressure, and respiratory rate were each one of the six most important predictors in three of the four boosted classification trees.

Figure 2.

Variable importance plot: AMI mortality.

The variability in the predictive accuracy of boosted classification trees and classical classification trees across the 1,000 random splits of the original AMI sample into derivation and validation samples is reported in Table 4. For each classification method, we report the minimum, first quartile, median, third quartile, and maximum of each measure of classification accuracy across the 1,000 splits of the original sample. One observes that variation in both sensitivity and positive predictive value was substantially reduced by using boosting compared to that observed with classical classification trees. Similarly, variation in specificity was reduced by using boosting compared to when using conventional classification trees.

Table 4.

Variation in accuracy of classification across 1,000 random splits of AMI sample

Depth of base classifier	Minimum	Lower Quartile	Median	Upper Quartile	Maximum
Sensitivity
1	0.181	0.231	0.246	0.261	0.330
2	0.180	0.246	0.261	0.278	0.335
3	0.202	0.264	0.280	0.297	0.352
4	0.206	0.267	0.284	0.301	0.360
Conventional tree	0.000	0.106	0.159	0.190	0.321
Specificity
1	0.965	0.973	0.976	0.978	0.986
2	0.954	0.970	0.973	0.975	0.984
3	0.946	0.963	0.966	0.969	0.982
4	0.947	0.958	0.961	0.965	0.976
Conventional tree	0.950	0.976	0.984	0.990	1.000
Positive predictive value
1	0.447	0.538	0.563	0.588	0.701
2	0.411	0.523	0.548	0.573	0.675
3	0.405	0.488	0.512	0.536	0.673
4	0.390	0.458	0.481	0.507	0.611
Conventional tree	0.342	0.488	0.529	0.574	1.000
Negative predictive value
1	0.893	0.908	0.911	0.914	0.928
2	0.896	0.909	0.912	0.916	0.929
3	0.894	0.911	0.914	0.917	0.929
4	0.899	0.911	0.914	0.917	0.930
Conventional tree	0.874	0.895	0.902	0.906	0.921
Misclassification rate
1	0.092	0.103	0.106	0.109	0.119
2	0.095	0.104	0.107	0.110	0.121
3	0.096	0.107	0.111	0.114	0.129
4	0.097	0.111	0.115	0.118	0.131
Conventional tree	0.096	0.108	0.111	0.114	0.127

CHF sample

The accuracy of the boosted classification tree generated in the derivation sample when applied to the validation sample is reported in Table 3. As the depth of the base classifier increased from 1 to 4, the misclassification rate increased from 10.6% to 12.4%. As the depth of the base classifier increased, sensitivity increased from 0.07 to 0.13. For all four base classifiers, specificity was high, ranging from 0.97 to 0.99. As in the AMI sample, the choice of depth of the base classifier reflected the classic tradeoff between sensitivity and specificity. The negative predictive value was 0.90 for all four base classifiers. The 30-day mortality rate for patients classified as dying within 30 days of admission is equal to the positive predictive value. Thus, the observed 30-day mortality rate in patients classified as dying within 30-days of admission ranged from 0.31 to 0.55. The 30-day mortality rate for patients classified as not dying within 30-days of admission is equal to one minus the negative predictive value. Thus, the observed 30-day mortality rate for patients classified as not dying within 30-days of admission was equal to 0.10.

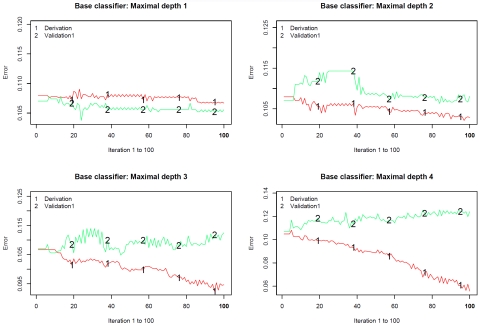
Figure 3 describes the misclassification rate in both the derivation and validation sample at each of the 100 iterations of the classification algorithm. Figure 3 consists of four panels, one for each of the base classifiers employed. Several results are worth noting. First, the misclassification rate in the derivation sample tended to decrease as the iteration number increased. Furthermore, the rate of decrease was greater when the depth of the classification tree used as the base classifier increased. However, the misclassification rate in the validation sample tended to either attain a plateau after approximately 40 iterations or to increase modestly from this point onwards. Second, the misclassification rate in the derivation sample tended to decrease as the depth of the base classifier increased. Third, the discordance between the misclassification rate in the derivation sample and that in the validation sample increased as the depth of the base classifier increased. When the depth of the base classifier was four, the discordance in misclassification rates between the two samples was particularly pronounced between iterations 50 and 100.

Figure 3.

Classification error for predicting CHF mortality in derivation and validation samples.

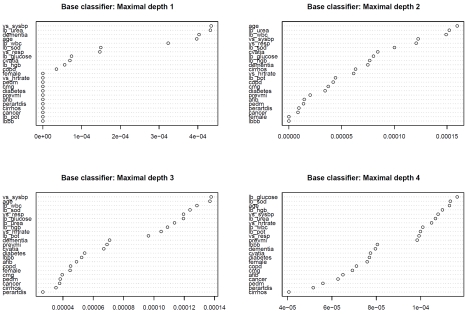
Variable importance plots for each of the four boosted classification trees are described in Figure 4. The top left panel describes the variable importance plots when ‘stumps’ were used as the base classifier (classification trees of depth 1). Twelve of the covariates (gender, heart rate, pulmonary edema, cardiomegaly, diabetes, previous AMI, atrial fibrillation, peripheral arterial disease, cirrhosis, cancer, potassium, and left bundle branch block) had variable importance scores of zero, indicating that they were uninformative in predicting 30-day CHF mortality. Systolic blood pressure and urea were the two most important variables for predicting 30-day AMI mortality, followed by dementia and age. When the base classifier was modified to allow for greater depth, some of the variables than initially had no role in classification changed to having a modest importance in classification. Systolic blood pressure and age were each one of the five most important predictors in each of the four boosted classification trees. White blood count was one of the five most important predictors in three of the four boosted classification trees.

Figure 4.

Variable importance plot: CHF mortality.

The variability in the predictive accuracy of boosted classification trees and classical classification trees across the 1,000 random splits of the original CHF sample into derivation and validation samples is reported in Table 5. One notes that greater variability in accuracy was observed for the boosted classification trees than for the conventional classification trees. The smaller variability in accuracy observed for the conventional classification tree is primarily due to the fact that for 992 of the 1,000 classification trees, no subjects were classified as dying within 30 days of admission. Thus, sensitivity and specificity were equal to 0 and 1, respectively, in 992 of the 1,000 random splits.

Table 5.

Variation in accuracy of classification across 1,000 random splits of CHF sample

Variable	Minimum	Lower quartile	Median	Upper quartile	Maximum
Sensitivity
1	0.020	0.058	0.068	0.079	0.123
2	0.028	0.077	0.088	0.103	0.159
3	0.049	0.101	0.115	0.128	0.179
4	0.079	0.119	0.132	0.146	0.212
Conventional tree	0.000	0.000	0.000	0.000	0.071
Specificity
1	0.983	0.990	0.992	0.993	0.997
2	0.974	0.985	0.987	0.989	0.996
3	0.964	0.977	0.980	0.982	0.991
4	0.952	0.968	0.971	0.974	0.986
Conventional tree	0.983	1.000	1.000	1.000	1.000
Positive predictive value
1	0.276	0.452	0.500	0.553	0.774
2	0.244	0.409	0.450	0.500	0.675
3	0.237	0.371	0.404	0.440	0.566
4	0.240	0.330	0.359	0.386	0.526
Conventional tree	0.200	0.281	0.321	0.336	0.389
Negative predictive value
1	0.882	0.895	0.899	0.902	0.914
2	0.884	0.897	0.900	0.904	0.916
3	0.884	0.899	0.902	0.905	0.916
4	0.888	0.900	0.903	0.906	0.918
Conventional tree	0.878	0.889	0.893	0.896	0.907
Misclassification rate
1	0.091	0.104	0.107	0.111	0.125
2	0.095	0.106	0.110	0.113	0.128
3	0.099	0.110	0.113	0.116	0.133
4	0.100	0.115	0.119	0.122	0.135
Conventional tree	0.093	0.104	0.107	0.111	0.122

Classical classification trees

The pruned classification tree for predicting 30-day AMI mortality was of depth of three and had six terminal nodes. The following five variables were used in the resultant tree: age, glucose, systolic blood pressure, urea, and white blood count. When applied to the validation sample, all subjects were classified as not dying within 30 days of admission for AMI. Thus the sensitivity was 0 (0%) and the specificity was 1 (100%). The misclassification rate was in the validation sample was 11.9%.

The pruned classification tree for predicting 30-day CHF mortality was of depth of two and had four terminal nodes. The following three variables were used in the resultant tree: urea, dementia, systolic blood pressure. When applied to the validation sample, all subjects were classified as not dying within 30 days of admission for AMI. Thus the sensitivity was 0 (0%) and the specificity was 1 (100%). The misclassification rate in the validation sample was 10.7%.

Discussion

There is an increasing interest in using classification methods in clinical research. The objective of binary classification schemes or algorithms is to classify subjects into one of two mutually exclusive categories based upon their observed baseline characteristics. Common binary categories in clinical research include death/survival, diseased/non-diseased, disease recurrence/disease remission and readmitted to hospital/not readmitted to hospital. In medical research, classification trees are a commonly-used binary classification method. In the data mining and machine learning fields, improvements to classical classification trees have been developed. However, many in the medical research community appear to be unaware of these recent developments, and these more recently developed classification methods are rarely employed in clinical research.

Comparison of the accuracy of classifications obtained using boosted classification trees with those obtained using conventional classification trees requires a nuanced interpretation. For predicting AMI mortality, conventional classification trees had a misclassification rate of 11.9%, whereas that for the boosted classification trees ranged from 10.6% to 11.9%, depending on the depth of the classification tree used as the base classifier. Thus, there was a minor improvement in accuracy of classification compared to that reported in some non-medical settings [4]. However, when accuracy was assessed using sensitivity and specificity, then a more dramatic improvement in accuracy was observed when boosted classification trees were used. With conventional classification trees, sensitivity and specificity were 0 and 1, respectively. When stumps were used as the base classifier, sensitivity increased substantially to 0.25, whereas specificity decreased only negligibly to 0.98. For predicting CHF mortality, conventional classification trees had a misclassification rate of 10.7%, whereas that for the boosted classification trees ranged from 10.6% to 12.4%, depending on the depth of the classification tree used as the base classifier. Thus, with the use of ‘stumps’, there was a negligible improvement in the misclassification rate, whereas the misclassification rate increased when base classifiers with depths greater than one were used. However, when accuracy was assessed using sensitivity and specificity, then a modest improvement in accuracy was observed when boosted classification trees were used. With conventional classification trees, sensitivity and specificity were 0 and 1, respectively. Depending on the depth of the base classifiers, sensitivity ranged from 0.07 to 0.13, while specificity exhibited only a minor decrease.

These findings suggest that potential improvement in the accuracy of classification when using boosting compared to conventional classification trees is dependent on the context. We observed that greater improvement in the accuracy of classification was observed for 30-day AMI mortality than was observed for 30-day CHF mortality. However, the improvements in the misclassification rates were less impressive than those that have been reported in some non-medical settings [4]. We hypothesize that the less than impressive observed accuracy of the classifications is due to the inherent difficulty in predicting health outcomes for individual patients.

There are certain limitations to the use of boosted classification trees. As Hastie, Tibshirani and Friedman note, the interpretation of conventional regression and classification trees is straightforward and transparent, and can be represented using a two-dimensional graphic [4]. However, as they note, “Linear combinations of trees lose this important feature, and must therefore be interpreted in a different way.” (Page 331). Many physicians find classification and regression trees attractive because of the simplicity of interpreting the final decision tree. Furthermore, predictions and classifications for new patients can easily be made by the physician. Boosted classification trees do not inherit this ability for the physician to quickly and simply obtain classifications for new patients. In selecting between conventional classification trees and boosted classification trees one must balance the minor to modest gains in predictive accuracy with the loss in interpretability and the increased difficulty of applicability of the final boosted tree.

In the current study we have focused on classification rather than regression. In the context of dichotomous outcomes, the focus of regression is on predicting each subject's probability of one outcome occurring compared to the alternate outcome. In contrast, the focus of classification is to classify subjects into two mutually exclusive groups according to the predicted outcome. Classification plays an important role in clinical medicine. When the outcome is the presence or absence of a specific disease, classifying subjects according to disease status permits physicians to target treatment and therapy at diseased subjects. When disease is ruled out for a set of subjects, then further potentially invasive investigations and treatments may justifiably be avoided. When the presence of disease is ruled in, subsequent investigations and treatment may be justified and actively pursued. Accurate classification of disease status allows for a more efficient use of limited health care resources. When the outcome is an event such as mortality, then subsequent treatments and actions may be mandated depending on whether the outcome is ruled in or ruled out. For instance, palliative care may be offered to patients who are classified as likely to die shortly. Alternatively, depending on the clinical context, aggressive treatment may be directed at those who have been classified as likely to die, in an attempt to arrest the natural trajectory of the disease state. Clinicians may also be more receptive to the boosted classification tree, which will generate a dichotomous outcome (e.g. death vs. survival) instead of the potential uncertainty that could be generated if the output is presented as a probability. In our examples, the boosted classification trees had high specificity relative to sensitivity, and also a high negative predictive value. Although the boosted classification trees in this study have not been formally tested for their clinical utility, diagnostic tools with very high specificity are generally useful to clinicians because they more clearly delineate those who will experience the outcome of interest and are independent of baseline prevalence.

In summary, boosting can be applied to classification methods to mitigate the inaccuracies of conventional classification trees. When assessed using the misclassification rate, improvements in accuracy using boosted classification trees were at best minor compared to when conventional classification trees were used. When assessed using sensitivity, then minor to modest improvements to sensitivity were observed, with only a negligible reduction in specificity.