Abstract
In the past several decades, the fields of ultrasound and magnetic resonance elastography have shown promising results in noninvasive estimates of mechanical properties of soft tissues. These techniques often rely on measuring shear wave velocity due to an external or internal source of force and relating the velocity to viscoelasticity of the tissue. The mathematical relationship between the measured velocity and material properties of the myocardial wall, arteries, and other organs with non-negligible boundary conditions is often complicated and computationally expensive. A simple relationship between the Lamb–Rayleigh dispersion and the shear wave dispersion is derived for both the velocity and attenuation. The relationship shows that the shear wave velocity is around 20% higher than the Lamb–Rayleigh velocity and that the shear wave attenuation is about 20% lower than the Lamb–Rayleigh attenuation. Results of numerical simulations in the frequency range 0–500 Hz are presented.
INTRODUCTION
In the past several decades, the field of elastography has offered various techniques for measuring stiffness of different organs to evaluate the presence of pathophysiological conditions and aid the treatment of diseases.1 A majority of the techniques rely on tracking the deformation of the tissue due to intrinsic physiological motion or external force due to a mechanical driver or focused ultrasound radiation force. Tissue undergoing displacement due to wave propagation is used to estimate shear wave velocity, which is directly related to the shear modulus of elasticity, μ. Geometry of organs such as the liver, kidney, and the breast allows one to assume that propagating shear waves in the middle of the organ (“far” from the edges) would not be affected by the boundaries. In the case of the liver, for example, the tissue can be modeled as an infinite elastic or viscoelastic medium, which allows for decomposition of the excitatory wave into the compressional and shear components.2 The advantage of this approach is that the compressional and shear waves are separable and measuring the shear wave velocity in the plane orthogonal to the excitation beam is sufficient to estimate the shear modulus.
Organs like the left ventricular (LV) free-wall of the heart (10–15 mm thick) and arteries (∼5 mm in diameter) can be approximated as plates since they are “thin” compared to the excitation force beam (focal length of 2–4 mm). The use of radiation force in plate-like organs excites guided waves that arise as a result of combining shear and compressional waves. The use of the curl operator has shown promising results in extracting the shear wave component alone,3, 4 but the curl operator requires information about the tissue deformation in all three dimensions of motion, which is not available in traditional ultrasound elasticity imaging techniques.
Several groups have reported the use of Lamb waves to model the motion and deformation of the myocardial septum, LV free-wall, and the arteries.5, 6, 7 These approaches are based on measuring the dispersion velocity and fitting the Lamb wave dispersion equation model to the data to estimate elasticity and viscosity. This adds computational costs to evaluating the mechanical properties of organs and also requires validation that Lamb-like motion occurs in the given organ. The A0 mode of anti-symmetric Lamb wave motion is characterized by preserved phase through the thickness of the plate-shaped object, in this case the myocardial wall. Thus, in vivo excitation of an anti-symmetric Lamb wave requires focusing ultrasound radiation force in the middle of the LV free-wall. This might prove to be difficult due to physiological periodic motion of the heart and higher power necessary to move the entire heart wall.
We have previously reported the use of Lamb wave dispersion ultrasound vibrometry to quantify viscoelasticity of various materials,7, 8 as well as advantages of using Rayleigh wave excitation to obtain similar results.9 Here, we present a simplification of the Rayleigh wave approach by showing its relationship to the “pure” shear wave (shear wave in the infinite medium). This approach would decrease computational costs and allow for more accurate estimation of shear wave velocity and attenuation, and would lead to model-free measurements of mechanical properties of soft tissues.
METHODS
The anti-symmetric Lamb wave dispersion equation for a viscoelastic plate submerged in a fluid, assuming that the compressional wave number for the plate and fluid are very small compared to the Lamb wave number and that the plate and fluid have similar densities, is as follows:5, 7, 9
| (1) |
where , kL = ω/cL is the Lamb wave number, ω is the angular frequency, cL is the frequency dependent Lamb wave velocity, is the shear wave number, ρm is the density of the sample (the same as that of water ∼ 1 000 kg/m3), h is the half-thickness of the sample, and μ is the shear modulus. Here, the shear modulus μ can be expressed in terms of the Voigt, generalized Maxwell, or other viscoelastic rheological model. By dividing both sides of Eq. 1 by , Eq. 1 is analogous to
| (2) |
Since for and since βL and kL increase as a function of frequency and the sample thickness is constant, the real part of Eq. 2 converges analytically to the real part of Eq. 3, which is the Rayleigh wave dispersion equation for a viscoelastic plate in a fluid of similar density. Here kR = ω/cR is the Rayleigh wave number, and cR is the frequency dependent Rayleigh wave velocity,9
| (3) |
By inserting the definition of into Eq. 3 and introducing the substitution , the third order polynomial (7) is obtained:
| (4) |
| (5) |
| (6) |
| (7) |
Equation 7 has one real solution and a pair of complex conjugate solutions that do not have a physical meaning. The real solution, , is of particular interest as it gives a ratio between the Lamb–Rayleigh wave number and the shear wave number ks/kR = 0.839 or kR/ks = 1.1915, where ks = ω/cs − iαs, kR = ω/cR − iαR, cs, cR, αs, and αR being the shear and Rayleigh wave velocities and attentuations, respectively. While the imaginary parts of Eqs. 2, 3 do not necessarily converge, the real parts of Eqs. 2, 3 depend on cs, cR, αs, and αR due to cross terms. Therefore, the 1.1915 relationship holds for both the real and imaginary components of kR and ks.
The Rayleigh wave dispersion equation for a solid with vacuum or air loading is similar to Eq. 7 except for the right hand side term:
| (8) |
Similar treatment of Eq. 8 yields the ratio ,10 which has been experimentally determined by Zhang et al.11
RESULTS
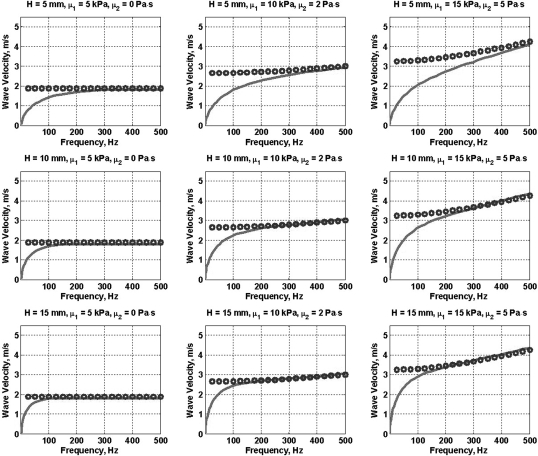
The anti-symmetric Lamb wave dispersion equation for a plate submerged in a water-like fluid [Eq. 1] was used to calculate the Lamb wave velocities in the frequency range 0–500 Hz. The frequency response of the plate was assumed to obey the Voigt model so that the shear modulus μ is expressed as μ = μ1 + iωμ2, where μ1 and μ2 are the elastic and viscous moduli, respectively. Solid lines in Fig. 1 show Eq. 1 plotted for various combinations of the plate thicknesses H = 2 h and elasticity (μ1) and viscosity (μ2) values in the range of those previously reported in soft tissues.7
Figure 1.
(Color online) Comparison between the Lamb wave dispersion (solid line) and corrected shear wave dispersion (cs/1.1915) (open circles) for plates of various thicknesses and values of elasticity and viscosity.
The shear wave velocity cs for the same values of μ1 and μ2 was calculated using , where μ = μ1 + iωμ2, and the real part of ks = ω/cs − iαs. Shear wave velocity divided by 1.1915 (cs/1.1915), also referred to as corrected shear wave velocity, is plotted as open circles for comparison. Note that the shear wave velocities divided by 1.1915 and the Rayleigh wave velocities are mathematically analogous for the given mechanical properties so the latter converges to the former similar to the way the A0 Lamb wave mode converges to the Rayleigh velocity, as previously reported by our group.9
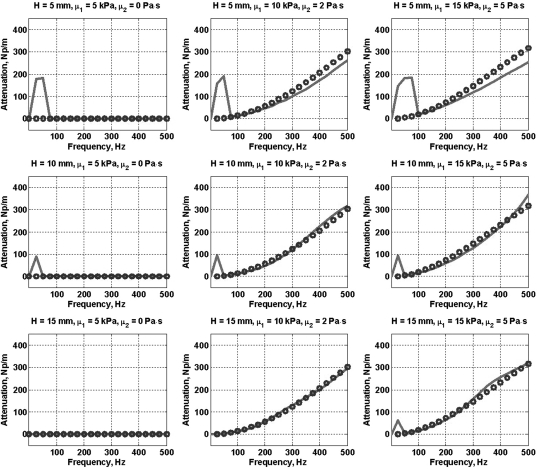
With the known values of shear wave velocity and attenuation (complex shear wave number) and the Lamb wave velocity, Eq. 1 was used to determine the Lamb wave attenuation. The relationship between the shear wave and the Lamb wave attenuation according to our theory is αs/αR = 1.1915. Figure 2 shows the values of corrected shear wave attenuation (αs/1.1915) as open circles for various combinations of plate thicknesses H = 2h, μ1, and μ2. Estimated Lamb wave attenuation divided by 1.1915 (αs/1.1915) is shown as solid lines.
Figure 2.
(Color online) Comparison between the Lamb wave attenuation (solid line) and corrected shear wave attenuation (αs/1.1915) (open circles) for plates of various thicknesses and values of elasticity and viscosity.
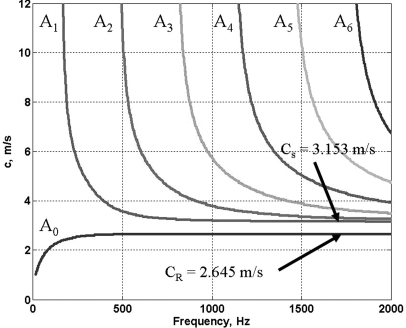
Figure 3 shows a typical set of anti-symmetric Lamb wave dispersion curves for an elastic plate 10 mm in thickness and shear modulus of 10 kPa submerged in a fluid of equal density. Table TABLE I. summarizes the convergence velocities at high frequencies of A0 and A1 modes for various values of elasticity and thickness and the ratio of the two. Note that all the Lamb wave modes of the order higher than A0 converge to the shear wave velocity (cs) and that the A0 Lamb and Rayleigh velocity (cR) are the same for higher frequencies.
Figure 3.
(Color online) Anti-symmetric Lamb wave dispersion curves for an elastic plate submerged in a noncompressible fluid (thickness of the plate H = 10 mm, shear modulus μ = 10 kPa).
Table 1.
Summary of Rayleigh wave velocities (A0) and the shear wave velocities (A1) for elastic plates submerged in a noncompressible fluid.
| μ (kPa) | H (mm) | A0 (m/s) | A1 (m/s) | A1/A0 |
|---|---|---|---|---|
| 10 | 10 | 2.645 | 3.153 | 1.1921 |
| 20 | 10 | 3.733 | 4.507 | 1.2073 |
| 30 | 20 | 4.580 | 5.475 | 1.1954 |
| 40 | 20 | 5.305 | 6.345 | 1.1960 |
DISCUSSION
Our analysis suggests that shear wave velocity and attenuation can be recovered by measuring the velocity and attenuation of propagating Lamb–Rayleigh waves without cumbersome and costly Lamb wave fitting.
A drawback to this approach is that the relationship need not hold for frequencies less than the Lamb–Rayleigh convergence frequency. This is manifested in Fig. 2, where for H = 5 mm, the 50 Hz attenuation measurements are significantly different. The attenuation estimates follow the trend of the Lamb and shear wave velocity values. To our advantage, the LV free-wall myocardium is usually thicker than 10 mm for which the Lamb and Rayleigh velocities converge at lower frequencies.
It is important to note that the relationship between the Lamb and shear wave velocity and attenuation presented here is derived for a fixed value of the Poisson’s ratio of ν = 0.5. In addition, it was assumed that the density of the fluid surrounding the plate is similar to that of the plate, a reasonable assumption when dealing with soft biological tissues such as the myocardium and arteries. In materials with a different Poisson’s ratio and density this relationship need not hold and a more generalized expression could be derived.
In a recent publication by Couade et al.,6 the authors proposed an empirical method for measuring shear wave modulus of elasticity of arteries by fitting a Lamb wave dispersion model to the experimental dispersion velocities. The empirical model includes a correction factor of , which is the ratio between the observed Lamb wave velocity and the expected Lamb wave velocity, suggesting that the experimental Lamb wave velocities should be lower than the measured values. This might be due to the fact that the ratio between the A1 and A0 modes is about 1.19 in water and that the reported paper is tracking the convergence velocity of the An modes (n = 1, 2,…) rather than the A0 mode. We have performed similar experiments in which we compared the velocities of urethane rubber plates and tubes where the thickness of the plates and diameters of tubes were the same, and have noticed that the same ratio holds. The results of these studies are beyond the scope of this study.
CONCLUSION
An algebraic relationship between the shear wave and Rayleigh wave velocity of a plate submerged in a fluid of similar density is derived. Due to convergence of Lamb and Rayleigh waves and the use of Lamb waves to quantify mechanical properties of the heart wall and arteries, this theory allows for simplification of equations and decreased computational cost.
ACKNOWLEDGMENTS
This research is supported in part by NIH Grant No. EB002167.
References
- Greenleaf J. F., Fatemi M., and Insana M., “Selected methods for imaging elastic properties of biological tissues,” Annu. Rev. Biomed. Eng. 5, 57–78 (2003). 10.1146/annurev.bioeng.5.040202.121623 [DOI] [PubMed] [Google Scholar]
- Chen S., Fatemi M., and Greenleaf J. F., “Quantifying elasticity and viscosity from measurement of shear wave speed dispersion,” J. Acoust. Soc. Am. 115, 2781–2785 (2004). 10.1121/1.1739480 [DOI] [PubMed] [Google Scholar]
- Sinkus R., Tanter M., Xydeas T., Catheline S., Bercoff J., and Fink M., “Viscoelastic shear properties of in vivo breast lesions measured by MR elastography,” Magn. Reson. Imaging 23, 159–165 (2005). 10.1016/j.mri.2004.11.060 [DOI] [PubMed] [Google Scholar]
- Sinkus R., Tanter M., Catheline S., Lorenzen J., Kuhl C., Sondermann E., and Fink M., “Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography,” Magn. Reson. Med. 53, 372–387 (2005). 10.1002/mrm.v53:2 [DOI] [PubMed] [Google Scholar]
- Kanai H., “Propagation of spontaneously actuated pulsive vibration in human heart wall and in vivo viscoelasticity estimation,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 1931–1942 (2005). 10.1109/TUFFC.2005.1561662 [DOI] [PubMed] [Google Scholar]
- Couade M., Pernot M., Prada C., Messas E., Emmerich J., Bruneval P., Criton A., Fink M., and Tanter M., “Quantitative assessment of arterial wall biomechanical properties using shear wave imaging,” Ultrasound Med. Biol. 36, 1662–1676 (2010). 10.1016/j.ultrasmedbio.2010.07.004 [DOI] [PubMed] [Google Scholar]
- Nenadic I. Z., Urban M. W., Mitchell S. A., and Greenleaf J. F., “Lamb wave dispersion ultrasound vibrometry (LDUV) method for quantifying mechanical properties of viscoelastic solids,” Phys. Med. Biol. 56, 2245–2264 (2011). 10.1088/0031-9155/56/7/021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal M., Nenadic I., Urban M. W., and Greenleaf J. F., “Material property estimation for tubes and arteries using ultrasound radiation force and analysis of propagating modes,” J. Acoust. Soc. Am. 129, 1344 (2011). 10.1121/1.3533735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nenadic I., Urban M. W., and Greenleaf J., “Ex vivo measurements of mechanical properties of myocardium using Lamb and Rayleigh wave dispersion velocities,” in IEEE International Ultrasonics Symposium (IUS), Rome, Italy (2009), pp. 2785–2788.
- Zhang X. and Greenleaf J. F., “Estimation of tissue’s elasticity with surface wave speed,” J. Acoust. Soc. Am. 122, 2522–2525 (2007). 10.1121/1.2785045 [DOI] [PubMed] [Google Scholar]
- Zhang X., Qiang B., and Greenleaf J., “Comparison of the surface wave method and the indentation method for measuring the elasticity of gelatin phantoms of different concentrations,” Ultrasonics 51, 157–164 (2011). 10.1016/j.ultras.2010.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]