Abstract
The effect of carrier level on tuning in modulation masking was investigated for noise and tonal carriers. Bandwidths of the modulation filters, estimated from the masked detection thresholds using an envelope power spectrum model, were independent of level for the noise carrier but seemed to decrease with increasing level for the tonal carrier. However, the apparently sharper tuning could be explained by increased modulation sensitivity and modulation dynamic range with increasing level rather than improved modulation-frequency selectivity. Consistent with this interpretation, the addition of a high-pass noise with a level adjusted to maintain the same threshold for the detection of the signal modulation for each carrier level used eliminated the effect of level on tuning. Overall, modulation filters estimated from psychophysical data do not depend on level in contrast to the modulation transfer functions obtained from neural recordings in the inferior colliculus in physiological studies. The results highlight differences between the characteristics of modulation processing obtained from neural data and perception. The discrepancies indicate the need for further investigation into physiological correlates of tuning in modulation processing.
INTRODUCTION
Temporal envelopes of sounds play an important role in speech perception (e.g., Drullman et al., 1996) and, more generally, in auditory tasks that require segregating sounds with overlapping spectra (e.g., Grimault et al., 2002; Roberts et al., 2002). To perform these tasks, listeners may use cues available in differences between the envelopes of the sounds, which in turn can be considered in terms of the spectral composition of the temporal envelope. Such a strategy would require at least some degree of selectivity in the processing of the modulation rates that comprise the envelopes. This has motivated many studies to investigate the hypothesis that the auditory system performs a spectral decomposition of the temporal envelope, analogous to the way in which the peripheral auditory system performs a spectral analysis of the acoustic waveform.
Psychophysical studies of adaptation to amplitude modulation (AM; Tansley and Regan, 1979; Kay, 1982; Tansley and Suffield, 1983; Wojtczak and Viemeister, 2003) and studies of modulation masking (Bacon and Grantham, 1989; Houtgast, 1989; Takahashi and Bacon, 1992; Ewert and Dau, 2000) have shown tuning in the modulation-rate domain. The psychophysical techniques used to measure masking in the AM-rate domain were analogous to those used to estimate tuning of peripheral auditory filters. However, unlike with the peripheral tuning, which has a strong physiological basis in the cochlear mechanics (e.g., Rhode, 1971; Ruggero, 1992), finding the physiological basis for tuning in the AM-rate domain has proven challenging (see Joris et al., 2004, for a review). In the auditory nerve—the only site with a homogenous neural population—AM is coded via synchronized responses of neural fibers to the AM rate (i.e., via phase locking to AM). In all auditory-nerve fibers, modulation transfer functions (MTFs) are represented by a low-pass characteristic with the cutoff frequency determined primarily by the bandwidth of the peripheral auditory filter that provides the input to a given fiber (Møller, 1976a; Joris and Yin, 1992). In contrast to the auditory nerve, a variety of patterns in response to AM are found in the cochlear nucleus, including band-pass shapes of synchronized-response (i.e., phase-locked to the modulation rate) MTFs emerging mainly at high stimulus levels (Møller, 1974, 1976b; Frisina et al., 1990; Frisina et al., 1994; Rhode, 1994; Rhode and Greenberg, 1994). The different response patterns are not robust to changes in stimulus parameters, and they appear to be indigenous to the types of cells as characterized by their responses to pure tones (Glattke, 1969). Band-pass MTFs are much more prevalent in the inferior colliculus (IC). Because AM rate is represented by both synchrony to the AM phase (temporal code) and by the average spike rate (rate code) in the IC, physiological studies often use both measures when analyzing responses to AM. The temporal and rate-based MTFs are typically referred to as tMTFs and rMTFs, respectively (e.g., see Joris et al., 2004). Because of the relative prevalence of band-pass responses to AM, physiological studies have focused on the IC when searching for neural resonances to AM rate (Rees and Møller, 1983; Langner and Schreiner, 1988; Schreiner and Langner, 1988; Heil et al., 1995; Krishna and Semple, 2000). Langner and Schreiner (Langner and Schreiner, 1988; Schreiner and Langner, 1988) suggested that there exists a topographic map of AM rate in the IC of the cat that is orthogonal to the tonotopic axis of audio frequencies. Their observations inspired models of envelope processing that implement a bank of modulation filters receiving inputs from separate peripheral auditory channels (Dau et al., 1997a,b; Ewert and Dau, 2000, 2004). The models are based on the assumption that the envelope of an incoming sound extracted in each channel of the peripheral processing stage is subsequently analyzed in relatively broadly tuned modulation-rate selective neural channels located at more central sites. The models have been successful in accounting for a large body of psychophysical data from studies of modulation perception and masking, lending support to the idea of modulation-rate selective neural channels.
Although band-pass tMTFs and rMTFs are relatively common in the IC (see Joris et al., 2004), they are not invariant with changes of stimulus parameters, in particular stimulus level (Rees and Møller, 1987; Rees and Palmer, 1989; Krishna and Semple, 2000). Rees and Møller (1987) found that tMTFs in the IC of the anesthetized rat changed from low-pass to band-pass as the level of the stimulus increased. In addition, band-pass tMTFs for a noise carrier had a substantially shallower low-frequency slope than band-pass tMTFs for a tonal carrier presented at the same dB SPL. Rees and Møller also showed that adding background noise to a modulated tonal carrier resulted in changing the shape of the tMTF from band-pass to low-pass. Similarly, changes to the shape of tMTFs from low-pass to band-pass with increasing level have been found in the anesthetized guinea pig (Rees and Palmer, 1989) and the anesthetized Mongolian gerbil (Krishna and Semple, 2000). The rMTFs show less orderly changes in the overall shape with level, with regions of suppression often becoming regions of excitation, and vice versa, as level increases (Krishna and Semple, 2000). Krishna and Semple also reported sizeable (frequently larger than an octave) changes in the best modulation frequency (i.e., the modulation frequency eliciting the strongest firing rate) with level.
Despite the ubiquitous dependence of physiological MTFs on stimulus level, the effect of level on masking patterns in the AM domain has not yet been investigated using psychophysical methods. Noise and tonal carriers have been used to measure modulation masking, but all the stimuli were limited to a narrow range of medium levels, around 50–65 dB SPL across all the studies. Furthermore, the use of different noise bandwidths, different experimental techniques and different methods for generating stimuli (e.g., the use of a product versus the sum of the masker and signal AM offset by the dc) complicate comparisons of masking patterns across different studies (Bacon and Grantham, 1989; Houtgast, 1989; Strickland and Viemeister, 1996; Dau et al., 1997a; Ewert and Dau, 2000; Ewert et al., 2002).
In this study, the effect of carrier level on modulation masking was measured for a tonal carrier, a noise carrier, and a tonal carrier presented with an unmodulated high-pass noise. The aim of the study was to investigate to what extent single-neuron recordings in the IC are representative of putative modulation filters derived from patterns of modulation masking measured psychophysically. The data show that despite the often complicated level dependence of neural MTFs, psychophysical modulation masking patterns behave in an orderly way with no strong level dependence, beyond some effects that relate to the dynamic range of modulation perception, rather than to tuning per se. The results highlight differences between the pictures emerging from neural recordings in animals and human perception of AM and they underscore the importance of incorporating peripheral auditory filtering in the models of AM processing.
EXPERIMENT 1: AM MASKING FUNCTIONS FOR TONAL AND NOISE CARRIERS
Methods
Detection of 40-Hz AM (signal) was measured in the presence of simultaneous masking AM using a three-interval forced-choice (3IFC) procedure combined with an adaptive three-down, one-up tracking technique (Levitt, 1971). The masker and signal AM were imposed on the same carrier, and the stimulus in the signal interval was described by
| (1) |
where c(t) denotes the carrier, and mm, ms, and fm, fs are the modulation indices and modulation rates of the masker and signal, respectively. In the non-signal intervals, ms was set to zero. The modulation depth of the masker was fixed at −8 dB in units of 20 log(mm). The choice of the masker modulation depth was dictated by the need to avoid overmodulation (which could occur when mm + ms > 1) during the adaptive tracking of the signal. The rms amplitudes of the stimuli in the signal and non-signal intervals were equated before each trial, and thus an increase in overall intensity resulting from adding the signal AM could not be used as a cue for detecting the signal. Two types of carrier were used, broadband noise with a bandwidth extending from 0.1 to 10 kHz and a 5.5-kHz tone. Masked modulation detection thresholds were measured using two spectrum levels of the noise carrier, 5 and 25 dB SPL (overall levels of 45 and 65 dB SPL), and three levels of the tonal carrier, 40, 65, and 80 dB SPL. Modulation rates of the masker AM ranged from 2 to 256 Hz for the noise carrier, and from 4 to 256 Hz for the tonal carrier, in one-octave steps with the addition of the modulation rate equal to that of the signal, i.e., 40 Hz. The carrier was gated on for 500 ms, including 5-ms raised-cosine ramps, and was modulated over the entire duration.
During the adaptive tracking, the modulation depth of the signal, in units of 20 log(m), was varied in 2-dB steps until the fourth reversal and in 1-dB steps for the subsequent eight reversals. A run terminated after a total of 12 reversals, and the masked threshold from a single run was estimated by averaging signal modulation depths at the final eight reversal points. Three to six threshold estimates were averaged to compute the final threshold. The observation intervals were separated by 300-ms silent intervals and were marked by lights on a computer screen. Visual feedback indicating the correct (i.e., the signal) interval was provided after each listener’s response. A run was aborted when the modulation depth of the signal reached a value yielding overmodulation. For the modulation depth of the masker used, this happened only on a few occasions for the masker rates of 32 and 40 Hz and never more than once for the same masker modulation rate for a given listener.
For each carrier level, threshold for detecting the signal AM was also measured without the masker modulation (i.e., for mm set to zero in the three observation intervals). The adaptive tracking procedure was the same as for measuring masked thresholds.
The stimuli were generated digitally on a PC using a 24-bit soundcard (Echo-Gina 24/96) and a sampling rate of 44.1 kHz. The noise carrier was generated in the frequency domain with the components outside of the passband set to zero. A new sample of noise was generated for each presentation. The stimuli were presented monaurally to the left ear via an earphone of a Sony MDR-V6 headset.
Subjects
Three listeners participated in the study. The listeners had normal hearing (thresholds below 15 dB HL) in the range of audiometric frequencies between 250 and 8000 Hz measured in 1-octave steps. All the three listeners had at least 20 h of practice in tasks involving detection of AM. Two listeners (S1 and S3) were paid for their services, and listener S2 was the author. Listeners S1 and S3 provided informed consent prior to their participation, and the protocol for the study was approved by the Institutional Review Board at the University of Minnesota.
Results
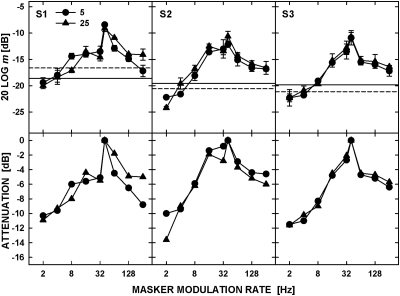
The data for the individual listeners obtained for the noise carrier are shown in Fig. 1. The top row of panels shows masked thresholds for detecting the 40-Hz signal AM plotted as a function of the modulation rate of masker AM, for two spectrum levels of the carrier, 5 (circles) and 25 (triangles) dB SPL. The solid and dashed horizontal lines show thresholds for unmasked detection of the signal AM for the same two spectrum levels, respectively. All the statistical analyses of the data were performed using a repeated-measures ANOVA with the Greenhouse--Geisser correction applied in cases where Mauchly’s test indicated that the assumption of sphericity was violated. The effects were considered significant for p < 0.05. The ANOVA showed that there was no significant effect of the noise-carrier level on the detection of unmasked signal AM [F(1,2) = 0.32, p = 0.63]. For all three listeners, masked threshold was the highest for the masker rate equal to that of the signal and decreased as the difference between the masker and signal rates increased. The decrease was particularly large for the masker rates that were most similar (but not equal) to the signal rate. The sharp drop in masked threshold was likely due to the detection of the second-order modulation resulting from beating between the masker and signal modulation rates (Ewert et al., 2002). This effect is analogous to the effect of beating between two tones on the shape of masking patterns measured in the domain of audio frequencies (Derleth and Dau, 2000).
Figure 1.
Modulation masking for noise carriers presented at a spectrum level of 5 and 25 dB SPL. The symbols in the top panels show thresholds for detecting the 40-Hz signal AM for different rates of the masker modulation with the modulation depth of −8 dB (20 log m). The horizontal lines show unmasked detection of the 40-Hz modulation for the two carrier levels. The lower panels show attenuation functions obtained from the data in the top panel by assigning a 0-dB attenuation to the highest masked threshold.
For the masker rate of 2 Hz (and in some cases, 4 Hz), masked threshold fell below the modulation depth needed for detecting the signal without the masker. This negative masking has been observed in earlier studies (e.g., Bacon and Grantham, 1989), and it is believed to reflect the ability of listeners to use local temporal features to detect the signal in the valleys of the masker modulation, where the local modulation depth of the signal is temporarily increased (Strickland and Viemeister, 1996).
The bottom row of panels shows attenuation functions obtained from modulation masking data by assigning a 0-dB attenuation to the peaks of the masked-threshold patterns and using it as a reference to infer attenuation for all the masker rates used. When derived from modulation-masking data uncontaminated by the use of temporal cues, these functions can be viewed as the transfer characteristics of putative modulation filters tuned to the signal rate under the assumption that a masked threshold is observed for a constant criterion ratio of powers of the masker and signal AM at the output of the modulation filter (Ewert and Dau, 2000). Although the data in Fig. 1 suggest that beats between the masker and signal AM and the local temporal cues played a role in the detection of signal AM, the contribution of these factors appears to be similar at the two carrier levels. The plots in the bottom panels of Fig. 1 show that there were no consistent differences between the shapes of the attenuation functions for the two levels. A repeated-measures ANOVA showed no effect of carrier level on the attenuation functions [F(1,2) = 0.000, p = 0.995], and no significant interaction between the carrier level and the masker modulation rate [F(1.47,2.95) = 1.48, p = 0.34].
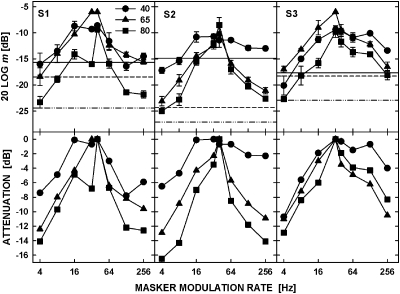
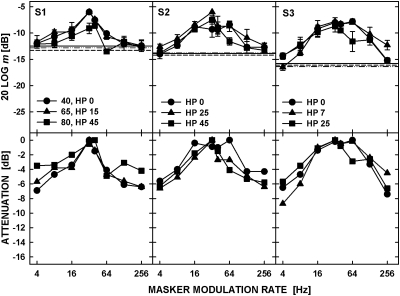
Figure 2 shows the data (top panels) and the attenuation functions (bottom panels) for the 5.5-kHz tonal carrier. Detection of the unmasked signal AM (horizontal lines) showed a systematic improvement (i.e., a decrease in threshold) with increasing carrier level. The ANOVA showed that the effect of carrier level was significant [F(2,4) = 9.68, p = 0.03]. Masked thresholds showed tuning with the peak at or near the signal rate, but unlike for the noise carrier, the tuning of modulation masking became sharper as the tone carrier level increased. The attenuation functions shown in the bottom row of panels indicate that the sharper tuning resulted from thresholds on both sides of the peak falling faster and reaching lower values as the level increased. The effect of carrier level on the attenuation functions was significant [ANOVA, F(2,4) = 44.46, p = 0.03], but the interaction between the carrier level and the masker modulation rate did not reach significance [F(1.25,2.50) = 9.04, p = 0.07].
Figure 2.
As in Fig. 1 but for the 5.5-kHz carrier presented at 40, 65, and 80 dB SPL.
Estimating modulation filter bandwidths from an envelope power spectrum model
An envelope power spectrum model (EPSM) similar to that described by Ewert and Dau (2000) was used to derive modulation filters from the masked AM-detection thresholds measured in Experiment 1 and to estimate the bandwidths of the filters. Following Ewert and Dau, peripheral filtering was not included. In the context of the EPSM, omitting the peripheral filter was inconsequential because the frequency of the tonal carrier was high (5.5 kHz), and thus the attenuation of the sidebands resulting from modulation by the peripheral filter was likely negligible for the modulation rates used. The envelope processing stage consisted of a second-order band-pass Butterworth filter followed by the first-order low-pass Butterworth filter with a cutoff frequency of 150 Hz. It was assumed that for all masker AM rates, masked threshold was obtained when the envelope power at the output of this combined filter increased by a constant ratio (and thus a fixed criterion amount in dB) when the signal AM was added to the masker AM. To calculate the envelope power at the output of the envelope-processing stage for the stimulus with and without the signal AM, the magnitude spectrum of the ac-coupled envelope, as defined in the square bracket in Eq. 1, was multiplied by the squared product of the magnitude transfer characteristics of the two Butterworth filters. The modulation filter was estimated by minimizing the sum of squared deviations between the measured masked thresholds and the power of the signal AM (in dB) that produced the criterion increase at the output of the combined (band-pass and low-pass) filter, using the MATLAB’Sfminsearch function. As was done by Ewert and Dau (2000), for each condition, the power of the signal AM corresponding to threshold observed without the masker AM was added to the output to provide the lower limit of performance. Ewert and Dau used second-order band-pass filters and directly adjusted the Q-values of the filters to obtain the best fits to the data. In this study, the free parameters in the model were the ratio of the cutoff frequencies and the center frequency of the band-pass filter. The center frequency was allowed to vary instead of being set to 40 Hz (the rate of the signal AM) because in many cases, the masked-threshold patterns were strongly asymmetric on the log-frequency scale and fixing the center frequency resulted in poor agreement between the data and the predictions.
Ewert and Dau (2000) used a constant criterion increase of 1 dB in envelope power at the output of the modulation filter. Using a 1-dB criterion, the model underestimated (often substantially) the masked thresholds in all conditions of this study, and other attempted values could not satisfactorily account well for the masked-threshold patterns for the two types of carriers and for all levels. Because of that, the criterion was chosen separately (and arbitrarily) for each masked-threshold pattern to produce a reasonable range of masked thresholds during the fitting procedure. The assumed criterion increase in envelope power at the output of the EPSM ranged from 1.3 to 4 dB across different conditions.
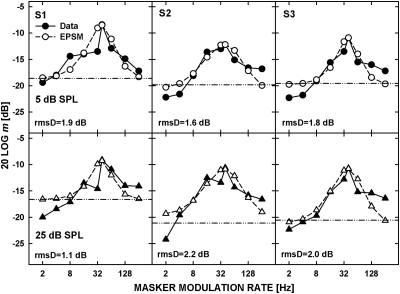
Figure 3 shows the data replotted from the top panels of Fig. 1 (filled symbols) and the predictions from the EPSM (open symbols), for the noise carrier presented at a spectrum level of 5 dB SPL (top panels) and 25 dB SPL (bottom panels). The rms deviations (rmsD) between the measured and predicted thresholds are shown in each panel.
Figure 3.
Masked AM thresholds replotted from the upper panels of Fig. 1 (filled symbols) and predictions by the EPSM (open symbols) for the noise carrier presented at a spectrum level of 5 dB SPL (upper panels) and 25 dB SPL (lower panels). The horizontal lines represent threshold for detecting the 40-Hz signal AM without the masker AM. The values of rms deviation (rmsD) between the data and model predictions are shown for each set of data.
For both carrier levels, there were systematic discrepancies between the data and model predictions, some resulting from the purely spectral approach of the EPSM to envelope processing. Because the long-term power spectra at the output of the modulation filter are used as the input to the decision stage of the EPSM and the envelope power necessary for AM detection without the masker is used to limit performance, the model cannot predict the effects of local temporal features, such as the locally enhanced modulation depth of the 40-Hz signal AM in the valleys of a low-rate masker AM (Strickland and Viemeister, 1996). Consequently, the thresholds predicted by the model for a masking rate of 2 Hz, and in some cases 4 Hz, were higher than those observed in the data. The data often exhibited a sharp decrease in threshold for masker rates around the modulation rate of the signal AM that was not reflected by the model predictions. This discrepancy is consistent with the hypothesis that beats between the masker and the signal AM rates provide a salient cue that can be used by the listeners in modulation-masking tasks.
For the highest modulation rates of the masker AM used, the model underestimated the amount of masking. The masker rates above the cutoff frequency of 150 Hz were attenuated in the model by the low-pass filter rendering these maskers less effective. It appears that a better agreement between the data and the model predictions for the highest masker rates used could be obtained by using a cutoff frequency higher than 150 Hz. Another reason for the discrepancy could be that the inherent fluctuations in the noise carrier were not taken into account because the ac-coupled modulator rather than the Hilbert transform of the stimulus envelope was used as the input to the modulation filter. The effect of the inherent fluctuations in the noise envelope on the detection of the signal AM was reflected in “absolute” threshold for detecting AM and the power of the signal AM at threshold was used to limit performance in the model. However, it may be that the combined effect of the high-rate masker AM and the components in the envelope spectrum of the noise carrier led to an increase in the amount of masking compared with that produced by the masker AM alone.
The effects of detecting beats and local temporal features were present and, based on the results in Fig. 3, they were similar at both carrier levels. Thus, despite these effects, filters derived from the EPSM were used to evaluate the dependence of the modulation-filter bandwidth (or lack thereof) on carrier level.
To compare the bandwidths of the modulation filters at the two carrier levels, Q3dB values were calculated for each fitted filter. These values are shown in Table TABLE I.. The Q3dB values in Table TABLE I. fall within the range of those reported by Ewert and Dau (2000) for the different noise carriers and the signal modulation rates below (16 Hz) and above (64 Hz) the rate of 40 Hz used in this study. A repeated-measures ANOVA performed on the Q3dB values showed that the bandwidth of the estimated modulation filter did not depend on the level of the noise carrier [F(1,2) = 0.06, p = 0.83].
Table 1.
Q3dB values of the modulation filters derived using the EPSM for the noise carrier presented at a spectrum level of 5 and 25 dB SPL.
| L (dB) | S1 | S2 | S3 |
|---|---|---|---|
| 5 | 0.91 | 0.53 | 1.08 |
| 25 | 1.08 | 0.57 | 0.75 |
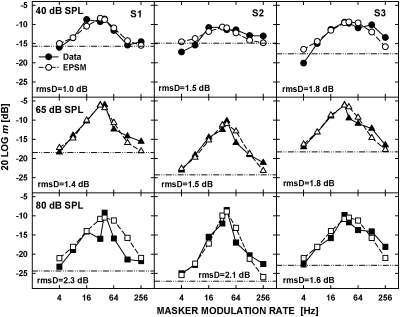
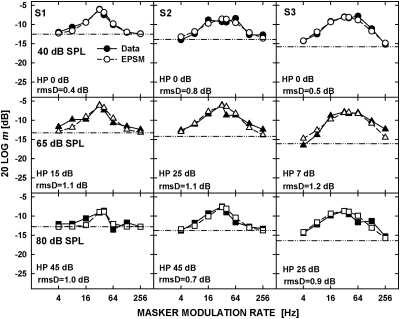
Figure 4 shows the data replotted from the top panel of Fig. 2 (filled symbols) and the predictions by the EPSM (open symbols) for the 5.5-kHz carrier. The data for different carrier levels are plotted in the upper (40 dB SPL), middle (65 dB SPL), and lower (80 dB SPL) panels. Because the masker rate of 2 Hz was not used for the tonal carrier, the effect of using locally enhanced signal modulation depth as a cue was less apparent, although it was observed in a few conditions for the 4-Hz masker (e.g., for S2 and S3 at 40 dB SPL). The sharp decrease in threshold around the peaks of the masked-threshold patterns, suggesting that the listeners used second-order beats as a cue for detecting the signal AM, was observed for the two higher carrier levels, resulting in visible discrepancies between the data and model predictions. Similar to the noise carrier, there was a trend for the model to underestimate the masked threshold for the masker rate of 256 Hz despite the fact that the tonal carrier did not contain intrinsic envelope fluctuations. This suggests that increasing the cutoff frequency of the low-pass filter in the EPSM would improve the model predictions for the highest masker rates, for both the noise and tonal carriers.
Figure 4.
Masked AM thresholds replotted from upper panels of Fig. 2 (filled symbols) and predictions by the EPSM (open symbols) for the 5.5-kHz carrier presented at 40 dB SPL (upper panels), 65 dB SPL (middle panels), and 85 dB SPL (lower panels). The unmasked threshold for detecting the signal AM and the rms deviations between the data and model predictions are shown in each panel.
The Q3dB values of the modulation filters estimated for the tonal carrier are shown in Table TABLE II.. A repeated-measures ANOVA showed that the effect of carrier level on Q3dB values reached significance [F(1.03,2.05) = 37.05, p = 0.02]. Additionally, the ANOVA showed a significant linear contrast for the effect of level [F(1,2) = 243.032, p = 0.004].
Table 2.
Q3dB values of the modulation filters derived using the EPSM for the 5.5-kHz carrier presented at a level of 40, 65, and 80 dB SPL.
| L (dB) | S1 | S2 | S3 |
|---|---|---|---|
| 40 | 0.65 | 0.56 | 0.39 |
| 65 | 0.87 | 0.70 | 0.54 |
| 80 | 0.89 | 0.87 | 0.66 |
Thus both the data and the predictions from the EPSM showed that the bandwidth of the estimated modulation filter tuned to the signal AM rate did not depend on level for the noise carrier, whereas the fitted bandwidths seemed to decrease with increasing level of the tonal carrier. However, the apparent decrease in bandwidth with increasing tonal carrier level covaried with increasing detectability of signal modulation in the absence of a masker (see horizontal lines in Figs. 24), and hence increasing modulation dynamic range. The following experiment was designed to test the hypothesis that the apparent level-dependence of the modulation-filter bandwidth on level is a byproduct of changing dynamic range due to peripheral processing, rather than a reflection of changes in tuning of the neural responses to AM.
EXPERIMENT 2: AM MASKING WITH RESTRICTED SPREAD OF EXCITATION
In agreement with earlier studies of AM processing, thresholds for detecting AM in Experiment 1 decreased with increasing level for the tonal carrier (Wojtczak and Viemeister, 1999; Kohlrausch et al., 2000) but not for the noise carrier (Viemeister, 1979). The improvement in sensitivity to AM for tonal carriers has been attributed to the use of spread of excitation along the basilar membrane and could be explained by two (not mutually exclusive) mechanisms. One explanation is that as the level increases, excitation spreads over a larger area and more neurons responding to AM are recruited. Integration of information across the increasing neural population would lead to an improvement in sensitivity to AM. The second explanation is that nonlinear basilar-membrane processing may contribute to the level dependence of AM detection for tonal carriers; Listeners can improve performance by attending to the upper side of the excitation pattern where changes in excitation level over the AM period are increasingly linear (and thus, larger) as the excitation spreads towards places with higher characteristic frequencies with increasing carrier level. Because unmasked AM detection thresholds for the noise carrier were similar to those for the tonal carrier at the lowest level used (respective horizontal lines in Figs. 12), despite a large difference in the size of the neural populations responding to the two stimuli, the explanation in terms of nonlinear peripheral processing appears more convincing. However, such direct comparison of the two carriers may not be justified because AM detection is limited by inherent envelope fluctuations in the noise carrier and by internal noise for the tonal carrier (Ewert and Dau, 2004). In either case, the covariance of threshold for detecting the signal AM in the absence of the masker and the bandwidth of the estimated modulation filter suggests that the sharpening of tuning in modulation masking may not be due to sharpening of putative physiological modulation filters with increasing level, but it may simply be a byproduct of an increased dynamic range due to the improved unmasked AM detection. Thus the sharpening could result from the same mechanism that contributes to the improved sensitivity to AM with increasing level, such as the use of spread of excitation at the level of peripheral auditory processing. To investigate this hypothesis, tuning of AM masking for a tonal carrier was measured as a function of level in the presence of a high-pass masking noise.
One way to ensure that upward spread of excitation does not contribute to the improvement in AM detection with level is to mask frequency regions on the basilar membrane above the carrier frequency with a high-pass noise with appropriately selected levels (Zwicker, 1956). Because of the nonlinear BM response, it is not intuitively clear how the noise level should change with the level of the tonal carrier. In this experiment, it was assumed that the availability of spread of excitation on the BM was equated by selecting noise levels yielding equal AM detection threshold in the absence of a masker modulation at different carrier levels.
Methods
Prior to the experiment proper, for each level of the 5.5-kHz carrier used in Experiment 1, the 3IFC procedure described in the preceding text was used to measure detection of 40-Hz AM as a function of the level of a high-pass noise. The high-pass noise had a cutoff frequency of 6.2 kHz and was gated on and off with the carrier. The levels of the noise were chosen to produce AM detection thresholds between that observed for each level of the tonal carrier in quiet and a threshold at least 2 dB above that observed for the lowest carrier level (40 dB SPL) in quiet. For each carrier level, the thresholds were then plotted as a function of the level of the high-pass noise and a straight line was fitted to each subject’s data, starting with the highest level of the noise for which the threshold measured in quiet did not differ from that measured in the presence of the noise. At least three data points contributed to each fitted line. The straight-line fits were then used to determine the levels of the high-pass noise that produced the same threshold for detecting the 40-Hz AM for all three carrier levels. These noise levels were paired with the appropriate level of the 5.5-kHz carrier in the modulation-masking experiment.
A 3IFC procedure identical to that used in Experiment 1 was used to measure detection of the 40-Hz signal AM as a function of the modulation rate of the masker AM in the presence of a high-pass noise. For each selected noise level, threshold for detecting the signal without the masker AM was first measured to verify that equal thresholds were obtained at all three carrier levels. In cases where the threshold differed by more than 2 dB from the expected value, small adjustments to the noise level were made, and the threshold was remeasured to make sure that the difference criterion (<2 dB) was satisfied.
Apart from adding the high-pass noise, the parameters of the stimuli, the equipment and experimental procedures were the same as in Experiment 1. The high-pass masker was created by generating Gaussian noise in the frequency domain and then setting the amplitudes of frequency components below 6.2 kHz (and above 10 kHz) to zero. The same sample of the high-pass noise was used in all presentations.
Subjects
The same three listeners who participated in Experiment 1 were recruited to participate in Experiment 2
Results
The detection thresholds and the attenuation functions are shown in the top and bottom panels of Fig. 5, respectively.
Figure 5.
As in Fig. 2 but for the tonal carrier presented with a high-pass noise set to levels equalizing unmasked detection of the 40-Hz signal AM across carrier levels. The spectrum levels of the high-pass noise (HP) are provided in the insets for each carrier level. They were adjusted individually for each listener.
A repeated-measures ANOVA showed that the selection of high-pass noise levels eliminated the effect of carrier level on the detection of signal AM alone [F(2,4) = 2.49, p = 0.20]. The presence of high-pass noise also eliminated negative masking observed for some listeners in Experiment 1 for the masker modulation rate of 4 Hz. The attenuation functions shown in the bottom row were similar for the three levels used. Indeed, there was no effect of level on the data as indicated by the ANOVA [F(2,4) = 0.15, p = 0.87]. Figure 6 shows the data replotted from the top panels of Fig. 5 (filled symbols) and predictions from the EPSM (open symbols).
Figure 6.
As in Fig. 4, but for the 5.5-kHz carrier presented with a high-pass noise. As in Fig. 5, the level of the noise (HP) is provided in each panel.
In contrast to the data for the tonal carrier in quiet (see Fig. 4) and the tone-on-tone AM masking patterns in the study by Ewert et al. (2002), the effect of beats was greatly diminished in the presence of the high-pass noise as evidenced by reduced discrepancies between the data and the EPSM predictions. It is possible that the intrinsic fluctuations in the envelope of the high-pass noise interfered with the detection of beats between the masker and signal AM. However, noticeable effects of beats were apparent for the noise carrier (see Fig. 3), for which the intrinsic fluctuations would be expected to have the same effect on the beats. The Q3dB values calculated for the derived modulation filter are shown in Table TABLE III.. A repeated-measures ANOVA showed no effect of carrier level on the Q3dB value of the modulation filter estimated for the tonal carrier presented with the high-pass noise [F(1.01,2.03) = 1.44, p = 0.35].
Table 3.
Q3dB values of the modulation filters derived using the EPSM for the 5.5-kHz carrier presented at a level of 40, 65, and 80 dB SPL with a high-pass noise the level of which was chosen to produce the same thresholds for detecting the unmasked signal AM.
| L (dB) | S1 | S2 | S3 |
|---|---|---|---|
| 40 | 1.03 | 0.45 | 0.39 |
| 65 | 0.86 | 0.54 | 0.39 |
| 80 | 2.25 | 0.70 | 0.38 |
Thus both the data and the predictions by the EPSM show that in the presence of a high-pass noise the bandwidth of the modulation filter estimated from the masked-threshold patterns for a tonal carrier did not depend on carrier level.
DISCUSSION AND CONCLUSIONS
MTFs obtained from physiological recordings in the IC are predominantly band-pass, but they are not robust to changes in stimulus parameters. This study investigated the effect of level on patterns of modulation masking. Under the assumptions of the envelope power spectrum model, AM masked-threshold patterns reflect the shapes of the underlying modulation filters (Ewert and Dau, 2000). It is not clear what metric used to describe physiological responses to AM best represents perception and thus, what metric should be used to compare psychophysical data with physiology. The metrics typically considered are the degree of synchronization to AM as a function of the modulation rate (tMTFs; Rees and Møller, 1987; Rees and Palmer, 1989; Krishna and Semple, 2000) and the average firing rate in response to an AM carrier as a function of the modulation rate (rMTFs; Langner and Schreiner, 1988; Schreiner and Langner, 1988; Krishna and Semple, 2000). A product of the two metrics, often referred to as “a synchronized rate” has also been used to represent MTFs (e.g., Joris et al., 2004; Nelson and Carney, 2007), but there are no systematic data regarding the effect of level on the synchronized-rate MTFs.
Level effects in tuning of modulation masking and neural tMTFs
Physiological tMTFs show a change in shape from low-pass to band-pass as the carrier level increases (Rees and Møller, 1987; Rees and Palmer, 1989; Krishna and Semple, 2000). The change in slope occurs only on the low-frequency side of the tMTF with the high-frequency slope remaining approximately constant. The attenuation functions obtained from Experiment 1 did not reveal systematic differences in either high- or low-frequency slopes for the noise carrier (bottom panels in Fig. 1) between the two levels used. For the tonal carrier, the attenuation functions (bottom panels in Fig. 2) generally became sharper with increasing level, but both the low- and high-frequency slopes of the functions became steeper as the level increased. Thus no obvious correspondence between the tMTFs and the attenuation functions obtained in this study was apparent.
It is in principle possible that a low-pass tMTF may yield a band-pass masked-thresholds pattern measured psychophysically if it is assumed that listeners can use locally increased modulation depth of the signal AM in the dips of the lower-frequency masker AM (Strickland and Viemeister, 1996). However, assuming that the slope of the underlying neural tMTF increased with increasing carrier level, the opportunity for using the increased local signal AM would diminish due to a greater attenuation of the masker AM and, consequently, a greater response to the masker minima. A perfect trade-off between the decreased strength of the local temporal cues and the decreased strength of the masker AM would be needed to yield the coinciding attenuation functions observed for the noise carrier at the two levels tested. Although not impossible this scenario seems rather unlikely especially because it could not explain the steepening of both sides of the filter attenuation function observed for the tonal carrier.
Level effects in tuning of modulation masking and neural rMTFs
The rMTFs often exhibit irregular changes to the band-pass shape as the level increases due to non-monotonic rate-level functions that are observed for a given carrier for some AM rates and not others (Rees and Palmer, 1989; Krishna and Semple, 2000). In contrast, psychophysical masked-threshold patterns and the derived attenuation functions show orderly steepening of the slopes for the tonal carrier and no changes for the noise carrier. It is important to note that most band-pass MTFs that were used to provide evidence for a topographic map for selective modulation-rate processing in the IC were derived using the average-rate metric (Schreiner and Langner, 1988). However, the changes in the shape of rMTFs with level are hard to reconcile with the orderly patterns of the psychophysical data in this study.
In addition to exhibiting irregular changes in shape, rMTFs exhibit changes in best modulation frequency (i.e., the modulation rate eliciting the peak average rate) with level. These changes often span a range of a few octaves (Krishna and Semple, 2000). The modulation-masking paradigm used in this study would not reveal changes in best modulation frequency and thus, the position of the peak of the filter function with level if at different levels, the processing of the signal AM was carried out by a set of neurons tuned to the signal rate at the level used. To reveal the shifts of the peaks of the attenuation functions, one would have to make sure the stimuli are processed by the same isolated set of neurons in the IC for all the levels tested. At present, the knowledge of the neural processing in the IC is too limited to develop an experimental design that could fulfill this requirement.
The role of spread of excitation on tuning in modulation masking
Thresholds for detecting AM without the masker did not depend on carrier level for the noise carrier but decreased with increasing level for the tonal carrier. The improvement in sensitivity to AM with level has been attributed to peripheral spread of excitation (Wojtczak and Viemeister, 1999; Kohlrausch et al., 2000) and could occur via integration of information over an increasing population of neurons or/and though monitoring increasingly more linear (and thus, greater) changes on the upper side of the excitation pattern. Both explanations (recruitment of more neurons and BM nonlinearity) for improved AM detection with level imply that the effect of level should not be observed in single-neuron recordings. Indeed, Nelson and Carney (2007) reported no systematic change in AM detection with carrier level in the awake rabbit IC.
Tuning of modulation masking in this study covaried with threshold for detecting the signal AM without the masker, suggesting that the apparent change in tuning to AM may simply be a byproduct of an increased dynamic range of perceived modulation. Adding a high-pass noise to the modulated tonal carrier with the level selected to equate thresholds for detecting signal AM measured without the masker AM affected the tuning of the attenuation functions. In the presence of the noise, both sides of the attenuation functions became shallower, and the effect of carrier level was eliminated (lower panels in Fig. 5). This result suggests that the level effect on tuning in modulation masking seen for tonal carriers was not mediated by the level dependence of the putative physiological modulation filters, but instead it was due to changes in the modulation dynamic range, produced by peripheral spread of excitation with increasing level.
Modulation filter bandwidths estimated from the EPSM
For the noise carrier and the tonal carrier presented with a high-pass noise, the EPSM (Ewert and Dau, 2000) yielded estimates of modulation filter bandwidths that did not depend on carrier level. For the tonal carrier presented without the high-pass noise, the estimated Q3dB values increased with increasing level. The results suggest that the increase in the dynamic range of modulation caused by the decrease in detection threshold for unmasked signal AM with carrier level contributed to the apparent sharpening of the derived modulation filters. In addition to the extended dynamic range, the masked-threshold patterns shown in the upper panels of Fig. 2 and in Fig. 4 (filled symbols in the middle and lower panels) exhibit a sharper drop in masked thresholds around the peak of the patterns at the two higher levels (65 and 80 dB SPL) than at the lowest level used (40 dB SPL). This suggests that beats between the masker and signal AM rates might have been used for detecting the signal AM at the higher levels. Because the detection of beats produces a sharper peak, the beats could also contribute to the sharpening of the estimated modulation filter with carrier level. However, the Q3dB values estimated from the data for the tonal carrier were all lower than those reported by Ewert et al. (2002) for the same carrier frequency (they ranged from 0.54 to 0.87 across listeners in this study and from 1.03 to 1.25 across different signal AM rates tested for the same carrier level of 65 dB SPL in the study by Ewert et al.). Unlike in this study, the masker AM used by Ewert et al. was not a sinusoid but a narrowband noise chosen specifically to eliminate the effects of beats. Because detecting beats would have an effect of producing sharper filter estimates and the estimated modulation filters were slightly broader than those in the Ewert et al. study, the effect of beats on the filter bandwidth was probably small. This might be because the effect of beats was restricted to a relatively small range of masker modulation rates, and thus resulted in greater discrepancies between the data and predictions around the peak, as shown in Fig. 4, but had little effect on the overall best-fitting filter.
To incorporate the effects of beats within the EPSM, a more elaborate version would have to be used, as proposed by Ewert et al. (2002). The expanded version includes a stage extracting the second-order envelope and adding its attenuated version to the first-order envelope prior to feeding the resulting magnitude spectrum to the modulation filter bank. The decision would have to be based on monitoring the outputs of multiple modulation filters to detect the components corresponding to the beat rates in remote filters instead of just one filter tuned to the signal AM as was done in this study. Because the estimated filter bandwidths suggest that the effect of detecting the second-order modulation was small, the modeling undertaken here was restricted to the basic version of the EPSM.
Other factors in comparisons between psychophysics and physiology
The modulation filters derived from the modulation-masking data in Experiments 1 and 2 suggest that the shape and bandwidth of the putative underlying physiological modulation filters are independent of carrier level once the effects of peripheral spread of excitation have been accounted for. The MTFs measured in single neurons are not affected by the spread of excitation, and yet they can be strongly level-dependent for both noise and tonal carriers. The level dependence is observed with both metrics commonly used to characterize neural responses to AM, synchrony to the modulation and the average firing rate although its exact form is different for the tMTFs than the rMTFs. The discrepancy between the level effects on psychophysical data and the neural MTFs in the IC does not necessarily imply that neural resonances in the IC or other mechanisms such as, for example, an interplay between inhibitory and excitatory inputs to the IC (Nelson and Carney, 2004) cannot be considered as physiological correlates of modulation filters. Other factors, such as the use of anesthesia in physiological studies, differences among species, or poor understanding of how responses from different types of neurons combine and translate into perception, may contribute to the lack of correspondence between psychophysics and physiology of AM processing.
Conclusions
Tuning in modulation masking has been considered as indicative of modulation-rate selective processing of temporal envelopes. The following conclusions can be drawn based on the measurements of modulation masking as a function of carrier level.
-
(1)
For noise carriers, modulation filters derived from modulation masking data under the assumption of the envelope power spectrum model did not vary with carrier level.
-
(2)
For tonal carriers, tuning in modulation masking data seemed to become sharper as the carrier level increased. The sharper tuning resulted from both the lower- and higher-frequency side of the filter becoming steeper with increasing level. This result does not have direct correspondence in changes with level of neural MTFs obtained using either a metric based on synchrony to AM or the average rate.
-
(3)
A high-pass noise presented at levels that yielded equal AM detection thresholds for different levels of the tonal carrier eliminated the apparent level dependence of tuning in modulation masking.
-
(4)
The data suggest that the effect of level on tuning in modulation masking for tonal carriers can be accounted for by the effects of peripheral spread of excitation. In contrast to neural MTFs in the IC which show level dependence, tuning in modulation masking does not depend on carrier level when spread of excitation cannot be used to detect signal AM.
ACKNOWLEDGMENTS
The study was supported by the NIH Grant No. DC006804. The author thanks Andrew Oxenham and two anonymous reviewers for helpful comments on the earlier version of the manuscript.
Portions of these data were presented at the 149th Meeting of the Acoustical Society of America [M. Wojtczak and Neal F. Viemeister, J. Acoust Soc. Am. 117, 2535(A) (2005)].
References
- Bacon, S. P., and Grantham, D. W. (1989). “Modulation masking: Effects of modulation frequency, depth and phase,” J. Acoust. Soc. Am. 85, 2575–2580. 10.1121/1.397751 [DOI] [PubMed] [Google Scholar]
- Dau, T., Kollmeier, B., and Kohlrausch, A. (1997a). “Modeling auditory processing of amplitude modulation. I. Detection and masking with narrowband carriers,” J. Acoust. Soc. Am. 102, 2892–2905. 10.1121/1.420344 [DOI] [PubMed] [Google Scholar]
- Dau, T., Kollmeier, B., and Kohlrausch, A. (1997b). “Modeling auditory processing of amplitude modulation. II. Spectral and temporal integration,” J. Acoust. Soc. Am. 102, 2906–2919. 10.1121/1.420345 [DOI] [PubMed] [Google Scholar]
- Derleth, R. P., and Dau, T. (2000). “On the role of envelope fluctuation processing in spectral masking,” J. Acoust. Soc. Am. 108, 285–296. 10.1121/1.429464 [DOI] [PubMed] [Google Scholar]
- Drullman, R., Festen, J. M., and Houtgast, T. (1996). “Effect of temporal modulation reduction on spectral contrasts in speech,” J. Acoust. Soc. Am. 99, 2358–2364. 10.1121/1.415423 [DOI] [PubMed] [Google Scholar]
- Ewert, S. D., and Dau, T. (2000). “Characterizing frequency selectivity for envelope fluctuations,” J. Acoust. Soc. Am. 108, 1181–1196. 10.1121/1.1288665 [DOI] [PubMed] [Google Scholar]
- Ewert, S. D., and Dau, T. (2004). “External and internal limitations in amplitude-modulation processing,” J. Acoust. Soc. Am. 116, 478–490. 10.1121/1.1737399 [DOI] [PubMed] [Google Scholar]
- Ewert, S. D., Verhey, J. L., and Dau, T. (2002). “Spectro-temporal processing in the envelope-frequency domain,” J. Acoust. Soc. Am. 112, 2921–2931. 10.1121/1.1515735 [DOI] [PubMed] [Google Scholar]
- Frisina, R. D., Smith, R. L., and Chamberlain, S. C. (1990). “Encoding of amplitude modulation in the gerbil cochlear nucleus. I. A hierarchy of enhancement,” Hear. Res. 44, 99–122. 10.1016/0378-5955(90)90074-Y [DOI] [PubMed] [Google Scholar]
- Frisina, R. D., Walton, J. P., and Karcich, K. J. (1994). “Dorsal cochlear nucleus single neurons can enhance temporal processing capabilities in background noise,” Exp. Brain Res. 102, 160–164. 10.1007/BF00232448 [DOI] [PubMed] [Google Scholar]
- Glattke, T. J. (1969). “Unit responses of the cat cochlear nucleus to amplitude-modulated stimuli,” J. Acoust. Soc. Am. 45, 419–425. 10.1121/1.1911390 [DOI] [PubMed] [Google Scholar]
- Grimault, N., Bacon, S. P., and Micheyl, C. (2002). “Auditory stream segregation on the basis of amplitude-modulation rate,” J. Acoust. Soc. Am. 111, 1340–1348. 10.1121/1.1452740 [DOI] [PubMed] [Google Scholar]
- Heil, P., Schulze, H., and Langner, G. (1995). “Ontogenic development of periodicity in the inferior colliculus of the mongolian gerbil,” Audit. Neurosci. 1, 363–383. [Google Scholar]
- Houtgast, T. (1989). “Frequency selectivity in amplitude-modulation detection,” J. Acoust. Soc. Am. 85, 1676–1680. 10.1121/1.397956 [DOI] [PubMed] [Google Scholar]
- Joris, P. X., Schreiner, C. E., and Rees, A. (2004). “Neural processing of amplitude-modulated sounds,” Physiol. Rev. 84, 541–577. 10.1152/physrev.00029.2003 [DOI] [PubMed] [Google Scholar]
- Joris, P. X., and Yin, T. C. (1992). “Responses to amplitude-modulated tones in the auditory nerve of the cat,” J. Acoust. Soc. Am. 91, 215–232. 10.1121/1.402757 [DOI] [PubMed] [Google Scholar]
- Kay, R. H. (1982). “Hearing of modulation in sounds,” Physiol. Rev. 62, 894–975. [DOI] [PubMed] [Google Scholar]
- Kohlrausch, A., Fassel, R., and Dau, T. (2000). “The influence of carrier level and frequency on modulation and beat-detection thresholds for sinusoidal carriers,” J. Acoust. Soc. Am. 108, 723–734. 10.1121/1.429605 [DOI] [PubMed] [Google Scholar]
- Krishna, B. S., and Semple, M. N. (2000). “Auditory temporal processing: Responses to sinusoidally amplitude-modulated tones in the inferior colliculus,” J. Neurophysiol. 84, 255–273. [DOI] [PubMed] [Google Scholar]
- Langner, G., and Schreiner, C. E. (1988). “Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms,” J. Neurophysiol. 60, 1799–1822. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 49, 467–477. 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- Møller, A. R. (1974). “Responses of units in the cochlear nucleus to sinusoidally amplitude-modulated tones,” Exp. Neurol. 45, 105–117. [DOI] [PubMed] [Google Scholar]
- Møller, A. R. (1976a). “Dynamic properties of primary auditory fibers compared with cells in the cochlear nucleus,” Acta Physiol. Scand. 98, 157–167. 10.1111/j.1748-1716.1976.tb00235.x [DOI] [PubMed] [Google Scholar]
- Møller, A. R. (1976b). “Dynamic properties of the responses of single neurones in the cochlear nucleus of the rat,” J. Physiol. 259, 63–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson, P. C., and Carney, L. H. (2004). “A phenomenological model of peripheral and central neural responses to amplitude-modulated tones,” J. Acoust. Soc. Am. 116, 2173–2186. 10.1121/1.1784442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson, P. C., and Carney, L. H. (2007). “Neural rate and timing cues for detection and discrimination of amplitude-modulated tones in the awake rabbit inferior colliculus,” J. Neurophysiol. 97, 522–539. 10.1152/jn.00776.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees, A., and Møller, A. R. (1983). “Responses of neurons in the inferior colliculus of the rat to AM and FM tones,” Hear. Res. 10, 301–310. 10.1016/0378-5955(83)90095-3 [DOI] [PubMed] [Google Scholar]
- Rees, A., and Møller, A. R. (1987). “Stimulus properties influencing the responses of inferior colliculus neurons to amplitude-modulated sounds,” Hear. Res. 27, 129–143. 10.1016/0378-5955(87)90014-1 [DOI] [PubMed] [Google Scholar]
- Rees, A., and Palmer, A. R. (1989). “Neuronal responses to amplitude-modulated amd pure-tone stimuli in the guinea pig inferior colliculus, and their modulation by broadband noise,” J. Acoust. Soc. Am. 85, 1978–1994. 10.1121/1.397851 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S. (1971). “Observations of the vibration of the basilar membrane in squirrel monkeys using the Mössbauer technique,” J. Acoust. Soc. Am. 49, 1218–1231. 10.1121/1.1912485 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S. (1994). “Temporal coding of 200% amplitude modulated signals in the ventral cochlear nucleus of cat,” Hear. Res. 77, 43–68. 10.1016/0378-5955(94)90252-6 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S., and Greenberg, S. (1994). “Encoding of amplitude modulation in the cochlear nucleus of the cat,” J. Neurophysiol. 71, 1797–1825. [DOI] [PubMed] [Google Scholar]
- Roberts, B., Glasberg, B. R., and Moore, B. C. (2002). “Primitive stream segregation of tone sequences without differences in fundamental frequency or passband,” J. Acoust. Soc. Am. 112, 2074–2085. 10.1121/1.1508784 [DOI] [PubMed] [Google Scholar]
- Ruggero, M. A. (1992). “Responses to sound of the basilar membrane of the mammalian cochlea,” Curr. Opin. Neurobiol. 2, 449–456. 10.1016/0959-4388(92)90179-O [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiner, C. E., and Langner, G. (1988). “Periodicity coding in the inferior colliculus of the cat. II. Topographical organization,” J. Neurophysiol. 60, 1823–1840. [DOI] [PubMed] [Google Scholar]
- Strickland, E. A., and Viemeister, N. F. (1996). “Cues for discrimination of envelopes,” J. Acoust. Soc. Am. 99, 3638–3646. 10.1121/1.414962 [DOI] [PubMed] [Google Scholar]
- Takahashi, G. A., and Bacon, S. P. (1992). “Modulation detection, modulation masking, and speech understanding in noise in the elderly,” J. Speech Hear. Res. 35, 1410–1421. [DOI] [PubMed] [Google Scholar]
- Tansley, B. W., and Regan, D. (1979). “Separate auditory channels for undirectional frequency modulation and unidirectional amplitude modulation,” Sen. Process. 3, 132–140. [PubMed] [Google Scholar]
- Tansley, B. W., and Suffield, J. B. (1983). “Time course of adaptation and recovery of channels selectively sensitive to frequency and amplitude modulation,” J. Acoust. Soc. Am. 74, 765–775. 10.1121/1.389864 [DOI] [PubMed] [Google Scholar]
- Viemeister, N. F. (1979). “Temporal modulation transfer functions based on modulation thresholds,” J. Acoust. Soc. Am. 66, 1364–1380. 10.1121/1.383531 [DOI] [PubMed] [Google Scholar]
- Wojtczak, M., and Viemeister, N. F. (1999). “Intensity discrimination and detection of amplitude modulation,” J. Acoust. Soc. Am. 106, 1917–1924. 10.1121/1.427940 [DOI] [PubMed] [Google Scholar]
- Wojtczak, M., and Viemeister, N. F. (2003). “Suprathreshold effects of adaptation produced by amplitude modulation,” J. Acoust. Soc. Am. 114, 991–997. 10.1121/1.1593067 [DOI] [PubMed] [Google Scholar]
- Zwicker, E. (1956). “Die elementaren Grundlagen zur Bestimmung der Informationskapazität des Gehörs (The foundations for determining the information capacity of the auditory system),” Acustica 6, 356–381. [Google Scholar]