Abstract
Recent experimental studies showed that isotropic vocal fold models were often blown wide apart and thus not able to maintain adductory position, resulting in voice production with noticeable breathy quality. This study showed that the capability of the vocal fold to resist deformation against airflow and maintain adductory position can be improved by stiffening the body-layer stiffness or increasing the anterior-posterior tension of the vocal folds, which presumably can be achieved through the contraction of the thyroarytenoid (TA) and cricothyroid (CT) muscles, respectively. Experiments in both physical models and excised larynges showed that, when these restraining mechanisms were activated, the vocal folds were better able to maintain effective adduction, resulting in voice production with much clearer quality and reduced breathiness. In humans, one or more restraining mechanisms may be activated at different levels to accommodate the varying degree of restraining required under different voice conditions.
INTRODUCTION
An important feature of normal phonation is the adduction of the two vocal folds toward glottal midline to close the glottis or maintain small glottal opening. Statically, small glottal opening facilitates the establishment of sufficient subglottal pressure needed to initiate phonation. Dynamically, small glottal opening enhances the fluid-structure interaction and thus lowers phonation threshold pressure (Titze, 1988; Zhang et al., 2007; Zhang, 2010a). For a given vibration amplitude, small glottal opening leads to strong vocal fold collision and longer glottal closure, which produce higher-order harmonics in the resulting sound spectrum that are important to normal voice quality (Klatt and Klatt, 1990). Complete glottal closure during each oscillation cycle also disrupts the development and persistence of a turbulent jet flow downstream of the glottis, which further reduces broadband noise production and the overall breathiness of the produced voice. Thus, the ability to achieve and maintain small glottal opening or a certain degree of glottal closure under different aerodynamic conditions is critical to normal voice production.
It is generally understood that glottal closure is achieved by approximation of the vocal folds through activation of laryngeal adductory muscles. However, recent experimental studies using isotropic self-oscillating vocal fold models (Z. Zhang et al., 2006a, 2009) suggested that vocal fold adduction, or approximation of the vocal folds, alone does not always guarantee glottal closure during phonation. These studies showed that isotropic one-layer vocal fold models had a tendency to be blown wide open at onset despite that the two vocal folds were brought into contact at rest (Z. Zhang et al., 2006a), resulting in incomplete glottal closure during the entire oscillation cycle and sound production of breathy quality (Zhang et al., 2009). The isotropic model exhibited excessively large motion in the inferior-superior direction that does not directly modulate glottal flow and is often not observed in humans. Increasing the Young’s modulus of the isotropic one-layer vocal fold did not improve the resisting capability of the vocal fold against airflow because phonation threshold pressure increased proportionally with vocal fold stiffness.
This inability of the isotropic vocal fold model to maintain glottal closure against airflow is in sharp contrast with human vocal folds which are capable of maintaining adduction when airflow is applied during normal phonation. Therefore, in addition to adduction, vocal fold posturing must also activate some restraining mechanisms so that the vocal folds are able to maintain effective adduction against the continuously time-varying subglottal pressure. These mechanisms are obviously missing in the isotropic physical models used in Z. Zhang et al. (2006a) Considering that the capability to control and maintain desirable glottal configuration is highly critical to normal voice production, it is thus important to obtain a better understanding of the possible restraining mechanisms available in human phonation. Because activation of such restraining mechanisms is likely to affect vocal fold biomechanics, such improved understanding of restraining mechanisms in phonation may also provide new insights toward other aspects of voice production such as control of voice intensity and fundamental frequency.
The concept that some restraining mechanisms are required to maintain vocal fold adduction is not new in voice production research. Van den Berg and Tan (1959) observed in their excised larynx experiments that, for small or negative longitudinal tension, vibration was only possible at small values of the flow rate or subglottal pressure. At large flow rates, the vocal folds were blown wide apart with no vibration. In a study on the laryngeal mechanisms of intensity control, Isshiki (1964, 1969) argued that, “in order to keep the glottis closed longer, withstanding the increasing pressure below the glottis, greater force to close the glottis is required.” In humans, such “greater force” or restraining function may be provided by the contraction of the thyroarytenoid (TA) muscle, which stiffens the deep body layer of the vocal fold, and the cricothyroid (CT) muscle, which stretches and stiffens the vocal fold tension in the anterior-posterior (AP) direction. Although the importance of TA and CT muscle contraction in regulating phonation has long been recognized and has been the subject of numerous studies (e.g., Isshiki, 1964; Hirano et al., 1969; Gay et al., 1972; Tanabe et al., 1972; Ward et al., 1977; Moore et al., 1987; Choi et al., 1993), most of these studies focused on the roles of TA and CT muscle contraction in pitch and vocal loudness control. There has essentially no systematic investigation regarding the possible restraining effects that contraction of the TA and CT muscles may provide to maintain vocal fold position against the subglottal pressure.
The aims of this paper are to investigate the effectiveness of CT and TA muscle contraction in maintaining effective vocal fold adduction against the subglottal pressure and to understand the effects of activation of these restraining mechanisms on regulating glottal opening during phonation and the produced sound quality. In the following (Sec. 2), the effectiveness of stiffening the body layer (stimulating TA contraction) and increasing the AP tension (stimulating CT contraction) is numerically evaluated by comparing static deformation of vocal fold models of different stiffness conditions when subjected to a constant uniform pressure over the inferior surface. In Sec. 3, experimental data from physical-model and excised larynx experiments are presented to further illustrate the need for restraining mechanisms and their importance to regulating glottal closure and the production of clear voice. The implications of the results of this study on the regulation of voice production in general are further discussed in Sec. 4.
NUMERICAL STUDIES
Considering that vocal fold vibration involves motion mostly in the transverse plane, it is preferable that the restraining effect is achieved without increasing the transverse stiffness of the vocal fold, particularly in the cover layer. This can be achieved in at least two ways: one is to stiffen the body layer, which is discussed in Sec. 2B using an isotropic vocal fold model, and the other is to stiffen the vocal fold in the AP direction (in either the body or cover layer or both layers), which is considered in Sec. 2C in a transversely isotropic vocal fold model. In humans, these two approaches roughly correspond to activation of the TA and CT muscles, respectively. Although the vocal folds are known to exhibit nonlinear material properties, the vocal fold in this study was treated as a linear elastic material, and the increased stress or tension due to muscle activation was modeled by an increase in corresponding Young’s modulus or shear modulus.
Numerical model and methods
The effectiveness of different restraining mechanisms was quantified by comparing static deformations of vocal fold models of different stiffness conditions when subjected to a constant pressure uniformly applied to the inferior surface of the vocal fold model. Although a uniform pressure over the inferior surface is an oversimplification of the spatially dependent flow pressure distribution in realistic phonation, this approach allows a quick and direct evaluation of the capability of the vocal folds to maintain their position against the subglottal pressure.
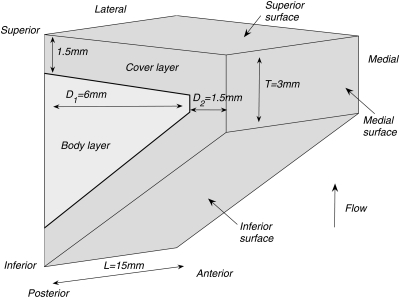
Figure 1 shows a sketch of the three-dimensional two-layer vocal fold model used in this study. A body-cover two-layer structure for the vocal folds was adopted as suggested by Hirano (1974). For simplicity, the vocal fold model was assumed to have a uniform cross-sectional geometry along the AP direction. The coronal cross-sectional geometry of the vocal fold model was defined in the same way as the two-dimensional vocal fold model investigated in Zhang (2009). The vocal fold model was fixed at the lateral surface and the two side surfaces at the anterior and posterior ends. A constant pressure of 500 Pa was applied to the inferior surface of the vocal fold model.
Figure 1.
Sketch of the three-dimensional vocal fold model used in the numerical studies. The vocal fold model has a uniform cross-sectional geometry along the AP direction.
For each stiffness condition, an eigenmode analysis was also performed to calculate the frequencies and modal shapes of the first ten eigenmodes of the vocal fold model. Previous studies showed that phonation onset occurs as two vocal fold eigenmodes are synchronized to the same frequency by the glottal flow, and the frequencies and modal shapes of the synchronizing eigenmodes determine the frequency and vibration pattern of the resulting vocal fold vibration (Ishizaka, 1981; Zhang et al., 2007; Zhang, 2009, 2010a). Thus, the eigenmode analysis allows an indirect evaluation of the influence of vocal fold stiffening on the flow-induced vocal fold vibration.
Both the static and eigenfrequency analysis were performed using the finite-element software COMSOL.
Stiffening body layer in isotropic models
This subsection considers the effect of stiffening the body-layer in a two-layer isotropic linear elastic material. The cover-layer Young’s modulus Eci was kept constant at 4 kPa whereas the body-layer Young’s modulus Ebi was varied between 4 kPa and 400 kPa. A Poisson’s ratio of 0.4995 was used for all conditions.
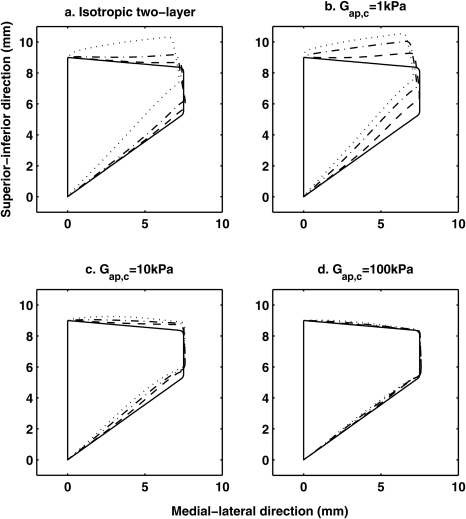
Figure 2a compares the deformed shape of the two-layer isotropic vocal fold model for different values of the body-layer Young’s modulus. The deformation was shown for a coronal slice located in the middle along the AP direction, at which maximum deformation occurred. For the unrestrained model (Ebi = Eci), the vocal fold exhibited large deformation in both the vertical and lateral direction, resulting in a divergent medial surface. Stiffening the body layer in a two-layer isotropic model reduced the vocal fold deformation in both the medial-lateral and inferior-superior direction. The divergence of the deformed medial surface was also significantly reduced, indicating an improved capability of the vocal fold to maintain its geometry and position against subglottal pressure.
Figure 2.
Deformed vocal fold shape in the coronal plane located in the middle along the anterior-posterior direction for (a) an isotropic two-layer vocal fold model and a transversely isotropic vocal fold model with longitudinal shear modulus (b) Gap,c = 1 kPa, (c) Gap,c = 10 kPa, and (d) Gap,c = 100 kPa. In subplot (a), – – –: Ebi = 400 kPa; – · – · – : Ebi = 40 kPa; ···· : Ebi = 4 kPa. In subplots (b), (c), and (d),: – – – Gap,b = 100 kPa; – · – –: Gap,b = 10 kPa; ····: Gap,b = 1 kPa. In all subplots, — : undeformed vocal fold geometry. The vocal fold was subjected to a 500 Pa flow pressure uniformly applied to the inferior surface. For all transversely isotropic conditions, Et=4 kPa, and Eap=4Gap for both layers.
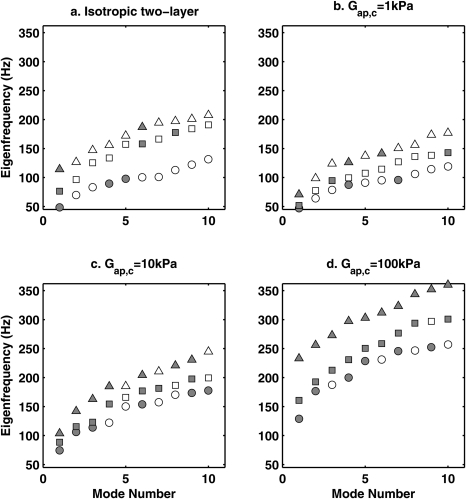
The first ten eigenfrequencies of vocal fold models are shown in Fig. 3a. As expected, increasing body-layer stiffness increased the eigenfrequencies of the vocal fold model. Compared to stiffening the entire vocal fold volume, stiffening only the body-layer is preferable because it allows the cover-layer to remain soft, which allows the restraining capability to be improved without significant increase in overall stiffness [and probably also phonation threshold pressure and phonation frequency as they are related (Zhang et al., 2007; Zhang, 2010a)].
Figure 3.
The first ten eigenfrequencies of (a) an isotropic two-layer vocal fold model and a transversely isotropic vocal fold model with longitudinal shear modulus (b) Gap,c=1 kPa, (c) Gap,c = 10 kPa, and (d) Gap,c = 100 kPa. In subplot (a), ○: Ebi = 4 kPa; □: Ebi = 40 kPa; △: Ebi = 400 kPa. In subplots (b), (c), and (d), ○: Gap,b = 1 kPa; □: Gap,b = 10 kPa; △: Gap,b = 100 kPa. The closed symbols indicate non-AP modes.
It is worth noting that many of the low-order modes of the isotropic models exhibited non-in-phase motion along the AP direction. These modes are referred to as AP modes below in the rest of the text. Because of the out-of-phase motion, the AP modes, particularly the high-order AP modes, generally do not provide efficient flow modulation and thus are undesirable in phonation. Figure 3a shows that stiffening the body-layer in the two-layer isotropic model in this case caused more AP modes to occur at low-order modes. As low-order eigenmodes are relatively easy to be excited due to lower structural damping, this suggests that AP modes are likely to be excited in isotropic models.
Increasing AP tension in transversely isotropic models
In order to consider the effect of increasing AP tension, each layer of the two-layer vocal fold structure was modeled as a transversely isotropic, nearly incompressible, linear elastic material with a plane of isotropy perpendicular to the AP direction, similar to previous studies (Berry and Titze, 1996; Cook et al., 2008; Itskov and Askel, 2002). In the results presented below, a constant transverse Young’s modulus Et of 4 kPa was used based on previous material properties measurements (Hirano and Kakita, 1985; K. Zhang et al., 2006; Chhetri et al., 2011). The longitudinal shear modulus for both the cover layer Gap,c and the body layer Gap,b were varied between 1 kPa and 100 kPa, in order to encompass the possible physiological range that may occur in normal and pathological phonation. It was further assumed in this study that the longitudinal Young’s moduli of both layers co-varied with the corresponding longitudinal shear moduli. Specifically, the results presented below were obtained by assuming Eap/Gap = 4 for both layers. The results are shown in Figs. 2b, 2c, 2d and Figs. 3b, 3c, 3d.
Figures 2b, 2c, 2d show that increasing the AP tension in both layers reduced vocal fold deformation. Comparing to the case of stiffening the body layer in an isotropic model [Fig. 2a], increasing the AP tension in the cover layer provided the maximum restraining effect whereas increasing the AP tension in the body layer provided the least restraining effect. In fact, for large values of the cover longitudinal shear modulus, the restraining effect remained more or less the same as the body layer longitudinal shear modulus was varied in a large range [Fig. 2d].
The AP tension of the cover-layer also had larger influence on vocal fold eigenfrequencies [Figs. 3b, 3c, 3d]. For a given transverse Young’s modulus, the eigenfrequencies of the transversely isotropic two-layer model were determined primarily by the cover layer longitudinal shear modulus and secondarily by the body layer longitudinal shear modulus, with eigenfrequencies increasing with an increase in the longitudinal shear modulus of either vocal fold layer.
In contrast to that of increasing body-layer stiffness (Sec. 2B), Fig. 3 shows that increasing the cover-layer longitudinal shear modulus shifted AP modes to high-order eigenmodes. This is particularly the case when the longitudinal shear modulus were increased in both the body and cover layers. For example, for Gap,c = Gap,b = 100 kPa [2.5 times of Et, similar to the condition considered in Berry (2001)], the first ten in vacuo eigenmodes were all non-AP modes. This suggests that AP modes are less likely to occur during phonation when the CT muscle is activated.
Influence on vocal fold eigenmodes
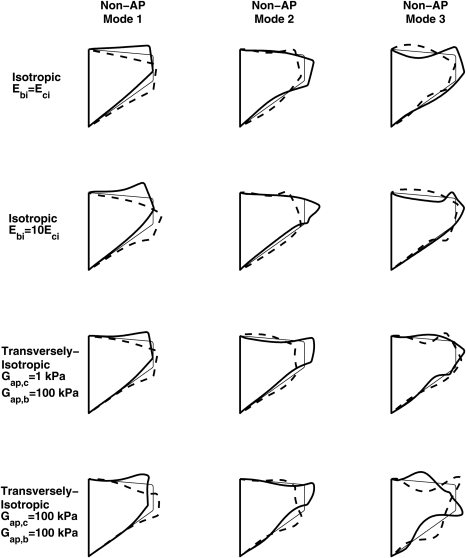
Figure 4 compares the modal shape of the first few non-AP eigenmodes of the unrestrained and restrained vocal fold models. Again, the modal shape was shown only in the coronal plane located in the middle along the AP direction. Although both restraining mechanisms reduce the body-layer motion (e.g., see the motion along the lateral part of the superior surface), increasing AP tension generally leads to a smaller wavelength in motion along the surface. For example, in the bottom case of Fig. 4, the third mode exhibited four strong antinodes in motion along the vocal fold surface, whereas only two or three strong antinodes were present in the isotropic cases. Thus, it is possible that a large AP stiffness (in comparison to the stiffness in the transverse plane) is critical to the so-called mucosal wave motion often observed in normal phonation. Indeed, such wave-like motion was not observed in previous experimental studies using isotropic vocal fold models.
Figure 4.
The first three non-AP eigenmodes of (a) the isotropic one-layer vocal fold model, (b) isotropic two-layer vocal fold model with Ebi = 10Eci, (c) the transversely isotropic model with Gap,c = 1 kPa and Gap,b = 100 kPa, and (d) the transversely isotropic model with Gap,c = 100 kPa and Gap,b = 100 kPa. In each plot, the thick solid line and the dashed line indicate extreme positions of the corresponding eigenmode, spaced 180° apart in a vibratory cycle, and the thin solid line indicates equilibrium positions.
EXPERIMENTAL STUDIES
In this section, experimental data regarding the influence of stiffening the body layer (Sec. 3B) and increasing the AP tension in the entire vocal fold (Sec. 3C) on voice production are presented. The discussion focuses on the influence on the mean glottal opening and the quality of the produced sound.
Experimental setup
The experimental setup was the same as used in previous studies (Z. Zhang et al., 2006a,b, 2009; Zhang, 2010b). More details of the setup can be found in these previous studies. The setup consisted of an expansion chamber (with a rectangular cross-section of the dimension 23.5 × 25.4 cm and 50.8-cm long) simulating the lungs, a 13-cm straight circular PVC tube (inner diameter of 2.54 cm) simulating the tracheal tube, and a vocal fold model (either physical model or excised larynx). No vocal tract was used. Airflow was provided through a pressurized flow supply. For the physical model experiments, the vocal fold physical models were constructed by mixing a two-component liquid polymer solution (Ecoflex 0030, Smooth On, Inc.) with a silicone thinner solution. The two vocal fold models were mounted on two supporting plates and were slightly compressed medially towards each other so that the glottis at rest was completely closed.
For each physical model or larynx condition, the flow rate was increased in discrete increments from zero to a value above onset, and then decreased back to zero in discrete decrements. At each step, after a delay of about 2–3 s after the flow rate change, the mean subglottal pressure (measured at 2 cm from the entrance of the glottis), mean flow rate, acoustic pressure inside the tracheal tube (2 cm from the entrance of the glottis), and outside acoustic pressure (about 20 cm downstream and about 30° off axis) were measured for a 1-s period. These data were recorded at a sampling rate of 50 kHz and saved for later analysis.
Stiffening body-layer (physical models)
A series of two-layer isotropic physical models were constructed with identical geometry (similar to that shown in Fig. 1) and cover-layer Young’s modulus but with different body-layer Young’s modulus. For all models, the cover-layer Young’s modulus was approximately 3.25 kPa. The body-layer Young’s modulus varied between 3.25 kPa and 73.16 kPa. Figure 5 compares the mean glottal opening and outside acoustic pressure as a function of the subglottal pressure between two vocal fold models of extreme body-layer stiffness: the softest model (body and cover had the same Young’s modulus, thus referred to as the unstrained one-layer model below) and the model with the highest body-layer Young’s modulus (referred to as the restrained model). The superior view of these two models during one oscillation cycle was also shown in Fig. 6, which was recorded at a subglottal pressure slightly above onset.
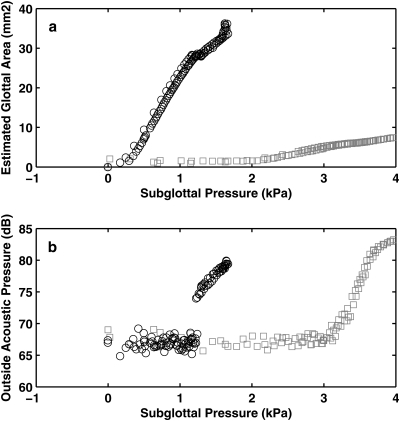
Figure 5.
(a) Estimated mean glottal opening area and (b) outside sound pressure amplitude as a function of the subglottal pressure in the unrestrained one-layer model (○) and the restrained two-layer model (□). The mean glottal opening area was estimated from the measured pressure-flow relationship as Q/(2Ps/ρ)1/2, where Q is the mean flow rate, Ps is the mean subglottal pressure, and ρ is air density.
Figure 6.
Superior view of (a) the unrestrained one-layer model and (b) the restrained two-layer physical model during one oscillation cycle. Both recordings were taken at a subglottal pressure slightly above onset.
Figure 5 shows that stiffening the body-layer increased phonation threshold pressure, but it allowed vocal fold model to vibrate with much reduced glottal opening.
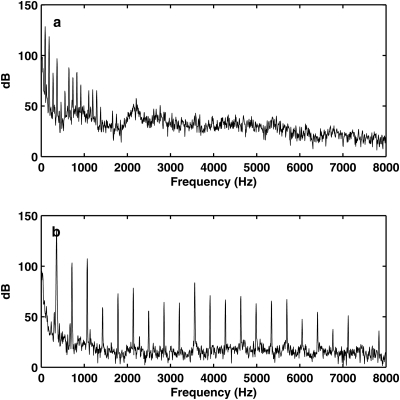
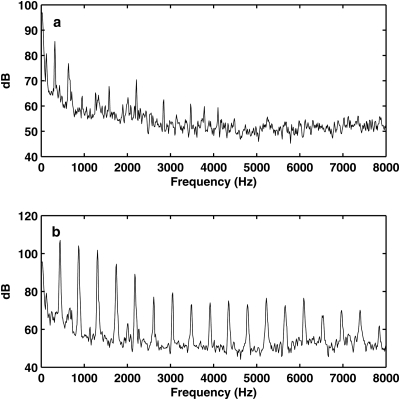
In Fig. 6, the unrestrained model showed consistently large glottal opening than the restrained model, despite that the recording for the unrestrained model was taken at a much lower subglottal pressure. The sound produced by the unrestrained physical model was dominated with noise, presumably because of the turbulence associated with the large glottal opening, and thus very breathy. This high-level turbulence noise can be observed in the outside sound spectrum [Fig. 7a], which was about 20 dB higher than that produced by the restrained vocal fold model [Fig. 7b]. The outside sound produced by the unrestrained vocal fold also had a harmonic structure confined to the frequency range below 1500 Hz. In contrast, the outside sound produced by the restrained model had a much richer harmonic structure, with strong harmonics present up to 8 kHz. As a result, the sound produced by the restrained model was much less breathy and much brighter.
Figure 7.
Spectra of the outside acoustic pressure measured in (a) the unrestrained one-layer isotropic physical model and (b) the restrained two-layer physical model. No vocal tract was used. For both cases the subglottal pressure was slightly above onset.
Note that similar observations were made in Zhang (2010b) which considered a vocal fold model with an extremely stiff body layer. In another study, Z. Zhang et al. (2006b) used a vertical restrainer applied to the lateral half of the superior surface of the vocal fold to suppress the inferior-superior motion and thus prevent the vocal fold model from being pushed wide open by the airflow. They also reported reduced glottal opening at onset and reduced breathiness in the produced sound (Zhang et al., 2009).
It is worth noting that the restrained physical model [Fig. 6a] exhibited slight phase difference in vocal fold motion along the AP direction, suggesting that some AP modes were excited. In our experiments, such phase difference was also observed for models with large body-layer stiffness. This is consistent with the discussion in Sec. 2 that AP modes are likely to be excited in isotropic models.
Increasing AP tension (excised canine larynx)
To illustrate the effectiveness of increasing AP tension as a restraining mechanism, results from excised larynx experiment are presented in this section. CT contraction, which increases AP tension of the vocal fold, can be reproduced in excised larynx models. In the following, voice production in conditions with and without CT contraction was contrasted to illustrate the effect of increasing AP tension on glottal opening and acoustics of the produced sound.
Similar to that in the physical model experiments, the vocal folds were adducted so that they were in contact when no airflow was applied. This was achieved by adducting the two arytenoids using sutures attached to the muscular process. CT contraction was achieved by attaching a 200 g weight anteriorly to the thyroid cartilage, which elongates and tensions the vocal folds.
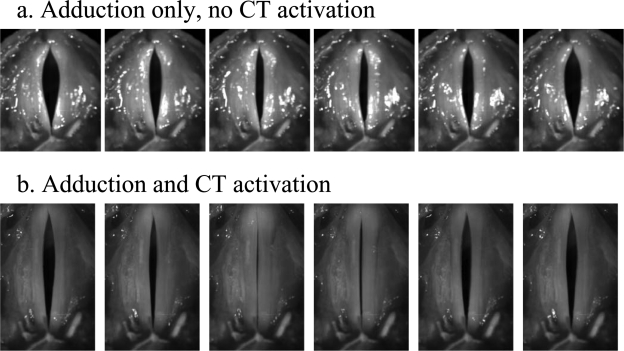
Figure 8 shows the estimated mean glottal opening and the outside acoustic pressure amplitude as a function of the mean subglottal pressure, for both two conditions. Figure 9 shows the superior view of the excised larynx during one oscillation cycle at a subglottal pressure of 2.4 kPa. For the condition without CT approximation, the glottis was gradually pushed open as the subglottal pressure was increased, in spite of the fact that the glottis was closed at rest. Similar to that in physical model experiments, vocal fold vibration was observed but without complete glottal closure except at very high values of subglottal pressure [Fig. 9a]. The produced sound was breathy in nature, with only a few harmonics excited, as shown in Fig. 10a.
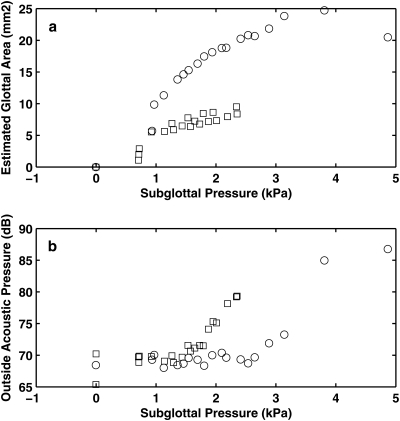
Figure 8.
Estimated mean glottal opening area (a) and outside sound pressure amplitude (b) as a function of the subglottal pressure in the canine larynx model. ○: the larynx was adducted but without CT activation; □: the larynx was adducted and with CT activation. The mean glottal opening area was estimated from the measured pressure-flow relationship as Q/(2Ps/ρ)1/2, where Q is the mean flow rate, Ps is the mean subglottal pressure, and ρ is air density.
Figure 9.
Superior view of the canine larynx (a) without and (b) with CT approximation. The subglottal pressure was around 2.4 kPa for both two cases.
Figure 10.
Spectra of the outside acoustic pressure measured in the canine larynx model. (a) The larynx was adducted but without CT activation; (b) the larynx was adducted with CT activation. No vocal tract was used. The subglottal pressure was around 2.4 kPa for both cases.
With CT approximation, the larynx was better able to maintain its adductory position with increasing subglottal pressure, as indicated by the reduced glottal opening in Fig. 8a. Consequently, complete closure was achieved for a considerable portion of one oscillation cycle [Fig. 9b]. The corresponding sound spectrum [Fig. 10b] had a much richer harmonic structure with strong harmonics up to 8 kHz. The noise level at high frequencies was also slightly lower than that in the case without CT contraction. As a result, the produced sound was much clearer and brighter compared to that produced in the case without CT contraction.
DISCUSSION
In summary, this study showed that, without proper restraining mechanisms, the vocal folds are often blown open (both laterally and vertically) and thus not able to maintain effective adduction, resulting in voice production with noticeably breathy quality. The capability of the vocal fold to resist deformation against the subglottal pressure can be improved by stiffening the body layer or increasing the AP tension in the vocal fold, both of which restrict vertical deformation of the vocal folds. In humans, these two approaches correspond approximately to TA and CT muscle contraction. Experimental results using both physical models and excised larynx models showed that, with reduced mean glottal opening, both restraining approaches were able to reduce the noise level at high frequencies and excite a richer harmonic structure in the produced sound spectra, resulting in much clearer voice quality and reduced breathiness. These results indicate that, in addition to maintain a soft cover layer, normal voice production also requires activation of proper restraining mechanisms, particularly in high-intensity voice production. For pathological conditions in which such restraining mechanisms are weakened or lost, one of the goals of clinical intervention thus should be to restore or provide replacement restraining mechanisms (e.g., vocal fold augmentation by injection or implants for treatment of vocal fold paralysis).
It is reasonable to expect the required level of restraining to vary under different voice conditions. The lowest voice intensity, presumably produced with low subglottal pressure, requires minimum restraining effect and thus minimum TA and CT contraction (unless for high-pitch tones for which muscle contractions are required to increase pitch), and thus is likely to have a breathy quality, as demonstrated by van den Berg and Tan (1959) and also in this study. As one attempts to increase vocal intensity, the restraining level also needs to be increased to match the increasing subglottal pressure in order to maintain at least the same degree of glottal closure during vibration. Although humans do not have voluntary selective control of the TA and CT muscles, some general rules regarding the relative roles of these two muscles in restraining the vocal fold can be noted based on the following differences between the two restraining approaches (stiffening either the body-layer or the cover layer). First, increasing AP tension in the cover layer leads to a much larger increase in vocal fold eigenfrequencies (and presumably phonation frequency) than that induced by stiffening the body layer. Thus, strong CT muscle contraction is less likely in low-pitch voice production. Secondly, stiffening the cover layer is shown to be more effective than stiffening the body layer. This suggests that CT muscle contraction (and thus a high pitch) is likely to be adopted as the primary restraining mechanism in high intensity sound production. On the other hand, this also suggests that TA muscle contraction is not necessary for high-pitch sound production in which sufficient restraining function is already provided by CT muscle contraction. This reduced role of TA muscle in high-pitch voice production (especially in falsetto voice) is consistent with the findings of previous studies (Hirano et al., 1969; Gay et al., 1972). Lastly, the low-order eigenmodes of vocal folds under low AP tension tend to exhibit out-of-phase motion in the AP direction. Thus, to prevent excitation of these AP modes (as in normal phonation in which the vocal folds vibrate in phase along the AP direction), certain degree of CT muscle contraction may be needed, particularly in the presence of strong contraction of the TA muscle. This is consistent with the observation of van den Berg and Tan (1959) that phase difference in vocal fold motion along the AP direction was observed for small values of longitudinal tension but disappeared with increasing longitudinal force.
It is worth noting that improvement on the restraining effect is the largest when the current vocal fold tension is low, i.e., the vocal fold is in a relaxed state with minimal TA or CT contraction. Beyond certain point, further stiffening will not result in any noticeable difference in the restraining effect [e.g., Fig. 3d]. This confirms Isshiki’s (1964) hypothesis that control of vocal intensity through adjusting the glottal resistance (presumably through contraction of primarily the CT and TA muscles) is most effective for low-pitch voices for which “the vocal folds are relaxed and the resistance of the glottis is so low that it can be further increased.”
There are other restraining mechanisms that are not considered in this study but may be also present in phonation. For example, in addition to stiffening the body layer, contraction of the TA muscle is known to cause the vocal fold bulge towards midline (Kreiman and Sidtis, 2011), thus creating medial compression force to close the glottis against the subglottal pressure. This medial compression is likely to further enhance the restraining effect of body-layer stiffening due to TA contraction. The medial bulging may also lead to increased vocal fold thickness in the flow direction, which may allow the vocal fold to better resist deformation against the subglottal pressure (Zhang, 2009).
While these different restraining mechanisms may combine together to achieve optimal restraining effect, the availability of multiple restraining mechanisms allows one to compensate for the loss or weakening of one restraining mechanism by over-activating another restraining mechanism. For example, one may contract the CT muscle more strongly to compensate for TA paralysis, and thus lead to higher fundamental frequency.
This study considers only the influence of vocal fold stiffening on vocal fold eigenmodes and static deformation of the vocal folds under a constant subglottal pressure. No attempts were made to evaluate its influence on glottal fluid-structure interaction. It is possible that a certain stiffness manipulation allows the vocal fold to better resist a given constant subglottal pressure but also significantly increases phonation threshold pressure so that there is no overall improvement on reducing glottal opening at onset. Different stiffening approaches may also lead to significant and possibly qualitative changes in the vibratory pattern and voice quality (other than breathy/clear quality). Such issues require further investigation, either in experiments or simulations using a fully coupled fluid-structure interaction approach (e.g., Luo et al., 2009; Zhang, 2009). Such studies would also need to consider the influence of changes in vocal fold geometry associated with stiffness changes [e.g., CT contraction is known to slightly open the glottis (van den Berg and Tan, 1959)], which, when coupled with a proper muscular model, would allow a better understanding of how different laryngeal muscles combine to achieve optimal restraining effect and maintain desirable glottal configurations under different voice conditions.
CONCLUSIONS
This study has shown that in addition to vocal fold approximation, vocal fold posturing also needs to activate some restraining mechanisms so that the vocal folds are able to maintain effective adduction against the subglottal pressure. Without such restraining mechanisms, the vocal folds were often pushed wide apart, resulting in voice production with noticeably breathy quality. In humans, such restraining mechanisms can be provided by contraction of the TA and CT muscles, which regulate the body layer stiffness and the AP tension, respectively. With proper restraining mechanisms activated, the vocal folds were better able to maintain the adductory position and produce voice with much clearer quality and reduced breathiness. It is further hypothesized that TA contraction may be used as the dominant restraining mechanism in low-pitch voice production whereas CT contraction may be used in high-pitch high-intensity voice production.
ACKNOWLEDGMENTS
This study was supported by Research Grant Nos. R01 DC009229 and R01 DC011299 from the National Institute on Deafness and Other Communication Disorders, National Institutes of Health. The author is grateful to Dr. Bruce Gerratt for many stimulating discussions and Dr. Dinesh Chhetri for his help in the excised larynx experiments.
References
- Berry, D. A. (2001). “Mechanisms of modal and nonmodal phonation,” J. Phonetics 29, 431–450. 10.1006/jpho.2001.0148 [DOI] [Google Scholar]
- Berry, D. A., and Titze, I. R. (1996). “Normal modes in a continuum model of vocal fold tissues,” J. Acoust. Soc. Am. 100, 3345–3354. 10.1121/1.416975 [DOI] [PubMed] [Google Scholar]
- Chhetri, D. K., Zhang, Z., and Neubauer, J. (2011). “Measurement of Young’s modulus of vocal fold by indentation,” J. Voice 25, 1–7. 10.1016/j.jvoice.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, H. S., Berke, G. S., Ye, M., and Kreiman, J. (1993). “Function of the thyroarytenoid muscle in a canine laryngeal model,” Ann. Otol. Rhinol. Laryngol. 102, 769–776. [DOI] [PubMed] [Google Scholar]
- Cook, D., Nauman, E., and Mongeau, L. (2008). “Reducing the number of vocal fold mechanical tissue properties: Evaluation of the incompressibility and planar displacement assumptions,” J. Acoust. Soc. Am. 124, 3888–3896. 10.1121/1.2996300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gay, T., Hirose, H., Strome, M., and Sawashima, M. (1972). “Electromyography of the intrinsic laryngeal muscles during phonation,” Ann. Otol. Rhinol. Laryngol. 81, 401–409. [DOI] [PubMed] [Google Scholar]
- Klatt, D. H., and Klatt, L. C. (1990). “Analysis, synthesis and perception of voice quality variations among male and female talkers,” J. Acoust. Soc. Am. 87, 820–856. 10.1121/1.398894 [DOI] [PubMed] [Google Scholar]
- Kreiman, J., and Sidtis, D. (2011). Foundations of Voice Studies: An Interdisciplinary Approach to Voice Production and Perception (Wiley-Blackwell, Hoboken, NJ: ), pp. 40. [Google Scholar]
- Luo, H., Mittal, R., and Bielamowicz, S. A. (2009). “Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method,” J. Acoust. Soc. Am. 126, 816–824. 10.1121/1.3158942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirano, M. (1974). “Morphological structure of the vocal cord as a vibrator and its variations,” Folia Phoniatr. (Basel) 26, 89–94. 10.1159/000263771 [DOI] [PubMed] [Google Scholar]
- Hirano, M., and Kakita, Y. (1985). “Cover-body theory of vocal fold vibration,” in Speech Science: Recent Advances, edited by Daniloff R. G. (College-Hill Press, San Diego: ), pp. 1–46. [Google Scholar]
- Hirano, M., Ohala, J., and Vennard, W. (1969). “The function of laryngeal muscles in regulating fundamental frequency and intensity of phonation,” J. Speech Hear Res. 12, 616–628. [DOI] [PubMed] [Google Scholar]
- Ishizaka, K. (1981). “Equivalent lumped-mass models of vocal fold vibration,” in Vocal Fold Physiology, edited by Stevens K. N. and Hirano M. (University of Tokyo, Tokyo: ), pp. 231–244. [Google Scholar]
- Isshiki, N. (1964). “Regulatory mechanism of voice intensity variation,” J. Speech Hear Res. 7, 17–29. [DOI] [PubMed] [Google Scholar]
- Isshiki, N. (1969). “Remarks on mechanism for vocal intensity variation,” J. Speech Hear Res. 12, 669–672. [Google Scholar]
- Itskov, M., and Aksel, N. (2002). “Elastic constants and their admissible values for incompressible and slightly compressible anisotropic materials,” Acta Mech. 157, 1–96. 10.1007/BF01182156 [DOI] [Google Scholar]
- Moore, D. M., Berke, G. S., Hanson, D. G., and Ward, P. H. (1987). “Videostroboscopy of the canine larynx: The effects of asymmetric laryngeal tension,” Laryngoscope 97, 543–553. [DOI] [PubMed] [Google Scholar]
- Tanabe, M., Isshiki, N., and Kitajima, K. (1972). “Vibratory pattern of the vocal cord in unilateral paralysis of the cricothyroid muscle,” Acta Oto-laryngol. 74, 339–345. 10.3109/00016487209128460 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (1988). “The physics of small-amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83, 1536–1552. 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
- van den Berg, J. W., and Tan, T. S. (1959). “Results of experiments with human larynxes,” Pract. Otorhinolaryngol. 21, 425–450. [DOI] [PubMed] [Google Scholar]
- Ward. P. H., Berci, G., and Calcaterra, T. C. (1977). “Superior laryngeal nerve paralysis: An often overlooked entity,” Trans. Am. Acad. Ophthalmol. Otolaryngol. 84(1), 78–89. [PubMed] [Google Scholar]
- Zhang, K., Siegmund, T., and Chan, R. W. (2006). “A constitutive model of the human vocal fold cover for fundamental frequency regulation,” J. Acoust. Soc. Am. 119, 1050–1062. 10.1121/1.2159433 [DOI] [PubMed] [Google Scholar]
- Zhang, Z. (2009). “Characteristics of phonation onset in a two-layer vocal fold model,” J. Acoust. Soc. Am. 125, 1091–1102. 10.1121/1.3050285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Z. (2010a). “Dependence of phonation threshold pressure and frequency on vocal fold geometry and biomechanics,” J. Acoust. Soc. Am. 127, 2554–2562. 10.1121/1.3308410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Z. (2010b). “Vibration in a self-oscillating vocal fold model with left-right asymmetry in body-layer stiffness,” J. Acoust. Soc. Am. 128(5), EL279–EL285. 10.1121/1.3492798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2006a). “The influence of subglottal acoustics on laboratory models of phonation,” J. Acoust. Soc. Am. 120, 1558–1569. 10.1121/1.2225682 [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2006b). “Aerodynamically and acoustically driven modes of vibration in a physical model of the vocal folds,” J. Acoust. Soc. Am. 120, 2841–2849. 10.1121/1.2354025 [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2007). “Physical mechanisms of phonation onset: A linear stability analysis of an aeroelastic continuum model of phonation,” J. Acoust. Soc. Am. 122, 2279–2295. 10.1121/1.2773949 [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2009). “Influence of vocal fold stiffness and acoustic loading on flow-induced vibration of a single-layer vocal fold model,” J. Sound Vibr. 322, 299–313. 10.1016/j.jsv.2008.11.009 [DOI] [PMC free article] [PubMed] [Google Scholar]