Abstract
The present analysis is based on the complete first law flow equation i.e. it includes the kinetic energy term that was neglected in earlier papers. It is shown that the results obtained with the proposed equations, derived from an Entropy Maximizing Principle, agree quite well with reliable data published in the scientific/technical literature.
The validity of the “theorem” of minimum entropy production (per unit time) was assessed in Refs 1 and 2 for the well documented case of single – phase fluid tube flow bifurcation from laminar to turbulent regimes. The analysis led to the following two main conclusions: 1) This theorem is not generally valid. 2) The stable type of flow regime is associated with a maximum specific (per unit mass) entropy change. More general broader statements of optimality in thermodynamics are now available in3.
In order to avoid the range of Re in the so called “transition region” the analysis in1,2 was limited to Reynolds numbers one order of magnitude above the estimated critical Reynolds number Rcr for the transition to turbulent flow and the kinetic energy term of the first law flow equation was neglected in line with normal engineering practice.
In the present report the analysis is carried out down to Re∞< Recrand based on the complete flow equation i.e. it includes the kinetic term. As a result a new independent variable: the relative tube length or its inverse L/D or D/L as well as two parameters: the laminar and turbulent kinetic energy factors Ml and Mt respectively, appear in the analysis and its solution. As the kinetic energy factors, or multipliers M play a key role in our analysis, a few words may be useful to clarify the definition of these parameters and provide a brief explanation on the methods adopted to assess their values under fully developed flow conditions for Newtonian fluids flowing in straight horizontal circular pipes.
The kinetic energy term V2/2g is only valid in the idealized world of inviscid fluid mechanics; due to the absence of friction the average velocity V also represents the local velocity that remains constant within the whole tube flow area. With real Newtonian fluids the local velocity is no longer constant and diminishes to zero at the pipe innerwall for both flow regimes. In the specific case of laminar regimes the actual local velocities could be determined accurately on the basis of Newton's laws of mechanics and from this a constant factor Ml = 2 determined to compute the correct kinetic energy term according to 2 (V2/2g). For turbulent regimes no exact theories are available to determine Mt(as well ft) and we depend entirely on experiments. Fortunately Mt≈ 1 and its impact on the prediction of Recris negligible compared to the laminar kinetic energy factor Ml.
The same end results are obtained in4 and the present report; the basic difference between these two communications lies in the method adopted to predict the critical Reynolds number Recr. In4 a quasi “empirical” approach was selected based on numerous plots produced with EXCEL. In the present report a purely analytical method was adopted based on a single premise: the extension of the validity of the Entropy Maximizing Principle proposed in1,2 to any Reynolds number, including the singularity at Re∞ where D/L = O and L/D →∞.
Although this topic may be of interest to some physicists, the theoretical prediction of the critical Reynolds number should prove particularly useful to scientists and engineers engaged in fluid mechanics and heat transfer mainly for several reasons that can be highlighted as follows. Soon after he demonstrated the existence of a “sinuous flow” regime and proposed an excellent estimate of Recr = 2200 for smooth circular tubes, Reynolds derived what became known as the”Reynolds analogy”, This shows that the internal hear transfer coefficient h for a circular pipe is directly proportional to the friction factor ft.. Since the ht is usually much larger than hlit is advantageous to operate in turbulent regimes. Therefore an advanced knowledge of Recrfor instance in such radically new applications as micro-channel heat exchangers is quite important4.
Results
Analysis
The well known5 first law flow equation can be expressed as follows
where H is the total head, V the average velocity and f the Darcy-Weissbach friction factor. Equation (1) is valid for laminar with fl, Ml and ft, Mt for turbulent flow. It is convenient to define a dimensionless relative head
where H frict,∞ is the head loss due only to friction at Re∞ where the laminar and turbulent friction factor curves intersect or
with
Since according to1,2,6a, H = T Δs and Hfrict,∞ = T Δsfrict,∞ with T and Δs the absolute temperature and specific entropy change, it is clear that under constant temperature conditions
and in view of (1) to (5)
The relative dimensionless entropy change Δsrel is used from here on instead of Hrel. and it follows from (6)
By treating both Δsrel,t and Δsrel,l as independent mathematical functions, it is permissible to set
yielding with (7) and (8)
noting that (10) is now independent of f∞; and can be reduced to
It is interesting to note that as long as Ml > Mt and ( Ml − Mt) is a finite number, then (11) yields D/L = 0, therefore L/D → ∞ at Re∞ , as it should.
If Ml and Mt were exactly equal (11) would yield D/L = 0/0; however the two kinetic terms in (10) would cancel each other and the result would be: fl = ft = f∞ = fcr and Re∞ = Recr . It is due to the fact that Ml / Mt = 2 > 1 in the case of smooth circular tubes with fully developed flow at inlet that Recr/Re∞ = 2.55 > 1 as shown in4.
Minimum Recr, fdwith fully developed flow at inlet of circular pipes
According to5 Ml = 2 and Mt ≈ 1; introducing these values in (11) then the expression of D/L thus obtained in both sides of (10) yields the same equation for Δsrel, l and Δsrel, t
As this mathematical function of Re has a maximum, we postulate that Re∞ occurs there in order to maximize the entropy change according to1,2. Therefore Recr can be determined from
or, with (12)
which means that the bifurcation to turbulent flow occurs at Re = Recr where, in a linear coordinate system, the slope of ft is one half that of fl.
Maximum Recr, fudwith fully undeveloped flow at inlet of circular pipes
This occurs when Ml → 1, for instance 1.01 or 1.001…. and Mt = 1. Following the same procedure as in the previous case yields as a limit
The slope of ft is identical to that of fl. in this limiting case, meaning that Recr, fud must be significantly larger than Recr, fd. This is corroborated to some extent by the following excerpts from the abstract of7 presented at the 2007 Annual Review of Fluid Mechanics: “Experiments on pipe flow,…. show that triggering turbulence depends sensitively on initial conditions.”
General case Recr, fd < Recr < Recr, fud with Partially Developed Flow at pipe Inlet
It is easy to show that (14) and (15) are individual cases of the following more general equations
for circular pipes:
It is noteworthy that the above equations were derived without using any explicit equations or correlations for fl or ft, on the basis of an “Entropy Maximizing Principle”, equation (13), and should therefore be applicable with any reliable empirical correlation of ft and valid for any pipe size, including micro tubes and channels.
Prediction of Recr, fdwith fully developed flow at inlet of smooth circular pipes
To validate the proposed theoretical equations it is necessary to compute Recr with equation (14) and demonstrate that the critical Reynolds numbers obtained in this manner substantially agree with the most reliable data published in the scientific/technical literature. As the exact equation of flin terms of Re is well known the right hand side of (14) presents no problem. For the left hand side we are faced with the following challenge: which one among the many empirical correlations proposed for the turbulent friction factor is best suited to our present purpose? Koo's excellent empirical correlation7 based on his 1932 thesis at MIT is selected here for the following reasons.
The values of ft obtained with four different correlations are shown in [5b]. Two of them, are clearly more accurate than the others, namely Petukhov's9 and Koo's7 correlations with the following Re validity limits 10,000 to 3,000,000 and 3,000 to 300,000 respectively. Since we focus in this study on Re below 10,000, Koo's correlation is the better choice; furthermore the maximum deviation between these two correlations being less than 1.5%, Petukhov's correlation is contained within the ±5% accuracy band of Koo's correlation based on 1380 most reliable test resuls.
By introducing in (14) Koo's correlation for ft and the exact equation of fl for the laminar regime, we obtain d(0.0056 + o.5 Re− 0,32 ) / dRe = 0.5 d( 64 Re− 1 ) / dRe, yielding Re0.68 = 200 resulting in Recr = 2400. In order to make allowance for its ± 5 % accuracy, it is only necessary to multiply Koo's correlation by 0.95 and 1.05, resulting in a possible range of Recr = 2160 to 2610.
The uppermost value Recr = 2610 < 3000, as it should, since this is the lower validity limit of Koo's correlation for turbulent flow based on tests with fully developed flow at tube inlet extending down to Re = 3000.
The lowest value Recr = 2160 ≈ 2200, below which the flow remains laminar regardless of inlet conditions according to5,6b. It is noteworthy that Osborne Reynolds, following his discovery of Sinuous Flows9 in 1884, proposed a value of 2200 for what was later called the Reynolds Number!
These positive results validate the proposed basic equation (17) with which they were obtained.
Conversely, if one accepts this conclusion and remembers that (17) was derived from the application of the Principle of Entropy Maximization (13), then the principle itself has been validated.
Estimate of Recr, fud with fully undeveloped flow at inlet of smooth circular pipe
The impact of the laminar factor Ml on Recr can be roughly estimated (as Koo's correlation based on tests with fully developed inlet flow is no longer as accurate) with (17) and 0.95.ft thus obtaining Re0.68 ≈ 420 and Recr ≈ 7300.
This estimate is sufficiently accurate to demonstrate the significant impact of Mlon Recr and to explain why Recr > 3000 have been reported with smooth tubes as indicated in the 2009 Moody Chart shown in5.
Discussion
A most succinct definition11 of engineering thermodynamics is: The Science of Energy and Entropy. Accordingly our analysis moved from conventional Fluid Mechanics to Classical Thermodynamics from equation (7) onwards and led, based on an entropy maximization principle, to the main equations (9), (11), (12), (13), (16) and (17).
At some point it became clear to the authors that equation (16) would lead to an incompressible fluid Fanno flow curve. Indeed all individual curves of Δsrelin terms of Re produced with (16) can be reduced to a single common curve by changing the coordinates as follows: Replace Δsrel by Δsrel/(Δsrel)max with (Δsrel)max obtained with (16) at Recr and substitute V/Vcr = Re/Recr for Re. The curve obtained in this manner shown in Fig. 1 (reproduced from4) is a FANNO FLOW curve according to the Extended Definition of Fanno Flow in12. The notes in green in figure 1 show the similarity with the more complex transition from sub-sonic to super-sonic flow regimes.
Figure 1. FANNO Flow Curve for Incompressible Fluids.
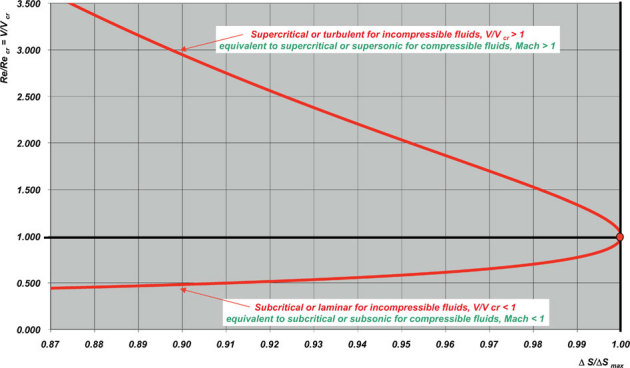
One of the important features of classical thermodynamics is that its laws are independent of the size and geometry of the systems under consideration. This fact permits extending the application of (17) beyond smooth tubes to include non-smooth pipes and constant cross section channels of any shape and size i. e. including micro tubes and channels used in micro heat exchangers3, provided suitably accurate ft and fl correlations as well as inlet parameters Ml and Mt are available with fully developed flow at pipe inlet.
The need and means of suppressing the laminar flow regimes in order to reduce the size of compact tubular heat exchangers is illustrated with the help of an internally finned tube design (INF) of rather complex geometry compared to standard circular pipes in4. This INF design patented in the 1940's was basically a forerunner of modern micro-channels heat exchangers.
For scientists/engineers active in thermal sciences the following list of key words may be helpful to identify the novel or little known features included in this short report: Fluid flow thermodynamics; Maximizing entropy; Incompressible FANNO flow; laminar kinetic energy factor and; Impact of relative tube length.
Author Contributions
Both authors contributed equally to the writing and both reviewed the manuscript.
References
- Soumerai H. On the Application of an “Entropy Maximizing Principle” in Flow Regime Prediction, International Communications Heat and Mass Transfer, 14, 303–312 (1987). [Google Scholar]
- Soumerai H. Thermodynamic aspects of Adiabatic and Diabatic Tube Flow Regime Transition – Single Phase Fluids, as paper number 1384 published in AIAA/ASME 4th Joint Thermophysics and Heat Transfer Conference June 2 – 4, 1986/Boston Mass.
- Bejan A. & Lorente S. The constructal law of design and evolution in nature, Philosophical Transactions of the Royal Society B, 365, 1335–47 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soumerai H. Application of a Novel Fanno Flow Equation, International Institute of Refrigeration's Web site, scheduled for publication in 2011. [Google Scholar]
- 2009 ASHRAE Handbook - Fundamentals (I-P Edition). American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. Online version available at: http://www.knovel.com/web/portal/browse/display?_EXT_KNOVEL_DISPLAY_bookid=2554&VerticalID=0, Chapter 3 Fluid Flow.
- Soumerai H. Practical Thermodynamic Tools for Heat Exchanger Design Engineers, a) Chapt. 2, Sect. 2.2 From Reversible to Irreversible Fluid Flow p.20, b) Chapt 3, Sect. 3.2 Laminar and Turbulent Flow Regimes p. 26, 1987, Wiley Interscience Publications, John Wiley & Sons.
- Koo E. Mechanisms of isothermal and non-isothermal flow of fluids in pipes, Sc D Thesis, Mass. Inst. of Technology, Dept. of Chemical Engineering, (1932). [Google Scholar]
- Eckhardt B. Schneider T., Hof B. & Westerweel J. Turbulence Transition in Pipe Flow. Annual Review of Fluid Mechanics 39; 447–468 (2007). [Google Scholar]
- Petukhov B. S. Heat Transfer and Friction in Turbulent Pipe Flow with Variable Physical Properties in Advances in Heat Transfer, J. P. Hartnett and T. F. Irvine, J,R.(EDS.), 6, 503–564, Academic Press, New York , 1970.
- Reynolds O. On the Two Motions of Water, Proc R. Inst Great Britain, 1884.
- Sonntag R. Gordon J. & Van Wylen. Introduction to Thermodynamics, Classical and Statistical, 2nd ed., Chap.2, p. 16, Wiley, New York, 1982.
- Webster's Extended Definition of Fanno Flow, May 2011, www.webster-online-dictionary.org.


