Skip to main content
PMC home page
Acta Crystallographica Section F: Structural Biology and Crystallization Communications logoLink to Acta Crystallographica Section F: Structural Biology and Crystallization Communications
. 2011 Dec 24;68(Pt 1):111–114. doi: 10.1107/S1744309111054029

Measurement of the equilibrium relative humidity for common precipitant concentrations: facilitating controlled dehydration experiments

Matthew J Wheeler a, Silvia Russi b, Michael G Bowler c, Matthew W Bowler a,*
PMCID: PMC3253849  PMID: 22232186

The equilibrium relative humidity values for a number of the most commonly used precipitants in macromolecular crystallization have been measured using a humidity-control device and compared with independent values where available. The results will simplify experiments using the device.

Keywords: controlled dehydration, macromolecular crystallography, humidity control, automation

Abstract

The dehydration of crystals of macromolecules has long been known to have the potential to increase their diffraction quality. A number of methods exist to change the relative humidity that surrounds crystals, but for reproducible results, with complete characterization of the changes induced, a precise humidity-control device coupled with an X-ray source is required. The first step in these experiments is to define the relative humidity in equilibrium with the mother liquor of the system under study; this can often be quite time-consuming. In order to reduce the time spent on this stage of the experiment, the equilibrium relative humidity for a range of concentrations of the most commonly used precipitants has been measured. The relationship between the precipitant solution and equilibrium relative humidity is explained by Raoult’s law for the equilibrium vapour pressure of water above a solution. The results also have implications for the choice of cryoprotectant and solutions used to dehydrate crystals. For the most commonly used precipitants (10–30% PEG 2000–8000), the starting point will be a relative humidity of 99.5%.

1. Introduction

Inducing phase changes in crystals of macromolecules can often result in an improvement in the order of the crystal lattice and as a result improve the quality of the observed diffraction of X-rays. This effect has been known since the early days of macromolecular crystallography (Berthou et al., 1972 ▶; Einstein & Low, 1962 ▶; Huxley & Kendrew, 1953 ▶; Perutz, 1946 ▶) and can be effected by changing the molar fraction of water in the mother liquor or by changing the relative humidity (RH) of the air surrounding a crystal, with many successful examples in the literature (Fratini et al., 1982 ▶; Gupta et al., 2010 ▶; Heras et al., 2003 ▶; Heras & Martin, 2005 ▶; Kadlec et al., 2011 ▶; Kuo et al., 2003 ▶; Sam et al., 2006 ▶; Zerrad et al., 2011 ▶; Adachi et al., 2009 ▶; Cramer et al., 2000 ▶; Nakamura et al., 2007 ▶; Vijayalakshmi et al., 2008 ▶; Yap et al., 2007 ▶; Bowler et al., 2006 ▶; Hu et al., 2011 ▶; Weiss & Hilgenfeld, 1999 ▶). Several devices have been developed to precisely control the humidity surrounding a crystal (Einstein, 1961 ▶; Pickford et al., 1993 ▶; Sjögren et al., 2002 ▶), with the most recent being mounted on in-house X-ray sources or synchrotron beamlines (Kiefersauer et al., 2000 ▶; Russi et al., 2011 ▶; Sanchez-Weatherby et al., 2009 ▶). The ability to control the relative humidity online allows the changes undergone by the crystal to be characterized and increases the chances of defining a beneficial phase change.

At the start of a dehydration experiment, the RH in equilibrium with the mother liquor of the crystal being studied must be determined. If the value to which the crystal is exposed is too high it will dissolve and if it is too low changes in the crystal may occur too quickly. The equilibrium RH is found experimentally by placing a drop of the mother liquor in a loop at a chosen starting RH and monitoring the size of a defined region of the drop using specific image-processing software. An increase in size indicates that the RH is too high; a decreasing size indicates that the RH is too low. Once the point of RH equilibrium has been determined this is used as the starting point for all further experiments with this particular mother liquor. The device is also increasingly used for room-temperature data collection (Russi et al., 2011 ▶), where the RH equilibrium point is needed in order to prevent crystal dehydration during data collection. This stage of the experiment can be quite time-consuming as an initial starting point is often unknown. In order to simplify this process, we have measured the equilibrium RH for a range of concentrations of the most commonly used precipitants. The data provide a starting point for most dehydration experiments, and Raoult’s law for the equilibrium vapour pressure of water above a solution can be used to understand the observations and make predictions for precipitant concentrations commonly in use. For the most frequently used PEGs the concentration has very little effect on the equilibrium vapour pressure, even though the effect on protein solubility is large (Atha & Ingham, 1981 ▶). For the concentrations of salt typically used as additives (∼200 mM) the effect is also negligible.

2. Experimental procedure: relative humidity measurements

Solutions of PEGs and glycerol were made gravimetrically at con­centrations between 50 and 10%(w/w). Stock solutions of salts at 3 M were made and then diluted to reach the desired concentration. A round 400 µm MicroMount (MiTeGen, Ithaca, New York, USA) was mounted on the humidity-control device (HC1b; Sanchez-Weatherby et al., 2009 ▶) and a drop of solution was placed on the loop with a pipette. The diameter of the drop was measured using specific image-analysis software. The humidity was adjusted until the drop diameter was stable. This was repeated a few times until the drop diameter was stable upon initial placement on the loop. Each measurement was repeated three times at ambient temperature between 296.5 and 297.0 K. All data are available in the Supplementary Material.1

3. Results and discussion

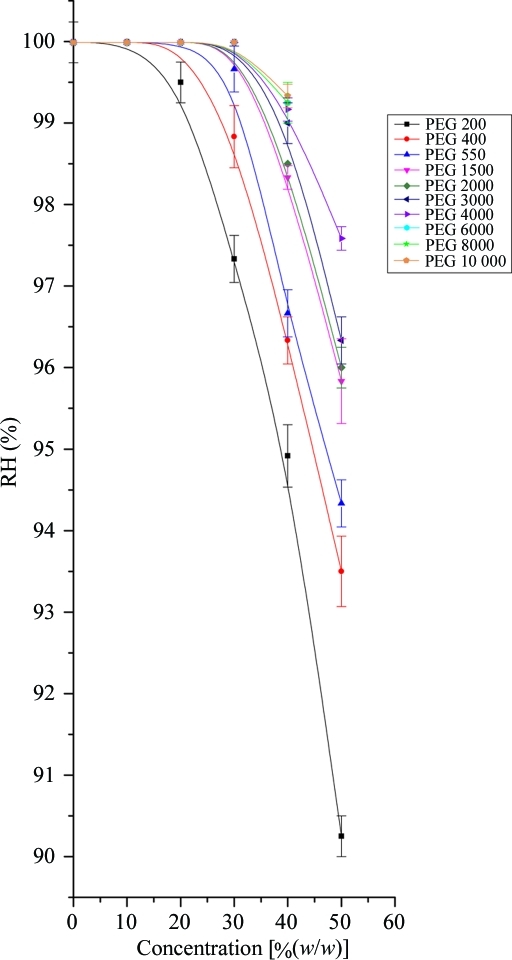
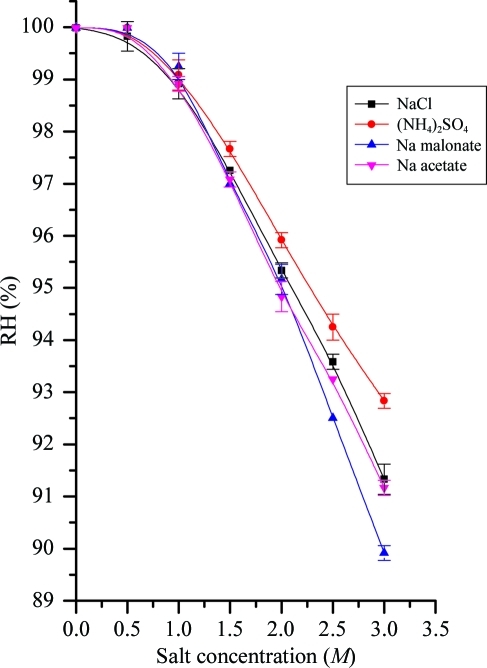
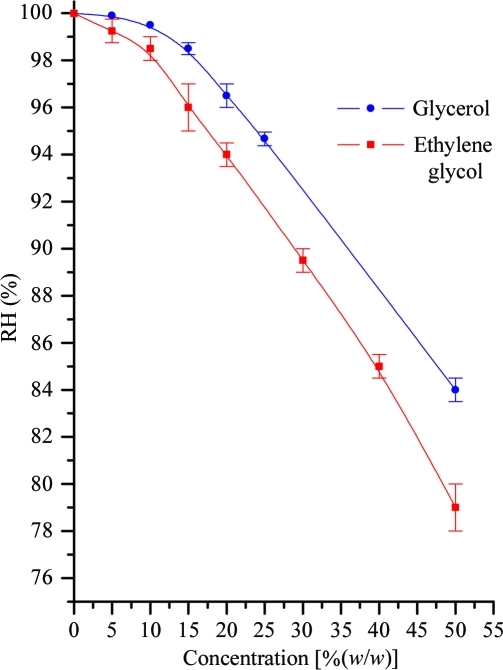
As a result of measuring the RH values across a broad range of concentrations of the most commonly used precipitants in macromolecular crystallogenesis, we hope to reduce the time taken finding the RH that is in equilibrium with the mother liquor. As previously determined, we found that increasing the molecular weight of the PEG (for a given w/w concentration) increased the RH in equilibrium with the solution (Russi et al., 2011 ▶). Surprisingly, we observed a steep increase in RH equilibrium point with decreasing PEG concentration (Fig. 1 ▶). This implies that for the concentrations most typically used in crystal-growth experiments [typically 10–30%(w/w)], with the exceptions of PEGs 200–550, the RH equilibrium point will be around 99.5%. The RH equilibrium points for some typical salts and cryoprotection agents displayed a steady decline in equilibrium RH with increasing concentration (Figs. 2 ▶ and 3 ▶). However, at low con­centrations [below 1 M or 15%(w/w) concentration] the equilibrium RH swiftly approaches 100%. What is also clear is that the equilibrium point converges at a concentration of around 1 M and it is only at high concentrations that salt solutions demonstrate a variety of RH equilibria using the HC1b. Measurements were also made of typical buffer solutions (100 mM) and detergents [1%(w/v)] and these were found to have an RH equilibrium point of 100% RH (data not shown) and therefore not to affect the RH equilibrium for precipitant solutions. This implies that the vast majority of crystallization mother liquors (typically 20–30% mid-range PEG, 200 mM salt and low concentrations of additives) will have an equilibrium RH of 99.5%, as measured by our device.

Figure 1.

Figure 1

Open in a new tab

Plot showing the equilibrium relative humidity for PEG concentrations commonly used in macromolecular crystallogenesis. The lines are B-spline fits to the points.

Figure 2.

Figure 2

Open in a new tab

Plot showing the equilibrium relative humidity for salt solutions commonly used as precipitants or additives in macromolecular crystallogenesis. The lines are B-spline fits to the points.

Figure 3.

Figure 3

Open in a new tab

Plot showing the equilibrium relative humidity for glycerol and ethylene glycol concentrations. The lines are B-spline fits to the points.

The so-called ‘non-ideal’ behaviour of PEG solutions has been observed previously when attempts were made to find concentrations of ammonium sulfate that were in equilibrium with PEG 8000 solutions (Arakali et al., 1995 ▶; Luft & DeTitta, 1995 ▶). The implications of the lack of dehydration in crystallization experiments using PEG 8000 were discussed. In fact, the behaviour of all solutions presented here can be understood in terms of Raoult’s law (Raoult, 1887 ▶),

3.

where the vapour pressure above the solution is p s, the vapour pressure above pure water is p 0 and x w is the mole fraction of water. It has two aspects that are counter-intuitive and lead to some surprising observations. The first is that the number of equivalent molecules in solution must be accounted for. This means that for sodium chloride, each ion in solution counts as a molecular equivalent. This requires knowledge of the ionization behaviour of the substance in solution. For example, ammonium sulfate effectively dissociates into two ions [NH4 + and (NH4SO4)−] and not three as might be expected. Therefore, the number of molecular equivalents is the same as for sodium chloride, whereas sodium malonate probably dissociates into three ions, contributing three molecular equivalents and leading to a lower RH equilibrium for a given concentration (Fig. 2 ▶). The second aspect is that it is the number of species in solution that affects the equilibrium vapour pressure and not the nature of the species. This means that one molecule of PEG 200 has an equivalent contribution as a sodium ion. This accounts for the increasing equilibrium RH with increasing molecular weight of PEG, as the number of molecules decreases for a given weight. Raoult’s law also accounts for the apparent nonlinear relationship; if the molecular concentration is used in place of molar or mass concentration, the relationship is linear (for those solutes for which Raoult’s law holds). We retain the latter measurements here as they are more familiar to those using the device.

The dominant effect in reducing the equilibrium RH is the entropy of mixing, which is the same effect that drives osmosis. The more molecules present in a solution, the more disordered the state becomes and the higher the entropy of the system; this in turn decreases the chemical potential of the water molecules. At equilibrium, the chemical potential of the water molecules in the vapour and in solution are equal; therefore, decreasing the chemical potential of the water molecules in solution by adding a solute decreases the vapour pressure above the solution correspondingly. This relationship, Raoult’s law, provides a close approximation for a large range of solutes at comparatively low molecular concentrations but breaks down at high concentrations, particularly for deliquescent salts and high-molecular-weight polymers, with the equilibrium RH being lower than predicted.

Using this relationship, the equilibrium relative humidity can be predicted for many of the precipitants used in macromolecular crystallogenesis. We have found that the measurements presented here are consistently higher than those predicted by Raoult’s law: around 1% higher for polymers and 3% for salt solutions. Some data on the equilibrium RHs for solutions of PEGs (Sadeghi & Ziamajidi, 2006 ▶; Sadeghi & Shahebrahimi, 2011 ▶) and salts (Wishaw & Stokes, 1954 ▶; Robinson, 1945 ▶) exist in which the equilibrium RHs have been measured by different methods. These data fit well to Raoult’s law (except for PEGs with a molecular weight above 1000 Da), implying inaccuracies in the measurements presented here. Extensive tests using two different devices have led to the conclusion that this is most likely owing to the way in which the RH is calculated by the con­denser, accompanied by differences in the measurements themselves, derived from the fact that drop swelling and shrinking are used. Additionally, the RH values produced by the device are less reliable above an RH of 96%, leading to the flat tops of the curves at values approaching 100% (Figs. 1 ▶, 2 ▶ and 3 ▶). Nevertheless, Raoult’s law can be used to calculate an approximate starting point for dehydration experiments using the following formulae.

For PEGs, glycerol and ethylene glycol (2) can be used,

3.

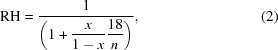where x is the mass fraction of solute and n is the molecular weight of the molecule.

For salts, equation (3) can be used,

3.

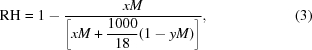where M is the concentration in moles, x is the number of ions in solution per molecule and y accounts for the specific volume of the solute (for sodium chloride y = 0.027 M, for ammonium sulfate y = 0.074 M, for sodium acetate y = 0.054 M and for sodium malonate y = 0.095 M). These equations can be used to predict the equilibrium RH for almost any dehydration experiment as they can be adjusted to apply to specific precipitants. For the higher molecular weight PEGs, where Raoult’s law breaks down, the starting point will be between an RH of 99.5 and 100% for the concentrations used in crystallization experiments, so a calculated predication is not required. Raoult’s law will provide a starting point for most precipitant solutions that will be a few percent below the value used by the device; the charts presented here can be used as an additional guide to the starting point. As each mother liquor must be measured anyway, this will provide a useful starting point that will facilitate the start of crystal-dehydration experiments.

The equations presented here will also allow the calculation of matching RH equilibria between different precipitants and also the calculation of specific dehydration protocols in vapour-diffusion experiments (Luft & DeTitta, 1995 ▶). The relationship between RH and PEG concentrations implies that for almost all PEG solutions with a molecular weight over 1500 Da used as precipitants, the vapour pressure exerted on the drop solution by the well solution in vapour-diffusion experiments will be negligible. This does not imply that PEG solutions cannot be used to dehydrate crystals during soaking experiments, but that in vapour diffusion concentrations of PEG above 1500 Da will not equilibrate. Instead, the most crucial factor will be the effect that the precipitant concentration has on protein solubility (Atha & Ingham, 1981 ▶).

Determining the starting point for these experiments is the first step in automation. Work is currently under way to provide an interface to these experiments through the beamline GUI MXCuBE (Gabadinho et al., 2010 ▶). The integration of dehydration experiments into the ESRF software environment will allow the inclusion of burning strategies (Leal et al., 2011 ▶), in which a crystal is sacrificed to determine the lifetime of a crystal in the beam (particularly important at ambient temperatures); mesh and helical scans (Bowler et al., 2010 ▶; Flot et al., 2010 ▶) to automate the use of multiple positions within crystals; and online data analysis with EDNA (Incardona et al., 2009 ▶; Bourenkov & Popov, 2010 ▶) to analyse diffraction images and determine changes in unit-cell parameters and diffraction intensities. RH equilibrium matching will be automated after starting from a point determined from the data presented here. We hope that the automation of these experiments will increase the use of the device and the number of successful experiments.

Supplementary Material

Supplementary material file. DOI: 10.1107/S1744309111054029/wd5171sup1.xls

Acknowledgments

The authors thank the Partnership for Structural Biology (PSB), Grenoble for an integrated structural biology environment. We also thank D. R. Bowler (Department of Physics and Astronomy, University College London, England) for helpful discussions.

Footnotes

1

Supplementary material has been deposited in the IUCr electronic archive (Reference: WD5171).

References

  1. Adachi, H., Umena, Y., Enami, I., Henmi, T., Kamiya, N. & Shen, J.-R. (2009). Biochim. Biophys. Acta, 1787, 121–128. [DOI] [PubMed]
  2. Arakali, S. V., Luft, J. R. & DeTitta, G. T. (1995). Acta Cryst. D51, 772–779. [DOI] [PubMed]
  3. Atha, D. H. & Ingham, K. C. (1981). J. Biol. Chem. 256, 12108–12117. [PubMed]
  4. Berthou, J., Cesbron, F. & Laurent, A. (1972). J. Mol. Biol. 71, 809–813. [DOI] [PubMed]
  5. Bourenkov, G. P. & Popov, A. N. (2010). Acta Cryst. D66, 409–419. [DOI] [PMC free article] [PubMed]
  6. Bowler, M. W., Guijarro, M., Petitdemange, S., Baker, I., Svensson, O., Burghammer, M., Mueller-Dieckmann, C., Gordon, E. J., Flot, D., McSweeney, S. M. & Leonard, G. A. (2010). Acta Cryst. D66, 855–864. [DOI] [PubMed]
  7. Bowler, M. W., Montgomery, M. G., Leslie, A. G. W. & Walker, J. E. (2006). Acta Cryst. D62, 991–995. [DOI] [PubMed]
  8. Cramer, P., Bushnell, D. A., Fu, J., Gnatt, A. L., Maier-Davis, B., Thompson, N. E., Burgess, R. R., Edwards, A. M., David, P. R. & Kornberg, R. D. (2000). Science, 288, 640–649. [DOI] [PubMed]
  9. Einstein, J. R. (1961). J. Sci. Instrum. 38, 449–451.
  10. Einstein, J. R. & Low, B. W. (1962). Acta Cryst. 15, 32–34.
  11. Flot, D., Mairs, T., Giraud, T., Guijarro, M., Lesourd, M., Rey, V., van Brussel, D., Morawe, C., Borel, C., Hignette, O., Chavanne, J., Nurizzo, D., McSweeney, S. & Mitchell, E. (2010). J. Synchrotron Rad. 17, 107–118. [DOI] [PMC free article] [PubMed]
  12. Fratini, A. V., Kopka, M. L., Drew, H. R. & Dickerson, R. E. (1982). J. Biol. Chem. 257, 4686–4707. [PubMed]
  13. Gabadinho, J. et al. (2010). J. Synchrotron Rad. 17, 700–707. [DOI] [PMC free article] [PubMed]
  14. Gupta, V., Gupta, R. K., Khare, G., Salunke, D. M., Surolia, A. & Tyagi, A. K. (2010). PLoS One, 5, e9222. [DOI] [PMC free article] [PubMed]
  15. Heras, B., Edeling, M. A., Byriel, K. A., Jones, A., Raina, S. & Martin, J. L. (2003). Structure, 11, 139–145. [DOI] [PubMed]
  16. Heras, B. & Martin, J. L. (2005). Acta Cryst. D61, 1173–1180. [DOI] [PubMed]
  17. Hu, N.-J., Iwata, S., Cameron, A. D. & Drew, D. (2011). Nature (London), 478, 408–411. [DOI] [PMC free article] [PubMed]
  18. Huxley, H. E. & Kendrew, J. C. (1953). Acta Cryst. 6, 76–80.
  19. Incardona, M.-F., Bourenkov, G. P., Levik, K., Pieritz, R. A., Popov, A. N. & Svensson, O. (2009). J. Synchrotron Rad. 16, 872–879. [DOI] [PubMed]
  20. Kadlec, J., Hallacli, E., Lipp, M., Holz, H., Sanchez-Weatherby, J., Cusack, S. & Akhtar, A. (2011). Nature Struct. Mol. Biol. 18, 142–149. [DOI] [PubMed]
  21. Kiefersauer, R., Than, M. E., Dobbek, H., Gremer, L., Melero, M., Strobl, S., Dias, J. M., Soulimane, T. & Huber, R. (2000). J. Appl. Cryst. 33, 1223–1230.
  22. Kuo, A., Bowler, M. W., Zimmer, J., Antcliff, J. F. & Doyle, D. A. (2003). J. Struct. Biol. 141, 97–102. [DOI] [PubMed]
  23. Leal, R. M. F., Bourenkov, G. P., Svensson, O., Spruce, D., Guijarro, M. & Popov, A. N. (2011). J. Synchrotron Rad. 18, 381–386. [DOI] [PMC free article] [PubMed]
  24. Luft, J. R. & DeTitta, G. T. (1995). Acta Cryst. D51, 780–785. [DOI] [PubMed]
  25. Nakamura, A., Wada, C. & Miki, K. (2007). Acta Cryst. F63, 346–349. [DOI] [PMC free article] [PubMed]
  26. Perutz, M. F. (1946). Trans. Faraday Soc. B, 42, 187–195.
  27. Pickford, M. G., Garman, E. F., Jones, E. Y. & Stuart, D. I. (1993). J. Appl. Cryst. 26, 465–466.
  28. Raoult, F.-M. (1887). C. R. Acad. Sci. Paris, 104, 1430–1433.
  29. Robinson, R. A. (1945). Trans. R. Soc. N. Z. 75, 203–217.
  30. Russi, S., Juers, D. H., Sanchez-Weatherby, J., Pellegrini, E., Mossou, E., Forsyth, V. T., Huet, J., Gobbo, A., Felisaz, F., Moya, R., McSweeney, S. M., Cusack, S., Cipriani, F. & Bowler, M. W. (2011). J. Struct. Biol. 175, 236–243. [DOI] [PubMed]
  31. Sadeghi, R. & Shahebrahimi, Y. (2011). J. Chem. Eng. Data, 56, 789–799.
  32. Sadeghi, R. & Ziamajidi, F. (2006). J. Chem. Thermodyn. 38, 1335–1343.
  33. Sam, M. D., Abbani, M. A., Cascio, D., Johnson, R. C. & Clubb, R. T. (2006). Acta Cryst. F62, 825–828. [DOI] [PMC free article] [PubMed]
  34. Sanchez-Weatherby, J., Bowler, M. W., Huet, J., Gobbo, A., Felisaz, F., Lavault, B., Moya, R., Kadlec, J., Ravelli, R. B. G. & Cipriani, F. (2009). Acta Cryst. D65, 1237–1246. [DOI] [PubMed]
  35. Sjögren, T., Carlsson, G., Larsson, G., Hajdu, A., Andersson, C., Pettersson, H. & Hajdu, J. (2002). J. Appl. Cryst. 35, 113–116.
  36. Vijayalakshmi, L., Krishna, R., Sankaranarayanan, R. & Vijayan, M. (2008). Proteins, 71, 241–249. [DOI] [PubMed]
  37. Weiss, M. S. & Hilgenfeld, R. (1999). Acta Cryst. D55, 1858–1862. [DOI] [PubMed]
  38. Wishaw, B. F. & Stokes, R. H. (1954). Trans. Faraday Soc. 50, 952–954.
  39. Yap, T. L., Chen, Y. L., Xu, T., Wen, D., Vasudevan, S. G. & Lescar, J. (2007). Acta Cryst. F63, 78–83. [DOI] [PMC free article] [PubMed]
  40. Zerrad, L., Merli, A., Schröder, G. F., Varga, A., Gráczer, É, Pernot, P., Round, A., Vas, M. & Bowler, M. W. (2011). J. Biol. Chem. 286, 14040–14048. [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material file. DOI: 10.1107/S1744309111054029/wd5171sup1.xls

Articles from Acta Crystallographica Section F: Structural Biology and Crystallization Communications are provided here courtesy of International Union of Crystallography

RESOURCES