Modeling the host response to inhalation anthrax

Abstract

Inhalation anthrax, an often fatal infection, is initiated by endospores of the bacterium Bacillus anthracis that are introduced into the lung. To better understand the pathogenesis of an inhalation anthrax infection, we propose a two compartment mathematical model which takes into account the documented early events of such an infection. Anthrax spores, once inhaled, are readily taken up by alveolar phagocytes which then migrate rather quickly out of the lung and into the thoracic/mediastinal lymph nodes. En route, these spores germinate to become vegetative bacteria. In the lymph nodes, the bacteria kill the host cells and are released into the extracellular environment where they can be disseminated into the blood stream and grow to a very high level, often resulting in death of the infected person. Using this framework as the basis of our model, we explore the probability of survival of an infected individual. This is dependent on several factors, such as the rate of migration and germination events and treatment with antibiotics.

1. Introduction

Although a disease of antiquity², anthrax still poses a potential threat to those exposed to the gram-positive bacterium that causes it: Bacillus anthracis. This is especially true in cases of inhalation anthrax, since it remains a potential bio-terror threat. While cutaneous anthrax infections are mostly curable, inhalational anthrax infections have a much higher mortality. This is largely due to the fact that diagnosis is delayed since early indicators of the disease resemble flu-like symptoms and can easily be overlooked by medical personnel.

The progression of an inhalation anthrax infection begins with the entry of bacteria into the airways of a host in the form of dormant endospores that remain highly resistant to a number of harsh conditions (Hanna, 1998). These spores, which are 1–2 microns in diameter, are an ideal size to be easily inhaled into the alveolar space (Dixon, 1999; Kobzik, 2009). Upon deposition in the alveoli, spores are readily taken up by resident alveolar phagocytes (Ross, 1957). After phagocytosing spores, host cells migrate rather quickly out of the lung and into the mediastinal lymph nodes (Ross, 1957; Maldonando-Arocho, 2009; Shetron-Rama, 2010). En route, the spores germinate in the conducive, intracellular environment and become vegetative bacteria that begin to multiply within the host cell (Ross, 1957; Guidi-Rontani, 1999; Ruthel, 2004). In the lymph nodes, the bacteria kill the host cell and vegetative bacteria are then released into the extracellular environment where they can be disseminated into the blood stream and grow to levels as high as 10⁸ bacteria per mL of blood (Dixon, 1999).

In this work, a mathematical model describing the above events is developed to explore the early events of an inhalation anthrax infection and explore possible points of intervention with respect to antibiotics. In the pathogenesis of inhalation anthrax, it is not entirely clear what kind of immune response is initiated after bacteria are released into the lymph nodes (Dixon, 1999), since the outgrowth of the bacteria is rapid and can overwhelm the host in a time frame on the order of days. Additionally, the host response to cutaneous infections appears to be quite different, or at least occurring on a different time scale, than the response to respiratory infections.

In monkey studies, the subjects seem to succumb even to low dose aerosol exposures of anthrax spores (Twenhafel, 2007; Vasconcelos, 2003). However, in general, there appears to be a minimum infective dose (Coleman, 2008; Fennelly, 2004) and there are documented cases (human and animal) in which the host survived exposure to airborne spores (Cote, 2004; Cote, 2006; Kaln, 2002; Guarner, 2003). In various fatal cases of inhalation anthrax, pathology reports (human and animal) mostly concur that hemorrhagic mediastinitis (i.e., inflammation of the mediastinum) was evident, indicating that some kind of response is initiated.

Virulence factors of B. anthracis include the antiphagocytic capsule and secreted toxins. The secreted toxins are important in pathogenesis and include lethal toxin and edema toxin (Baldari, 2006; Ribot, 2006; Cote, 2008). The nature of the inflammatory response to these toxins is highly regulated and varies depending on the cell type engaged, the biological system used and the time point studied during infection (early or late). In general, both lethal and edema toxins appear to suppress the immune response to bacteria, thus paralyzing the host defense (Baldari, 2006). However, it has been recently shown that lethal toxin can induce the proinflammatory programmed cell death pathway of pyroptosis in macrophages and dendritic cells (Fink, 2008; Popov, 2004). Neutrophils are actively recruited during infection and play a critical and complex role in the host response to B. anthracis. The work of Mayer-Scholl and colleagues reported that neutrophil killing of B. anthracis is independent of the generation of reactive oxygen species, which are typically associated with inflammatory conditions (Mayer-Scholl, 2005). There is also evidence that anthrax and its toxins do not necessarily induce the typical “cytokine storm” induced during sepsis (Erwin, 2001; Popov, 2002b; Pellizzari, 1999). Prince suggests that toxin-induced death is mediated not by cytokine release but by hypoxia-induced liver failure (Prince, 2003). It was recently suggested that toxin alone may not be responsible for death (Popov, 2008). Thus, the cause of death in anthrax is still widely debated (Popov, 2004; Popov_2008).

In a previous mathematical model of anthrax infection, Kumar and colleagues modified a general model of sepsis (Clermont, 2004; Chow, 2005) to take into account anthrax specific effects (Kumar, 2008). The general model that they modified described an acute inflammatory response to a generic gram negative pathogen, resulting in the clinical manifestation of sepsis, an often fatal condition. While their work is the first (to our knowledge) to mathematically model the host response to an anthrax infection³, it assumes an identical pathogenesis for multiple routes of entry. We propose that for inhalation anthrax, the environments of the lung and mediastinal lymph nodes determine a different immune progression unique from other routes of entry. Further, we chose not to base the host response on the typical cascade of cellular and molecular events leading to sepsis, but instead wanted to use only those events documented in the literature that were specific to the initiation and progression of an inhalation anthrax infection. Due to many gaps and sparse data in the literature regarding these events for anthrax, we present a less detailed model than that of Kumar and colleagues, but also one that contains fewer variables and parameter values.

Additionally, the incubation period of anthrax is typically defined as the time between initial exposure and symptom onset. However, defining “symptom onset” in a model is problematic. Indeed, Kumar et al., mention the use of an incubation period (0–10 days) but do not define exactly how this is incorporated in their model nor explore how varying the incubation period affects outcome or treatment strategies. Thus, we look at an analogous quantity that describes the length of time in which spores are inhaled, phagocytosed, transported, and germinated (what we term the “PMG period” ) and explore the effect of differing PMG period lengths on bacterial numbers. This is addressed in detail in Section5.

Lastly, Kumar et al. explored various treatment strategies with their model, concluding that a combination of vaccination and antibiotic administration proved most effective in protecting against a fatal anthrax infection, as defined in their model (Kumar, 2007). In this work, we choose to focus on antibiotic treatments and, in contrast with Kumar et al., include two antibiotics which combat the anthrax bacteria via differing mechanisms. (Friedlander, 1993; Kalns, 2002; Dixon, 1999). In defining outcome in our model, we interpret high sustained bacterial numbers as a sign of mortality. This is always accompanied by high sustained numbers of neutrophils as well. Using high bacterial load accompanied by high neutrophil density as mortality indicators is consistent with what is reported in the literature regarding the pathogenesis of inhalation anthrax.

2. Modeling Methods

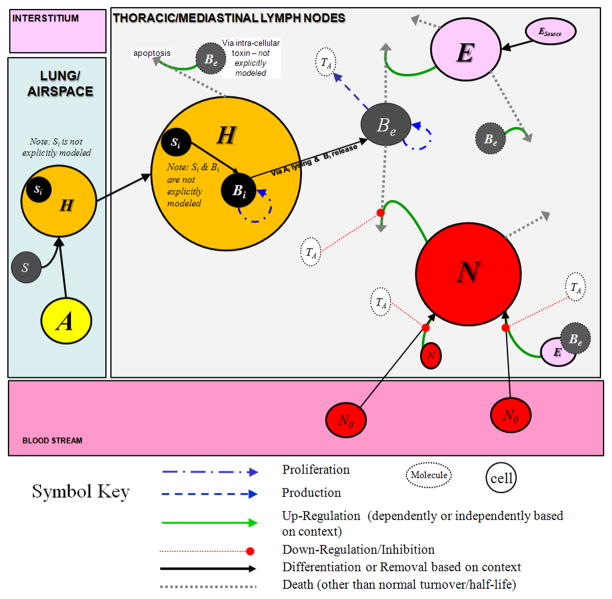
We develop a two compartment ordinary differential equations model which includes the lung and the thoracic/mediastinal lymph nodes (TMLN). Our model is meant to be primarily representative of a human host, although some of the assumptions regarding anthrax pathogenesis and estimation of model parameters are taken from animal data (e.g. non-human primate) when human data are unavailable. For simplicity, we assume that the TMLN are one entity and are representative of the condition of other organ tissues in the body. The lung model feeds into the lymph node model, but there is no feedback from the lymph node compartment into the lung. Figure 1, pictorially summarizes the interactions described in this section. A description of the model variables and parameters in the equations developed below along with the values used can be found in Table 1.

Figure 1.

Diagram of interactions between various cell types and anthrax toxin considered in the model equations, given by Eqs. 1–6 in the text. Spores (S) enter the airway and are readily phagocytosed by resident alveolar phagocytes (A) which become host cells (H). After phagocytosis, the host cells (H) migrate to the Thoracic/Mediastinal Lymph Nodes (TMLN) compartment. The intracellular spores (S_i) germinate en route to the TMLN into vegetative intracellular bacteria (B_i) which can replicate before destroying their host cell via the production of toxins. (S_i, B_i, and intracellular toxins are not modeled explicitly.) After destroying the host cell, the bacteria are released and become extracellular bacteria (B_e) which grow and produce anthrax toxins (T_A). Resident cells (E) as well as soluble components of the innate immune system in the TMLN are the first to encounter the anthrax bacteria and attempt to kill some of the bacteria; however, anthrax induces lysis of these cells after their interaction, keeping killing of bacteria by these resident cells to a minimum. Signals elicited upon death of these cells, attract neutrophils (N) from the blood stream into the TMLN. Neutrophils are partially effective against the bacteria, although the anthrax toxins inhibit neutrophil priming, mobility, and phagocytosis.

Table 1.

Model variables and parameters used in the simulations of the model equations (1) – (6)

Symbol	Description	Units	Initial Condition
S	Free/extracellular anthrax spores	spores	variable
A	Alveolar phagocyte population (Set to quasi-steady state)	Cells	n/a
H	Alveolar host cell; assume that there are nS spores per H	Cells	0.0
E	Resident immune cells in MLN (Early response in MLN)	Cells	2×109
Be	Extracellular bacteria	CFU	0.0
N	Neutrophils	Cells	0.0
TA	Anthrax Toxins	TA-units	0.0

Name	Description	Value Used	Sources/Ranges/Explanations
BeMAX	Carrying capacity for the Be population;	5×1011 Be	Estimated; (Hanna, 1999) reports that bacterial levels in the blood can reach as high as 108/ml. We assume a (0–1) mL volume for a mediastinal lymph node and approximately 20–50 mediastinal lymph nodes (MLN) (Dietrich, 1998; Schmidt, 2007), giving a range of (0–50) mL for total MLN volume. Using Hanna’s number and 50 mL volume, this gives 5×109 bacteria total and we assume that greater numbers of bacteria can pack into the lymph node tissues than in the blood and thus increase this number to 5×1011
ct1, ct2,ct3	Controls the effectiveness of the anthrax toxins, TA, to inhibit neutrophil processes (phagocytosis/killing, recruitment and chemotaxis)	1 TA-units	Estimated; The inhibition is at 50% when the anthrax toxin reaches its maximum level of 1 TA-unit;
ctb	Saturation of the production of anthrax toxin by bacteria	1000 Be	Estimated;
C	Ciprofloxacin antibiotic treatment amount	0.675	Estimated such that its effects on bacteria would not be negligible nor unrealistically successful in all scenarios
D	Doxycycline antibiotic treatment amount	1.23	Estimated such that its effects on bacteria would not be negligible nor unrealistically successful in all scenarios
k1	Rate of apoptosis of resident immune cells in MLN after interaction with Be (i.e. via intracellular anthrax toxin, not specifically modeled)	10−5 /Be per hr	Estimated; (DeLeo, 2004)
k2	Rate at which resident lung cells (which we call host cells), H, phagocytose anthrax spores	10−10/H per hr	Estimated; when all the spores are taken up, there should be S/ns # of infected host cells. k2 determines how quickly/slowly that happens. that k2=10–10 has all spores taken up by resident lung cells around 10 hours.
k3	Rate at which spore-containing host cells migrate to MLN and release vegetative bacteria (which came about from the germinated spores inside the host cell – we assume that some intra-cellular growth has occurred)	0.05/hr	Estimated (Hanna, 1993; Hanna, 1998; Hanna, 1999; Shetron-Rama, 2010). This is computed from simulations such that all infected host cells are gone from the lung compartment by 4 days, for initial spore counts ≤ 2×104. (See paper for more details.)
k4	Rate of production of anthrax toxins by bacteria	2 TA-units per hr	Estimated;
k5	Growth rate of extracellular bacteria, Be	0.8/hr	Doubling time =0.78 hour → growth rate of 0.88865/hr (Kalns, 2002). We took the growth rate to be slightly smaller since under normal circumstances growth conditions are not ideal.
k6	Rate at which resident immune cells in MLN kill Be	5×10−10/E per hr	Estimated; Figure 9 in (Cote, 2006) implies there exists other mechanisms other than neutrophils that are involved in killing anthrax but that these are overwhelmed with larger initial spore counts.
k8	Rate of phagocytosis and killing of Be by N	6×10−10/N per hr	Estimated; (Hampton, 1994)
k9	Rate at which resting neutrophils are activated by Be	5×10−10/BeE per hr	Estimated
k10	Rate at which resting neutrophils are activated by already activated neutrophils	1×10−5/N per hr	Estimated
N0	Source of resting neutrophils	5500 N	Estimated such that maximum neutrophil infiltration is not greater than 2.5×109. We assume that a maximum of 5×107 neutrophils can occupy a milliliter of volume. Assuming a volume of 50mL of lymph nodes (See explanation in BeMAX), gives a maximum neutrophil capacity of 2.5×109.
nb	Number of bacteria (on average) inside a host cell after migration of the cell to the MLN and after anthrax spores have germinated, become vegetative bacteria and grown intracellularly before lysing the cell.	5 Be	Estimated
ns	Number of spores (on average) phagocytosed by resident lung host cells	3 S	Estimated
sA	Source of resident lung host cells (like alveolar macrophages or dendritic cells, prior to phagocytosing spores)	3×108 H/hr	Previous work: Day, 2009
sE	Source of resident immune cells in MLN	1×108 E/hr	Estimated
μA	Death rate of resident lung host cells (like alveolar macrophages or dendritic cell, prior to phagocytosing spores)	0.05/hr	Previous work: Day, 2009
μE	Death rate of resident immune cells in MLN	0.05/hr	Estimated; based on μA;
μN	Death rate of primed neutrophils;	0.06/hr	Reynolds, 2006; Half-life 1–2 days (24–48 hours) → (0.01444, 0.02888)/hr- Wikipedia; We use a larger value to include other removal mechanisms of neutrophils (e.g. by macrophages)
μTA	Decay of anthrax toxins	2/hr	Estimated; Watson_2007 reports PA half-lives of 10–20 minutes → decay rates of (ln(2)/20)*60 to (ln(2)/10)*60 per hour → (2.07944, 4.15888)

The Lung submodel is developed to account for the entry of spores into the airway, to emulate inhalation anthrax. Spores (S) enter the airway and we assume that, because of their small size, they are easily lodged in the airway and alveoli, so that any clearance via bronchial mucociliary mechanisms is negligible (spore size: Dixon, 1999 pg 819; Kobzik, 2009). In addition, we consider a given initial spore load to be the number of spores delivered into the lung and not the amount of spores to which the host is exposed. Spores in the alveoli are readily phagocytosed by resident alveolar phagocytes (A) and we assume that all spores are taken up by these alveolar phagocytes by 10 hours post inoculation. Some have reported that these host cells are alveolar macrophages (Guidi-Rontani, 2002) while others have shown evidence that dendritic cells primarily play this role (Brittingham, 2005; Cleret, 2007; Shetron-Rama, 2010). In our model, we simply consider both cell types as alveolar host cells and that an average of n_S spores reside in each host cell (H) that is involved in the phagocytois of spores. After phagocytosis, these host cells migrate to the TMLN compartment (Ross, 1957; Maldonado-Arocho, 2009; Shetron-Rama, 2010) and we assume that for low to moderately high aerosol challenges (i.e. up to 2×10⁴ spores) the migration is completed by approximately 100 hours post inoculation. We refer to the time period which encompasses initial exposure and phagocytosis of spores, migration to TMLN, and germination as the PMG period and explore this further in in Section 5: Antibiotic Treatment and the Phagocytosis-Migration-Germination (PMG) period. Following are the equations for spores (S), the alveolar phagocytes (A), and the host cells (H):

$$\begin{array}{l}\frac{dA}{dt}=\underset{\begin{array}{c}\text{Internalization}\\ \text{of}\text{spores}\text{to}\\ \text{become}\text{a}\text{host}\text{cell}\end{array}}{\underbrace{-k_{2}SA}}+\underset{\begin{array}{c}\text{Source}\text{of}\\ \text{alveolar}\\ \text{phagocytes}\end{array}}{\underbrace{S_A}}-\underset{\begin{array}{c}\text{Natural}\\ \text{Turnover}\end{array}}{\underbrace{{\mu }_{2}A}}\\ \frac{dS}{dt}=\underset{\begin{array}{c}\text{Internalization}\\ \text{of}\text{spores}\text{by}\\ \text{alveolar}\text{phagocytes}\end{array}}{\underbrace{-k_{2}SA}},S(0)=\text{variable}\end{array}$$

$$\frac{dH}{dt}=\underset{\begin{array}{c}\text{Internalization}\text{of}\\ \text{spores};\\ n_S\text{spores}\text{per}H\end{array}}{\underbrace{\frac{k_{2}SA}{n_s}}}-\underset{\begin{array}{c}\text{migration}\\ \text{of}H\text{to}\text{TMLN}\end{array}}{\underbrace{k_{3}H}}$$

We assume that phagocytosis of spores by the alveolar macrophages happens quickly and as such, set the equation for A to quasi-steady state to arrive at the following formula for A:

$$A=\frac{s_A}{k_{2}S+{\mu }_A}$$

We incorporate this formula into the equation for S and H above as shown below in equations (1)–(2). The host cell provides a suitable environment for spores to germinate and germination occurs quickly en route to the TMLN (Dixon, 2000; Ruthel, 2004; Guidi-Rontani, 1999). Based on the work of Dixon and colleagues, host cells burst soon after migrating to the TMLN, most likely via toxin effects rather than mechanical lysis due to host cell carrying capacity constraints (Dixon, 2000). We combine migration, germination, and bursting into the term -k₃H in equation (2) below.

$$\frac{dS}{dt}=\underset{\begin{array}{c}\text{Internalization}\\ \text{of}\text{spores}\text{by}\\ \text{alveolar}\text{phagocytes}\end{array}}{\underbrace{-k_{2}S\frac{s_A}{k_{2}S+{\mu }_A}}}$$ (1)

$$\frac{dH}{dt}=\underset{\begin{array}{c}\text{Internalization}\text{of}\\ \text{spores};\\ n_S\text{spores}\text{per}H\end{array}}{\underbrace{\frac{k_{2}S\frac{s_A}{k_{2}S+{\mu }_A}}{n_s}}}\underset{\begin{array}{c}\text{migration}\\ \text{of}H\text{to}\text{TMLN};\\ \text{encompasses}\text{germination}\\ \text{process}\text{and}\text{bursting}\end{array}}{\underbrace{-k_{3}H}}$$ (2)

Whether or not alveolar macrophages kill or inhibit B. anthracis growth is an unresolved issue, yet Cote and colleagues suggest that something other than neutrophils must be at work to protect against low dose aerosol exposure (Cote, 2006). Thus, we assume that resident cells (such as macrophages, dendritic cells, and lymphocytes) as well as soluble components of the innate immune system in the TMLN respond to the released vegetative bacteria but are not capable of clearing bacterial load amounts over some critical threshold (Kalns, 2002; Banks, 2005; Popov, 2002a; Banks, 2006; Baldari, 2006; Hanna, 1999). Subsequently, these resident cells via signals elicited upon death (Fink, 2008; Popov, 2004) may serve to draw neutrophils to the area, which are partially effective at killing anthrax bacteria (Mayer-Scholl, 2005). Anthrax toxins inhibit neutrophil priming, (Wright, 1986), neutrophil mobility (chemotaxis), (During, 2005; Baldari, 2006) and phagocytosis of bacteria (O’Brian, 1985; Banks, 2006; Baldari, 2006). The above suggests that neutrophils cannot effectively kill all bacteria. Furthermore, we assume that spores have not only germinated inside their host cell but have become vegetative bacteria capable of at least some intracellular replication before killing their host cell. Hence, we assume that for each infected host cell, n_B bacteria are released into the TMLN when the host cell bursts. We also assume that no bacteria are released in the lung since inhalational anthrax does not, at least initially, cause pneumonia (Swartz, 2001).

The TMLN submodel is the main site of bacterial infection in our model. We assume that it is representative of the host’s overall condition since hemorrhagic mediastinitis seems to be evident in the majority of the fatal anthrax cases (Dixon, 1999; Guarner, 2003). The TMLN submodel consists of the early lymphocyte mediators (E), extracellular vegetative anthrax bacteria (B_e), neutrophils (N), and anthrax toxins (T_A). Below are the equations for the TMLN submodel:

$$\frac{dE}{dt}=\underset{\begin{array}{c}\text{Source}\\ \text{of}\text{lympocytes}\end{array}}{\underbrace{s_E}}\underset{\begin{array}{c}\text{Natural}\\ \text{turnover}\end{array}}{\underbrace{-{\mu }_{E}E}}\underset{\begin{array}{c}\text{Bacterial}/\text{toxin}\\ \text{induced}\text{death}\end{array}}{\underbrace{-k_1{B}_{e}E}}$$ (3)

$$\frac{{dB}_e}{dt}=\underset{\begin{array}{c}\text{Gain}\text{from}\text{germinated}\\ \text{spores}\backslash \text{vegetative}\\ \text{bacteria}\text{released}\\ \text{from}\text{the}\text{host}\text{cell}\end{array}}{\underbrace{k_3{n}_{B}H}}+\underset{\begin{array}{c}\text{extracellular}\\ \text{baceterial}\text{growth}\end{array}}{\underbrace{k_5{B}_e\left(1-\frac{B_e}{B_{\mathit{eMAX}}}\right)}}\underset{\begin{array}{c}\text{Killing}\text{of}\text{Be}\text{by}\\ \text{early}\text{immune}\\ \text{response}\text{in}\text{TMLN}\end{array}}{\underbrace{-k_6{EB}_e}}\underset{\begin{array}{c}\text{Killing}\text{of}{\text{B}}_{\text{e}}\text{by}\text{N}\\ \text{inhibited}\text{by}\text{anthrax}\text{toxins}\end{array}}{\underbrace{-\frac{k_8{NB}_e}{1+\frac{T_A}{c_{t1}}}}}$$ (4)

$$\frac{dN}{dt}=\underset{\begin{array}{c}\text{Recruitment}/\text{priming}\\ \text{by}\text{siganls}\text{from}\\ \text{dying}\text{lymphocytes};\\ \text{inhibited}\text{by}\text{anthrax}\text{toxin}\end{array}}{\underbrace{\frac{k_9{B}_e{EN}_0}{1+\frac{T_A}{c_{t2}}}}}+\underset{\begin{array}{c}\text{Recruitment}/\text{priming}\\ \text{by}\text{primed}\\ \text{neutrophils};\\ \text{inhibited}\text{by}\text{antrhax}\text{toxin}\end{array}}{\underbrace{\frac{k_{10}{NN}_0}{1+\frac{T_A}{c_{t3}}}}}-\underset{\text{decay}}{\underbrace{{\mu }_{N}N}}$$ (5)

where N₀ is a constant source of circulating neutrophils.

$$\frac{{dT}_A}{dt}=\underset{\begin{array}{c}\text{Production}\text{of}\text{toxin}\text{by}\\ \text{extracellular}\text{bacteria}\end{array}}{\underbrace{k_4\frac{B_e}{c_{tb}+B_e}}}-\underset{\text{decay}}{\underbrace{{\mu }_{TA}T}}$$ (6)

This four-equations sub-model of the lymph node allows for bacterial clearance for small inocula of B_e, while higher B_e inocula show uncontrolled bacterial growth, coupled with high neutrophil numbers. Equations (1)–(6) complete the present model. All simulations were performed using XPPAUT, courtesy of Bard Ermentrout of the University of Pittsburgh (available at www.math.pitt.edu/xpp/xhtml) numerically integrated using CVODE method with a step size of 0.01. MATLAB® (version R2008a Mathworks) was used to generate Figure 2 and to compute the sensitivity analysis (where XPPAUT was used to carry out the numerical integration method). Microsoft® Excel 2007 was used to generate Figures 3 and 4.

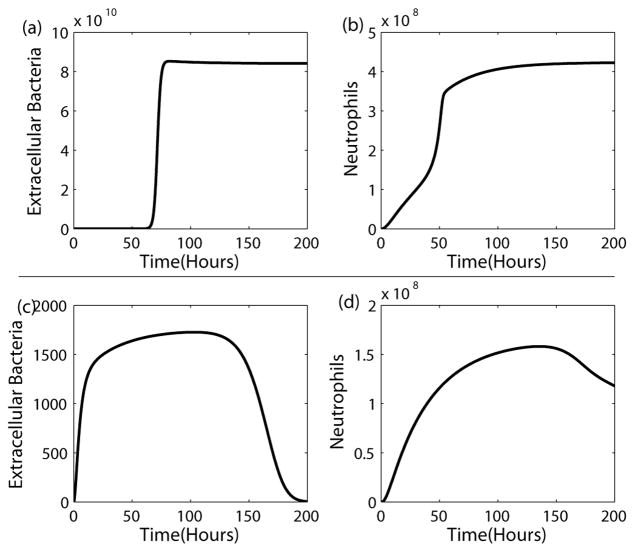
Figure 2.

Mortality and Survival Scenarios. The top panel shows a mortality scenario with persistently elevated bacterial levels, (a), accompanied by elevated neutrophil counts, (b). The bottom panel illustrates a survival scenario where bacterial levels, (c), are decreasing toward zero and neutrophils, (d), are also decreasing toward zero. In each scenario only the initial spore level is different. Parameter values for each scenario are the identical.

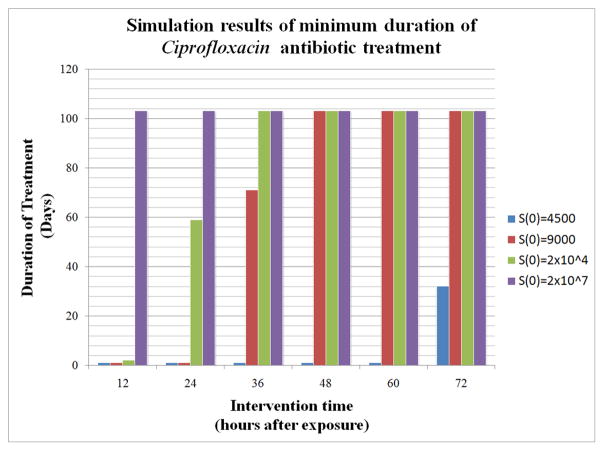
Figure 3.

The x-axis represents the number of hours after initial exposure at which treatment is started. This ranges from 12 hours after exposure up to 72 hours after exposure. The y-axis indicates the minimum duration (in days) of treatment needed for survival given one of four different initial spore counts, S(0), ranging from 4500 to 2×10⁷. For example, consider the third set of columns above 36. For this group, treatment began 36 hours after exposure. At least 1 day of Ciprofloxacin treatment is needed if S(0)=4500, 71 days if S(0)=9000, and 103 days if S(0)=2×10⁴ or S(0)=2×10⁷. In the latter 2 cases, we assume that such lengthy treatment for this antibiotic is unreasonable and that the subject would have already died before completion of the antibiotic regimen.

Figure 4.

The x-axis represents the number of hours after initial exposure at which treatment is started. This ranges from 12 hours after exposure up to 72 hours after exposure. The y-axis indicates the minimum duration (in days) of treatment needed for survival given one of four different initial spore counts, S(0), ranging from 4500 to 2×10⁷. For example, consider the third set of columns above 36. Treatment began 36 hours after exposure. At least 1 day of Doxycycline treatment is needed if S(0)=4500, 42 days if S(0)=9000, and greater than 73 days if S(0)=2×10⁴ or S(0)=2×10⁷. In the latter two cases, we assume that such lengthy treatment for this antibiotic is unreasonable and that the subject would have already died before completion of the antibiotic regimen.

Table 1 provides information about the variables and parameter values used. We assume that there is a resident population of lymphocytes (E) in the TMLN tissue that does not need to be recruited from the blood stream. We also assume that when anthrax toxin reaches its maximum level, processes affected by the toxin are inhibited by 50%.

3. Baseline Simulation Results

As previously stated, we interpret a high bacterial load accompanied by a large neutrophil population as evidence of mortality. Survival is identified in the model by all model variables, including bacterial and neutrophil numbers, approaching zero or background levels (in the case of the variable E). The time at which “death” occurs is a more ambiguous entity to define, but generally, we assume that if bacterial levels remain high for the duration of the simulation, then the “time of death” occurs shortly after bacterial numbers have reached their carrying capacity. However, the specific time is not necessarily important for our analysis, for we are simply interested in whether or not the system has resolved, which indicates a survival or fatal outcome.

When the initial spore count is high, the model shows the fatal state with persistently elevated bacterial levels accompanied by high levels of neutrophils, and when the initial spore count is below a critical threshold, survival is possible, as illustrated in Figure 2. The model allows for low spore doses to be overcome without neutrophils, as shown in (Cote, 2006), but that at higher doses, neutrophils are important and that without them, the host dies. Without the presence of anthrax toxins, the model is able to resolve the bacterial burden by approximately 300 hours even with very high initial spore counts (i.e. 2×10⁸); not shown here. We assume that the units of anthrax toxin are arbitrary, since we combine the toxins into one variable and there is a lack of literature regarding the amount of toxin produced by B. anthracis. Toxin is coupled to equations (4) and (5) through its inhibition effects. We assume that at T_A=0 there is no inhibition, while at T_A=1, there is 50% inhibition. Hence we take c_t1=c_t2=c_t3=1.

We performed a sensitivity analysis on 15 of the 23 model parameters using the methods outlined in Marino et al. to determine those parameters that most affect bacteria and neutrophil loads, since these two populations give an indication of the “healthiness” of the system. We are interested in bacterial levels and neutrophil levels at 100 hours and at 500 hours post infection because we expect that in a 100 hour (~4 day) time frame there will be early indicators of outcome (e.g. bacteria and neutrophil levels will be on the rise), whereas, by 500 hours (~21 days) outcome is usually determined. Thus, we wish to see which parameters the bacteria and neutrophil levels are most sensitive to at these two different time points. We are also interested in which parameters affect the PMG period and how the different PMG period lengths may correlate with bacterial load. We look at results for three different initial spore loads: 4000 (low), 2×10⁴ (mid-range), and 10⁷ (high). A complete account of these results is given in supplementary materials.

In summary, among all three initial spore loads, the parameters that proved to be among the most significant in negatively affecting bacteria load (i.e. an increase in these parameters resulted in a decrease in bacterial load) were those that were related to the killing of B_e: k₆ (rate at which resident immune cells, E, in MLN kill B_e), E(0) (initial level or resident immune cells in MLN), and k₁₀ (the rate at which resting neutrophils are activated by already activated neutrophils). The parameters k₄ (rate of production of anthrax toxins by bacteria) and k₁ (rate of apoptosis of resident immune cells in MLN after interaction with B_e) were the only significant parameters that positively affected the bacterial load (i.e. an increase in these parameters resulted in an increase in bacterial load) and only came up as significant for mid-range or high initial spore load. For all three initial spore loads, k₁₀ (the rate at which resting neutrophils are activated by already activated neutrophils) consistently showed up as most significant in positively affecting neutrophil levels at 100 and 500 hours.

Additionally, we noticed that under some of the parameter selections the behavior of the system was not “biologically plausible” for an anthrax infection. For instance, oscillations of the bacteria and neutrophil populations appeared or the neutrophil population would grow exponentially even after bacteria levels had been reduced below 1 bacterium. Thus, while our parameter values are estimated, we maintain that the baseline values that we use (i.e. those in Table 1) give a good characterization of the pathogenesis of anthrax.

As expected, the PMG period is most affected by the parameter k₃ (rate at which spore-containing host cells migrate to MLN and release vegetative bacteria). The parameters n_S (number of spores (on average) phagocytosed by resident lung host cells) and k₂ (rate at which resident lung host cells, H, phagocytose anthrax spores) are also significant. In comparing the length of the PMG period with bacterial load, there appears to be no correlation between the two at either 100 or 500 hours. We discuss this more at the end of Section 5: Antibiotic Treatment and the Phagocytosis-Migration-Germination (PMG) period.

4. Phagocytosis and Intracellular Bacterial Growth

It is not exactly known how many bacteria are phagocytosed by each lung host cell, nor what the number of bacteria released is upon lysis of the host cell. Therefore, we wished to explore in the model the effects of the parameters n_S (average number of spores phagocytosed by a host cell), n_B (average number of bacteria released by host cells in the TMLN), and, in particular, their ratio, n_b/n_s. The model also shows that for a moderately large dose of 2×10⁴ spores, survival still occurs if n_B can be made significantly smaller than n_S (e.g., n_B=35 if n_S=100); this raises the intriguing question as to whether a drug can be designed to render n_B less than n_S. In other words, drugs aimed at killing intracellular spores and/or bacteria may prove to be a more effective strategy than just killing extracellular bacteria. In the present parameter regime, n_S=3 and n_B=5, implying that some of the intracellular bacteria have replicated (once) and some have not due to time constraints (since we assumed host cells are lysed rather quickly after migrating) or possible inhibitory mechanisms that the host cell has.

5. Antibiotic Treatment and the Phagocytosis-Migration-Germination (PMG) period

Two primary antibiotics are FDA-approved for the treatment of inhalation anthrax: Ciprofloxacin or Doxycycline (Stern, 2008; CDC, 2005; CDC, 2010). Ciprofloxacin (or Cipro, for short) belongs to the family of antibiotics known as fluoroquinolones. It is bactericidal in that it inhibits enzymes required for proper bacterial DNA functions, such as replication, transcription, repair, and recombination. Thus, bacteria exposed to Cipro die upon cell division. This killing mechanism is distinct from that of penicillins and other classes of antibiotics and makes Cipro desirable in light of antibiotic resistance. (Bayer Healthcare Pharmaceuticals, 2009)

Doxycycline (or Doxy, for short) is a member of the tetracycline family of antibiotics. In contrast to Cipro, Doxycycline is bacteriostatic, meaning that it does not kill the bacteria but instead prevents bacteria from growing. Thus, bacteria affected by Doxycycline are prevented from replicating and thereby made susceptible to immune defenses while not being able to add to the bacterial load in the host. However, it appears that the mechanism of action which is to prevent aminoacyl-tRNA from binding to the ribosome is reversible (Doxycycline-an overview; Mayer, 2010).

We incorporate the action of Ciprofloxacin and Doxycycline in our model and explore the effects of either antibiotic on outcome. Since the Centers for Disease Control and Prevention (CDC) recommends treatment with either and not both, we chose not to explore the use of both antibiotics at the same time. In order to model the bactericidal or bacteriostatic effects of Ciprofloaxin or Doxycycline, respectively, we track the population of bacteria that is affected by an antibiotic. When either antibiotic affects the bacterial population, B_e, the newly effected bacteria become part of a differently tracked bacterial population. For instance, the B_c population of bacteria refers to the bacteria that are affected by Ciprofloxacin and as such, this bacterial population dies upon division. The B_d population of bacteria refers to the bacteria that are affected by Doxycycline which prevents bacteria from dividing, and whose effects are reversible.

Since antibiotic dosing regimens are constructed to keep the level of the drug at a consistently effective level in the body for a particular time period, we chose to simply model the level of an antibiotic as a constant value (C or D for Ciprofloxacin and Doxycycline, respectively). This value is set to a prescribed amount (given in Table 1) for a particular time window, depending on the simulation scenario. Otherwise, the value is zero. Hence, we have the following modification to equation (4) and the addition of two other equations, for B_c and B_d:

$$\frac{{dB}_e}{dt}=\underset{\begin{array}{c}\text{Gain}\text{from}\text{germinated}\\ \text{spores}/\text{vegetative}\\ \text{bacteria}\text{released}\\ \text{from}\text{the}\text{host}\text{cell}\end{array}}{\underbrace{k_3{n}_{B}H}}+\underset{\begin{array}{c}\text{extracellular}\\ \text{bacterial}\text{growth}\end{array}}{\underbrace{k_5{B}_e\left(1-\frac{(B_e+B_c+B_d)}{B_{\mathit{eMAX}}}\right)}}-\underset{\begin{array}{c}\text{Killing}\text{of}\text{Be}\text{by}\\ \text{early}\text{immune}\\ \text{response}\text{in}\text{TMLN}\end{array}}{\underbrace{k_6{EB}_e}}-\underset{\begin{array}{c}\text{Killing}\text{of}{\text{B}}_{\text{e}}\text{by}\text{N}\\ \text{inhibited}\text{by}\text{anthrax}\text{toxins}\end{array}}{\underbrace{\frac{k_8{NB}_e}{1+\frac{T_A}{c_{t1}}}}}\underset{\begin{array}{c}\text{Cipro}\\ \text{effected}\\ \text{bacteria}\end{array}}{\underbrace{-B_{e}C}}\underset{\begin{array}{c}\text{Doxy}-\text{effected}\\ \text{bacteria}\end{array}}{\underbrace{-B_{e}D}}+\underset{\begin{array}{c}\text{unbound}\\ \text{Doxy}-\text{effected}\\ \text{bacteria}\end{array}}{\underbrace{k_d{B}_d}}$$ (7)

$$\frac{{dB}_c}{dt}=\underset{\begin{array}{c}\text{gain}\text{of}\\ B_c\text{by}\\ \text{cipro}-\text{effected}\\ \text{bacteria}\end{array}}{\underbrace{B_{3}C}}\underset{\begin{array}{c}\text{Cipro}-\text{effected}\text{bacteria}\text{are}\\ \text{killed}\text{during}\text{the}\text{division}\text{process}\end{array}}{\underbrace{-k_5{B}_c\left(1-\frac{(B_e+B_c+B_d)}{B_{\mathit{eMAX}}}\right)}}-\underset{\begin{array}{c}\text{Killing}\text{of}\text{Bc}\\ \text{by}\text{local}\text{TMLN}\\ \text{immune}\text{response}\end{array}}{\underbrace{k_6{EB}_c}}-\underset{\begin{array}{c}\text{Phagocytosis}\text{and}\\ \text{killing}\text{of}{\text{B}}_{\text{c}}\text{by}\text{N};\\ \text{inhibited}\text{by}\\ \text{anthrax}\text{toxins}\end{array}}{\underbrace{\frac{k_8{NB}_c}{1+\frac{T_A}{c_{t1}}}}}$$ (8)

$$\frac{{dB}_d}{dt}=\underset{\begin{array}{c}\text{gain}\text{of}\\ B_d\text{by}\\ \text{Doxy}-\text{effected}\\ \text{bacteria}\end{array}}{\underbrace{B_{e}D}}-\underset{\begin{array}{c}\text{Killing}\text{of}\text{Bd}\\ \text{by}\text{local}\text{TMLN}\\ \text{immune}\text{response}\end{array}}{\underbrace{k_6{EB}_d}}-\underset{\begin{array}{c}\text{Phagocutosis}\text{and}\\ \text{killing}\text{of}{\text{B}}_{\text{d}}\text{by}\text{N}\\ \text{inhibited}\text{by}\\ \text{anthrax}\text{toxins}\end{array}}{\underbrace{\frac{k_8{NB}_d}{1+\frac{T_A}{c_{t1}}}}}-\underset{\begin{array}{c}\text{unbound}\text{Doxy}-\text{effected}\\ \text{bacteria}\end{array}}{\underbrace{k_d{B}_d}}$$ (9)

We chose parameter values for C and D (given in Table 1) such that their effects, on the one hand, would not be negligible nor, on the other hand, be unrealistically successful in all scenarios. We explored a range of initial intervention times (from 12 to 72 hours at 12 hour increments) to determine the minimum duration of antibiotic therapy that proved sufficient to eliminate the bacteria. This minimum duration time is defined as the smallest length of time (to the nearest hour) for which an antibiotic can be given such that when the treatment is stopped, the host can recover. Figures 3 and 4 display bar graphs of these results for each of the antibiotics we chose to simulate. For inhalation anthrax, the CDC recommends that post-exposure prophylaxis includes 60 days of antibiotic treatment (CDC, 2005). In general, with either treatment, the longer it is delayed, the longer the duration of therapy needs to last. However, the initial spore count plays a critical role, showing that for high spore counts, regardless of treatment time, the duration of treatment required is very long and in many cases unreasonable (i.e. greater than 60–70 days). In addition, around four days after exposure, bacterial levels in the model are close to carrying capacity, which we are considering a marker of nonsurvival in the model. In other words, even though the antibiotic treatment simulations show survival is possible if antibiotics are given long enough, it is likely that such patients would have already succumbed to the effects of having a high bacterial load for an extended period of time. Despite the fact that the two drugs have different mechanisms of action, the results in the model show that they each lead to similar outcomes.

The CDC’s recommendation of an antibiotic treatment window of 60 days is based on several factors, including data from the 1979 Sverdlovsk anthrax outbreak and studies in nonhuman primates (Meselson, 1994). The studies reported a 2–90 day incubation period for spores in the lung. The incubation period was defined to be the time between initial exposure and symptom onset. In our model, we instead look at the time frame from initial exposure and phagocytosis of spores in the lung to migration of host cells into the TMLN and germination of spores. More specifically, we define the PMG period as the length of time from t=0 hours to the time when the total number of infected host cells, H, in the lung falls below a value of 50 cells, which we regard as a negligible number of spore-laden host cells. This differs from the incubation period in that it does not use symptoms of the disease as a marker and may therefore occur on a shorter time scale than the incubation period would. Using the parameter values outlined in Table 1, the PMG period occurs over a time period of approximately four days for low to moderate initial spore counts (i.e. less than 2×10⁴ spores). The PMG period in our model is primarily governed by the parameter k₃. The process of migration/germination takes a longer time to be completed if the initial spore count is larger. Indeed, for initial spore counts of greater than 2×10⁴ the parameter value of k₃ would need to be increased in order to maintain the same PMG period of four days. While for simplicity we only used one value for k₃ for most all of our simulations, regardless of initial spore count, we wanted to explore the effects of the length of the PMG period on outcome.

Thus, modulating the PMG period (via the parameter k₃) allows us to explore the possibility of some spores remaining without germination for longer periods of time. This is especially important in light of the fact that the duration of antibiotic treatment is currently based on the idea that germination could be delayed from initial exposure or occurs over an extended period of time (CDC, 2005). Our model suggests that an extension of the PMG time window actually enables survival (without therapy) of a larger initial spore exposure. For example, decreasing the baseline value of k₃ from 0.05 to k₃=0.01, which corresponds to an increased PMG period, increases the maximum survivable initial spore count by greater than 2.2 times. Figure 5 shows survival vs. death outcomes with regard to initial spore count and length of PMG (up to 90 days). Differing values of k₃ were chosen so that the incubation period was approximately 4, 30, 60, or 90 days, depending on the initial spore counts shown. For instance, the values of k₃ that were used for an initial spore count of 9000 were 0.06, 0.008, 0.004, and 0.0026, corresponding to a 4, 30, 60, and 90 day PMG period, respectively.

Figure 5.

Effect of PMG (Phagocytosis, Migration, Germination) period length on survival (without drug intervention) with respect to initial spore count. Differing values of k₃ were computed from model simulations so that the PMG period was approximately 4, 30, 60, or 90 days, depending on the initial spore counts shown. For instance, the values of k₃ that were used for an initial spore count of 9000 were 0.06, 0.008, 0.004, and 0.0026, corresponding to a 4, 30, 60, and 90 day PMG period, respectively. Generally, survival increases as the PMG period increases; however for very high initial spore counts, death occurs even with a PMG period of 90, as seen in the last column.

Using this convention, we carried out simulations using initial spore values that lead to death with either a short (4 days) or long (21 days) PMG period. These simulations show a delay in the onset of death when the PMG period is longer (not represented in figure). However, even though survival is increased with a longer PMG period, this does not correspond to a shorter duration of antibiotic treatment, and in fact, longer treatment is required (not shown here). Our simulations suggest that in this case longer treatment is required because at earlier time points, the bacterial growth rate is slow (i.e. not in its exponential growth phase yet). Hence, there is a window of time from initial exposure in which the bacteria are dividing but not very rapidly. Since Ciprofloxacin kills bacteria when it divides and Doxycycline prevents division, this semi-quiescent growth phase tends to render the antibiotics less effective. With a shorter PMG period, the exponential growth phase of bacteria commences earlier than with a longer PMG period and thus, the antibiotic treatment becomes effective sooner, allowing for a shorter duration of treatment. Understanding the different states of bacterial division/metabolism in vivo are critical factors in assessing drug efficacy.

The different simulations generated in the sensitivity analysis show that the length of the PMG period does not correlate to bacterial loads, with various PMG values close in length corresponding to either low or high bacterial levels at various selected time points. In addition, there is also no correlation between the length of the PMG period and peak bacterial loads or the time at which the peak occurs. (see Supplementary Text). This result was seen under all three initial bacterial loads and implies that other factors are playing a more defining role in determining bacterial load when differing parameter regimes are explored. Our baseline parameter values that we use give plausible outcomes for various initial spore loads; however, it is unclear that when we choose randomized parameter values from ranges varying from 10%–200% of the baseline that we are always getting results that are biologically plausible. Thus, it is difficult to compare the effect of the PMG period length on bacterial levels when using the baseline parameter values versus using a set of parameter values chosen randomly from various ranges, as is done in the sensitivity analysis.

6. Conclusion

Inhalation anthrax is a deadly disease whose progression seems to differ from other bacterial infections that lead to acute inflammation and classical sepsis. In this paper, we developed a mathematical model based on those events documented in the literature that are specific to the initiation and progression of inhalation anthrax infection. Thus, the formulation of the model is specific to anthrax pathogenesis. For instance, during an inhalation anthrax infection, migration of host cells occurs rather rapidly such that the main battlefield for an inhalation anthrax infection turns out to be the lymph nodes and not the lung. The pathogenesis of a tuberculosis infection, for example, does not share this characteristic and instead has several other unique features that differ from an inhalation anthrax infection (Day, 2009). There may be other respiratory pathogens that have a similar pathogenesis to inhalation anthrax; however, it seems more likely that the interaction of a given pathogen with a host will be quite specialized. Thus, different cell types and molecules may need to be considered and the equations would be formulated to reflect the specific nature of the interactions. However, the general approach of formulating the equations would be similar to the process outlined here or in (Day, 2009), for instance.

The inhalation anthrax model consists of two compartments: the lung airspace and the thoracic/mediastinal lymph nodes (TMLN). Anthrax spores are inhaled in the lung airspace where they are internalized by the alveolar phagocytes. These host cells then migrate to the TMLN while the internalized spores germinate into bacteria, lyse the host cells and are released to the TMLN space. The model includes the toxin released by the bacteria, the early immune response in the TMLN, and the recruitment of neutrophils.

The goal of the paper is to explore the probability of survival of an infected individual. This probability depends on several factors:

1. the amount of inhaled spores;

2. the rate of migration from the lung airspace to the TMLN and germination events;

3. the average number of bacteria released from a lysed host cell; and

4. the timing of drug treatment with Ciprofloxacin or Doxycycline.

In particular, we show that if the inhaled spore count is less than some critical threshold then the infected individual will survive without any treatment. Above this threshold, the individual will die unless treated by a drug and only if the number of initial spores is low enough. For instance, if the initial number of spores is 2×10⁴ and treatment with Cipro or Doxy begins no later than 36 hours after exposure, then survival is possible. On the other hand, if the initial spore count is, for instance 2×10⁷, then death is imminent even if treatment is started 12 hours after exposure. See Figure 4. Our model is based on what is currently known about the disease. The model could be further developed as more information and data about inhalation anthrax become available and/or more drugs are developed.