Human Annulus Fibrosus Dynamic Tensile Modulus Increases with Degeneration

Abstract

The annulus fibrosus (AF) of the intervertebral disc experiences cyclic tensile loading in vivo at various states of mechanical equilibrium. Disc degeneration is associated with alterations in the biochemical composition of the AF including decreased water content, decreased proteoglycan concentration, and increased collagen deposition that affect mechanical function of the AF in compression and shear. Such changes may also affect the dynamic viscoelastic properties of the AF and thus alter the disc's ability to dissipate energy under physiologic loading. The objectives of this study were to quantify the dynamic viscoelastic properties of human AF in circumferential tension and to determine the effect of degeneration on these properties. Nondegenerated and degenerated human AF tensile samples were tested in uniaxial tension over a spectrum of loading frequencies spanning 0.01Hz to 2Hz at several states of equilibrium strain to determine the dynamic viscoelastic properties (dynamic modulus, phase angle) using a linear viscoelastic model. The AF dynamic modulus increased at higher equilibrium strain levels. The AF behaved more elastically at higher frequencies with a decreased phase angle. Degeneration resulted in a higher dynamic modulus at all strain levels but had no effect on phase angle. The findings from this study elucidate the effect of degeneration on the dynamic viscoelastic properties of human AF and lend insight into the mechanical role of the AF in cyclic loading conditions.

INTRODUCTION

The intervertebral disc functions mechanically to permit motion, allow spinal flexibility, and dissipate energy during activities of daily living. Physiologically, the intervertebral disc experiences complex deformations under combinations of compression, tension, torsion, and bending. The composition and structure of the disc are organized to withstand such loading conditions and do so at a spectrum of loading frequencies and at various states of mechanical equilibrium (Andersson et al., 1978; Wilke et al., 1999). Specifically, the nucleus pulposus permits compressive loads of the disc to be transmitted radially in the form of circumferential hoop stresses that load the fibers of the annulus fibrosus (AF) in tension. Structurally, the AF lamellar architecture progressively transitions from densely packed aligned collagen I fibers in the outer AF to a less densely packed more collagen II rich fibrous matrix towards the inner AF. Within lamellae, collagen fibers embedded in a proteoglycan rich network are aligned in a crossply manner at ± 30° to the transverse plane, with alternations in the prevailing fiber direction between adjacent lamellae (Cassidy et al., 1989). The AF fiber network, together with the extrafibrillar matrix, behaves as a nonlinear inhomogeneous anisotropic viscoelastic material (Acaroglu et al., 1995; Elliott and Setton, 2001; Guerin and Elliott, 2007).

The AF tensile mechanical properties have been determined primarily under uniaxial quasi-static loading conditions where rate-dependent viscous effects have dissipated (Acaroglu et al., 1995; Ebara et al., 1996; Elliott and Setton, 2001; Galante, 1967; O'Connell et al., 2009; Skaggs et al., 1994). However, the disc also experiences cyclic loading in vivo at a variety of frequencies where rate dependent viscous effects may play an important role in the disc's ability to dissipate energy. In the axial direction of ovine AF, increasing cyclic strain rate resulted in an increased linear region dynamic modulus and decreased hysteresis suggesting decreased energy dissipation at higher strain rates (Kasra et al., 2004). These rate-dependent effects have not been studied in circumferential tension, a primary AF loading mode. Furthermore, disc degeneration is known to accompany AF biochemical changes, including a decrease in water and proteoglycan content and an increase in collagen deposition, leading to stiffer mechanical behavior in shear and compression (Antoniou et al., 1996; Eyre, 1979; Le Maitre et al., 2007; Iatridis et al., 1999; Iatridis et al., 1998). Degeneration does not affect the circumferential quasi-static tensile modulus, although the Poisson's ratio decreases, fiber reorientation decreases, and fiber-matrix interactions determined from modeling tensile mechanics are altered with degeneration (Acaroglu et al., 1995; Guerin and Elliott, 2007; O'Connell et al., 2009). It is unknown how degeneration affects the dynamic tensile mechanical behavior of the AF.

Thus, the objectives of this study were to quantify dynamic viscoelastic properties of human AF in circumferential tension over a range of equilibrium strains and loading frequencies and to determine the effect of degeneration on these properties. We hypothesized that the AF would be stiffer (increased dynamic modulus) at higher equilibrium strains and at faster loading frequencies, and that the AF would behave more elastically (reduced phase angle) at faster loading frequencies. Further, we hypothesized that degeneration would result in a stiffer AF under dynamic loading.

METHODS

Sample Preparation

Lumbar discs from L1/L2 and L2/L3 levels were excised from human cadaveric spines via sharp dissection. Prior to dissection, three separate reviewers graded the discs using the Pfirrmann classification system using previously acquired mid-sagittal T2-weighted MRI images. An average grade of less than 2.5 was considered nondegenerated while an average grade of greater than 2.5 was considered degenerated. The outer AF from the anterior disc was isolated and cryo-microtomed to uniform thickness in the circumferential-axial plane. Tensile samples were prepared with the loading axis aligned in the circumferential direction from nondegenerate (n=8, average age 49, range 25–76) and degenerate (n=7, average age 60, range 29–80) discs (Pfirrmann et al., 2001). Tissue samples were airbrushed with speckle pattern for image capture and optical strain analysis of 2D Lagrangian strain (O'Connell et al., 2009).

Mechanical Testing

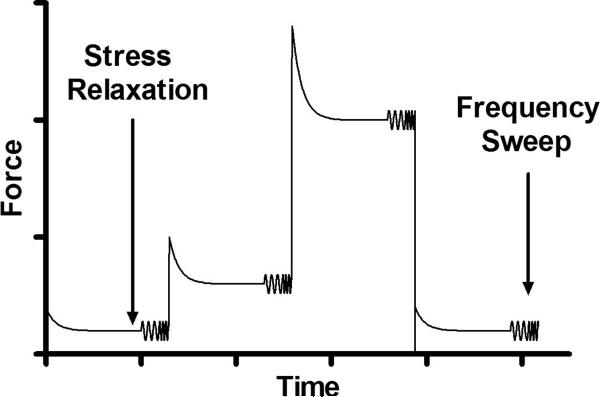
Testing was performed on an Instron 5848 (Canton, MA) system in a phosphate buffered saline bath at room temperature. Samples were preconditioned for 10 cycles between 0 and 10% strain at 0.025 Hz, followed by a 20 min unloaded recovery. Following recovery, a 2% step strain, 30 min relaxation, and a frequency sweep (5 cycles each at 0.01, 0.1, 0.2, 1, and 2 Hz) with an oscillatory amplitude of ±0.5% strain were performed. This protocol (step strain, followed by a 30 min relaxation and a frequency sweep) was repeated for 6 and 10% step strains (Figure 1). Finally, a second frequency sweep at 2% strain was performed at the end of the protocol to confirm repeatability and that no damage occurred during the test protocol. Images at the end of each step-relaxation were captured with a high resolution camera (Model A102f, 1280 × 960 pixel resolution; Basler, Exton, PA). 2D Lagrangian strains were computed from these images using Vic2D software (Correlated Solutions Inc., Columbia, SC) to confirm equilibrium tissue strain values (O'Connell et al., 2009).

Figure 1.

Dynamic tensile testing with an oscillatory amplitude of ±0.5% at frequencies between 0.01 and 2 Hz at equilibrium strain levels of 2%, 6%, and 10% strain. A repeat frequency sweep at 2% was performed at the end of the testing sequence. To achieve equilibrium, a step strain followed by a stress relaxation was applied to each tensile specimen prior to dynamic loading.

Data Analysis

Stress and strain were calculated from the force and displacement data. Stress was computed as force divided by original cross-sectional area and strain was computed as displacement divided by the initial gauge length. The stress strain data were analyzed by transforming the data into the frequency domain using the Fast Fourier Transform in a custom written Matlab program (The Mathworks Inc., Natick, MA). The magnitude and phase of the prevailing frequency was calculated to determine the dynamic modulus and viscous phase angle at each frequency. Dynamic modulus was calculated as the ratio of the magnitudes of the transformed stress and strain data at the prevailing frequency during each cyclic test. The viscous phase angle was calculated as the difference between the phase shifts of the transformed stress and strain data during each cyclic test (Lakes, 1999). A two-way repeated measures ANOVA with Bonferroni post-hoc analysis was performed to compare mechanical properties with respect to frequency and strain level. A Student's t-test was used to determine the difference between degenerate and nondegenerate properties at each strain level. Significance was set at p<0.05.

RESULTS

Effects of Equilibrium Strain and Frequency

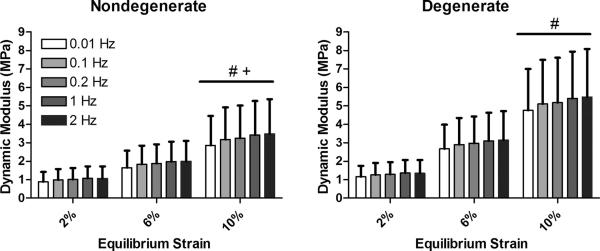
The dynamic modulus significantly increased with increasing equilibrium strain but was not significantly altered by changes in loading frequency (Figure 3). As a result, the data across all frequencies at a given equilibrium strain level were pooled for comparison (Figure 4). Specifically, the mean dynamic modulus increased from 1.00 MPa at 2% strain to 3.23 MPa at 10% strain for nondegenerate tissue. In the degenerated group, the mean dynamic modulus increased from 1.28 MPa at 2% strain to 5.18 MPa at 10% strain.

Figure 3.

Dynamic modulus increased with increasing equilibrium strain (# vs. 2% strain, + vs. 6% strain, p<0.05 post-hoc Bonferroni test). Dynamic modulus was not significantly altered by frequency. Error bars represent standard deviation.

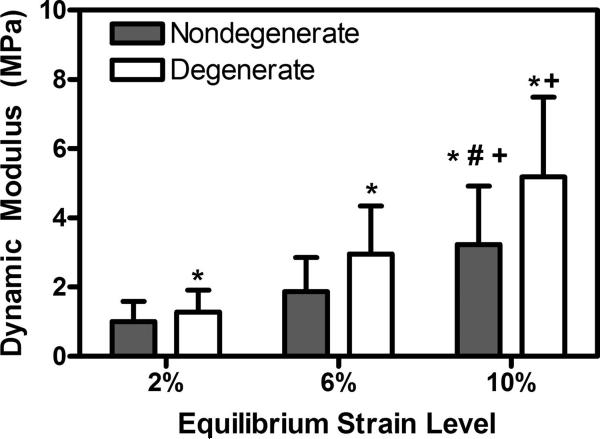
Figure 4.

Dynamic modulus was significantly altered with degeneration. Dynamic modulus was significantly greater in the degenerate group at all equilibrium strain levels. * vs. nondegenerate at a given strain, # vs. 2% strain, + vs. 6% strain, p<0.05, error bars represent standard deviation.

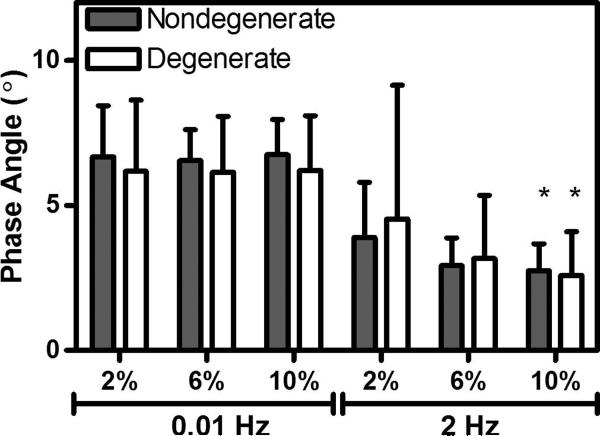
The phase angle significantly decreased with increasing loading frequency (Figure 5), but was not significantly altered with increasing equilibrium strain (except at 2 Hz), or with degeneration (Figure 5). At 2 Hz, the highest frequency tested, the phase angle at 2% strain was significantly higher than at 10% strain for both degenerate and nondegenerate samples (Figure 5). For nondegenerate samples at 2% strain, the phase angle ranged from 6.68 ± 1.76° at 0.01 Hz to 3.90 ± 1.91° at 2 Hz; whereas at 10% strain, the phase angle ranged from 6.76 ± 1.20° at 0.01 Hz to 2.75 ± 0.93° at 2 Hz.

Figure 5.

Phase Angle (nondegenerate) decreased with increasing frequency. At 2Hz, the phase angle at 2% strain was significantly higher than the phase angle at 10% strain. * = p<0.05, error bars represent standard deviation.

Effects of Degeneration

The dynamic modulus in degenerate samples was significantly greater compared to nondegenerate samples at all strain levels (Figure 4). Specifically, degenerate tissue was 28, 58, and 60% stiffer than nondegenerate tissue at 2, 6, 10% equilibrium strains, respectively. There was no significant effect of degeneration on the phase angle (Figure 6).

Figure 6.

Phase Angle significantly decreased with increasing frequency in both degenerate and nondegenerate groups at 10% strain. * = p<0.05 with respect to phase angle at 10% strain at 0.01Hz. Error bars represent standard deviation.

Linear Viscoelastic Model and Repeatability

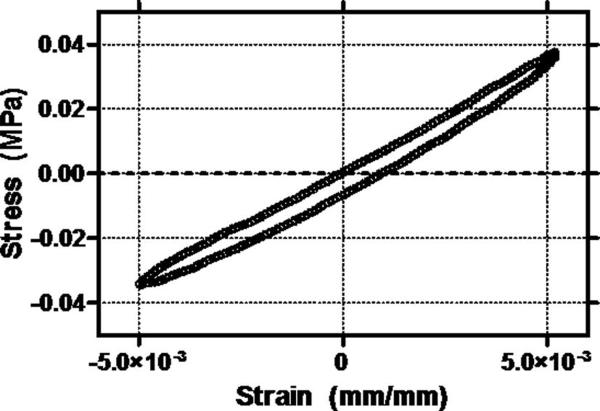
The stress-strain responses at all equilibrium strain levels and frequencies behaved linearly for the small oscillatory amplitudes prescribed by the testing protocol. Elliptical stress-strain responses were observed for all combinations of equilibrium strain and loading frequency, confirming the linear behavior in dynamic tension and allowing for the use of a linear viscoelastic model to quantify dynamic properties (Figure 2). The frequency sweep at 2% strain at the end of the testing protocol demonstrated no difference in any property compared to the initial frequency sweep at 2% strain demonstrating the repeatability of the testing protocol (paired t-test, p>0.27). Optical strain analysis confirmed that the tissue strain at each equilibrium strain level was not significantly different from the prescribed strains (t-test, p>0.3).

Figure 2.

Representative elliptical stress-strain response at 10% strain and 1Hz that demonstrates that linear viscoelastic theory can be appropriately utilized at small oscillatory amplitudes. All equilibrium strain/frequency combinations displayed similar elliptical stress-strain responses.

DISCUSSION

Physiologic loading behavior of the intervertebral disc occurs over a range of compressive loads and a spectrum of loading frequencies causing the AF to experience dynamic loads in circumferential tension. Thus, it is important to quantify the AF tensile mechanical behavior and the effect of degeneration in dynamic loading conditions as altered AF function may relate to mechanical progression of disc degeneration. This study showed that (1) the dynamic modulus increases with increasing equilibrium strain in circumferential tension, (2) the AF behaves more closely to an elastic solid as loading frequency increases, and (3) the dynamic modulus of the AF increases with degeneration.

The AF dynamic modulus increased with increasing equilibrium strain which is consistent with the nonlinear response of the AF in quasi-static tension (Acaroglu et al., 1995; Ebara et al., 1996; Elliott and Setton, 2001; Galante, 1967; Guerin and Elliott, 2007; O'Connell et al., 2009; Wagner and Lotz, 2004). Similar to quasi-static tension, it is likely that the degree of fiber reorientation within the extrafibrillar matrix at various equilibrium strains is the predominant mechanism for the observed response non-linearity. Despite the observed non-linear overall behavior, displacements applied during frequency sweeps at each equilibrium strain were of sufficiently small amplitude that linear viscoelastic theory could be utilized to quantify the dynamic material properties of the AF (Bonifasi-Lista et al., 2005; Boxberger et al., 2009; Lujan et al., 2009)

Conversely, dynamic modulus was not significantly affected by increasing loading frequency within any given equilibrium strain. This finding is in contrast to ovine bone-AF tissue-bone segments tested in the axial loading direction, where the linear region modulus was significantly greater at 6.25 Hz compared to 0.0625 Hz and 0.0313 Hz (Kasra et al., 2004). In addition to detecting differences in dynamic modulus only for frequencies greater than those tested in this study, differences may have arisen due to the differing boundary conditions (bone-tissue-bone), orientation (axial), and species (ovine). In addition to AF tissue, the strain-rate effect has also been determined for the medial collateral ligament, another fiber-reinforced soft tissue. Here, dynamic modulus increased with increasing loading frequency (Bonifasi-Lista et al., 2005). However, the differences reported were modest and most pronounced between the lowest (0.01 Hz) and highest frequencies tested (10–15 Hz). It is possible that similar increases in dynamic modulus would be observed for loading frequencies beyond the 2 Hz tested in this study; however, we chose to focus on loading frequencies experienced during the activities of daily living.

The phase angle, a relative ratio of the quantity of energy a material dissipates to that which it stores, decreased with frequency at all equilibrium strain levels, indicating that the AF is able to dissipate less energy as loading frequency increases. However, phase angle was less than 8° for all loading conditions, which suggests that the overall behavior of the tissue more closely resembles that of an elastic solid. Interestingly, the phase angle was significantly greater (AF more viscous) at 2% strain compared to 10% strain at 2 Hz (Figure 5). Assuming a Poisson's ratio of 0.33, we can estimate water loss of 0.7% and 3% for an applied 2% and 10% strain, respectively. It is possible that the higher equilibrium strain expelled more fluid out of the tissue, reducing the viscous capabilities of the tissue.

The decrease in phase angle in human AF reported here is consistent with the decreases in hysteresis area and phase angle with increasing frequency in ovine AF, rat disc segments, and human ligament (Bonifasi-Lista et al., 2005; Boxberger et al., 2009; Kasra et al., 2004). While the AF has an energy dissipation role in circumferential tension, overall disc energy dissipation is shared between all the disc substructures and the nucleus pulposus has an important role. Indeed, the nucleus pulposus has a higher phase angle in dynamic shear compared to the AF (Iatridis et al., 1999; Iatridis et al., 1997).

Degeneration had pronounced effects on the dynamic modulus, where degenerate tissue was significantly stiffer than nondegenerate tissue. This finding is in contrast to quasi-static tensile modulus, which is unchanged with degeneration (Acaroglu et al., 1995), but is consistent with AF dynamic compressive shear (Iatridis et al., 1999). Quasi-static modulus is dependent on collagen organization, whereas the effect of degeneration on the dynamic tensile modulus implicates the role of extrafibrillar matrix stiffening in addition to collagen organization on the AF mechanical behavior. While one possible mechanism of extrafibrillar matrix stiffening may be through a reduction in glycosaminoglycan and water content characteristic of the biochemical changes in degeneration, previous studies on tendon demonstrate that the mechanical interactions between glycosaminoglycans and collagen fibrils may not have a predominant role in the viscoelastic behavior of ligament (Lujan et al., 2009). In light of these findings, it is possible that advanced glycation end products (Wagner et al., 2006) and deposition of non-fibrillar proteins in the extrafibrillar matrix may contribute to the observed increase in dynamic modulus ultimately affecting the solid-fluid interactions responsible for tissue viscoelasticity.

The findings presented here are not without limitations. This study tested tissue in circumferential tension which is a primary loading mode of the AF. While the free edge boundary conditions in uniaxial tension may not accurately approximate the in-situ boundary conditions during physiologic loading, this testing modality provides a convenient and rigorous way to quantify mechanical properties for comparative analysis. This study tested a maximum loading frequency of 2 Hz. It is evident that frequency dependent changes may occur at frequencies greater than 2 Hz based on previous work on both AF and ligament. While there is a limit on what is considered physiologically relevant, testing at higher frequencies may lend insight into putative mechanisms responsible for tissue viscoelasticity that are playing a more modest role at lower frequencies. In addition, the dynamic modulus values were lower than previously reported quasi-static modulus values (Acaroglu et al., 1995; Elliott and Setton, 2001; Galante, 1967). To calculate the dynamic modulus and phase angle, it is important that small displacement oscillations occur about a steady-state condition. Therefore, a 30 min stress-relaxation was performed before applying frequency sweeps. This, in combination with the slow loading rates at the low end of the frequency spectrum, resulted in extended periods of time in a PBS bath, which is known to decrease the modulus, likely due to swelling effects (Han, 2011; Screen et al., 2006). However, a second frequency sweep at 2% strain was performed at the end of the protocol to confirm repeatability and that no damage occurred during the test protocol. No significant differences were observed for dynamic modulus or phase angle between the repeated frequency sweep at the end of the protocol and the initial frequency sweep, indicating that the significant differences reported in this study between different loading frequencies, equilibrium strain level, and condition (nondegenerate vs. degenerate) remain valid. In summary, this study determined the dynamic behavior of AF in circumferential tension and quantified the effects of degeneration. Dynamic modulus significantly increased with increasing equilibrium strain and the phase angle significantly decreased with increasing frequency. In addition, degeneration led to an increase in the dynamic modulus of the AF. Overall, the data presented here lend insight into the mechanical outcomes of degeneration in dynamic loading schemes.