Protecting High Energy Barriers: A New Equation to Regulate Boost Energy in Accelerated Molecular Dynamics Simulations

Abstract

Molecular dynamics (MD) is one of the most common tools in computational chemistry. Recently, our group has employed accelerated molecular dynamics (aMD) to improve the conformational sampling over conventional molecular dynamics techniques. In the original aMD implementation, sampling is greatly improved by raising energy wells below a predefined energy level. Recently, our group presented an alternative aMD implementation where simulations are accelerated by lowering energy barriers of the potential energy surface. When coupled with thermodynamic integration simulations, this implementation showed very promising results. However, when applied to large systems, such as proteins, the simulation tends to be biased to high energy regions of the potential landscape. The reason for this behavior lies in the boost equation used since the highest energy barriers are dramatically more affected than the lower ones. To address this issue, in this work, we present a new boost equation that prevents oversampling of unfavorable high energy conformational states. The new boost potential provides not only better recovery of statistics throughout the simulation but also enhanced sampling of statistically relevant regions in explicit solvent MD simulations.

Introduction

Molecular dynamics simulation (MD) is one of the most common tools used by computational chemists to study the dynamic behavior of biomolecules.^1,2 However, conventional MD techniques (cMD) are still limited to relatively short time scales, which hinder observation of conformational transitions that are essential for protein function.^1,3 Most of these transitions occur on a time scale of milliseconds to seconds or longer and often involve the rare crossing of high energy barriers. In an effort to extend the time scale of all-atom molecular dynamics simulations of biomolecules, our group recently proposed an enhanced sampling technique called accelerated molecular dynamics (aMD). This method, which is based on the hyperdynamics technique introduced by Voter,⁴ has been shown to increase conformational sampling of biomolecules over cMD.³ Recently, our group has been successfully using aMD in a wide range of applications and biological systems.^3,5−11

Two major implementations of the boost equation for aMD have been proposed. In the original implementation, the boost potential is defined according to eq 1.^3,5

1

A continuous non-negative boost potential function, ΔV^a, is added the original potential surface, V(r), such that regions around the energy minima are raised and those near high barriers or saddle points are left unaffected. Thus, whenever V(r) is below a chosen threshold boost energy, E₁, the simulation is performed on the modified potential V*(r) = V(r) + ΔV^a; otherwise, sampling is performed on the original potential V*(r) = V(r). The parameter α₁ modulates roughness and the depth of the energy minima on the modified surface.

To recover the correct canonical ensemble, each frame of the simulation must be reweighted using the Boltzmann factor e^βΔV[r]. Since the lowest energy wells may be associated with the largest boost values, the reweighting can have a detrimental effect on the statistics.^8,12

To address this issue, a second implementation was introduced in which energy barriers are modified, instead of energy minima.⁸

2

A continuous negative boost potential function, ΔV^b(r), is added to the original potential surface, V(r), such that regions around the energy barriers are lowered and those near the minima are left unaffected. Thus, whenever V(r) is above the boost energy, E₁, the simulation is performed on the modified potential V*(r) = V(r) – ΔV^b; otherwise, sampling is performed on the original potential V*(r) = V(r).

This implementation improves the statistical reweighting problem by allowing much of the simulation to remain in the original potential surface, which in this case needs no reweighing. However, application of ΔV^b tends to oversample high energy regions of the potential landscape. As can be seen in eq 2, the boost potential is proportional to the difference V(r) – E, and as a consequence regions of the potential surface displaying large V(r) (or high-energy regions) are affected significantly more than regions with relatively low energy barriers. When applied to large systems, such as proteins, the simulation tends to be biased toward high energy regions of the potential landscape. In small systems, application of ΔV^b revealed promising results when combined with free energy calculations, such as thermodynamic integration (TI).⁸

In this work, we describe a new boost potential (eq 3) in an attempt to combine the strengths of the two previous implementations.

Results and Discussion

A possible way to overcome the sampling issues associated with ΔV^b is to modify the boost potential equation so that its magnitude reduces significantly at large values of V(r) – E.

New equation ΔV^c:

3

We defined a second energy level (E₂) in order to return the modified potential surface back to the original one whenever the potential energy of the system is larger than E₂. This boost equation is shown above as ΔV^c (eq 3). The second energy level allows the user to define a window of acceleration between E₁ and E₂. To regulate the return to the original potential upon crossing E₂, a second parameter α is required (α₂). The term in the large brackets in the denominator is responsible for bringing the boost to zero when the potential energy V(r) is higher than E₂. Thus, when V(r) is higher than E₂, (1 + e^{–(E₂–v(r))/α₂}) tends to a very large positive number, and as a result, the modified potential converges to the original one, V(r). On the other hand, when V(r) is lower than E₂, the term (1 + e^{–(E₂–v(r))/α₂}) tends to 1, which results in ΔV^c = ΔV^b or eq 2.

We explored the new boost equation by creating a hypothetical one-dimensional potential using the analytical equation below:

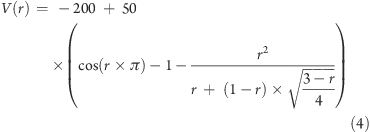4

Figure 1 displays the effect of boost energy E (E₁ and E₂) and α (α₁ and α₂) on eqs 2 and 3. The upper solid black line represents the unmodified potential V(r), while the lower solid black line represents modified potential V(r)* generated after the application of eq 2, ΔV^b. Boost energies E are shown as dashed lines. The solid colored lines represent different modified potentials, V(r)*, generated by ΔV^c with different sets of parameters. Figure 1A shows that high energy barriers can be selectively protected by setting different values of E₂. It is worth noting that the modified potential generated by ΔV^c follows closely along ΔV^b until the difference between E₂ and E₁ is similar to the difference between V(r) and E₁ (Figure 1A and B).

Figure 1.

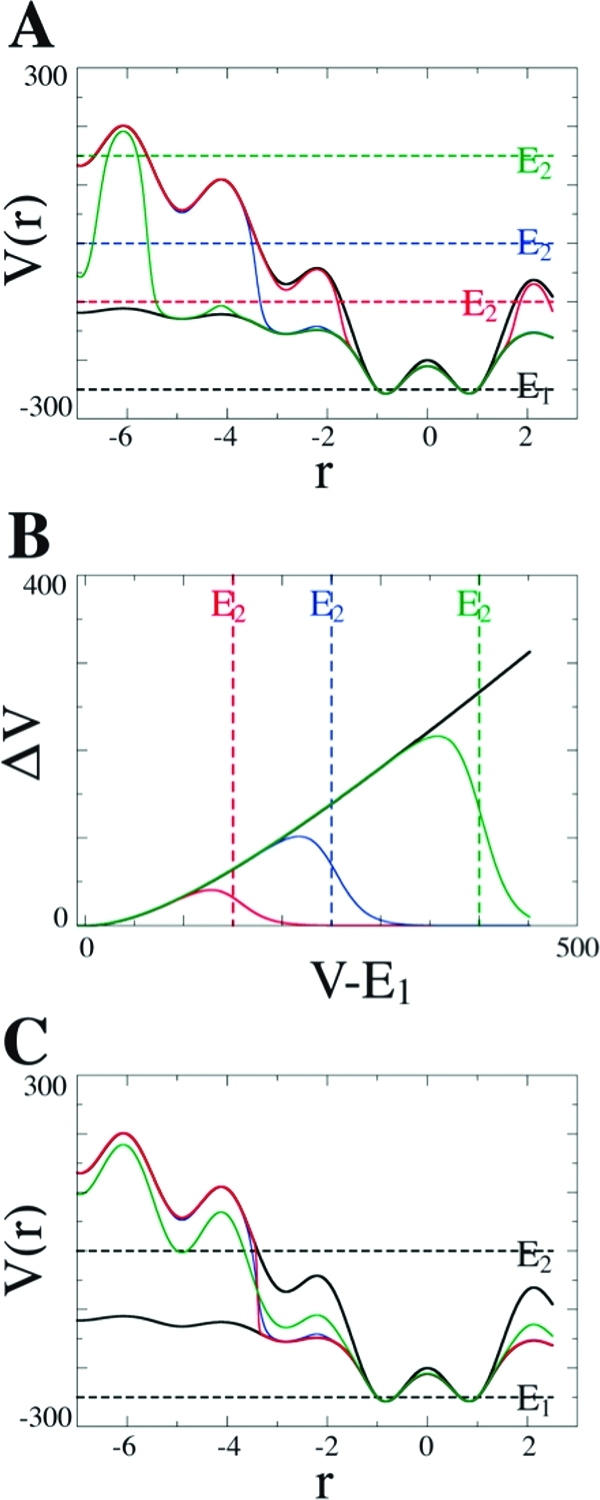
Hypothetical one-dimensional potential representing the effect of ΔV^c. In all charts, α₁ = 200 and E₁ = −250. The upper and lower solid black lines represent the original potential and the modified potential generated with ΔV^b, respectively. This color scheme is used throughout. (A) Effects of different parameters E₂ (dashed colored lines) on the modified potential generated with ΔV^c (solid colored lines). (B) Boost levels ΔV^b (solid black line) and ΔV^c (colored lines) as V(r) moves away from E₁. For both A and B, α₂=15 and E₂ = −100 (red), 0 (blue), and 150 (green). (C) Effect of varying α₂ parameter on ΔV^c: α₂= 3 (red), 15 (blue), and 75 (green) with E₂ = 0.

Like in the original implementation, the degree of acceleration is controlled by the parameter α₁ and E₁. Parameter α₂ controls how strongly energy barriers higher than E₂ are protected. For instance, when V is higher than E₂, in the limit α₂→∞, the term (1 + e^{–(E₂-v(r))/α₂})→2 and ΔV^c converges to 1/2ΔV^b, and as a result, large energy barriers are not effectively protected anymore. On the other hand, when α₂→0, the term (1 + e^{–(E₂–v(r))/α₂})→∞ and ΔV^c→0, thus keeping all energy regions, where V(r) is higher than E₂, unchanged. Figure 1C displays the effects of α₂ on V*(r).

Although this new implementation introduces two new parameters, E₂ and α₂ are easily estimated. Initial guesses for α₂ are based on the hypothetical one-dimensional potential shown in Figure 1. To keep the underlying shape of the original potential surface and effectively protect energy barriers higher than E₂, α₂ is recommended to be proportional to the difference ∼ (E₂ – E₁). More specifically, we estimate α₂ to be between 20 and 60% of the difference (E₂ – E₁). Energy levels E₁ and E₂ are estimated from short cMD simulations. Since ΔV^c is only effectively applied to the system whenever the potential V(r) is higher than E₁, it is important to not set E₁ much higher than the average potential energy of system, ⟨V(r)⟩, in order to guarantee a minimum degree of acceleration. In this work, V(r) and ⟨V(r)⟩ correspond to the instantaneous and average dihedral energy, respectively. E₂ is simply defined as E₂ = E₁ + ΔE, where ΔE is the highest energy barrier that is allowed to be crossed. The selection of optimum boost parameters is bound to be system dependent. For this reason, short aMD runs are strongly recommended to fine-tune parameters α₁ and E₁. Failure in obtaining suitable parameters may lead to two possible scenarios: (i) No or extremely low acceleration is effectively applied to the system. In this case, aMD and cMD will likely generate very similar trajectories. (ii) Extremely high acceleration is applied to system, which results in serious structural and energetic instabilities.

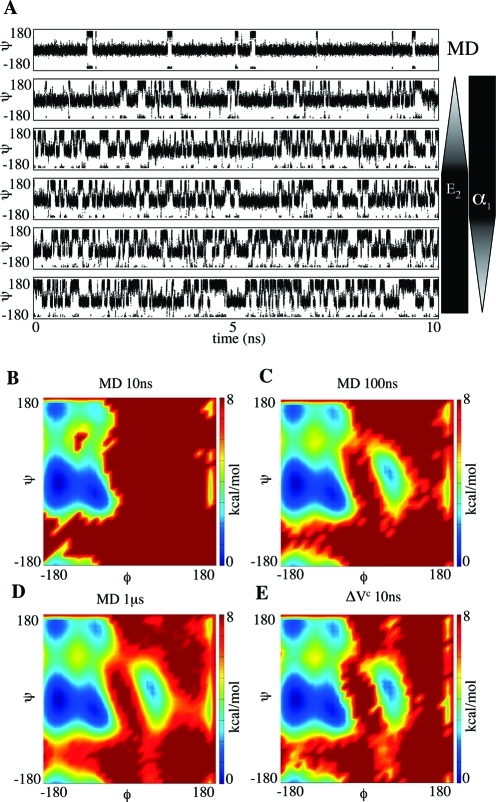
Unless otherwise stated, all simulations were performed applying the boost potential ΔV^c to the dihedral terms of the potential energy function. Enhanced sampling techniques, such as aMD, based on the dihedral energy contributions have been successfully used to effectively enhance conformational sampling of biomolecules.^10,13−17 The approach presented in this work can be easily extended to the nonbonded energy terms via the dual boost method.⁹ To investigate the use of the new boost equation ΔV^c, we first compared our aMD simulations results of fully solvated alanine dipeptide to cMD protocols. Alanine dipeptide has been extensively studied as a model system to evaluate free energy and conformational change in biomolecular simulations.¹⁸⁻²⁴ Figure 2A displays the time evolution of the Ψ angle during the cMD and five aMD simulations of 10 ns. As can be clearly seen, the number of Ψ transitions dramatically increases as we modify boost parameters E₂ and α₂. Figure 2B–E show the free-energy density plots obtained from cMD simulations of 10 ns, 100 ns, and 1 μs and an aMD simulation of 10 ns. The free-energy density plots were calculated from the population of states sampled on each simulation. To recover the corrected canonical ensemble, each frame of the aMD trajectory was Boltzmann weighted by its respective boost factor. Figure 2B reveals that the conformational sampling obtained from 10 ns of cMD is mainly restricted to α-helical (Φ < 0° and −60° < Ψ < 0°) and β-strand regions (Φ < 0° and 120° < Ψ < 180°), with the α-helical region displaying the most populated states. A significant increase in conformational sampling is evident when the cMD is extended to 100 ns (Figure 2C). The most pronounced change can be seen in the left-handed α-helix region (Φ ∼ 50 and Ψ ∼ 50), which is now well sampled and is not observed in the cMD of 10 ns. A dramatic increase in the number of transitions between the α-helical and β-strand regions is also noted. To provide some insights concerning the time scale accessed by our aMD runs, we further extended the cMD simulation to 1 μs. A comparison of Figure 2D and E clearly shows that there is good agreement between the regions sampled by our short aMD of 10 ns and the cMD of 100 ns and 1 μs. For the alanine dipeptide system, these results suggest that aMD simulations with ΔV^c can accelerate conformational sampling by at least 10–100 fold.

Figure 2.

Alanine dipeptide simulation results. (A) Ψ angle values obtained from cMD and five different aMD simulations. From top to bottom, aMD parameters were set to E₂ = E₁ + 15 and α₁ = 5, E₂ = E₁ + 20 and α₁ = 5, E₂ = E₁ + 25 and α₁ = 5, E₂ = E₁ + 25 and α₁ = 2.5, and E₂ = E₁ + 25 and α₁ = 1.25. In all simulations, E₁ and α₂ were set to 10 and 5, respectively. Weighted free energy density plots obtained from cMD (B, C, D) and aMD with ΔV^c (E). All values are in kcal/mol.

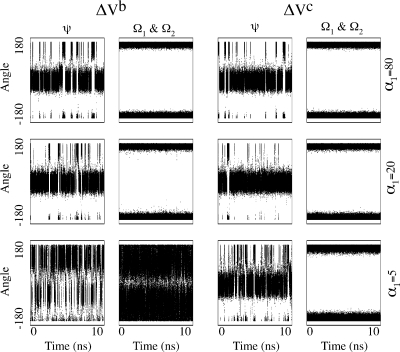
While boosting through energy barriers is important for sampling, limiting the boost to reduce the population of thermodynamically unfavorable states is equally important. To illustrate the advantage of ΔV^c and its boost limiting capabilities over ΔV^b, we analyzed and compared the Ψ and Ω angle transitions (cis/trans isomerization) obtained from the alanine dipeptide simulations in both implementations. As seen in Figure 3, as the degree of acceleration is increased (by reducing the value of parameter α₁), ΔV^b dramatically increases not only Ψ but also Ω dihedral transitions. Conversely, ΔV^c promotes a very similar increase in Ψ dihedral transitions without affecting the Ω dihedral angles. This result confirms the capability of ΔV^c to accelerate conformational transitions by selectively crossing energy barriers lower than the predefined energy level. It is worth mentioning that ΔV^b notably undersamples the normally preferred region −50 > Ψ > +50 under high acceleration conditions.

Figure 3.

ψ and Ω angle values obtained from aMD simulations with boost potentials ΔV^b and ΔV^c. In all simulations, E₁ = 10.0 and α₁ were set as shown on the far right. Additional parameters for aMD with ΔV^c were set to E₂ = E₁ + 15 and α₂ = 5. All values are in kcal/mol.

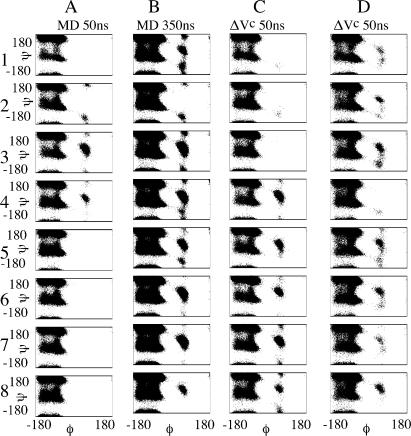
To evaluate the applicability of equation ΔV^c to biomolecules, we also performed aMD studies on a more complex model system, decalanine.²⁵ Figure 4 displays the distribution of eight Φ–Ψ angles monitored along two cMD simulations of 50 and 350 ns and two independent aMD of 50 ns. All simulations started from a fully solvated and extended conformation. As expected, there is a substantial improvement in conformational sampling when the cMD simulation is extended from 50 ns to 350 ns (Figure 4A and B). Similar results are obtained for Φ–Ψ angles 4–8 when we compare aMD with both cMD simulations (Figure 4A, B, and C). Interestingly, the opposite behavior is observed for Φ–Ψ angles 1–3 (Figure 4C). We attribute this result to the low degree of acceleration used on the aMD simulation. Even though application of ΔV^c enhances conformational transitions of decalanine, the small boost used in this simulation, as a test case, may not generate the 7-fold acceleration expected from Figure 4C and B. To investigate this issue and further explore the capability of ΔV^c, we carried out two extra aMD simulations of 50 ns in which we (a) increased the acceleration by reducing the α₁ value by a factor of 2 (result is shown in Figure 4D) and (b) increased the degree of acceleration by raising the energy level E₂ (E₂ = E₁ + 35 kcal/mol), in addition to reducing α₁ by a factor of 2 (Figure S1, Supporting Information). As expected, the different aMD simulations of 50 ns each (Figure 4C,D and Figure S1) cover different regions of the Φ–Ψ subspace, with the more accelerated ones (Figure 4D) showing better agreement with the cMD simulation of 350 ns (Figure 4B). These results also agree with the fact that, by lowering energy barriers, aMD increases the rate of escape from minimum wells and thus generates more diverse trajectories for complex systems with multidimensional energy landscapes such as decalanine. Figure S1 displays the Φ–Ψ angle distributions obtained with the highest degree of acceleration tested. It is worth noting that there is better agreement with the conformational sampling obtained from the 350 ns of cMD, as a result of the longer time scale accessed by this aMD simulation.

Figure 4.

Decalanine Φ–Ψ angles distribution obtained from cMD and aMD simulations. For the aMD simulations with ΔV^c parameters were set to E₁ = 74, E₂ = E₁ + 25, α₂ = 5, α₁ = 30 (C), and α₁ = 15 (D). All values are in kcal/mol.

Decalanine can adopt numerous secondary structures making it a challenging test case for enhanced sampling methods.²⁵ Principal component analysis (PCA) shows that our ΔV^c aMD simulation explores energy wells that are not adequately sampled by 350 ns of cMD simulation (Figure 5A, B, C). One of these regions represents the state in which decalanine adopts an α-helical conformation, energetically the most stable configuration.²⁵ This folding event is evident in the aMD simulations, but not in the cMD simulations despite the latter being 7-fold longer (Figure 2S).

Figure 5.

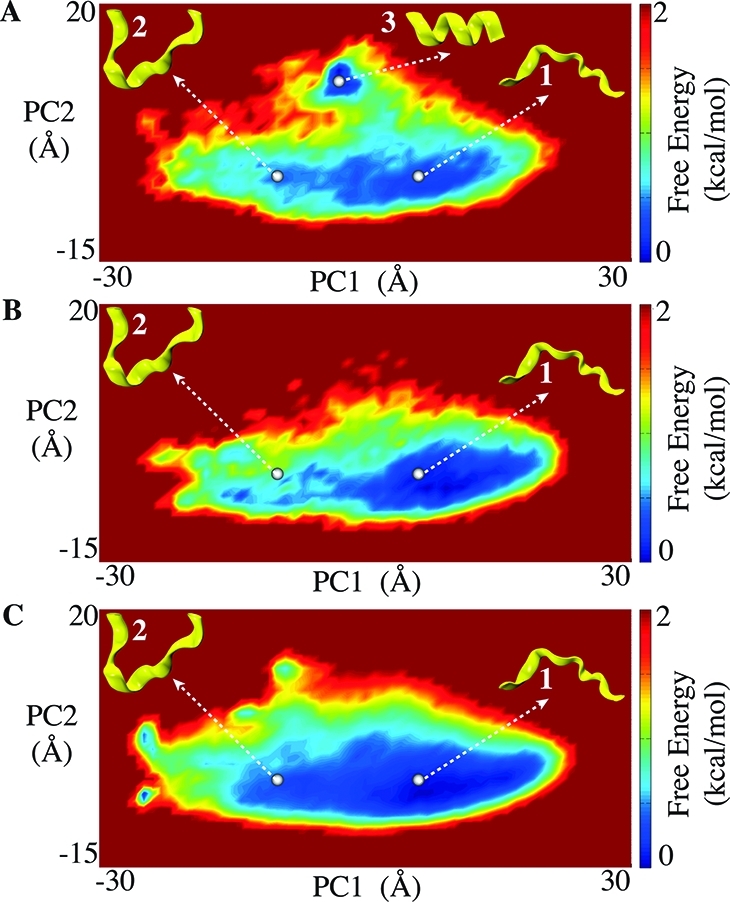
Principle component analysis obtained from decalanine MD simulations. (A) 50 ns of aMD simulation with ΔV^c. Parameters were set to E₁ = 74, E₂ = E₁ + 25, α₂ = 5, and α₁ = 15, same as in Figure 4D. (B) 50 ns of cMD simulation and (C) 350 ns of cMD simulation. Structures 1, 2, and 3 shown in yellow represent relevant populated states in PC subspace sampled by aMD and cMD.

Free energy calculations are useful in the optimization of compounds for biological targets and host systems.²⁶ However, these calculations usually require a computationally expensive ensemble generation either from Monte Carlo calculations or MD simulations.^27,28 As previously shown, coupling of aMD methods with free energy calculations, such as thermodynamic integration (TI), revealed promising results when applied to simple model systems.⁸ To further extend the applicability of aMD-based approaches to free energy calculations, in this work, we modified our original implementation by incorporating the boost equation ΔV^c into the TI simulations. As a test case, we calculated the relative free energy difference between Ac_2-L-Lys_-D-Ala_-D-Ala and Ac_2-L-Lys_-D-Ala_-D-Lac bound to vancomycin. This mutation, Ala to Lac, confers to bacteria a resistance against vancomycin.²⁹ The experimental change in binding free energy has been determined to be 4.1 kcal/mol, which corresponds to an approximately 1000-fold decrease in affinity from _DAla to _DLac.³⁰

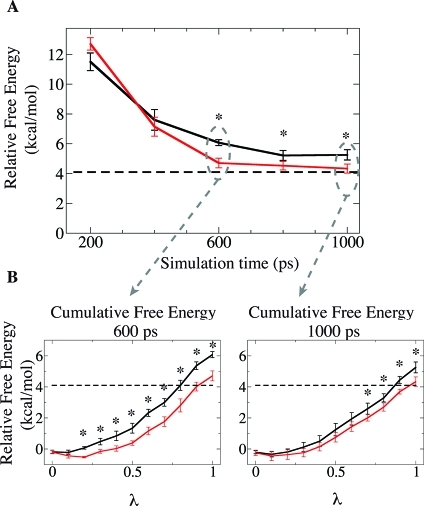
Figure 6A compares the relative free energy of binding (ΔΔG) calculated from TI simulations using cMD and aMD with ΔV^c. To calculate the final free energy values, we divided the trajectories in blocks of 200 ps, with the last block representing the production phase. For example, a TI simulation of 800 ps corresponds to an equilibration phase of 600 ps (three blocks) followed by a collecting data phase of 200 ps, and a TI simulation of 1000 ps corresponds to an equilibration phase of 800 ps (four blocks) followed by the collecting data phase of 200 ps. Thus, the points displayed in Figure 6A reveals how the calculated ΔΔG changes as a function of the equilibration time.

Figure 6.

(A) Relative free energy of binding between Ac_2-L-Lys_-D-Ala_–-D-Ala and Ac_2-L-Lys_-D-Ala_-D-Lac to vancomycin calculated from cMD (solid black line) and aMD with ΔV^c (solid red line). A dashed line displays the experimental value, 4.1 kcal/mol. (B) Cumulative free energy curves calculated from simulations of 600 ps (left) and 1000 ps (right) per λ point. The ∗ shows points where there is no overlapping between error bars.

It is worth mentioning that application of ΔV^c notably improves the convergence of ΔΔG when compared to standard cMD TI simulation. In addition, the final free energy value obtained with ΔV^c (4.3 ± 0.3 kcal/mol) shows very good agreement with the experimental value of 4.1 kcal/mol,³⁰ while the final free energy value from TI with cMD is 5.3 ± 0.3 kcal/mol. Since the same force field and simulation conditions were applied to both TI simulations, we attribute this difference solely on the conformational sampling enhancement provided by the ΔV^c. Moreover, the error associated with each point suggests that the faster convergence toward the final free energy value is statistically relevant. Interestingly, the cumulative free energy values (Figure 6B) demonstrate that the TI simulations coupled with cMD are indeed converging toward the ones coupled with aMD as we increase the simulation time. Hence, inaccuracies in the final value are likely to be primarily due to the lack of convergence on λ points. These results indicate that ΔV^c can effectively enhance conformational sampling when coupled with TI simulations and hence shorten the equilibration period required for accurate free energy calculation.

Computational Methods

ΔV^c was implemented in the AMBER10 code³¹ as previously reported.⁸

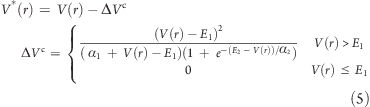5

All cMD, aMD and TI simulations were performed using a modified version of the sander module of the AMBER10 package.³¹ TIP3P water molecules were used to solvate both the alanine dipeptide and decalanine systems.³² A buffer region of 10 or 12 Å was used in all systems. To eliminate any steric clashes, 100 steps of conjugate gradient minimization were performed on all systems. To bring the systems to the right density, we carried out cMD simulations of 50 ps in which the NPT ensemble was applied. Then, long cMD and aMD simulations were performed in which the NVT ensemble was applied. All bonds involving hydrogen atoms were constrained using the SHAKE algorithm.³³ The temperature and pressure were controlled using weak coupling to external temperature and pressure baths.³⁴ Electrostatic interactions were computed via PME (particle mesh Ewald summation) with a cutoff of 8.0 Å. All simulations were performed at temperature of 300 K. In all accelerated simulations, the boost potential was based on the dihedral energy. Principal components analysis was performed using the ptraj module of the AMBER10 package. All cMD simulations were projected onto the PC subspace obtained from the aMD simulation displayed at Figure 4D. Alignment of the trajectory was performed on backbone atoms of decalanine.

To study the use of the new boost equation on thermodynamic integration calculations, we calculated the relative difference in the free energy of binding of Ac_2-L-Lys_-D-Ala_-D-Ala and Ac_2-L-Lys_-D-Ala_–D-Lac to a vancomycin dimer, starting from the crystal structure of Ac_2-L-Lys_-D-Ala_-D-Ala bound to vancomycin (PDB ID: 1FVM). The glycopeptides and vancomycin were parametrized using Antechamber. The system was solvated in a cubic box of TIP3P water molecules, with a buffer region of 10 Å.³¹ Owing to the strong correlation between glycopeptides binding affinity and vancomycin dimerization,³⁵ we simulated the “back to back” homodimer of vancomycin, as present in the X-ray crystal structure. Both ligands were included in the model and modified alchemically.

TI simulations were performed with nine equally spaced λ parameters (λ = 0.1 to 0.9) in solution and in the vancomycin receptor. In all transformations, electrostatic and van der Waals contributions were decoupled and computed separately. More specifically, in this work, the alchemical transformation of _DAla to _DLac was carried out in three steps: (i) removal of partial charges of the NH group from _DAla, (ii) transformation of van der Waals parameters of the NH group to the O (oxygen) atom, and (iii) partial charge creation on the O (oxygen) atom. Softcore potentials were used for step ii.^36,37 The ΔV/Δλ values were calculated over a production period of 200 ps along with five equilibration periods 0, 200, 400, 600, and 800 ps. The final free energy values were averaged over three independent (with reassigned initial atomic velocities) cMD or aMD simulations. As previously shown, in order to recover the correct canonical ensemble, ΔV/Δλ values collected from aMD runs were reweighted by their respective boost factor e^βΔV[r].^3,8

Error bars were calculated using, σ_⟨A⟩ ≈ σ/√M where M is the number of independent simulations and σ_⟨A⟩ is the standard deviation of the average value A obtained from M independent data values (M = 3 in all cases). An analysis of the trajectories was performed using ptraj.³¹

Our aMD parameters were estimated on the basis of the average dihedral energy term obtained from short cMD simulations. For all alanine dipeptide aMD simulations, parameter E₁ was set to 10 kcal/mol. Parameter α₂ was set to 5 kcal/mol, which corresponds to 0.2 to 0.33(E₂ – E₁). In Figure 2A, from top to bottom, aMD simulations used the following parameters: E₂ = E₁ + 15 and α₁ = 5, E₂ = E₁ + 20 and α₁ = 5, E₂ = E₁ + 25 and α₁ = 5, E₂ = E₁ + 25 and α₁ = 2.5, and E₂ = E₁ + 25 and α₁ = 1.25. In Figure 2E, the aMD simulation used the parameters E₂ = E₁ + 15and α₁ = 5. In Figure 3, E₂ = E₁ + 15 (for ΔV^c) and α₁ were varied as indicated in the far right column.

Boost parameters for decalanine simulations were E₁ = 74, E₂ = E₁ + 25, α₁ = 30, and α₂ = 5. Boost parameters for the vancomycin-glycopeptides simulations were E₁ = 211, E₂ = E₁ + 25, α₁ = 30, and α₂ = 15.

Conclusion

In this work, we introduced a new boost equation, ΔV^c, for aMD simulations aiming to overcome sampling issues introduced by ΔV^b. Since energy barriers located above a predefined energy level can now be protected, the new boost equation ΔV^c provided much better control over high energy regions of the conformational landscape when compared to ΔV^b. We used two model systems, alanine dipeptide and decalanine, to study the applicability and efficiency of ΔV^c in enhancing conformational sampling. In both cases, the new boost potential not only provides better recovery of statistics throughout the simulation but also enhanced sampling of statistically relevant regions in explicit solvent MD simulations. When coupled with thermodynamic integration, our results indicate that ΔV^c can effectively enhance conformational sampling and accelerate convergence for a more accurate free energy calculation.

Supporting Information Available

Additional simulation and analysis of decalanine including the Φ–Ψ angles distribution for an aMD simulation and calculation of the RMS deviation from the α-helix conformation. This information is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Author Contributions

^∥ These authors contributed equally.

Funding Statement

National Institutes of Health, United States