Nursing Home Care Quality: Insights From a Bayesian Network Approach

Abstract

Purpose

The purpose of this research is twofold. The first purpose is to utilize a new methodology (Bayesian networks) for aggregating various quality indicators to measure the overall quality of care in nursing homes. The second is to provide new insight into the relationships that exist among various measures of quality and how such measures affect the overall quality of nursing home care as measured by the Observable Indicators of Nursing Home Care Quality Instrument. In contrast to many methods used for the same purpose, our method yields both qualitative and quantitative insight into nursing home care quality.

Design and Methods

We construct several Bayesian networks to study the influences among factors associated with the quality of nursing home care; we compare and measure their accuracy against other predictive models.

Results

We find the best Bayesian network to perform better than other commonly used methods. We also identify key factors, including number of certified nurse assistant hours, prevalence of bedfast residents, and prevalence of daily physical restraints, that significantly affect the quality of nursing home care. Furthermore, the results of our analysis identify their probabilistic relationships.

Implications

The findings of this research indicate that nursing home care quality is most accurately represented through a mix of structural, process, and outcome measures of quality. We also observe that the factors affecting the quality of nursing home care collectively determine the overall quality. Hence, focusing on only key factors without addressing other related factors may not substantially improve the quality of nursing home care.

Determining what factors significantly influence the quality of care in nursing homes has presented a difficult challenge and is a growing concern. Despite calls for reform (Institute of Medicine, 1986), recent reports conclude that the quality of care provided in some facilities still leaves much to be desired (Institute of Medicine, 1996, 2001). As the United States will encounter an unprecedented number of Americans who require skilled nursing care in the upcoming decades, the need for a more thorough understanding of nursing home care quality has never been more prominent.

In this study we examine what factors influence the quality of nursing home care through a multivariate framework known as Bayesian networks. The intent of our research is twofold. We seek to utilize a new methodology for aggregating various quality indicators to measure the overall quality of care in nursing homes. We also seek to provide new insight into the relationships that exist among various measures of quality and how such measures affect the overall quality of nursing home care as measured by the Observable Indicators of Nursing Home Care Quality Instrument (Rantz & Zwygart-Stauffacher, 2006; Rantz, Mehr, et al., 2006). Two aspects of the study provide such insight. First, the Bayesian network framework allows us to examine previous research to determine which combinations of variables most significantly influence the quality of care. Second, an inspection of the structure and parameters that characterize a Bayesian network both qualify and quantify aspects of nursing home care quality. The insights gained from this analysis not only provide a unique perspective on the makeup of nursing home care quality, but they also afford practical applications for quality improvement.

Background

In recent decades, researchers have conducted numerous studies to gain a better understanding of the quality of nursing home care. In this section we do not intend to provide an exhaustive review of such studies. Rather, we offer a survey of studies, many of which we think are representative of important advances in this field. The survey is divided into two sections. The first addresses studies focusing on specific factors that influence nursing home care quality; the second is devoted to studies that aggregate information to measure the overall quality of care in nursing homes.

Factors Influencing the Quality of Nursing Home Care

Factors influencing the quality of nursing home care delivery can be separated into three categories: structure, process, and outcome. Common structural measures of quality include facility size, occupancy, ownership type, staffing, and percentage of Medicaid and Medicare residents. Most studies concur that larger facilities exhibit lower levels of quality than do smaller facilities (Harrington, O’Meara, Kitchener, Simon, & Schnelle, 2003; O’Neill, Harrington, Kitchener, & Saliba, 2003). Research examining the relationship between the quality of nursing home care and occupancy rate has produced mixed results. Some studies show that higher occupancy rates are associated with a higher use of restraints, more pressure sores, a greater use of psychoactive drugs, and lower total nurse and registered nurse staffing hours (Castle, 2001; Harrington & Swan, 2003). In contrast, research conducted by Zinn, Aaronson, and Rosko (1993) indicates that higher mortality rates are associated with lower occupancy rates. Investigations into the relationship between the proprietary status of nursing homes and the quality of care overwhelmingly favor nonprofit institutions over for-profit institutions (Aaronson, Zinn, & Rosko, 1994; Harrington, Woolhandler, Mullan, Carrillo, & Himmelstein, 2001; O’Neill et al.). Although one study reports that staffing levels account for only a small portion of the total variation in quality of care (Harrington, Zimmerman, Karon, Robinson, & Beutel, 2000), the general consensus of research is that more staffing of all types improves nursing quality (Schnelle et al., 2004).

According to the authors of some studies, higher percentages of Medicaid residents tend to negatively influence nursing quality and staff levels (Grabowski, 2001; Harrington & Swan, 2003). However, Chesteen, Helgheim, Randall, and Wardell (2005) posited that, in their study, the percentage of Medicaid residents did not contribute adversely to outcome quality. Research conducted by Harrington and colleagues (2001, 2003) seems to indicate that the percentage of Medicare residents has a positive affect on the quality of care in nursing homes. Although research to date has yielded various results on the relationship of structural measures to overall nursing home quality, such measures are clearly an influential aspect of the quality of nursing home care.

Process measures of nursing home quality describe the process of care provided. Outcome quality measures, in contrast, measure the results of nursing care processes. An often utilized set of clinical quality indicators (which encompass both process and outcome measures) was developed by researchers at the Center for Health Systems Research and Analysis (CHSRA) at the University of Wisconsin–Madison. These quality indicators (QIs) measure the proportion of nursing home residents with the QI condition. The latter portion of Table 1 lists the 24 CHSRA QIs (QI variable names followed by the letter N were revised in 1997). Despite their widespread use, clinical QIs are not without criticism. Critics point to flaws with the Minimum Data Set as well as with the QIs themselves (General Accounting Office, 2002; Office of the Inspector General, 2001). Although a number of studies indicate that clinical QIs require further validation and testing in order for researchers to determine how accurately they predict the quality of care in nursing homes, critics admit that facilities with better quality can be differentiated among those with average or poorer quality on the basis of such indicators (Harrington et al., 2003).

Table 1.

Variable Descriptions and Model Composition

Variable	Description	Model(s)
QOC	The QOC as determined by the total OIQ score	All
BedSz	Number of beds in a facility	BN2
Occupancy	Number of beds occupied in a facility	BN3; Reg2
Medicare	Indicates whether or not a facility accepts Medicare residents	BN2
Chain	Indicates whether or not a facility is part of a nursing home chain	BN2; Reg2
RNhrs	The number of RN hours per resident day	BN2; Reg2
CNAhrs	The number of CNA hours per resident day	BN2,3
Totalhrs	The number of total staff hours per resident day	BN2; Reg2
Deficiencies	The number of deficiencies issued to a facility	BN3; Reg1, Reg2
FP	Indicates FP facilities	BN2
NP	Indicates NP facilities	BN2
GOV	Indicates GOV facilities	BN2
QI1N	Prevalence of any injury	BN1, Reg2
QI2	Prevalence of falls	BN1
QI3	Prevalence of behavioral symptoms affecting others	BN1
QI4N	Prevalence of diagnosis or symptoms of depression	BN1
QI5N	Prevalence of depression with no treatment	BN1
QI6	Use of 9 or more different medications	BN1
QI7N	Onset of cognitive impairment	BN1
QI8	Prevalence of bladder or bowel incontinence	BN1
QI9	Prevalence of occasional bladder or bowel incontinence without a toileting plan	BN1
QI10	Prevalence of indwelling catheters	BN1
QI11	Prevalence of fecal impaction	BN1
QI12	Prevalence of urinary tract infections	BN1
QI14	Prevalence of weight loss	BN1
QI15	Prevalence of tube feeding	BN1; Reg2
QI16	Prevalence of dehydration	BN1
QI17	Prevalence of bedfast residents	BN1,3
QI18	Incidence of decline in late-loss ADLs	BN1
QI20N	Lack of training–skill practice or ROM for mobility-dependent residents	BN1
QI21N	Prevalence of antipsychotic use, in the absence of psychotic and related conditions	BN1; Reg2
QI23N	Prevalence of antianxiety or hypnotic use	BN1
QI24	Prevalence of hypnotic use more than two times in past week	BN1
QI26	Prevalence of daily physical restraints	BN1,3
QI27	Prevalence of little or no activity	BN1; Reg2
QI29	Prevalence of Stage 1–4 pressure ulcers	BN1

Note: BN1, BN2, BN3 = Bayesian networks; QOC = quality of care; OIQ = Observable Indicators of Nursing Home Care Quality Instrument; RN = registered nurse; CNA = certified nurse assistant; FP = for profit; NP = not for profit; GOV = government; ADLs = activities of daily living; ROM = range of motion. Reg1 = the first benchmark model (a simple regression); Reg2 = the second benchmark model (a multiple regression), in which variables were chosen by means of a stepwise selection procedure.

When a facility does not comply with federally imposed standards, the facility may receive a deficiency. As deficiencies may address standards related to processes or outcomes (or both) in a nursing home, they have often been utilized as process and outcome measures, depending on their type and severity. In addition, the number and type of deficiencies have often been utilized as a measure of overall quality in nursing homes. Consequently, relationships between deficiencies and many of the aforementioned structural measures of quality have been rigorously researched.

Models for Assessing the Quality of Nursing Home Care

A popular model that has been applied to the assessment of nursing home care quality was developed by Donabedian (1988). Donabedian proposed three aspects of quality assessment: structure, process, and outcome, known as the SPO framework. The SPO framework served as the foundation for two notable models. Atchley (1991) modified the framework to include a time dimension. Unruh and Wan (2004), noting the lack of causality among structure, process, and outcomes in models utilizing the SPO framework, constructed a “framework for nursing home quality that links contextual components of quality with structure, structure with process, and process with outcomes, focusing on nursing care quality.” The authors suggest further development of the model through structural equation modeling.

Two studies have utilized clinical QIs as predictors of overall nursing home quality. Karon, Sainfort, and Zimmerman (1999) established the stability of QIs over time by ordering facilities by their QI ranks. The QI rank (or percentile), therefore, provides a relative measure of overall quality within a group of nursing homes. Instead of employing the QI rank method, Rantz and colleagues (2004) classified nursing homes on the basis of their individual QI scores and compared them to established QI thresholds (Rantz, Petroski, et al., 2000). The conglomeration of the individual QI ratings yielded an overall classification for the facility—good, average, or poor. Table 2 (where G, A, and P denote the number of QIs in the good, average, and poor ranges, respectively) illustrates the number of QIs within a certain range required to arrive at an overall facility rating.

Table 2.

Criteria for the Quality Indicator Classification Model

Classification	Criteria
Good (G)	G ≥ 5 and G–P ≥ 2
Poor (P)	P ≥ 5 and P–G ≥ 5
Average (A)	A ≥ 15 and neither G nor P

The Observable Indicators of Nursing Home Care Quality Instrument (OIQ) measures the overall quality of a nursing facility during an on-site visit to a nursing home. Development of the OIQ began through a series of qualitative studies to identify and describe the many dimensions of the quality of care in nursing homes of importance to consumers, providers, and regulators (Rantz et al., 1999). As a result of these studies, Rantz and colleagues proposed two theoretical models of nursing home care quality: one from the point of view of direct-care providers and regulators, and one from the view of consumers. The researchers merged the dimensions from the models into one comprehensive model defining nursing home care quality as a multidimensional concept with seven dimensions: central focus of the agency is on residents, families, staff, and community; care; communication; staff; environment; home; and family involvement. On the basis of this qualitative work, Rantz and colleagues constructed an initial instrument from the descriptive statements of study participants. They constructed items to measure each of the dimensions of the theoretical model of nursing home care quality. As the instrument name implies, each item refers to some directly observable aspect of any nursing home. Four field tests in 123 Missouri nursing homes and a small international sample delivered promising reliability and validity results (Rantz, Mehr, et al., 2000). Subsequent field testing, refinement, and psychometric evaluation were conducted as a field test in 407 nursing homes in three states. Based on the results of exploratory factor analysis, confirmatory factor analysis, classical test theory, and generalizability theory, Rantz and colleagues determined the OIQ to be a valid and reliable instrument for measuring the quality of care in nursing homes (Rantz & Zwygart-Stauffacher, 2006; Rantz et al., 2006).

Because we employ the OIQ as a measure of overall quality in this study, we give a brief explanation of how the instrument gauges nursing home quality. During an on-site visit to a nursing home, an evaluator answers a series of questions related to the aforementioned dimensions of quality. To answer each question, the evaluator chooses from answers associated with a Likert scale. The sum total of the answers constitutes a score for the facility. The score is then transformed into a facility classification of Below Average, Average, or Above Average. The thresholds for these classifications correspond to the 20th and 80th percentiles of nursing homes examined in the studies mentioned earlier. The authors of the OIQ provide more details regarding the OIQ at their Web site (www.nursinghomehelp.org).

Bayesian Networks

Bayesian networks (BNs) are a multivariate method that is useful in modeling complex relationships among variables. Using Bayesian probability theory, BNs estimate the probability distributions of unknown variables from known probabilistic relationships. In this section we address three key components of BNs: structure, parameters, and inference. We illustrate each of these aspects with a simple hypothetical example, and we provide appropriate references for readers seeking additional information. In addition, we also discuss the advantages and weaknesses of BNs as a modeling tool.

Structure

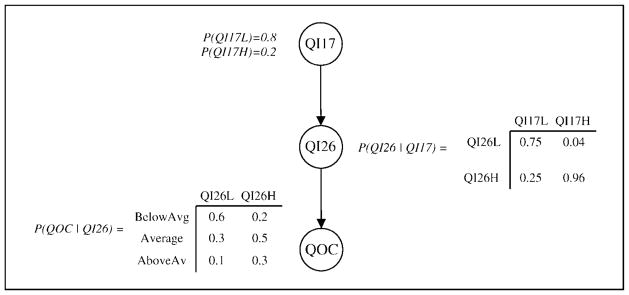
The structure of a BN is a graph, composed of a set of nodes V={X₁, …, X_n} and a set of edges E. The nodes of the graph represent random variables, each of which may take on certain values, whereas the edges represent influence among variables. Consider, for example, the hypothetical BN depicted in Figure 1 with variable definitions in Table 3. In this example V = {QI17, QI26, QOC} and E = {(QI17, QI26), (QI26, QOC)}. The structure suggests that the overall quality of care (QOC) in a nursing home is directly affected by the prevalence of daily physical restraints (QI26), which in turn is influenced by the prevalence of bedfast residents (QI17).

Figure 1.

Hypothetical Bayesian network.

Table 3.

Hypothetical Bayesian Network Variable Definitions

Variable	Value	When the Variable Takes on This Value
QI17	QI17L	<50% of residents are bedfast
	QI17H	>50% of residents are bedfast
QI26	QI26L	<50% of residents have daily physical restraints
	QI26H	>50% of residents have daily physical restraints
QOC	BelowAvg	The QOC delivered is below average
	Average	The QOC delivered is average
	AboveAvg	The QOC delivered is above average

Note: QOC = quality of care.

Given a set of variables, one can develop the structure of a BN in two ways. First, a domain expert may place edges among variables to represent his or her understanding of how the variables interact. Second, one may determine the structure of BNs by means of structure-learning algorithms. Such methods seek for a network structure that maximizes the probability of a particular network configuration, G, given a set of data, d, which one may write as P(G|d). One calculates this quantity by using Bayes’ theorem, which states that P(G|d) is proportional to P(d|G)P(G), where P(d|G) is the likelihood of G and P(G) is the prior probability. The details of structure-learning algorithms are found in the research of Geiger and Heckerman (1994) and Bøttcher (2001).

Parameters

The parameters of a BN provide additional details as to the relationships among variables. Each node in a BN contains a conditional probability table that provides the conditional probability distribution of the node given the various states of its parents (node A is a parent of node B if the BN contains a directed edge from A to B). For example, associated with node QOC in Figure 1 is a conditional probability table that gives the probability of QOC given the two possible values of QI26. The qualitative relationships imposed by a BN’s structure are thereby quantified by its parameters.

Given a network structure, the parameters of a BN may be developed in two ways. First, a domain expert may determine the conditional probability distributions on the basis of his or her knowledge. Parameters may also be developed through parameter-learning algorithms. Such methods determine conditional probability distributions based on a provided data set with known values for each variable. As each nursing home in the data set is presented to the BN, an estimate of the conditional probability distributions is gradually revised. As the details of parameter-learning algorithms are beyond the scope of this article, the interested reader is referred to Spiegelhalter, Dawid, Lauritzen, and Cowell (1993) and Geiger and Heckerman (1994).

Inference

With the structure and parameters of a BN in place, probabilistic inference can be performed within the network. More specifically, one may query the BN for the probability distribution of one or more variables of unknown value given the known values of other nodes in the network. Methods for performing inference in a BN use Bayes’ rule to predict the outcome of events that are dependent on other events, where dependence is given by the network structure.

As an example of inference, the probability distribution of QOC in Figure 1 may be of interest. For purposes of comparison, we begin by calculating this distribution when none of the values of the variables in Figure 1 are known. An outline of the basic calculations involved is given in the following set of equations, which yields P(QOC) = {0.443, 0.378, 0.178}.

$$\begin{array}{l}P(\text{QI}26\text{L})=P(\text{QI}26\text{L}\mid \text{QI}17\text{L})P(\text{QI}17\text{L})+P(\text{QI}26\text{L}\mid \text{QI}17\text{H})P(\text{QI}17\text{H})\\ =(0.75)(0.8)+(0.04)(0.2)=0.608\\ P(\text{Below}\text{Avg})=P(\text{Below}\text{Avg}\mid \text{QI}26\text{L})P(\text{QI}26\text{L})+P(\text{Below}\text{Avg}\mid \text{QI}26\text{H})P(\text{QI}26\text{H})\\ =(0.6)(0.608)+(0.2)(1-0.608)\\ =\mathrm{0.443.}\end{array}$$

If it is known that QI26 = QI26L, then similar calculations yield P(QOC) = {0.600, 0.300, 0.100}. Thus, as additional information becomes available, one adjusts the distribution of QOC accordingly. The various types of inference that can be performed in a BN and the associated algorithms are found in the books by Jensen (1996) and Pearl (1988).

Advantages and Weaknesses of BN Modeling

The primary advantage of a BN is an efficient representation of the joint probability distribution of a set of variables V, denoted P(V). Normally, P(V) would require an entry for each combination of the variables in V and their associated states. As the number of variables increases, the number of entries in P(V) increases exponentially, thereby making it intractable to determine and update P(V) even for moderate numbers of variables. BNs overcome this intractability by exploiting the conditional probability relationships among variables. More specifically, the joint probability distribution can be represented as a product of conditional probabilities,

$$P(V)=\prod _{i}P\left[X_i\mid pa(X_i)\right],$$

where pa(X_i) denotes the parents of variable X_i (Jensen, 1996).

As we mentioned earlier, establishing the structure and parameters of a BN by means of learning algorithms may uncover relationships among variables missed by conventional statistical methods. Because these relationships may be highly nonlinear, a BN approach is likely to provide a more instructive model than traditional methods, such as regression. A particularly salient benefit of a BN approach is the ability to obtain rich insight into nursing home care quality. As illustrated in the examples given herein, rich qualitative and quantitative insight is available by inspecting a BN’s structure and parameters. Further insight is available upon querying the BN for the probability distributions of key variables, such as QOC. A simultaneous disadvantage is the unfamiliarity of such measures. For example, regression coefficients and correlation measures may be more familiar to researchers than are conditional probabilities.

Another disadvantage of a BN approach is the method of evaluation. Although some standard classification measures may be applied to a BN, much of a network’s evaluation is application dependent. As an example of this, in a subsequent section we use two measures to evaluate potential BNs. Although we believe these measures are well suited for this study, they may not be applicable for BNs developed for other purposes.

To summarize, BN methodology is in a period of development analogous to structural equation modeling in the 1970s. Additional improvements in search strategy and estimation will likely emerge. For the time being, however, the current state of the methodology provides a very practicable means for studying nursing home care quality. Further explanation of BNs, directed toward nurse researchers, is given by Lee and Abbott (2003).

Methods

Data and Software

As is the case in many modeling studies, the quality of the data was of paramount importance. In this work, the BN structure and parameter-learning algorithms required a preexisting overall measure of nursing home care quality with which to build models that would subsequently serve as a means to gain insight. Of particular interest to this study was the availability of the overall quality score (QOC in Table 1) as determined by the OIQ. As we discussed in the Background section, the OIQ has been determined to be a valid and reliable instrument for measuring the QOC in nursing homes. Therefore, the OIQ score served as our overall measure of nursing home care quality for each nursing home in our analysis.

The data that we analyzed in this study were provided by the University of Missouri–Columbia Sinclair School of Nursing and were gathered as part of a 3-year research project funded by the National Institute of Nursing Research of the National Institutes of Health. Data collected for each nursing home included the items listed in Table 1. The first variable, QOC, is derived from the OIQ. The next 11 variables constitute structural quality measures often utilized in previous research to evaluate the quality of nursing home care. The remaining portion of Table 1 depicts the 24 CHSRA QIs. The far right column of Table 1 specifies variable inclusion in the resulting models. QI data were collected within a 90-day period prior to the determination of the OIQ score. The average time between QI assessment and OIQ assessment was 43 days, with a standard deviation of 26 days. We decreased the initial data set of 256 nursing homes to 234 nursing homes by removing facilities with missing information and potential OIQ scoring errors.

For the purpose of constructing BN models, we transformed the data items in Table 1 into discrete ranges as follows. We labeled the QOC score for each facility as Below Average, Average, or Above Average on the basis of the classification scheme discussed in the Background section. We divided the variables of number of beds in a facility, number of beds occupied in a facility (occupancy), number of registered nurse hours per resident day, number of certified nurse assistant hours per resident day (CNAhrs), number of total staff hours per resident day, and number of deficiencies issued to a facility (deficiencies) into three levels (high, average, and low) based on the 20th and 80th percentiles of the facilities in the data set. We did not modify the variables of whether or not a facility accepts Medicare residents, whether or not a facility is part of a nursing home chain, and whether the facility is for profit, not for profit, or government, as they were binary variables to begin with. Finally, we divided the QIs into three levels on the basis of established QI thresholds. These thresholds, established by experts, classify a nursing home’s performance on a particular QI as good, average, or poor (Rantz, Petroski, et al., 2000).

We partitioned the data set into two sets—a learning set (n = 184) to be used in determining BN structures and parameters and a validation set (n = 50) to be used in validating the BNs. We repeated this process a total of 10 times, resulting in 10 randomly partitioned learning and validation data set pairs. All data sets were proportional to the original data set, with respect to the OIQ score (20% with a Below Average OIQ score, 60% with Average, and 20% with Above Average). Such a method, similar to cross-validation, is a standard procedure for the testing and validation of classifiers (Tan, Steinbach, & Kumar, 2005).

Using the learning data sets, we created BN models with two software packages. We used Deal, a BN software package developed in Denmark by Bøttcher and Dethlefsen (2004), to learn the structures of the BN models. We conducted subsequent parameter learning in Netica, developed by Norsys Corporation. Using the validation data sets, we then evaluated the models with the assistance of Netica as described in the following paragraphs.

Model Creation and Variable Selection

To utilize the BN framework to better understand the relationships among various measures of quality and the overall QOC in nursing homes, we created three BN models (denoted by BN1, BN2, and BN3). We designed the models to utilize research discussed in the Background section of this article and to uncover previously undiscovered relationships among quality measures and the overall QOC. The following paragraphs give a description of the variables included in each model. The far right column of Table 1 also indicates variable inclusion in specific models.

We included variable QOC in each model with the aim of examining relationships among QOC and other sets of variables. The variables in BN1 include the 24 CHSRA QIs; the variables in BN2 are composed of structural measures of quality; and we selected the variables in BN3 by means of the Pearson chi-square test of independence. This standard test, which is useful in detecting associations between categorical variables, assesses whether or not paired observations on two variables (expressed as a contingency table) are independent of each other (Hogg, Craig, & McKean, 2004). We performed the test for each pairwise combination of QOC and the other variables listed in Table 1. We selected variables with a chi-square probability of 0.10 or smaller for inclusion in BN3. Such a method for variable selection in BNs is not uncommon (Marshall, McClean, Shapcott, Hastie, & Millard, 2001).

Evaluation Measures

In this section we describe three models used as a benchmark for comparison with the BN models. Because this is the first application of BNs to nursing home care quality, a point of comparison is necessary to justify the use of BNs. We also describe the evaluation criteria employed to assess the performance of the BN models and the benchmark models. We use these criteria to select the most appropriate BN model with which to gain insight into nursing home care quality.

The first benchmark model (labeled Reg1 in Tables 1 and 4) is a simple regression and follows a more common approach to the examination of nursing home care quality by utilizing the number of deficiencies as a representation of the QOC (Grabowski, 2001; Harrington & Swan, 2003; Harrington et al., 2000, 2001; O’Neill et al., 2003). In this model, (number of) deficiencies is the independent variable employed to predict QOC (the numeric OIQ scores, in this case). The second benchmark model is a multiple regression (labeled Reg2 in Tables 1 and 4) in which we chose variables by means of a stepwise selection procedure. Again, we use these variables to predict the numeric OIQ scores. To calculate prediction accuracy (subsequently described), we transformed the OIQ score predicted by the regression models into Below Average, Average, or Above Average by using the classification criteria of Rantz and colleagues (2006). The third benchmark model is the QI classification method put forth by Rantz and associates (2004). An explanation of this model is provided in the Background section and Table 2.

Table 4.

Model Performance

Model	Prediction Accuracy	Correlation
BN1	0.494	0.211
BN2	0.568	0.186
BN3	0.560	0.364
Regression1	0.590	0.213
Regression2	0.568	0.293
QI Classification	0.460

Note: BN = Bayesian network; QI = quality indicator.

After we created the BN and benchmark models with the learning data sets, we used two criteria to evaluate them by means of the validation data sets. The criteria—prediction accuracy and correlation—each provide a different perspective as to what associations do or do not exist among variables in the models and the overall QOC.

Prediction accuracy indicates how accurately each model predicted the likelihood of QOC. For each of the 50 facilities in a validation data set, each model was given knowledge of all variables in the model except for the actual QOC. By means of probabilistic inference schemes for BNs, we obtained the probability distribution of QOC. We considered the state of QOC corresponding to the highest value of the probability distribution to be what the model predicted as the overall quality of care. For example, if the distribution for QOC was determined to be {Pr(QOC = Above Average) = 0.2, Pr(QOC = Average) = 0.3, Pr(QOC = Below Average) = 0.5}, then the model predicted the QOC to be below average for this nursing home. A model’s prediction accuracy is then composed of a comparison of the model’s prediction to the actual QOC for each of the 50 nursing homes in a validation data set.

The correlation measure builds upon prediction accuracy by further utilizing the probability distribution of QOC. For the BN models, each nursing home in a validation set is assigned a score of −1 × Pr(QOC = Below Average) + 0 × Pr(QOC = Average) + 1 ×Pr(QOC = Above Average). The resulting scores are then correlated (using the Pearson product–moment correlation) with the actual QOC values (the numeric OIQ scores). For the regression models, the numeric output is simply correlated with the actual QOC values. A higher correlation is indicative of a higher degree of association between the selected variables and the overall QOC, whereas a lower correlation implies the opposite.

Results

Performance of the three BN models, the regression models, and the QI classification model based on the aforementioned criteria are displayed in Table 4. The prediction accuracy and correlation measures represent the average value for the 10 data sets (any measure referenced hereafter is an average value). The following first compares the performance of the BN models among themselves and then compares BN3 (deemed to be the most accurate BN model) with the regression and QI classification models.

In comparison with the other BNs, BN1 (which includes the 24 CHSRA QIs) incurred the lowest prediction accuracy and posted mediocre correlation. This led us to concur with other researchers that Minimum Data Set QIs, when used as the sole variables, are not very effective in a predictive model (Rantz et al., 2004; Schnelle et al., 2004).

BN2 provides insights into the relationships among structural measures of quality and the overall QOC in nursing homes. The inclusion of only structural variables resulted in an improvement of 7.4% in prediction accuracy when BN2 was compared with BN1. This led us to conclude that structural variables tend to have a greater influence on the overall QOC than do QIs. Despite this improvement, the sole consideration of structural variables as predictors of the overall QOC does not present the most effective network.

Variables selected by the chi-square test of independence for BN3 resulted in a marked improvement in correlation and performed as well as or better than the other models with respect to prediction accuracy. An examination of the structure and parameters of BN3, given in the next section, provides additional insight into the factors that affect nursing home care quality.

Additionally, BN3 constitutes a more accurate representation of the factors influencing the quality of care than do the regression and QI classification models. When comparing Reg1 to BN3, we find that Reg1 achieves a higher rate of prediction accuracy.

However, a more in-depth look reveals that Reg1 almost always predicts the QOC to be average for all of the nursing homes. This is confirmed by its low correlation value. Although it is not shown in Table 4, Reg1 also performs poorly with respect to other relative measures of accuracy. Compared with BN3, Reg2 makes a marginal improvement in prediction accuracy but falls short with respect to correlation. The QI classification method substantially underperforms BN3 on prediction accuracy. In addition, the QI classification method often predicts a facility with above average quality as below average quality and vice versa. The rate of these totally wrong predictions is 13.5%; the BNs rarely make such a prediction error.

Discussion

One strength of the BN approach is its ability to provide both qualitative and quantitative insight into the multidimensional makeup of nursing home care quality. Accordingly, we examine BN3 in more detail. The qualitative insight gained from BN3’s structure depicts how various factors interact with each other to produce certain levels of nursing home care quality. We obtain further understanding of these interactions from the quantitative analysis of BN3’s parameters. Considered together, the quantitative and qualitative aspects of the BN afford a more complete perspective of the QOC in nursing homes. We conclude this section by highlighting the differences between BN methodology and the methods employed in other studies.

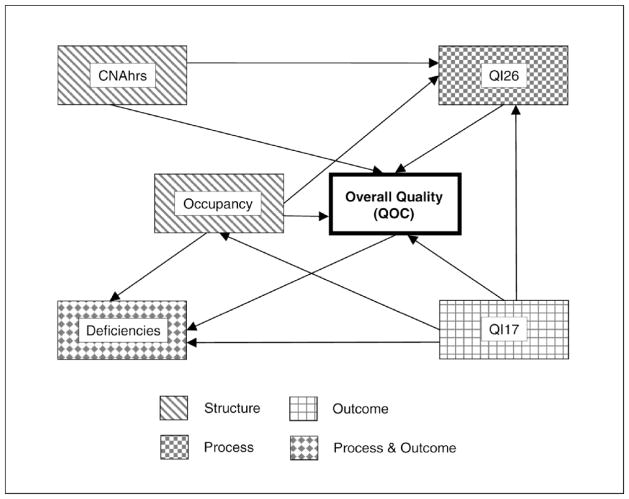
Structure

The structure of BN3 (see Figure 2) indicates that the overall quality of nursing home care is tightly related to five quality measures: certified nurse assistant staffing levels (CNAhrs), occupancy rate (occupancy), prevalence of bedfast residents (QI17), prevalence of daily physical restraints (QI26), and number of deficiencies (deficiencies). The direction of the arc between QOC and deficiencies implies that the overall QOC is indicative of the number of deficiencies issued to a facility. This direction of causation makes sense from an evaluation perspective (i.e., the number of deficiencies results from the QOC provided). Conversely, the arc direction between QOC and the remaining variables implies that CNAhrs, occupancy, QI17, and QI26 each influence the overall quality.

Figure 2.

Bayesian network 3 (BN3).

A further analysis of BN3’s structure reveals that it is composed of structural, process, and outcome measures. As illustrated in Figure 2, CNAhrs and occupancy provide structural quality measures, QI26 provides a process measure, QI17 supplies an outcome measure, and the variable of deficiencies encompasses both process and outcome measures of nursing home care quality. The inclusion of quality measures from each group provides a more complete view of the QOC in nursing facilities.

Insights from the structure of BN3 also have significant practical implications because the identification of factors that directly influence the overall quality of nursing home care provides direction for nursing home administrators.

Parameters

We obtain further understanding of how the quality of nursing home care is influenced by the aforementioned factors through an examination of the parameters of BN3. To illustrate how the parameters provide insight into the QOC, we present excerpts from the conditional probability tables of BN3 in Table 5.

Table 5.

Conditional Probability Table Excerpts

QI17 (Bedfast)	CNAhrs	Occupancy	QI26 (Restraints)	Pr(QOC = Above Average)
Good	Good	High	Good	0.674
Average	Good	High	Good	0.542
Poor	Good	High	Good	0.276
Good	Good	High	Good	0.674
Good	Average	High	Good	0.250
Good	Poor	High	Good	0.155
Poor	Poor	High	Poor	0.150
Poor	Poor	Average	Poor	0.150
Poor	Poor	Low	Poor	0.150

Note: QI = quality indicator; QOC = quality of care; Pr = probability; QI17 (Bedfast) = prevalence of bedfast residents; CNAhrs = the number of CNA hours per resident day; Occupancy = number of beds occupied in a facility; QI26 (Restraints) = prevalence of daily physical restraints.

The first portion of Table 5 inspects the relationship between the overall quality of nursing home care (QOC) and the prevalence of bedfast residents (QI17). To facilitate this examination, we hold the levels of CNAhrs, occupancy, and QI26 constant while we vary the level of QI17. As shown, the probability that the overall quality of nursing home care is above average decreases with an increased likelihood of poor levels of QI17. In other words, the probability of above average QOC declines as the instances of bedfast residents increase. This is an important observation for nursing home administrators seeking to improve the overall QOC. The magnitude of decline is not severe when the level of QI17 is average, and hence, relatively good overall quality of nursing home care can be maintained as long as the level of QI17 is average or good.

We examine the relationship between certified nurse assistant staffing levels and overall QOC in the second portion of Table 5. As before, we hold the other variables at a constant level while we allow the level of CNAhrs to vary. Similar to the relationship between QI17 and QOC, decreased CNA staffing levels significantly shift the probability distribution for the overall QOC. Unlike the previous case, it is imperative to have good CNA staffing levels to keep above average QOC.

The last portion of Table 5 reveals an interesting observation: The occupancy rate has no affect on the overall QOC when QI17, CNAhrs, and QI26 are at their lowest levels. This is apparent from the repetitive probability distribution of QOC as occupancy moves from high to average to low. Therefore, despite a facility’s occupancy rate, one can achieve little or no QOC improvement without first addressing the prevalence of bedfast residents, the prevalence of daily physical restraints, and certified nurse assistant staffing levels. When other factors such as QI17, CNAhrs, and QI26 are held at their middle and upper levels (as opposed to their lower levels in the preceding scenario), the distribution for QOC changes when the occupancy rate is varied (not shown in Table 5).

The analysis just presented demonstrates the complicated nature of nursing home care quality. Although it is evident that some factors have a greater influence on the overall QOC, the effect of other factors is not readily apparent. Knowledge of such interdependencies has important implications for QOC improvement. Nursing home administrators should recognize the relative significance of each factor influencing the overall quality of nursing home care. Accordingly, attention should not only be given to key factors but also to closely related factors in an effort to further improve the overall QOC. In other words, focusing on only one key factor while ignoring closely related factors may not result in the desired outcome.

Methodological Differences

We conclude this section by highlighting the differences between our method and the methods utilized in other studies. As we discussed in the Background section, many studies have been conducted that focus on specific factors influencing nursing home care quality. The methods employed in these studies include ordinary least-squares regression, two-stage and three-stage least-squares regression, Tobit multivariate techniques, logistic regression, and various experimental designs. Studies devoted to aggregating information to measure the overall QOC in nursing homes have used additional methods. These methods include conceptual frameworks, analysis of deficiencies, hierarchical decomposition, factor analysis, path analysis, cluster analysis, structural equation modeling, QI rank and classification techniques, and methods utilizing on-site surveys.

In contrast to methods used in previous studies, this work relies on BN methodology. This methodology is fundamentally different from the other approaches. We use BN methodology in this study for two purposes. First, it serves as a method to aggregate various indicators of quality to predict an overall measure of nursing home care quality. Second, it is used to gain qualitative and quantitative insight into nursing home care quality through an analysis of BN structure and parameters. Thus, this research makes contributions to both types of studies addressed in the Background section.

Conclusion

The analysis and results presented in this article provide researchers, administrators, and policy makers alike with valuable insight into the multidimensional nature of the quality of nursing home care. Consideration of the new perspective afforded by the BN approach, in combination with previous research in this area, will yet provide heretofore unattained insight and understanding. Toward this end, the salient points of this research include the following.

First, a more accurate representation of nursing home care quality is obtained through a mix of structural, process, and outcome measures of quality. Moreover, sole consideration of variables belonging to any of these three categories is not as powerful in describing nursing home care quality as is their collective influence.

Second, a BN framework for nursing home care quality provides both qualitative and quantitative explanations of the factors that influence the overall QOC in nursing homes. Consequently, previously unattained insight into the quality of nursing home care delivery can be afforded through a BN approach.

Third, nursing home administrators seeking to improve the overall QOC should first consider ensuring good staffing levels of certified nurse assistants, decreasing the prevalence of bedfast residents, and reducing the prevalence of daily physical restraints. In addition to improving quality, such efforts are likely to result in a decreased number of deficiencies.

Fourth, the factors affecting nursing home care quality collectively determine the overall quality. Hence, focusing on only key factors without addressing other related factors may not substantially improve the quality of nursing home care.

Future research with BNs may provide additional utility when they are used in conjunction with a larger data set. This would provide more data for structure and parameter learning, which may in turn yield a model that provides more in-depth insights into nursing home care quality. Furthermore, a larger data set would allow for more extensive testing of the networks.

In addition to augmenting the data set, future efforts may benefit from considering further measures for the overall QOC. In this research, we used the OIQ for this purpose. Although the OIQ has provided valuable insights into the QOC in nursing homes, other measures may offer further insight and may yield more accurate results. Despite the need for some improvements in future research, the positive implications of assessing the QOC in nursing homes through a Bayesian network—as illustrated in this analysis—outweigh any limitations or difficulties encountered in this research.