Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs

Summary

Directed acyclic graphs are commonly used to represent causal relationships among random variables in graphical models. Applications of these models arise in the study of physical and biological systems where directed edges between nodes represent the influence of components of the system on each other. Estimation of directed graphs from observational data is computationally NP-hard. In addition, directed graphs with the same structure may be indistinguishable based on observations alone. When the nodes exhibit a natural ordering, the problem of estimating directed graphs reduces to the problem of estimating the structure of the network. In this paper, we propose an efficient penalized likelihood method for estimation of the adjacency matrix of directed acyclic graphs, when variables inherit a natural ordering. We study variable selection consistency of lasso and adaptive lasso penalties in high-dimensional sparse settings, and propose an error-based choice for selecting the tuning parameter. We show that although the lasso is only variable selection consistent under stringent conditions, the adaptive lasso can consistently estimate the true graph under the usual regularity assumptions.

1. Introduction

Graphical models are efficient tools for the study of statistical models through a compact representation of the joint probability distribution of the underlying random variables. The nodes of the graph represent the random variables, while the edges capture the relationships among them. Both directed and undirected edges are used to represent interactions among random variables. However, there is a conceptual difference between these two types of graphs: while undirected graphs are used to represent conditional dependence, directed graphs often represent causal relationships (see Pearl, 2000). Directed acyclic graphs, also known as Bayesian networks, are a special class of directed graphs, where all the edges of the graph are directed and the graph has no cycles. Such graphs are the main focus of this paper and unless otherwise specified, any reference to directed graphs below refers to directed acyclic graphs.

Directed graphs are used in graphical models and belief networks and have been the focus of research in the computer science literature (Pearl, 2000). Important applications involving directed graphs also arise in the study of biological systems, including cell signalling pathways and gene regulatory networks (Markowetz & Spang, 2007).

Estimation of directed acyclic graphs is an NP-hard problem, and estimation of the direction of edges may not be possible due to observational equivalence. Most of the earlier estimation methods involve greedy algorithms that search through the space of possible graphs. A number of methods are available for estimating directed graphs with a small to moderate number of nodes. The max-min hill-climbing algorithm (Tsamardinos et al., 2006), and the PC-algorithm (Spirtes et al., 2000) are two such examples. However, the space of directed graphs grows super-exponentially with the number of nodes (Robinson, 1977), and estimation using search-based methods, especially in high-dimensional settings, becomes impractical. Bayesian methods (e.g Heckerman et al., 1995) are also computationally very intensive and therefore not particularly appropriate for high-dimensional settings. Recently, Kalisch & Bühlmann (2007) proposed an implementation of the PC-algorithm with polynomial complexity in high-dimensional sparse settings. When the variables inherit a natural ordering, estimation of directed graphs is reduced to estimating their structure or skeleton. Applications with a natural ordering of variables include estimation of causal relationships from temporal observations, estimation of transcriptional regulatory networks from gene expression data and settings where additional experimental data can determine the ordering of variables. Examples of such applications are given in § 6.

For Gaussian random variables, conditional independence relations among random variables are represented using an undirected graph, known as the conditional independence graph. The edges of this graph represent conditional dependencies among random variables, and correspond to nonzero elements of the inverse covariance matrix, also known as the precision matrix. Different penalization methods have been recently proposed to obtain sparse estimates of the precision matrix. Meinshausen & Bühlmann (2006) considered an approximation to the problem of sparse inverse covariance estimation using the lasso penalty. They showed, under appropriate assumptions, that their proposed method correctly determines the neighbourhood of each node. Banerjee et al. (2008) and Friedman et al. (2008) explored different aspects of the problem of estimating the precision matrix using the lasso penalty, while Yuan & Lin (2007) considered other choices for the penalty. Rothman et al. (2008) proved consistency in Frobenius norm, as well as in matrix norm, of the ℓ₁-regularized estimate of the precision matrix when p ≫ n, while Lam & Fan (2009) extended their result and considered estimation of matrices related to the precision matrix, including the Cholesky factor of the inverse covariance matrix, using general penalties. Penalization of the Cholesky factor of the inverse covariance matrix has also been considered by Huang et al. (2006) and Levina et al. (2008), who used the lasso penalty in order to obtain a sparse estimate of the inverse covariance matrix. This method is based on the regression interpretation of the Cholesky factorization model and therefore requires the variables to be ordered a priori.

In this paper, we consider the problem of estimating the skeleton of directed acyclic graphs, where the variables exhibit a natural ordering. The known ordering of variables is exploited to reformulate the likelihood as a function of the adjacency matrix of the graph, which results in an efficient algorithm for estimation of structure of directed graphs using penalized likelihood methods. Although the results of this paper are presented for the case of Gaussian observations, the proposed method can also be applied to non-Gaussian observations, provided the underlying causal mechanisms in the network are linear.

2. Representation of directed acyclic graphs

2.1. Background and notation

Consider a graph 𝒢 = (V, E), where V corresponds to the set of nodes with p elements and E ⊂ V × V to the edge set. The nodes of the graph represent random variables X₁,..., X_p and the edges capture the associations among them. An edge is called directed if (j, i) ∉ E whenever (i, j) ∈ E, and undirected when (i, j) ∈ E if and only if (j, i) ∈ E. We denote by pa_i the set of parents of node i and for j ∈ pa_i, we denote j → i. The skeleton of a directed graph is the undirected graph that is obtained by replacing directed edges in E with undirected ones. We represent E using the adjacency matrix A of the graph; i.e. a p × p matrix whose (j, i)th entry is nonzero if there is an edge between nodes j and i.

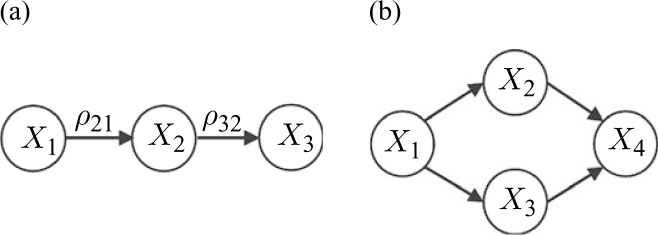
The estimation of directed graphs is a challenging problem due to the so-called observational equivalence with respect to the same probability distribution. More specifically, regardless of the sample size, it may not be possible to infer the direction of causation among random variables from observational data. As an illustration, consider the simple graph in Fig. 1(a). Reversing the direction of all edges of the graph results in a new graph, which is isomorphic to the original graph, and hence not distinguishable from observations alone.

Fig. 1.

Directed graphs. (a) A simple directed graph; and (b), an illustration of observational equivalence in directed graphs.

The second challenge in estimating directed graphs is that conditional independence among random variables may not reveal the skeleton. The notion of conditional independence in directed graphs is represented using the concept of d-separation (Pearl, 2000), or equivalently, the moral graph, obtained by removing the directions of the edges and joining the parents of each node (Lauritzen, 1996). Therefore, estimation of the conditional independence structure reveals the structure of the moral graph, which includes additional edges between parents of each node. For instance, X₂ and X₃ are connected in the moral graph of the graph in Fig. 1(b).

2.2. The latent variable model

The causal effect of random variables in a directed acyclic graph is often explained using structural equation models (Pearl, 2000). In particular,

$$X_i=f_i({\text{pa}}_i,\hspace{0.17em}{Z}_i)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}p),$$ (1)

where the random variables Z_i are the latent variables representing the unexplained variation in each node. To model the association among the nodes, we consider a simplification of (1) with linear f_i. More specifically, let ρ_ij represent the effect of node j on i for j ∈ pa_i. Then

$$X_i=\sum _{j\in {\text{pa}}_i}{\rho }_{ij}{X}_j+Z_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}p).$$ (2)

If the random variables are Gaussian, equations (1) and (2) are equivalent, in the sense that ρ_ij are the coefficients of the linear regression model of X_i on X_j, for j ∈ pa_i. It is known in the normal case that ρ_ij = 0, if j ∉ pa_i.

Consider the graph in Fig. 1(a); denoting the influence matrix of the graph by Λ, (2) can be written in compact form as X = Λ Z, where for the example above, we have

$$\mathrm{\Lambda }=\left(\begin{array}{ccc}1& 0& 0\\ {\rho }_{12}& 1& 0\\ {\rho }_{12}{\rho }_{23}& {\rho }_{23}& 1\end{array}\right).$$

Let the latent variables Z_i be independent with mean μ_i and variance ${\sigma }_i^2$. Then, E(X) = Λμ and Σ = var(X) = ΛDΛ^T, where D = diag ( ${\sigma }_i^2$) and Λ^T denotes the transpose of the matrix Λ.

The following result from Shojaie & Michailidis (2009) establishes the relationship between the influence matrix Λ, and the adjacency matrix A of the graph. The second part of the lemma establishes a compact relationship between Λ and A in the case of directed graphs, which is explored in § 3 to directly formulate the problem of estimating the skeleton of the graph.

Lemma 1. For any graph 𝒢, with the adjacency matrix A, and influence matrix Λ,

1. Λ = A⁰ + A¹ + A² + … = ${\sum }_{r=0}^{\infty }{A}^r$, where A⁰ ≡ I.

2. If 𝒢 is a directed acyclic graph, then Λ has full rank and Λ = (I – A)⁻¹.

Remark 1. Part (ii) of Lemma 1 and the fact that Σ = ΛDΛ^T imply that for any directed acyclic graph, if D_ii > 0 for all i, then Σ is full rank. More specifically, let ϕ_j (Σ) denote the jth eigenvalue of matrix Σ. Then, ϕ_min(Σ) > 0, or ϕ_max(Σ⁻¹) < ∞. Similarly, since Σ⁻¹ = Λ^−T D⁻¹Λ⁻¹, then Λ having full rank implies that ϕ_min(Σ⁻¹) > 0, or equivalently ϕ_max(Σ) < ∞. This result also applies to all subgraphs of a directed graph.

The properties of the proposed latent variable model established in Lemma 1 are independent of the choice of probability distribution. In fact, since the latent variables Z_i in (2) are assumed independent, given the entries of the adjacency matrix, the distribution of each random variable X_i in the graph only depends on the values of pa_i. Hence, regardless of the choice of the probability distribution, the joint distribution of the random variables is compatible with 𝒢 (Pearl, 2000, p. 16). Therefore, based on the equivalence of conditional independence and d-separation, if the joint probability distribution of random variables on a directed graph is generated according to the latent variable model (2), zeros of the adjacency matrix, A, determine conditional independence relations among random variables. As mentioned before, under the normality assumption, the latent variable model is equivalent to the general structural equation model. Although we focus on Gaussian random variables in the remainder of this paper, the estimation procedure proposed in § 3 can be applied to a variety of other distributions, if one is willing to assume the linear structure in equation (2).

3. Penalized likelihood estimation of directed graphs

3.1. Problem formulation

Consider the latent variable model of § 2.2 and denote by 𝒳 the n × p data matrix. We assume, without loss of generality, that the X_i s are centred and scaled, so that μ_i = 0 and ${\sigma }_i^2=1\hspace{0.17em}(i=1,\hspace{0.17em}\dots ,\hspace{0.17em}p)$.

Denote by Ω ≡ Σ⁻¹ the precision matrix of a p-vector of Gaussian random variables and consider a general penalty function J (Ω). The penalized estimate of Ω is then given by

$$\widehat{\mathrm{\Omega }}=\underset{\mathrm{\Omega }\succ 0}{\text{arg}\hspace{0.17em}\text{min}}\{-\text{log}\hspace{0.17em}\text{det}(\mathrm{\Omega })+\text{tr}(\mathrm{\Omega }S)+\lambda J(\mathrm{\Omega })\},$$ (3)

where S = n⁻¹ 𝒳^T 𝒳 denotes the empirical covariance matrix and λ is the tuning parameter controlling the size of the penalty. Applications in biological and social networks often involve sparse networks. It is therefore desirable to find a sparse solution for (3). This becomes more important in the small n, large p setting, where the unpenalized solution is unreliable. The lasso penalty and the adaptive lasso penalty (Zou, 2006) are singular at zero and therefore result in sparse solutions. We consider these two penalties in order to find a sparse estimate of the adjacency matrix. However, the optimization algorithm proposed here can also be used with other choices of penalty function, if the penalty is applied to each individual component of the adjacency matrix.

Using the latent variable model of § 2.2, and the relationship between the covariance matrix and the adjacency matrix of directed graphs established in Lemma 1, the problem of estimating the adjacency matrix of the graph can be directly formulated as an optimization problem based on A. Specifically, if the underlying graph is directed, and the ordering of the variables is known, then, A is a lower triangular matrix with zeros on the diagonal. Let 𝒜 ={A : A_ij = 0, j ⩾ i}. Then, using the facts that det(A) = 1 and ${\sigma }_i^2=1$, A can be estimated by:

$$\widehat{A}=\underset{A\in 𝒜}{\text{arg}\hspace{0.17em}\text{min}}[\text{tr}\{{(I-A)}^{\text{T}}(I-A)S\}+\lambda J(A)].$$ (4)

In this paper, we consider the general weighted lasso problem, where

$$J(A)=\sum _{i,\hspace{0.17em}j=1:p,\hspace{0.17em}j<i}{w}_{ij}|A_{ij}|.$$

The lasso and adaptive lasso problems are special cases of this general penalty. In the case of the lasso, w_ij = 1. In the original proposal of Zou (2006), the weights for the adaptive lasso are obtained by setting w_ij =|Ã_ij|^−γ, for some initial estimate of the adjacency matrix à and some power γ. We consider the following modification of the original weights:

$$w_{ij}=1\hspace{0.17em}\vee \hspace{0.17em}|{\tilde{A}}_{ij}{|}^{-\gamma },$$ (5)

where the initial estimates à are obtained from the regular lasso estimates, and x ∨ y represents the maximum of x and y. Aside from the truncation of weights from below, which is implemented to facilitate the study of asymptotic properties, the main difference between the adaptive lasso penalty using (5) and the proposal of Zou (2006) is the use of the lasso estimates to construct the weights. In §§ 4 and 5, we show that this modification, which could also be considered a two-stage or iterated lasso penalty, results in improvements over the regular lasso penalty in terms of both asymptotic properties and numerical performance.

The objective functions for the lasso and adaptive lasso problems are convex. However, since the ℓ₁ penalty is nondifferentiable, these problems can be reformulated using matrices A₊ = max(A, 0) and A_– = – min(A, 0). To that end, let W be the p × p matrix of weights for the adaptive lasso, or the matrix of ones for the lasso estimation problem. Problem (4) can then be formulated as

$$\underset{A_{+},\hspace{0.17em}{A}_{-}\succcurlyeq 0}{\text{min}}\text{tr}\{S{(I-A_{+}+A_{-})}^{\text{T}}(I-A_{+}+A_{-})+\lambda (A_{+}+A_{-})W+\mathrm{\Delta }(A_{+}+A_{-})1_{u^{+}}\},$$ (6)

where ≽ 0 is interpreted componentwise, Δ is a large positive number and 1_u⁺ is the indicator matrix for upper triangular elements of a p × p matrix, including the diagonal elements. The last term of the objective function, tr {Δ(A₊ + A_–)1_u⁺}, prevents the upper triangular elements of the matrices A₊ and A_– being nonzero.

Problem (6) corresponds to a quadratic optimization problem with nonnegativity constraints and can be solved using standard interior point algorithms. However, such algorithms do not scale well with dimension and are only applicable if p ranges in the hundreds. In § 3.2, we present an alternative formulation of the problem, which leads to more efficient algorithms.

3.2. Optimization algorithm

Consider again the problem of estimating the adjacency matrix of directed graphs with the general weighted lasso penalty. Let 𝔞_i be the ith row of matrix A, and denote by l^- the set of indices up to l – 1, i.e. l^-={j : j = 1,..., l – 1}. Then (4) can be written as

$$\widehat{A}=\underset{A\in 𝒜}{\text{arg}\hspace{0.17em}\text{min}}\left\{\sum _{i=1}^p({𝔞}_{i}S{𝔞}_i^T-2{𝔞}_i{S}_i+\lambda |{𝔞}_i|W_i)\right\}.$$ (7)

It can be seen that the objective function in (7) is separable and therefore it suffices to solve the optimization problem over each row of matrix A. Then, taking advantage of the lower triangular structure of A and noting that A₁₁ = 0, solving (7) is equivalent to solving the p – 1 optimization problems:

$${\widehat{A}}_{i,i^{-}}=\underset{\theta \in {ℝ}^{i-1}}{\text{arg}\hspace{0.17em}\text{min}}\left\{{\theta }^T{S}_{i^{-},i^{-}}\theta -2S_{i,i^{-}}\theta +\lambda \sum _{j=1}^{i-1}|{\theta }_j|w_{ij}\right\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=2,\hspace{0.17em}\dots ,\hspace{0.17em}p).$$ (8)

In addition, S_i^-,i^- = n⁻¹(𝒳_i^-)^T𝒳_i^- and S_i,i^- = n⁻¹(𝒳_i)^T𝒳_i^-, and hence the problem in (8) can be reformulated as the following ℓ₁-regularized least-squares problems:

$${\widehat{A}}_{i,i^{-}}=\underset{\theta \in {ℝ}^{i-1}}{\text{arg}\hspace{0.17em}\text{min}}\left\{n^{-1}{\Vert {𝒳}_i-{𝒳}_{i^{-}}\theta \Vert }_2^2+\lambda \sum _{j=1}^{i-1}|{\theta }_j|w_{ij}\right\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=2,\hspace{0.17em}\dots \hspace{0.17em},p).$$ (9)

The formulation in (9) indicates that the ith row of matrix A includes the coefficient of projection of X_i on X_j (j = 1,..., i – 1), in agreement with the discussion in § 2.2. It also reveals a connection between estimation of the underlying graphs and the neighbourhood selection approach of Meinshausen & Bühlmann (2006): when the underlying graph is directed, the approximate solution of the neighbourhood selection problem is exact, if the regression model is fitted on the set of parents of each node instead of all other nodes in the graph.

Using (9), the problem of estimating directed graphs can be solved very efficiently. In fact, it suffices to solve p – 1 lasso problems for estimation of least-squares coefficients, with dimensions ranging from 1 to p – 1. To solve these problems, we use the efficient pathwise coordinate optimization algorithm of Friedman et al. (2007), implemented in the R-package glmnet (R Development Core Team, 2010). The proposed procedure is summarized in Algorithm 1.

Algorithm 1. Penalized likelihood estimation of directed graphs.

1. Given the ordering 𝒪, order the columns of observation matrix 𝒳 in increasing order.

2. For i = 2, 3,..., p,

   • 2.1. Denote y = 𝒳_i, X = 𝒳_i^-. Given the weight matrix W, let w = W_i,i^-, and solve

$${\widehat{A}}_{i,i^{-}}=\text{arg}\hspace{0.17em}\text{min}\left\{n^{-1}{\Vert y-X\theta \Vert }_2^2+{\lambda }_i\sum _{j=1}^{i-1}|{\theta }_j|w_j\right\}$$

3.3. Analysis of computational complexity

As mentioned in § 1, the space of all possible directed graphs is super-exponential in the number of nodes and hence it is not surprising that the PC-algorithm, without any restriction on the space, has exponential complexity. Kalisch & Bühlmann (2007) recently proposed an efficient implementation of the PC-algorithm for sparse graphs; its complexity when the maximal neighbourhood size q is small, is bounded with high probability by O(p^q). Although this is a considerable improvement over the original algorithm, in many applications it can become fairly expensive. For instance, gene regulatory networks and signaling pathways include many hub genes, which lead to large values for q.

The reformulation of the directed graph estimation problem in (9) requires solving p – 1 lasso regression problems. The cost of solving a lasso problem comprised of k covariates and n observations using the pathwise coordinate optimization algorithm is O(nk); hence, the total cost of estimating the adjacency matrix of the graph is O(np²), which is the same as the cost of calculating the empirical covariance matrix S. Moreover, the formulation in (9) includes a set of non-overlapping subproblems. Therefore, for problems with very large number of nodes and/or observations, the performance of the algorithm can be further improved by parallelizing the estimation of these subproblems. The adaptive lasso version of the problem is similarly solved using the modification of the regular lasso problem proposed in Zou (2006), which results in the same computational cost as the regular lasso problem.

To evaluate the performance of these algorithms, we compared the average CPU time, over 10 simulation runs, for estimation of directed graphs with different numbers of nodes, p = 100, 1000, and different sample sizes, n = 100, 1000. The computational time for the PC-algorithm increases with larger values of the average neighbourhood size and the significance level α. Therefore, to control the computational complexity of the PC-algorithm, these parameters are set to 5 and 0.01, respectively. In addition, in order to compare equivalent quantities, we only consider the CPU time that the PC-algorithm requires for estimation of the graph skeleton. Based on this simulation study, while for p = 100, the computation time for the PC-algorithm is comparable to the time for the penalized likelihood algorithm, in a graph with p = 1000 and n = 1000, the average CPU time for the PC-algorithm could be up to two orders of magnitude larger than the equivalent time for Algorithm 1.

4. Asymptotic properties

4.1. Preliminaries

Next, we establish theoretical properties of the lasso and adaptive lasso estimates of the adjacency matrix of directed graphs. Asymptotic properties of the lasso-type estimates with fixed design matrices have been studied by a number of researchers (Knight & Fu, 2000; Zou, 2006; Huang et al., 2008), while random design matrices have been considered by Meinshausen & Bühlmann (2006). Rothman et al. (2008) and Lam & Fan (2009), among others, have studied asymptotic properties of estimates of covariance and precision matrices.

As discussed in § 3.2, the problem of estimating the adjacency matrix of a directed graph is equivalent to solving the p – 1 non-overlapping penalized least-squares problems described in (9). In order to study the asymptotic properties of the proposed estimators, we focus on the asymptotic consistency of network estimation, i.e. the probability of correctly estimating the network structure, in terms of Type I and Type II errors. We allow the total number of nodes in the graph to grow as an arbitrary polynomial function of the sample size, while assuming that the true underlying network is sparse.

4.2. Assumptions

Let X = (X₁,..., X_p) be a collection of p zero-mean Gaussian random variables with covariance matrix Σ, and let 𝒳 and S be defined as in § 3.1. To simplify the notation, denote by θⁱ = A_i,i^- the entries of the ith row of A to the left of the diagonal. Further, let θ^i,ℐ be the estimate for the ith row, with values outside the set of indices ℐ set to zero; i.e. θ^i,ℐ ≡ A_i,i^- and A_{i, j} = 0, j ∉ ℐ.

The following assumptions are used in establishing the consistency of network estimation.

• Assumption 1. For some a > 0, p = p(n) = O(n^a) as n → ∞, and there exists a 0 ⩽ b < 1 such that max_i∈V card (pa_i) = O(n^b)as n → ∞.

• Assumption 2. There exists ν > 0 such that for all n ∈ 𝑁 and all i ∈ V, var(X_i | X_i^-) ⩾ ν.

• Assumption 3. There exists δ > 0 and some ξ > b, with b defined above, such that for all i ∈ V and for every j ∈ pa_i, |π_ij | ⩾ δn^{−(1−ξ)/2}, where π_ij is the partial correlation between X_i and X_j after removing the effect of the remaining variables.

• Assumption 4. There exists Ψ < ∞ such that for all n ∈ ℕ and every i ∈ V and j ∈ pa_i, ‖θ^j,pa_i‖₂ ⩽ Ψ.

• Assumption 5. There exists κ < 1 such that for all i ∈ V and j ∉ pa_i, $|{\sum }_{k\in {\text{pa}}_i}\text{sign}\hspace{0.17em}({\theta }_k^{i,{\text{pa}}_i}){\theta }_k^{j,{\text{pa}}_i}|<\kappa$.

Assumption 1 determines the permissible rates of increase in the number of variables and the neighbourhood size, as a function of n, Assumption 2 prevents singular or near-singular covariance matrices, and Assumption 3 guarantees that true partial correlations are bounded away from zero.

Assumption 4 limits the magnitude of the shared ancestral effect between each node in the network and any of its parents. This is less restrictive than the equivalent assumption for the neighbourhood selection problem, where the effects over all neighbouring nodes are assumed to be bounded. In fact, in the case of gene regulatory networks, empirical data indicate that the average number of upstream-regulators per gene is less than two (Leclerc, 2008). Thus, the number of parents of each node is small, while each hub node can affect many downstream nodes.

Assumption 5 is referred to as neighbourhood stability and is equivalent to the irrepresentability assumption of Huang et al. (2008). It has been shown that the lasso estimates are not in general variable selection consistent if this assumption is violated. Huang et al. (2008) considered the adaptive lasso estimates with general initial weights and proved their variable selection consistency under a weaker form of irrepresentability assumption, referred to as adaptive irrepresentability. We will show that when the initial weights for the adaptive lasso are derived from the regular lasso estimates as in (5), the assumption of neighbourhood stability, and the less stringent Assumption 4 are not required for establishing variable selection consistency of the adaptive lasso. This relaxation in assumptions required for variable selection consistency, is a result of the consistency of the regular lasso estimates, and the special structure of directed graphs. Similar results can be obtained for the adaptive lasso estimates of the precision matrix, as well as regression models with fixed and random design matrices, under additional mild assumptions.

4.3. Asymptotic consistency of directed graph estimation

Our first result studies the variable selection consistency of the lasso estimate. In this theorem, (i) corresponds to sign consistency, (ii) and (iii) establish control of Type I and Type II errors and (iv) addresses the consistency of network estimation. We denote by Ê the estimate of the edge set of the graph, and by x ∼ y the asymptotic equivalence between x and y.

Theorem 1. Suppose that Assumption 1–5 hold and λ ∼ dn^{−(1−ζ)/2} for some b < ζ <ξ and d > 0. Then for the lasso estimate there exist constants c_(i),..., c_(iv) > 0 such that for all i ∈ V, as n → ∞,

1. pr{sign ( ${\widehat{\theta }}_j^{i,{\text{pa}}_i}$) = sign ( ${\theta }_j^{i,{\text{pa}}_i}$) for all j ∈ pa_i}= 1 – O{exp (–c_(i)n^ζ)},

2. pr( ${\widehat{\text{pa}}}_i\subseteq {\text{pa}}_i$) = 1 – O{exp (–c_(ii)n^ζ)},

3. pr( ${\text{pa}}_i\subseteq {\widehat{\text{pa}}}_i$) = 1 – O{exp (–c_(iii)n^ζ)} and

4. pr(Ê = E) = 1 – O{exp (–c_(iv)n^ζ)}.

Proof. The proof of this theorem follows from arguments similar to those presented in Meinshausen & Bühlmann (2006) with minor modifications and replacing conditional independence for undirected graphs with d-separation for directed graphs, and hence is omitted.

The next result establishes similar properties for the adaptive lasso estimates, without the assumptions of neighbourhood stability. The proof of Theorem 3 makes use of the consistency of sparse estimates of the Cholesky factor of covariance matrices, established in Theorem 9 of Lam & Fan (2009). For completeness, we restate a simplified version of the theorem for our lasso problem, for which σ_i = 1 (i = 1,... p), and the eigenvalues of the covariance matrix are bounded; see Remark 1. Throughout this section, we denote by s the total number of nonzero elements of the true adjacency matrix A.

Theorem 2 (Lam & Fan 2009). If n⁻¹(s + 1) log p = o(1) and λ = O{(log p/n)^1/2}, then ‖Â – A‖_F = O_p{(n⁻¹s log p)^1/2}.

It can be seen from Theorem 2 that the lasso estimates are consistent as long as n⁻¹(s + 1) log p = o(1). To take advantage of this result, we replace Assumption 1 with the following assumption.

Assumption 1′. For some a > 0, p = p(n) = O(n^a) as n → ∞. Also, max_i∈V card (pa_i) = O(n^b) as n → ∞, where sn^2b−1 log n = o(1) as n → ∞.

Assumption 1′ further restricts the number of parents of each node and also enforces a restriction on the total number of nonzero elements of the adjacency matrix. Condition sn^2b−1 log n = o(1) implies that b < 1/2. Therefore, although the consistency of the adaptive lasso in Theorem 3 is established without making any further assumptions on the structure of the network, it is achieved at the price of requiring a higher degree of sparsity in the network.

Theorem 3. Consider the adaptive lasso estimation problem, where the initial weights are calculated using the regular lasso estimates of the adjacency matrix of the graph in (9). Suppose Assumptions 1′, 2 and 3 hold and λ ∼ dn^{−(1−ζ)/2} for some b < ζ < ξ and d > 0. Also suppose that the initial lasso estimates are found using a penalty parameter λ⁰ that satisfies λ⁰ = O{(log p/n)^1/2}. Then there exist constants c_(i),..., c_(iv) > 0 such that for all i ∈ V, as n → ∞, (i)–(iv) in Theorem 1 hold.

Proof. See the Appendix.

4.4. Choice of the tuning parameter

Both lasso and adaptive lasso estimates of the adjacency matrix depend on the choice of the tuning parameter λ. Different methods have been proposed for selecting the value of the tuning parameter, including crossvalidation (Rothman et al., 2008) and the Bayesian information criterion (Yuan & Lin, 2007). However, choices of λ that result in the optimal classification error do not guarantee a small error for network reconstruction. We propose next a choice of λ for the general weighted lasso problem with weights w_ij. Let $Z_q^{*}$ denote the (1 – q)th quantile of standard normal distribution, and define

$${\lambda }_i(\alpha )=2n^{-1/2}{Z}_{\alpha /\{2p(i-1)\}}^{*}.$$ (10)

The following result establishes that such a choice controls the probability of falsely joining two distinct ancestral sets, defined next.

Definition 1. For every node i ∈ V, the ancestral set of node i, AN_i, consists of all nodes j, such that j is an ancestor of i or i is an ancestor of j or i and j have a common ancestor k.

Theorem 4. Under the assumptions of Theorems 1 and 3 above, for the lasso and adaptive lasso, respectively, for all n ∈ 𝑁 the solution of the general weighted lasso estimation problem with tuning parameter determined in (10) satisfies

$$\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}i\in V:{\widehat{AN}}_i⊈A{N}_i)⩽\alpha .$$

Proof. See the Appendix.

Theorem 4 is true for all values of p and n, but it does not provide any guarantee for the probability of false positive error for individual edges in the graph. We also need to determine the optimal choice of penalty parameter λ⁰ for the first phase of the adaptive lasso, where the weights are estimated using the lasso. Since the goal of the first phase is to achieve prediction consistency, crossvalidation can be used to determine the optimal choice of λ⁰. On the other hand, it is easy to see that the error-based proposal in (10) satisfies the requirement of Theorem 2 and can therefore be used to define λ⁰. It is, however, recommended to use a higher value of significance level in estimating the initial weights, in order to prevent an oversparse solution.

5. Performance analysis

5.1. Preliminaries

In this section, we consider examples of estimating directed graphs of a varying number of edges from randomly generated data. To randomly generate data, one needs to generate lower-triangular adjacency matrices with sparse nonzero elements, ρ_ij. In order to control the computational complexity of the PC-algorithm, we use the random directed graph generator in the R-package pcalg (Kalisch & Bühlmann, 2007), which generates graphs with given values of the average neighbourhood size. The sparsity levels of graphs with different sizes are set according to the theoretical bounds in § 4, as well as the recommendations of Kalisch & Bühlmann (2007) for the neighbourhood size. We use an average neighbourhood size of five, while limiting the total number of true edges to be equal to the sample size n.

Different measures of structural difference can be used to evaluate the performance of estimators. The structural Hamming distance represents the number of edges that are not in common between the estimated and true graphs, i.e. shd = card (Ê\E) + card (E\Ê), where Ê and E are defined as in Theorem 1. The main drawback of this measure is its dependency on the number of nodes, as well as the sparsity of the network. The second measure of goodness of estimation considered here is the Matthew’s correlation coefficient, which is commonly used to assess the performance of binary classification methods, and is defined as

$$\text{MCC}=\frac{(\text{TP}\times \text{TN})-(\text{FP}\times \text{FN})}{{\{(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\text{FP})(\text{TN}+\text{FN})\}}^{1/2}},$$ (11)

where tp, tn, fp and fn denote the total number of true positive, true negative, false positive and false negative edges, respectively. The value of Matthew’s correlation coefficient ranges from −1 to 1 with larger values corresponding to better fits, and −1 and 1 representing worst and best fits, respectively. Finally, in order to compare the performance of different estimation methods with theoretical bounds established in § 4.3, we also report the values of true and false positive rates.

The performances of the PC-algorithm and our proposed estimators based on the choice of tuning parameter in (10), vary with different values of significance level α. In the following experiments, we first investigate the appropriate choice of α for each estimator. We then compare the performance of the estimators with an optimal choice of α. The results reported in this section are based on estimates obtained from 100 replications; to offset the effect of numerical instability, we consider an edge present only if |Â_ij| > 10⁻⁴.

5.2. Estimation of directed graphs from normally distributed observations

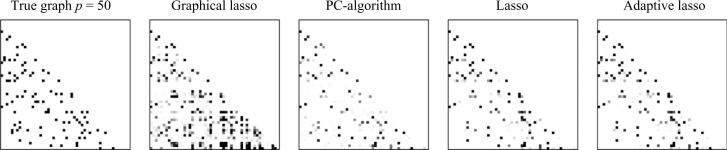
We begin with an example that illustrates the differences between estimation of directed graphs and conditional independence graphs. The first two images in Fig. 2 represent a randomly generated directed graph of size p = 50 and the greyscale image of the average precision matrix estimated based on a sample of size n = 100 using the graphical lasso algorithm (Friedman et al., 2008). The image is obtained by calculating the proportion of times that a specific edge is present in 100 replications. To control the probability of falsely connecting two components of the graph, the value of the tuning parameter for the graphical lasso is defined based on the error-based proposal in Banerjee et al. (2008, Theorem 2). It can be seen that the conditional independence graph has many more edges, 8% false positive rate compared to 1% for the lasso and adaptive lasso, and does not reveal the true structure of the underlying directed graph. Therefore, although methods of estimating conditional independence graphs are computationally efficient, they should not be used in applications, such as estimation of gene regulatory networks, where the underlying graph is directed.

Fig. 2.

True directed graph along with estimates from Gaussian observations. The greyscale represents the percentage of inclusion of edges.

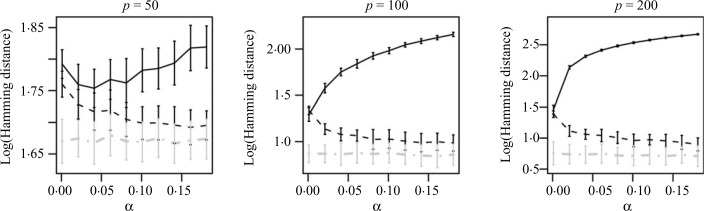
In simulations throughout this section, the sample size is fixed at n = 100, and estimators are evaluated for an increasing number of nodes, p = 50, 100, 200. Figure 3 shows the mean and standard deviation of the Hamming distances, expressed in base 10 logarithmic scale, for estimates based on the PC-algorithm, as well as the proposed lasso, and adaptive lasso methods for different values of the tuning parameter α and different network sizes. It can be seen that for all values of p and α, the adaptive lasso estimate produces the best results, and the proposed penalized likelihood methods outperform the PC-algorithm. This difference becomes more significant as the size of the network increases.

Fig. 3.

Logarithm, in base 10, of the Hamming distances for estimation of directed graphs using the PC-algorithm (black solid), lasso (black dashes) and adaptive lasso (grey dot-dashes) from normal observations.

As mentioned in § 2, it is not always possible to estimate the direction of the edges of a directed graph and therefore, the estimate from the PC-algorithm may include undirected edges. Since our penalized likelihood methods assume knowledge of the ordering of variables and estimate the structure of the network, in the simulations considered here, we only estimate the skeleton of the network using the PC-algorithm. We then use the ordering of the variables to determine the direction of the edges. The performance of the PC-algorithm for estimation of partially completed directed graphs may therefore be worse than the results reported here.

In our simulation results, observations are generated according to the linear structural equation model (2) with standard normal latent variables and ρ_ij = ρ = 0.8. Additional simulation studies with different values of σ and ρ indicate that changes in σ do not have a considerable effect on the performance of the proposed models. As the magnitude of ρ decreases, the performance of the proposed methods, as well as the PC-algorithm deteriorates, but the findings remain unchanged.

The above simulation results suggest that the optimal performance of the PC-algorithm is achieved when α = 0.01. The performance of the lasso and adaptive lasso methods is less sensitive to the choice of α; however, a value of α = 0.10 seems to deliver more reliable estimates. Our extended simulations indicate that the performance of the adaptive lasso does not vary significantly with the value of power γ and therefore we present the results for γ = 1.

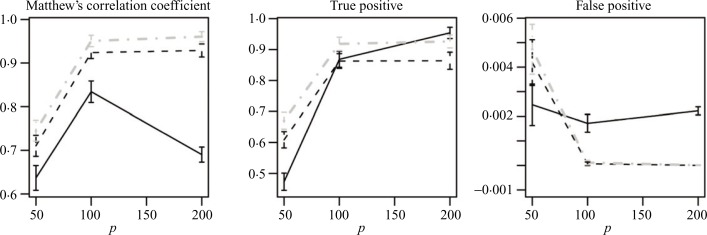
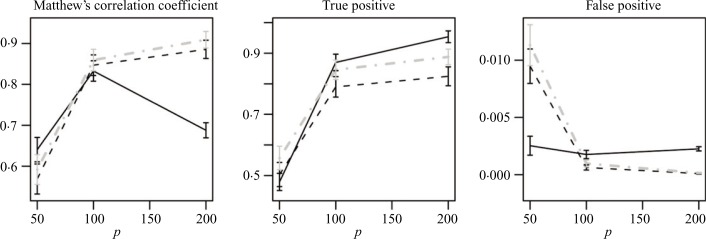
Figure 2 represents images of estimated and true directed graphs created based on the above considerations for tuning parameters for p = 50. Similar results were also observed for larger values of p, p = 100, 200, and are excluded due to space considerations. Plots in Fig. 4 compare the performance of the three methods with the optimal settings of tuning parameters, over a range of values of p. It can be seen that the values of Matthew’s correlation coefficient confirm the above findings based on the Hamming distance. On the other hand, false positive and true positive rates only focus on one aspect of estimation at a time and do not provide a clear distinction between the methods.

Fig. 4.

Matthew’s correlation coefficient, true and false positives for estimation of directed graphs using the PC-algorithm (black solid), lasso (black dashes) and adaptive lasso (grey dot-dashes) from normal observations.

The representation of conditional independence in directed graphs adapted in our algorithm is not restricted to normally distributed random variables; if the underlying structural equations are linear, the method proposed in this paper can correctly estimate the underlying graph. In order to assess the sensitivity of the estimates to the underlying distribution, we performed two simulation studies with nonnormal observations. In both simulations, observations were generated according to a linear structural model. In the first simulation, the latent variables were generated from a mixture of a standard normal and a t-distribution with three degrees of freedom, while in the second simulation, a t-distribution with four degrees of freedom was used. The performance of the proposed algorithm for nonnormal observations was similar to the case of Gaussian observations, with the adaptive lasso providing the best estimates, and the performance of penalized methods improving in sparse settings.

5.3. Sensitivity to perturbations in the ordering of the variables

Algorithm 1 assumes a known ordering of the variables. The superior performance of the proposed penalized likelihood methods in comparison to the PC-algorithm may be explained by the fact that additional information about the order of the variables significantly simplifies the problem of estimating directed graphs. Therefore, when such additional information is available, estimates using the PC-algorithm suffer from a disadvantage. However, as the underlying network becomes more sparse, the network includes fewer complex structures and the ordering of variables should play a less significant role.

Next, we study the performances of the proposed methods, and the PC-algorithm in problems where the ordering of variables is unknown. To this end, we generate normally distributed observations from the latent variable model of § 2.2. We then randomly permute the order of variables in the observation matrix and use the permuted matrix to estimate the original directed graph. Figure 5 illustrates the performance of the three methods for choices of α described in § 5.2. It can be seen that for small, dense networks, the PC-algorithm outperforms the proposed methods. This is expected since the change in the order of variables causes the proposed algorithm to include unnecessary moral edges, while failing to recognize some of the existing associations. However, as the size of the network and correspondingly the degree of sparsity increase, the local structures become simpler and therefore the ordering of the variables becomes less crucial. Thus, the performance of penalized likelihood algorithms is improved compared to that of the PC-algorithm. For the high-dimensional sparse case, where the computational cost of the PC-algorithm becomes more significant, the penalized likelihood methods provide better estimates.

Fig. 5.

Matthew’s correlation coefficient, true and false positives for estimation of directed graphs using the PC-algorithm (black solid), lasso (black dashes) and adaptive lasso (grey dot-dashes) with random ordering.

6. Real data application

6.1. Analysis of cell signalling pathway data

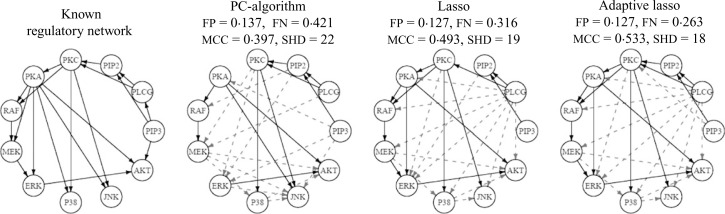
Sachs et al. (2003) carried out a set of flow cytometry experiments on signaling networks of human immune system cells. The ordering of the connections between pathway components was established based on perturbations in cells using molecular interventions and we consider it to be known a priori. The dataset includes p = 11 proteins and n = 7466 samples.

Friedman et al. (2008) analyzed this dataset using the graphical lasso algorithm. They estimated the graph for a range of values of the ℓ₁ penalty and reported moderate agreement, around 50% false positive and false negative rates, between one of their estimates and the findings of Sachs et al. (2003). True and estimated signaling networks using the PC-algorithm, with α = 0.01, and the lasso and adaptive lasso algorithms, with α = 0.1, along with the corresponding performance measures, are given in Fig. 6. The estimated network using the PC-algorithm includes a number of undirected edges. As in the simulation studies, we only estimate the structure of the network using the PC-algorithm and determine the direction of edges by enforcing the ordering of nodes. It can be seen that the adaptive lasso and lasso provide estimates that are closer to the true structure.

Fig. 6.

Known and estimated networks for human cell signalling data. True and false edges are marked with solid and dashed arrows, respectively. mcc, Matthew’s correlation coefficient; fn, False negative; fp, False positive; shd, structural Hamming distance.

6.2. Transcription regulatory network of E. coli

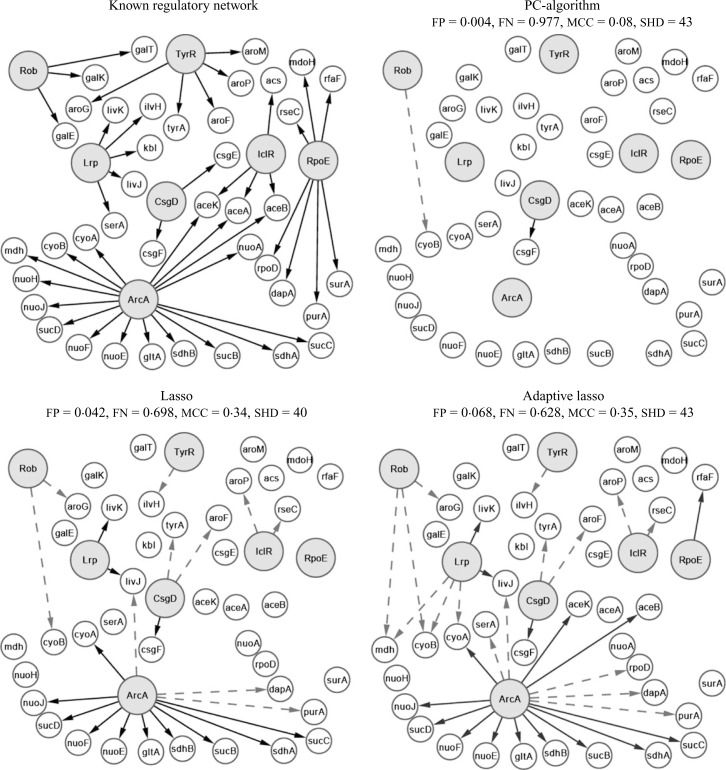
Transcriptional regulatory networks play an important role in controlling the gene expression in cells and incorporating the underlying regulatory network results in more efficient estimation and inference (Shojaie & Michailidis, 2009, 2010). Kao et al. (2004) proposed the network component analysis method to infer the transcriptional regulatory network of Escherichia coli, E. coli. They also provided whole genome expression data over time, with n = 24, as well as information about the known regulatory network of E. coli.

In this application, the set of transcription factors are known a priori and the goal is to find connections among transcription factors and regulated genes through analysis of whole genome transcriptomic data. The algorithm proposed in this paper can be used by exploiting the natural hierarchy of transcription factors and regulated genes. Kao et al. (2004) provide gene expression data for seven transcription factors and 40 regulated genes, i.e. p = 47. Figure 7 presents the known regulatory network of E. coli along with the estimated networks and the corresponding performance measures using the PC-algorithm, lasso and adaptive lasso. The values of α are set as in § 6.1. The relatively poor performance of the algorithms in this example can be partially attributed to the small sample size. However, it is also known that no single source of transcriptomic data is expected to successfully reveal the regulatory network and better estimates are obtained by combining different sources of data. It can be seen that the PC-algorithm can only detect one of the true regulatory connections, and both the lasso and adaptive lasso offer significant improvements, mostly due to the considerable drop in the false negative rate, from 97% for the PC-algorithm to 63% for the adaptive lasso. In this case, the lasso and adaptive lasso estimates are very similar, and the choice of the best estimate depends on the performance evaluation criterion.

Fig. 7.

Known and estimated transcription regulatory network of E. coli. Large grey nodes indicate the transcription factors, and true and false edges are marked with solid and dashed arrows, respectively.

APPENDIX

Technical proofs

The following lemma is a consequence of the Karush–Kuhn–Tucker conditions for the general weighted lasso problem and is used in the proof of Theorems 3 and 4.

Lemma A1. Let θ̂^i,ℐ be the general weighted lasso estimate of θ^i,ℐ, i.e.

$${\widehat{\theta }}^{i,ℐ}=\underset{\theta :{\theta }_k=0,k\notin I}{\text{arg}\hspace{0.17em}\text{min}}\left\{n^{-1}{\Vert {𝒳}_i-𝒳\theta \Vert }_2^2+\lambda \sum _{k=1}^p|{\theta }_k|w_{ik}\right\}.$$ (A1)

Define

$$G_j(\theta )=-2n^{-1}{𝒳}_j^{\text{T}}({𝒳}_i-𝒳\theta ),$$

and let w_i be the vector of initial weights in the adaptive lasso estimation problem. Then a vector θ̂ with θ̂_k = 0, for all k ∉ ℐ is a solution of (A1) if and only if for all j ∈ ℐ, G_j (θ) = – sign (θ̂_j)w_ij λ if θ̂_j ≠ 0 and |G_j (θ)| ⩽ w_ij λ if θ̂_j = 0. Moreover, if the solution is not unique and |G_j (θ)| <w_ij λ for some solution θ̂, then θ̂_j = 0 for all solutions of (A1).

Proof. The proof of the lemma is identical to the proof of Lemma (A1) in Meinshausen & Bühlmann (2006), except for inclusion of general weights w_ij, and is therefore omitted.

Proof of Theorem 3. To prove (i), note that by Bonferroni’s inequality, and the fact that card (pa_i) = o(n) as n → ∞, it suffices to show that there exists some c_(i) > 0 such that for all i ∈ V and for every j ∈ pa_i, pr{sign ( ${\widehat{\theta }}_j^{i,{\text{pa}}_i}$) = sign ( ${\theta }_j^{i,p{a}_i}$)}= 1 – O{exp (–c_(i)n^ζ)} as n → ∞.

Let θ̂^i,pa_i (β) be the estimate of θ^i,pa_i in (A1), with the jth component fixed at a constant value β,

$${\widehat{\theta }}^{i,{\text{pa}}_i}(\beta )=\underset{\theta \in {\mathrm{\Theta }}_{\beta }}{\text{arg}\hspace{0.17em}\text{min}}\left\{n^{-1}{\Vert {𝒳}_i-𝒳\theta \Vert }_2^2+\lambda \sum _{k=1}^p|{\theta }_k|w_k\right\},$$ (A2)

where Θ_β ≡{θ ∈ 𝕉^p : θ_j = β, θ_k = 0, k ∉ pa_i}. Note that for $\beta ={\widehat{\theta }}_j^{i,{\text{pa}}_i}$, θ̂^i,pa_i (β) is identical to θ̂^i,pa_i. Thus, if sign ( ${\widehat{\theta }}_j^{i,{\text{pa}}_i}$) ≠ sign ( ${\theta }_j^i$), there would exist some β with sign (β) sign ( ${\theta }_j^i$) ⩽ 0 such that θ̂^i,pa_i (β) is a solution to (A2). Since ${\theta }_j^i\ne 0$, for all j ∈ pa_i, it suffices to show that for all β with sign (β) sign $({\theta }_j^i)<0$, with high probability, θ̂^i,pa_i (β) cannot be a solution to (A2).

Without loss of generality, we consider the case where ${\theta }_j^i>0$; ${\theta }_j^i<0$ can be shown similarly. Then if β ⩽ 0, from Lemma A1, θ̂^i,pa_i (β) can be a solution to (A2) only if G_j {θ̂ⁱ (β)} ⩾ – λw_ij. Hence, it suffices to show that for some c_(i) > 0 and all j ∈ pa_i with ${\theta }_j^i>0$,

$$\text{pr}\left(\underset{\beta ⩽0}{\text{sup}}[G_j\{{\widehat{\theta }}^i(\beta )\}<-\lambda w_{ij}]\right)=1-O\{\text{exp}(-c_{(i)}{n}^{\zeta })\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\to \infty .$$

Define, 𝒭_i (β) = 𝒳_i – 𝒳θ̂ⁱ (β). Then for every j ∈ pa_i we can write

$$X_j=\sum _{k\in {\text{pa}}_i\backslash \{j\}}{\theta }_k^{j,{\text{pa}}_i\backslash \{j\}}{X}_k+Z_j,$$ (A3)

where Z_j is independent of {X_k; k ∈ pa_i \{j}}. Then by (A3),

$$G_j\{{\widehat{\theta }}^i(\beta )\}=-2n^{-1}{Ƶ}_j^{\text{T}}{𝒭}_i(\beta )-\sum _{k\in {\text{pa}}_i\backslash \{j\}}{\theta }^{j,{\text{pa}}_i\backslash \{j\}}2n^{-1}{𝒳}_k^{\text{T}}{𝒭}_i(\beta ).$$

By Lemma A1, it follows that for all k ∈ pa_i \{j}, $|G_k\{{\widehat{\theta }}^i(\beta )\}|=|2n^{-1}{𝒳}_k^{\text{T}}{𝒭}_i(\beta )|⩽\lambda w_{ik}$, and hence,

$$G_j\{{\widehat{\theta }}^i(\beta )\}⩽-2n^{-1}{Ƶ}_j^{\text{T}}{𝒭}_i(\beta )+\lambda \sum _{k\in {\text{pa}}_i\backslash \{j\}}|{\theta }^{j,{\text{pa}}_i\backslash \{j\}}|w_{ik}.$$

Using the fact that |θ^j,pa_i\{j}| ⩽ 1, it suffices to show that

$$\text{pr}\left[\underset{\beta ⩽0}{\text{sup}}\{-2n^{-1}{Ƶ}_j^{\text{T}}{𝒭}_i(\beta )\}<-\lambda \sum _{k\in {\text{pa}}_i}{w}_{ik}\right]=1-O\{\text{exp}(-c_{(i)}{n}^{\zeta })\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\to \infty .$$

It is shown in Lemma A.2. of Meinshausen & Bühlmann (2006) that for any q > 0, there exists c_(i) > 0 such that for all j ∈ pa_i with ${\theta }_j^i>0$,

$$\text{pr}\left[\underset{\beta ⩽0}{\text{inf}}\{2n^{-1}{Ƶ}_j^{\text{T}}{𝒭}_i(\beta )\}>q\lambda \right]=1-O\{\text{exp}(-c_{(i)}{n}^{\zeta })\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\to \infty .$$ (A4)

However, by definition w_ik ⩾ 1 and therefore, Σ_k∈pai w_ik ⩾ card (pa_i) ⩾ 1, and (i) follows from (A4).

To prove (ii), note that the event $\widehat{{\text{pa}}_i}\not\subset \hspace{0.17em}{\text{pa}}_i$ is equivalent to the event that there exists a node j ∈ i^-\pa_i such that ${\widehat{\theta }}_j^i\ne 0$. In other words, denoting the latter event by 𝒟, pr( ${\widehat{\text{pa}}}_i\subseteq {\text{pa}}_i$) = 1 – pr(𝒟).

However, by Lemma A1, and since w_ij ⩾ 1,

$$\begin{array}{lll}\text{pr}(𝒟)\hfill & =\hfill & \text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\in i^{-}{\backslash \text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}|G_j({\widehat{\theta }}^{i,{\text{pa}}_i})|⩾w_{ij}\lambda )\hfill \\ \hfill & ⩽\hfill & \text{pr}\{\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\in i^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}|G_j({\widehat{\theta }}^{i,{\text{pa}}_i})|⩾q\lambda \hspace{0.17em}\text{and\hspace{0.17em}}{w}_{ij}\lambda ⩽q\lambda \hspace{0.17em}\text{for\hspace{0.17em}some\hspace{0.17em}}q⩾1\}\hfill \\ \hfill & ⩽\hfill & \text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\in i^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{w}_{ij}⩽q\hspace{0.17em}\text{for\hspace{0.17em}some\hspace{0.17em}}q⩾1).\hfill \end{array}$$

But $w_{ij}=1\vee |{\tilde{\theta }}_j^i{|}^{-\gamma }$, with ${\tilde{\theta }}_j^i$ the lasso estimate of the adjacency matrix from (9). Hence, letting 𝐹 be the event that there exists j ∈ i^-\pa_i such that w_ij ⩽ q for some q > 0, and using Lemma A1 we can write

$$\begin{array}{lll}\text{pr}(𝒡)\hfill & =\hfill & \text{pr}\left(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}|{\tilde{\theta }}_j^i|\hspace{0.17em}⩾\hspace{0.17em}{q}^{-1/\gamma }\hspace{0.17em}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}q\hspace{0.17em}⩾\hspace{0.17em}1\right)\hfill \\ \hfill & ⩽\hfill & \text{pr}\left(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}|{\tilde{\theta }}_j^i|\hspace{0.17em}⩾\hspace{0.17em}{q}^{\prime }\hspace{0.17em}\text{for\hspace{0.17em}some\hspace{0.17em}}{q}^{\prime }>0\right)\hfill \\ \hfill & ⩽\hfill & \text{pr}\left(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\tilde{\theta }}_j^i\hspace{0.17em}\ne \hspace{0.17em}0\right)\hfill \\ \hfill & =\hfill & \text{pr}\left(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}|G_j({\tilde{\theta }}^{i,{\text{pa}}_i})|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0\right).\hfill \end{array}$$

Since card (pa_i) = o(n), we can assume, without loss of generality, that card (pa_i) < n, which implies that θ̃^i,pa_i is an almost sure unique solution to (A1) with ℐ = pa_i. Let ℰ ={max_j∈i^-\pai|G_j (θ̃^i,pa_i)| <λ⁰}. Then conditional on the event ℰ, it follows from the first part of Lemma A1 that θ̃^i,pa_i is also a solution of the unrestricted weighted lasso problem (A1) with ℐ = i^-. Since ${\tilde{\theta }}_j^{i,{\text{pa}}_i}=0$, for all j ∈ i^-\pa_i, it follows from the second part of Lemma A1 that ${\tilde{\theta }}_j^i=0$, for all j ∈ i^-\pa_i. Hence,

$$\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash {\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\tilde{\theta }}_j^i\ne 0)\hspace{0.17em}⩽\hspace{0.17em}1-\text{pr}(ℰ)=\text{pr}\left\{\underset{j\in i^{-}\backslash {\text{pa}}_i}{\text{max}}|G_j({\tilde{\theta }}^{i,{\text{pa}}_i})|⩾{\lambda }^0\right\},$$

where $G_j({\tilde{\theta }}^{i,{\text{pa}}_i})=-2n^{-1}{𝒳}_j^{\text{T}}({𝒳}_i-𝒳{\tilde{\theta }}^{i,{\text{pa}}_i})$.

Since card (V) = O(n^a) for some a > 0, Bonferroni’s inequality implies that to verify (ii) it suffices to show that there exists a constant c_(ii) > 0 such that for all j ∈ i^-\pa_i,

$$\text{pr}(|G_j({\tilde{\theta }}^{i,{\text{pa}}_i})|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0)=O\{\text{exp}(-c_{(ii)}{n}^{\zeta })\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\hspace{0.17em}\to \hspace{0.17em}\infty ,$$

where $R_j\sim N(0,\hspace{0.17em}{\sigma }_j^2)$, ${\sigma }_j^2⩽1$ and R_j is independent of X_l, l ∈ pa_i. Similarly, with R_i satisfying the same requirements as R_j, we get $X_i={\sum }_{k\in {\text{pa}}_i}{\theta }_k^{i,{\text{pa}}_i}{X}_k+R_i$. Denote by 𝒳_pai the columns of 𝒳 corresponding to pa_i and let θ_pai be the column vector of coefficients with dimension card (pa_i) corresponding to pa_i. Then,

$$\begin{array}{lll}\text{pr}\{|G_j({\tilde{\theta }}^{i,{\text{pa}}_i})|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0\}\hfill & =\hfill & \text{pr}\{|-2n^{-1}{𝒳}_j^{\text{T}}({𝒳}_i-𝒳{\tilde{\theta }}^{i,{\text{pa}}_i})|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0\}\hfill \\ \hfill & =\hfill & \text{pr}[|-2n^{-1}{\{{𝒳}_{{\text{pa}}_i}{\theta }_{{\text{pa}}_i}^{j,{\text{pa}}_i}+{𝒭}_j\}}^{\text{T}}\{{𝒳}_{{\text{pa}}_i}({\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i})+{𝒭}_i\}|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0]\hfill \\ \hfill & ⩽\hfill & \text{pr}\{|-2n^{-1}{({\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i})}^{\text{T}}{𝒳}_{{\text{pa}}_i}^{\text{T}}{𝒳}_{{\text{pa}}_i}{\theta }_{{\text{pa}}_i}^{j,{\text{pa}}_i}|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0/3\}\hfill \\ \hfill & \hfill & +\text{pr}\{|-2n^{-1}{({\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i})}^{\text{T}}{𝒳}_{{\text{pa}}_i}^{\text{T}}{𝒭}_j|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0/3\}\hfill \\ \hfill & \hfill & +\text{pr}\{|-2n^{-1}{({𝒳}_{{\text{pa}}_i}{\theta }_{{\text{pa}}_i}^{j,{\text{pa}}_i}+{𝒭}_j)}^{\text{T}}{𝒭}_i|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0/3\}\hfill \\ \hfill & \equiv \hfill & \text{I}+\text{II}+\text{III},\hfill \end{array}$$

say. Let 1_pai denote a vector of 1s of dimension card (pa_i). Then using the fact that $|{\theta }_l^{j,{\text{pa}}_i}|\hspace{0.17em}⩽\hspace{0.17em}1$, for all l ∈ pa_i, we can write $\text{I}⩽\text{pr}\{2{\Vert {\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i}\Vert }_{\infty }{n}^{-1}{({𝒳}_{{\text{pa}}_i}{1}_{{\text{pa}}_i})}^{\text{T}}{𝒳}_{{\text{pa}}_i}{1}_{{\text{pa}}_i}⩾{\lambda }^0/3\}$. Then ${𝒳}_{{\text{pa}}_i}^{\text{T}}$ 𝒳_pai ∼ 𝕎_{card (pai)}(Σ_pai, n) where 𝕎_m(Σ, n) denotes a Wishart distribution with mean n Σ. Hence, from properties of the Wishart distribution, we get ${({𝒳}_{{\text{pa}}_i}{1}_{{\text{pa}}_i})}^{\text{T}}{𝒳}_{{\text{pa}}_i}{1}_{{\text{pa}}_i}\sim {𝕎}_1(1_{{\text{pa}}_i}^{\text{T}}\hspace{0.17em}{\mathrm{\Sigma }}_{{\text{pa}}_i}\hspace{0.17em}{1}_{{\text{pa}}_i},\hspace{0.17em}n)$.

Since pa_i also forms a directed acyclic graph, the eigenvalues Σ_pai are bounded, see Remark 1, and hence

$$1_{{\text{pa}}_i}^{\text{T}}{\mathrm{\Sigma }}_{{\text{pa}}_i}{1}_{{\text{pa}}_i}\hspace{0.17em}⩽\hspace{0.17em}\text{card\hspace{0.17em}}({\text{pa}}_i){\varphi }_{\text{max}}({\mathrm{\Sigma }}_{{\text{pa}}_i}).$$ (A5)

Therefore, if $Z\sim {\chi }_1^2$, then n⁻¹(𝒳_pai 1_pai)^T 𝒳_pai 1_pai is stochastically smaller than card (pa_i)ϕ_max(Σ_pai)Z. On the other hand, by Theorem 2, ‖A – Ã‖_F = O_p{(n⁻¹s log p)^1/2}, and hence,

$${\Vert {\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i}\Vert }_{\infty }=O_p\{{(n^{-1}s\hspace{0.17em}\text{log}\hspace{0.17em}p)}^{1/2}\}.$$ (A6)

Noting that card (pa_i) = O(n^b), b < 1/2 and p = O(n^a), a > 0, (A5) and (A6) imply that

$${\Vert {\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i}\Vert }_{\infty }\hspace{0.17em}\text{card}\hspace{0.17em}({\text{pa}}_i){\varphi }_{\text{max}}({\mathrm{\Sigma }}_{{\text{pa}}_i})=O_p\{{(s{n}^{2b-1}a\hspace{0.17em}\text{log}\hspace{0.17em}n)}^{1/2}\}.$$

By Assumption 1′, sn^2b−1 log n = o(1) and hence by Slutsky’s Theorem and properties of the χ²-distribution, there exists c_(I) > 0 such that for all j ∈ i^-\pa_i, I = O{exp (–c_(I)n^ζ)} as n → ∞.

Using a similar argument, $\text{II}⩽\hspace{0.17em}\text{pr}(2n^{-1}{\Vert {\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i}\Vert }_{\infty }|1_{{\text{pa}}_i}{𝒳}_{{\text{pa}}_i}^{\text{T}}{𝒭}_j|⩾{\lambda }^0/3)$. But columns of 𝒳_pai have mean zero and are all independent of 𝒭_j, so it suffices to show that there exists c_(II) > 0 such that for all j ∈ i^-\pa_i and for all k ∈ pa_i,

$$\text{pr}\{2n^{-1}{\Vert {\theta }_{{\text{pa}}_i}^{i,{\text{pa}}_i}-{\tilde{\theta }}_{{\text{pa}}_i}^{i,{\text{pa}}_i}\Vert }_{\infty }\hspace{0.17em}\text{card\hspace{0.17em}}({\text{pa}}_i)\hspace{0.17em}|{𝒳}_k^{\text{T}}{𝒭}_j|\hspace{0.17em}⩾\hspace{0.17em}{\lambda }^0/3\}=O\{\text{exp}(-c_{(\text{II})}{n}^{\zeta })\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{as\hspace{0.17em}}n\hspace{0.17em}\to \hspace{0.17em}\infty .$$ (A7)

By (A6) and Assumption 1′, the random variable on the left-hand side of (A7) is stochastically smaller than 2n⁻¹|𝒳_k𝒭_j|. By independence of X_k and R_j, E(X_k R_j) = 0. Also, using Gaussianity of both X_k and R_j, there exists g < ∞ such that E{exp (|X_k R_j|)} ⩽ g. Since λ⁰ = O{(log p/n)^1/2}, by Bernstein’s inequality (Van der Vaart & Wellner, 1996), pr(2n⁻¹|𝒳_k𝒭_j| > λ⁰/3) ⩽ exp(–c_(II)n^ζ) for some c_(II) > 0 and hence (A7) is satisfied.

Finally, $\text{pr}\{|-2n^{-1}{({𝒳}_{{\text{pa}}_i}{\theta }_{{\text{pa}}_i}^{j,{\text{pa}}_i}+{𝒭}_i)}^{\text{T}}{𝒭}_j|⩾{\lambda }^0/3\}=\text{pr}\{|-2n^{-1}{𝒳}_i^{\text{T}}{𝒭}_j|⩾{\lambda }^0/3\}$, and using the Bernstein’s inequality we conclude that there exists c_(III) > 0 such that for all j ∈ i^-\pa_i and for all k ∈ pa_i, III = O{exp (–c_(III)n^ζ)} as n → ∞. The proof of (ii) is then completed by taking c_(ii) to be the minimum of c_(I),..., c_(III).

To prove (iii), note that $\text{pr}({\text{pa}}_i\subseteq {\widehat{\text{pa}}}_i)=1-\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\widehat{\theta }}_j^i=0)$, and let ℰ = {max_k∈i^-\pai|G_j (θ̂^i,pa_i)| <λw_ij}. It then follows from an argument similar to the proof of (ii) that conditional on ℰ, θ̂^i,pa_i is an almost sure unique solution of the unrestricted adaptive lasso problem (A1) with ℐ = i^-. Therefore,

$$\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\widehat{\theta }}_j^i=0)\hspace{0.17em}⩽\hspace{0.17em}\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{\text{pa}}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\widehat{\theta }}_j^i=0)+\text{pr}({ℰ}^c).$$

From (i), there exists a c₁ > 0 such that pr(there exists j ∈ pa_i such that ${\widehat{\theta }}_j^i=0$) = O{exp (–c₁n^ζ)} and it was shown in (ii) that pr(ℰ^c) = O{exp (–c₂n^ζ)} for some c₂ > 0. Thus (iii) follows from Bonferroni’s inequality.

The claim in (iv) follows from (ii) and (iii), and Bonferroni’s inequality as p = O(n^a).

Proof of Theorem 4. We first show that if AN_i ∩ AN_j = ∅, then i and j are independent. Since Σ = Λ Λ^T and Λ is lower triangular,

$${\mathrm{\Sigma }}_{ij}=\sum _{k=1}^{\text{min}(i,j)}{\mathrm{\Lambda }}_{ik}{\mathrm{\Lambda }}_{jk}.$$ (A8)

We assume without loss of generality that i < j. The argument for j > i is similar. Suppose for all k = 1 ,..., i, that Λ_ik = 0 or Λ_jk = 0. Then by (A8) i and j are independent. However, by Lemma 1, Λ_jk is the influence of kth node on j, and this is zero only if there is no path from k to j. If i is an ancestor of j, we have Σ_ij ≠ 0. On the other hand, if there is no node k ∈ i^- such that k influences both i and j, i.e. k is a common ancestor of i and j, then for all k = 1,..., i we have Λ_ik Λ_jk = 0 and the claim follows.

Using Bonferroni’s inequality twice and Lemma A1, we get

$$\begin{array}{lll}\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}i\hspace{0.17em}\in \hspace{0.17em}V\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{\widehat{AN}}_i⊈\hspace{0.17em}A{N}_i)\hfill & ⩽\hfill & p\hspace{0.17em}\underset{i\in V}{\text{max}}\text{pr}(\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{i}^{-}\backslash A{N}_i\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}j\hspace{0.17em}\in \hspace{0.17em}{\widehat{\text{pa}}}_i)\hfill \\ \hfill & ⩽\hfill & p(i-1)\hspace{0.17em}\underset{i\in V,\hspace{0.17em}j\in i^{-}\backslash A{N}_i}{\text{max}}\text{pr}(j\hspace{0.17em}\in \hspace{0.17em}{\widehat{\text{pa}}}_i)\hfill \\ \hfill & ⩽\hfill & p(i-1)\hspace{0.17em}\underset{i\in V,\hspace{0.17em}j\in i^{-}\backslash A{N}_i}{\text{max}}\text{pr}\{|G_j({\widehat{\theta }}^{i,A{N}_i})|\hspace{0.17em}⩾\hspace{0.17em}\lambda w_{ij}\}.\hfill \end{array}$$

However, by definition w_ij ⩾ 1, and hence it suffices to show that

$$(i-1)p\hspace{0.17em}\underset{i\in V,\hspace{0.17em}j\in i^{-1}\backslash A{N}_i}{\text{max}}\text{pr}\{|G_j({\widehat{\theta }}^{i,A{N}_i})\hspace{0.17em}|\hspace{0.17em}⩾\hspace{0.17em}\lambda \}\hspace{0.17em}⩽\hspace{0.17em}\alpha .$$

Note that $G_j({\widehat{\theta }}^{i,A{N}_i})=-2n^{-1}{𝒳}_j^{\text{T}}({𝒳}_i-𝒳{\widehat{\theta }}^{i,A{N}_i})$ and X_j is independent of X_k for all k ∈ AN_i. Therefore, conditional on 𝒳_ANi, G_j (θ̂^i,AN_i) ∼ (0, 4R²/n), where $R^2=n^{-1}{\Vert {𝒳}_i-𝒳{\widehat{\theta }}^{i,A{N}_i}\Vert }_2^2⩽n^{-1}{\Vert {𝒳}_i\Vert }_2^2=1$, by definition of θ̂^i,AN_i and the fact that columns of the data matrix are scaled.

It follows that for all j ∈ i^-\AN_i, pr{|G_j (θ̂^i,AN_i)| ⩾ λ | 𝒳_ANi} ⩽ 2{1 – Φ(n^1/2λ/2)}, where Φ is the cumulative distribution function for standard normal random variable. Using the choice of λ proposed in (10), we get pr{|G_j (θ̂^i,AN_i)| ⩾ λ | 𝒳_ANi} ⩽ α{(i – 1) p}⁻¹, and the result follows.