Encapsulation of a polyelectrolyte chain by an oppositely charged spherical surface

Abstract

Using the ground state dominance approximation and a variational theory, we study the encapsulation of a polyelectrolyte chain by an oppositely charged spherical surface. The electrostatic attraction between the polyelectrolyte and the surface and the entropy loss of the encapsulated polyelectrolyte chain dictate the optimum conditions for encapsulation. Two scenarios of encapsulation are identified: entropy-dominated and adsorption-dominated encapsulation. In the entropy-dominated encapsulation regime, the polyelectrolyte chain is delocalized, and the optimum radius of the encapsulating sphere decreases with increasing the attraction. In the adsorption-dominated encapsulation regime, the polyelectrolyte chain is strongly localized near the surface, and the optimum radius increases with increasing the attraction. After identifying a universal encapsulation parameter, the dependencies of the optimum radius on the salt concentration, surface charge density, polymer charge density, and polymer length are explored.

INTRODUCTION

Adsorption of polyelectrolytes by oppositely charged surfaces is a central issue in surface and colloidal science.^{1, 2, 3} Due to the electrostatic attraction between polyelectrolytes and surfaces, polyelectrolytes tend to be adsorbed onto the surface. This in turn induces confinement and consequent entropy loss of polyelectrolytes. The competition between the electrostatic attraction and entropy loss of the adsorbed polyelectrolytes leads to a critical adsorption temperature T_c, below which adsorption occurs.^{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} The general theoretical ideas are consistent with simulations^{15, 16, 17, 18, 19, 20} and experiments.^{21, 22, 23} For the adsorption of polyelectrolytes onto a curved surface, the critical adsorption temperature depends also on surface curvature. In addition to the critical adsorption temperature, the question of optimum surface curvature for the adsorption of a fixed amount of polyelectrolyte chains is of interest. This question is motivated by extensive adsorption phenomena of charged bio-macromolecules in cells. Most bio-macromolecules including DNA, RNA and proteins, as well as cell membranes are charged, and electrostatic interaction is critical for cell self-organization.^{24, 25, 26, 27, 28} An example is the electrostatically induced endocytosis of polyelectrolytes.^{29, 30, 31, 32} Similar issues also appear in experiments involving vesicles.^{33, 34} In these experiments, some polyelectrolyte chains are placed into a vesicle to study the interaction between the polyelectrolyte and the membrane. If the size of the vesicle does not match the adsorption of polyelectrolyte chains, the loading of polyelectrolytes induces stress in the vesicle, and sometimes, even leads to rupture and re-assembly of the vesicle.³⁵

The simplest problem in the above context is the encapsulation of a polyelectrolyte chain by an oppositely charged spherical surface, which is addressed in this paper. The spherical surface can be a rigid virus capsid, nano-cavity or soft cell membrane. Our study attempts to find the spatial distribution of the polyelectrolyte chain encapsulated in the sphere, and the optimum radius of the spherical surface for the encapsulation of polyelectrolyte with a fixed chain length, for different values of salt concentration, polymer charge density, and surface charge density.

The theoretical approach used in this paper is the ground state dominance approximation for the polyelectrolyte distributions. Usually, the distributions of the adsorbed polyelectrolytes can be determined in the self-consistent field theory (SCFT) without additional approximations by numerically solving the diffusion equation.¹ To avoid complicated numerical calculation in the self-consistent field theory, the ground state dominance approximation is adopted to simplify the solution.³⁶ The approximation method has been used successfully in previous studies on polymer adsorption by electrostatic interaction.^{4, 6, 25} We expect the approximation method to provide qualitatively correct results for the issues addressed here.

The outline of this paper is as follows: Sec. 2 describes the theoretical model. We present the self-consistent field equations for the system, and then instead of solving the full SCFT equations, the ground state dominance approximation is introduced to simplify the solution. Moreover, we also solve this equations by approximating the interacting polyelectrolyte chain using an effective Gaussian chain. In Sec. 3, the main results from the two approaches are presented and discussed. The density profiles are compared at different values of the attraction parameter. Two scenarios of encapsulation are revealed. The dependencies of the optimum radius on various parameters are analyzed in connection with the two scenarios of encapsulation. In Sec. 4, the main conclusions are summarized and the constraints on our theoretical methods are pointed out.

THEORETICAL MODEL

We assume that a positively charged polyelectrolyte chain of Kuhn length b is confined inside a negatively charged spherical surface of radius R. The distribution of the polyelectrolyte chain can be described by a propagator G(r,r₀;s), which gives the probability of appearance of segment s at site r with segment 0 at site r₀. According to the Gaussian chain model, the propagator satisfies the modified diffusion equation,

$$\begin{array}{c}\hfill \left[\frac{\partial }{\partial s}-\frac{b^2}{6}{\nabla }^2+\beta \omega \left(\mathbf{r}\right)\right]G(\mathbf{r},{\mathbf{r}}_0;s)=\delta (\mathbf{r}-{\mathbf{r}}_0)\delta \left(s\right),\end{array}$$ (1)

where, β = 1/(k_BT) and ω(r) is the space-dependent potential field acting on the chain segment at r. k_BT is the Boltzmann constant times the absolute temperature. For the polymer chain with interactions between segments, such as the excluded volume interaction or the electrostatic interaction, the potential field should depend on the propagator G self-consistently. For the system concerned here, the self-consistent potential in Eq. 1 consists of three parts: the external electrostatic potential ω_ex, the excluded volume interaction ω_ev, and the electrostatic repulsion between chain segments ω_ep,

$$\begin{array}{ccc}\hfill \beta \omega & =& \beta {\omega }_{ex}+\beta {\omega }_{ev}+\beta {\omega }_{ep},\hfill \end{array}$$ (2)

with

$$\begin{array}{ccc}\hfill \beta {\omega }_{ev}& =& \int d{\mathbf{r}}^{\prime }\rho \left({\mathbf{r}}^{\prime }\right)v\delta (\mathbf{r}-{\mathbf{r}}^{\prime }),\hfill \end{array}$$ (3)

where v is the excluded volume interaction parameter. For simplicity, the electrostatic interaction is formulated in the framework of the Debye-Hückel theory,⁶

$$\begin{array}{ccc}\hfill \beta {\omega }_{ex}& =& -4\pi |\sigma z_p|l_{B}R\exp (-{\kappa }_{D}R)\frac{\sinh \left({\kappa }_{D}r\right)}{{\kappa }_{D}r},\hfill \end{array}$$ (4)

and

$$\begin{array}{ccc}\hfill \beta {\omega }_{ep}& =& \int d{\mathbf{r}}^{\prime }\rho \left({\mathbf{r}}^{\prime }\right)z_p^2{l}_B\frac{\exp (-{\kappa }_D|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|},\hfill \end{array}$$ (5)

where, z_pe is the effective charge per segment of the polymer chain, and σe is the charge density of the surface. The inverse Debye-Hückel screening length is defined as ${\kappa }_D=\sqrt{8\pi l_B{c}_s}$ of the monovalent salt concentration c_s and Bjerrum length $l_B=\frac{e^2}{4\pi \epsilon k_{B}T}$ (where e is the elementary charge and ε is the permittivity). In addition, the electrostatic potential distribution inside the sphere due to the charged surface in Eq. 4 can be rewritten as

$$\begin{array}{c}\hfill \beta {\omega }_{ex}={\omega }_{ex}^b\frac{R}{\sinh \left({\kappa }_{D}R\right)}\frac{\sinh \left({\kappa }_{D}r\right)}{r}={\omega }_{ex}^0\frac{\sinh \left({\kappa }_{D}r\right)}{{\kappa }_{D}r},\end{array}$$ (6)

where, ${\omega }_{ex}^b=-4\pi |\sigma z_p|l_B\frac{1-\exp (-2{\kappa }_{D}R)}{2{\kappa }_D}$ is the potential on the surface and ${\omega }_{ex}^0=-4\pi |\sigma z_p|l_{B}R\exp (-{\kappa }_{D}R)$ is the potential at the center. Obviously, the potential inside the sphere decreases by $\frac{\sinh \left({\kappa }_{D}r\right)}{r}$ from ${\omega }_{ex}^b$ on the surface to ${\omega }_{ex}^0$ at the center. ${\omega }_{ex}^b$ is a monotonically increasing function of radius R, and approaches to the potential of infinite plane when κ_DR ≫1.

ρ is the density of polymer segment, which can be related to the propagator by

$$\begin{array}{c}\hfill \rho \left(\mathbf{r}\right)=\frac{{\int }_0^{N_p}ds\int d{\mathbf{r}}^{\prime }G(\mathbf{r},{\mathbf{r}}^{\prime },s)\int d{\mathbf{r}}^{\prime \prime }G(\mathbf{r},{\mathbf{r}}^{\prime \prime },N_p-s)}{\int d{\mathbf{r}}^{\prime }\int d\mathbf{r}G(\mathbf{r},{\mathbf{r}}^{\prime \prime },N_p)},\end{array}$$ (7)

where N_p is the chain length of the polymer chain.

Equations 1, 2, 7 form a close and self-consistent equation set, which need to be solved simultaneously and self-consistently. So far, there is no exact analytical solution, and usually it is solved numerically.

Using the solution to the above SCFT equations, the free energy of the system can be written as

$$\begin{array}{ccc}\hfill \beta F& =& -\ln Q\left(\beta \omega \right)-\int d\mathbf{r}\rho \left(\mathbf{r}\right)\beta \omega \left(\mathbf{r}\right)\hfill \\ & & +\int d\mathbf{r}\beta {\omega }_{ex}\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)+\frac{v}{2}\int d\mathbf{r}\rho {\left(\mathbf{r}\right)}^2\hfill \\ & & +\frac{z_p^2{l}_B}{2}\int d\mathbf{r}d{\mathbf{r}}^{\prime }\rho \left(\mathbf{r}\right)\rho \left({\mathbf{r}}^{\prime }\right)\frac{\exp (-{\kappa }_D|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}\hfill \\ & =& -\ln Q\left(\beta \omega \right)-\frac{v}{2}\int d\mathbf{r}\rho {\left(\mathbf{r}\right)}^2-\frac{z_p^2{l}_B}{2}\int d\mathbf{r}d{\mathbf{r}}^{\prime }\rho \left(\mathbf{r}\right)\rho \left({\mathbf{r}}^{\prime }\right)\hfill \\ & & \times \frac{\exp (-{\kappa }_D|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|},\hfill \end{array}$$ (8)

where the single chain partition function Q is

$$\begin{array}{c}\hfill Q\left(\beta \omega \right)=\int d\mathbf{r}d{\mathbf{r}}^{\prime }G(\mathbf{r},{\mathbf{r}}^{\prime },N).\end{array}$$ (9)

Here, instead of solving the full self-consistent field equations numerically, we use the ground state dominance approximation, and leave the full numerical self-consistent field approach to another paper.

Self-consistent ground state dominance approximation (ScGSDA)

The propagator G can be written as bilinear expansion,

$$\begin{array}{c}\hfill G(\mathbf{r},{\mathbf{r}}^{\prime },s)=\sum _{i=0}^{\infty }{\varphi }_i\left(\mathbf{r}\right){\varphi }_i\left({\mathbf{r}}^{\prime }\right)\exp (-{\lambda }_{i}s),\end{array}$$ (10)

with ϕ_i(r) being the ith eigenfunction of the equation,

$$\begin{array}{c}\hfill \left[-\frac{b^2}{6}{\nabla }^2+\beta \omega \right]{\varphi }_i={\lambda }_i{\varphi }_i,\end{array}$$ (11)

with the corresponding eigenvalue λ_i.

In the ground state dominance approximation, the propagator can be approximated by

$$\begin{array}{c}\hfill G(\mathbf{r},{\mathbf{r}}^{\prime },s)\simeq {\varphi }_0\left(\mathbf{r}\right){\varphi }_0\left({\mathbf{r}}^{\prime }\right)\exp (-{\lambda }_{0}s),\end{array}$$ (12)

and correspondingly, the density is

$$\begin{array}{c}\hfill \rho \left(r\right)=N_p{\varphi }_0^2,\end{array}$$ (13)

and −ln Q is

$$\begin{array}{ccc}\hfill -\ln Q\left(\beta \omega \right)& =& N_p{\lambda }_0-\ln \int d\mathbf{r}\int d{\mathbf{r}}^{\prime }{\varphi }_0\left(\mathbf{r}\right){\varphi }_0\left({\mathbf{r}}^{\prime }\right)\hfill \\ & \simeq & N_p{\lambda }_0,\hfill \end{array}$$ (14)

where the trivial constant term is neglected in the last equality.

Using spherical coordinates, the equation for the ground state eigenfunction φ₀ can be written as

$$\begin{array}{c}\hfill H{\varphi }_0\equiv -\frac{b^2}{6}\frac{1}{r}\frac{{\partial }^2}{\partial r^2}\left[r{\varphi }_0\left(r\right)\right]+\beta [{\omega }_{ex}+{\omega }_{ev}+{\omega }_{ep}]{\varphi }_0={\lambda }_0{\varphi }_0.\end{array}$$ (15)

Even for the ground state equation in Eq. 15, the exact solution is unknown. Here we use a variational method analogous to Ref. 6, to approximate the solution. For the problem concerned here, the wavefunction of the ground state should satisfy the following boundary conditions:

$$\begin{array}{c}\hfill {\varphi }_0\left(R\right)=0,\end{array}$$ (16)

and

$$\begin{array}{c}\hfill {\partial }_r{\varphi }_0\left(0\right)=0.\end{array}$$ (17)

Accordingly, we choose the variational ground state functional as³⁷

$$\begin{array}{c}\hfill {\varphi }_0=\mathcal{N}\left[1-{\left(\frac{r}{R}\right)}^2\right]\exp \left(\alpha \frac{r^2}{R^2}\right),\end{array}$$ (18)

where N is the normalization factor to satisfy $4\pi {\int }_0^{R}dr{r}^2{\varphi }_0^2=1$.

Using the ground state eigenfunction in Eq. 18, we can get the density distribution as

$$\begin{array}{c}\hfill \rho \left(r\right)=N_p\frac{64{\alpha }^{7∕2}{\left[\left(1-{\left(\frac{r}{R}\right)}^2\right)\exp \left(\alpha \frac{r^2}{R^2}\right)\right]}^2}{\pi R^3[4e^{2\alpha }\sqrt{\alpha }(15+4\alpha )-\sqrt{2\pi }(15+24\alpha +16{\alpha }^2)\mathrm{erfi}\left(\sqrt{2\alpha }\right)]},\end{array}$$ (19)

and −ln Q

$$\begin{array}{ccc}\hfill -\ln Q\left(\beta \omega \right)& =& N_{p}4\pi {\int }_0^{R}dr{r}^2{\varphi }_{0}H{\varphi }_0.\hfill \end{array}$$ (20)

Therefore, the free energy can be written as

$$\begin{array}{ccc}\hfill \beta F& =& -\frac{2\pi N_p{b}^2}{3}{\int }_0^{R}drr{\varphi }_0\frac{{\partial }^2}{\partial r^2}\left[r{\varphi }_0\left(r\right)\right]\hfill \\ & & +\int d\mathbf{r}\beta {\omega }_{ex}\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)+\frac{\nu }{2}\int d\mathbf{r}\rho {\left(\mathbf{r}\right)}^2\hfill \\ & & +\frac{z_p^2{l}_B}{2}\int d\mathbf{r}d{\mathbf{r}}^{\prime }\rho \left(\mathbf{r}\right)\rho {\left(\mathbf{r}\right)}^{\prime }\frac{\exp (-{\kappa }_D|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}.\hfill \end{array}$$ (21)

The free energy is a function of the variational parameter α which can be determined by minimizing the free energy F.

Effective Gaussian chain approximation (EGCA)

In the above approach (ScGSDA), the interaction between segments is considered explicitly, and the distribution of the polyelectrolyte should be determined in a self-consistent way. Another method is to approximate the self-excluding and interacting polyelectrolyte chain by a Gaussian chain with an effective Kuhn length,^{4, 6} and the distribution of the effective chain is affected only by external potential. The effective Kuhn length b_eff of the Gaussian chain is determined by a variational method,^{4, 6}

$$\begin{array}{ccc}& & {\left(\frac{b_{eff}}{b}\right)}^{5∕2}-{\left(\frac{b_{eff}}{b}\right)}^{3∕2}\hfill \\ & & =\frac{4}{3}{\left(\frac{3}{2\pi }\right)}^{3∕2}v{N}_p^{1∕2}+\frac{4}{45}{\left(\frac{6}{\pi }\right)}^{1∕2}{z}_p^2{l}_B{N}_p^{3∕2}\frac{b_{eff}}{b}\hfill \\ & & \times \left(\frac{15\sqrt{\pi }{e}^a}{2a^{5∕2}}(a^2-4a+6)\mathrm{erfc}\left[\sqrt{a}\right]\right.\hfill \\ & & \left.-\frac{3\pi }{a^{5∕2}}+\frac{\pi }{a^{3∕2}}+\frac{6\sqrt{\pi }}{a^2}\right),\hfill \end{array}$$ (22)

with $a\equiv \frac{{\kappa }_D^2{N}_{p}b{b}_{eff}}{6}$. The dimensionless effective Kuhn length b_eff/b is a function of N_p, κ_Db, z_p, l_B, and v, and reflects the chain expansion and consequent entropy loss due to self-interaction between segments. As the strength of the excluded volume and electrostatic interactions increases, the entropy loss increases and b_eff/b increases correspondingly. In this way, the interaction between segments is reflected implicitly through b_eff/b. Now, the problem is transformed into finding the distribution of an effective Gaussian chain under the external potential ω_ex, that is,

$$\begin{array}{c}\hfill \left[\frac{\partial }{\partial s}-\frac{b{b}_{eff}}{6}{\nabla }^2+\beta {\omega }_{ex}\left(\mathbf{r}\right)\right]G(\mathbf{r},{\mathbf{r}}_0;s)=\delta (\mathbf{r}-{\mathbf{r}}_0)\delta \left(s\right).\end{array}$$ (23)

Here, we still adopt the ground state dominance approximation, and then the ground state equation becomes

$$\begin{array}{ccc}\hfill H{\varphi }_0& \equiv & -\frac{b_{eff}}{b}\frac{b^2}{6}\frac{1}{r}\frac{{\partial }^2}{\partial r^2}\left[r{\varphi }_0\left(r\right)\right]\hfill \\ & -& BR\exp (-{\kappa }_{D}R)\frac{\sinh \left({\kappa }_{D}r\right)}{{\kappa }_{D}r}{\varphi }_0={\lambda }_0{\varphi }_0,\hfill \end{array}$$ (24)

with λ₀ the eigenvalue of the ground state and B = 4π|σz_p|l_B. Using γ = κ_DR and ζ = κ_Dr, we have

$$\begin{array}{c}\hfill -\frac{1}{\zeta }\frac{{\partial }^2}{\partial {\zeta }^2}\left[\zeta {\varphi }_0\left(\zeta \right)\right]-B^{\prime }\gamma \exp (-\gamma )\frac{\sinh \left(\zeta \right)}{\zeta }{\varphi }_0={\lambda }_0^{\prime }{\varphi }_0,\end{array}$$ (25)

with

$$\begin{array}{ccc}\hfill B^{\prime }& =& 24\pi |\sigma b^2{z}_p|\frac{l_B}{b}\frac{b}{b_{eff}}\frac{1}{{\kappa }_D^3{b}^3}\hfill \\ \hfill {\lambda }_0^{\prime }& =& 6\frac{b}{b_{eff}}\frac{1}{{\kappa }_D^2{b}^2}{\lambda }_0.\hfill \end{array}$$ (26)

Here, B^′ reflects the attraction strength between polyelectrolyte and membrane and also includes chain expansion given by b_eff.

The same trial function in Eq. 18 is used to approximate the solution to Eq. 24, satisfying the same boundary conditions in Eqs. 16, 17. The same density profiles in Eq. 19 are obtained.

In the ground state dominance approximation, we have

$$\begin{array}{ccc}\hfill \beta F=-\ln Q\left(\beta \omega \right)& \simeq & N_p{\lambda }_0.\hfill \end{array}$$ (27)

Similarly, the free energy is a function of the variational parameter α, which needs to be determined by minimization of free energy.

The effective Gaussian chain approximation (EGCA) has been used to study the critical temperature for the adsorption of polyelectrolyte chain onto oppositely charged curved surfaces.⁶ In the effective Gaussian chain approximation, all relevant parameters (N_p, κ_D, z_p, l_B, and v) are lumped into a combined parameter B^′. The free energy βF = N_pλ₀ and the determination of variational parameter α depend only on B^′. So the advantage of EGCA is that we can get a universal dependence ${\lambda }_0^{\prime }\left(B^{\prime }\right)$. From this universal dependence, we can deduce the effect of various parameters.

RESULTS AND DISCUSSION

In this section, the main results are presented and discussed with emphasis on the optimum radius of the spherical surface for the encapsulation of a polyelectrolyte chain of a fixed chain length. We first describe the general feature of encapsulation under different adsorption strengths. Then we define the optimum radius for the spherical surface as the location of the minimum of free energy and discuss the dependence of the optimum radius on various parameters. Our calculation shows that in most cases, the results from EGCA and ScGSDA are qualitatively consistent. Therefore, in the following, the general feature of encapsulation is revealed using the results from EGCA in terms of the combined parameter B^′, and then effects of various parameters are discussed based on results from EGCA, supplemented by results from ScGSDA.

For the description of results, we choose b as length unit and 1/β = k_BT as energy unit. Correspondingly the following dimensionless parameters σ = σb², κ_D = κ_Db, b_eff = b_eff/b, ${\lambda }_0^{\prime }∕\left(4\pi \right)$, and F = βF/(4π) are used. We set l_B = 1, and expect no new qualitative results when varying l_B value.

Two scenarios of encapsulation

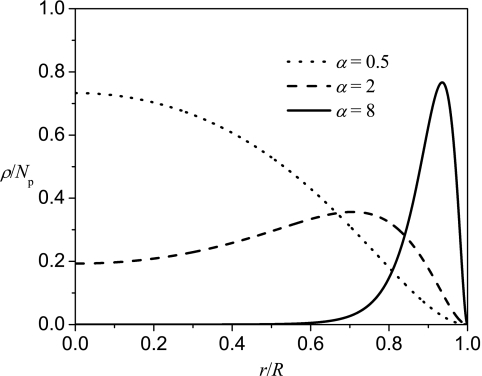
The variational parameter α determines the density profiles of the polyelectrolyte according to Eq. 19. As shown in Fig. 1 (where ρR³/N_p is plotted against r/R), the polyelectrolyte is delocalized for small values of α, while the polyelectrolyte is localized near the surface for large values of α. By increasing α values, the distribution of the polyelectrolyte switches from the delocalized to the localized chain. This change from delocalization to localization is gradual as shown in Fig. 1. The extent of chain localization near the surface versus delocalization is captured by the density profiles. It is possible to construct moments of the density profiles as measures of the thickness of the adsorbed layer. However, this is not pursued here, due to the finite size of the confinement. For the adsorption of a polyelectrolyte onto the inner spherical surface, localized states as well as delocalized states could be bound states due to the confinement effect by the closed surface. This is different from the adsorption of a polyelectrolyte on an open surface, e.g., planar surface, where only the localized polyelectrolyte could be a bound state.^{4, 6, 14}

Figure 1.

Typical density profiles of the encapsulated polyelectrolyte with α = 0.5, 2, and 8.

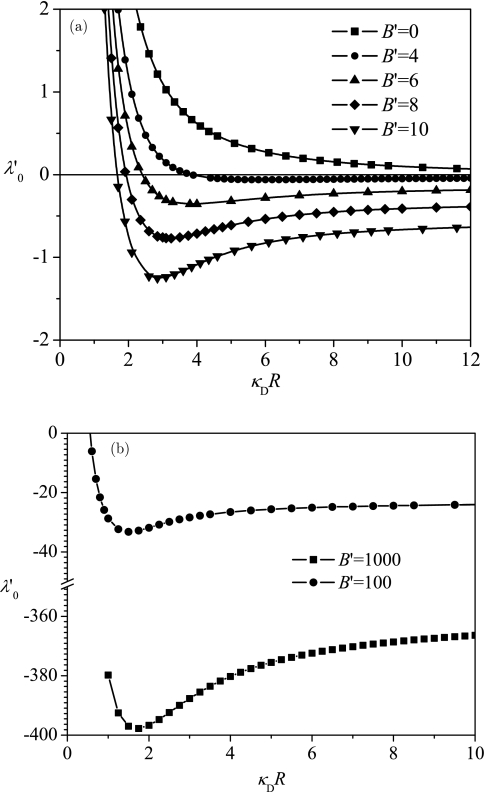
We have calculated the optimum size of the encapsulating sphere for a polyelectrolyte chain of a prescribed length and charge density at a given salt concentration, by the following protocol. First we minimize the free energy with respect to the variational parameter α for different values of R and B^′ to determine the density profile and free energy. In the effective Gaussian chain approximation, $\beta F=\frac{N_p}{6}\frac{b_{eff}}{b}{\kappa }_D^2{b}^2{\lambda }_0^{\prime }$; therefore, ${\lambda }_0^{\prime }$ plays the role as a free energy, and a minimization of F over R is equivalent to a minimization of ${\lambda }_0^{\prime }$ over R. We have found that, only for B^′ larger than the critical value $B_c^{\prime }\simeq 3.207$, bound states implying polyelectrolyte encapsulation are allowed by Eq. 25. The free energy ${\lambda }_0^{\prime }$ given in Eq. 25 is plotted in Fig. 2 as a function of κ_DR for different values of B^′. For all values of $B^{\prime }>B_c^{\prime }$, we observe that ${\lambda }_0^{\prime }$ shows a minimum at a certain value of R, labelled as R^*, which is computed by minimizing the free energy with respect to R. Following this step, we calculate the dependence of R^* on B^′, and explicitly on σ, c_s, z_p, and N_p.

Figure 2.

Typical dependence of the free energy ${\lambda }_0^{\prime }$ on the vesicle radius R (a) at small values of B^′, and (b) at large values of B^′. The curve has a minimum when $B^{\prime }>B_c^{\prime }$, which we define as the optimum radius R^*.

In an effort to seek an understanding of the computed results on the dependence of R^* on B^′, we resolve the entropic ${\lambda }_{0,s}^{\prime }$ and energetic ${\lambda }_{0,u}^{\prime }$ contributions to the free energy, at different values of B^′. ${\lambda }_{0,u}^{\prime }$ and ${\lambda }_{0,s}^{\prime }$ are given by Eqs. 28, 29 as

$$\begin{array}{c}\hfill {\lambda }_{o,u}^{\prime }=-4\pi \gamma \exp (-\gamma ){\int }_0^{\gamma }d\zeta {\zeta }^2{\varphi }_0^2{B}^{\prime }\frac{\sinh \left(\zeta \right)}{\zeta },\end{array}$$ (28)

and

$$\begin{array}{c}\hfill {\lambda }_{0,s}^{\prime }=-4\pi {\int }_0^{\gamma }d\zeta \zeta {\varphi }_0\frac{{\partial }^2}{\partial {\zeta }^2}\left[\zeta {\varphi }_0\left(\zeta \right)\right].\end{array}$$ (29)

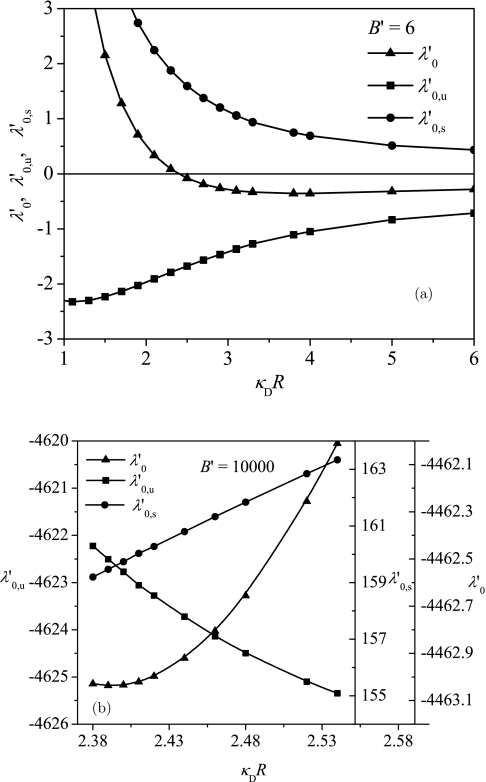
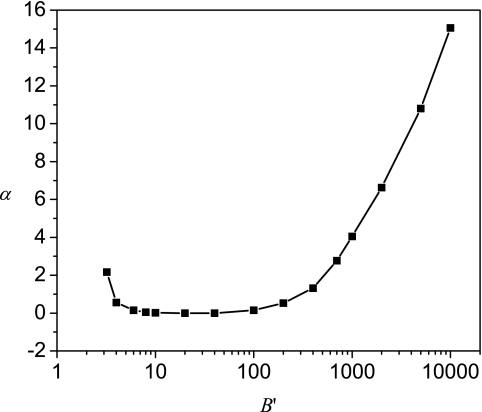
The relative contribution of the entropic part in comparison with ${\lambda }_{0,u}^{\prime }$ depends on the value of B^′. Representative results are given in Fig. 3, where ${\lambda }_{0,u}^{\prime }$ and ${\lambda }_{0,s}^{\prime }$ are plotted against κ_DR at B^′ = 6 and 100 00. As shown in Fig. 3a, for small values of B^′, an increase in the sphere radius R leads to a decrease in ${\lambda }_{o,s}^{\prime }$ and an increase in ${\lambda }_{0,u}^{\prime }$. These opposing trends lead to a minimum in the dependence of ${\lambda }_0^{\prime }$ on R. Although a similar minimum in ${\lambda }_0^{\prime }$ occurs for large B^′ values in Fig. 3b, the dependencies of the entropic and the energetic contributions on the radius are different from those for small values of B^′. For large B^′ values, ${\lambda }_{o,s}^{\prime }$ increases but ${\lambda }_{o,u}^{\prime }$ decreases when the radius is increased. It is to be noted that although the magnitude of the entropic part is an order of magnitude smaller than the energetic part for very large B^′ values, their changes with R are comparable. The different behaviors of ${\lambda }_{o,s}^{\prime }$ and ${\lambda }_{o,u}^{\prime }$ at different values of B^′ can be explained from the different distributions of the polyelectrolyte at various B^′ values. To corroborate further, the value of α that corresponds to R^* is plotted in Fig. 4 against B^′. Using α values, the distribution of polyelectrolyte chain can be obtained by referring to Fig. 1. For small B^′ values, the polyelectrolyte is delocalized. Now an increase in the radius of the sphere leads to less confinement of the polyelectrolyte so that ${\lambda }_{0,s}^{\prime }$ decreases. The ${\lambda }_{0,u}^{\prime }$ naturally becomes less attractive for large R values due to lesser number of monomer contacts at the surface. These are seen in Fig. 3a. On the other hand, for large B^′ values, the polyelectrolyte is strongly adsorbed at the spherical surface. In this case, by increasing the radius, the space near the surface with high attractive potential $\beta {\omega }_{ex}^b$ increases by R² as shown in Eq. 6. Therefore, there are more polymer segments near the surface, which leads to an increase in ${\lambda }_{o,s}^{\prime }$ and a decrease in ${\lambda }_{o,u}^{\prime }$. These trends are clearly seen in Fig. 3b. Therefore, depending on the attraction strength B^′, the encapsulation can be dominated by the attraction or by the entropy.

Figure 3.

R-dependence of the entropic and energetic contributions (${\lambda }_{0,s}^{\prime }$ and ${\lambda }_{0,u}^{\prime }$) to the free energy ${\lambda }_0^{\prime }$ at (a) B^′ = 6 and (b) B^′ = 100 00. Different trends of ${\lambda }_{0,s}^{\prime }$ and ${\lambda }_{0,u}^{\prime }$ lead to a minimum in ${\lambda }_0^{\prime }$.

Figure 4.

B^′-dependence of the variational parameter α at R = R^*.

For the attraction-dominated encapsulation at large B^′ values, the polyelectrolyte chain is absorbed strongly to the sphere; For the entropy-dominated encapsulation at small B^′ values, the polyelectrolyte chain is delocalized in the sphere.

Optimum radius

We now consider the optimum radius of the spherical surface required for the adsorption of the polyelectrolyte of a fixed length. The existence of a minimum of the free energy with respect to a particular sphere radius R implies that the adsorption of the polyelectrolyte and the entropic reduction due to confinement select the radius of the spherical surface. The radius where the minimum free energy appears is defined as the optimum radius R^* and its reciprocal as the spontaneous curvature 1/R^*.

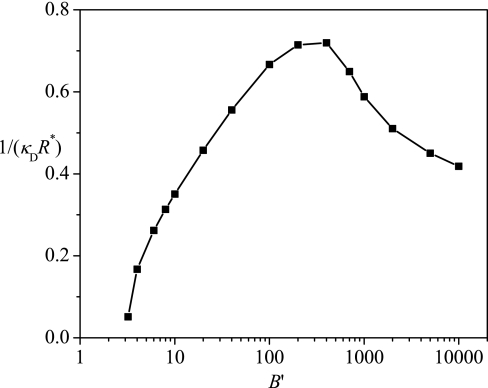
The optimum radius is a function of the parameter B^′. As shown in Fig. 5, the spontaneous curvature varies non-monotonically with B^′. The curve of the B^′-dependent spontaneous curvature can be divided into two branches. For the first branch at smaller B^′ values, the spontaneous curvature increases with increasing B^′ and for the second branch at higher B^′ values, it decreases with increasing B^′. The two-branch behavior of the spontaneous curvature is correlated to the two scenarios of encapsulation discussed above. As already pointed out, for large values of B^′, the chain is localized near the spherical surface so that the chain entropy plays a minor role. However, the R-dependent ${\lambda }_{0,u}^{\prime }$ becomes more attractive as B^′ is increased with a consequent effect of shifting R^* to higher values at higher B^′ values. We call this branch to be the energy-dominated encapsulation. In contract, the other branch of small values of B^′ is dominated by entropic considerations associated with the lack of chain localization. For smaller values of B^′, the chain is considerably delocalized in the interior of the sphere. As B^′ is increased (which being small enough), these are an increasing number of contacts between the surface and the polymer, which then reduces the confinement entropy. Thus, ${\lambda }_{0,u}^{\prime }$ becomes more negative and ${\lambda }_{0,s}^{\prime }$ becomes more positive as B^′ increases. In consideration of these two trends, the free energy minimum shifts to lower values of R^*. We call this branch to be the entropy-dominated branched.

Figure 5.

Dependence of the spontaneous curvature 1/(κ_DR^*) on B^′.

We must point out that the dependence of 1/R^* on B^′ as shown in Fig. 5 is universal and depends on the only parameter B^′ which is a combination of various specific parameters of the model. Because $B^{\prime }=24\pi |\sigma b^2{z}_p|\frac{l_B}{b}\frac{b}{b_{eff}}\frac{1}{{\kappa }_D^3{b}^3}$ and b_eff is a function of z_p, c_s, N_p, and v, we need to work out the dependence of B^′ on these parameters, in order to analyze effects of various parameters on the spontaneous curvature. After getting B^′(σ, z_p, c_s, N_p, v), Fig. 5 can provide a reference to obtain the dependence of the optimum radius on these parameters.

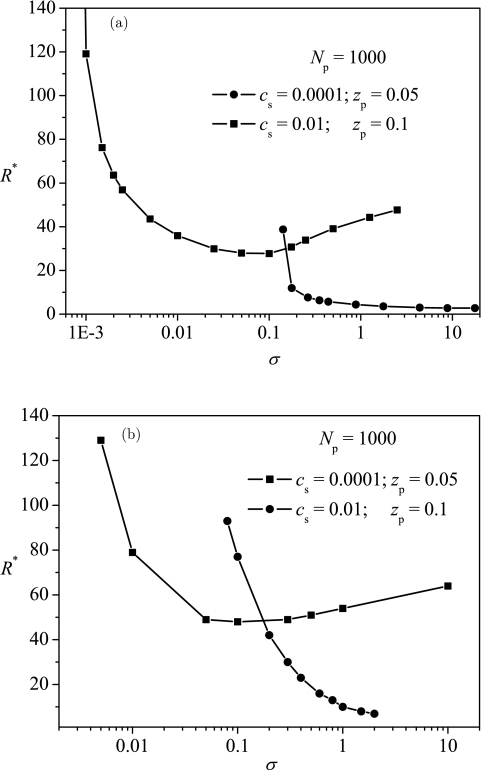
It is easy to obtain the effect of surface charge density σ on R^*. B^′ is linear in σ, so the dependence of R^* on σ is just similar to that on B^′, as shown in Fig. 6a. There will be a critical surface charge density, above which the polyelectrolyte can be encapsulated. At a low surface charge density, an entropy-dominated encapsulation occurs, and the distribution of the polyelectrolyte is delocalized. At a high surface charge density, an attraction-dominated encapsulation occurs, and the distribution of the polyelectrolyte is highly localized near the surface. The results from ScGSDA as shown in Fig. 6b confirm the predictions from EGCA. The effect of salt concentration is also included in Fig. 6.

Figure 6.

Typical dependence of the optimum radius R^* on the charge density of the surface σ with results in (a) from EGCA and results in (b) from ScGSDA.

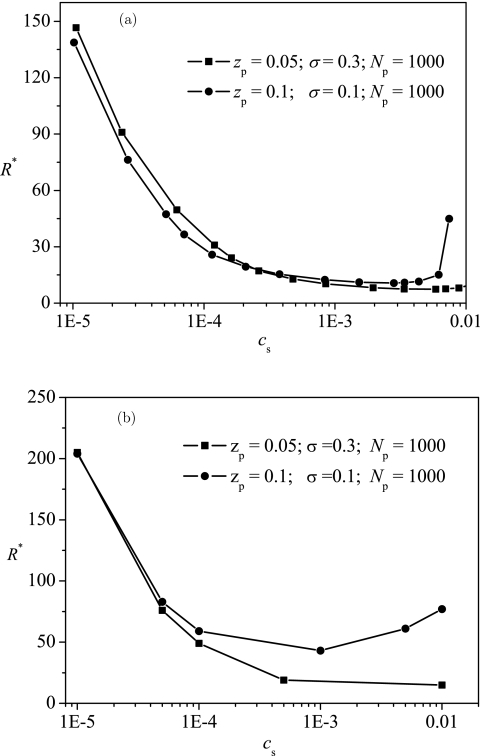
Salt concentration influences both the attraction between the polyelectrolyte and the surface, and the expansion of the polyelectrolyte. Due to the screening effect considered in Debye-Hückel theory used here, by increasing the salt concentration, the attraction decreases by $1∕{\kappa }_D^3$ and the chain expansion also decreases through a decrease in b_eff in EGCA. Our results show that the screening effect is dominant and B^′ decreases monotonically with increasing the salt concentration. According to the relation between 1/R^* and B^′ shown in Fig. 5, it is predicted that by increasing the salt concentration the optimum radius decreases at a low salt concentration but increases at a high salt concentration as shown in Fig. 7a. At a low salt concentration, the attraction is strong, an attraction-dominated encapsulation occurs, and a decrease in the attraction by increasing the salt concentration leads to a decrease the optimum radius. At a high salt concentration, the attraction is weak, an entropy-dominated encapsulation occurs, and a decrease in the attraction by increasing the salt concentration leads to an increase in the optimum radius. The results from ScGSDA shown in Fig. 7b are analogous to the results from EGCA given in Fig. 7a.

Figure 7.

Typical dependence of the optimum radius R^* on the salt concentration c_s with results in (a) from EGCA and results in (b) from ScGSDA.

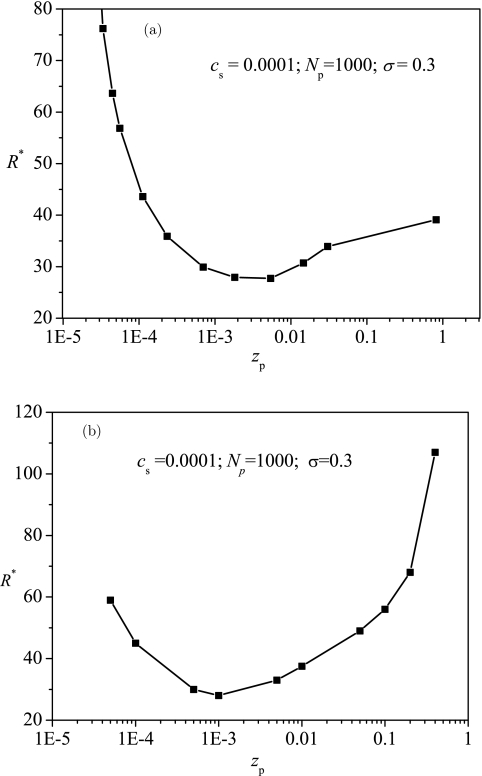
Charge density of the polyelectrolyte also affects both the attraction between the polyelectrolyte and the surface and the expansion of the polyelectrolyte. Roughly speaking, increasing the charge density of the polyelectrolyte, the attraction increases linearly with z_p and the self-repulsion increases by $z_p^2$. The latter leads to an increase in b_eff. The net effect is that B^′ increases monotonically with increasing z_p. With reference to Fig. 5, we get that by increasing z_p, the optimum radius R^* decreases at low z_p values, but increases at high z_p values as shown in Fig. 8a. This result is also confirmed by the results from ScGSDA shown in Fig. 8b. This behavior is explained by the fact that entropy dominates at low z_p and attraction dominates at high z_p. The results from EGCA and ScGSDA are in qualitative agreement. The relatively larger discrepancy at higher values of z_p can be traced to the uniform expansion approximation used in EGCA.

Figure 8.

Typical dependence of the optimum radius R^* on the charge density of the polyelectrolyte z_p with results in (a) from EGCA and results in (b) from ScGSDA.

The above results of the effects of various parameters on the optimum radius R^* further support two scenarios of encapsulation. We know that the encapsulation depends on the competition between the energy gain of adsorption and the entropy loss of confinement. An increase in the salt concentration or a decrease in the charge density of the polyelectrolyte or the surface usually leads to a decrease in attraction. When salt concentration is high enough or the charge density of the polyelectrolyte or the surface is low enough, the entropy loss will dominate over the attraction. In this case, if we decrease the attraction, by increasing the salt concentration or decreasing charge densities of polyelectrolyte or surface, the optimum radius tends to increase. On the other hand, when salt concentration is low enough and the charge density of polyelectrolyte and surface is high enough, the attraction will dominate. In this case, if we decrease the attraction, by increasing the salt concentration or decreasing charge densities of polymer chain or membrane, the optimum radius tends to decrease.

Similar to the above deduction, we can analyze the effect of the excluded volume interaction. In EGCA, the excluded volume interaction only affects the expansion of polyelectrolyte. Larger excluded volume interaction v (improving the quality of solvent) leads to larger b_eff and smaller B^′. So improving the solvent quality, we conjecture that the encapsulation evolves from an attraction dominated scenario to an entropy dominated case.

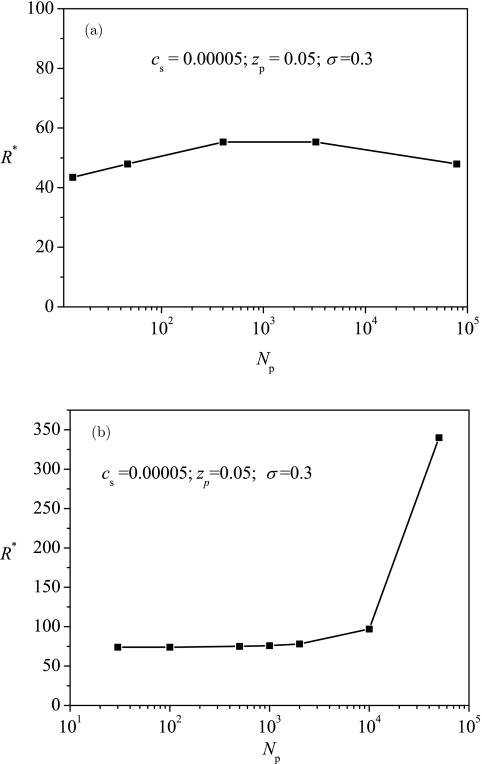
Despite the good qualitative agreement between the EGCA and ScGSDA results for the above considered parameters, an exception arises for the chain length dependence of R^*. In EGCA, the chain length of polyelectrolyte affects B^′ only weakly through b_eff. As a consequence, R^* depends on chain length only weakly, as shown in Fig. 9a. Under the same conditions of Fig. 9a, ScGSDA results in Fig. 9b show that the optimum radius increases with increasing the chain length. For small values of N_p, the increase is very slight, but for large values of N_p, the increase is rapid. The results from ScGSDA are consistent with the two scenarios of encapsulation. At small values of N_p, the attraction is relatively strong because the expansion is weak, and consequently the polyelectrolyte is strongly adsorbed to the surface. Both the adsorption and entropy are apparently proportional to the polymer chain length. Therefore, in this case, the polyelectrolyte chain length only has a small effect on the optimum radius. On the other hand, For large values of N_p, the attraction is relatively weak because the expansion is strong, and consequently the polyelectrolyte is delocalized and thus the electrostatic self-repulsion of polyelectrolyte chain is dominant. The electrostatic self-repulsion is $N_p^2$-dependent and therefore the optimum radius should increase rapidly as the chain length is increased.

Figure 9.

Typical dependence of the optimum radius R^* on the chain length of the polyelectrolyte N_p with results in (a) from EGCA and results in (b) from ScGSDA.

CONCLUSIONS

The encapsulation of a polyelectrolyte chain by an oppositely charged spherical surface is studied using the ground state dominance approximation, with emphasis on the optimum radius of the spherical surface to encapsulate the polyelectrolyte. The encapsulation is governed by the competition between the electrostatic attraction between the polyelectrolyte and the surface and the entropy loss of the encapsulated polyelectrolyte. Two scenarios of encapsulation are identified: when the attraction is dominant, the polyelectrolyte is localized around the surface, and the optimum radius increases with increasing the attraction; when the polymer-surface interaction is weak, the polyelectrolyte is delocalized and the optimum radius decreases with increasing attraction.

Here we only consider the free energy of the polyelectrolyte and neglect the self-interaction of the charged surface. The present model is valid for a polyelectrolyte encapsulated in a solid cavity. If the surface is a fluid membrane, as in endocytosis, the self-interaction and the elasticity of the membrane should be considered. In this case the spontaneous curvature, we get in this paper, is an additional spontaneous curvature of the membrane induced by the encapsulated polyelectrolyte.

All of our results presented are based on the ground state dominance approximation. The approximation is valid in the limit of long chain polyelectrolyte and dilute solution condition. In systems where the polyelectrolyte concentration is not dilute, the entropy of solvent should be taken into account and more eigenfunctions should be included. In addition, the electrostatic self-energy of the confinement,³⁸ the entropy of counterions and salt ions are also neglected in this paper.