Perceptual Sensitivity to High-Frequency Interaural Time Differences Created by Rustling Sounds

Abstract

Interaural time differences (ITDs) can be used to localize sounds in the horizontal plane. ITDs can be extracted from either the fine structure of low-frequency sounds or from the envelopes of high-frequency sounds. Studies of the latter have included stimuli with periodic envelopes like amplitude-modulated tones or transposed stimuli, and high-pass filtered Gaussian noises. Here, four experiments are presented investigating the perceptual relevance of ITD cues in synthetic and recorded “rustling” sounds. Both share the broad long-term power spectrum with Gaussian noise but provide more pronounced envelope fluctuations than Gaussian noise, quantified by an increased waveform fourth moment, W. The current data show that the JNDs in ITD for band-pass rustling sounds tended to improve with increasing W and with increasing bandwidth when the sounds were band limited. In contrast, no influence of W on JND was observed for broadband sounds, apparently because of listeners' sensitivity to ITD in low-frequency fine structure, present in the broadband sounds. Second, it is shown that for high-frequency rustling sounds ITD JNDs can be as low as 30 μs. The third result was that the amount of dominance for ITD extraction of low frequencies decreases systematically with increasing amount of envelope fluctuations. Finally, it is shown that despite the exceptionally good envelope ITD sensitivity evident with high-frequency rustling sounds, minimum audible angles of both synthetic and recorded high-frequency rustling sounds in virtual acoustic space are still best when the angular information is mediated by interaural level differences.

Introduction

Evolution has shaped the mammalian binaural system for fast and accurate sound localization in the horizontal plane. The duplex theory (Rayleigh 1907) states that the binaural system relies on the analysis of interaural time differences (ITDs) and level differences (ILDs) for low-frequency and high-frequency sounds, respectively. Meanwhile, it is well documented that the binaural system can also analyze ITDs of the envelopes of both periodic and aperiodic high-frequency sounds (e.g., Klumpp and Eady 1956; Tobias and Schubert 1959; Yost et al. 1971; Henning 1974; McFadden and Pasanen 1976; Amenta III et al. 1987).

To quantify localization acuity in the horizontal plane, ITD just noticeable differences (JNDs) have been measured for various types of modulators imposed on high-frequency, pure-tone carriers: with a simple sinusoidal modulator, ITD JNDs were as good as about 100 μs (Nuetzel and Hafter 1976; Bernstein and Trahiotis 1985). Dye et al. (1994) investigated the effect of the number and phase of individual harmonics of harmonic modulators imposed on a high-frequency pure-tone carrier. They showed that envelope ITD JNDs improved with increasing degree of envelope fluctuations. Van de Par and Kohlrausch (1997) introduced a new family of high-frequency stimuli, transposed tones, which were designed to carry the phase-locked temporal information of a low-frequency pure tone in the envelope of a high-frequency tone. Bernstein and Trahiotis (2002, 2003, 2007) subsequently showed that envelope ITD JNDs with transposed tones can be almost as good as for their low-frequency, pure-tone counterparts. Similarly, raised-sine stimuli, where the modulator of a pure-tone carrier is passed through a power-law expansion, lead to ITD JND improvements with increasing exponent (Bernstein and Trahiotis 2009). In general, however, envelope ITD JNDs are rarely smaller than about 100 μs (Ewert et al. 2009; Klein-Hennig et al. 2011).

With respect to the effect of aperiodic vs. periodic envelope fluctuations on ITD JNDs, Hafter and Buell (1990) have shown that an interruption of a periodic envelope fluctuation can elicit a recovery from binaural adaptation, i.e., the decline in the usefulness of interaural information after the signal's onset when the clicks in a click train are presented at a high rate. Thus, localization acuity may be enhanced by aperiodic envelope fluctuations. Using filtered Gaussian noise stimuli or clicks, several authors have shown that envelope ITD JNDs are quite good with aperiodic stimuli and that JNDs improve with increasing bandwidth (Klumpp and Eady 1956; Yost et al. 1971; McFadden and Pasanen 1976; Amenta, III et al. 1987).

Aperiodic high-frequency sounds have a strong behavioral relevance: rustling sounds, generated by, e.g., a prey animal or predator approaching over a leaf-littered ground need to be located fast and accurately. Such sounds are dominated by high frequencies and extend well even into the ultrasonic range. As natural masking sounds originating from, e.g., wind or water are typically low-pass shaped as a consequence of atmospheric attenuation and occlusion, they will result in more masking in the low-frequency range emphasizing the importance of high-frequency components for rustling-sound localization. Although rustling sounds can be considered as stochastic, noise-like sounds, their envelope characteristics can be very different from those of Gaussian noise: specifically, the degree of envelope fluctuation of rustling sounds can be much higher than that of Gaussian noise, a feature which may facilitate the exploitation of envelope ITDs for sound localization. For periodic envelope fluctuations, this facilitation has been demonstrated (Dye et al. 1994; Bernstein and Trahiotis 2007).

The aim of the current study was to investigate the salience of ITD cues for the localization of rustling sounds. First, ITD JNDs were measured for rustling sounds, both broadband and band-pass filtered, to assess the extent to which ITD JNDs improve with increasing envelope fluctuations. Second, it was assessed whether the spectral dominance region for ITD sensitivity, which has been shown to lie around 700 Hz (Stern and Colburn 1978; Raatgever 1980; Stern et al. 1988), is affected by envelope fluctuations. Finally, it was investigated whether envelope ITD cues provided by rustling sounds may be strong enough to dominate ILD cues for horizontal sound localization. It was assessed to what extent the rustling-sound data can be modeled with existing models, which have been mainly tested with periodic stimuli in the past.

Experiment I: ITD JNDs for Broadband and Band-Pass Rustling Sounds

Stimuli

Stimuli were “sparse noises” (Hübner and Wiegrebe 2003; Grunwald et al. 2004) which were generated by modulating a Gaussian noise with an aperiodic pulse-train modulator. The modulator consisted of pulses which had a value of one for only a single sample (22.7 μs at 44.1-kHz sampling rate) separated by random-duration temporal gaps. The gap duration was randomly drawn with a uniform distribution between zero and a fixed maximum number of samples. The higher this maximum value was, the higher was the resulting degree of envelope fluctuation. The amplitude distribution of the resulting sounds thus deviates from Gaussian noise, showing a strong overrepresentation of low amplitude values imposed on the otherwise Gaussian amplitude distribution. Hartmann and Pumplin (1988) have provided means to quantify noise power fluctuations, among them the fourth moment of the envelope (Y), as investigated by, e.g., Bernstein and Trahiotis (2007) or the fourth moment of the waveform (W), as has been used by, e.g., Huebner and Wiegrebe (2003) and Grunwald et al. (2004). Bernstein and Trahiotis (2007, 2010) have shown that perceptually, Y is not a good predictor of envelope ITD sensitivity. The same must be assumed to apply for W given that for band-limited stimuli Y is equal to two thirds of W (Hartmann and Pumplin 1988). Here, W is used only as a physical descriptor for the degree of power fluctuations of the stimuli. W offers the advantage that it does not require the calculation of the Hilbert envelope which is not properly defined for broadband stimuli.

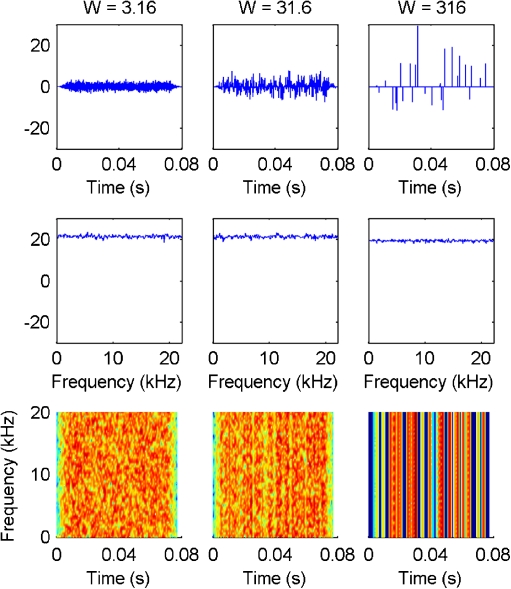
Waveforms, power spectra, and spectrograms for three sparse noises with three different values of W are shown in Figure 1. A W of 3.16 corresponds to a gap duration of 0 μs, i.e., Gaussian noise. A W of 31.6 is generated with a maximum gap width of 362 μs. A W of 316 is generated with a maximum gap width of 5.8 ms. While the long-term power spectra of the stimuli are not affected by an increase in W, the spectrograms reveal an increasing degree of comodulation (represented by the vertical stripes) with increasing W. The stimuli were either presented broad band (20–20,000 Hz) or were band-pass filtered. Band-pass filters were geometrically centered around 4 kHz with bandwidths of 770, 1,470, 3,330, and 6,000 Hz. The filters were fourth-order Butterworth high- and low-pass filters resulting in a slope of 24 dB/octave. Filtering was always performed after the application of the modulator. Thus, the band-pass filtering decreased the effective degree of fluctuation with decreasing bandwidth (see below). In the case of the band-pass filtered stimuli, a continuous, dichotic background (Gaussian) noise, low-pass filtered at 1 kHz (24 dB/octave) was presented at a level of 50 dB SPL to mask aural distortions. The stimulus duration was 300 ms, including 20-ms raised-cosine ramps. ITDs were applied in the frequency domain by manipulating the phase spectrum. The gating was applied after the ITD, i.e., the raised-cosine ramps for the two ears had always zero ITD. Sounds were digitally generated at a sampling rate of 44.1 kHz. They were played back via an RME Audio Digi 96/8 PST sound card and AKG K240 DF circumaural headphones at an average level of 60 dB SPL (with a ±6 dB level roving). Headphones were calibrated, both in magnitude and phase, on a Bruel and Kjaer 4153 artificial ear. All stimuli were convolved with the resulting compensation impulse response before digital-to-analog conversion. Independent noise realizations were used for each presentation.

FIG. 1.

Waveforms (upper row), power spectra (middle row), and spectrograms (lower row) of sparse noise as a function of different degrees of power fluctuations (W). All three stimuli share the same long-term power spectrum and the same RMS. The increase in W is reflected in the emergence of vertical stripes in the spectrogram. The color code in the spectrograms spans a range from 0 dB (blue) to 50 dB (red).

Procedure

An adaptive, four-interval, two-alternative, forced-choice paradigm with visual feedback was used to measure envelope ITD JNDs. Three of the four stimuli were presented at an ITD of 0 μs (diotically), and either the second or the third stimulus had a non-zero ITD. At the beginning of the adaptive track, the test ITD was randomly chosen between 300 and 600 μs. This test ITD was changed by factors of 1.5, 1.2, and 1.1 for reversals one to three, four to five, and six to 11, respectively. The ITD threshold for an adaptive run was taken as the arithmetic mean of reversals six to 11. Presented thresholds were averaged across at least three runs per listener for the broadband condition and six runs per listener for the narrowband conditions. The occurrence of intervals and the feedback was presented via a graphical user interface on an 8-in. touch screen which was also used by the listeners to indicate their response.

Listeners were three normal-hearing females and one male, aged between 24 and 30 years. They were individually seated in a double-walled sound attenuating booth (G + H Schallschutz). Listeners were given extensive training before data acquisition.

Results and discussion

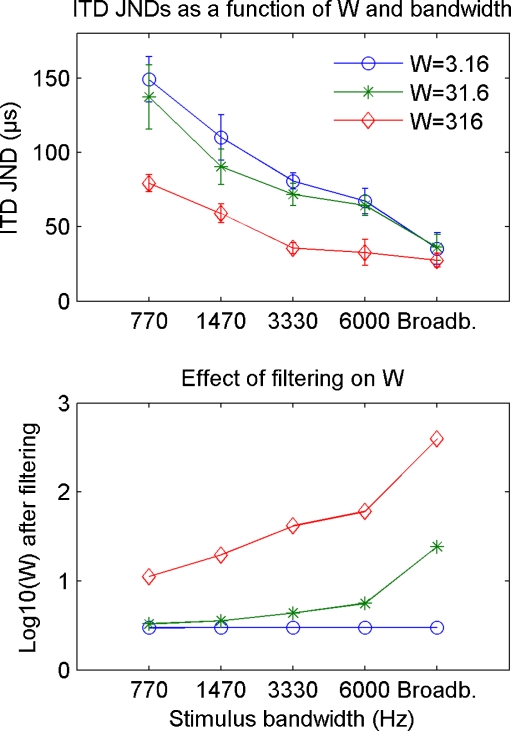
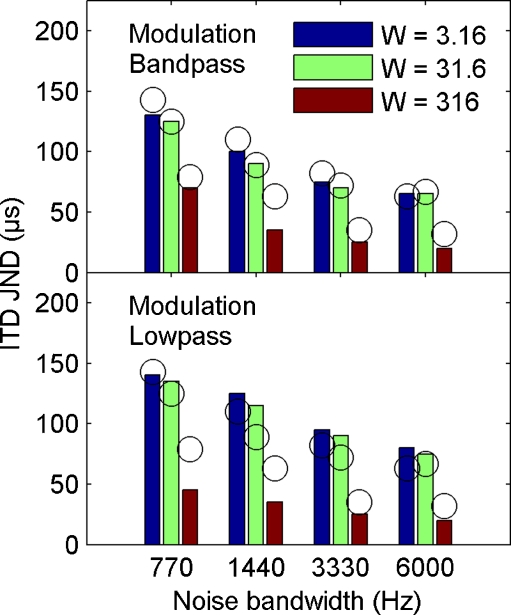
ITD JNDs are shown as a function of stimulus bandwidth in Figure 2. The data show that ITD JNDs improve significantly with increasing bandwidth. ITD JNDs also improve with increasing W, especially for the band-pass filtered stimuli. This improvement is particularly pronounced when W was increased from 31.6 to 316. For the band-limited conditions, both the effect of bandwidth and the effect of W on the ITD JND are significant (see figure caption). The data show that, in line with previous reports on the effect of envelope fluctuations on ITD JNDs (Dye et al. 1994; Bernstein and Trahiotis 2007), an increased W of high-frequency rustling sounds improves ITD JNDs. For the broadband condition, there was no significant effect of W on ITD JNDs (p = 0.87, df = 2, χ² = 0.27; Kruskal–Wallis non-parametric one-way ANOVA).

FIG. 2.

Upper panel: mean ITD JNDs of broadband and band-pass filtered sparse noises as a function of bandwidth. The different colors represent data for different degrees of power fluctuations (W). Error bars represent standard errors across four listeners. ITD JNDs improve both with increasing bandwidth and with increasing W. For the band-limited conditions, both the effect of bandwidth and the effect of W on the ITD JND are significant (df = 2, χ² = 26.61, p < 0.0001 for the effect of W; df = 2, χ² = 30.55, p < 0.0001 for the effect of bandwidth, Friedman’s non-parametric two-way ANOVA). The lower panel shows the distribution of W of the stimuli after filtering. For the stimuli with higher broadband W (31.6 and 316), decreasing the bandwidth decreases W but this effect is absent for W = 3.16 (Gaussian noise). These data show that the effect of filtering on W cannot fully describe the pattern of results.

Band-pass filtered stimuli with a W of 316 allow for very good ITD JNDs between 30 and 40 μs (red line in upper panel of Fig. 2). Compared to previously reported envelope ITD JNDs (Bernstein and Trahiotis 2002, 2007; Dietz et al. 2009) which are typically not lower than about 80 μs even for transposed harmonic series, the current ITD JNDs appear exceptionally good. Possible reasons are given in the general discussion below.

Band-pass filtering of the stimuli decreased their effective W. This is illustrated in the lower panel of Figure 2 where the base-10 logarithm of W of the stimuli is plotted as a function of stimulus bandwidth. It is obvious that for the higher values of W (31.6 and 316) the band-pass filtering results in a systematic decrease of W with decreasing bandwidth. This is consistent with the idea that stimuli with a higher W produce smaller ITD JNDs. It should be noted, however, that for the smoothest stimulus, Gaussian noise (W = 3.16), the effective W is not affected by filtering. The strong improvement in ITD JNDs with increasing bandwidth for these stimuli thus cannot be accounted for by stronger envelope fluctuations but by bandwidth per se. Consequently, the JND improvements observed for the stimuli with higher broadband W (31.6 and 316) should be regarded as resulting from both increased bandwidth and increased W.

To quantify the relative effects of W and bandwidth, a second-order polynomial was fitted to the data. The non-linear model with the two parameters base-10 log of W after filtering and base-10 log of the bandwidth in hertz could explain 96.5% of the variance of the experimental data. When only the base-10 log of W before filtering was given as the parameter, the model predictions were considerably worse, explaining only 24.5% of the variance. With the base-10 log of W after filtering (cf. lower panel in Fig. 2) as the only parameter, agreement between data and predictions was also poor; only 46.9% of the variance was explained. Likewise, when only the base-10 log of the bandwidth in hertz was given as a parameter, 68.6% of the variance was explained by the model. In conclusion, both bandwidth and W after filtering contribute to the observed ITD JNDs to a roughly similar extent.

The fact that an improvement of ITD JNDs with increasing W was not observed with broadband stimuli indicates that the advantage the listeners receive from increasing envelope fluctuations at high frequencies may be swamped by the salience of low-frequency ITD information mediated by the noise fine structure. The relative salience of ITDs in different frequency regions was investigated in more detail in the following experiment II.

Experiment II: Spectral Dominance of ITD Extraction

Earlier studies have shown that for Gaussian-noise ITDs, the spectral dominance region lies around 700 Hz (Stern and Colburn 1978; Raatgever 1980; Bilsen and Raatgever 2000). Considering the result of experiment I that the salience of envelope ITDs increases with increasing W, the question arises whether W affects the spectral dominance region for ITD extraction. This experiment quantifies the extent to which the ITDs occurring in different frequency regions of a broadband stimulus contribute to the overall perception of laterality. The experimental design chosen to address this question is motivated by classical measures of spectral dominance of pitch perception (Ritsma 1967; Moore et al. 1985): listeners were required to trade opposing ITDs applied to a target-band region and the complementary band-stop (“outside the target band”) region of a broadband noise. The hypothesis was that if the selected target-band region contributed strongly to ITD sensitivity, a large leftward ITD in the corresponding outside-target-band region would be required to compensate for a rightward ITD in the target band. Here, the same paradigm was used for broadband stimuli with different values of W. The current paradigm can only describe the salience of different frequency regions relative to each other. Unlike in the work of, e.g., Macpherson and Middlebrooks (2002), the current paradigm does not allow assigning absolute weights to given frequency regions of a broadband sound.

Stimuli

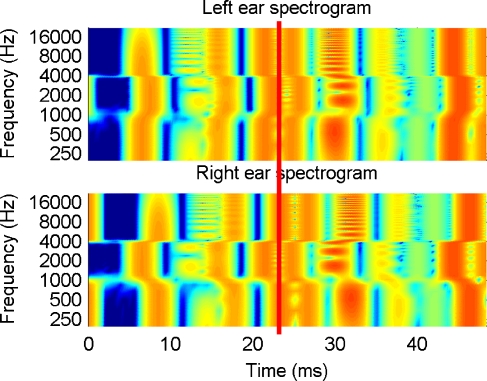
Stimuli were the broadband noises (full audio bandwidth) with the three different values of W from experiment I. In the test stimulus, different ITDs were applied to different frequency regions: in a two-octave target-band region, a 300 μs, rightward ITD was applied. In the corresponding outside-target-band region of the test stimulus, an adjustable ITD (dependent variable) was applied. Target-band center frequencies were equally spaced on a log frequency axis between 250 and 8,000 Hz. Filtering was implemented as frequency-domain (“brickwall”) filtering with very steep slopes, limited only by the Fourier window which was set equal to the stimulus duration of 300 ms. As in experiment I, ITDs were applied as phase manipulations in the frequency domain to allow for ITD changes smaller than one sample, in this case independent in the two different frequency regions. Stimuli were gated on and off with 20-ms raised-cosine ramps. An illustration of the spectro-temporal structure of the test stimuli is shown in Figure 3. The reference stimulus was a diotic broadband noise with the same W as the test stimulus. Stimulus duration and level were identical to experiment I. In contrast to experiment I, there was no dichotic, continuous background noise.

FIG. 3.

Spectrograms for left- and right-ear sparse-noise stimulus with different ITDs applied to different frequency regions. The target-band region between 1 and 4 kHz has a 1-ms ITD with the right ear leading, the complementary outside-target-band frequency range has a 1-ms ITD with the left ear leading. Thus, identical temporal features occur earlier in the right ear in the 1–4-kHz target band, and earlier in the left ear in the outside-target band. For illustrative clarity, the chosen ITDs are larger than those used in the experiment. Sound levels are again color coded (blue = −20 dB, red = +40 dB).

Procedure

ITD–ITD trading matches were determined using an adaptive two-interval, two-alternative forced-choice paradigm without feedback. Each trial consisted of two stimuli with the first stimulus being the reference (with zero ITD in any frequency region) and the second being the test stimulus with different ITDs in different frequency regions. Listeners indicated whether they lateralized the test left or right of the reference. If the listeners lateralized the test stimulus left of the reference, the leftward ITD of the outside-target-band region of the test stimulus was decreased for the next trial; otherwise, it was increased. In some experimental conditions, listeners reported to perceive two spectrally different images with different lateralizations (see “Results” section below). Listeners were instructed to estimate an average lateralization forming the center of gravity of the split images in this case and to compare this average lateralization with that of the (diotic) reference stimulus. ITD step sizes were 50 μs for the first two reversals, 20 μs for reversals three to five, and 10 μs for reversals six to 11. The adjusted outside-target-band ITD was taken as the arithmetic mean across reversals six to 11. The outside-target-band ITD at the beginning of each adaptive run was set randomly between 300 and 600 μs leading on the left side. The presented trading data are based on the average across three adaptive runs. In addition to the four listeners (L1–L4) who already participated in experiment I, three additional listeners (two females, one male, aged between 23 and 25 years) took part in this experiment.

Results

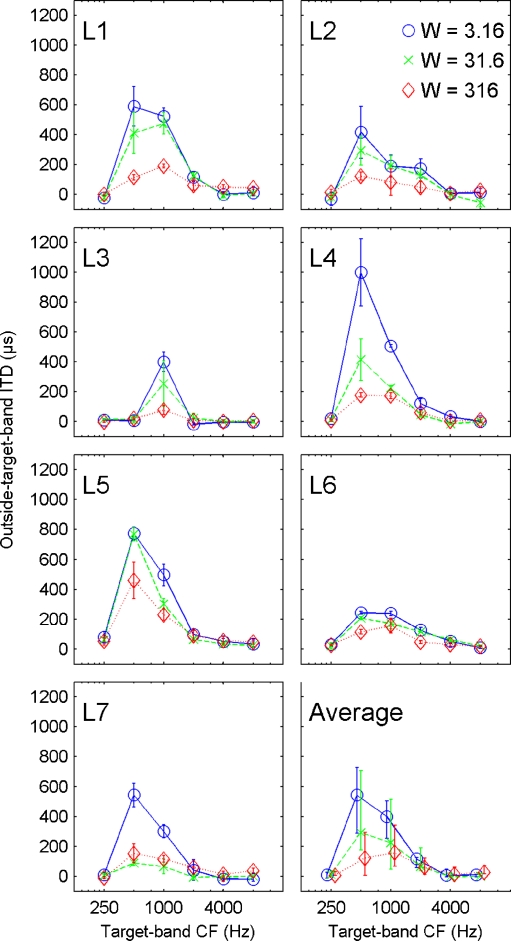
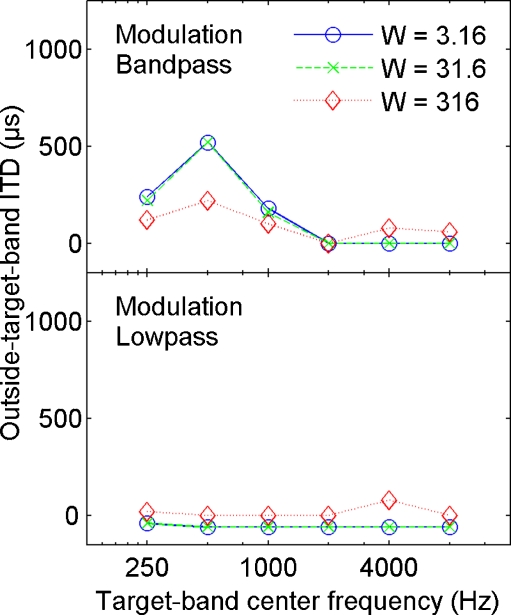
The leftward ITD adjusted in the outside-target-band region of a broadband noise to compensate for a rightward ITD in the target-band region of the same noise is plotted as a function of target-band center frequency in Figure 4. Data for stimuli with different W are shown with different colors and symbols. Panels represent individual data (L1–L7); the medians and interquartiles across listeners are shown in the lower right panel. It is observed that the largest outside-target-band ITDs were required for a compensation of perceived lateralization when the target-band center frequency was 500 or 1,000 Hz. This observation confirms earlier results that a two-octave frequency region around these center frequencies dominates ITD extraction in broadband stimuli (Stern and Colburn 1978; Raatgever 1980; Bilsen and Raatgever 2000). In the current data, a systematic effect of W on the outside-target-band ITD is observed: the largest outside-target-band ITD was always required for compensation for stimuli with the lowest W (3.16). The ITD of the outside-target-band region required to compensate for the opposing ITD in the target-band region decreases with increasing W. In the average data (lower right panel of Fig. 4), this decrease is significant for a center frequency of 1,000 Hz (Kruskal–Wallis, p < 0.01, df = 2, χ² = 9.24).

FIG. 4.

Spectral dominance of ITD extraction and the effect of W. Each panel shows the left-ward ITD in the outside-target-band frequency range around the CF to perceptually compensate for a right-ward ITD in the band-pass frequency range around the same CF (target band). Data are shown for three values of W, 3.16 (blue, open circles and solid lines), 31.6 (green, x symbols and dashed lines), and 316 (red, open diamonds and dotted lines). The figure shows both individual data (VP1–7) and the average data (lower right panel, median and interquartile ranges). For each listener, the required outside-target-band ITD to compensate for a target-band ITD is highest for target bands around 500 or 1,000 Hz, indicating that this frequency range dominates ITD extraction. This low-frequency dominance, however, appears to decrease systematically with increasing W. In the average data, this decrease is significant for a CF of 1 kHz (Kruskal–Wallis, df = 2, χ² = 9.24, p < 0.01).

It is important to note that in the test stimulus, listeners often reported to perceive two distinct images with different lateralizations corresponding to the spectral region of the target-band and the outside-target-band. In this case, they had to weight these images against each other to form a summary lateralization (center of gravity) which was matched with the lateralization of the (diotic) reference stimulus. To confirm that the listeners could reliably perform the comparison of the center of gravity with the diotic reference stimulus in case of split image percepts, a control experiment was performed which gave nearly identical results. In the control experiment, the reference stimulus was a left-right flipped version of the test stimulus (compare to experiments 3 and 4 of Dietz et al. 2009) which produced corresponding split images with flipped left–right direction. In this case, subjects had to match the lateralization of the estimated center of gravity for test and reference while any potential bias effects related to the fixed direction of the target-band ITD were removed.

In conclusion, the data demonstrate that with increasing W, high frequencies become more effective at countering the target-band ITDs in the low-frequency region (with fine structure assessable by the auditory system) of broad-band stimuli.

Model simulations

The results from experiments I and II show that although perceptual sensitivity to ITDs of rustling sounds does not appear to improve with increasing W for broadband stimuli, an increase of W leads to improvements of ITD JNDs for high-frequency, band-limited rustling sounds where ITD JNDs are mediated by the envelope. In the following, these data, and the data of experiment II (effect of the envelope fluctuations on the dominance region) are compared to model simulations based on the established cross-correlation model of binaural processing (Stern et al. 1988; Hartung and Trahiotis 2001; Bernstein and Trahiotis 2002, 2007). Two model versions were implemented. The first model (in the following referred to as modulation lowpass model) used the preprocessing stages of the model of Bernstein and Trahiotis (2002) while some stages were modified in the second model (referred to as modulation bandpass model) to better account for the current data. The implementation of the modulation lowpass model consisted of a combined middle-outer-ear filter (first-order highpass at 1,000 Hz, first-order lowpass at 4,000 Hz; Breebaart et al. 2001) followed by a gammatone filterbank with center frequencies equally spaced on an ERB (equivalent rectangular bandwidth; Glasberg and Moore 1982) axis. The center frequencies of the filters were between 1 and 10 kHz for experiment I and between 100 Hz and 10 kHz for the broadband stimuli used in experiment II. The next stages were half-wave rectification, power-law compression (exponent = 0.46), and lowpass filtering (425-Hz fourth-order; Weiss and Rose 1988). For the auditory channels with center frequencies at and above 1 kHz, an additional modulation lowpass filter (first-order, 150 Hz) was the final stage of the preprocessing.

In the modulation bandpass model, the following preprocessing stages were modified: the exponent in the power-law compression was changed to 0.4 and a 770-Hz fifth-order lowpass filter was used as in Breebart et al. (2001). The modulation lowpass filter in the auditory channels at and above 1 kHz was replaced by a second-order modulation band-pass filter (Ewert and Dau 2000; Ewert et al. 2002) with a center frequency of 300 Hz.

The preprocessing of both models was followed by a channel-wise binaural cross-correlation with a maximum correlation lag of 3 ms. Finally, cross-correlation functions were summed across frequency to create a summary cross-correlogram. In contrast to the model by Bernstein and Trahiotis (2002), the cross-correlations in the different frequency channels were not normalized. As a consequence, frequency channels with weaker auditory excitation contributed less to the summary cross-correlogram. In contrast to the classical simulations, e.g., Stern et al. (1988), no specifically adjusted frequency weighting function was applied but the middle-outer-ear filter combined with the un-normalized cross-correlation resulted in effectively larger weights of the 1,000–4,000-Hz frequency region.

For experiment I, the decision device was based on the root-mean-square (RMS) distance between the summary crosscorrelogram of the diotic (zero ITD) stimulus and the summary cross-correlogram of the stimulus with non-zero ITD. The RMS distance was calculated for ITDs between 0 and 300 μs in 5-μs steps. Predicted ITD JNDs were based on a fixed RMS distance criterion for all experimental conditions. The RMS distance criterion was chosen to minimize the RMS error between the model predictions and the data.

For the simulation of the dominance region experiment (experiment II), the summary cross-correlograms were calculated for the reference stimulus and for test stimuli with the experimentally applied rightward target-band ITD of 300 μs, and with a range of outside-target-band ITDs from 60 μs towards the right to 600 μs towards the left in 20-μs steps. The decision device was based on the center of gravity of the summary cross-correlograms. The outside-target-band ITD which, together with the fixed target-band ITD of 300 μs, resulted in a center of gravity closest to that of the reference stimulus (0 μs ITD at all frequencies) was selected as simulation result. The center of gravity was chosen to mimic the perception of the subjects who matched the center of gravity of two spatial images for the two spectral regions to the single spatial image of the reference stimulus.

The model predictions for experiment 1 are shown in Figure 5. The upper panel shows the predictions of the modulation bandpass model while the lower panel is for the modulation lowpass model. The open circles indicate the experimental results from Figure 2. Both models predict the general improvement of ITD JNDs with increasing bandwidth. Both models also predict considerably improved ITD JNDs when W increases from 31.6 to 316. The modulation bandpass model additionally accounts for the JND differences between the W = 3.16 and 31.6 conditions for bandwidth up to 3,330 Hz, and shows no difference between these conditions at a noise bandwidth of 6,000 Hz. In contrast, the modulation lowpass model cannot account for this change between 3,330 and 6,000 Hz. Furthermore, the modulation lowpass model predicts a too small ITD JND for W = 316 and a noise bandwidth of 770 Hz. Overall, the modulation bandpass model performs better, predicting 94.4% of the variance in the data (modulation lowpass model = 81.2%). The root-mean-square error (RMSE) between model predictions and data amount to 30.4 μs and 58.7 μs for the modulation bandpass and lowpass model, respectively.

FIG. 5.

Simulation of ITD JNDs for rustling sounds for the modulation bandpass (upper panel) and lowpass model (lower panel). Experimental data are shown with open circles; simulation results are shown with colored bars. Both models capture the dependence of ITD JNDs on bandwidth and W reasonably well. The modulation bandpass model shows an overall better agreement with the data.

Model predictions for experiment II are shown in Figure 6 in the same format as the experimental data (cf. Fig. 4, lower right). Again, the upper panel displays predictions for the modulation bandpass model while the lower panel is for the modulation lowpass model. In qualitative agreement with the experimental data, the modulation bandpass model predicts that the strongest outside-target-band ITDs are required to counteract a target-band ITD centered around 500 Hz. This is an emergent property of the model and is not a simple reflection of the middle-ear band-pass filter. When the band-pass cutoff frequencies were changed from 1,000 and 4,000 Hz to (physiologically implausible) 100 and 14,000 Hz, the dominance of the 500-Hz center frequency persisted.

FIG. 6.

Simulation of the spectral dominance experiment (experiment II). Upper and lower panels are for the modulation bandpass and lowpass model, respectively. In qualitative agreement with the experimental data (cf. Fig. 4, lower right), the modulation bandpass model predicts the largest outside-target-band ITDs to compensate a target-band ITD applied at 500 Hz. The model also predicts that this required outside-target-band ITD decreases with increasing W of the stimuli, at least when W increases from 31.6 to 316. The modulation lowpass model in the lower panel fails to account for the data.

Also in qualitative agreement with the data, the predicted outside-target-band ITD of the modulation bandpass model is smaller for the stimuli with the highest W while there is no difference in the predicted values between the broadband W of 3.16 or 31.6. This result can be explained by the effective W at the output of a 500-Hz gammatone filter: when this filter is fed with stimuli with a broadband W of 3.16 or 31.6, the resulting effective W of the filter output is virtually identical. Only when the broadband W is increased to 316, the envelope fluctuations are strong enough to be partially retained at the filter output.

The modulation lowpass model (lower panel of Fig. 6) completely fails to predict the effects observed in the data. The model predicts outside-target-band ITDs close to zero for all target-band center frequencies. This property of the model is related to the modulation lowpass characteristic which passes the DC component of the envelope (corresponding to the stimulus power) and the slow envelope fluctuations. This resulted in generally quite flat cross-correlograms with a corresponding center of gravity near zero.

As an alternative approach, the RMS distance measure, as utilized in the model predictions of experiment I, was employed here and the results are described in the following. In this case, the decision device selected that outside-target-band ITD which, together with the fixed target-band ITD of 300 μs, resulted in the minimum RMS distance between summary cross-correlograms of the test and the reference stimulus (0 μs ITD at all frequencies). This approach was additionally tested with the inclusion of the correlation tau-weighting function of Stern et al. (1988). The predictions for the modulation bandpass model were in both cases qualitatively similar to the data and to the predictions with the center-of-gravity decision device as shown in the upper panel of Figure 6. The modulation lowpass model could predict a small peak of the outside-target-band ITD at 500 Hz for the smallest W of 3.16 when no tau-weighting was applied. With tau-weighting included, the modulation lowpass model accounted very well for the data with a W of 3.16 and showed nearly identical and slightly lower peaked functions for W = 31.6 and 316.

Overall, the current simulations show that the modulation bandpass model, which had been designed to predict temporal binaural processing mostly of periodic or Gaussian noise stimuli, is well capable of capturing the binaural temporal processing of the complex and aperiodic modulations as they occur in rustling sounds. The modulation bandpass model is also relatively robust against different detector mechanisms in experiment II. The modulation lowpass model can only account for the data of experiment II if the RMS difference detector in combination with the tau weighting is used.

Experiment III: Contribution of Envelope ITDs and IIDs to the Minimum Audible Angle for Rustling Sounds

The previous experiments have shown that, with increasing W, ITD JNDs for high-frequency, band-pass filtered stimuli improve (experiment I), and that the relative dominance of low frequencies in the evaluation of broadband ITDs decreases (experiment II). It is still unclear, however, to what extent envelope ITDs can contribute to the localization of high-frequency rustling sounds. In their comprehensive review of the duplex theory of hearing, Macpherson and Middlebrooks (2002) have shown that, for the range of stimuli tested in that study, the perceptual weight of envelope ITDs of high-frequency sounds for sound localization was always low compared to the perceptual weight for the IIDs. Here, it is addressed how envelope ITDs and IIDs contribute to the minimum audible angle (MAAs) of rustling sounds.

Stimuli

The stimuli were again sparse noises with a W of 3.16, 31.6, and 316. As in the largest-bandwidth condition of experiment I, the stimuli were band-pass filtered with a 6,000-Hz bandwidth geometrically centered around 4 kHz (corner frequencies of 2,000 and 8,000 Hz). As in experiment I, a low-pass noise was presented to preclude the use of low-frequency aural distortions. After gating the stimuli with 20-ms raised-cosine ramps, the stimuli were convolved with generic head-related impulse responses (HRIRs) from measurements of the KEMAR audio manikin (Knowles Electronics Mannequin for Acoustics Research), available from the CIPIC database (Center for Image Processing and Integrated Computing, University of California, Davis). The high-resolution measurements with 5° spacing in the horizontal plane were used. As human MAAs are typically on the order of 1° to 2° in the frontal horizontal plane (Mills 1958; Grantham et al. 2003), the HRIRs of the KEMAR audio manikin database offering an angular resolution of 5° were not suited to measure MAAs. Thus, the 5° HRIRs were linearly interpolated, in terms of their magnitude spectrum and their unwrapped phase spectrum, to generate intermediate HRIRs with a 0.1° spacing. HRIRs were used in three different experimental conditions: first, the unmodified (only interpolated) HRIRs were used, providing ITD and IID information. In the second condition, the HRIRs were manipulated to keep the original magnitude spectra for the left and right ear while the phase spectra were replaced with those of a diotic impulse (linear phase). This manipulation also affects W of the HRIRs while it preserves the IID information but sets the ITD to 0 μs. In the third condition, the HRIR phase spectra were preserved for the left and right ear, but the magnitude spectra were replaced with those of a diotic impulse. In this case, the ITD information is preserved while the IID is set to 0 dB. Stimuli were generated at a sampling rate of 44.1 kHz with a duration of 371.5 ms including 20-ms, raised-cosine ramps. After the stimuli were convolved with the corresponding HRIRs, they were played back using the same setup and level as in the previous experiments. Sound levels depended somewhat on the HRIRs but were always in the range between 55 and 65 dB SPL. Considering the stochastical nature of the stimuli, they were regenerated for each trial.

To complement the sparse-noise synthetic stimuli with real-life rustling sounds, sounds of a thin plastic bag and a piece of aluminum foil being crushed were additionally recorded. Recordings were performed in a small anechoic chamber using a high-quality condenser microphone (Sanken CO100k) and a Digidesign Mbox audio interface connected to a PC. The same sampling rate of 44.1 kHz was used. Stimuli were cut from the recording using the same duration and ramps as for the synthetic stimuli. The W was 3.98 and 100 for the plastic bag and the aluminum foil, respectively.

Procedure

In an adaptive four-interval, two-alternative forced-choice task, listeners were asked to detect whether the test stimulus in the second or the third interval of a trial was played from a non-zero azimuth position in virtual acoustic space. The three reference stimuli always had a central (zero-azimuth) position. Responses were recorded and feedback was provided via a graphical user interface. The initial horizontal angle of the test stimulus was randomized between 20° and 40°. Following a three-down, one-up rule, the azimuth angle of the test stimulus was changed with a factor of two (halving or doubling), for reversals one and two, and with a factor of 1.1 for reversals three to 11. Thresholds were extracted as the mean of reversals six to 11. Individual data are based on four adaptive runs per condition. An experimental session consisted of three runs. Across the three runs, the HRIR condition (original HRIR, IID only, and ITD only) was randomized, without informing the listeners. There were four listeners, three females and one male, aged between 22 and 25 years. Listeners were different from those in the previous experiments.

Results

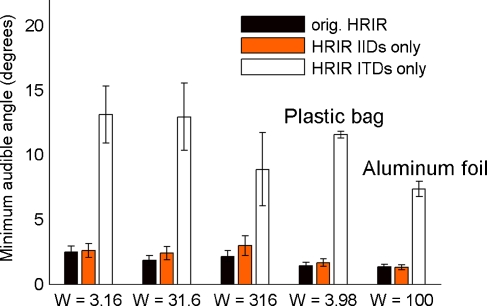
Figure 7 shows MAAs for the sparse noises with three values of W, the two recorded stimuli, and the three types of HRIRs. For the original HRIRs which contained both the ITD and the IID information (black bars), MAAs were about 2°, independent of the stimulus. When the ITDs were set to 0 μs but the IIDs were preserved in the HRIRs (IID only, orange bars), MAAs remained virtually unchanged. When, however, the IIDs were set to 0 dB and only the ITDs were preserved in the HRIRs (ITD only, white bars), MAAs were significantly higher (Friedman’s non-parametric two-way ANOVA, p < 0.0001, df = 2, χ² = 0.62), independent of the W of the sparse noises. In the ITD-only condition, there is a trend for MAA improvement in the synthetic stimuli when W increases from 31.6 to 316. This trend is not significant; however, it qualitatively supports the results of experiment I, in which significant ITD-JND improvements were observed with increasing W. MAAs measured for the recorded sounds, plastic bag and aluminum foil, produced very similar results.

FIG. 7.

Minimum audible angles (MAA) measured in virtual acoustic space using generic HRIRs. HRIRs were either used with full information (black bars), with IID information only (orange bars), or with ITD information only (white bars). Error bars represent across-listeners standard errors. MAAs were measured for sparse noises of three different Ws (3.16, 31.6, and 316) and for two recorded rustling sounds, a plastic bag and an aluminum foil being crushed with Ws of 3.98 and 100, respectively. The data show that MAAs are very good (1° to 3°) either with both ITD and IID information or with IID information only. With ITDs only, performance decreases considerably but the differences in W are still reflected in the MAAs.

In line with experiment I, MAAs were smaller for the aluminum foil (with the higher W) than for the plastic bag when only ITD information of the HRIR was preserved.

Overall, the data of experiment III show that for both synthetic and natural high-frequency rustling sounds, listeners achieved their best performance in terms of MAAs when the angular information was mediated by IIDs. This is true despite the fact that, as shown in experiment I, rustling sounds provide very salient ITDs.

General Discussion

The current study presents a set of experiments designed to assess the salience of envelope cues to extract spatial information from rustling sounds. Synthetic rustling sounds, in which the degree of envelope fluctuation can be carefully controlled, as well as two recorded samples of “natural” rustling sounds were used.

The synthetic rustling sounds recruited for the current experiments were derived from Gaussian noise by multiplication with the aperiodic pulse-train modulator in order to create sparse noise with systematically increased envelope fluctuations. Perceptually, these noises are similar to rustling sounds as they occur for example by movements of a predator or prey in leaf litter. The existential importance of these sounds for survival may have contributed significantly to the structure and function of binaural neural circuits in mammals and birds.

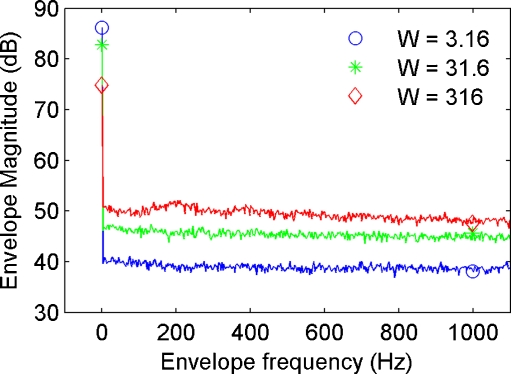
One difference between the current stimuli and those used in most earlier experiments on envelope ITD sensitivity is that the modulators used here are aperiodic and they were imposed on noise carriers. Thus, the manipulations used here did not introduce systematic changes to the shape of the long-term power spectrum of the waveform with increasing W (cf. power spectra in Fig. 1). In contrast to other stimuli that have been used to investigate the salience of envelope ITDs (e.g., band-pass noises, sinusoidally amplitude modulated tones, or transposed tones), also the long-term power spectrum of the envelope reveals no distinct peaks or shape changes with increasing W except for an increase of the magnitude for all envelope frequencies (Fig. 8). Thus, these stimuli represent an interesting extension for the hypothesis that sensitivity to ITDs is governed by the interaural correlation function of their envelopes (Bernstein and Trahiotis 2007, 2009, 2010). The interaural correlation function of the envelope is the inverse Fourier transform of the interaural envelope cross-power spectrum. In terms of the envelope power spectra, which in case of a pure ITD manipulation can replace the interaural envelope cross-power spectra (cf. Fig. 8), only the AC-to-DC ratio can be exploited to predict the measured ITD JNDs.

FIG. 8.

Envelope power spectra for sparse noises with a W of 3.16, 31.6, and 316. The DC component of the envelope spectra are shown with open circles on the Y-axis. While the envelope spectra reveal no conspicuous envelope frequencies that change with W, the AC-to-DC ratio increases systematically with increasing W.

Buell and Hafter (1988) have shown that for high-pass filtered click trains, ITD JNDs improve when the inter-click interval increases up to 10 ms. In the same line, Ewert et al. (2009) and Klein-Hennig et al. (2011) have shown that two stimulus parameters dominate envelope ITD JNDs, namely the rise time (attack) of the envelope of high-frequency tone pips and the duration of the temporal gap preceding the attack, comparable to the inter-click interval of the Buell and Hafter (1988) study. As outlined in the methods, the sparse noises used here were generated with an aperiodic impulse-train modulator. The W of the sparse noise is determined by the maximum gap width in the modulator. For the current stimuli with a W of 3.16, 31.6, and 316, the maximum gap widths are 0, 0.36, and 5.8 ms, respectively. Thus, the sparse noise with a W of 316 includes gap widths approaching and sometimes exceeding the 5-ms threshold for effective envelope extraction as suggested by Ewert et al. (2009) and Klein-Hennig et al. (2011). Due to the impulse-train nature of the modulator, the attack following a gap has the maximum rise time in any given frequency region.

A second advantage of using such sparse noise to quantify envelope ITD JNDs is that, due to the aperiodic modulator, sparse noises impede the detrimental effect of binaural adaptation on envelope ITD sensitivity, as it has been shown in previous studies (Hafter and Buell 1990; Laback and Majdak 2008; Goupell et al. 2009).

In experiment I, a systematic improvement of ITD JNDs not only with W but also with bandwidth was found. This bandwidth effect has been described in several earlier studies (Yost et al. 1971; McFadden and Pasanen 1976; Amenta III et al. 1987). As the band-pass cutoff frequencies were geometrically centered around 4 kHz, the high-pass cutoff decreases with increasing bandwidth: at the largest bandwidth, 6 kHz, the high-pass cutoff was at 2 kHz. It is conceivable that the observed ITD JND improvement results not from the increase in bandwidth per se but from the lower cutoff frequency of the noise moving down into a frequency region of slightly improved phase locking. Indirect evidence against this hypothesis comes from experiment III: the MAAs measured in the “ITD only” condition of that experiment with an “aluminum foil” stimulus, high-pass filtered at 4 kHz, were about 8°. Assuming a head radius of 9 cm, this 8° threshold corresponds to an ITD of about 74 μs. This value is in the same range as the ITD JND of about 70 μs obtained in experiment I for the 2–8-kHz bandwidth sparse noise with a W value of 31.6 (compared to the W value of 100 for the “aluminum foil” stimulus). For both stimuli, the effective bandwidth could be regarded similar. Thus, it can be argued that the ITD JND improvement with increasing bandwidth in experiment I is more closely related to bandwidth per se than to the lower cutoff moving in the region of improved phase locking. It should be noted that for monaural temporal acuity, quantified as sensitivity to sinusoidal amplitude modulation, the effect of bandwidth also dominates over the effect of absolute frequency (Eddins 1993, 1999).

Laback and Majdak (2008) and Goupell et al. (2009) have shown that jittering the inter-click interval of high-pass filtered click trains improves temporal encoding in both electric (via cochlear implants) and acoustic hearing. The introduction of a jitter, however, will not change W for click-train stimuli. Thus, while these stimuli share a “randomness” feature with the current ones, the effect of jitter in those experiments argue against W (or Y) as a predictor for envelope ITD sensitivity. It is possible that the resetting of binaural adaptation (Hafter and Buell 1990) contributes to the exceptionally good envelope ITD JNDs found in the current experiment I. As the current model was adjusted to predict ITD JNDs for the current random stimuli, the predicted thresholds for the Bernstein and Trahiotis (2007) periodic stimuli may be too good because their periodic stimuli are more strongly affected by binaural adaptation. Again, one should note that none of the current measures of envelope fluctuation are sensitive to the degree of periodicity of the envelope fluctuations.

Experiment II showed a systematic decrease in the relative dominance of frequencies around 500 to 1,000 Hz with increasing W. It can be hypothesized that this decrease was mediated by the improvement of (high-frequency) envelope ITDs with increasing W. The more pronounced temporal gaps in stimuli with higher W improve, according to Buell and Hafter (1988) and Ewert et al. (2009), the extraction of envelope ITDs in high-frequency channels. Thus, it is likely that with increasing W, envelope ITDs contribute more and more to the overall lateralization, in line with improving ITD JNDs as quantified in experiment I. The fact that for broadband stimuli in experiment I, ITD JNDs did not improve with increasing W, however, indicates that the effect of increasing W on the envelope ITDs is swamped by the high sensitivity to low-frequency, fine-structure ITDs when available.

The results of experiments I and II could be reasonably well accounted for by a modified version of the cross-correlation model by Bernstein and Trahiotis (2002). The main modification was the inclusion of a band-pass modulation filter to extract the fast fluctuations (as they are produced by steep onsets) prior to the cross-correlation mechanism. With a “classical” modulation lowpass filter instead of the band-pass filter, the model of Bernstein and Trahiotis could also capture the general trends in the data of experiment I; however, the model failed in experiment II, at least with the center-of-gravity-based detector mechanism. The successful inclusion of the modulation band-pass filter in the model scheme supports the modulation frequency selective processing in the recent binaural model of Dietz et al. (2008, 2009).

Experiment III shows, in line with previous studies using different stimuli (Macpherson and Middlebrooks 2002), that although human listeners can extract envelope ITDs of high-frequency rustling sounds with high acuity, the IID information still dominates localization acuity in the horizontal plane. This finding highlights the necessity to investigate temporal aspects of neural IID extraction. The following argument is based on the assumption that the precision of neural extraction of IIDs is related to the steepness of electrophysiologically measured rate-level functions: recent physiological experiments have highlighted the dynamic adjustment of rate-level functions to the statistics of level fluctuations (Dean et al. 2005). Considering these data, one could assume that rate-level functions in response to stimuli with pronounced level fluctuations should be shallower than in response to stimuli with small-level fluctuations. This would in turn lead to larger IID JNDs for strongly fluctuating stimuli than for smooth stimuli. The fact that IID sensitivity appears rather insensitive to W (cf. “IID-only” condition in experiment III), however, argues that IID sensitivity is very little affected by level fluctuations. The fact that the lateral superior olive as the main processing unit of IIDs exhibits also good sensitivity to envelope ITDs (Joris and Yin 1995; Tollin and Yin 2005; Tollin et al. 2008) highlights the need to explore time constants of perceptual IID extraction in more detail.

Taken together, the current experiments show that temporal characteristics of ecologically relevant rustling sounds are well exploitable in terms of envelope ITDs. With broadband stimulation of increasing W, the relative contribution of envelope ITDs to overall ITD JNDs increases. However, the data show that while envelope ITD JNDs systematically improve with increasing W of rustling sounds, despite of the very good ITD JNDs, high-frequency envelope ITDs are still an inferior cue compared to high-frequency IIDs when MAAs for rustling sounds are measured. Thus, the current study highlights the need to explore temporal aspects of the neural analysis of IIDs which appear to be still the dominant spatial cue for high-frequency sounds even in the presence of strong envelope fluctuations.

Conclusions

The current study shows that (1) with broadband stimulation, increasing waveform fourth moment (W) did not yield better ITD JNDs, while with high-frequency, band-pass filtered stimuli, ITD JNDs improved with increasing W (experiment I). (2) The dominance of low-frequency components of broadband stimuli for ITD extraction decreases systematically with increasing W. (3) A binaural model based on interaural crosscorrelation captures the rustling-sound results quite well. (4) Although ITD JNDs for complex high-frequency sounds can be as good as those for low-frequency sounds, frontal MAAs in virtual acoustic space are still best when the angular information is mediated by IIDs generated by the acoustic head shadow.