Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion

Abstract

Here, we demonstrate that subject motion produces substantial changes in the timecourses of resting state functional connectivity MRI (rs-fcMRI) data despite compensatory spatial registration and regression of motion estimates from the data. These changes cause systematic but spurious correlation structures throughout the brain. Specifically, many long-distance correlations are decreased by subject motion, whereas many short-distance correlations are increased. These changes in rs-fcMRI correlations do not arise from, nor are they adequately countered by, some common functional connectivity processing steps. Two indices of data quality are proposed, and a simple method to reduce motion-related effects in rs-fcMRI analyses is demonstrated that should be flexibly implementable across a variety of software platforms. We demonstrate how application of this technique impacts our own data, modifying previous conclusions about brain development. These results suggest the need for greater care in dealing with subject motion, and the need to critically revisit previous rs-fcMRI work that may not have adequately controlled for effects of transient subject movements.

Introduction

It is well-established that head motion is undesirable in fMRI studies (Friston et al., 1996; Hutton et al., 2002; Jiang et al., 1995; Johnstone et al., 2006; Oakes et al., 2005; Wu et al., 1997). Blood oxygen level dependent (BOLD) signal acquisition depends upon precise spatial and temporal placement of magnetic gradients on scales of millimeters and milliseconds. Movement of the head during scans not only shifts the position of brain matter in space, it fundamentally disrupts the establishment of magnetic gradients and subsequent readout of the BOLD signal. To compensate for these effects, it is common practice to realign data (here, a part of fMRI preprocessing). Spatial realignment corrects motion-induced shifts in space but does not correct intensity changes resulting from disruption of the physical principles underlying MRI. Therefore additional measures are often taken (here, a part of functional connectivity processing), such as ICA decomposition or regression of motion estimates, to remove spurious motion-related signal from the data (Beckmann and Smith, 2005; Erhardt et al., 2010; Fox et al., 2009; Robinson et al., 2009a; Weissenbacher et al., 2009). In this paper, we demonstrate that at least some of these approaches to motion correction do not fully remove motion-related signal from the data. Critically, we also find that the inclusion of motion-contaminated data introduces colored noise into the study of functional brain organization via resting state functional connectivity MRI (rs-fcMRI).

Subject movement is often measured with summary statistics based upon head realignment parameters. Since subjects move during scans, it is standard practice to estimate the position of the head in space at each volume of the data and to realign all volumes using rigid body transforms. In a rigid body transform, head position is described at each timepoint by six parameters (translational displacements along X, Y, and Z axes and rotational displacements of pitch, yaw, and roll). These realignment parameters can be condensed into a single summary statistic, such as root mean squared head position change (RMS movement). Summary statistics are often used to describe subject motion and to make decisions about cohort formation or matching. When forming cohorts, scans with summary statistics above some threshold (e.g., RMS movement over half a voxel’s width) are considered essentially unusable, and these scans are discarded from the analysis. When multiple cohorts are compared, motion matching is often accomplished using means or t-tests of summary statistics between cohorts.

Summary statistics of motion are quite useful, but they do not always distinguish between qualitatively different types of subject movement. Consider two subjects: Subject A who is perfectly still but moves suddenly once to arrive at a very different head position, and Subject B who has frequent small to moderate movements about the original head position. It is possible for these two subjects to have similar, or even identical, RMS movement estimates, despite the substantial qualitative differences in how they moved. Since head displacement disrupts the spin history assumptions upon which BOLD signal establishment and readout depend, all other things being equal, Subject A will have data of acceptable quality throughout the scan except during and immediately after head motion, whereas the data of Subject B will be somewhat compromised throughout much of the scan. In an effort to counter such effects, head realignment estimates or other indices of movement are often regressed from data (for example, within GLMs for task fMRI, or during functional connectivity processing for rs-fcMRI). Here, we demonstrate that clear artifacts remain in the data even after such regressions, and that these artifacts have systematic effects upon rs-fcMRI correlations.

Following a regression-based approach to motion correction (Fox et al., 2009), this report begins by demonstrating a correspondence between head displacement and large-amplitude changes in rs-fcMRI BOLD signal. These changes are evident in single rs-fcMRI timecourses, and occur throughout the brain and across subjects. Based upon the suspicious co-occurrence of head movement and changes in rs-fcMRI signal, two indices of data quality that operate on a frame-by-frame basis to flag suspect frames of MR data are proposed. In four cohorts, removal of flagged frames produces structured changes in patterns of correlation, such that some short-distance correlations are weakened, and some medium- to long-distance correlations are strengthened. Some similar effects related to motion in functional connectivity data have recently been described (Van Dijk et al., 2011). Control analyses demonstrate that the artifact does not arise from (and is not adequately countered by) regressions performed during functional connectivity processing, nor is it simply a product of frame removal from data. We conclude by demonstrating how this artifact has impacted our own data and how removing the artifact modifies our previous conclusions.

One of the principal attractions of rs-fcMRI is that the minimal burden upon subjects allows investigators to explore populations (especially pediatric and clinical) that are typically difficult to study. The present results indicate that systematic but spurious rs-fcMRI correlation structures are induced by subject motion in ways that are not always detected or dealt with in common approaches to rs-fcMRI analysis. These effects can obscure patterns of functional connectivity within single cohorts and create spurious differences between cohorts. This characterization suggests the need to critically revisit previous work that may not have adequately controlled for frame-by-frame head displacement, and the need for greater care when dealing with subject movement.

Before moving to data we wish to clarify the intent of this paper. Although this paper suggests a method to dampen or remove the influences of movement on rs-fcMRI analyses, this paper is intended to be descriptive rather than proscriptive. Also note that the basis for the artifactual effects described herein is not specific to rs-fcMRI, but is a general feature of fMRI, and should also be present in diffusion imaging or task fMRI studies. The approach described in this paper may be adapted to these modalities.

Methods

Subjects

Subjects were recruited from the Washington University in St. Louis campus and the surrounding community. Individuals were excluded if there was a history of metal implants or other contraindications to the MRI environment, or a history of developmental delay, neurological or psychiatric illness, including the use of psychotropic medications. All subjects were native English speakers. All adult subjects gave informed consent, and all children gave assent with parental consent, in accordance with the guidelines and approval of the Washington University Human Studies Committee. Subjects were compensated for their participation.

Datasets and Data Collection

This study utilized multiple datasets, divided into 4 cohorts (see Table 1).

Table 1. The four cohorts presented in this report.

Within each cohort studied, the number of subjects, sex distribution, digital age in years, and percent of data cut by motion scrubbing are shown. Additionally, the RMS movement estimates are shown for unscrubbed and scrubbed datasets.

	# subjects	Sex (M/F)	Age in years mean (sd)	% data cut	Unscrubbed RMS motion in mm mean (sd)	Scrubbed RMS motion in mm mean (sd)
Cohort 1: 3T children	22	11/11	8.5 (1)	26 (14)	0.51 (0.29)	0.41 (0.23)
Cohort 2: 3T adolescents	29	22/7	12.1 (1.1)	16 (14)	0.38 (0.24)	0.33 (0.21)
Cohort 3: 3T adults	26	4/22	23.5 (1.4)	12 (6)	0.38 (0.16)	0.35 (0.14)
Cohort 4: 1.5T children	42	19/23	8.8 (0.7)	58 (20)	0.70 (0.31)	0.58 (0.20)

The data for the first 3 cohorts (N=77) were acquired on a Siemens MAGNETOM Tim Trio 3.0T Scanner with a Siemens 12 channel Head Matrix Coil (Erlangen, Germany). A T1-weighted sagittal MP-RAGE structural image was obtained (TE = 3.06 ms, TR-partition = 2.4 s, TI = 1000 ms, flip angle = 8°, 176 slices with 1×1×1 mm voxels). A T2-weighted turbo spin echo structural image (TE = 84 ms, TR = 6.8 s, 32 slices with 2×1×4 mm voxels) in the same anatomical plane as the BOLD images was also obtained to improve alignment to an atlas. Functional images were obtained using a BOLD contrast sensitive gradient echo echo-planar sequence (TE = 27 ms, flip angle = 90°, in-plane resolution= 4×4 mm; volume TR = 2.5 s). Whole brain coverage for the functional data was obtained using 32 contiguous interleaved 4 mm axial slices.

The data for the fourth cohort (N=42) were acquired on a Siemens 1.5 Tesla MAGNETOM Vision MRI scanner (Erlangen, Germany). Structural images were obtained using a sagittal magnetization-prepared rapid gradient echo (MP-RAGE) three-dimensional T1-weighted sequence (TE = 4 ms, TR = 9.7 ms, TI = 300 ms, flip angle = 12°, 128 slices with 1.25×1×1 mm voxels). Functional images were obtained using an asymmetric gradient echo echo-planar sequence sensitive to blood oxygen level-dependent (BOLD) contrast (T2* evolution time = 50 ms, flip angle = 90°, in-plane resolution 3.75×3.75 mm; volume TR = 2.5 s). Magnetization steady state was assumed after 10 seconds. Whole brain coverage for the functional data was obtained using 16 contiguous interleaved 8 mm axial slices, acquired parallel to the plane transecting the anterior and posterior commissure (AC-PC plane).

fMRI preprocessing

Figure S1 provides a complete overview of the workflow for data analysis. Functional images underwent standard fMRI preprocessing to reduce artifacts (Shulman et al., 2010). These steps included: (i) removal of a central spike caused by MR signal offset (in 1.5T data only), (ii) correction of odd versus even slice intensity differences attributable to interleaved acquisition without gaps (temporal realignment using sinc interpolation of all slices to the temporal midpoint of the first slice, accounting for differences in the acquisition time of each individual slice), (iii) correction for head movement within and across runs and (iv) within run intensity normalization to a whole brain mode value of 1000. Of note, mode 1000 normalization defines 100% signal at every voxel identically as the modal value across all voxels throughout the entire scan. BOLD values are presented in mode 1000 scale, where 10 units = 1% signal change (see Figures). Atlas transformation of the functional data was computed for each individual via the MP-RAGE scan. Each run was then resampled in atlas space on an isotropic 3 mm grid combining movement correction and atlas transformation in a single interpolation (Shulman et al., 2010).

Head realignment estimate calculations

Head motion estimation involved a series of rigid body transforms, T_i, where i indexes frame (volume) and T_i spatially registers frame i to a selected reference frame. Each transform was computed by minimizing the registration error,

$${\epsilon }_i=\langle {\left(s{I}_i\left(T\left(\overrightarrow{x}\right)\right)-I_0\left(\overrightarrow{x}\right)\right)}^2\rangle ,$$

where $I\left(\overrightarrow{x}\right)$ is image intensity at locus $\overrightarrow{x}$, angle brackets denote the spatial average over the brain, subscript 0 denotes the reference frame (here, taken as the run midpoint) and s is scalar factor that compensates for small changes in mean signal intensity. Each transform can be expressed as a combination of rotation and displacement components. Thus,

$$T_i=\left[\begin{array}{cc}\hfill R_i\hfill & \hfill {\stackrel{.}{d}}_i\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],$$

where R_i is a 3 × 3 rotation matrix and ${\stackrel{.}{d}}_i$ is a 3 × 1 column vector of displacements. R_i can be factored into three elementary rotations about each of the three axes. Thus, R_i = R_iαR_iβR_iγ, where

$$R_{i\alpha }=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos {\alpha }_i\hfill & \hfill -\sin {\alpha }_i\hfill \\ \hfill 0\hfill & \hfill \sin {\alpha }_i\hfill & \hfill \cos {\alpha }_i\hfill \end{array}\right],R_{i\beta }=\left[\begin{array}{ccc}\hfill \cos {\beta }_i\hfill & \hfill 0\hfill & \hfill \sin {\beta }_i\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sin {\beta }_i\hfill & \hfill 0\hfill & \hfill \cos {\beta }_i\hfill \end{array}\right],\text{and}{R}_{i\gamma }=\left[\begin{array}{ccc}\hfill \cos {\gamma }_i\hfill & \hfill -\sin {\gamma }_i\hfill & \hfill 0\hfill \\ \hfill \sin {\gamma }_i\hfill & \hfill \cos {\gamma }_i\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

Thus, each rigid body transform is defined by six parameters.

Framewise displacement (FD) calculations

Differentiating head realignment parameters across frames yields a six dimensional timeseries that represents instantaneous head motion. To express instantaneous head motion as a scalar quantity we used the empirical formula, $F{D}_i=\mid \Delta d_{ix}\mid +\mid \Delta d_{iy}\mid +\mid \Delta d_{iz}\mid +\mid \Delta {\alpha }_i\mid +\mid \Delta {\beta }_i\mid +\mid {\Delta }_{\gamma i}\mid$, where $\Delta d_{ix}=d_{(i-1)x}-d_{ix}$, and similarly for the other rigid body parameters $\left[d_{ix}{d}_{iy}{d}_{iz}{\alpha }_i{\beta }_i{\gamma }_i\right]$. Rotational displacements were converted from degrees to millimeters by calculating displacement on the surface of a sphere of radius 50 mm, which is approximately the mean distance from the cerebral cortex to the center of the head.

Functional connectivity (rs-fcMRI) processing

For rs-fcMRI analyses, standard additional functional connectivity processing steps were utilized to reduce spurious variance unlikely to reflect neuronal activity (Fox et al., 2006; Fox et al., 2005; Fox et al., 2009). These steps included: (i) spatial smoothing (6 mm full width at half maximum), (ii) a temporal band-pass filter (0.009 Hz < f < 0.08 Hz), and (iii) a multiple regression of nuisance variables from the BOLD data. Nuisance regressions included ventricular signal averaged from ventricular regions of interest (ROIs), white matter signal averaged from white matter ROIs, whole brain signal averaged across the whole brain, six head realignment parameters obtained by rigid body head motion correction, and the derivatives of each of these signals. Where indicated in the text, data was reprocessed identically using only the indicated nuisance regressors (e.g. no motion regressors means that the 12 motion-related regressors were not included, no whole brain regression means that the two whole-brain-related regressors were withheld, etc.).

DVARS calculations

DVARS (D referring to temporal derivative of timecourses, VARS referring to RMS variance over voxels) indexes the rate of change of BOLD signal across the entire brain at each frame of data. To calculate DVARS, the volumetric timeseries is differentiated (by backwards differences) and RMS signal change is calculated over the whole brain. DVARS is thus a measure of how much the intensity of a brain image changes in comparison to the previous timepoint (as opposed to the global signal, which is the average value of a brain image at a timepoint). The global measure of signal change is

$$DVARS{\left(\Delta I\right)}_i=\sqrt{\langle {\left[\Delta I_i\left(\overrightarrow{x}\right)\right]}^2\rangle }=\sqrt{\langle {[I_i\left(\overrightarrow{x}\right)-I_{i-1}\left(\overrightarrow{x}\right)]}^2\rangle }$$

where, as before, $I_i\left(\overrightarrow{x}\right)$ is image intensity at locus $\overrightarrow{x}$ on frame i and angle brackets denote the spatial average over the whole brain. A computationally important detail is to note that this spatial average should count only voxels that, during acquisition, were within the field of view at all times, i.e., completely sampled voxels. DVARS was first described and applied in (Smyser et al., 2010). In this report,DVARS was calculated upon final functional connectivity images. Note that DVARS could, in principle, be calculated at other points of the processing stream (e.g., prior to functional connectivity processing).

ROI definition

All timecourses and correlations presented in this paper were drawn from a set of 264 regions of interest (ROIs) that were defined with our lab (Dosenbach et al., 2010; Power et al., in press). These ROIs were defined through several meta-analyses of task fMRI data, and with the fc-Mapping technique (Cohen et al., 2008; Nelson et al., 2010) applied to rs-fcMRI data (no subjects in the present study were used to define ROIs). All ROIs are modeled as 10 mm diameter spheres centered upon ROI coordinates.

Correlation calculations and graph formation

Following standard techniques, correlations were calculated as the Pearson product moment between the timecourses extracted from pairs of ROIs. The 264 × 264 correlation matrix averaged across a cohort defines a weighted network (nodes = ROIs, edges = correlation coefficients), and community detection algorithms (Infomap (Fortunato, 2010; Rosvall and Bergstrom, 2008)) were applied to the graph to detect sub-networks within the brain-wide network. To avoid effects of smoothing and reslicing, only correlations between ROIs separated by more than 20 mm were considered. Networks were analyzed at a variety of thresholds, and a representative analysis performed at 10% edge density is presented in Figure 10. Normalized mutual information is a measure of shared information between probability distributions, and is a standard measure of the similarity of community assignments in networks (Newman, 2010). Values of 1 indicate that two sets of assignments are identical (knowledge of one distribution gives full information about the other distribution), whereas values of 0 indicate that an observer gains no information about one distribution from the other.

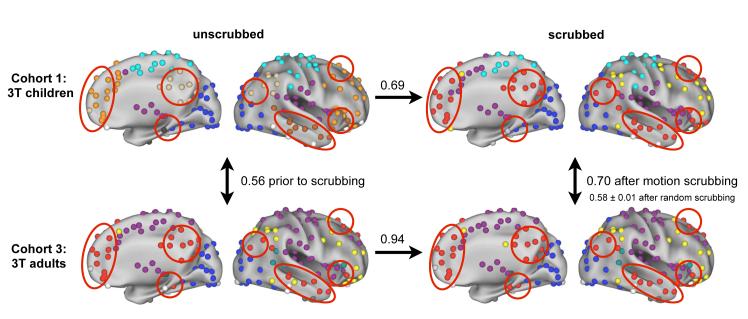
Figure 10. The modular organization of brain-wide networks is fundamentally altered by head motion.

Top and bottom rows depict data from children and adults, respectively. Left and right columns depict unscrubbed and scrubbed data, respectively. Each panel shows the sub-network (community) organization within the appropriate dataset of a network composed of the 264 ROIs studied in this report. Colors indicate sub-networks, and are independent in each panel, though congruent colors have been chosen across panels for ease of visual comparison. Only right hemispheres are shown, but results are generally symmetric across hemispheres. The numbers between panels indicate the normalized mutual information of community assignments between panels, a standard measure of how similar two sets of community assignments are (values of 1 indicate identical assignments). Scrubbing adult data produced little change in community assignments (NMI = 0.94), whereas scrubbing child data produced substantial changes in community assignments (NMI = 0.69). Moreover, though network organization in children and adults was initially quite dissimilar (NMI = 0.56), it became more similar with scrubbing (NMI = 0.70). This increase in similarity is not observed with random scrubbing (NMI = 0.58 ± 0.01 over 10 repetitions of random scrubbing in children and adults). The reorganization of functional network in children can be seen in the large contiguous patches of color (e.g. orange) in unscrubbed data, which become parts of distributed communities in scrubbed data (see red circles for an example). All graphs are thresholded at 10% edge density (r > 0.16, 0.15, 0.15, and 0.15 clockwise from upper left). For ease of visualization, nodes in communities with fewer than 4 members are colored white, and thus white nodes are explicitly not a single community.

Computations and Visualizations

MRI images were processed using in-house software. Network calculations were performed using MATLAB (2007a, The Mathworks, Natick, MA). Brain surface visualizations were created using Caret software and the PALS surface (Van Essen, 2005; Van Essen et al., 2001).

Results

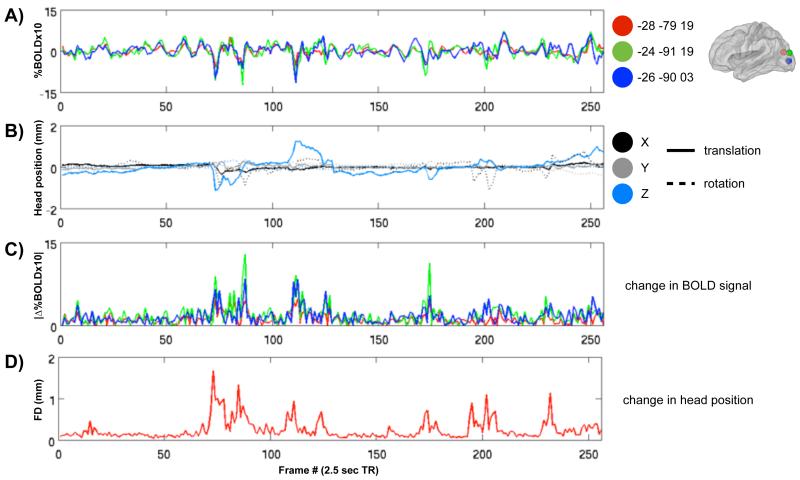
Single timecourses in a single subject demonstrate a relationship between head motion and changes in the BOLD signal, even after data realignment and regression of realignment estimates and their derivatives from the data. Figure 1A shows rs-fcMRI timecourses at 3 left occipital regions of interest (ROIs) in a single subject. These data are from a single child with RMS movement of 0.50 mm (processed data are 3 mm isotropic voxels derived from 3.75 × 3.75 × 4 mm acquisition voxels). The extent of movement in this scan would be considered low (i.e., of high quality) by many investigators. The timecourses are all quite similar, and there are several major peaks and troughs in the data. Figure 1B displays the six head realignment estimates for this subject. Figure 1C shows the absolute values of the differentials of the timecourses, identifying the periods in which the rs-fcMRI signal was most rapidly changing. These periods correspond to the peaks and troughs of Figure 1A, and Figure 1D compresses the six realignment parameters into a single index of framewise displacement (FD) by summing the absolute values of the differentials of the six parameters. There is evident correspondence between plots in Figures 1C and 1D. As Figure S2 shows, such relationships between timecourses and head displacement are not unique to occipital cortex, and can be seen throughout the brain. The pattern is quite similar across ROIs, but there are differences in the sensitivity of particular timecourses to particular movements, which might result from the proximity of ROIs to gray/white matter or gray matter/CSF interfaces in particular directions.

Figure 1. Frame-by-frame changes in rs-fcMRI signal are related to frame-by-frame changes in head position even after motion regression.

(A) rs-fcMRI timecourses from 3 ROIs in a single subject. Each ROI is a 10 mm diameter sphere centered on the coordinates listed at the right, which are all left occipital locations (see Figure S2 for further examples elsewhere in the brain). (B) The six parameters calculated for frame-by-frame realignment of the subject’s data, which indicate the translational (solid line) and rotational (dotted line) displacements of the head from a fixed position in space. Rotational displacements were calculated at a 50 mm radius. (C) The absolute values of the differential of each of the timecourses in (A). (D) The framewise displacement (FD) of head position, calculated as the sum of the absolute values of the differential of the realignment estimates in (B). Note the correspondence of high values in (C) and (D) indicating that large changes in BOLD signal co-occur with large changes in head position. RMS movement for this subject is 0.50 mm, which is well within traditionally acceptable limits of subject motion (e.g. 1.5 mm RMS movement with 3 mm isotropic voxels). Coordinates are in MNI space, and ROIs are shown on a PALS fiducial surface (Van Essen, 2005).

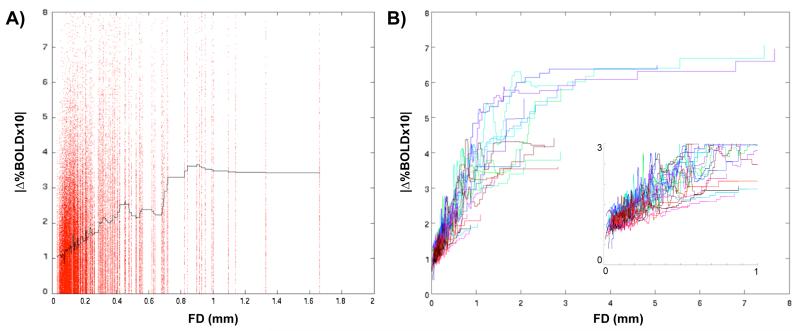
A general relationship between head motion and changes in BOLD signal across the brain can be seen in every subject examined in this paper (N=119 in four cohorts). A brain-wide collection of 264 ROIs based upon meta-analytic fMRI data and resting state functional connectivity data (independent of the present data) (Power et al., in press) was used to produce rs-fcMRI timecourses in each subject (see Methods, Table S1 for coordinates, Figure S3 for locations on a brain surface). Figure 2A plots the absolute values of the derivatives of the 264 timecourses as a function of framewise displacement for the same subject shown in Figure 1. A loess curve using a quadratic fit over the adjacent 5000 data points is shown in black. The data are scattered, but there is an unmistakable trend for frames with high movement to be frames with large changes in many timecourses. Figure 2B plots such loess curves for all 22 children in Cohort 1, demonstrating that this trend is a general feature of the data, and is not particular to any subject. As the inset shows, there is a strong relationship of motion and rs-fcMRI signal change down to a framewise displacement of 0, suggesting that any and all movement tends to increase the amplitude of rs-fcMRI signal changes.

Figure 2. Frame-by-frame head displacement is related to frame-by-frame changes in rs-fcMRI signal throughout the brain and across subjects.

(A) For each frame of data in the same subject used in Figure 1, the framewise displacement (FD) of a frame of data is plotted against the absolute values of the differentials of rs-fcMRI timecourses of 264 ROIs (locations listed and shown in Table S1 and Figure S3). These data are fitted with a loess curve (black line) sampling the nearest 5000 data points. (B) Identically produced loess curves from all 22 subjects in Cohort 1 are plotted against framewise displacement. There is a clear trend for larger frame-by-frame head displacement to co-occur with larger changes in rs-fcMRI signal. The inset magnifies the plot between framewise displacements of 0 and 1, demonstrating that this relationship exists even for very small movements.

It is now clear that across subjects, periods of head movement tend to contain rs-fcMRI data in which BOLD signal is rapidly and substantially changing. Neural activity representing movement planning and execution is surely present at such times, but the signal changes observed during movement do not correspond to the neuroanatomical patterns one would predict for motor-related neural activity. For example, as Figure S4 shows, during head motion, signal changes are not confined to primary motor, pre-motor, or supplementary motor regions, but are instead found throughout the entire brain. Moreover, the amplitude of these signal excursions are often very large - far greater than the signal changes produced by typical motor tasks (e.g., button-pushing or speaking). It is therefore unlikely that these signal changes reflect motor-related neural activity to any great extent. Instead, it is far more likely that movement disrupts magnetic gradient establishment or BOLD signal readout (Hutton et al., 2002), that many slices or entire volumes of data have been contaminated with artifact during periods of movement, and that this contamination has not been completely removed by fMRI preprocessing and functional connectivity processing. In fMRI studies, such noise in single subjects is dampened through trial averaging. This averaging is impossible in rs-fcMRI studies, which depend upon covariance estimated in long timecourses. If large-amplitude changes contaminate rs-fcMRI timecourses, they will alter patterns of covariance according to their prevalence, magnitude, and spatial distribution, and could lead to distorted estimates of rs-fcMRI correlation between brain regions.

Given the presence of motion-related artifact in the data, how might one detect and/or minimize its impact? All functional connectivity processing streams involve some method of “artifact removal” that is aimed to reduce such artifacts. One approach to removing or minimizing motion-related effects has been to use head realignment parameters or other motion estimates as nuisance regressors, and to attempt to regress movement effects from the data (e.g., (Fox et al., 2006; Fox et al., 2005; Fox et al., 2009; Weissenbacher et al., 2009)). However, the data presented thus far have already undergone such a procedure, and subsequent figures will show how regression neither causes the effects shown here, nor is it capable of completely removing the effects shown here. This may be because there is not a strong, simple, linear relationship between movement estimates and changes in the BOLD signal throughout the brain, or because the regressions used here were not tailored to every voxel’s displacement. Another approach is to use covariance-based approaches such as component analysis (e.g. ICA, implemented in software packages such as MELODIC or GIFT) to identify and remove “artifactual” components in the data (e.g., (Beckmann and Smith, 2004; Erhardt et al., 2010; Robinson et al., 2009a)). Although some artifactual signals (e.g. “ringing”) are easily identified and removed using such procedures, other artifactual signals may be more ambiguous, and decisions about retaining or discarding such components are somewhat subjective. Since regressions do not fully remove motion-related signal, and because component removal entails subjective decisions about what constitutes artifact, we adopt a different approach, described below.

Head motion tends to occur sporadically in cooperative subjects. Thus, motion-induced signal changes tend to behave as burst noise. Rather than attempting to parse “true” from “artifactual” signal within all frames, we propose to identify and entirely eliminate frames of suspect quality from our rs-fcMRI analyses to detect and characterize motion-related artifact. Previous studies that have examined the concatenation of discontinuous rs-fcMRI data have found no deleterious effects upon functional connectivity (Fair et al., 2007; Van Dijk et al., 2010), and similar “temporal masking” approaches have been used in other rs-fcMRI studies (e.g. (Barnes et al., 2011; Fransson et al., 2007; Jones et al., 2010; Kennedy and Courchesne, 2008; Smyser et al., 2010; Smyser et al., 2011)) and in task fMRI (e.g., (Birn et al., 2004)). Generally, we propose two indices of data quality that can be used to flag frames of suspect quality, creating temporal masks of the data. These temporal masks can be augmented and combined in various ways to produce a final temporal mask, which specifies frames to ignore when performing calculations upon the data (similar approaches using frame elimination or weighting could be implemented in AFNI or SPM’s ArtRepair). We refer to this process as “scrubbing”.

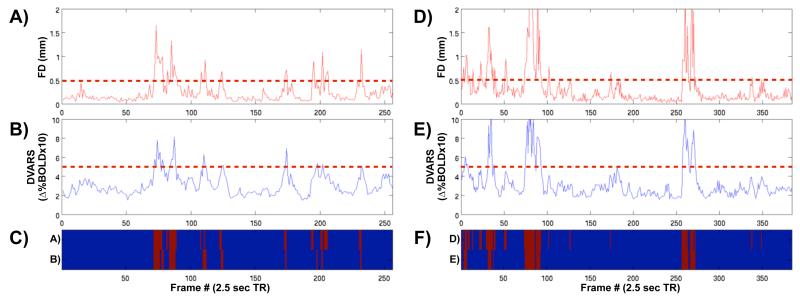
Specifically, we begin our procedure after functional connectivity processing has finished, because bandpassing, often an integral part of functional connectivity processing, cannot be performed properly upon temporally discontinuous data. The first framewise data quality index is framewise displacement (e.g., Figure 1D), calculated as the sum of the absolute values of the derivatives of the six realignment parameters. Framewise displacement thus measures how much the head changed position from one frame to the next. Figure 3A and 3D show framewise displacement values for two subjects (see Figure S5 for further examples). The second framewise data quality index is called DVARS, which is calculated in each volume as the RMS of the derivatives of the timecourses of all within-brain voxels. DVARS thus measures how much image intensity has changed from one frame to the next. This measure was conceived of as a logical extension of the trends shown in Figures 1 and 2, where epochs of head movement coincide with epochs of high-amplitude BOLD signal changes. Such plots are shown in Figure 3B and 3E for two subjects (see also Figure S5). Note that the plots of framewise displacement and DVARS are similar but not identical. In particular, framewise displacement measures tend to be temporally focused (sharp peaks) in contrast to the broader peaks of the DVARS measure. Additionally, the signal-to-noise ratio is larger for framewise displacement than for DVARS (Figures S5, S6). For moderate to large movements, both indices identify very similar portions of the data (big peaks occur at nearly identical timepoints). If one also wishes to identify small movements, framewise displacement may more sensitive due to the lower “floor” in the signal (see Figures S5, S6). Note that framewise displacement arises from realignment parameters calculated in fMRI preprocessing steps, whereas the DVARS measure reflects image intensity, which (if no realignment parameters are regressed) has no explicit relation to the movement measures other than the alignment process itself. It is presently unclear whether one index captures data quality better than the other, but the ease of producing either measure and the similarity of frame indexing that each measure produces render the issue moot in operational terms when only large movements are sought. After studying the plots of dozens of healthy adults, values of 0.5 for framewise displacement and 0.5% ΔBOLD for DVARS were chosen to represent values well above the norm found in still subjects (see Figure S5 for examples of still subjects).

Figure 3. Two framewise indices of data quality, and a method for flagging frames of suspect quality.

(A) The framewise displacement (FD) of head position, calculated as the sum of the absolute values of the 6 translational and rotational realignment parameters (see Figure 1C,D). (B) The DVARS measure, calculated as the RMS of the differential of all timecourses of all voxels within a spatial brain mask at each frame. (C) Two temporal masks, indicating frames of suspect quality in red. Here, the upper row indicates frames that were flagged as having FD over 0.5 (see the dotted red line in (A)), and the bottom row indicates frames that were flagged as having DVARS over 5 (dotted red line in (B)). These temporal masks are quite similar, but not identical, just as the plots in (A) and (B) are quite similar, but not identical. (A-C) show data for the same subject examined in Figure 1 (RMS movement = 0.50 mm), and (D-F) show data from another subject, whose RMS movement is 0.82 mm. Here, thresholds are chosen to simply identify the most egregiously suspect frames.

A temporal mask was generated from each index, marking frames whose framewise displacement or DVARS exceeded the cutoffs set above. Figures 3C and 3F show the temporal masks generated from each index in two subjects, and the cutoffs themselves are shown as dotted lines in the plots above. These temporal masks were augmented by also marking the frames 1 back and 2 forward from any marked frames to accommodate temporal smoothing of BOLD data in functional connectivity processing and re-establishment of steady-state spins. Since reasonable arguments underlie each measure as an index of data quality, we conservatively chose to use an intersection of the two temporal masks to generate a final temporal mask. All removed frames must thus 1) be high-motion frames, and 2) display evidence of widespread and/or large amplitude changes in BOLD signal. When any operations were performed upon a subject’s data, the temporal mask was applied to eliminate marked frames from the analysis. Importantly, the current analysis is designed to identify only the most egregiously suspect frames of data in order to explore how a relatively small number of “bad” frames impact the data, rather than to completely excise movement-related artifact.

Even with this conservative approach to identifying periods of motion in a relatively still cohort of children, the temporal masks indicated that approximately 25% of the data from Cohort 1 was severely contaminated with motion artifact (Table 1). The subject inclusion criteria for this study were identical to the traditional criteria employed in our laboratory, with the added requirement that at least 125 frames (~5 min) of data must remain after scrubbing. No limitations were placed on the percentage of data that scrubbing could remove as long as this minimum amount of data remained. These inclusion criteria were employed because our aim was a) to describe what happened if (any amount of) motion-contaminated data was removed from a scan and b) to recover as much data from compromised scans as possible. Figure S7 shows the proportion of data removed from each subject in this study. Importantly, periods of motion could be brief or extended: although many motion epochs last only one or two TRs, many epochs lasting 5, 10, or even dozens of TRs were also identified (see Figure S8). The varying extents of periods of movement suggest that the induced BOLD signal changes may have varying durations, some of which may be within the low-frequency window that characterizes rs-fcMRI data.

To test the effects of high-motion frames on rs-fcMRI correlations, this scrubbing procedure was applied to four cohorts of healthy subjects to produce four unscrubbed and four scrubbed datasets. Within each cohort (for N subjects), the 264 ROIs described previously were applied to the scrubbed and the unscrubbed data to produce timecourses and seed correlation maps. Pearson correlations between seed timecourses were calculated to produce 264×264×N matrices of scrubbed and unscrubbed data in each subject. The unscrubbed matrices were subtracted from the scrubbed matrices to produce Δr matrices.

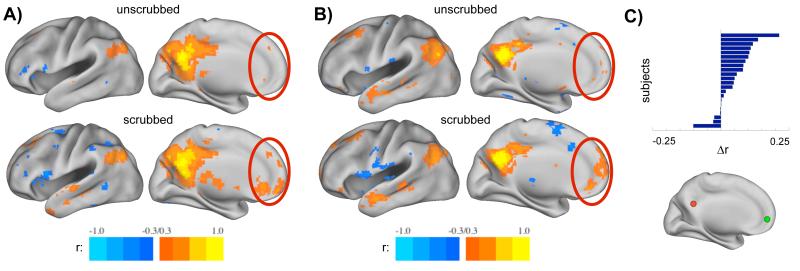
The effects of scrubbing high-motion frames from the data are readily visible on inspection. Figure 4A and 4B display seed correlation maps from a seed in medial parietal cortex (−7 −55 27) in unscrubbed (top) and scrubbed (bottom) data from two subjects in Cohort 1. Scrubbing removed 35% and 39% of the data from these subjects, respectively. The seed ROI is a member of the default mode network, and the correlation maps in scrubbed data demonstrate more characteristic topography (see the differences in medial prefrontal cortex, for example) than the maps from unscrubbed data. Prior to scrubbing, one is struck by the incompleteness of correlations within the default mode network, whereas after scrubbing, it is clear that the seed is correlated with the canonical regions of the entire default mode network. Such changes in correlation patterns can be found in many subjects. Figure 4C displays changes in correlation values between medial parietal and medial prefrontal cortex seeds for the 22 subjects in Cohort 1 in unscrubbed and scrubbed data. Correlations between these two ROIs, which are both members of the default mode network, are substantially increased in most subjects. A natural reaction is to ask whether such changes are significant and to demand direct comparisons or t-tests before taking these results seriously. As we will demonstrate shortly, the changes in correlations depend (naturally) upon the amount of data that is removed by scrubbing, which is in turn dependent upon framewise displacement and DVARS measures. For a given threshold, greater amounts of movement will produce greater (and more often significant) changes. Likewise, for a given amount of movement, more stringent scrubbing settings will remove more data and produce greater effects.

Figure 4. Examples of how motion scrubbing impacts rs-fcMRI data.

(A,B) Seed correlation maps in unscrubbed and scrubbed data in two subjects using a medial parietal seed (−7 −55 27). Scrubbing removed 35% of the data in (A) and 39% of the data in (B), leaving 265 and 151 frames for analysis, respectively. The red ovals indicate locations where correlations are clearly altered. Seed maps produced from scrubbed data demonstrate much greater resemblance to the canonical default mode network. (C) Changes in the strength of rs-fcMRI correlations between medial parietal (−7 −55 27, red sphere) and medial prefrontal cortex (−7 50 −1, green sphere) across all 22 subjects in Cohort 1. Δr is produced by subtracting unscrubbed correlation values from scrubbed correlation values. Note that scrubbing increases this long-distance correlation in most subjects, does not substantially alter it in others, and reduces it in a small number of subjects.

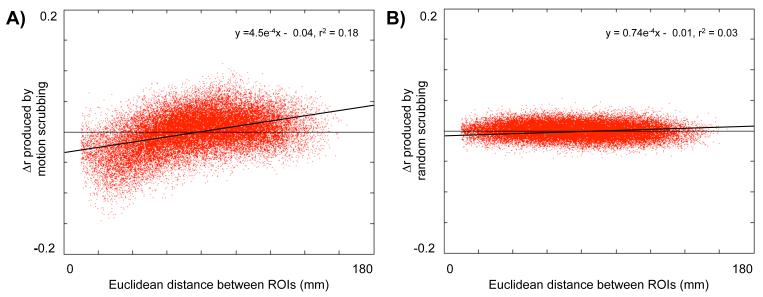
More comprehensive investigations of motion scrubbing reveal systematic effects throughout the brain. Figure 5 plots the mean Δr matrix from Cohort 1 against the Euclidean distance between the ROIs that produced the correlations. Motion scrubbing tends to decrease many short-range correlations, and to increase many medium- to long-range correlations. To check that these changes did not arise simply as a result of removing frames, the temporal masks within each subject were randomized to remove an identical amount of data, in identical-sized chunks, but at random. This “random scrubbing” was performed 10 times, always with the result shown in Figure 5B, which shows no systematic effects of distance upon Δr. The difference in the amplitudes of Δr effects is highly significant (paired two-tail t-test, t = 251; p=0). A linear fit of Δr in motion scrubbed data to Euclidean distance has a slope of 4.5 ± 0.01 × 10⁻⁴ Δr/mm with an r² of 0.18, whereas a fit to random scrubbing data has a much shallower slope of 0.74 ± 0.04 × 10⁻⁴ Δr/mm and an r² of 0.03, explaining almost no variance in the data.

Figure 5. Scrubbing high-motion frames from rs-fcMRI data decreases short-distance correlations and augments long-distance correlations.

(A) Within the 22 subjects of Cohort 1, 264 ROIs were applied to scrubbed and unscrubbed data to produce two 264×264×22 correlation matrices. The unscrubbed matrix was subtracted from the scrubbed matrix and then averaged over subjects to produce a difference matrix (Δr). The values of this matrix are plotted as a function of the Euclidean distance between ROIs. Scrubbing high-motion frames from the data substantially decreases short-distance correlations and increases medium- to long-distance correlations. (B) To demonstrate that these effects arise from the removal of high-motion frames and not frame removal in general, the number of frames and the size of contiguous chunks of removed data were calculated for each subject, and identical sized chunks of data and numbers of frames were removed at random from each subject’s data. Difference matrices were calculated as in (A), and data are presented after (A). This process was repeated 10 times with similar results. Motion scrubbing has a much greater impact upon Δr values than random scrubbing (paired two-tail t-test: t = 305; p = 0). Linear fits are plotted over each dataset, demonstrating a relationship between distance and Δr when motion-targeted scrubbing is performed (r² = 0.18), but not when random scrubbing is performed (r² = 0.03).

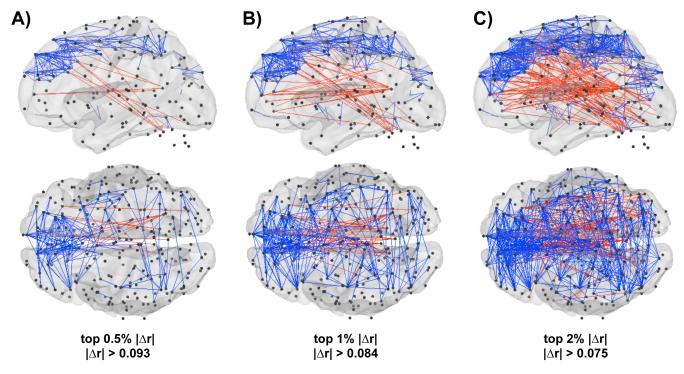
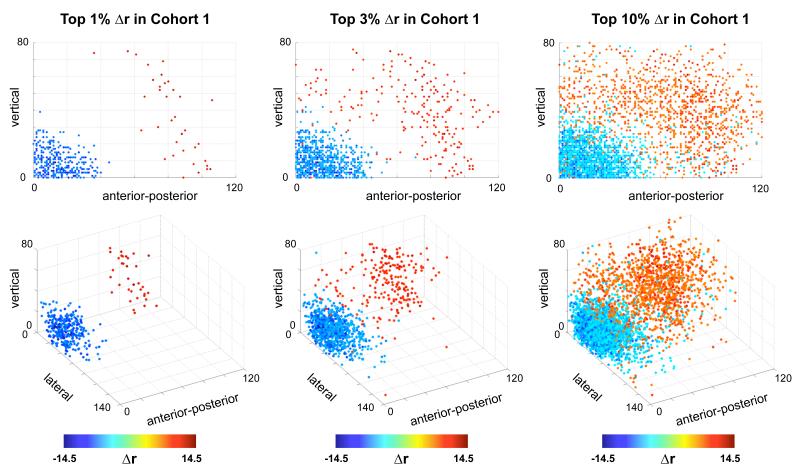
The spatial distribution of these changes is shown in Figure 6, which plots changes in correlation on a brain. Blue vectors decrease with scrubbing, red vectors increase with scrubbing, and black spheres identify ROI locations. As indexed by absolute value of the change, the top 0.5%, 1%, and 2% of Δr are shown. Short blue vectors pepper the cortex, and long red lines connect distant ROIs. Figure 7 plots Δr in terms of the projection of pairwise correlations onto the X, Y, and Z axes of the brain. Here, again, the dependence of Δr upon distance is clear. Additionally, these plots show that lateral relationships (along the X axis) tend to be decreased by scrubbing, whereas vertical or anterior-posterior relationships tend to be increased by scrubbing. This set of observations is consonant with the effects shown in Figure S4, in which head motion produced symmetric effects about the X axis, but produced strong BOLD signal changes of opposite sign in the anterior-posterior and dorsal-ventral directions. Changes in pitch (e.g., head nodding) are a predominant form of motion in many scans, and could produce such effects.

Figure 6. The spatial distribution of scrubbing effects upon correlations.

The top 0.5% (A) and 1% (B), and 2% (C) of Δr changes, as indexed by the absolute value of the change. Blue vectors represent correlations that decrease with scrubbing, and red vectors are correlations that increase with scrubbing. Most blue vectors are short- to medium-range, while most red vectors are medium- to long-range. The locations of the 264 ROIs are shown as small black spheres. Data are shown on a transparent PALS fiducial surface (Van Essen, 2005), and cerebellar ROIs are shown without a cerebellar surface.

Figure 7. Scrubbing produces direction- and distance-dependent changes in correlations.

For Cohort 1, the top 1%, 3%, and 10% of changes in correlation are plotted as a function of the projection of each pairwise correlation vector onto the X, Y, and Z axes of Tailarach space. Here, X is the lateral axis, Y is the anterior-posterior axis, and Z is the vertical axis. In addition to the dependence of Δr upon distance, it appears that strongly lateral correlations tend to be mainly weakened by scrubbing, whereas more vertical or anterior-posterior correlations tend to be strengthened by scrubbing.

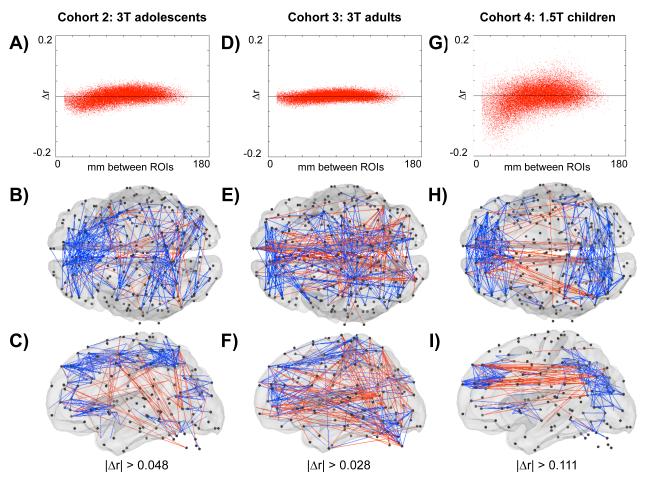
Similar results are found in three additional cohorts (Cohorts 2-4). Figures 8A, 8D, and 8G all show the trend for scrubbing to decrease short-distance correlations and to augment medium- to long-distance correlations. It is clear that the effect is strongest in children, intermediate in adolescents, and weakest in adults. The magnitude of the Δr effect is significantly different between cohorts (one-factor ANOVA, main effect of cohort: p = 0; post-hoc two-sample two-tail t-tests demonstrate that 55.3% of child-adult, 8.5% of child-adolescent, and 2.1% of adolescent-adult comparisons of Δr were significant beyond p < 0.05, FDR corrected), and is related to how much data was scrubbed from the dataset, which in turn is related to the amount of movement the cohorts possessed (see Table 1). Although the effects are weaker in adolescents and adults, they are certainly present, as the plots of motion scrubbing and random scrubbing in Figure S9 make clear. The brain surfaces in Figure 8 present the spatial distribution of the top 2% of Δr changes in each cohort. No particular spatial patterning is clear across cohorts, other than the tendency for blue vectors to be shorter than the red vectors.

Figure 8. Similar effects of scrubbing are found in 3 additional cohorts.

(A-C): Cohort 2, (D-F): Cohort 3, (G-I): Cohort 4. (A) The Δr values plotted against the Euclidean distance between ROIs. (B,C) Dorsal and lateral views of the top 1% of Δr changes, indexed by the absolute value of the change. Blue vectors represent correlations that decrease with scrubbing, and red vectors are correlations that increase with scrubbing. (D-F) and (G-I) are after (A-C) in different cohorts. The trend for scrubbing to augment long-distance correlations and to decrease short-distance correlations is present in each cohort (A,D,G), but the precise distribution of maximal change in correlation varies between cohorts. The magnitude of scrubbing effects reflects the average RMS movement of the cohort, and by extension the amount of data that is removed in the scrubbing process (see Table 1). An ANOVA comparing the magnitude of Δr across all cohorts was significant for a main effect of cohort (p = 0), and post-hoc two-sample two-tail t-tests demonstrated that 55.3% of child-adult, 8.5% of child-adolescent, and 2.1% of adolescent-adult comparisons of Δr were significant beyond p < 0.05, FDR corrected (children are Cohort 1 for these t-tests).

A question of particular interest to the neuroimaging community is whether these findings generalize beyond particular scanners, institutions, study populations, and acquisition sequences. The datasets reported in this paper represent a single institution, two scanners with two field strengths and two acquisition sequences, and three age ranges (see Methods). Scrubbing methods have also been applied to several datasets other than the ones reported here, and the effects are present in every dataset from every site examined thus far (at present, four sites). This represents data acquired in several scanners (Philips and Siemens) at multiple field strengths (1.5T and 3T) using multiple acquisition sequences. The effects do not appear to be particular to any study population (they are present in clinical adult cohorts, in neonatal cohorts, etc.). As such, this artifact appears to be a general feature of functional connectivity MRI. It is probable that particular aspects of acquisition (e.g. gradient sequence, spatial or temporal resolution, etc) may render data more or less sensitive to motion-related effects, though we are unable to offer any specific observations or recommendations at this point. It is worth noting that framewise displacement estimates should be relatively uniform across sites, scanners, and sequences, but that the DVARs measure may vary across these parameters, since it indexes changes in signal intensity.

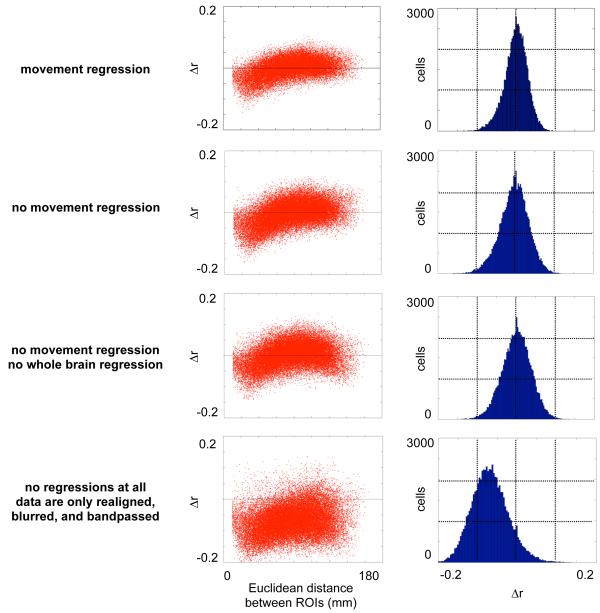
A related question is whether this artifact is produced and/or countered by particular aspects of data processing. For any analysis it is standard practice to realign fMRI data across scans. After fMRI preprocessing, a variety of functional connectivity processing strategies may be used to form rs-fcMRI data. These approaches typically include spatial blurring, temporal bandpassing, and some version of “artifact removal”, whether by regression of nuisance variables or component removal or other methods. The data presented in this paper follows a functional connectivity processing stream that uses a multiple regression of nuisance variables as a method to reduce noise and artifact in functional connectivity data (Fox et al., 2009). Typical regressors include signals from white matter, ventricles, and the whole brain, the derivatives of those 3 signals, the 6 head realignment estimates, and the derivatives of each of those estimates (18 regressors total). An important concern is that motion-related artifacts might actually have been introduced to the data in the regression process. Figure 9 plots Δr against Euclidean distance for Cohort 1 beginning with the standard functional connectivity processing stream, then progressively removing elements of the regression, and finally removing the regression altogether (so that the data have only been realigned, registered, blurred, and bandpassed). In each case the artifact is present, excluding these regressions as a source of this effect. This indicates that the motion-related dependence of correlation strength upon distance is either inherent in the data (presumably, due to motion), or that it is produced by the widely used processes of data realignment, blurring, or bandpassing. In terms of countering the motion-induced correlations, the regressions in this processing stream have a partial but incomplete effect: the spread of the histogram of Δr values is clearly reduced by the regressions, but the artifact persists through all aspects of functional connectivity processing. It is possible that other approaches to functional connectivity processing (e.g., ICA) may fare better in removing this motion-related artifact, and we encourage users of other approaches to test their data for similar effects.

Figure 9. Motion-induced colored noise does not arise from standard regressions in functional connectivity processing.

Each row presents analyses performed on Cohort 1 using functional connectivity data processing streams that differed only in the nuisance variables included in the multiple regression performed as the final step of functional connectivity processing. Each row plots the changes in correlation produced by motion scrubbing as a function of distance between ROIs, and also shows a histogram of these correlations. Nuisance variables in the top row included movement estimates at each frame (the 6 head realignment parameters and their temporal derivatives), as well as whole-brain signal and its derivative, white matter signal and its derivative, and ventricular signal and its derivative. Progressive analyses removed regressors (including derivatives) as indicated, and the bottom panels use no regression at all. Motion regression does not produce (or completely eliminate) the artifact in question, though it does produce a modest reduction in the changes in correlation produced by motion scrubbing.

We now demonstrate how scrubbing can alter fundamental conclusions about patterns of functional connectivity. Across typical development, several groups, including our own, have reported a reorganization of functional connectivity, such that short-distance correlations tend to decrease with age, whereas long-distance relationships between functionally related brain regions tend to increase with age (for a review of the developmental literature, see (Power et al., 2010)). This pattern is, unfortunately, also what one would predict from a motion-related artifact (Table 1). Figure 10 presents the community assignments of child and adult datasets (Cohorts 1 and 3, see Table 1) before and after scrubbing. Here, colors in each panel indicate sub-networks within the brain-wide network of 264 ROIs. Scrubbing produced little change in the community structure of adult functional networks, but it produced substantial changes in the child functional networks. What began as largely local, non-distributed communities in children (e.g. the orange community in children) became distributed modules with closer resemblance to adult modules (e.g. the yellow or red modules) upon scrubbing. This reflects a fundamental reorganization of the child network into a more adult-like distributed architecture that includes intact default and fronto-parietal sub-networks. These changes in network architecture can be quantified by normalized mutual information, which indicates that community assignments between children and adults before scrubbing (NMI = 0.56) become more similar after scrubbing (NMI = 0.70). This increase is not seen upon random scrubbing (over 10 repetitions, NMI = 0.58 ± 0.01). Another way to quantify this set of observations is to note that scrubbing reduces the number of significant differences in pairwise correlations between children and adults by over 30% (from 608 to 401, p < 0.05 FDR corrected, two-tail two-sample t-test). These findings suggest that at least some of the developmental differences previously reported can be accounted for by motion-related artifact.

These analyses employed the standard scrubbing regime used throughout this manuscript, and are intended as proof-of-principle that even a modest amount of data removal can alter patterns of functional connectivity. A more definitive and comprehensive investigation of developmental functional connectivity is in preparation, utilizing more stringent scrubbing criteria (see Figure S10 for an example of how scrubbing affects statistical power). Additionally, we are exploring the incorporation of temporal masks in the multiple regression stage, since large-amplitude motion-related changes are likely to decrease the beta weights of regressors, which could differentially impact subject data across development.

Discussion

We have demonstrated that small movements produce colored noise in rs-fcMRI networks. Evidence for this artifact was first observed in timecourses, where movement of the head visibly coincided with large changes in the rs-fcMRI signal. This relationship was found in ROIs throughout the brain, and in all subjects studied. To explore the effects of this motion-containing data on rs-fcMRI analyses, two semi-independent indices of data quality were proposed that operate on a frame-by-frame basis to flag frames of suspect quality. In four independent cohorts, removal of frames with high values on each index reduced many short-distance rs-fcMRI correlations and increased many long-distance rs-fcMRI correlations. This effect was not due to frame removal, and the artifact did not arise from regressions in functional connectivity processing. On-line scanner corrections for head motion also did not ameliorate this effect (Thesen et al., 2000) (data not shown).

The presence of this artifact has substantial implications. All subjects analyzed in this article are healthy control subjects and would meet inclusion criteria for analysis in most MRI laboratories. The motion-induced artifacts occur with movements on the order of a few tenths of a millimeter or less (subjects for this study were selected with our former standard inclusion criteria – RMS movement under 1.5 mm). Within single cohorts, motion scrubbing can substantially alter seed correlation maps, and commonly studied rs-fcMRI correlations such as those between medial prefrontal and medial parietal cortex are among the correlations that are affected by this artifact. A clear implication is that many rs-fcMRI results (both negative and positive) in clinical populations and across the lifespan may need to be critically revisited. In our own developmental data, some of our previous conclusions must be modified, though definitive analyses are not yet complete.

The analyses presented in this paper were crafted to demonstrate the effects of small movements upon rs-fcMRI correlations, not to completely remove motion-induced artifact from the data. An important topic for further study will be how such artifacts should be dealt with. There are two fundamental approaches to artifact removal: excision of entire contaminated frames of data, and parsing “artifactual” from “real” signal within frames. If one adopts the former approach, the news is both encouraging and discouraging. The discouraging news is that, as Figure 2 shows, any and all movement tends to increase changes in BOLD signal, which suggests that there is no threshold below which movement creates no artifactual changes in signal. However, as the still subjects in Figure S5 demonstrate, there does appear to be a floor in framewise displacement and DVARS values, and if one wished to excise motion-contaminated signal as thoroughly as possible, thresholds close to those floors would seem appropriate. Additionally, unions of the flagged frames from framewise displacement and DVARS, rather than intersections, could be used to generate more liberal temporal masks. If the latter approach is favored, several possibilities exist. Linear regression of head realignment estimates showed some utility in reducing the effects of motion-related artifact on rs-fcMRI correlations (see Figure 8). We currently perform these regressions using single parameters applied over the entire brain. However, one could craft voxel-specific regressors that more precisely account for the direction and amplitude of displacement at every voxel in the brain. Such regressions may prove more effective than the current, blunter regressions. Alternatively, covariance-based methods may prove to be effective in countering such artifacts (e.g., (Beckmann and Smith, 2004; Erhardt et al., 2010; Robinson et al., 2009a)). We hope that groups with functional connectivity processing strategies that differ from the one used in this report will examine their data to see whether motion-induced correlations reside in their analyses.

A variety of artifacts are present in fMRI data, including susceptibility artifact, cardiac artifact, respiratory artifact, etc. It is useful to distinguish between static vs. dynamic artifacts. Susceptibility inhomogeneity leads to image distortions and signal voids that are especially problematic in particular brain regions, such as orbitofrontal cortex and temporal cortex above the petrous bone (Ojemann et al., 1997; Robinson et al., 2009b; Simmons et al., 2009). Susceptibility artifacts shift in space approximately with the rest of the brain as the head moves, and their effects should be mitigated by conventional realignment procedures. However, head movement can alter magnetization gradients in the Z-direction, resulting in head position-dependent image warping and signal dropout. Head motion could thus potentially interact with artifacts of all types in spatially inhomogeneous ways. It is therefore important to note that no consistent spatial patterning over the brain was evident in our data (Figures 6 and 8). Since our collection of ROIs only sparsely populates the ventral surface of the brain, it is possible that future investigations may reveal that ventral regions are particularly sensitive to motion-induced changes in correlations. Recently, temporal SNR has been used to measure the quality of functional connectivity data in relation to head motion (Van Dijk et al., 2011). Similar approaches may shed light on specific spatial locations of interest for the motion-related changes in correlation we describe here. Other avenues for future inquiry will include determining whether particular acquisition sequences are less susceptible to this artifact, or whether particular processing choices (e.g., voxel size, region size and placement, smoothing, etc.) render analyses less susceptible to this artifact.

How does a systematic artifact arise from head movement? Figure S4 demonstrates that a single movement can produce changes in BOLD signal throughout the brain in a regionally specific manner, such that one portion of the brain displays increased signal, whereas other portions display decreased signal. This effect introduces an element of anti-correlation between such different portions, and causes the timecourses of nearby voxels within a portion to resemble one another more closely, providing a natural explanation for the increased short-distance and decreased long-distance correlations seen when high-motion frames are retained. In our experience, the predominant head motion is a change in pitch (e.g., head nodding). This motion, which is symmetric about the X (lateral) axis, could lead to artifactual signal changes of opposite sign in the anterior and posterior parts of the head, and in dorsal and ventral parts of the head (a clear example of this is shown in Figure S4). The data of Figure 7 are in accord with such an interpretation, because the greatest increases in correlation upon scrubbing are predominantly in relationships oriented in anterior-posterior and dorsal-ventral directions, whereas laterally-oriented correlations tend to decrease upon scrubbing. Also note that head movements tend to produce large amplitude changes in BOLD signal. Since correlation calculations are based upon differences of individual measures from means, these large displacements in BOLD signal carry substantial weight in such computations.

In conclusion, subject head motion-induced artifacts contribute substantially to the rs-fcMRI signal, and produce systematic but spurious patterns in correlation. This effect is present in healthy control subjects, and is likely to be larger in developing, aging, or clinical populations that, as groups, have more movement of all forms. Optimal handling of rs-fcMRI data will need to take into account the consequence of motion artifact that is only incompletely addressed with standard realignment and motion regression analysis strategies.

Highlights.

Large changes in rs-fcMRI timecourses coincide with motion despite motion regression.

Motion increases short-distance correlations and decreases long-distance correlations.

Motion artifacts do not arise from, and are not fully countered by, motion regressions.

Framewise indices of data quality and methods to remove motion artifact are proposed.